Abstracts
The ready availability of very strong permanent magnets in the form of rare-earth magnetic alloys such as neodymium-iron-boron has lead to renewed interest in one of the oldest types of electric motors - the homopolar motor. The ease with which a demonstration homopolar motor can now be built and operated when neodymium magnets are used is quite remarkable. In this paper some simple homopolar motors employing neodymium magnets suitable for demonstrational purposes are described and discussed.
homopolar motor; homopolar roller; neodymium magnets; driven wheel; Lambert W function
A atual disponibilidade de ímãs permanentes muito fortes na forma de ligas magnéticas de terras raras, como neodímio-ferro-boro, levou ao interesse renovado em um dos mais antigos motores elétricos - o motor homopolar.É notável a facilidade com que as demonstrações com ímãs de neodímio podem ser construídas e operacionalizadas. Neste artigo são descritos alguns simples motores homopolares que usam ímãs de neodímio apropriados para demonstrações no ensino.
motores homopolares; ímãs de rolete homopolares; neodímio; função W de Lambert
PRODUTOS DE MATERIAIS DIDÁTICOS
Some simple demonstration experiments involving homopolar motors
Algumas experiências simples de demonstração envolvendo motores homopolares
Seán M. Stewart1 1 E-mail: ersilva@if.usp.br.
Core Program, The Petroleum Institute, Abu Dhabi, United Arab Emirates
ABSTRACT
The ready availability of very strong permanent magnets in the form of rare-earth magnetic alloys such as neodymium-iron-boron has lead to renewed interest in one of the oldest types of electric motors the homopolar motor. The ease with which a demonstration homopolar motor can now be built and operated when neodymium magnets are used is quite remarkable. In this paper some simple homopolar motors employing neodymium magnets suitable for demonstrational purposes are described and discussed.
Keywords: homopolar motor, homopolar roller, neodymium magnets, driven wheel, Lambert W function.
RESUMO
A atual disponibilidade de ímãs permanentes muito fortes na forma de ligas magnéticas de terras raras, como neodímio-ferro-boro, levou ao interesse renovado em um dos mais antigos motores elétricos - o motor homopolar.É notável a facilidade com que as demonstrações com ímãs de neodímio podem ser construídas e operacionalizadas. Neste artigo são descritos alguns simples motores homopolares que usam ímãs de neodímio apropriados para demonstrações no ensino.
Palavras-chave: motores homopolares, ímãs de rolete homopolares, neodímio, função W de Lambert.
1. Introduction
The importance and use of carefully selected demonstration experiments in the teaching of physics should not be underestimated. Cliff Swartz, the highly regarded American teacher of physics writes that "Physics instruction without demonstrations is like dinner without food" [1]. Pedagogically, demonstration experiments provide those we teach with an opportunity to gain and develop basic familiarity with a range of physically important phenomena [2]. Often it is those demonstrations performed with the simplest of equipment using arrangements easily and readily understood that are most likely to be long remembered.
Simple electric motors are always sure to please. First invented in 1821 by the famous nineteenth century English scientist Michael Faraday (17911867), he built a type of electric motor which nowadays is referred to as a homopolar motor [3]. In essence such a motor consists of a conducting disc in the neighbourhood of a permanent magnet that is free to rotate.2 2 Faraday's original 1821 motor consisted of a rigid, vertically hanging wire. Its upper end was free to rotate while its lower end was dipped into a pool of mercury. Positioned in the centre of the pool of mercury was a permanent magnet. On passing current through this arrangement the hanging wire rotated about the magnet like a conical pendulum. A source of direct current is then allowed to pass through two arbitrary points on the disc. A well-known early example of such a motor, which until quite recently was a familiar demonstration apparatus in many physics laboratories, was the Barlow Wheel [4, 5], first conceived and built by Peter Barlow (1776{1862) in 1822 [6].
In contrast to most dc motors found today where commutators are used to reverse the direction of current fow in order to maintain continuous rotation, a homopolar motor is able to produce continuous rotation without the need for any such reversal in current. In fact, it is the only known example of a true direct current motor and it is from its very means of operation the motor takes its name. Since the motor requires only the same electric polarity for its operation, the Greek root homos, meaning 'same', used in a combining form with polarity leads to the term homopolar. Occasionally a homopolar motor in English may also be referred to as unipolar for similar etymological reasons.
The cheap and ready availability of very strong permanent magnets in the form of rare-earth magnetic alloys such a neodymium-iron-boron (NeFeB) - so-called neodymium magnets - has revived interest in the design and development of ever simpler forms of this very old motor. The aim of this paper is to describe and explain several of these recently proposed homopolar motors that teachers and lecturers of introductory-level physics may consider using to demonstrate the so-called motor e®ect. Particular attention is paid to an intriguing little motor I shall refer to as a homopolar roller. Here a simple, non-trivial modification briefly pointed out by the author [7] to the design of a recently proposed homopolar roller [8] is expanded upon. An analysis of the dynamics of the roller is also presented here for the first time.
2. A simple homopolar motor
Based on a modification first suggested by Strickler [9], replacement of the conducting disc used in a homopolar motor with a conducting disc that produces a magnetic field of its own allows for a surprising simplification with which a homopolar motor can be built. Recently, interest in this very old form of motor was revived when very strong neodymium disc magnets were used in place of substantially weaker alnico (aluminium-nickel-cobalt) permanent disc magnets for the conducting disc of the motor [10, 11].
In its most recent form one side of a small neodymium disc magnet is stuck to the level head of a ferromagnetic screw. The screw, in turn, becomes magnetised owing to the strength of the neodymium magnet. The pointy end of the screw can now be stuck to the bottom terminal of a 1.5 V D-cell battery where it hangs freely under gravity since the battery's casing is ferromagnetic and provides a very low friction connection between the hanging magnet and the battery. If one end of a copper wire is pressed against the top terminal of the battery using your finger, brushing the other end of the wire against the rim of the disc magnet completes the circuit and not only causes current to ºow but leads to a spinning in the disc (see Fig. 1). With its elegantly simple arrangement and a total of four components used, one has to ask is this not the simplest motor in the world?
Understanding what causes the disc to rotate provides students with an excellent example of the application of the right-hand rule used to determine the direction a magnetic force acts on a current-carrying conductor in the presence of an external magnetic field. Referring to Fig. 2, on brushing the wire up against the outer periphery of the disc, current flows from the rim to the central connection point at the head of the attached screw. As the disc magnet itself now takes on a current-carrying function, a Lorentz force acts tangentially to the inwardly ºowing radial component of the current in accordance with the right-hand rule. The resultant torque causes the disc to spin about its attached axle (for directions, refer to Fig. 2).
Two surprising features of the motor are sure to amaze onlookers the readiness with which the disc magnet rotates, and the size of the final rotation speeds achievable. From the arrangement shown in Fig. 1, twenty seconds after closing the circuit with the connecting wire speeds in excess of 5000 rpm are typical. Both the above features are possible since neodymium magnets have remnant magnetic field strengths close to their surface significantly larger than those found in ordinary alnico magnets.3 3 Field strengths of the order of 1 Tesla are quite common for neodymium magnets [12]. Attempting to spin an alnico disc magnet of similar size using an arrangement identical to that shown in Fig. 1 is simply not possible, despite the size of the very large currents which flow in the almost resistanceless circuit, because of their substantially weaker surface magnetic field strengths.
It is important to recognise that the disc magnet will only rotate provided it is mechanically decoupled from the closing wire as relative motion between the two is necessary [13]. Brushing the wire up against the rim of the disc magnet allows the latter to slide pass the former whilst maintaining electrical contact between the two. To show relative motion between the two is necessary for rotation to occur, one end of the connecting wire can be permanently attached (by either taping or soldering it) to the rim of the disc magnet. On completing the circuit no initial start-up motion in the freely hanging disc magnet is ever observed.
A number of modifications to the above arrangement are possible and seem to be limited only by the imagination and ingenuity of teacher and student alike. One such arrangement is a simple upright version [14]. Here a spherical neodymium magnet is used in place of the disc magnet. The magnet is set spinning on the top terminal of a battery on closing the circuit with a hand-held wire. With suitable modification it is also possible to change the basic elements of the motor which actually rotate. In one refinement, the connecting wire rather than the disc magnet can be made to rotate [15, 16]. In another, both the battery and the disc magnet rotate while a connecting copper wire frame in the form of a tripod remains stationary [17]. The latter two refinements result in an operation of the motor which is completely hands-free.
3. A simple homopolar roller
A more recent incarnation of the homopolar motor using neodymium magnets is of the rolling type a type herein referred to as a homopolar roller. While not a completely new idea in itself [18, 19], it was Sugimoto and Kawada who showed most elegantly how the former spin of the simple homopolar motor could be made to roll [8]. This was achieved by sticking two neodymium disc magnets to either terminal of an AA battery. The electric circuit was then completed by placing the entire arrangement onto a flat conducting surface (or conducting rails) from where it was observed to roll. Torques act on each of the disc magnets in a manner identical to those described previously with the exception that the conducting surface replaces the connecting wire. In order to get both of these torques to act in the same sense it is necessary to orientate each end magnet so that like poles face one another.
As ingenious as Sugimoto and Kawada's homopolar roller is, it suffers from two significant drawbacks. Firstly, getting the double disc magnet and battery arrangement to roll over a conducting surface is difficult since one needs to ensure good electrical contact between the two. For suitable contact chemical polishing of the surface was found to be necessary. Secondly, once the roller is in motion, final rolling speeds attainable are significantly impeded by the effects of magnetic breaking resulting from eddy currents induced within the conducting surface itself.
Problems associated with ensuring good electrical contact and avoiding unwanted magnetic braking effects can both be overcome if the arrangement were to roll over a non-conducting surface. If the circuit between the rims of the disc magnets is completed using a short, non-ferromagnetic connecting U-shaped wire, su±cient electrical contact between the upper rim of each disc magnet and the wire can be maintained as its rolls by moulding either of its ends into an arc of a circle (see Fig. 3). As the circuit is now complete, current flows over the ends of the disc magnets and results in magnetic forces acting on either wheel. Provided the connecting wire is placed on the side of the roller behind its forward direction of motion, the resultant torques which act on each wheel cause the double disc magnets and battery to roll off with the U-shaped wire trailing behind. On a smooth, flat surface the homopolar roller can roll at a comfortable walking pace over a reasonable distance before the connecting wire becomes dislodged.4 4 A collection of short video clips showing the simple homopolar roller in action can be found at http://martha.cabspace.com/jalbum/science/.
On connection, the U-shaped wire experiences a downwardly directed magnetic force as one has a current-carrying wire in the presence of an external magnetic field. This force tends to help hold each end of the connecting wire onto the rims of the disc magnets as the arrangement rolls. For all current, magnetic field, and magnetic force directions in the roller arrangement refer to Fig. 4.
As with the simple homopolar motor, relative motion between the disc magnets and the connecting U-shaped wire in the homopolar roller is maintained as the arrangement rolls. Free rotation in the U-shaped wire, is, however, prevented by the floor while free rotation in the disc and axle combination is possible. For insuffcient traction between the surface and the lower rims of the disc magnets, slippage will occur and the wheels of the driven roller can be made to spin on the spot. If rolling of the homopolar roller is prevented by anchoring it to the floor, placing the connecting wire on the forward side of the roller if unanchored, allows the equal but opposite torque which acts on the connecting wire to be observed. For a suffciently short connecting wire such a placement leads to the wire being swung through, in dramatic fashion, from one side of the roller If a rechargeable AA Nickel-Cadmium (NiCd) battery is used instead of a normal non-rechargeable alkaline cell battery, much higher currents can be delivered into a short circuit (of the order of 10 A for the former compared to 5 A, and then only briefly, for the latter). Higher sustained currents lead to greater sustained torques. With such a substitution in battery the homopolar roller tends to roll faster over a flat surface, though the connecting wire was found to dislodge far more readily. More interestingly, the roller could be made to roll up an incline. Rolling up inclines with inclination angles as large as 5º were possible. At inclination angles close to 5º it may be necessary to give the roller a small push to start it off since relative motion between the disc magnets and the connecting wire is necessary before it can roll.
Guala-Valverde has suggested that closing the circuit in the homopolar roller using a moulded U-shaped connecting wire is more than a trivial modification it may at first appear to be [20]. Compared to the roller described by Sugimoto and Kawada, use of a U-shaped connecting wire for the roller provides a configuration that is particularly suited to the verification of Newton's third law as applied to electromechanical engines since it allows the fundamental action{reaction torque pairs acting between the connecting wire and the disc magnets to be readily observed.
4. Dynamics of the driven wheel homopolar roller
A complete analysis leading to a calculation for the torques which act on each disc magnet in the roller configuration is no easy task. In particular, the path followed by the current as it flows through an extended conductor such as the disc magnet is not well defined. In what follows a simplified analysis for the dynamics of the homopolar roller whose dominant contribution to the torques arise from radial current flows over the surface of the disc magnets is presented.
Consider a disc magnet of mass M and radius r. Assume the path followed by the current as it passes through the disc magnet is over its surface. Furthermore, all current will be assumed to flow along straight line paths. Thus current ºows horizontally from the upper rim to the edge of the disc and then radially inwards towards the centre of the disc. The total torque which acts on the disc magnets is therefore taken to be dominated by a surface radial flow of current inwards towards the centre of the disc.
For a steady current i flowing along an element of conductor dl directed along the direction of current flow and in an external magnetic field B, the total force acting on each element is [21]
The total force on the conductor is obtained by integrating along the path C followed by the current
while the total torque acting on the conductor is
Here r is a position vector directed from the origin to the current element
Consider a right-handed Cartesian coordinator system with unit basis vectors á x,
x, y,
y, zñ whose origin is centred at the centre of the disc. If the xy-plane lies on the inner surface of the disc magnet, aligning the radial path followed by the current with the y-axis one can immediately write dl = dy
zñ whose origin is centred at the centre of the disc. If the xy-plane lies on the inner surface of the disc magnet, aligning the radial path followed by the current with the y-axis one can immediately write dl = dy  y and r = y
y and r = y  y. Furthermore, if the magnetic field at the surface of the disc magnet is assumed to be uniform and normal to the surface, B = B
y. Furthermore, if the magnetic field at the surface of the disc magnet is assumed to be uniform and normal to the surface, B = B z. Since the current follows along a straight line path given by the positive y-axis, from Eqs. (2) and (3) one has for the total magnetic force
z. Since the current follows along a straight line path given by the positive y-axis, from Eqs. (2) and (3) one has for the total magnetic force
and the total torque
for each disc respectively.
Once the disc is rotating a back emf in the motor resulting from a changing magnetic flux through the rotating disc will be set up. The size of the current flowing in the closed circuit therefore reduces over time and approaches some fixed value whose size depends on the speed of rotation of the disc. The size of the induced emf set up between the centre and rim of a disc rotating with angular speed w in a constant external magnetic field can be found from Faraday's law. Its value is [22]
The current flowing in the closed series circuit formed by the double disc magnet arrangement can therefore be expressed as
Here V is the voltage across the terminals of the battery while R is the total resistance in the circuit.
Proceeding with an analysis of the dynamics for the roller one recognises the homopolar roller forms a driven wheel system. Here each wheel formed by the disc magnets is driven by a magnetically produced torque such that the two wheels and axle (battery) roll off together in unison about the system's axis of symmetry. Approximating the homopolar roller as a rigid system consisting of two uniform discs (the magnets) connected concentrically to a third, slightly smaller but longer uniform cylinder (the battery), since the arrangement rotates about its axis of symmetry the moment of inertia for the system will be
Here mb and b are the mass and radius of the battery respectively.
For a driven wheel which rolls without slipping, the surface exerts a frictional force on the wheel in the same direction as the direction the wheel rolls. If the effects of rolling friction are ignored, from Newton's second law, for translational centre of mass motion along the horizontal one has
Here f is the frictional force exerted by the surface on each of the wheels, a is the acceleration of the centre of mass of the roller while 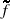 is the frictional force exerted by the connecting wire on the upper rim of each wheel and is assumed to act in the horizontal direction. From the rotational form of Newton's second law, for rotational motion about the axis of symmetry of the roller one has
is the frictional force exerted by the connecting wire on the upper rim of each wheel and is assumed to act in the horizontal direction. From the rotational form of Newton's second law, for rotational motion about the axis of symmetry of the roller one has
Here a is the angular acceleration of the roller. Finally, for rolling without slipping the linear and angular accelerations are related by
Upon eliminating a from Eq. (10) and solving Eqs. (9) and (10) simultaneously for a one finds
where we have defined
Using Eq. (7) to eliminate the current from expression (12), one arrives at
Here the non-slip condition of v = rw has been used, v being the linear speed of the centre of mass of the roller.
Initially the roller is taken to be at rest. Since a = dv/dt, on separating and integrating Eq. (14) the linear speed of the centre of mass of the roller as a function of time can be expressed as
Here
corresponds to the terminal speed of the roller while
is identified as a time constant for the system since it has the dimensions of time.
Equation (16) imposes an upper bound on the size of the frictional force 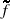 that can be applied to each rim of the roller if it is to move. For rolling to occur one requires vt > 0. Hence
that can be applied to each rim of the roller if it is to move. For rolling to occur one requires vt > 0. Hence
Since v = dx/dt, the distance x travelled by the roller as a function of time is found on separating and integrating Eq. (15). Doing so yields
Equation (19) can be used to estimate the distance travelled by the roller in a given time. Experimentally it is however far easier and more accurate to measure the time taken by the homopolar roller to roll over a fixed distance. It is therefore more useful to express Eq. (19) in terms of the time taken as a function of distance travelled. Even though Eq. (19) is traditionally thought of as a transcendental equation, recently it has become possible to solve such equations in closedform in terms of what is now known as the Lambert W function [23].
The Lambert W function, W(x), is defined to be the inverse of the function y = xex. It is a rapidly emerging 'implicitly' elementary function of mathematical physics which is being applied with increasing frequency to a range of problems [24] and is included as an in-built library function in many computer algebra systems.5 5 For example, LambertW[x] in Maple and ProductLog[x] in Mathematica. The LambertW function therefore solves the transcendental equation
When x is real, Eq. (20) can have either two real solutions W0(x) (defined to be the principal branch, and satisfies W(x) > 1) and W1(x) (the secondary real branch, and satisfies W(x) < 1) for 1/e < x < 0, one real solution W0(x) for x > 0, or no real solutions for x < 1/e.
Setting µ = x=vt+t , on rearranging terms Eq. (19) can be written as
Since Eq. (21) is now exactly in the form of the defining equation for the Lambert W function, on solving for the time t one has
Note that the principal branch is chosen since physically the time must be positive.
For the homopolar roller used, the disc magnets had mass M = 2.3 × 102 kg and radius r = 1.0 × 102 m while for the AA alkaline battery mb = 2.45 × 102 kg and b = 7.0 × 103 m. Thus  = 3.3 × 106 kg m2. The resistance between the centre and the middle of the rim of the disc magnet was measured to be about 0:3 W. If the U-shaped wire is considered to be of negligible resistance compared to the disc magnet, the total resistance of the circuit is about R ~ 0.6 W since the two disc magnets are connected in series with one another. Taking the magnetic field strength at the surface of the disc magnet to be about 1 tesla, then t ~ 199 s. Finally, for the AA alkaline battery used, V = 1:5 V.
= 3.3 × 106 kg m2. The resistance between the centre and the middle of the rim of the disc magnet was measured to be about 0:3 W. If the U-shaped wire is considered to be of negligible resistance compared to the disc magnet, the total resistance of the circuit is about R ~ 0.6 W since the two disc magnets are connected in series with one another. Taking the magnetic field strength at the surface of the disc magnet to be about 1 tesla, then t ~ 199 s. Finally, for the AA alkaline battery used, V = 1:5 V.
As a first estimate, ignore the frictional force between the connecting wire and the upper rim of the disc magnet. Thus 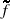 = 0 and vt = 150 m s1. When the roller was allowed to roll over a fixed distance of 2:1 metres, times in the neighbourhood of 4 seconds were recorded. On the other hand, Eq. (22) predicates a time of t ~ 2:4 s, a result surprisingly close to that observed. Inclusion of a non-zero frictional force
= 0 and vt = 150 m s1. When the roller was allowed to roll over a fixed distance of 2:1 metres, times in the neighbourhood of 4 seconds were recorded. On the other hand, Eq. (22) predicates a time of t ~ 2:4 s, a result surprisingly close to that observed. Inclusion of a non-zero frictional force 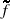 would lengthen the time taken for the roller to travel the fixed distance.
would lengthen the time taken for the roller to travel the fixed distance.
As a check on the self-consistency of the model, from the parameters given above an upper bound on the size of the frictional force predicated by Eq. (18) is
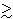 1.9 × 102 N. On the other hand, using the experimentally measured times of t ~ 4 s for the roller to roll a distance of x = 2.1 m, an estimate for the size of the frictional force present leads to
1.9 × 102 N. On the other hand, using the experimentally measured times of t ~ 4 s for the roller to roll a distance of x = 2.1 m, an estimate for the size of the frictional force present leads to 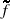 ~ 1.2 × 102 N, a value well within the limit imposed by the upper bound if rolling is to occur.
~ 1.2 × 102 N, a value well within the limit imposed by the upper bound if rolling is to occur.
5. Conclusion
Physics is hard, its concepts are di±cult, not obvious, and often seem to be counter-intuitive. Simple demonstration experiments are one epistemic tool teachers of physics can use to counter such perceptions. In this paper two simple homopolar motors relying on strong neodymium permanent magnets suitable for demonstrational use in an introductory-level physics course have been described and a brief analysis accompanying the dynamics of the driven wheel homopolar roller developed. Each is sure to engage and intrigue students and colleagues alike.
Acknowledgments
Discussions held with Mark Worthington, Jorge Guala-Valverde and Dave Keenan are gratefully acknowledged. I am also grateful to Marinus Dirks for translating the abstract into Portuguese.
Recebido em 14/9/2006; Aceito em 23/10/2006
- [1] C. Swartz, Cliff's Nodes: Editorials from The Physics Teacher (The Johns Hopkins University Press, Maryland, 2006), p. 101.
- [2] R.D. Knight, Five Essay Lessons: Strategies for successful physics teaching (Addison-Wesley, San Francisco, 2004).
- [3] M. Faraday, Quart. J. Sci. 12, 74 (1821).
- [4] R.M. Sutton, Demonstration Experiments in Physics (American Association of Physics Teachers, College Park, MD, 2003), n. E-136, p. 306.
- [5] H.C. Jensen, Am. J. Phys. 21, 692 (1953).
- [6] The original sketch of the wheel accompanied a letter Peter Barlow sent to Michael Faraday in March of 1822. See http://www.scienceandsociety.co.uk, accessed on July 2006.
- [7] S.M. Stewart, Phys. Teacher (Letter to the Editor, submitted for publication).
- [8] N. Sugimoto and H. Kawada, Phys. Teacher 44, 313 (2006).
- [9] T.D. Strickler, Am. J. Phys. 29, 635 (1961).
- [10] C. Chiaverina, Phys. Teacher 42, 553 (2004).
- [11] H.J. Schlichting and C. Ucke, Phys. Unserer Zeit 35, 272 (2004).
- [12] A.K. Geim, M.D. Simon, M.I. Boamfa and L.O. Heflinger, Nature 400, 323 (1999).
- [13] J. Guala-Valverde, P. Mazzoni and R. Achilles, Am. J. Phys. 70, 1052 (2002).
- [14] D. Kagan, Phys. Teacher 43, 68 (2005).
- [15] S.Q. Field, Return of Gonzo Gizmos: More Projects and Devices to Channel Your Inner Geek (Chicago Review Press, Chicago, 2006), p. 55-61.
- [16] D. Featonby, Phys. Education 41, 292 (2006).
- [17] D. Keenan, http://scitoys.com/ board/messages/8/1257.html?1128906028, accessed on July 2006.
- [18] A. Serra-Valis and C. Gago-Bousquet, Am. J. Phys. 38, 1273 (1970).
- [19] B. Layton and M. Simon, Phys. Teacher 36, 474 (1998).
- [20] J. Guala-Valverde, Private Communication, 19 June 2006; Apeiron (submitted for publication).
- [21] I.S. Grant and W.R. Phillips, Electromagnetism (John Wiley & Sons, Chichester, 1990), 2nd ed., p. 150.
- [22] H.D. Young and R.A. Freedman, University Physics (Addison Wesley, San Francisco, 2004), 11th ed., p. 1122-1123.
- [23] R.M. Corless, G.H. Gonnet, D.E.G. Hare, D.J. Jeffrey and D.E. Knuth, Adv. Comput. Math. 5, 329 (1996).
- [24] See, for example, S.M. Stewart, Int. J. Math. Educ. Sci. Technol. 37, 411 (2006) and references therein.
Publication Dates
-
Publication in this collection
17 Sept 2007 -
Date of issue
2007
History
-
Accepted
23 Oct 2006 -
Received
14 Sept 2006



























