Abstract
The eclipse of the Sun of 1919 was fundamental in the development of physics and earns a high place in the history of science. Several players took part in this adventure. The most important are Einstein, Dyson, Eddington, the Sun, the Moon, Sobral, and Principe. Einstein's theory of gravitation, general relativity, had the prediction that the gravitational field of the Sun deflects an incoming light ray from a background star on its way to Earth. The calculation gave that the shift in the star's position was 1.75 arcseconds for light rays passing at the Sun's rim. So to test it definitely it was necessary to be in the right places on May 29, 1919, the day of the eclipse. That indeed happened, with a Royal Greenwich Observatory team composed of Crommelin and Davidson that went to Sobral, and that was led at a distance by the Astronomer Royal Frank Dyson, and with Eddington of Cambridge University that went to Principe with his assistant Cottingham. The adventure is fascinating, from the preparations, to the day of the eclipse, the data analysis, the results, and the history that has been made. It confirmed general relativity, and marked an epoch that helped in delineating science in the post eclipse era up to now and into the future. This year of 2019 we are celebrating this enormous breakthrough.
Keywords:
Light deflection; General relativity; Eclipse 1919
1. Introduction
It was written in the stars that the May 29, 1919, eclipse of the Sun would be the most important eclipse in the history of humankind.
In a total eclipse of the Sun, the Moon blocks the sunlight and casts a shadow on the Earth, turning the sky dark and letting the stars shine like it was night, the whole scene yielding back to the normal daylight as the required alignment is slowly undone with the turning of the celestial sphere at the place. The totality, i.e., the period during which an eclipse is total, takes about 5 minutes.
In ancient times the phenomenon was not understood in rational terms, only after the emergence of the recent civilizations, like the Babylonian and Assyrian, eclipses started to be understood as natural phenomena explained by an alignment between the Sun, Moon and Earth. The Earth was fixed, the celestial sphere with its stars turned around day after day, the Moon moved in the celestial sphere with a period of a month, and the Sun moved along the ecliptic, the great circle on the celestial sphere representing the Sun's path during the year.
With the advent of the Copernican revolution, that the Sun is at the center and the planets move around it, the understanding of the movements in the celestial sphere became highly simplified. One could now explain the motion of the Sun along the ecliptic through the motion of the Earth around the Sun. As the Earth moves the projection of the Sun into the celestial sphere changes, returning to the same point after tracing the ecliptic during one year. The Moon moves around the Earth during one month with an orbit slightly inclined relatively to the plane of the Earth's orbit. So, when it occurs that the Moon is new and the Moon's path is crossing the plane of the Earth's path there is an eclipse of the Sun, in case the cross is with a full Moon the eclipse is of the Moon, and this is the reason for the name ecliptic, the path where eclipses occur.
With the emergence of Newton's gravitation and precise celestial mechanics, eclipses and their places could be predicted with ease. With the development of telescopes through the use of photography and spectroscopy and the rise of astrophysics, it was possible to make observations of the Sun's cromosphere and corona during eclipses helping thus to determine its composition and physical properties.
But suddenly, solar eclipses started to have a new significance. They could be used to prove or disprove fundamental physics. Indeed, general relativity was completed by 1915, and Einstein, its author, predicted that the gravitational field of the Sun should deflect an incoming light ray from a background star on its way to Earth, such that the shift in the star's position was 1.75 arcseconds for light rays passing at the Sun's rim. If correct, one would know that the world is governed by general relativity, a theory of gravitation that connects space, time, and matter at a fundamental level. To confirm the light deflection prediction of general relativity one needed a solar eclipse such that the stars near the Sun's rim could be seen and their displacements measured.
In May 29, 1919, there was an eclipse with several bright stars in the background near the Sun giving the perfect conditions to measure the deflection effect, the more bright stars one has the better the results can be trusted. Due to the narrow bandwidth shadow that the Moon projects, solar eclipses usually are in remote parts of the world, so preparations to transport the telescopes and have the correct equipment and provisions took months. On the day of the eclipse all had to be ready so that during the five minutes of totality observations and photographic plates would work perfectly and give good results. If it rained or the sky were filled with heavy clouds all the work would have been for nothing. The 1919 eclipse would be no exception, one would have to go to Sobral, north of Brazil, and Principe, a Portuguese island at the time off the coast of west Africa.
British astronomers and astrophysicists decided it was time to test general relativity. Dyson, the Astronomer Royal, would collaborate with Crommelin and Davidson that would make the observations in Sobral, and Eddington would go with Cottingham to Principe. The enterprise was a success, with Einstein's general relativity being confirmed when the announcement of the results was made in London, in a joint meeting of the Royal Society and Royal Astronomical Society, on November 6, 1919.
This year of 2019 we celebrate one hundred years of this adventure. It is worth to register the seven main protagonists that took part in it, to understand the principles that lead to light deflection in general relativity, and to go through the 1919 eclipse in detail, namely, the preparations, the day of the eclipse, the data analysis, the results, and how history looks back at it. In confirming general relativity the 1919 eclipse science accomplishment outlined in some way the post eclipse era up to now and into the future. So let us wander through the 1919 eclipse wonders.
2. The protagonists
2.1. Einstein
Einstein, see Fig. 1, had a very important role in a number of areas in physics but the pinnacle is without a doubt the creation of general relativity. After great persistence from a work that started with the idea of the principle of equivalence in 1907 [1[1] A. Einstein, Jahrbuch der Radioaktivität und Elektronik 4, 411 (1907)., 2[2] A. Einstein, Annalen der Physik 35, 898 (1911).] and continued through the collaboration with Grossmann in the entwurf theory of gravitation [3[3] A. Einstein and M. Grossmann, Zeitschrift für Mathematik und Physik 62, 225 (1914). [4] A. Einstein, Naturforschende Gesellschaft in Zürich 58, 284 (1914).–5[5] A. Einstein, Naturforschende Gesellschaft in Zürich 59, IV (1914).], Einstein presented to the Prussian Academy of Sciences, in November 18 and 25, 1915 [6[6] A. Einstein, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 831 (1915)., 7[7] A. Einstein, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 844 (1915).], see also [8][8] A. Einstein, Annalen der Physik 49, 769 (1916)., a totally new theory, namely, a covariant, tensorial, and relativistic theory, that he immediately called the general theory of relativity, or simply, general relativity. Einstein equation that governs general relativity is
where is a quantity that represents the geometry of spacetime called the Einstein tensor, is a quantity that represents the matter content of the spacetime called the energy-momentum tensor, G is the constant of gravitation, and c is the speed of light, see [9][9] J. Renn and M. Schemmel, The Genesis of General Relativity (Springer, Dordrecht, 2007). for the genesis of this equation. In a stroke, the theory confirms the Minkowskian spacetime notion, states that gravitation is geometry, spacetime is curved, and particles follow geodesics. For accounts of this period in Einstein's life see [10[10] R.W. Clark, Einstein, the Life and Times (Avon Books, New York, 1971). [11] A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein (Oxford University Press, Oxford, 1982).–12[12] A. Pais, Einstein Lived Here (Oxford University Press, Oxford, 1994).].
In its more than one hundred years, general relativity has passed through very rigorous tests, it is accepted as the standard theory of gravitation, and is considered one of the great feats in history. Notwithstanding all these achievements, gravitation is the most intriguing of all the known interactions.
The tests and implications of general relativity are many and profound. Weak field classical tests within the solar system are the perihelion precession of Mercury, the light deflection in the gravitational field of the Sun, the gravitational redshift Doppler effect, and the Shapiro gravitational time delay in the radar echo. Technological applications of general relativity, are now current, as the global position system, or GPS, would not work at all without the general relativistic corrections related to the gravitational redshift Doppler effect, necessary to synchronize clocks in the satellites with clocks on the Earth's surface. Gravitational lensing is an abundant special case of light deflection and of great importance to understand the gravitational mass and gravitational structure of the Universe. Cosmology, the dynamical and physical study of the Universe, was started by Einstein in 1917 with a static finite universe, continued with the proposal by Friedmann, Lemaitre, and Hubble for an expanding universe, along with the establishment of the big bang scenario through the discovery of the cosmic microwave background radiation, up to the establishment of the acceleration of the Universe, and to the most recent astonishing developments, that converged in the awarding of the shared 2019 Nobel Prize in Physics to Peebles of Princeton University, one of the exponents in the field throughout the last six decades. Fundamental theories, theories that make the unification of gravitation and electromagnetism, were initiated by Weyl in 1918, and continued by Eddington and Einstein. Now they are called theories of everything and try to unify the four fundamental fields in a unique quantum scheme. Black holes, the geometric object par excellence in general relativity, were found by Oppenheimer and Snyder in 1939 as the endpoint of gravitational collapse and thus occurring necessarily in nature. Millions of solar mass black holes float through our galaxy, and all, or almost all, galaxies contain a central supermassive black hole in its center. Gravitational waves, spacetime waves predicted by Einstein in 1916, were detected indirectly in the binary pulsar discovered by Hulse and Taylor in 1976, which gave the Nobel prize in 1993, and detected directly in 2015 by the LIGO antennas, from the collision of two black holes, which in turn gave the Nobel prize in 2017. General relativity has left an immense and amazing legacy and we are still in the middle of many of its developments.
2.2. Dyson
Frank Dyson, see Fig. 2, excelled in astronomy, was Astronomer Royal and Director of the Royal Greenwich Observatory. He had been a Cambridge student in Trinity College scoring Second Wrangler in 1889, was elected Fellow of the Royal Society, i.e., FRS, in 1901, and worked on the Astrographic Catalogue published in 1905.
Dyson was a world specialist in solar eclipses and an expert in the solar corona and chromosphere. He was present in six eclipses with success in all, in particular, his first eclipse was in Ovar, Portugal, for the May 28, 1900, eclipse, and was a member of the Joint Permanent Eclipse Committee, which was founded in 1884 by the British to strengthen expertise on the subject [13][13] A.S. Eddington, Biographical Memoirs of Fellows of the Royal Society 3, 159 (1940)..
Through Eddington, he understood the importance and possibilities of the 1919 eclipse that could prove or disprove general relativity and invited Eddington himself in turn to participate in the observations. After all the limelight had passed he knew that the eclipses' findings would be recorded as Eddington's.
Two Dyson's assistants at the Royal Greenwich Observatory participated in this adventure and were sent to Sobral to do the eclipse observations. Andrew Crommelin, see Fig. 3, Irish astronomer specialist in comets, led the expedition, and on the day was in charge of the 4 inch telescope that yielded the important data in the end. He substituted in the last minute Aloysius Cortie, a Jesuit astronomer that did not travel because of work, possibly he had to take immediate charge of being Director of the Stonyhurst College Observatory. Crommelin was president of the Royal Astronomical Society from 1929 to 1931. Charles Davidson, see Fig. 3, was a computer, i.e., did arithmetic calculations for problems in astronomy at the Royal Greenwich Observatory, and scaled up the hierarchy through his skills with instruments and telescopes. He accompanied Dyson and Eddington in other eclipses. He was elected FRS in 1931, showing his great competence. In Sobral, he operated the 13 inch astrographic telescope that did not work well.
2.3. Eddington
Eddington, see Fig. 4, professor in the University of Cambridge, shined in astrophysics and gravitation. He was the first and only second-year student that got the much aimed Senior Wrangler, i.e., First Wrangler. Was elected FRS in 1914, President of the Royal Astronomical Society in the period 1921-1923, and President of IAU in the period 1938-1944 [14][14] A. Vibert Douglas, Arthur Stanley Eddington (Thomas Nelson and Sons, London, 1956)., see also [15[15] C.W. Killmister, Eddington's Search for a Fundamental Theory: A Key to the Universe (Cambridge University Press, Cambridge, 1994)., 16[16] M. Stanley, Practical Mystic: Religion, Science, and A. S. Eddington (University of Chicago Press, Chicago, 2007).].
Eddington was the first to understand the physics of the stars at its center with temperatures of 10 million degrees. In 1918 he introduced general relativity to the British audience which were still grasping to understand special relativity. He wrote several outstanding books on the theory, read with enthusiasm worldwide for many generations up to now. He was the first to give the correct quadrupole formula for gravitational radiation as a 1/2 term was missing in Einstein's deduction, he introduced a parameterization scheme for general relativity through a post-Newtonian approximation which appeared in his book in mathematical relativity and was much later developed into the parameterized post-Newtonian, or PPN, formalism, he initiated the study of gravitational radiation emission using a rotating star mimicked by a rod, and he examined the problem of n bodies in general relativity with interesting results. He was lured into cosmology and tried frantically a theory of everything without success. He was the main name in the 1919 expeditions that detected the light deflection by the gravitational field of the Sun, he himself having made the observations in Principe. His many books for the public understanding of science are fascinating.
Edwin Cottingham, see Fig. 5, made fame and money through the making of clocks as he was a gifted mechanical and electric technician. His shop was in Thrapston, between Northampton and Cambridge, and Cambridge University would frequently called him to help in the maintenance of clocks and instruments. In Principe he helped Eddington in the mounting and maneuvering of the telescope. Eddington narrates that, on the day previous to the departure, in Greenwich, he and Dyson were discussing that Newtonian gravitation gave half the amount of the deflection predicted by Einstein's theory, and that Eddington expected to observe the full deflection. Cottingham was present and asked “What will it mean if we get double the Einstein deflection?” which prompted a response from Dyson, “Then Eddington will go mad, and you will have to come home alone!” [17][17] A.S. Eddington, in: Background to Modern Science, edited by J. Needham and W. Pagel (Cambridge University Press, Cambridge, 1940), p. 117., see also [14][14] A. Vibert Douglas, Arthur Stanley Eddington (Thomas Nelson and Sons, London, 1956)..
2.4. The Sun
The Sun, see Fig. 6, is our beloved star, it shines and deposits energy for terrestrial processes. However, here the interest is that the Sun is source of gravitational field, or in other words, it distorts spacetime.
There is a dictionary for trading words and concepts from Newtonian gravitation to general relativity, like gravitational force for spacetime distortion, but it is not exhaustive as the two theories have completely different ontologies with general relativity being much more comprehensive. We want to understand the motion of light in a gravitational field like the Sun through Newtonian gravitation and through general relativity.
In Newtonian mechanics a particle moves according to Newton's second law of motion , where F is the applied force, m is the particle's inertial mass, r is the particle's position, t is the time, and the particle's acceleration. Newtonian gravitation states that the force F exerted by the Sun in a particle is , where M and m are the Sun's and the particle's gravitational mass, respectively, r the distance between the Sun and the particle, and G Newton's universal constant, see, e.g., [18][18] V.D. Barger and M.G. Olsson, Classical Mechanics, a Modern Perspective (McGraw-Hill, New York, 1994). for more on Newtonian gravitation. By experiment, it is known that inertial and gravitational masses have the same value which for the particle we have called m. For the purposes of understanding the motion of light, considered as a massless particle, note that in Newtonian gravitation, the motion of a particle is generically governed by , since inertial and gravitational masses having the same value m, they cancel in the equation of motion, i.e., the particle's mass m does not enter into the problem. So, light moving in a gravitational field can indeed be thought as obeying Newtonian gravitation laws, the only hypothesis is that light is a particle. Whether the light particle has zero mass or any other effective mass, it does not matter, since even the zero mass case can be conceived as a particle of very tiny mass with that mass going to zero in the limit. However, in the 19th century light started to be considered as a wave, instead of a particle, in which case it would not be influenced by gravitation, there would be no coupling between light and gravitation, as it was thought. But even this idea of no coupling between waves and gravitation had to be rethought within the context of special relativity, as here light would have an effective mass corresponding to the special relativistic energy E, and where c is the velocity of light. Since then in special relativity a lightwave has an effective mass it would now indeed couple to gravitation and light, even as a wave, could follow Newton's laws. So, the motion of light in a gravitational field in Newtonian gravitation could not be settled so easily, it could be the case that light is a wave that does not couple to gravitation, or it could be the case that light is a particle of some mass, even zero mass, or a wave with effective mass , in both these cases light would couple and be influenced by the laws of gravitation as described by Newton.
Einstein's general relativity, based on the principle of equivalence that states that gravitational and inertial masses are the same thing, arrives at the notion that spacetime is curved, in particular is curved around the Sun, see Fig. 7, and a particle moves following this curvature. General relativity incorporates then naturally the motion of light within its spacetime formalism and describes it as geodesic motion.
Spacetime distortion by the Sun here represented as space distortion alone. The movement of massive particles and massless particles such as light is described as geodesic motion in spacetime.
2.5. The Moon
The Moon, see Fig. 8, has a very important effect on Earth: The tides. However, here the interest is that the Moon can put itself between the Earth and the Sun yielding a full shadow of the Moon, i.e., a total eclipse of the Sun.
A total eclipse of the Sun is relatively rare. The plane of the orbit of the Moon around the Earth makes a 5 angle with the ecliptic, the plane of the projected annual orbit of the Sun around the Earth onto the celestial sphere, see Fig. 9. This plane is of course the same as the plane of the orbit of the Earth around the Sun. The two orbits, Moon's and Sun's, cross at the nodes, one ascending the other descending. When the Moon is in between the Earth and the Sun one has a new moon. If the new moon happens to be on a node then there is a total eclipse of the Sun, At the eclipse, the disk of Moon barely hides the disk of the Sun. If in the eclipse the Moon's orbit is in the perigee, when it is closest to Earth, then the eclipse is total, if the Moon's orbit is in the apogee, when it is farthest from the Earth, then an annulus of the Sun can be seen and the eclipse is annular. When there is a total eclipse the shadow of the Moon on Earth is about 200Km wide and can run a track roughly from west to east of some 12 thousand Km, visiting countries and oceans. A typical eclipse photograph is seen in Fig. 10. For information on solar eclipses see, e.g., [19[19] M. Littmann, F. Espenak and K. Willcox, Totality: Eclipses of the Sun (Oxford University Press, Oxford, 2008)., 20[20] T. Nordgren, Sun, Moon, Earth: The History of Solar Eclipses from Omens of Doom to Einstein and Exoplanets (Basic Books, Philadelphia, 2016).].
Lunar orbit showing the nodes when the orbit crosses the ecliptic, the Sun's path on the celestial sphere along the year.
The July 11, 1991, shadow of the Moon from Playas del Coco, Costa Rica. This eclipse also passed some hours later in Amazonia.
2.6. Sobral
The 1919 eclipse would hit Earth along several places, in particular it would pass through the north of Brazil. Henrique Morize, the director of Observatorio Nacional in Rio de Janeiro, recommended to the British Sobral as the right place to do the eclipse observations.
Sobral is located 230 Km west from Fortaleza, the capital of the state of Ceará, and the port nearest to it is Camocim, see Fig. 11. Sobral is crossed by the river Acaraú. In 1919 it was a small town of 10 thousand people, it is now a fine city with a population of 200 thousand. It is worth to compare photos of Sobral city in 1919 and in 2019, see Fig. 12.
Left: Map of South America, with Brazil and the city of Fortaleza visible in the north. Right: Map of Ceará, where one can spot Sobral, Fortaleza, and Camocim, the nearest port to Sobral.
Left: Sobral in 1919 with the main church of Nossa Senhora da Conceição seen from the church of Patrocínio with a zoom. The Jockey Club where the English and American tents were mounted is just beyond the right boundary of the photograph. Courtesy of Carnegie Institute. Right: Sobral city today with the main church of Nossa Senhora da Conceição seen from near the river Acaraú, with the river itself on the picture. The old race horse track of the Jockey Club started from the riverbank at the constructed circular bay seen in the figure and ran perpendicular to the river.
The Brazilian astronomers, led by Morize, were also at Sobral to make observations of the Sun's cromosphere and corona. They mounted their tents with the telescopes in front of church of Patrocinio, see Fig. 13. Church of Patrocinio is now famous because of this. In 1999, Sobral inaugurated the Museum of the Eclipse precisely in the place where the Brazilian tents were, as can be ascertained from Fig. 13 and Fig. 14. The two stylish half moons format of the museum is due to the architect from Sobral Antenor Coelho. On one side of the museum there is a small dome that contains the Henrique Morize Observatory with its telescope, and since 2015 a planetarium was also installed. It is a true astronomy park. This year of 2019 a sculpture of Einstein was inaugurated and laid near the river, see Fig. 15.
Observatory camp of the Brazilian expedition with the church of Patrocinio in 1919. Courtesy of Observatorio Nacional, Rio de Janeiro.
Museum of the Eclipse, the planetarium, and church of Patrocinio today. The monument in between the two half moons of the museum was built in 1923 to celebrate the 150 years of the establishment of Sobral.
Einstein in Sobral: Einstein's statue inaugurated in 2019 for the one hundred years of the eclipse.
The two members of the British expedition, Crommelin and Davidson, were installed nearby in the house of the Saboya family, together with the two members of an American team of geophysicists from the Carnegie Institute that, jointly with other teams of geophysicists spread over several countries within the belt of the eclipse, wanted to measure the magnetic field of the Earth and the electricity of the air during the eclipse. The Saboya house is not in front of the church of Patrocinio, it is a three minute walk from it, to the back and to the right of Fig. 14, i.e., to the south of the church. In front of the Saboya house passed a horse race track that started in the Aracaú's riverbank, had 700 meters length, and belonged to the Jockey Club of Sobral. Since there were no races in the foreseeable future the British and American teams mounted the telescope tents precisely there. The Jockey Club, also called the Derby Club, has moved somewhat further to the northeast of the town along the river Aracaú.
2.7. Principe
The track of the eclipse would continue its trajectory through a narrow band on Earth. After Brazil, it would cross the Atlantic, would touch Cape Palmas in Liberia, pass through the island of Principe and spread through mainland Africa until disappearing in the east. The Joint Permanent Eclipse Committee with Dyson and Eddington in command chose the island of Principe. Principe, belongs to the São Tomé e Principe archipelago, was a Portuguese territory in 1919 that became independent in 1975. Why Principe was chosen instead of other point in mainland Africa is motif for speculation. It is known that Principe was chosen instead of Cape Palmas because it was thought that the chances of having good weather in Principe were better than in Cape Palmas, although on the day of the eclipse Cape Palmas had a sunny day, as reported by one of the geophysicists from the Carnegie Institute that composed the several teams spread along the eclipse's belt set to measure the magnetic field of the Earth [21][21] L.A. Bauer, Science 51, 301 (1920).. It is also known that Eddington and Davidson had passed in Lisbon in 1912 on the way to the total eclipse in Passa Quatro, Minas Gerais, Brazil, where they wanted to observe the solar corona. In this passage through Lisbon, Eddington met Campos Rodrigues and Frederico Oom, director and vice-director of the Lisbon Observatory, respectively, and surely considered himself at ease to ask for observing the 1919 eclipse in Principe. Moreover, the eclipse would strike Gabon, a French colony at the time, and certainly would be more delicate to pass by the French sensitivities, as the Europe powers were in another peak of national fanaticism. Thus, in the end Principe was the best choice, see Fig. 16.
Principe is in the Gulf of Guinea off the western coast of Africa just north of the equator, see Fig. 17. A map of Principe is shown in Fig. 18 with a few important locations, namely, Santo Antonio and Roça Sundy. In Santo Antonio, the capital of Principe, see Fig. 19, Eddington and Cottingham were received by several personalities of the island.
Left: The location of Principe in the Guinea Golf off the western equatorial coast of Africa. Right: A close up.
One of the personalities that took the British around to see the best site to mount the telescope was Jerónimo Carneiro, a landowner with headquarters at Roça Sundy. In 1919 he was a young man of 26 years old and had inherited the land from his father and from his grandfather. His grandsons, live in Lisbon, and remember him well, who is also nowadays remembered by the local old people of Principe. With the independence in 1975, the land became a state land and the family Carneiro did not return there. The land passed through a river, called the river Sundim, that was in a region that belonged to Senhor Dias probably in the beginning of the 19th century. Local people rounded his name for Sundim. So, from Senhor Dias it passed to Sundim, from Sundim it passed to Sundi and then from Sundi it changed to Sundy. It is possible that the first time it was written as Sundy, clearly an English spelling, was by Eddington when he was reporting on the eclipse preparations and results. With all the best possible infrastructure that could be offered in Principe the British opted to stay at Roça Sundy.
In Roça Sundy, in the surroundings of the house there is a stone commemorative of the 1919 eclipse and Eddington's observations that confirmed the generalized theory of relativity, see Fig. 21. On its base there are some mathematical formulas, like the Eddington luminosity expression, a line element representing curved spacetime, and the gravitational redshift formula. There is also a plate, now in front of one of the sides of the house, see Fig. 22, with a well-written small overview of the main achievements of the eclipse and an informative figure in the middle explaining the phenomenon of light deflection and with pictures of Eddington and Einstein.
A plate in Roça Sundy containing useful historical and scientific information about the findings of the 1919 eclipse.
3. The theory: what general relativity says about light deflection
In 1907 Einstein understood that in an accelerating field, e.g., in an accelerating elevator, the trajectory of a light ray would be bent, and through the equivalence principle inferred that light would be as well deflected in a gravitational field of a star, like the Sun for instance [1][1] A. Einstein, Jahrbuch der Radioaktivität und Elektronik 4, 411 (1907)., see Fig. 23 for a generic sketch of the phenomenon. The calculation gave that a light ray would be deflected by an angle given by the expression , where G is Newton's constant, M is the mass of the star, c is the velocity of light, and D is the distance of closest approach of the light ray to the star [2][2] A. Einstein, Annalen der Physik 35, 898 (1911).. This was a surprise because light was an electromagnetic wave and it was thought that waves would have zero mass and in the context of Newtonian gravitation would not be influenced by a gravitational field. Even with the appearance of the special relativistic mass formula , with E being the energy of the wave, in which case the lightwave would have precisely the effective mass and would suffer gravitational attraction, it seems no one thought of that gravitational influence on the wave, it was only through Einstein's equivalence principle that the idea and the effect of light deflection emerged [1[1] A. Einstein, Jahrbuch der Radioaktivität und Elektronik 4, 411 (1907)., 2[2] A. Einstein, Annalen der Physik 35, 898 (1911).].
Unbeknown to Einstein, and to everybody else interested in light deflection at the time, this deflection had been calculated in 1801 by Soldner [22[22] J.G. von Soldner, Berliner Astronomisches Jahrbuch, 161 (1801)., 23[23] S.L. Jaki, Foundations of Physics 8, 927 (1978).], a German astronomer, using Newtonian gravitation and considering light as a particle, yielding the same result as using the equivalence principle. Indeed, the inertial mass term in Newton's second law, cancels with the the gravitational mass in Newton's law of gravitation, this being the essence of the equivalence principle, and the equation of motion holds for any particle, including particles with zero mass in the limit. After all gravitation is universal. The only thing Soldner's assumed in the computation, apart from Newton's laws, was that the particle travels with the velocity of light. The calculation had also been done before by Cavendish but not published [24][24] R. McCormmach, British Journal for the History of Science 4, 126 (1968).. In 1704, Newton in the first query of his book Opticks, questions “Do not Bodies act upon Light at a distance, and by their action bend its Rays; and is not this action strongest at the least distance?” It is often said that Newton foresaw gravitational deflection in this query. It seems that this interpretation is not correct. In the query he never mentions gravitation, indeed the book is on opticks, so it is almost certain that he was thinking in other interactions of light with matter. When seventeen years before, he was writing the Principia on the laws of motion and gravitation, he would have thought that light could be deflected by a gravitational field, but he may have dismissed it as trivial, as gravitation was universal, and in his theory light had no special category, its motion being a particular case of unbound hyperbolic trajectories of particles. Clearly, if he had thought it important he would have done the calculation explicitly in the Principia or even afterwards.
Now, by 1915 there were competing relativistic theories of gravitation. Nordström's scalar theory [25][25] N.A. Doughty, Lagrangian Interaction (Addison-Wesley, New York, 1990)., on which Einstein was very interested although it yielded the wrong value for Mercury's precession, gave zero deflection for light travelling in a gravitational field, the same value as in Newtonian gravitation considering light as a wave with no coupling to it, and the entwurf theory of Einstein and Grossmann predicted, as the equivalence principle calculation had done, again the Newtonian deflection value of Soldner [3[3] A. Einstein and M. Grossmann, Zeitschrift für Mathematik und Physik 62, 225 (1914). [4] A. Einstein, Naturforschende Gesellschaft in Zürich 58, 284 (1914).–5[5] A. Einstein, Naturforschende Gesellschaft in Zürich 59, IV (1914).]. So, when Einstein had the equations of general relativity ready he of course thought important to redo the light deflection due to the Sun's gravitational field and got [6][6] A. Einstein, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 831 (1915).. This is twice the result he got using simply the principle of equivalence. Let us see how one obtains this .
If there is no central mass, i.e., no Sun, then the light ray propagates in a straight line, see Fig. 24. Clearly, in polar coordinates a straight line has equation , where D is the closest approach distance from the center of coordinates. It is sometimes better to use the variable in which case the straight line equation is .
Now, when the center of the polar coordinates has a central mass, e.g., the Sun, then the problem changes and a light trajectory gets curved. The spacetime for a central mass M is given in spherical coordinates where t, r, , and , are the time, radial, and angular coordinates, respectively, by the Schwarzschild line element interval
When one writes M in Eq. (2) one should bare in mind that one should have written , or conversely, if one uses units in which , , than one can stick to M simply. So, M is the geometrical mass with units of length. For the Sun, in kilograms , and in kilometers Km. The light trajectories follow geodesics, paths of minimal interval. One can think that there is a parameter that runs along a geodesic and so the geodesic trajectory can be written as , i.e., . One can assume that the light propagation is in the plane , so the angle along the light ray is inert, it does not change. Two equations for the light geodesic can be shown to be and , where a dot means derivative with respect to , and k and b are constants, actually constants of integration. Since the trajectory is light-like one has . Thus, a third equation for the geodesic can be find by putting in Eq. (2), and dividing each term of it by , one gets , where has been assumed. So putting the first two equations onto the third yields the geodesic equation . Now, define again our variable u as . Then, since by definition , one has , i.e., one trades a derivative with respect to by a derivative with respect to . Then the geodesic equation above turns into . Usually one wants to integrate, but here we take the derivative in relation to to get a better equation, which gives , as appears in all terms and can been eliminated. No central mass, , and the equation is , the solution being obvious, it is a sine, i.e., . Or putting back get a straight line in polar coordinates , as we have shown above. Now is small, as M is the geometric mass of the Sun, a small quantity, and D is the distance of closest approach of the light ray to the Sun's surface, a much bigger quantity. For small one uses perturbation methods and finds the solution . The light ray comes from the star, see Fig. 25, at , i.e., , and with say, so we get from the solution , i.e., . The light ray goes to the Earth, see Fig. 25, assumed at , so , and with say, so get from the solution , i.e., . We used the approximation for , as is the case here. Now, the total angle of deviation is , see Fig. 25, so summing the two results above one gets . Restoring G and c one has that the formula for the deflection taken from general relativity is
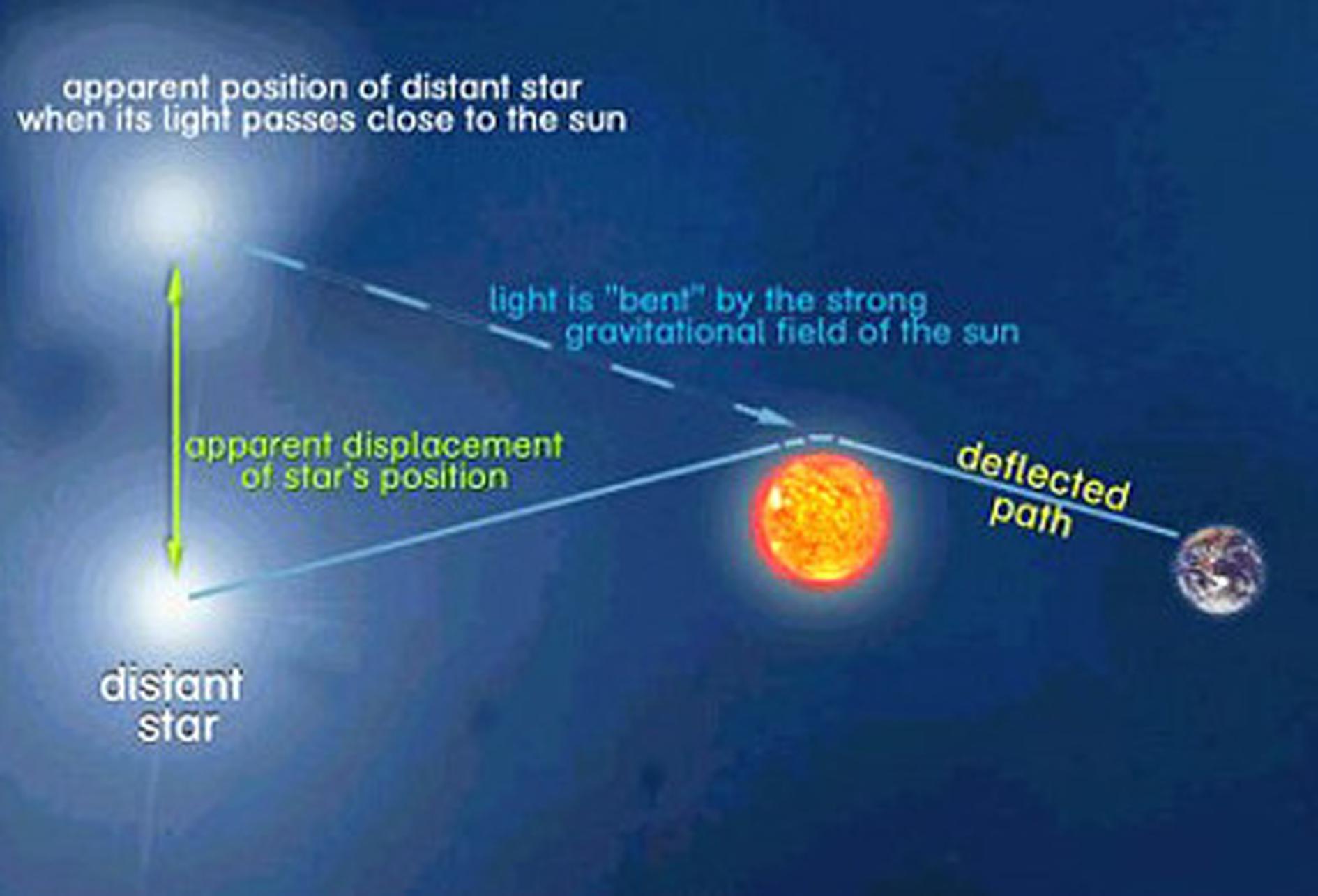
When there is an object of mass M like the Sun there is light deflection. Light rays come from a star at infinity. If there is no mass M they continue their travel in straight lines. Since the star is at infinity all these light rays are parallel and hit the line Sun-Earth at an angle , in particular one of them hits the observer at that angle. In the presence of a mass M these light rays get deflected and one of them hits the observer at an angle . The incoming light ray is thus deflected by an amount . Therefore the star has its position in the sky shifted by .
This is the law for light deflection, i.e., an hyperbolic law. Let us put numbers. The geometrical mass of the Sun is , and for a light ray that grazes the Sun's surface, D is the Sun's radius, i.e., . So arcseconds. The general relativistic deviation for a light ray that passes tangent to the Sun's surface is 1.75 arcseconds and so an apparent star shifted by this amount is seen in the sky instead of the star in its true position. Newtonian gravitation predicts half of that value. To see this one can follow Soldner's calculation, or for that matter Einstein's calculation using the equivalence principle, but simpler here is to consider that Newtonian gravitation can be mimicked by a line element interval of the form , where the term in front of takes care of the Newtonian gravitational potential , and there is no term as space is flat. Then redoing the calculations above, instead of having appearing twice as in Eq. (2), one has appearing only once, yielding half the value, , so that for a light ray passing at the Sun's rim arcseconds. Light deflection is treated in most textbooks on general relativity.
Admit that the Sun is eclipsed by the Moon, as in Fig. 26, and that there are four stars just at the rim of the Sun. Then due to the gravitational deflection effect the four field stars will pop out just outside the Sun's rim. This effect always exists, with or without eclipse, but only with an eclipse can the stars, and so the effect, be observed. Measure the positions of the four stars when the Sun is not there and measure the positions of the four stars when the Sun is there, subtract the results for each star, and obtain for each star. Compare this observed with the predicted by the theories of gravitation, namely, the zero value of Newtonian gravitation with no coupling to lightwaves or Nordström relativistic scalar theory of gravitation, the half value of Newtonian gravitation and treating light as a particle as considered by Soldner or considering light as a wave with an effective mass , and the full value of general relativity. This concept is what is needed to understand the light deflection test of theories of gravitation, in particular of general relativity, in eclipse observations. So now we turn into the heart of the 1919 eclipse and its light deflection.
Left: Field of four stars. Right: The Sun is eclipsed by the Moon and the field of four stars pops out in accord with the law for gravitational light deflection.
4. The 1919 eclipse: Preparations, the day, data analysis, results, and history
4.1. Preparations
Having understood that a light ray from a star behind the Sun is deflected by its gravitational field [1[1] A. Einstein, Jahrbuch der Radioaktivität und Elektronik 4, 411 (1907)., 2[2] A. Einstein, Annalen der Physik 35, 898 (1911).] Einstein immediately started to look for astronomers that could measure the effect. Freundlich, a young German astronomer, got very interested, and tried first to obtain from other astronomers around the world pictures of past eclipses, but these were not of the quality required. It was necessary to wait for a total eclipse of the Sun. The American astronomer Charles Perrine, originally from Lick Observatory and now director of the Cordoba Observatory in Argentina, heard from Freundlich the interest and importance of testing the light deflection in the gravitational field of the Sun. In October 10, 1912, there was an eclipse that passed in Minas Gerais, Brazil, and Perrine went there to observe the predicted Einsteinian equivalence principle half effect [26][26] C.D. Perrine, Astronomische Nachrichten 219, 281 (1923).. Eddington and Davidson happened also to be there but to observe the solar corona. At this time, Eddington was not familiar with Einstein's ideas. Many other teams from everywhere were also in Minas Gerais for the eclipse. It is speculated [27[27] J. Stachel, in: The Prism of Science, edited by E. Ullmann-Margalit (Boston Studies in the Philosophy of Science, Boston, 1986), p. 225., 28[28] A. Warwick, Masters of Theory: Cambridge and the Rise of Mathematical Physics (University of Chicago Press, Chicago, 2003).] that Eddington heard for the first time from Perrine the possibility of light deflection. Eddington was at Passa Quatro and Perrine at Cristina, both localities in the state of Minas Gerais separated by 80 Km through the road. It is indeed possible that they met somewhere in some city of Brazil before the eclipse, although that is not registered in the official report [29][29] A.S. Eddington and C. Davidson, Monthly Notices of the Royal Astronomical Society 73, 386 (1913).. Unfortunately, Perrine “suffered a total eclipse instead of observing one”, as he wrote after heavy rain set in [26][26] C.D. Perrine, Astronomische Nachrichten 219, 281 (1923)., and no light deflection could be checked. In August 21, 1914, there was a solar eclipse that passed in Crimea, Russia. It would test the zero prediction value in the case that light rays did not couple to gravitation at all as in Newtonian gravitation with no coupling to lightwaves or the relativistic Nordström's theory [25][25] N.A. Doughty, Lagrangian Interaction (Addison-Wesley, New York, 1990)., or it would give the Newtonian value also predicted by the equivalence principle [2][2] A. Einstein, Annalen der Physik 35, 898 (1911). and the entwurf theory [3[3] A. Einstein and M. Grossmann, Zeitschrift für Mathematik und Physik 62, 225 (1914)., 4[4] A. Einstein, Naturforschende Gesellschaft in Zürich 58, 284 (1914).], as Einstein was aware [5][5] A. Einstein, Naturforschende Gesellschaft in Zürich 59, IV (1914).. Or, perhaps, other value. To test it two expeditions were organized but were a total failure. Freundlich was made prisoner when he arrived in Russia as the first world war had just broken out, and Campbell of Lick Observatory in California, got rained washed on the day.
The eclipses in Brazil and Russia were set to test the zero value and the half value prediction, this latter given by the equivalence principle and the entwurf theory and also called the Newtonian value. From the end of 1915 onwards, the full value prediction of general relativity was also to be tested. The eclipse of June 8, 1918, that crossed the USA, could thus serve to test the zero value, the half value, and the full value. The 1918 eclipse passed almost through Lick Observatory, but Campbell and Curtis could not make proper measurements as the good instruments that went to Russia were still stuck somewhere because of the first world war. The next eclipse would be the one of May 29, 1919.
At the time, the observation of the Sun's rim through eclipses was in its highest point, and British astronomers and scientists, understanding the importance of the eclipses, formed eclipse committees that culminated in 1892 in the Joint Permanent Eclipse Committee in order to gather a coherent base of knowledge on eclipses. Eclipse expeditions were time consuming and laborious to prepare but to the British Empire this was no problem, it could put anyone anywhere. Dyson, being an authority on eclipses and Astronomer Royal, was a member of the committee.
During the first world war there were no communications between England and Germany. In England, most scientists, some of the caliber of Lodge, Larmor, and Jeans, were vaguely aware of special relativity and even less of general relativity, they were interested in what was called the electrical theory of matter that still included the ether, and that perhaps would explain the phenomenon of gravitation [28][28] A. Warwick, Masters of Theory: Cambridge and the Rise of Mathematical Physics (University of Chicago Press, Chicago, 2003).. There were two exceptions however, Cunningham from Cambridge that taught and published on special relativity, and the Lindemanns, father and son, the first a wealthy engineer and amateur astronomer of German origin, the second yet to become a prominent physicist at Oxford and adviser to Churchill in the second world war, that got interested in the light deflection effect of general relativity and published a paper on how one might proceed to measure it from daylight photography of stars [30][30] A.F. Lindemann and F.A. Lindemann, Monthly Notices of the Royal Astronomical Society 77, 140 (1916).. At about this time, in 1916, Eddington had access to general relativity through his friend de Sitter, a Dutch astronomer of Leiden, colleague of Lorentz and Ehrenfest that had a genuine keen interest in Einstein's ideas on gravitation. Earlier, de Sitter had attacked Mercury's perihelion problem by mixing Newtonian gravitation with special relativity, and by now he had a good command on general relativity. Eddington asked de Sitter to write a review on general relativity to the Monthly Notices of the Royal Astronomical Society readers which he did in a series of three remarkable papers. Eddington then immediately understood the power of the general theory and mastered it as quickly as he could, in about two years. He became particularly interested in the 1919 eclipse test of general relativity and his first book on general relativity was published [31][31] A.S. Eddington, Report on the Relativity Theory of Gravitation (Fleetway Press, London, 1918)..
Eddington and Dyson were colleagues that met several times a month in the Royal Astronomical Society, i.e., in Burlington House, London, and in other places around England. So, briefed by Eddington, Dyson understood the importance of the 1919 eclipse test and accordingly, in March 1917, he published in the Monthly Notices of the Royal Astronomical Society a paper with the title “On the opportunity afforded by the Eclipse of 1919 May 29 of verifying Einstein's theory of gravitation” [32][32] F.W. Dyson, Monthly Notices of the Royal Astronomical Society 77, 445 (1917)., in which he highlighted the fact that that eclipse was in front of the open cluster Hyades, a region of the sky containing many bright stars, see Fig. 27. A greater number of bright stars around the eclipsed Sun surely improves the probability of obtaining relevant results for light deflection.
Left: The Hyades open cluster in the Constellation of Taurus. Right: The Hyades in plenitude.
The May 29, 1919, eclipse was thus a great opportunity to test general relativity. Dyson, in turn, called Eddington to do the observations for obvious reasons, he was an excellent astronomer and astrophysicist, and a deep connoisseur of general relativity. In addition, Eddington was a quaker, and that religious confession professes peace and nonviolence. Thus, Eddington, a conscientious objector, asked to be dispensed of military service, and only by the intervention of Dyson the exemption from the authorities was conceded without further ado, with the justification of Eddington's importance in the expedition. The preparations started in 1917. The end of the first world war in November 1918 enabled definitely the realization of the new test to Einstein's law of gravitation. For narratives of this eclipse and its results see also [33[33] A.C.D. Crommelin, Nature 102, 444 (1919). [34] A.S. Eddington, Observatory 42 119 (1919). [35] A.C.D. Crommelin, Observatory 42, 368 (1919). [36] J.J. Thomson, Observatory 42, 388 (1919). [37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920). [38] A.S. Eddington, Space, Time, and Gravitation: An Outline of the General Relativity Theory (Cambridge University Press, Cambridge, 1920). [39] A.N. Whitehead, Science and the Modern World (The Macmillan Company, New York, 1925). [40] H. von Klüber, Vistas in Astronomy 3, 47 (1960). [41] S. Chandrasekhar, Notes and Records of the Royal Society of London 30, 249 (1976). [42] D.F. Moyer, in: On the Path of Albert Einstein, edited by A. Perlmutter and L.F. Scott (Plenum Press, New York, 1979), p. 55. [43] J. Earman and C. Glymour, Historical Studies in the Physical Sciences 11, 49 (1980). [44] C.M. Will, Classical and Quantum Gravity 32, 124001 (2015).–45][45] D. Kennefick, No Shadow of a Doubt: The 1919 Eclipse that Confirmed Einstein's Theory of Relativity (Princeton University Press, New Jersey, 2019)..
The track of the eclipse was known, see Fig. 28. The eclipse would run from west to east, would start at dawn in west of South American in Peru, then traverse Bolivia, pass through the north and northeast of Brazil, cross the Atlantic, hit Cape Palmas in Africa, reach Principe island, and finally arrive in Africa mainland until disappearance at twilight in the east in the border of Tanzania and Mozambique, running across 12 thousand Km.
World map with the track of the May 29, 1919, eclipse. The black belt 200Km wide yields the places of total eclipse. The gray belt is for partial eclipse.
Two sites were chosen by the Joint Permanent Eclipse Committee and accordingly two expeditions were planned. To have two expeditions would increase the chances of at least one being successful. One expedition would proceed with the astronomers Cortie and Davidson to Sobral, Brazil. Dyson could not go as he had several other important commitments as Astronomer Royal. In the last hour Cortie could not depart and was traded for Crommelin. The Sobral team was pure Royal Greenwich, with Dyson having the responsibility of supervising the data analysis and results after the expedition returned to England. The other expedition would proceed with Eddington and Cottingham to Principe. The two sites were certainly carefully chosen. The Sobral site was chosen with the help of Morize, Eddington and Morize met during the 1912 eclipse in Minas Gerais. The Principe site was chosen for Eddington's acquaintance with the main Portuguese astronomers, and for being the most convenient at the time taking into account all factors. Why Eddington went to Principe rather than Sobral is a question that seems beyond all conjectures. At last, all was set, and Crommelin, Davidson, Eddington, and Cottingham sailed on March 8 on the Anselm ship, passed in Lisbon where they were received by Frederico Oom, went for a city tour [35][35] A.C.D. Crommelin, Observatory 42, 368 (1919)., and followed to Funchal.
Crommelin and Davidson boarded then for Belém do Pará, stretched up to Manaus for sightseeing, and went to their destination in the steamboat Fortaleza, arriving in Camocim, the nearest port, on April 29, and in Sobral on April 30. The Sobral expedition had all the support from the Brazilian authorities. A team from Observatorio Nacional of Rio de Janeiro with Morize was present in Sobral. They accompanied the stay of the British and mounted its own camping observatory to observe the solar corona. The Americans from Carnegie had also arrived at about the same time. Crommelin describing the arrival writes [35][35] A.C.D. Crommelin, Observatory 42, 368 (1919).: “Several deputations were at the station to welcome us; it must be confessed that they were expecting Father Cortie, whose letter expressing his inability to go had never reached Sobral. However, the welcome was freely transferred to us.” This welcome from the Brazilians he restated in [36][36] J.J. Thomson, Observatory 42, 388 (1919).. Davidson in the 1920 report published in the Philosophical Transactions describing the preparations writes [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920).: “We were met at Sobral station by representatives of both the Civil and Ecclesiastical Authorities, headed respectively by Dr. Jacome d'Oliveira, the Prefect, and Mgr. Ferreira, and conducted to the house which had been placed at our disposal by the kindness of its owner, Col. Vicente Saboya, the Deputy for Sobral... A convenient site for the eclipse station offered itself just in front of the house; this was the race-course of the Jockey Club, and was provided with a covered grand stand, which we found most convenient for unpacking and storage and in the preparatory work.” They were thus received warmly and treated like princes.
In Funchal, Eddington and Cottingham boarded on April 9 in the ship Portugal to Principe arriving there on April 23. The Principe expedition had the support from the Observatorio Astronomico de Lisboa and from the Portuguese authorities. There was exchange of correspondence between Eddington and Campos Rodrigues and Frederico Oom, to finalize the logistics. Eddington, in the report published in 1920 describing the preparations and the arrival in Principe, writes [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920).: “Vice-Admiral Campos Rodrigues and Dr. F. Oom of the National Observatory, Lisbon, had kindly given us introductions, and everything possible was done by those on the island for the success of the work and the comfort of the observers. We were met on board by the Acting Administrator Sr. Vasconcelos, Sr. Carneiro, President of the Association of Planters, and Sr. Grageira, representing the Sociedade d'Agricultura Colonial, who made all necessary arrangements. The Portuguese Government dispensed with any customs examination of the baggage.” Further on he writes: “We were advised that the prospects of clear sky at the end of May were not very good, but that the best chance was on the north and west of the island. After inspecting two other sites on the property of the Sociedade d'Agricultura Colonial, we fixed on Roça Sundy, the headquarters of Sr. Carneiro's chief plantation. We were Sr. Carneiro's guests during our whole visit, and used freely his ample resources of labour and material at Sundy. We learnt later that he had postponed a visit to Europe in order to entertain us. We were also greatly indebted to his manager at Sundy, Sr. Atalaya, with whom we lived for five weeks; his help and attention were invaluable.” At Principe, an island with few people, they were received with great sympathy and treated as celebrities and science stars that they were.
The eclipse day was arriving and there are some nice stories to tell.
4.2. The day
In Sobral there are several photographs taken by the Brazilian astronomers, the two American geophysicists from Carnegie, and the two Britons. One of the photographs shows the the three teams, Brazilian, American, and British, posing together, see Fig. 29.
The three eclipse teams, Brazilian, British, and American, at Igreja do Patrocinio, Sobral. From left to right: Luiz Rodrigues, Theophilo Lee, Daniel Wise from Carnegie, Henrique Morize, Charles Davidson, Andrew Crommelin, Allyrio de Mattos, Andrew Thomson from Carnegie, Domingos da Costa, Lélio Gama, Antônio Lima, and Primo Flores. Courtesy from Observatorio Nacional, Rio de Janeiro.
In the Jockey race course, in front of the Saboya house in which Crommelin and Davidson stayed, it was mounted the two telescopes that would serve to make the light deflection observations. There was a 4 inch telescope and a 13 inch astrographic telescope, see Fig. 30 and Fig. 31. Since to mount anew a heavy telescope with all its accessories is a difficult task, each telescope was coupled to a coelostat, a device commonly used in eclipses to maintain the telescope rigid. It consists of a mirror that reflects the sky field to the telescope itself and turns slowly with the sky so that the image on the telescope is static. The coelostat was conceived by Lippmann in 1895, a French physicist that got the Nobel Prize in 1908 for inventing color photography.
The Jockey race course in Sobral with the tents and the instruments of the Carnegie team and the British tent. The British tent is closed and can be seen as a small square on the left corner. The Saboya house where the British and Americans stayed is the pleasant nice looking spacious loft house on the middle left. Courtesy of the Carnegie Institute.
Left: The British tent closed. The Saboya house is in the background. Compare with the previous photograph. Right: The British tent opened with the two telescopes used by Crommelin and Davidson, the 4 inch telescope on the right and the 13 inch astrographic telescope on the left, together with the respective ceolostats. The telescopes are pointing eastward as the eclipse was to be at 9:00am. Courtesy of the Royal Greenwich Observatory.
The eclipse in Sobral was in the morning at 9:00am, see Fig. 32 for a representation. Davidson in the report writes[37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920).: “As totality approached, the proportion of cloud diminished, and a large clear space reached the sun about one minute before second contact.” Then further on he says, “The region round the Sun was free from cloud, except for an interval of about a minute near the middle of totality when it was veiled by thin cloud, which prevented the photography of stars, though the inner corona remained visible to the eye and the plates exposed at this time show it and the large prominence excellently defined.” And then commenting on the after the eclipse, “On June 7, having completed the development, we left Sobral for Fortaleza, returning on July 9 for the purpose of securing comparison plates of the eclipse field.” So, Crommelin and Davidson developed the plates, were happy to leave for Fortaleza, capital of Ceará, to enjoy life on the beaches, and went back to Sobral to get comparison plates by photographing, the eclipse field that 7 weeks after the eclipse could be seen at night before dawn, as the Earth's translation, or equivalently the Sun's annual movement along the ecliptic, modifies slightly but surely the sky, night after night.
A view from the top of the Earth, Moon, Sun system yielding an eclipse at 9:00am local time in Sobral.
Indeed, the Sun moves about 1 degree per day on the ecliptic, so that 365 days after it is back in the same position. The stars in the celestial sphere stay fixed in the same place. Now, 24 hours is equivalent to 360 degrees, which means that 1 degree per 24 hours is equivalent to (24/360) =(1/15) hours, i.e., 4 minutes. Since this small 1 degree movement of the Sun is in the same sense of the Earth's rotation, it means that each day the Sun will be delayed 4 minutes per day relative to the fixed stars, for instance the stars of the eclipse. Now, the eclipse in Sobral was at 9:00am, thus in order that the Sun is sufficiently delayed to rise at 6:00am and the eclipse stars are in the same position and can now be seen just before dawn, one has to have a lag of 3 hours, i.e., 180 minutes, which is achieved in (180 minutes)/(4 minutes/day) = 45 days, i.e., about 6 and a half weeks. This is consistent with the 7 weeks that the British astronomers took to return Sobral, where they arrived on July 9.
Crommelin and Davidson left Sobral on July 22 and arrived back in Greenwich on August 25. A report on Sobral is also given in [38][38] A.S. Eddington, Space, Time, and Gravitation: An Outline of the General Relativity Theory (Cambridge University Press, Cambridge, 1920).. For details of the Sobral stay, stories, results, and history see [46[46] R.R.F. Mourão, A Teoria da Relatividade (Editora Tecnoprint, Rio de Janeiro, 1987). [47] R.R.F. Mourão, Einstein: de Sobral para o Mundo (Editora Universidade Estadual Vale do Acaraú, Sobral, 2003). [48] L.C.B. Crispino and M.C. de Lima, Physics in Perspective 18, 379 (2016). [49] L.C.B. Crispino, International Journal of Modern Physics D 27, 1843004 (2018). [50] L.C.B. Crispino and M.C. de Lima, Revista Brasileira de Ensino de Física 40, e1601 (2018). [51] L.C.B. Crispino and D.J. Kennefick, Nature Physics 15, 416 (2019).–52[52] J. Mota Rodrigues, Entre Telescópios e Potes De Barro: Expedições Científicas do Eclipse Solar na Comprovação da Teoria da Relatividade em Sobral-CE 1919 (Appris Editora, Curitiba, 2019).].
In Principe, incredibly, there are no photos to tell the story in pictures. Surely, Eddington and Cottingham forgot to take a camera with them. The eclipse in Principe was in the afternoon at 2:00pm, see Fig. 33 for a representation. The hour difference between Sobral and Principe is three hours, so taking that into account, the Principe totality had a lag of about two hours in relation to the totality in Sobral, as is clearly seen in the two figures, Fig. 32 and Fig. 33. These were old times, and certainly they would have liked to communicate via teleconference or otherwise, but could not.
A view from the top of the Earth, Moon, Sun system yielding an eclipse at 2:00pm local time in Principe.
Although no photographs were taken in situ in Principe, the expedition is well documented by Eddington, both in the 1920 report [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920). and in his book Space, Time, and Gravitation, published also in 1920 [38][38] A.S. Eddington, Space, Time, and Gravitation: An Outline of the General Relativity Theory (Cambridge University Press, Cambridge, 1920).. In the book he states, “On the day of the eclipse the weather was unfavourable. When totality began the dark disc of the Moon surrounded by the corona was visible through cloud, much as the Moon often appears through cloud on a night when no stars can be seen. There was nothing for it but to carry out the arranged programme and hope for the best. One observer was kept occupied changing the plates in rapid succession, whilst the other gave the exposures of the required length with a screen held in front of the object-glass to avoid shaking the telescope in any way.” And immediately after he says in a poetic tone, “We are conscious only of the weird half-light of the landscape and the hush of nature, broken by the calls of the observers, and beat of the metronome ticking out the 302 seconds of totality”. Yet, he writes [38][38] A.S. Eddington, Space, Time, and Gravitation: An Outline of the General Relativity Theory (Cambridge University Press, Cambridge, 1920)., “Sixteen photographs were obtained, with exposures ranging from 2 to 20 seconds.” Eddington then after reducing one plate made the necessary measurements, and not going mad after all, told Cottingham that he would not have to go alone [17][17] A.S. Eddington, in: Background to Modern Science, edited by J. Needham and W. Pagel (Cambridge University Press, Cambridge, 1940), p. 117.. In Eddington's notebook it is written [14][14] A. Vibert Douglas, Arthur Stanley Eddington (Thomas Nelson and Sons, London, 1956).: “June 3. We developed the photographs, 2 each night for 6 nights after the eclipse, and I spent the whole day measuring. The cloudy weather upset my plans, and I had to treat the measures in a different way from what I intended, consequently I have not been able to make any preliminary announcement of the result. But the one plate that I measure gave a result agreeing with Einstein.” As Eddington referred to it, this was “the most exciting event I recall in my own connection with astronomy” [17][17] A.S. Eddington, in: Background to Modern Science, edited by J. Needham and W. Pagel (Cambridge University Press, Cambridge, 1940), p. 117.. This echoes Einstein's words about the discovery of the principle of equivalence that it “was the happiest thought of my life”, see e.g. [11][11] A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein (Oxford University Press, Oxford, 1982)..
Since the eclipse had been at 2:00pm in Principe, in order that the Sun is rising at 6:00am and the eclipse stars are in the same position and can be seen before dawn, one has to have a lag of 8 hours, i.e., 480 minutes, which is achieved in (480 minutes)/(4 minutes/day) = 120 days, i.e. about 4 months.
So there was no point in staying that long, and after revealing some initial plates and reducing a few, they decided to march back on June 12, transhipped at Lisbon, and arrived in Liverpool on July 14. For details of the Principe stay, stories, results, and history see [53[53] P. Crawford, Revista Colóquio Ciências da Fundação Calouste Gulbenkian 16, 3 (1995). [54] P. Crawford and A. Simões, Gazeta de Física 32, 22 (2009). [55] E. Mota, A. Simões and P. Crawford, British Journal for the History of Science 42, 245 (2009). [56] A. Simões, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 4.–57[57] P. Crawford, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 8.].
4.3. Data analysis
As soon as the two expeditions arrived back in England the analysis of the data started. Dyson joined Crommelin and Davidson and they were busy analyzing the Sobral plates at the Royal Greenwich Observatory. Eddington in Cambridge was putting full effort in the analysis of the Principe plates. The analyses by the two teams were independent.
In Sobral there were two telescopes. There was the small aperture, 4 inch telescope, handled by Crommelin, that was taken on recommendation by Cortie as a back up, and that proved to be essential. There was the main astrographic telescope maneuvered by Davidson, with aperture of 13 inches that was reduced to 8 inches to get better images. The two telescopes can be seen clearly in Fig. 31. In Sobral, with the 4 inch telescope 8 plates were taken with 7 stars visible during the 5 minute and 13 seconds eclipse, see Fig. 34. With the astrographic telescope, 19 photographic plates were obtained with 12 stars visible on them. Crommelin and Davidson then took photographs of the same field in the night sky seven weeks later and got the comparison night plates.
Photograph of the field of stars in the 1919 eclipse by the 4 inch telescope in Sobral. Courtesy of The Royal Greenwich Observatory.
In Principe, Eddington and Cottingham used only one telescope, an astrographic telescope similar to Sobral's with its aperture also reduced to 8 inches coupled to a coelostat. Here, 16 plates were obtained, of which only 7 had stars, as the sky had a tenuous variable nebulosity at the time of the eclipse, with 6 stars well visible, see Fig. 35 for a glimpse. Eddington was able to develop immediately some photographic plates and in reducing one managed to measure the full shift, confirming general relativity. After returning to Cambridge he analyzed the other plates and in the end only two plates were of worth and 5 stars were used. No comparison night plates were taken in Principe and this obliged Eddington to solve the problem in a different way.
Having the photographic plates with the stars in the environment of the eclipsed Sun, one had now to quantify the shift in the stars' positions due to the gravitational field of the Sun. The procedure is similar to the measurement of stellar parallaxes and star proper motions in photographic plates and so was well-known. The snag here is that in an eclipse setting one is not at home, where all the equipment works well and at prescribed times, and moreover, the eclipse runs for a very short slot of time, of about five minutes. Another difficulty is that the maximum value for the displacement is for a star at the Sun's rim. However, stars at the rim are rare and not bright enough to be seen, the light from the corona shines them out. Thus, the stars observed in an eclipse are relatively far from the rim, say two times or more further away, and the star's displacement has a lower value in accordance to the hyperbolic 1/D law of Eq. (3). In order to see what is at stake, we note that the 1.75 arcseconds gravitational shift at the Sun's rim means, for the type of telescopes used, about 0.03mm in the plate, and for a star at three solar radius the gravitational shift is 0.58 arcseconds, about 0.01mm in the plate. Let us now look, in a nutshell, how both teams reduced the data to find the shift due to the gravitational field of the Sun.
Suppose one has eclipse plates and comparison night plates. To find the shifts of the stars one has to put the two plates together. In theory, one needs one star, one eclipse plate, and one comparison night plate only. If all is perfect, one measures the star's position in the comparison night plate, then measures the star's position in the eclipse plate, subtracts, and gets immediately the star's shift. But, in practice, there are many more things involved. There is mismanagement when putting the two plates together. The plates could be slightly translated and rotated in relation to each other without notice. Also, more importantly there could be a change of scale on one plate relatively to the other. This change in scale comes from a change in the location of the focus on the eclipse day and location of the focus on the comparison night day that might appear due to variations of temperature or some other factors. One then makes a rectangular grid on the plates and assigns an x and y position for each star in the comparison night plate. We follow closely, but not exactly, the report of 1920 [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920)., see [40][40] H. von Klüber, Vistas in Astronomy 3, 47 (1960). and also [42][42] D.F. Moyer, in: On the Path of Albert Einstein, edited by A. Perlmutter and L.F. Scott (Plenum Press, New York, 1979), p. 55.. By comparing in both plates the positions of the same star, the shifts and for that star can be obtained, see Fig. 36.
An equation for the displacement and for each star can be written as,
where c and f are translation shifts that can come from some anomaly in the clamping of the two plates, b and d are rotational shifts that can also come from the clamping of the two plates, a and e give the differences in scale value between the two plates, and and yield the light deflection, with . The form of the and terms comes from the 1/D dependence. Indeed, as the gravitational shift is proportion to 1/D, the respective shift in the x direction is proportional to and the respective shift in the y direction is proportional to , where here is the angle between the x direction and the radial direction associated to the radius D. One has four unknowns for Eq. (4) in , namely, c, b, a, , and four unknowns for Eq. (5) in , namely, f, d, e, . To solve the equations one needs a minimum of four stars. If one has n stars with then the system is overdetermined and one resorts to a least squares method. Now, one sees that a and scale both with x, and e and scale both with y, which can bring difficulties in the disentangling of a and and of e and . But, moreover, whereas the scaling increases the shift relative to the center, the gravitational effect decreases the shift relative to the center, and at some distance D they can be of the same order, possibly increasing the difficulties. On the other hand, since the gravitational effect obeys the 1/D law, stars far from the Sun, if there are any on the plates, have a negligible deflection and can in principle be used to set comparison points when the plates are matched. Further corrections that have to be taken into account are atmospheric refraction and aberration since the eclipse and comparison plates are taken at different dates and times of day. Also, turbulence in Earth's atmosphere makes the stars scintillate and effectively produces random deflection of the light from the stars which can be nonneglible as compared to the gravitational effect. Nevertheless this effect is random and balances to zero for a sufficient number of stars. The analysis of the random and systematic errors in the measurements then follow standard procedures.
The Sobral team, now enlarged to be the Greenwich team with the inclusion of Dyson to help in the data analysis, having eclipse plates, comparison night plates, and an intermediary scale plate to insure faithful comparison, did not bother with the scale problem. They simply solved Eqs. (4) and (5) to get c, f, b, d, a, e, and then finally the gravitational shift through and .
The Principe team, essentially Eddington, as Cottingham being an instrument maker could not help in the analysis, did not get comparison night plates, the eclipse had been at 2:00pm and the eclipse star field would appear before dawn, on the night sky, four months later only. Eddington managed to solve the scale change problem because photographs of another star field were taken months earlier. In fact, two different star fields in some January nights in Oxford were photographed. The photographs were made with the astrographic telescope that went to the eclipse, which belonged to Oxford. One star field that was photographed in Oxford was the star field that would pop in the eclipse day in Principe, called the comparison night field. The other star field that was photographed in Oxford was a given chosen star field, the check field. This check field was then also photographed in Principe nights in May. All this trouble was to take precautions against any change on the lens on the trip and to take care of systematic errors that could derive from the distinct conditions at Oxford and Principe. In the end the check field plates were essential in the analysis. This was because there were no sufficient stars to provide the data necessary to find the constants in Eqs. (4) and (5) and pick up in the end the pursued and . The check plates would thus function as appropriate for systematic error determinations as well as to settle the constants in Eqs. (4) and (5). Indeed, by applying Eqs. (4) and (5) to the two check field plates, without the and terms as there was no gravitational deflection for the check field, Eddington managed to get a and e for the scale change in an independent manner. He then compared the eclipse field in Principe with the comparison night field of Oxford, knowing beforehand the scale change factors a and e. Going then back to Eqs. (4) and (5) with a and e known, and correcting for refraction and aberration, he could determine and in an ingenious manner. This method, using several complementary layers to obtain the final result, was invented by Eddington by necessity and proved to be useful and used in other eclipses.
4.4. Results
After the return to England of the British teams, people interested in general relativity and positional astronomy started to get impatient. Certainly, the most anxious of all was Einstein. In September he inquired Dutch colleagues if there were developments from the eclipse expeditions. Then, just after, Lorentz hearing that Eddington had claimed in a meeting that the results indicated some amount of gravitational light deflection but could not tell yet the precise values, immediately sent a telegram to Einstein with the good news, see Fig. 37. Einstein jubilated. In that same day he wrote to his mother: “Good news today. H. Lorentz sent me a telegram saying that the British expeditions confirmed definitely the light deflection by the Sun.” Sometime later he then states his famous phrase when the student of philosophy Ilse Schneider asks what he would say if the eclipse results were otherwise, not confirming his predictions: “I would have to be sorry for the dear Lord. The theory is correct”, see e.g. [10][10] R.W. Clark, Einstein, the Life and Times (Avon Books, New York, 1971)..
Lorentz telegram to Einstein in September 22, 1919, stating “Eddington found stellar shift at solar limb, tentative value between nine-tenths of a second and twice that.”
The analysis at the Royal Greenwich Observatory and Cambridge, made along the lines already described, was performed from August to October. Eventually, on Thursday, November 6, 1919, in a joint meeting of the Royal Society and the Royal Astronomical Society, at the Royal Society with a room completely crowded, the results of the two expeditions were announced. J.J. Thomson, the man of the electron and the President of the Royal Society, opened the session.
The word was then passed to Dyson and Crommelin as representants of the Sobral expedition and of the Royal Greenwich Observatory analysis. They stated that the 4 inch telescope had 7 very good stars and the result for the angle of deflection by the gravitational field of the Sun at its rim was
Dyson then declared about the plates and the reduction process [36][36] J.J. Thomson, Observatory 42, 388 (1919).: “I am prepared to say that there can be no doubt that they confirm Einstein's prediction. A very definite result has been obtained that light is deflected in accordance with Einstein's law of gravitation.” Dyson and Crommelin also said that the 13 inch astrographic telescope system did not work properly, the stars' images were diffused and to explain this there were two possibilities, either the telescope was out of focus or it simply blurred the images. This had happened probably because the coelostat heated and in consequence mal-functioned. If it was assumed that there was a change of focus due to the mal-function and the eclipse plates were used to determine the scale, in the way mentioned above, then the value for the deflection was 0.98 arcseconds. If it was assumed that the stars were simply blurred with no change of scale and no mal-function of the telescope system then the value was 1.40 arcseconds. Thus, being hard to trust the astrographic telescope, the Royal Greenwich Observatory team decided to discard its results.
Then Eddington spoke on the Principe outcome [36][36] J.J. Thomson, Observatory 42, 388 (1919).. He said that the Principe 13 inch astrographic telescope and coelostat functioned well, admittedly because the temperature was not too high due to the cloudy veil. He stated that there were five good stars and the result for the angle of deflection by the gravitational field of the Sun at its rim was
He then interpreted the results. For the half effect Newtonian gravitation would be the correct theory. The full effect had been obtained and so gravitation obeys the law proposed by Einstein. He mentioned that the new law had already incorporated Mercury's perihelion precession and spoke of the possibility of detecting in the future the gravitational redshift in the surface of the Sun predicted by the law.
Then J. J. Thomson raised to the occasion and said [36][36] J.J. Thomson, Observatory 42, 388 (1919).:, “This is the most important result obtained in connection with the theory of gravitation since Newton's day, and it is fitting that it should be announced at a meeting of the Society so closely connected with him.” The moment was echoed by the philosopher Whitehead some years later musing about the meeting. He wrote [39][39] A.N. Whitehead, Science and the Modern World (The Macmillan Company, New York, 1925)., “in the background the picture of Newton to remind us that the greatest of scientific generalisations was now, after more than two centuries, to receive its first modification.” And then, “a great adventure in thought had at length come safe to shore.”
All the details of the data analysis and results of the two expeditions were then written down in the report of January 1, 1920 [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920). with Dyson, Eddington, and Davidson as authors. Why Crommelin was not an author in the report has not been explained. He led the Sobral expedition, he was in charge on the day of the 4 inch telescope that yielded the good data, he was in the data reduction process, he talked in the historical joint meeting of November 6, he published papers on the eclipse before and after the eclipse, but in the most important paper, the 1920 report, he is not an author. In concluding, the report states in the end that [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920). “In summarising the results of the two expeditions, the greatest weight must be attached to those obtained with the 4-inch lens at Sobral”. This judgement is certainly because the error of the results in Sobral were arcseconds whereas in Principe they were , two and a half times larger, and so admittedly less reliable.
It has often been said that the conclusion, that Einstein's theory has been proved on the 1919 eclipse observations by the two expeditions, has been taken on shaky data and shaky grounds, see, e.g., [43][43] J. Earman and C. Glymour, Historical Studies in the Physical Sciences 11, 49 (1980).. The last figure of the 1920 report [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920). plots gravitational shift due to light deflection versus the inverse distance from the center of the Sun 1/D, with , where R is the Sun's radius. Three straight lines popping from the origin (, i.e., ) are given in that figure. The lower straight line, the less inclined dotted line, is for the Newtonian prediction, the middle heavy line is for the Einstein prediction, and the upper straight line is for the observations carried on the two sites. This upper straight line, does not match the Einstein prediction, yields in fact values for the deflection along the 1/D abscissa that are slightly higher than the Einstein prediction. Thus, the maximum that one could say was that (i) no deflection is ruled out, (ii) Newtonian gravitation with light coupling to it is ruled out, and (iii) general relativity might be correct, which could only be tested by future observations. The authors nevertheless claim [37][37] F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920)., “Thus the results of the expeditions to Sobral and Principe can leave little doubt that a deflection of light takes place in the neighbourhood of the sun and that it is of the amount demanded by Einstein's generalised theory of relativity, as attributable to the sun's gravitational field.”
So, on what evidence and with what arguments could one say that Einstein's theory had been proved in 1919? There are several. First, Newtonian gravitation could no more be upheld on fundamental principles. By then it was known to some that the world was relativistic and the velocity of propagation of any signal was finite contradicting on its face Newton's law of gravitation where the propagation of the gravitational field is instantaneous, and thus its speed of propagation is infinite. Moreover the concept of mass was no more invariant, mass of a particle would change depending on the observer bringing further complications to Newton's laws. Second, Einstein had mounted a theory based on solid principles, namely, special relativity principles, the equivalence principle, the covariance principle, and the metric principle which states that the world is described by a spacetime metric, as Minkowski prescribed. Third, as soon as the theory was about to be ready, Einstein calculated Mercury's perihelion precession and found 43 arcseconds per century, the amount that was lacking in Newtonian gravitation, a problem without solution for decades. This is astonishing, as the conceptually complex theory, as general relativity is, when applied to the concrete problem of the trajectory of planets, has in its kernel and essence, the precise amount required by the data. However, wonderful as it was, this precession was an a posteriori confirmation, not an apriori prediction, and thus confirmation of new general relativistic predictions were necessary. Fourth, and finally, there was indeed the general relativistic definite prediction of 1.75 arcseconds for the light deflection by the gravitational field of the Sun.
Given that the eclipse data was surely on the full deflection side, it was clear that general relativity had been favored by a great margin, and that the other two possibilities, no deflection for the case light does not interact with gravitation, or half deflection for the case Newtonian gravitation was the correct theory and light coupled to it, had been ruled out, see also [45][45] D. Kennefick, No Shadow of a Doubt: The 1919 Eclipse that Confirmed Einstein's Theory of Relativity (Princeton University Press, New Jersey, 2019).. Moreover, given the other three points raised above, it was obvious, especially for a theorist that Eddington was, that the measurements had confirmed general relativity. Or in other words, it was highly probable given the four points above that general relativity was correct. One could think on extensions of general relativity which could include electromagnetism on its fundamental level, as Eddington was already thinking at this time, drawing on work by the German physicist and mathematician Hermann Weyl, but these extensions in principle would not affect the general relativistic light deflection result at least at some zeroth order level. Therefore Dyson and Eddington were right in betting without further ado on general relativity. With humor it is said that the 1919 data did not prove that Einstein was right, Dyson and Eddington did. It is also frequently quoted that Eddington said that he did not need to go to Principe to prove general relativity since he was fully convinced of the truth of the theory [41][41] S. Chandrasekhar, Notes and Records of the Royal Society of London 30, 249 (1976)..
Interestingly, the analysis of the plates and data from Sobral was repeated with all the new modern available techniques by Harvey from the Royal Greenwich Observatory in 1979 [58][58] G.M. Harvey, Observatory 99, 195 (1979)., which having passed unnoticed to Hawking [59][59] S.W. Hawking, A Brief History of Time, from the Big Bang to Black Holes (Bantam Books, New York, 1988)., elicited a comment by Wayman and Murray [60][60] P.A. Wayman and C.A. Murray, Observatory 109, 189 (1989).. The reanalysis revealed for the 4 inch object glass the value arcseconds, and for the 13 inch object glass the value arcseconds. The 4 inch telescope yielded trivially about the same results with less error, the the 13 inch telescope had, after all, utilizable data that gave results in harmony with the other telescopes. All is well that ends well. Unfortunately, most of Principe plates and Eddington's reductions inexplicably disappeared from the Observatories in Cambridge, probably into the litter, after Eddington's death.
4.5. History
The war had finished a year before, and there were still bitter feelings among the belligerent countries. This confirmation of the light deflection had international relevance. German science was being shun by the British and this event gave a hope to stop the ban on the Germans as was the desire of Eddington, a pacifist in character. The scientific cooperation was an example for all the world to see, that British science represented by the two eclipse expedition teams had confirmed a completely new and profound theory of gravitation proposed by a scientist on the other side. On the top of the scientific achievement many appreciated this peace effort accomplishment.
History had been done. The newspapers knew that and announced with jubilation the achievement of the observations which, in turn, spurred a huge enthusiasm from the public at large.
The major journals of England immediately reverberated the accomplishment of its scientists. General relativity was held as the new theory of gravitation and of the Universe. The Times of London, revealed the results in November 7, one day after the joint meeting of the two royal societies, writing shortly afterwards an article with the title “Revolution in science: The ideals of Aristotle, Euclides, and Newton, that are the basis of our conceptions, do not correspond to what can be observed in the structure of the universe”. In the USA, the New York Times announced the results in November 10, the O Jornal from Rio de Janeiro, in November 12, and the O Jornal O Século, from Lisbon, gave the information in November 15. The Illustrirte Zeitung from Berlin wrote in December 14, “A new celebrity in the world history: Albert Einstein, whose investigations lead to a complete revision of our concepts about Nature and are at the same level of those of Copernicus, Kepler, and Newton”. The German journalist forgot to include Galileu but that is another matter.
Einstein was acclaimed instantaneously. Up to then he was known as an outstanding theoretician within a circle of physicists working in areas related to his works. The announcement of the 1919 eclipse results catapulted him to celebrity. Indeed, Einstein's biographies [10[10] R.W. Clark, Einstein, the Life and Times (Avon Books, New York, 1971). [11] A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein (Oxford University Press, Oxford, 1982).–12[12] A. Pais, Einstein Lived Here (Oxford University Press, Oxford, 1994).] highlight the results of the Sobral and Principe expeditions. For instance the biography by Clarke [10][10] R.W. Clark, Einstein, the Life and Times (Avon Books, New York, 1971). opens a chapter of the biography stating “In the morning of November 7, 1919, Einstein woke up in Berlin as a famous man.” From that day onwards he became a world figure and started to be invited to all places around the planet.
As an example of his voyages, in March 11, 1925, on the way to Brazil, Argentina, and Uruguay, the ship he was travelling in stopped in Lisbon for two days. He visited the Castle of São Jorge, a fascinating site whose initial fortifications date back to the first century, and the Monastery of Jerónimos, a wonderful late Gothic Manueline style construction of 1500, but he was really impressed with the varinas, fisher women in downtown Lisbon, annotating in his onboard diary, “A fisher woman selling fish, photographed with a fish basket, proud gesture, naughty”. In Lisbon, nobody noticed his passage, in spite of being very famous by now; on the top of the 1919 eclipse results hype, he had already received the 1921 Nobel Prize in Physics [61][61] A.J.S. Fitas, e-Journal of Portuguese History 3, 2 (2005).. Perhaps this can be justified by the political turmoil the country was in. Mira Fernandes, a leading Portuguese mathematical physicist, working in Lisbon at Instituto Superior Técnico, was at this time starting to get interested in general relativity and in the ideas of unification of gravitation and electromagnetism [62[62] J.P.S. Lemos, in Proceedings of the 12th Marcel Grossmann Meeting on General Relativity - MG12, edited by R. Jantzen et al. (World Scientific, Singapore, 2012), p. 1745. [63] J.P.S. Lemos, in: Aureliano Mira Fernandes, edited by L. Saraiva and J.T. Pinto (Boletim da Sociedade Portuguesa de Matemática, Lisbon, 2010), p. 147.–64[64] J.P.S. Lemos, Gazeta de Física 34, 27 (2011).]. He was most probably not aware of Einstein's stay in the capital, otherwise he would have invited Einstein to give a talk or at least to meet him. He compensated this failure somehow by, under his suggestion, having Einstein together with Levi-Civita, elected as foreigner correspondents of the Lisbon Academy of Sciences in 1932, a year before Einstein left Berlin to Princeton. Interestingly, on the day following this election, March 18, 1932, the newspaper Pittsburgh Press announced this ceremony. Also, Santos Lucas, a professor of mathematics in the Faculty of Sciences of Lisbon, would have liked to meet Einstein in his passage in 1925. He had dedicated a whole semester to a course in general relativity, where the light deflection phenomenon is treated with rigor, surely one of the first courses in general relativity in the world [65][65] A. Santos Lucas, Lições sobre a Teoria da Relatividade: Apontamentos de Física-Matemática de António dos Santos Lucas Compilados por Francisco de Paula Leite Pinto (Manuscript edition from the author, Lisbon, 1922-1923)., see also [64][64] J.P.S. Lemos, Gazeta de Física 34, 27 (2011).. Much later, in 1946, António Gião, a physicist based in Lisbon, with works in general relativistic cosmological solutions and unification schemes, corresponded with Einstein, a fact he was very proud of [64][64] J.P.S. Lemos, Gazeta de Física 34, 27 (2011).. After leaving Lisbon the ship where Einstein was headed for Rio de Janeiro where he arrived in March 21, 1925, for a three day visit. He then proceeded to Buenos Aires to give a series of lectures in the university, continued to Montevideo, and passed again in Rio, where he now delivered lectures in several places, visited Henrique Morize in Observatorio Nacional in May 9, and socialized with high authorities. Finally, he returned to Hamburg on May 12. Einstein's visit in Rio is well documented, see e.g., [66[66] I.C. Moreira and A.A.P. Videira, Einstein e o Brasil (Editora Universidade Federal Rio de Janeiro, Rio de Janeiro, 1995)., 67[67] A.T. Tomasquim, Einstein: o Viajante da Relatividade na América do Sul (Vieira & Lent, Rio de Janeiro, 2003).].
As for Eddington he also became a figure not only in scientific circles, but in larger public circles, from 1919 onward. The 1919 events, of which he was the exponent, transformed the scene, signaling to the world the importance of general relativity as the correct theory of gravitation. How important was luck in all of this? As usual luck plays a part. Of course, sooner or later, general relativity would be vindicated, some eclipse would show the correctness of general relativity, but this one was spectacular and surely Eddington played the major role in its magnificentness. His influence was vast and profound. For instance, Dirac was so impressed by the inspiring 1919 eclipse test that he moved from Bristol to Cambridge to study relativity with Cunningham but ended up being a student of Fowler to work on quantum mechanics [68][68] D.F. Moyer, American Journal of Physics 49, 944 (1981)., see also [42][42] D.F. Moyer, in: On the Path of Albert Einstein, edited by A. Perlmutter and L.F. Scott (Plenum Press, New York, 1979), p. 55..
In 1930 Einstein finally went to Cambridge. He and Eddington corresponded along the years after the eclipse confirmation and Eddington invited Einstein to visit Cambridge. Fortunately a photograph of both was taken, see Fig. 38. It says all, two happy men posing for posterity.
Einstein and Eddington in front of the main building of the Observatories, in Madingley Road, Cambridge, in June 1930.
In the 1920s through to the 1930s general relativity was taken by mathematical works. Perhaps, the great exception is the work of Oppenheimer and Snyder of 1939 that discovered black holes by proving mathematically their existence [69][69] J.R. Oppenheimer and H. Snyder, Physical Review 56, 455 (1939).. Oppenheimer was aware of his discovery and that black holes were real [70][70] K.S. Thorne, Black Holes and Time Warps, Einstein's Outrageous Legacy (W.W. Norton and Company, New York, 1994)., but couldn't care less, he understood it as a minor contribution [71][71] F. Dyson, American Mathematical Monthly 103, 800 (1996)., an amazing fact on several grounds. This year we are thus also celebrating eighty years of black holes. The name black hole itself appeared only later through the hand of Wheeler [72][72] C.A.R. Herdeiro and J.P.S. Lemos, Gazeta de Física 41, 2 (2018).. Then after the second world war, in the 1950s, a renaissance of general relativity back into physics took place [73][73] J. Eisenstaedt, The Curious History of Relativity: How Einstein's Theory of Gravity Was Lost and Found Again (Princeton University Press, New Jersey, 2006)., with Wheeler and his group in Princeton where at its beginning Einstein was an inspirational figure still around, with Hoyle, Sciama, Penrose, Hawking, and Carter in Cambridge, surely in Eddington's tradition, and with Zel'dovich and his group in Moscow [74][74] W. Israel, in: 300 Years of Gravitation, edited by S.W. Hawking and W. Israel (Cambridge University Press, Cambridge, 1987), p. 198.. General relativity is now taught in most, if not all, undergraduate courses in physics. Books in general relativity abound and the student can learn relatively quickly this discipline. To cite some, there is the book of Eddington [75][75] A.S. Eddington, The Mathematical Theory of Relativity (Cambridge University Press, Cambridge, 1923)., a masterpiece, there is the book by Adler, Bazin, and Schiffer [76][76] R. Adler, M. Bazin and M. Schiffer, Introduction to General Relativity (McGeaw-Hill, New York, 1965)., written in 1965 and still a marvelous book in its modernity, there is the book by Weinberg [77][77] S. Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley, New York, 1972)., of 1972, with the calculations done in a beautiful way and with an emphasis on cosmology, carefully treating all its mathematical and physical aspects, there is the book by Misner, Thorne and Wheeler, Gravitation [78][78] C. Misner, K.S. Thorne and J.A. Wheeler, Gravitation (Freeman San Francisco, 1973)., written in 1973, an extraordinary treatise up-to-date in its approach and encompassing subjects, there is the book by Wald with advanced topics [79][79] R.M. Wald, General Relativity (University of Chicago Press, Chicago, 1984)., there is the book by D'Inverno [80][80] R. d'Inverno, Introducing Einstein's Relativity (Clarendon Press, Oxford, 1992)., that made general relativity a very easy subject to teach and learn, and there are others excellent books, e.g., [81[81] J. Plebański and A. Krasiński, An Introduction to General Relativity and Cosmology (Cambridge University Press, Cambridge, 2006)., 82[82] L. Ryder, Introduction to General Relativity (Cambridge University Press, Cambridge, 2009).].
Nowadays, general relativity is basic to understand the whole cosmos and its functioning, from cosmology to black holes, to gravitational waves, to gravitational lensing, to other disciplines, all are products of general relativity.
5. Post eclipse and the future
There is a long list of expeditions to eclipses to test the light deflection prediction by general relativity following the 1919 eclipse. We name a few. Campbell, after two failed attempts was desperate to get results. So, he took from the Lick Observatory all the necessary paraphernalia with 35 tons of equipment, to land in Wallal beach, in west Australia. It was September 21, 1922, and the weather was fine when the Moon darkened the Sun. Later he would report that the measurements gave arcseconds for the deflection angle, confirming general relativity's prediction right on target. It has been considered the best determination of the light deflection in an eclipse of the Sun. Other expeditions went to observe this eclipse, some were rain washed others got good results [40][40] H. von Klüber, Vistas in Astronomy 3, 47 (1960).. Freundlich, who together with Einstein had started all this business, had had permanent bad luck. In 1914 he was made prisoner in Crimea, in 1922 he chose Christmas Island, the wrong site, as it rained on the day, in 1923 he got rain in Mexico, in 1926 in Sumatra once again it rained, and finally in 1929 also in Sumatra the weather was fine, the measurement gave a deflection considerably greater then general relativity's prediction, 2.2 arcseconds [40][40] H. von Klüber, Vistas in Astronomy 3, 47 (1960)., and nobody else believed in it. A team from Austin, Texas, that included the relativists Bryce DeWitt, Cecile DeWitt, and Richard Matzner, organized an expedition to the Mauritania desert, for the eclipse of June 30, 1973. They witnessed a dust storm just before the eclipse, but even so they managed to find from the emulsion plates a light deflection of arcseconds [83][83] R.A. Brune, C.L. Cobb, B.S. DeWitt, C. DeWitt-Morette, D.S. Evans, J.E. Floyd, B.F. Jones, R.V. Lazenby, M. Marin, R.A. Matzner et al., Astronomical Journal 81, 452 (1976)., see also [19][19] M. Littmann, F. Espenak and K. Willcox, Totality: Eclipses of the Sun (Oxford University Press, Oxford, 2008).. In present times, amateur astronomers with high expertise on telescopes and optics, in possession of CCD cameras, can test the light deflection from the Sun, as was done by Bruns in the August 21, 2017, eclipse in Wyoming, USA, obtaining 1.7512 arcseconds for the deflection [84][84] D.G. Bruns, Classical and Quantum Gravity 35, 075009 (2018)..
The light deflection tests have improved in many directions. One is in gravitational lensing. Since a gravitational field deflects light it can act as a gravitational lens, in which case the light rays from behind the gravitational field source converge at the observational point. Light deflection from stars behind the Sun does not produce a lens at Earth, the light rays are not enough deflected to form a lens. Lensing is thus a special, though abundant, case of light deflection. Einstein in 1913 thought that stars themselves might be gravitational lenses of other stars, but found the effect negligible and opted for not publishing it until much later when in 1936 he was pressed to disclose these calculations. Just after, Zwicky, a Swiss astronomer working in Caltech that had several other influential insights, showed that the lensing effect was non negligible for galaxies and clusters of galaxies acting as gravitational deflectors of light coming behind them from, e.g., another galaxy or another cluster of galaxies. The effect was confirmed in 1979 when two quasars with the same properties were identified as one single quasar for which its light was suffering lensing from an intervening galaxy. Today, these lensing effects are detected all over, see Fig. 39, where an example of an Einstein ring is displayed in full glory. Gravitational lensing serves to measure the mass of the galaxy responsible for the effect as well as giving a measure for the dark energy that is responsible for the acceleration of the Universe [85][85] P. Schneider, C. Kochanek and J. Wambsganss, Gravitational Lensing: Strong, Weak and Micro (Springer Verlag, Berlin, 2006).. Gravitational lensing in cosmology will be done by the ESA mission Euclid and the NASA mission WFIRST, both of them designed to set constraints on the physics of the dark energy [86][86] I. Tereno, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 43.. Currently, black holes and accretion disks provide strong field light deflection and lensing, called black hole shadows, as the Event Horizon Telescope has showed, see e.g. [87][87] J.P.S. Lemos, C.A.R. Herdeiro and V. Cardoso, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 36..
Wonderful light deflection. A blue galaxy appearing several times along a ring is being lensed by a cluster of galaxies. Courtesy of the Hubble Space Telescope - NASA.
Another direction in which gravitational light deflection is proving important is optical astrometry. The ESA satellites, Hipparcus and Gaia, measured star positions up to milliarcsecond and microarcsecond precision, respectively. Gaia, still in operation, is measuring the positions of billions of stars. These positions have to to be corrected for the light deflection from the Sun, Jupiter, and other planets, as the measurements are so precise that without the corrections the star sky mapping would be incorrect, see, e.g., [88[88] M. Perryman, Astronomical Applications of Astro-metry Ten Years of Exploitation of the Hipparcos, Satellite Data (Cambridge University Press, Cambridge, 2009)., 89[89] M. Perryman, D.N. Spergel and L. Lindegren, Astrophysical Journal 789, 166 (2014).].
Yet another direction for light deflection is with the use of radio telescopes which can measure positions with great precision. Shapiro, an American astrophysicist that proposed the gravitational time delay, an effect that bears some relation to gravitational light deflection, also had the idea of testing gravitational deflection, but using radio waves and radio telescopes instead of light, by bouncing those waves back off an inner planet of the solar system when the Sun and the planet are in a correct alignment with the Earth [90][90] I.I. Shapiro, Science, 157, 806 (1967).. Radio wave interferometry to test light deflection proved to be much more effective by the use of quasars, objects at cosmological distances, many emit strongly in the radio. The quasars are fixed in the celestial sphere and some of them are in the plane of the ecliptic. When, as seen from the Earth, the Sun passes in front of such a quasar its angular separation from another quasar in a nearby place in the ecliptic changes due to the gravitational light deflection effect. A value that has been obtained is 1.75 arcseconds with a very small residual error [91[91] D.E. Lebach, B.E. Corey, I.I. Shapiro, M.I. Ratner, J.C. Webber, A.E.E. Rogers, J.L. Davis and T.A. Herring, Physical Review Letters 75, 1439 (1995)., 92[92] E. Fomalont, S. Kopeikin, G. Lanyi and J. Benson, Astrophysical Journal 699, 1395 (2009).], again in perfect accord with general relativity. The precision on the position of radio quasars is so great that it is now possible to measure the deflection due to the Sun of the radio waves emitted from quasars that are reasonably far from the Sun in the celestial sphere and even to measure the deflection due to the stars in our Galaxy of radio waves emitted from those quasars [93][93] M.V. Sazhin, V.E. Zharov, T.A. Kalinina and V.N. Sementsov, Astronomy Reports 62, 1026 (2018)..
The initial criticisms against general relativity soon died away, and instead a few physicists started to consistently build, after 1919, new theories of gravitation grounded in great part on the ideas of general relativity. Now, there is a plethora of such theories, and due to all the high precision in the optical and the radio telescopes, as well as due to gravitational wave detection, one can now test alternative theories to general relativity. All these alternative or modified theories of gravitation can be parameterized through the parameterized post-Newtonian, or PPN, formalism [94][94] C.M. Will, Living Reviews in Relativity 17, 4 (2014).. And so slowly and surely we will know at which level general relativity will go astray.
We end by coming back to the start. Mercury's precession, gravitational redshift, gravitational light deflection, and the gravitational time delay, were tests possible to do within the solar system and all have all confirmed general relativity. The gravitational redshift has found a direct technological application in the GPS, as to work properly with all its clocks synchronized the effect has to be taken into account. Gravitational light deflection has as a particular case gravitational lensing which serves to measure masses of the intervening objects and as a tool for cosmology. Cosmology, the study of the Universe as a whole, has showed that the Universe is in accelerated expansion. Fundamental theories, that started with tentative unifications of gravitation and electromagnetism, by Weyl, Eddington, and Einstein, continued to be pursued, now they are called theories of everything and try to unify the four fundamental fields in a unique quantum scheme. Black holes, the geometrical object par excellence of general relativity, can now be seen through spectacular light deflection, called black hole shadows, and also provide a tool to probe quantum gravity through the Hawking radiation effect. Gravitational waves, or spacetime waves, predicted by Einstein in 1916, have been detected directly in 2015 by LIGO and were generated by the collision of two black holes. In brief, general relativity has so far provided a great adventure that has been thoroughly enjoyable. Is the end in sight? Not yet.
6. One hundred years after: The 2019 celebrations
The year 2019 marks the one hundred years of the light deflection observations and consequent confirmation of general relativity. Given the historical character of this date several celebrations have been organized.
In Sobral there was a scientific conference and a public event from May 26 to May 31, 2019, that certainly lived up to the importance of the discovery, see [95][95] I.C. Moreira, in: Einstein, Eddington, Eclipse, editado por A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 32..
In Principe there was a scientific conference “From Einstein and Eddington to LIGO: 100 years of gravitational light deflection” with the main aim of celebrating such an important date with worldwide experts to reflect on the legacy left by Einstein and Eddington and to discuss the subsequent startling developments in the fields of astrophysics and gravitation, namely, black holes, gravitational waves, gravitational lensing, and cosmology. The meeting was held from May 26 to May 30, 2019, the webpage of it is https://science.esundy.tecnico.ulisboa.pt/en/, and the organizers were Vitor Cardoso, Carlos Herdeiro, and the author of this article. There was a public event at Roça Sundy on May 30, exactly one hundred years after the eclipse, see http://esundy.org/index.php/en/homepage/ and [96][96] J. Latas, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 30.. Sobral and Principe got together on May 29 on a videoconference where scientific and political personalities congratulated each other for this special moment. A special number of the Portuguese journal Gazeta de Física has been issued to celebrate the events in Sobral and Principe [97][97] A.J.S. Fitas, P. Crawford and J.P.S. Lemos, Einstein, Eddington, Eclipse (Gazeta de Física, Lisbon, 2019)..
Finally, in London there was a public evening event on November 6, 2019, organized by the Royal Astronomical Society to celebrate the one hundred years of the announcement of the results of the light deflection by Dyson, Crommelin, Davidson, and Eddington that confirmed Einstein's theory of gravitation.
Acknowledgments
I thank Nelson Studart for having invited me to write this article to the special number commemorating the 100 years of the eclipse in the prestigious journal Revista Brasileira do Ensino de Física of which he is editor.
I thank Júlio Fabris from Vitória-ES, Nelson Pinto Neto and Santiago Perez Bergliaffa from Rio de Janeiro, and Vilson Zanchin from São Paulo, for, on the understanding of the significant importance of the event, having organized on short notice a great scientific conference on the eclipse and general relativity in Sobral, which was the symmetric part of the scientific conference organized by us in Principe, and for very many conversations on general relativity and cosmology. I thank Ildeu Castro Moreira, President of the Sociedade Brasileira para o Progresso da Ciência SBPC and organizer of the main public event in Sobral, for all the help in the setting of the major videoconference across the Atlantic between Sobral and Principe, on May 29, 2019, eclipse times, celebrating the 100 years on the spot, that involved scientists and politicians from both sites, and also for conversations on the eclipse.
I thank Emerson Almeida, of University of Vale do Acaraú in Sobral, for, in February 2019, showing me all the important places where the expedition teams were located and made the observations, and for inviting me to give a colloquium on the eclipse in the university with a participation of more than 200 students. I thank Luis Carlos Crispino of Belém do Pará for many conversations on the Sobral eclipse, in particular for pressing me, and for that matter all the world, that Sobral of Crommelin, Davidson, and Dyson, has to have the same importance in the news as Principe of Eddington. I thank Claudio Bastos of Observatorio Nacional of Rio de Janeiro for many conversations on astronomy and astrophysics and on the eclipse.
I thank all my group CENTRA at IST Lisbon, for the support in the organization of the Principe scientific conference “From Einstein and Eddington to LIGO: 100 years of gravitational light deflection”, realized in May 26-30, 2019, Sérgio Almeida of CENTRA for the help in the administration of the conference's webpage, and Dulce Conceição of CENTRA for handling all the administrative processes for the conference. I thank our colleague Luis Viseu Melo, in charge of the IST finances, for simplifying the necessary internal procedures. I thank the conference coorganizers Vitor Cardoso and Carlos Herdeiro for all the good atmosphere created in the preparation of this event. I thank Phillipe Moreau and Beatriz Geraldes of HBD for assisting with great sympathy in the logistics of the conference in the resort Roça Bom Bom, and the manager Nuno Santos for all the help at the resort. I thank Joana Latas of NUCLIO for the help she gave in the arrangements for a smooth interface between the scientific activities in Roça Bom Bom and the general activities in Roça Sundy and in providing infrastructure for the videoconference between Sobral and Principe on May 29, 2019, eclipse times.
I thank André Ferreira Freitas from São Tomé for inviting me to give a seminar by teleconference on May 29, 2018, for the 99 years of the eclipse, for the students of the Portuguese School of São Tomé e Principe. I thank Paulo Crawford and Ana Simões of Faculdade de Ciências, Lisbon, for many conversations on the history of the eclipse and, together with Augusto Fitas, for the teamwork in the preparation of the special number of Gazeta de Física dedicated to Einstein, Eddington, and the eclipse. I thank Ismael Tereno of Faculdade de Ciências, Lisbon, for many conversations on the physics and astronomy of the 1919 eclipse and on gravitational lensing. I thank Ana Mourão and Ilidio Lopes of CENTRA and IST, Lisbon, for allowing me to speak on the 1919 eclipse and general relativistic light deflection in the stimulating XXIX Astronomy and Astrophysics National Meeting in Lisbon in September 2019, and Amaro Rica da Silva of CENTRA and IST, Lisbon, for the many conversations on eclipses and light deflection, in particular in helping in the light deflection drawing of Fig. 25. I thank David Hilditch of CENTRA and IST for conversations on the eclipse. I thank Diogo Bragança, MSc student at CENTRA and IST three years ago, now in Stanford finishing his PhD, for the careful reading of the manuscript.
I thank Donald Lynden-Bell, my PhD supervisor in the Institute of Astronomy, Cambridge, for the many enlightening conversations on physics and astrophysics, and on Eddington. He was a greater admirer of Eddington. In the Observatories he occupied what had been the famous Eddington's office with a curved door. Our conversations were usually there, and sometimes, weather permitted, in front of the main building where Einstein and Eddington took the photograph.
I thank António Luciano Videira, my MSc thesis supervisor in PUC-Rio de Janeiro, for allowing me to study what I wanted: black holes; and also through reading, studying and conversation, putting me in direct connection with Wheeler's tradition, and thus with Einstein and Oppenheimer, as well as with the works of Penrose, Hawking, and Carter.
In July 11, 1991, there was an eclipse that would end in Amazonia, Brazil, after passing through the Pacific Ocean, Hawaii, Mexico, Guatemala, Nicaragua, Costa Rica, Panama, and Colombia. I was in my first job in Observatorio Nacional, Rio de Janeiro, and being a general relativist thought opportune to test general relativity once again through light deflection. I start some demarches but soon I got stuck. I could not find financial support and several people, notably Antares Kleber of Observatorio Nacional, convinced me that it was a too risky enterprise, as the probability of rain in Amazonia was high, the eclipse would be in the end of the afternoon, and it was too difficult to find good instruments to be carried to the site, CCDs were not yet around in the corner shop. So I did not go and did not thought about it again until today.
I thank Fundação para a Ciência e Tecnologia (FCT), Portugal, for financial support through Grant No. UID/FIS/00099/2019.
Referências
-
[1]A. Einstein, Jahrbuch der Radioaktivität und Elektronik 4, 411 (1907).
-
[2]A. Einstein, Annalen der Physik 35, 898 (1911).
-
[3]A. Einstein and M. Grossmann, Zeitschrift für Mathematik und Physik 62, 225 (1914).
-
[4]A. Einstein, Naturforschende Gesellschaft in Zürich 58, 284 (1914).
-
[5]A. Einstein, Naturforschende Gesellschaft in Zürich 59, IV (1914).
-
[6]A. Einstein, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 831 (1915).
-
[7]A. Einstein, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, 844 (1915).
-
[8]A. Einstein, Annalen der Physik 49, 769 (1916).
-
[9]J. Renn and M. Schemmel, The Genesis of General Relativity (Springer, Dordrecht, 2007).
-
[10]R.W. Clark, Einstein, the Life and Times (Avon Books, New York, 1971).
-
[11]A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein (Oxford University Press, Oxford, 1982).
-
[12]A. Pais, Einstein Lived Here (Oxford University Press, Oxford, 1994).
-
[13]A.S. Eddington, Biographical Memoirs of Fellows of the Royal Society 3, 159 (1940).
-
[14]A. Vibert Douglas, Arthur Stanley Eddington (Thomas Nelson and Sons, London, 1956).
-
[15]C.W. Killmister, Eddington's Search for a Fundamental Theory: A Key to the Universe (Cambridge University Press, Cambridge, 1994).
-
[16]M. Stanley, Practical Mystic: Religion, Science, and A. S. Eddington (University of Chicago Press, Chicago, 2007).
-
[17]A.S. Eddington, in: Background to Modern Science, edited by J. Needham and W. Pagel (Cambridge University Press, Cambridge, 1940), p. 117.
-
[18]V.D. Barger and M.G. Olsson, Classical Mechanics, a Modern Perspective (McGraw-Hill, New York, 1994).
-
[19]M. Littmann, F. Espenak and K. Willcox, Totality: Eclipses of the Sun (Oxford University Press, Oxford, 2008).
-
[20]T. Nordgren, Sun, Moon, Earth: The History of Solar Eclipses from Omens of Doom to Einstein and Exoplanets (Basic Books, Philadelphia, 2016).
-
[21]L.A. Bauer, Science 51, 301 (1920).
-
[22]J.G. von Soldner, Berliner Astronomisches Jahrbuch, 161 (1801).
-
[23]S.L. Jaki, Foundations of Physics 8, 927 (1978).
-
[24]R. McCormmach, British Journal for the History of Science 4, 126 (1968).
-
[25]N.A. Doughty, Lagrangian Interaction (Addison-Wesley, New York, 1990).
-
[26]C.D. Perrine, Astronomische Nachrichten 219, 281 (1923).
-
[27]J. Stachel, in: The Prism of Science, edited by E. Ullmann-Margalit (Boston Studies in the Philosophy of Science, Boston, 1986), p. 225.
-
[28]A. Warwick, Masters of Theory: Cambridge and the Rise of Mathematical Physics (University of Chicago Press, Chicago, 2003).
-
[29]A.S. Eddington and C. Davidson, Monthly Notices of the Royal Astronomical Society 73, 386 (1913).
-
[30]A.F. Lindemann and F.A. Lindemann, Monthly Notices of the Royal Astronomical Society 77, 140 (1916).
-
[31]A.S. Eddington, Report on the Relativity Theory of Gravitation (Fleetway Press, London, 1918).
-
[32]F.W. Dyson, Monthly Notices of the Royal Astronomical Society 77, 445 (1917).
-
[33]A.C.D. Crommelin, Nature 102, 444 (1919).
-
[34]A.S. Eddington, Observatory 42 119 (1919).
-
[35]A.C.D. Crommelin, Observatory 42, 368 (1919).
-
[36]J.J. Thomson, Observatory 42, 388 (1919).
-
[37]F.W. Dyson, A.S. Eddington and C. Davidson, Philosophical Transactions of the Royal Society A 220, 291 (1920).
-
[38]A.S. Eddington, Space, Time, and Gravitation: An Outline of the General Relativity Theory (Cambridge University Press, Cambridge, 1920).
-
[39]A.N. Whitehead, Science and the Modern World (The Macmillan Company, New York, 1925).
-
[40]H. von Klüber, Vistas in Astronomy 3, 47 (1960).
-
[41]S. Chandrasekhar, Notes and Records of the Royal Society of London 30, 249 (1976).
-
[42]D.F. Moyer, in: On the Path of Albert Einstein, edited by A. Perlmutter and L.F. Scott (Plenum Press, New York, 1979), p. 55.
-
[43]J. Earman and C. Glymour, Historical Studies in the Physical Sciences 11, 49 (1980).
-
[44]C.M. Will, Classical and Quantum Gravity 32, 124001 (2015).
-
[45]D. Kennefick, No Shadow of a Doubt: The 1919 Eclipse that Confirmed Einstein's Theory of Relativity (Princeton University Press, New Jersey, 2019).
-
[46]R.R.F. Mourão, A Teoria da Relatividade (Editora Tecnoprint, Rio de Janeiro, 1987).
-
[47]R.R.F. Mourão, Einstein: de Sobral para o Mundo (Editora Universidade Estadual Vale do Acaraú, Sobral, 2003).
-
[48]L.C.B. Crispino and M.C. de Lima, Physics in Perspective 18, 379 (2016).
-
[49]L.C.B. Crispino, International Journal of Modern Physics D 27, 1843004 (2018).
-
[50]L.C.B. Crispino and M.C. de Lima, Revista Brasileira de Ensino de Física 40, e1601 (2018).
-
[51]L.C.B. Crispino and D.J. Kennefick, Nature Physics 15, 416 (2019).
-
[52]J. Mota Rodrigues, Entre Telescópios e Potes De Barro: Expedições Científicas do Eclipse Solar na Comprovação da Teoria da Relatividade em Sobral-CE 1919 (Appris Editora, Curitiba, 2019).
-
[53]P. Crawford, Revista Colóquio Ciências da Fundação Calouste Gulbenkian 16, 3 (1995).
-
[54]P. Crawford and A. Simões, Gazeta de Física 32, 22 (2009).
-
[55]E. Mota, A. Simões and P. Crawford, British Journal for the History of Science 42, 245 (2009).
-
[56]A. Simões, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 4.
-
[57]P. Crawford, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 8.
-
[58]G.M. Harvey, Observatory 99, 195 (1979).
-
[59]S.W. Hawking, A Brief History of Time, from the Big Bang to Black Holes (Bantam Books, New York, 1988).
-
[60]P.A. Wayman and C.A. Murray, Observatory 109, 189 (1989).
-
[61]A.J.S. Fitas, e-Journal of Portuguese History 3, 2 (2005).
-
[62]J.P.S. Lemos, in Proceedings of the 12th Marcel Grossmann Meeting on General Relativity - MG12, edited by R. Jantzen et al. (World Scientific, Singapore, 2012), p. 1745.
-
[63]J.P.S. Lemos, in: Aureliano Mira Fernandes, edited by L. Saraiva and J.T. Pinto (Boletim da Sociedade Portuguesa de Matemática, Lisbon, 2010), p. 147.
-
[64]J.P.S. Lemos, Gazeta de Física 34, 27 (2011).
-
[65]A. Santos Lucas, Lições sobre a Teoria da Relatividade: Apontamentos de Física-Matemática de António dos Santos Lucas Compilados por Francisco de Paula Leite Pinto (Manuscript edition from the author, Lisbon, 1922-1923).
-
[66]I.C. Moreira and A.A.P. Videira, Einstein e o Brasil (Editora Universidade Federal Rio de Janeiro, Rio de Janeiro, 1995).
-
[67]A.T. Tomasquim, Einstein: o Viajante da Relatividade na América do Sul (Vieira & Lent, Rio de Janeiro, 2003).
-
[68]D.F. Moyer, American Journal of Physics 49, 944 (1981).
-
[69]J.R. Oppenheimer and H. Snyder, Physical Review 56, 455 (1939).
-
[70]K.S. Thorne, Black Holes and Time Warps, Einstein's Outrageous Legacy (W.W. Norton and Company, New York, 1994).
-
[71]F. Dyson, American Mathematical Monthly 103, 800 (1996).
-
[72]C.A.R. Herdeiro and J.P.S. Lemos, Gazeta de Física 41, 2 (2018).
-
[73]J. Eisenstaedt, The Curious History of Relativity: How Einstein's Theory of Gravity Was Lost and Found Again (Princeton University Press, New Jersey, 2006).
-
[74]W. Israel, in: 300 Years of Gravitation, edited by S.W. Hawking and W. Israel (Cambridge University Press, Cambridge, 1987), p. 198.
-
[75]A.S. Eddington, The Mathematical Theory of Relativity (Cambridge University Press, Cambridge, 1923).
-
[76]R. Adler, M. Bazin and M. Schiffer, Introduction to General Relativity (McGeaw-Hill, New York, 1965).
-
[77]S. Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley, New York, 1972).
-
[78]C. Misner, K.S. Thorne and J.A. Wheeler, Gravitation (Freeman San Francisco, 1973).
-
[79]R.M. Wald, General Relativity (University of Chicago Press, Chicago, 1984).
-
[80]R. d'Inverno, Introducing Einstein's Relativity (Clarendon Press, Oxford, 1992).
-
[81]J. Plebański and A. Krasiński, An Introduction to General Relativity and Cosmology (Cambridge University Press, Cambridge, 2006).
-
[82]L. Ryder, Introduction to General Relativity (Cambridge University Press, Cambridge, 2009).
-
[83]R.A. Brune, C.L. Cobb, B.S. DeWitt, C. DeWitt-Morette, D.S. Evans, J.E. Floyd, B.F. Jones, R.V. Lazenby, M. Marin, R.A. Matzner et al., Astronomical Journal 81, 452 (1976).
-
[84]D.G. Bruns, Classical and Quantum Gravity 35, 075009 (2018).
-
[85]P. Schneider, C. Kochanek and J. Wambsganss, Gravitational Lensing: Strong, Weak and Micro (Springer Verlag, Berlin, 2006).
-
[86]I. Tereno, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 43.
-
[87]J.P.S. Lemos, C.A.R. Herdeiro and V. Cardoso, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 36.
-
[88]M. Perryman, Astronomical Applications of Astro-metry Ten Years of Exploitation of the Hipparcos, Satellite Data (Cambridge University Press, Cambridge, 2009).
-
[89]M. Perryman, D.N. Spergel and L. Lindegren, Astrophysical Journal 789, 166 (2014).
-
[90]I.I. Shapiro, Science, 157, 806 (1967).
-
[91]D.E. Lebach, B.E. Corey, I.I. Shapiro, M.I. Ratner, J.C. Webber, A.E.E. Rogers, J.L. Davis and T.A. Herring, Physical Review Letters 75, 1439 (1995).
-
[92]E. Fomalont, S. Kopeikin, G. Lanyi and J. Benson, Astrophysical Journal 699, 1395 (2009).
-
[93]M.V. Sazhin, V.E. Zharov, T.A. Kalinina and V.N. Sementsov, Astronomy Reports 62, 1026 (2018).
-
[94]C.M. Will, Living Reviews in Relativity 17, 4 (2014).
-
[95]I.C. Moreira, in: Einstein, Eddington, Eclipse, editado por A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 32.
-
[96]J. Latas, in: Einstein, Eddington, Eclipse, edited by A.J.S. Fitas, P. Crawford and J.P.S. Lemos (Gazeta de Física, Lisbon, 2019), p. 30.
-
[97]A.J.S. Fitas, P. Crawford and J.P.S. Lemos, Einstein, Eddington, Eclipse (Gazeta de Física, Lisbon, 2019).
Publication Dates
-
Publication in this collection
13 Dec 2019 -
Date of issue
2019
History
-
Received
23 Sept 2019 -
Accepted
27 Sept 2019