Abstracts
Most of the Brazilian bridges of federal road network are made of reinforced concrete and are more than 30 years old, with little information about the mechanical properties of their constitutive materials. Along the service life of these bridges much modification occurred on vehicles load and geometry and in design standard. Many of them show signs of concrete and steel deterioration and their stability conditions are unknown. With the aim of contributing to the structural evaluation of reinforced concrete bridges it was decided to analyze the stresses in reinforced concrete bridge sections to verify the effects due to reinforcement corrosion and variation of the concrete Young modulus on the stress distribution regarding several load patterns and cracking effects in a representative bridge of the Brazilian road network with different longitudinal reinforcement taxes and two concrete Young modulus, Ec and 0.5Ec, and with different percentage of reinforcement corrosion. The analysis considered two finite element models: frame and shell elements as well as solid elements. The results indicate that these variation effects are more significant in reinforcement bars than in concrete.
concrete bridges; reinforcement corrosion; stresses distribution
A maioria das pontes da malha de rodovias federais brasileiras é de concreto armado e tem idade superior a 30 anos, sendo escassas as informações sobre seus materiais constituintes e suas características mecânicas. Ao longo da vida útil dessas pontes ocorreram alterações de capacidade de carga e geometria dos veículos da frota circulante e alterações dos trens-tipo para o dimensionamento dessas estruturas. Muitas delas apresentam sinais perceptíveis de deterioração, tanto do concreto quanto da armadura, e não se conhece o grau de comprometimento dessas estruturas. Este trabalho pretende contribuir para a avaliação estrutural das pontes de concreto armado através da análise da variação da distribuição de tensões no concreto e na armadura, decorrentes da variação do módulo de elasticidade do concreto e da redução da taxa geométrica de armadura longitudinal por corrosão, em uma ponte representativa do estoque de pontes existentes. A análise foi feita com a utilização de dois modelos em elementos finitos, um com elementos de barras e cascas e outro com elementos sólidos, nos quais foram simuladas variações no módulo de elasticidade do concreto e diferentes condições de corrosão da armadura longitudinal das longarinas. Os resultados obtidos indicam que os efeitos da variação do módulo de elasticidade do concreto e da taxa geométrica de armadura são mais significativos nas tensões na armadura que no concreto.
pontes de concreto; corrosão da armadura; distribuição de tensões
Reinforced concrete bridges: effects due to corrosion and concrete young modulus variation
P. T. C. MendesI; M. L. T. MoreiraII; P. M. PimentaIII
IUniversidade Federal do Piauí, Depto. de Estruturas, Centro de Tecnologia, Coordenador de Engenharia Civil NOVAFAPI, paulo.tcm@uol.com.br , Campus da Ininga Teresina PI - Brasil CEP 64.049-550
IIUniversidade Federal do Piauí, Depto. de Estruturas, Centro de Tecnologia, mtmoreira@uol.com.br , Campus da Ininga Teresina PI Brasil CEP 64.049-550
IIIUniversidade de São Paulo, EPUSP, ppimenta@usp.br , Av. Prof. Almeida Prado, Trav. 2, 83, Cidade Universitária São Paulo SP Brasil CEP 05.508-900
ABSTRACT
Most of the Brazilian bridges of federal road network are made of reinforced concrete and are more than 30 years old, with little information about the mechanical properties of their constitutive materials. Along the service life of these bridges much modification occurred on vehicles load and geometry and in design standard. Many of them show signs of concrete and steel deterioration and their stability conditions are unknown. With the aim of contributing to the structural evaluation of reinforced concrete bridges it was decided to analyze the stresses in reinforced concrete bridge sections to verify the effects due to reinforcement corrosion and variation of the concrete Young modulus on the stress distribution regarding several load patterns and cracking effects in a representative bridge of the Brazilian road network with different longitudinal reinforcement taxes and two concrete Young modulus, Ec and 0.5Ec, and with different percentage of reinforcement corrosion. The analysis considered two finite element models: frame and shell elements as well as solid elements. The results indicate that these variation effects are more significant in reinforcement bars than in concrete.
Keywords: concrete bridges; reinforcement corrosion; stresses distribution.
1. Introduction
The research developed by Mendes [ 1 ] with information about 5.619 Brazilian bridges belong to Brazilian Federal Roads network allowed them to be characterized by age, dimension and the number of spans, structural systems, standard vehicle-load and the stability and durability conditions. The majority of these bridges are more than 30 years old, with no or little information about the mechanical characteristics of their materials. The changes occurred over time in the capacity and the geometry of the loads in the fleet of vehicles circulating, as well as the finding of the perceptible signs of the deterioration, both concrete as well as reinforcement of the bridges, conducted to an evaluation of the distribution of the stresses in the cross sections of the reinforced concrete bridges considering the effects of the variation of the module of elasticity of concrete and of the reinforcement corrosion.
The aim of this work is to contribute for structural evaluation in the reinforced concrete bridge through the analysis of the variation in the distribution of stresses in the concrete and in the reinforcement, resulting from the variation of the module of the elasticity of the concrete and of the reduction in the geometric longitudinal reinforcement ratio from corrosion, in a representative bridge from the stock of existing bridges.
In this work, a bridge with representative span and cross section existent on the Brazilian Federal Roads were analyzed, supposing different longitudinal reinforcement ratios, different configurations of reinforcement corrosion in each case and two values for the module of the elasticity of the concrete, Ec and 0.5Ec . The value of Ec was determined with the expression of NBR6118 [ 3 ] supposing a concrete with fck = 18.0 MPa. Due to the unknown real value of the strength characteristics of the older bridges and to consider the effect of the long-term deformation, opted to also consider the module of elasticity as half of Ec.
1.1 Justification of the adopted model
In Mendes [ 1 ] the distribution of bridges on the Federal roads by age group was obtained, highlighting the high number of bridges (41.2%) with unknown ages (Figure 1). Admitting that this sample is representative to the set, 70% of the bridges is more than 30 years old, from which naturally exists a significant growth in the pathologies [ 2 ]. It should be noted, however, that the bridges with unknown ages are probably the oldest ones, which will increase the percentage with more than 30 years old.
The large number of bridges for which are unknown (or not aware) the year of the construction constitutes only one sample of the difficulties found for a more detailed analysis of the existent situation and an evidence of little importance given to the register and treatment of the information.
Of the existing bridges on the Brazilian Federal Roads, 1,588 bridges had their structural systems not informed. Excluded bridges for which the structural system was not informed, 98% of the bridges are made of reinforced or prestressed concrete, in beam, slab or arc model (Figure 2).
From the total of bridges registered, 3,153 of them the vehicle-load adopted in the structural analysis is unknown (corresponding to 56% of the total number of bridges). Among the bridges which the vehicle-load is known, 642 were projected with standard vehicle-load of 240 KN (corresponding to 64%) and 237 were projected with standard vehicle-load of 450 KN (corresponding to 9.6%) (Figure 3). Probably most of non-informed bridges were analyzed with a 240 KN standard vehicle-load.
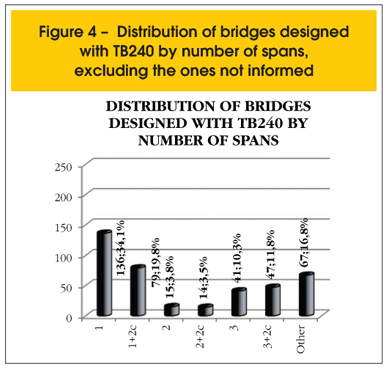
Among the 642 bridges projected with the 240 KN standard vehicle-load, there were no records of the spans for 243 of them. Figure 4 presents a distribution of the 399 bridges projected with 240 KN standard vehicle-load, by the number of spans, in which 54% of them are simply supported beam.
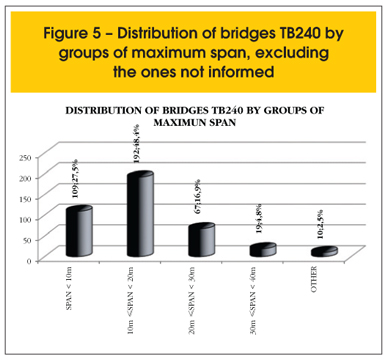
Among the 399 bridges projected with 240 KN standard vehicle-load with the number of spans known, two had the values of the spans not informed. Figure 5 presents the distribution of the 397 bridges projected with 240 KN standard vehicle-load, by bands of maximum spans emphasizing that 93% have maximum span inferior to 30.0 m and of these, 53.9% have only one span. Considering all the informed bridges, for all the standard vehicle-load, the percentage is practically the same (50%).
2. Characterization of models
In reason to the exposed, the representative adopted bridge for analysis is in simply supported beam by reinforced concrete, with a span of 20.0 m and with cross section dimensions according to Figure 6. For analysis effect concrete with fck = 18.0 MPa was admitted and reinforcement constituted of steel CA24 or CA50.
2.1 Computational models
The SAP2000-V11 program was used for the numerical evaluation of the bridge behavior. The first model consisted in the discretization of beams with finite elements of bar and the slabs with finite elements of shell (B-S), according to Figure 7. In this model, under bending moments acting on the longitudinal beams, the stresses on the concrete and in the reinforcement were obtained from the admission of Navier's hypothesis in maintenance of the plane section, in uncracked and cracked cross section, considering the resulting tensile in the reinforcement situated in its center of gravity. In the second model, the constituents of the superstructure of the bridge were discretizated with solid finite elements (SOL) representative of concrete and the different reinforced bars, with their mechanical characteristics, according to Figure 8. In this case the stresses in the concrete and in several bars of the reinforcement were provided directly by the program for each of the finite elements constituent to the model. For uncracked section was considered as a whole with perfect adherence between representative elements of concrete and the steel bars. For cracked section, the height of the neutral axis was estimated and the crack of the section was simulated with the removal of the concrete elements below the neutral axis in the vicinity of the cracks and in the other sections remained in the same conditions as in uncracked section.
2.2 Modulus of elasticity of concrete and steel
For the analysis of the models a module of elasticity on the concrete Ec = 23.8 GPa was adopted corresponding to the suggested value in the NBR 6118 [ 3 ].
Due to the scarcity of information relative to the mechanical characteristics of the concrete used on these bridges, it was chosen to analyze them considering the module of elasticity of the corresponding concrete at 50% of the Ec value with the objective of evaluating the influence of this factor in the distribution of the concrete and steel stresses. The module of elasticity of the steel was considered Es = 210.0 GPa.
2.3 Variation in the geometric reinforcement ratio
The geometric ratio of the longitudinal reinforcement of the beams was considered with the values of ρ1 = 3,78%, ρ2 = 3,22%, ρ3 = 2,68% and ρ4= 1,63%, corresponding to the possibility of details with the CA24 and the CA50 steel to various processes of design, according to Figure 9.
2.4 Configurations of corrosion
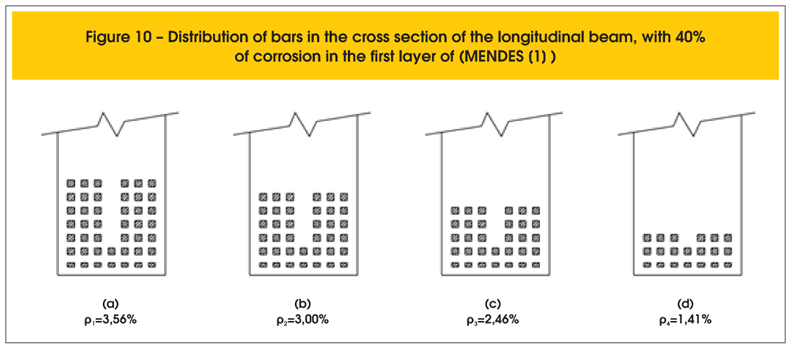
Taking into account the most frequently configuration of corrosion of the longitudinal reinforcement corresponds to the corrosion of the lower level of the bars, one opted to admit the reduction of the section of the bars in this layer in 40%and 100% according to Figures 10 and 11.
2.5 Loads
To analyze the designed bridges for the 240 KN standard vehicle-load (TB240), it was considered the dead loads and the 360 KN standard vehicle-load (TB360) of NB6 [ 4 ] and 450 KN standard vehicle-load (TB450) of NB6 [ 5 ], including the effect of the impact through the coefficient of impact φ.
3. Results of the analysis
3.1 Compressive stresses on the concrete cracking effect
For the models with elements of bar and shell (B-S), the maximum stress on the concrete , considered uniform along the width and the tensile stress in the reinforcement, determined in its center of gravity and both varying linearly along the height were obtained from the maximum bending moment and the geometric characteristics of the cross section [ 6 ].
In the model with solid elements, the longitudinal compression stress on the top of the flange varies considerably along the width of the flange, in the center of the elements from 1 to 12 indicated in Figure 12, depending on the type of applied load, as indicated in Figures 13 and 14 for load situations {DEAD} and {DEAD + φ.TB450} in uncracked section and Figures 15 and 16 in cracked section.
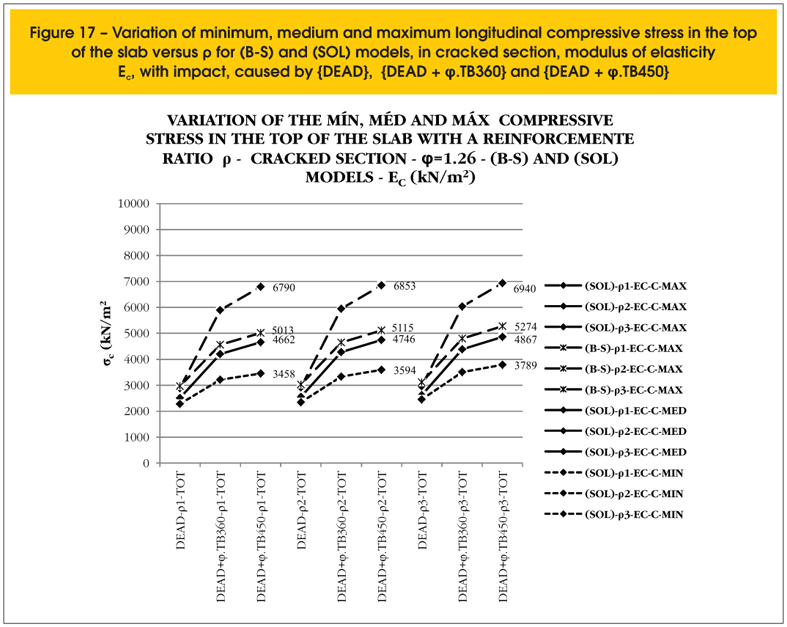
It is observed for the load {DEAD} that the maximum value of longitudinal compression stress on the top of the flange is 2,897 KN/m2 or 2.90 MPa (Figure 13), obtained with the uncracked section, and that in the most unfavorable load type, corresponding to the load combination {DEAD + φ.TB450}, the maximum value of longitudinal compression stress on the top of the flange is 6,790 KN/m2 or 6.79 MPa (figure 16), obtained with the cracked section. Therefore the maximum longitudinal compression stress varies between 2.90MPa and 6.79 MPa, with a section considered uncracked and cracked respectively.
It seems that the maximum compressive stress suffers an increase of 134.1% among the two extreme situations analyzed only load {DEAD} and uncracked section and load {DEAD + φ.TB450} with cracked section. However, considering the concrete with fck = 18.0 MPa the compressive stress varies from 16.1% to 37.7% of the characteristic compressive strength of concrete and from 22.6% to 52.8% of the design compressive strength of concrete. Considering the medium value on the top of the flange these percentages become from 13.6% to 25.9% of the characteristic compressive strength of concrete and from 19.0% to 36.3% of the design compressive strength of concrete, little significant take in account the strength of the material.
3.2 Compressive stress in concrete corrosion effect
Figures 17 and 18 present stress values of minimum, medium and maximum compressive stress on the top of the flange for each of the following situations:
-
Geometric reinforcement ratio equal to ρ
1 = 3.78%, ρ
2 = 3.22% and ρ
3 = 2.68% according to
-
Modulus of elasticity of concrete equal to E
c and 0.5.E
c;
-
Cracked section;
-
Models with bar and shell elements (B-S) and models with solid elements (SOL).
The variation of the reinforcement ratio of the section from ρ1 = 3.78% to ρ3 = 2.68% has little repercussion in the intensity of the maximum compressive stress, whose values vary from 6.79 MPa to 6.94 MPa, to the same modulus of elasticity of concrete Ec. A reduction of the modulus of elasticity of concrete from Ec to 0.5.Ec mobilizes a larger area of the compressive region of the section, which reduces the maximum values of the stresses that vary from 6.30 to 6.41 MPa.
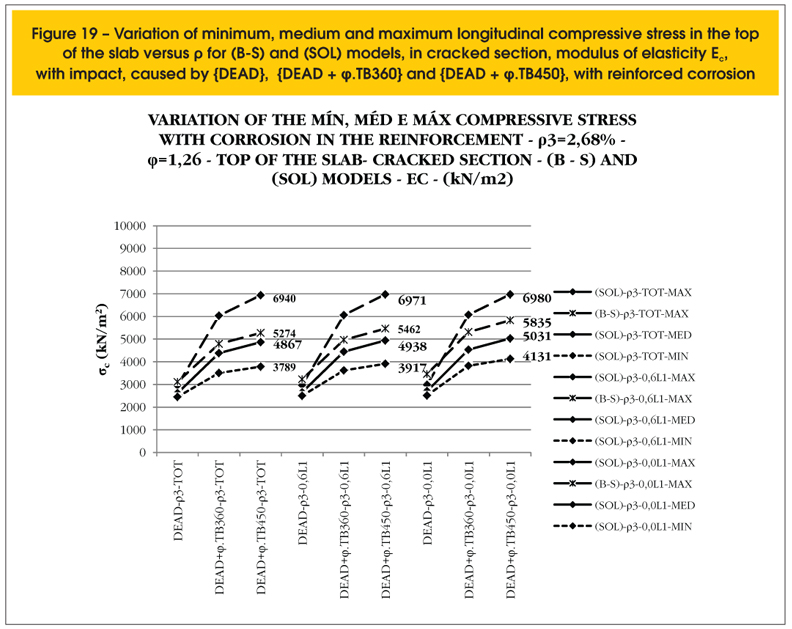
Figures 19 and 20 show the variations of minimum, medium and maximum compressive stresses in the top of the flange considering a longitudinal beam with geometric reinforcement ratio ρ3 = 2.68% variable with the corrosion, modulus of elasticity of concrete Ec and 0.5.Ec to the cracked section and load cases {DEAD}, {DEAD + φ.TB360} and {DEAD + φ.TB450}.
Considering the case of combination loads {DEAD + φ.TB450} the maximum compressive stress varies from 6.41 MPa (Figure 20) with non corroded reinforcement to 6.98 MPa (Figure 19) with the first layer totally corroded, for modulus of elasticity of concrete 0.5.Ec and Ec respectively, which indicates little influence on the corrosion of the reinforcement and modulus of elasticity of the concrete in the variation of intensity of these stresses.
3.3 The tensile stresses on the non corroded reinforcement
In the solid element model (SOL), the tensile stresses are supplied for each bar, which facilitates in the determination of the medium, maximum and minimum values, according to what is presented in Figures 21a and 22a, to the non cracked section, and 21b and 22b to the cracked section, corresponding to the loads {DEAD} and {DEAD + φ.TB450}.
One observe that the existence of cracks in the section completely changes the distributions of the stresses on the bars, making the more requested bar, that before the cracks belonged to the more distant layer of the neutral axis (L-1), becomes a bar situated in the nearest layer (L-7) arising from the stress redistribution due the presence of the crack and of the torsion effect of the positioning of the standard vehicle-load in the bridge. The deformation coming from the torsion provokes the warping of the section, invalidating the hypothesis of maintenance of the plane section.
Figure 23 presents the values of the medium stress on the reinforcement obtained with the models (B-S) and (SOL) in uncracked and in cracked sections, for the load {DEAD}. For cracked section the results obtained with the two models and different modules of elasticity are equivalent. For uncracked section, however, the values obtained with the two models are also equivalent but the variation of the modulus of elasticity has significant influence in the stress values, greater as smaller the modulus of elasticity of the concrete. Due to the symmetry of the {DEAD} load, the solicitant efforts are distributed equally between the two longitudinal beams, being applied approximately in its cross sectional principal planes, which explains the similarity of the results found for models (B-S) and (SOL).
Figure 24 presents the values of medium stresses on the reinforcement obtained from models (B-S) and (SOL) in uncracked section and in cracked section for the load {DEAD + φ.TB450}. The results present the same tendency, but the model (SOL) results are greater (inferior to 10%) than the model (B-S) results, attributed to the torsion effect of the positioning in the standard vehicle-load.
The convergence of the results obtained and presented in Figures 23 and 24 point to the pertinence of the models adopted.
In these figures markers in the form of asterisk relate to the models with bar and shell elements (B-S), while the markers in the form of a full rhombus relate to the models with solid elements (SOL). The full lines refer to uncracked section and the dashed lines to cracked section.
For the older bridges, built with CA-24 steel and reinforced ratio inferior to 2.68%, the reinforcement stress calculated in cracked section due to the actual standard vehicle-load TB450 exceeds the value of the design yield strength of reinforcement, signaling to the necessity of the strengthening structure.
3.4 Tensile stresses in the corroded reinforcement
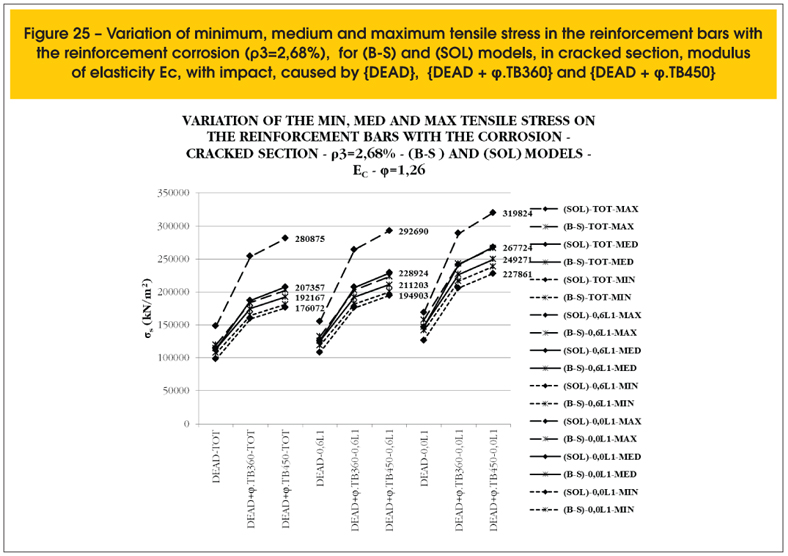
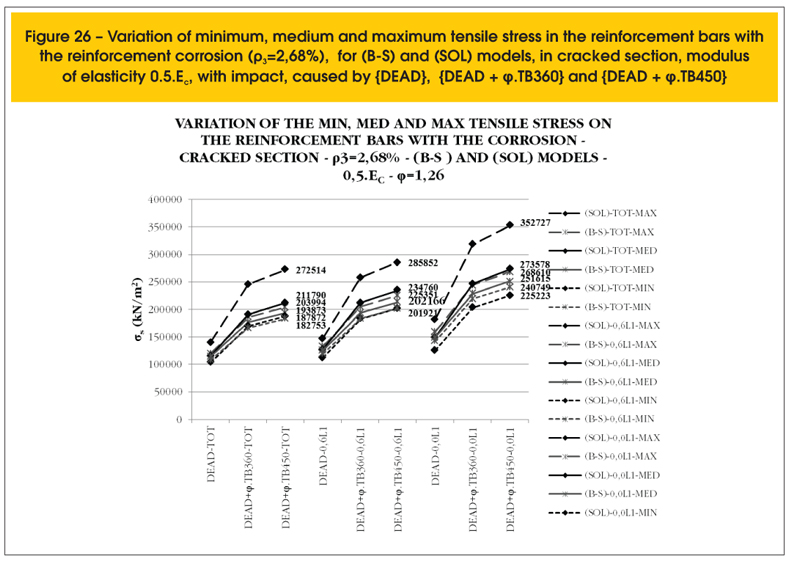
Figures 25 and 26 present the minimum, medium and maximum tensile stresses in the bars of the reinforcement for the conditions described in 3.2, with reinforcement ratio of 2.68% in cracked section. One observe the great difference between the reinforcement stresses for the (SOL) model compared with the difference obtained with the (B-S) model for each degree of reinforcement corrosion.
For the considered reinforcement ratio, for no corroded reinforcement, the stresses in the most solicited bar of the reinforcement due to the standard vehicle-loads TB360 and TB450 with the (SOL) model are greater than the design yield strength of reinforcement values designed with CA-24 steel, and this does not occur for the stresses obtained with the (B-S) model.
For the sections which the first layer of the reinforcement presents a corrosion of 40%, the tensile stresses on the most requested bars of the (SOL) model, obtained with the standard bridge-loads TB360 and TB450, are superior to the design yield strength of reinforcement CA-24 steel, which start to happen with the stresses obtained with the (B-S) model for the standard bridge-load TB450.
For the sections which the first layer of the reinforcement presents a corrosion of 100%, the tensile stresses on the most requested bars of the (SOL) model, obtained with the standard bridge-loads TB360 and TB450, are superior to the design yield strength of reinforcement CA-24 steel, which start to happen with the stresses obtained with the (B-S) model for the standard bridge-load TB360 and TB450.
Considering the case of load {DEAD + φ.TB450} and the modulus of elasticity Ec the maximum tensile stress varies from 280.88 MPa, with the no corroded reinforcement, to 319.82 MPa with the first layer totally corroded, which increases the stress intensity of 13.9% and decrease the reinforcement ratio of 20.9%, due to the total corrosion of the first layer. With the modulus of elasticity 0.5.Ec, the maximum tensile stress varies from 272.51 MPa, with a no corroded reinforcement, up to 352.73 MPa with the first layer totally corroded, corresponding to 29.4%. In these cases, the maximum stress of the bars exceeds the corresponding value of the design yield strength of CA24 steel, even considering the entire reinforcement, evidencing that these bridges do not obey the requirements imposed by the actual standard bridge-load.
4. Conclusions
With the above, one could conclude that the compression stresses on the concrete, coming from bending moment, had been little influenced by the cracking, by the variation of the modulus of elasticity of concrete and by the corrosion of the first layer of the reinforcement. In the worst situation, the highest level of the stress in the compressed concrete reached 37.7% of its arbitrated characteristic compressive strength or 52.8% of its design strength. For the older bridges, with strength of concrete in the same order of magnitude of the value arbitrated, the results obtained permit to conclude that the compressive stresses on the concrete are not a motive for major worries. For the new bridges, the requirements to their durability require the adoption of concrete with very high characteristic strength, which for the same levels of solicitations ensures a greater security reserve.
In relation to the tensile stress in reinforcement, on observe as expected a significant variation by the effect of cracking. The effect of the variation of the modulus of elasticity from Ec to 0.5.Ec in the cracked section, is not significant. The complete corrosion of the inferior layer of the reinforcement (L-1), with the reduction of the reinforcement ratio ρ3 = 2.68% in 20.9% raises the maximum stress value in the bars in 13.9% for the modulus of elasticity of concrete Ec and in 29.4% considering a reduction in the modulus of elasticity of concrete to 0.5.Ec .
From distributions of the stresses on the bars of the reinforcement in (SOL) model in the cracked section, one could conclude that an inadequate positioning of the deformation sensors in the reinforcement might not capture a real situation of the stresses on the bars, on the occasion of load tests or in the monitoring of the structures. This numerical finding suggests the realization of laboratory and field tests that sensors are adopted in all bars of the reinforcement of a same section, being adopted details of the execution that induces the occurrence of cracking in this section.
5. References
Received: 26 Sep 2011
Accepted: 19 Mar 2012
Available Online: 26 Jun 2012
- [01] MENDES, P. T. C.. Contribuições para um modelo de gestão de pontes de concreto aplicado à rede de rodovias brasileiras. Tese (Doutorado). Escola Politécnica da Universidade de São Paulo, São Paulo, 2009.
- [02] ASSOCIATION FRANÇAISE DE GÉNIE CIVIL AFGC. Concrete Design for a Given Structure Service Life. April, 2007. Paris, France.
- [03] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de Estruturas de Concreto - Procedimento. Rio de Janeiro: ABNT, 2007.
- [04] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NB 6: Carga Móvel em Pontes Rodoviárias. Rio de Janeiro: ABNT,1960.
- [05] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NB6: Carga Móvel em Ponte Rodoviária e Passarela de Pedestre. Rio de Janeiro: ABNT, 1982.
- [06] MENDES, P. T. C.. A influência da fissuração no comportamento das vigas de concreto armado. 1983. Dissertação (Mestrado em Engenharia). Escola Politécnica da Universidade de São Paulo, São Paulo.
Publication Dates
-
Publication in this collection
20 Sept 2012 -
Date of issue
June 2012