ABSTRACT
This paper does a review of the recent achievements on the knowledge of UHPFRC properties and in the development of design procedures. UHPFRC is defined as a new material, with unique properties (high ductility, low permeability, very high strength capacity in compression, higher toughness) in comparison to conventional concrete. It is important to know both material and mechanical properties to fully take advantage of its outstanding properties for structural applications. However, since this is a new material, the current design codes are not well suited and should be reviewed before being applied to UHPFRC. In the first part, the following material properties are addressed: hydration process; permeability; fibers role; mix design; fiber-matrix bond properties workability; mixing procedure; and curing. In the second part, the mechanical properties of the material are discussed, together with some design recommendations. The aspects herein examined are: size effect; compressive and flexural strength; tensile stress-strain relation; shear and punching shear capacity; creep and shrinkage; fracture energy; steel bars anchorage and adherence. Besides, the tensile mechanical characterization is described using inverse analysis based on bending tests data. In the last part, material behavior at high temperature is discussed, including physical-chemical transformations of the concrete, spalling effect, and transient creep. In the latter case, a new Load Induced Thermal Strain (LITS) semi-empirical model is described and compared with UHPC experimental results.
Keywords:
Ultra-High Performance Fiber Reinforced Concrete (UHPFRC); material properties; design procedures; mechanical behavior; high temperature
RESUMO
Este artigo faz uma análise dos recentes avanços nas pesquisas das propriedades do CUADRF e dos seus procedimentos normativos. O CUADRF pode ser definido como um novo material, com propriedades muito superiores (grande ductilidade, baixíssima permeabilidade, altíssima capacidade resistente à compressão e elevada tenacidade) às do concreto convencional. O conhecimento das propriedades mecânicas e do material do CUADRF é importante para que todo o seu potencial seja plenamente utilizado. Entretanto, como este é um novo material, as recomendações normativas atuais não são plenamente válidas. Na primeira parte, as seguintes propriedades do material são descritas: processo de hidratação; permeabilidade; efeito dos diferentes tipos de fibras; definição do traço; aderência entre as fibras e o concreto; trabalhabilidade; procedimentos de mistura; e cura. Na segunda parte, as propriedades mecânicas e algumas recomendações normativas são discutidas. Neste caso são examinados o efeito escala, a resistência à compressão e à flexão, a relação tensão-deformação à tração, a força de cisalhamento e de punção, a fluência e a retração, a energia de fratura, a ancoragem e aderência das barras de aço. Além disso, são descritos alguns métodos de análise inversa para a caracterização do material à tração por meio de ensaios à flexão. Na última parte, é analisado o comportamento do concreto em alta temperatura, incluindo as suas transformações físico-químicas, o efeito de lascamento (“spalling”) e a fluência transiente. Neste último caso, um novo modelo semi-empírico de fluência, baseado no conceito de deformação térmica induzida pelo carregamento ou LITS (Load induced Thermal Strain) é apresentado e comparado com resultados experimentais de CUAD.
Palavras-chave:
Concreto de Ultra Alto Desempenho Reforçado com Fibras (CUADRF); propriedades do material, especificações de projeto, comportamento mecânico, alta temperatura
1. Introduction
Ultra High Performance Concrete (UHPC) is a cementitious composite characterized by a significant amount of cement (higher than 600 kg), small aggregates size (lower than 6 mm), binder (pozzolana, fly ash, silica fume, reactive powder) and a low water/cement ratio (w/ c < 0.2). This mix design creates a dense and interconnected microstructure with high homogeneity, a capillary porosity lower than 1.5% and a compressive strength higher than 150 MPa. These characteristics result in a concrete with better performance, higher durability and increased bearing capacity and toughness compared to normal and high strength concretes. The incorporation of fibers significantly improves the tensile capacity, leading to a high deformability (above 1%) with a pseudo-plastic phase (multi-cracking) and an increase in the tensile capacity before crack localization and strength depletion. As a result, the UHPFRC can be classified as a new cementitious material. Its mechanical behavior should be adequately characterized to fully take advantage of its unique properties in structural design, making possible the construction of lighter, more durable, efficient and innovative structural elements.
It is worth mentioning that in concretes with high levels of compressive strength, there is a sub-proportional increase of both the tensile strength and the Modulus of Elasticity in relation to the compressive strength. To obtain a better response in tension, especially in the post-cracking regime, fibers can be incorporated in the concrete mix.
The Ultra High-Performance Fiber Reinforced Concrete (UHPFRC) contributes to improving durability, service life and performance of the structure. As stated by [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], during the last decades, the three major developments in cementitious composites were the significant increase in the compressive strength, ductility improvement, and workability enhancement. These achievements were the result of a granular packing optimization, the development of Fiber Reinforced Concrete (FRC) and the better understanding of the material rheology. In the latter case, the improvements in the models to describe concrete flow (Bingham fluid flow and stress growth method) lead to the development of Self-Compacting Concrete (SCC) and later to UHPC and UHPFRC.
The researches on FRC lead to an increase in concrete deformability and reduction of brittleness due to the improvement on the tensile properties and the achievement of a post-cracking behavior. The latter is characterized by a softening (crack localization and stable propagation due to fiber pull-out resistance) or hardening (multi-cracking state) response, which results in an increase in the material performance. A strain softening response is obtained due to a progressive fiber engagement and pull-out resistance, leading to a stable crack propagation and a reduction of the tensile strength as a result of a gradual fiber debonding. A strain hardening response is characterized by an increase in the tensile strength due to the development of finely distributed microcracks before crack localization (pseudo-plastic behavior), allowing the material to be used in the non-linear range without loss of performance.
According to [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], the primary transport mechanism of concrete, associated with durability in aggressive environments, is the capillary absorption of water combined with moisture and ion diffusion (chlorides and sulphates). Hence, the crack width limitation is the main concern with respect to Serviceability Limit State (SLS), since even narrow cracks are prone to water penetration. In this case, the UHPFRC can be applied as a concrete cover (ranging from 20 mm to 50 mm), serving as waterproofing and protective layer [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.]. The main advantage of UHPFRC in relation to conventional and high performance concrete (HPC) is its high propensity to avoid cracks due to the high tensile strength, limited shrinkage due to the small w/c ratio and significant viscous response, obtained by the very dense matrix which contributes to relax the eigenstresses [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.]. Concrete time-dependent deformation occurs due to calcium-silicate-hydrates (CSH) microprestress relaxation, owing to transport mechanisms (moisture diffusion). As the material reaches the post-cracking hardening phase, the stress redistributions and the increase of ductility (stress release) prevent further increase of the eigenstresses.
Numerical analysis carried out by [2[2] Oesterlee, C.; Sadouki, H. and Brühwiler, E. Structural analysis of a composite bridge girder combining UHPFRC and reinforced concrete. UHPC-2008: The Second International Symposium on Ultra High Performance Concrete, March 2008.] on a composite bridge girder, combining a top layer of UHPFRC and RC structure, demonstrated that the restrained shrinkage and external loads could generate stresses close to the elastic tensile strength. In this case, the UHPFRC top layer can act as an efficient mechanism to resist to additional tensile stresses transferred from the RC structure after the attainment of its maximum tensile strength capacity. The stress redistribution prevents the development of cracks, maintaining the structure’s low permeability (waterproofing resistance) and improving its durability.
Due to these properties, one of the most promising applications of UHPFRC is the rehabilitation of structural members, for example, bridges superstructure elements subjected to severe environmental and mechanical loads, allowing a higher durability (reduction of maintenance) and providing waterproofing layer. Besides, it has a broad range of applications. For example, in design, it is possible to produce furniture and architectural elements such as staircases with very thin layers (around 30 mm). In structural applications, it can be utilized for construction of wind towers structural elements, tall buildings, and bridges with reduced sections (reduction of weight). It can also be used for rehabilitation and repair of concrete elements such as pavements, bridge decks, columns, and slabs.
It is important to underline that, to obtain an optimum performance, UHPFRC mix design should be able simultaneously to satisfy the conditions of tensile strain hardening, low permeability, high tensile and compressive strength capacities and self-compacting properties in case of cast in situ applications [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.]. However, according to [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], very few mixes or almost none are able to fulfill all these requirements. Moreover, despite the main advantages of UHPFRC, design procedures still need to be developed to take advantage of the fully material properties. For example, FRC material classification and some of the testing procedures for the material characterization specified for normal and high strength concrete, as the tensile characterization through bending tests, may not be suitable for UHPFRC. As stated by [3[3] Walraven, J. C. High performance fiber reinforced concrete: progress in knowledge and design codes. Materials and Structures, vol. 42, p. 1247-1260, 2009.], standard flexural tests using notched and unnotched beams can lead to significant differences, since, in the first case, the notch allows the measurement of the crack opening, but the results disregard completely the hardening effect (multi-cracking). Moreover, the crack localization does not necessarily correspond to the weakest section of the element.
Besides, as stated by [3[3] Walraven, J. C. High performance fiber reinforced concrete: progress in knowledge and design codes. Materials and Structures, vol. 42, p. 1247-1260, 2009.], it is important to have design rules that are in agreement with existing code provisions to allow the development of hybrid structures, combining prestressing, rebars, fibers, conventional concrete and UHPC. It is worth mentioning that tests results from [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.] demonstrated that the limit states imposed in design codes to conventional concrete should be reviewed for the case of UHPFRC.
One of the greatest challenges facing fiber reinforced cementitious composites, according to [3[3] Walraven, J. C. High performance fiber reinforced concrete: progress in knowledge and design codes. Materials and Structures, vol. 42, p. 1247-1260, 2009.], is how to correct link the standard tests results to the behavior of a real structural element. For example, fibers orientation and distribution are strongly affected by casting and compacting procedures. Moreover, it is not completely clear the scale effect on large-scale tests [5[5] Sritharan, S. Design of UHPC Structural Members: Lessons Learned and ASTM Test Requirements. Advances in Civil Engineering Materials, vol. 4, p. 113-131, 2015.].
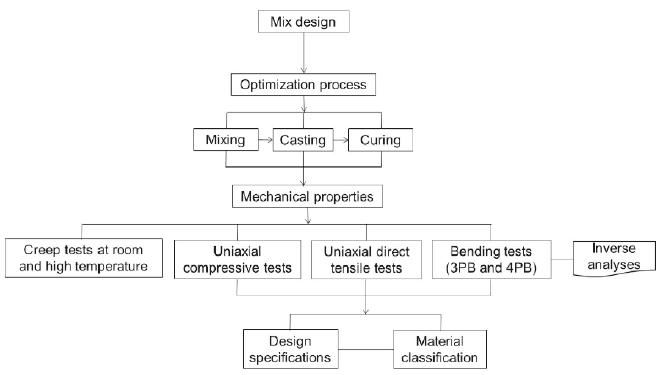
Said that, this paper aims at highlighting some UHPFRC unique properties and design rules, as is shown in Figure 1. To do so, a review of the recent achievements on the knowledge of the material properties, both at room and high temperature, is carried out, together with the description of the developments in the material mechanical characterization and design procedures.
2. Material properties
In this section, material properties of interest for the characterization of the UHPFRC are described: hydration, permeability, fiber-matrix bond properties, mix design, workability and curing regimes. The objective is to provide a better understanding of the unique material properties that are reflected in UHPFRC superior performance and improved mechanical properties.
2.1 Hydration process
Hydration is a thermo-activated process, which is directly affected by the temperature level. The chemical reactions of the different anhydrous cementitious components with water generate heat, increasing concrete temperature.
As stated by [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], the high amount of binder associated with the low w / cratio in the UHPFRC mix design changes the hydration kinetics and the mechanical properties of the material. UHPFRC hydration reaction is characterized by a long initial period of dormant (approximately 24 hours), followed by a fast reaction time, which leads to a rapid evolution of the mechanical properties. At the 7th day of hydration, the material reaches 60% of the tensile strength and more than 80% of both the compressive strength and the modulus of elasticity. After 90 days, the hydration process is virtually completed [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.].
On one hand, UHPFRC long period of dormant is caused by the incorporation of super and hyper plasticizers that lead to the separation of the cementitious grains from the pore water. On the other hand, the first contact of the moisture with anhydrous cementitious products creates an amorphous layer of hydration product around the cement particles, which separates them from the pore solution (water containing a variety of ionic species), preventing further rapid reactions.
After the dormant period, the hydration process effectively begins, with an initial phase, which lasts approximately 12 hours, characterized by a significant amount of energy release (thermal process) [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.]. This process leads to a non-negligible temperature increase in the inner concrete layers, even for relatively thin members, which could favor concrete microcracking. An investigation of UHPFRC composite beams carried out by [7[7] Habel, K. Structural behaviour of elements combining ultra-high performance fibre-reinforced concretes (UHPFRC) and concrete. PhD thesis, The Ecole Polytechnique Fédérale de Lausanne, 2004.] demonstrated an increase in temperature, from 20°C to 32°C, on the core of UHPFRC due to the hydration process. In this case, [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.] affirm that the Arrhenius equation seems to be adequate to take into account the temperature dependence of the binder reaction rates.
According to [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], the current reaction models (for example, Waller [8[8] Waller, V. Relations entre composition des bétons, exothermie en cours de prise et résistance à la compression. PhD thesis, Laboratoire Central des Ponst et Chaussées Nantes (LCPC), 2002.] and the extended Powers’ [9[9] van Breugel, K.; Jensen, O. M. and Lura, P. Autogenous shrinkage in high performance cement paste. An evaluation of basic mechanisms. Cement and Concrete Research , vol. 33, p. 223-232, 2003.] models) adopted for normal strength concrete to determine the theoretical degree of hydration can also be applied to UHPC. This is possible because both materials develop similar chemical reactions during hydration and show similarities with respect to the reaction kinetics. It is interesting to note that the value of the activation energy (Ea) calculated for UHPFRC in [10[10] Kamen, A.; Denarié, E.; Sadouki, H. and Bruhwiler, E. Evaluation of UHPFRC activation energy using empirical models. Materials and Structures , vol. 42, p. 527-537, 2009.] was equal to 33 kJ/mol, close to the one for normal strength concrete (40 kJ/mol).
For UHPC, as stated by [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], a closed system (no moisture transfer with the exterior) can be assumed, since the little porosity prevents water percolation into the bulk concrete. In the experimental investigation on UHPFRC carried out by [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], the final degree of hydration was relatively small (α = 0.31) compared to normal strength concrete, where: w/ c > 0.42;α =1. This is a consequence of UHPFRC self-desiccation since the low w/c ratio is not sufficient to hydrate all cement constituents.
Experimental tests carried out by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.] on UHPFRC demonstrate a fast growth of the hydration degree during the first seven days (reaching 50% at the end of this period), followed by a slower and gradual increase up to 28 days. Moreover, an increase of the amount of cement hydration was observed with the substitution of part of the cement by filler (for example, limestone and quartz powder). This is an indication that UHPFRC mix design optimization (reduction of binder volume and increase of filler content) can enhance the cement hydration degree and improve material’s efficiency (replacement of anhydrous cement grains by cheaper filler constituents) [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.].
2.2 Permeability
UHPFRC is characterized by a low w/ cratio that is not sufficient to hydrate all cement constituents. The anhydrous grains (portlandite and calcium silicates) in the matrix remain as inert filler, acting as a reserve of the system (healing capacity), that can be activated (hydration process) after concrete cracking to close or reduce crack opening. Moreover, the unhydrated binder helps to improve the matrix compactness, filling out the small gaps between cement particles (densification process), leading to a very low permeability.
The hydrated grains create a dense and interconnected microstructure with a higher fiber-matrix bond strength (interfacial transition zone with lower porosity) compared to normal and high strength concretes [12[12] Russell H. G. and Graybeal B. A. Ultra-High Performance Concrete: A State-of-the-Art Report for the Bridge Community. Report FHWA-HRT-13-060, Jun, 2013., 13[13] Moser, B. and Pfeifer, C. Microstructure and Durability of Ultra-High Performance Concrete. UHPC-2008: The Second International Symposium on Ultra High Performance Concrete, March 2008, pp. 417-424.].
The very low permeability of UHPFRC serves as a protection against aggressive agents, such as chloride ions that cause corrosion of steel bars and sulfate attack, which could lead to concrete expansion, crack propagation and loss of bond between the cement paste and the aggregates [14[14] Toutlemonde, F. and Resplendino, J. (eds.). Designing and Building with UHPFRC: State-of-the-Art and Development, John Wiley and Sons, 2011. , 15[15] Resplendino, J. First recommendations for Ultra-High-Performance Concretes and examples of application. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, pp. 79-90., 16[16] Carsten, V.; Matthias, G. and Bernhard, M. Seeing at the nanoscale: Hydration of pozzolanic and cementitious materials. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, pp. 143-152.]. It is worth noting that in UHPFRC, due to the hardening behavior, small microcracks are developed before crack localization, keeping the material permeability very low even at the post-cracking phase [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.].
Experimental tests carried out by [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.] demonstrated that the permeability degree of uncracked and cracked UHPFRC with a strain level up to 0.15% was practically the same. Beyond this limit, a progressive increase of permeability was observed.
2.3 Fibers role
According to [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], the incorporation of long fibers (lf > 10 mm) has an effect at the structural level, contributing to increasing the deformability of the material. Immediately after cracking, fibers are progressively engaged, leading to a multi-cracking pattern (pseudo-hardening phase) and crack localization (softening behavior).
In contrast, the addition of short and microfibers (a few mm length) has an effect at the material level, helping to improve the tensile strength associated to the pseudo-elastic domain. The microfibers are activated immediately after concrete microcracking, leading to a concrete behavior characterized by a longer elastic phase (elastic + pseudo-elastic).
Steel fibers (twisted, hooked-end, straight long and short) are regularly used in UHPFRC mixtures due to their high strength, high resistance in alkaline environment and high modulus of elasticity. It is worth mentioning that polypropylene fibers (PP) can be incorporated in the concrete mix to avoid explosive spalling in a fire scenario. In this case, PP fibers melting, around 180ºC, lead to the increase of the permeability, releasing the vapor pressure inside the matrix.
The different types of fibers are shown in Figure 2.
2.4 Mix design
In the last two decades, different mix designs were developed by different laboratories in partnership with commercial companies such as: Ductal commercialized by Lafarge-Holcim; CEMTEC developed by [17[17] Rossi, P.; Arca, A.; Parant; E. and Fakhria, P. Bending and compressive behaviours of a new cement composite. Cement and Concrete Research , vol. 35, p. 27-33, 2005.] in the French Laboratoire Central des Ponts et Chaussees (LCPC); BSI by Eiffage; COR-TUF from US Army Corps of Engineers.
In literature, most of concrete mix specifications are detailed without any theoretical background or detailed description of the mix design procedures [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.]. In fact, most of the mixtures are based on empirical processes, based on trial and error, suited to a specific field of investigation [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.]. As a result, a significant variability in the amount of cement (from 600 kg to more than 1000 kg) and aggregates sizes is observed from one mixture to another, which leads to a low optimization of the material. As observed by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.], it is possible that a large amount of binders and other particles (filler and aggregates) are not well utilized in UHPFRC. An optimization process can reduce concrete porosity and enhance matrix microstructure links, contributing to increasing concrete strength and reduce creep effects.
Fuller’s grading curve is not appropriate for materials with fine constituents (SCC, HSC and UHPC), since it results in less workable mixtures, with poor cement content [19[19] Brouwers, H. J. H. and Hadix, H. J. Self-compacting concrete: the role of the particle size distribution. First International Symposium on Design, Performance and Use of Self-Consolidating Concrete, Changsha, Hunan, China, 2005.]. Nonetheless, UHPC grain size distribution can be determined according to Andreasen and Andersen [18[18] Andreasen, A. and Andersen, J. Ueber die Beziehung zwischen Kornabstufung und Zwischenraum in Produkten aus losen Körnern (mit einigen Experimenten). Kolloid-Zeitschrift, vol. 50, p. 217-228, 1930.] particle packing procedure. In this case, the particles distribution is calculated according to Eq. 1, where: P (D i) is the fraction of the total solids smaller than the specified diameter D i; D maxis the maximum particle diameter; qis the distribution modulus, dependent on the type of concrete.
Fuller’s original grading curve [20[20] Fuller, W.B. and Thompson, S.E. The laws of proportioning concrete. Transactions of the ASCE, vol. 159, 1907.] assumed for Eq. 1 an exponent equal to 0.5, which is not suitable for UHPC mix design. As stated by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.], coarse mixtures are obtained when q > 0.5, while mixtures rich in fine particles are achieved when q < 0.25. Experimental tests on UHPFRC carried out by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.] assumed a value of qequal to 0.23.
Some researchers adopt a modified version of the Andreasen and Andersen model (Eq. 1) to introduce a minimum particle size (D min), as is shown in Eq. 2. According to [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.], this expression, proposed by [21[21] Funk, J. E. and Dinger, D.R. Particle Packing, Part VI - Applications of Particle Size Distribution Concepts. Interceram, vol. 43, pp. 350-3, 1994.], has been successfully adopted for optimization of normal strength concrete and lightweight concrete mix design.
In [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.] research, the modified Andreasen and Andersen model was implemented to determine the optimum packing distribution of a UHPFRC. In this case, an algorithm based on the Least Squared Method (LSM) was formulated to reach the best fitting between target and calculated mixtures. A comparison with optimized (using the modified Andreasen and Andersen model) and non-optimized concrete mixtures show that the compressive strength of both materials are equivalent, indicating that the optimizing process can reduce the amount of binder without changing significantly concrete strength [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.]. In the case analyzed, a compressive strength of 142 MPa was achieved with only 650 kg of binder. The results clearly indicate that an optimization packing process can produce a UHPFRC with relatively low binder volume.
2.5 Fiber-matrix bond properties
In normal and high strength concrete, the improvement of concrete micromechanical properties does not occur uniformly due to the matrix and fibers interfacial transition zone (ITZ) distinct microstructural properties evolution. As stated by [22[22] Chan, Y.-W. and Li, V. C. Age effect on the characteristics of fibre/cement interfacial properties. Journal of Materials Science, n. 32, p. 5287-5292, 1997.], fiber ITZ is markedly weaker compared to the bulk matrix due to its higher porosity, resulted from the formation of large calcium hydroxide (CH) crystals.
Long-term aging properties of Steel Fiber Reinforced Concrete (SFRC) were investigated in [23[23] Buttignol, T. E. T.; Colombo, M. and Di Prisco, M. Long-term aging effects on tensile characterization of steel fibre reinforced concrete. fib Structural Concrete, 2016.]. A comparison of 1- and 10-years-old specimens, using 4-point bending tests, demonstrated a large increase in both peak and SLS post-peak strengths (roughly by 50%), which was attributed to matrix improvements. In contrast, fiber pull-out resistance, affecting Ultimate Limit State (ULS) strength, was barely increased (approximately by 15%).
UHPFRC high tensile strength increases fiber frictional-adhesive and mechanical bond, ensuring a high pull-out strength without fiber rupture [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.]. Its complex microstructure enhances ITZ properties, which is characterized by a higher adhesion of the binder to the steel fiber surface, leading to an increase of the pull-out strength and a reduction of its weakness. According to [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], the reacted part of the binder helps to build a skeleton with an intricate and complex network (stronger links) with more connections and less porosity. As a result, more particles adhere to the steel fibers, enhancing the fiber-matrix ITZ and increasing the pull-out energy (better bond properties).
Experimental tests on UHPFRC performed by [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.] on mixtures incorporating different types of fibers (smooth, twisted and hooked end) show that improving fiber bond behavior (by increasing matrix density, fiber and matrix strengths and fiber mechanical bond by adding twisted or hooked end fibers) can lead to a higher performance of the material. The incorporation of 1.5% high strength twisted steel fibers led to a significant enhancement of concrete tensile properties in comparison with specimens reinforced with smooth steel fibers. In this case, a tensile strength up to 15 MPa and a strain at peak load of 0.6%, with a strain hardening response (multiple cracking with small crack widths and inelastic strain) was achieved.
It is worth mentioning that tests carried out by [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.] on UHPFRC show that fibers efficiency, measured by means of fiber tensile stress (ffpc ), as is shown in Eq. 3, did not change for different volume fractions of straight fibers. In contrast, an increase in hooked-end fibers volume led to a decrease of fiber tensile stress. This was attributed by [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.] to the effect of fibers localized mechanical anchorage, which induce peak stress concentrations in the bulk matrix, causing microcracks and, as a result, loss of performance.
where: ffpc is the average fiber tensile stress; σpc is the peak strength; α2is a parameter equal to 0.75; Vf is the fiber volume.
2.6 Workability
Workability on conventional concrete is regularly measured by means of the fresh mixture consistency determined on slump tests. These tests are largely utilized due to their simplicity (simple procedures and basic apparatus). However, the prediction of UHPFRC workability cannot rely simply on the basis of slump tests, since they only verify the level of flowability, but does not give any information about the mixture physical properties. Hence, rheological measurements should be used in order to find the range of workability.
Concrete workability is directly related to the w / cratio. In conventional concrete, the w / cratio ranges between 0.4 and 0.6. A moderate increase in the w/c ratio, within these limits, can lead to an increase of the slump without significantly affecting the durability and the strength of the material. However, high levels of water (w/c > 0.6) have a deleterious effect, causing particles segregation and water exudation (bleeding), which increases matrix porosity and reduces concrete strength. In UHPC, the control of water content is more critical, since the w/c ratio is around 0.2. In this case, an increase of water content can lead to a pronounced decrease of concrete strength. As a result, to guarantee the mixture workability, high levels of super and hyper plasticizers should be incorporated in the mixture.
In UHPFRC, flowability is directly related to the amount of fibers. A high flowability (high slump) is required to guarantee fibers dispersion (uniform distribution) and orientation during casting. However, the incorporation of fibers reduces the level of fresh mix flowability due to fiber friction, cohesive forces and changes in the skeleton structure [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.].
Tests carried out by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.] on UHPFRC, taking into account different steel fibers content, demonstrated a reduction of the relative slump flow due to the increase of the amount of fibers. Besides, tests considering the same mix design, but with different amounts of filler, have shown that replacing part of the cement with filler can significantly improve workability.
According to [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.], the fiber factor, as is shown in Eq. 4, can be adopted to evaluate the adequate level of workability on UHPFRC. Experimental tests performed by [17[17] Rossi, P.; Arca, A.; Parant; E. and Fakhria, P. Bending and compressive behaviours of a new cement composite. Cement and Concrete Research , vol. 35, p. 27-33, 2005.] show that the fiber factor ranged from 0.8 to 2.0. An upper bound limit of 2.5 for straight steel fibers is suggested in [25[25] Markovic, I. High-performance hybrid-fibre concrete-development and utilisation. phD thesis, Technische Universitat Delft.], while [26[26] Naaman, A. E. and Wille, K. Some correlation between high packing density, ultra-high performance, flow ability, and fiber reinforcement of a concrete matrix. 2nd Iberian congress on self compacting concrete - BAC2010 , University of Minho-Guimaraes, Portugal, 2010.] recommends a maximum value of 2.0.
where: Xf is the fiber factor; Vf is the volume of fibers; lf is the fiber length; df is the fiber diameter.
2.7 Mixing procedure
UHPFRC fresh mix is characterized by a high viscosity and thixotropy (time-dependent change in viscosity), which requires high standard quality levels to assure proper mixing and casting procedures (homogeneity and dispersion of particles) and the quality of the constituents (purity, RH and gradation). Moreover, the high amount of binder and the low w / cratio favor the formation of balls of cement, mixture overheating (thermo-activated chemical reactions generating heat) and self-desiccation (due to water evaporation and hydration) during preparation and placement. Besides, the size and shape of test samples can affect fiber orientation (wall effect) [5[5] Sritharan, S. Design of UHPC Structural Members: Lessons Learned and ASTM Test Requirements. Advances in Civil Engineering Materials, vol. 4, p. 113-131, 2015.].
In order to achieve a good workability, UHPFRC mixing procedure should guarantee fibers orientation and dispersion through the bulk concrete and assure a good packing density, avoiding materials agglomeration (formation of balls of cement). Due to the tendency of agglomeration, the fine particles (binder and sand) should be mixed first, before the addition of water. Fibers are incorporated in the last phase, after the addition of water and chemical admixtures (super and hyperplasticizers). The shear action of steel fibers helps to destroy the remaining agglomerates. The complete mixing procedure takes between 8 to 20 minutes.
2.8 Curing
UHPC compressive strength depends on the curing regime. Experimental tests performed by [27[27] Wipf, T. J.; Phares, B. M.; Sritharan, S.; Degen B. E. and Giesmann, M. T. Design and Evaluation of a Single-Span Bridge Using Ultra-High Performance Concrete. Iowa Department of Transportation, IHRB Project TR-529, 2009.] show that steam curing provided the highest strength values compared to air and tempered steam curing.
An experimental investigation on the thermal curing properties of UHPFRC was carried out by [10[10] Kamen, A.; Denarié, E.; Sadouki, H. and Bruhwiler, E. Evaluation of UHPFRC activation energy using empirical models. Materials and Structures , vol. 42, p. 527-537, 2009.] by means of Loss of Ignition (LOI) tests, assuming a linear relationship between the amount of bound water and the degree of hydration. The results demonstrated that the level of hydration was very low (close to zero) at the beginning of curing at 20ºC, with a non-linear increase in time: sharp increase in the level of hydration products in the first seven days, followed by a decrease in the growth rate of chemical reactions. In contrast, curing at 40ºC led to high chemical reactions even at the first day and a constant degree of hydration in time. At seven days of curing, the same degree of hydration was obtained for the specimens cured at 20°C, 30°C and 40°C. However, at 28 days, a higher level of hydration was achieved for the specimens cured at 20°C compared to the ones cured at 40°C.
2.9 Fibers orientation and alignment
Fiber distribution and alignment are affected by the size of the specimen, boundary conditions (wall effect), workability of the mixture, fiber volume and compaction procedures.
Experimental tests on round panels carried out by [28[28] Barnett, S. J.; Lataste, J.-F.; Parry, T.; Millard, S. G. and Soutsos, M. N. Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength. Materials and Structures , vol. 43, p. 1009-1023, 2010.], using X-ray computed tomography and electrical resistivity measurements, have shown that pouring concrete from the center produces the best results in terms of strength capacity. The flow of concrete outwards from the center of the panel led a preferential alignment of the fibers, perpendicular to the radius of the panel, increasing the numbers of fibers bridging the cracks.
3. Mechanical properties and design procedures of UHPFRC
In normal and high strength concretes, the compressive strength continues to increase even after many years. Experimental tests performed by [23[23] Buttignol, T. E. T.; Colombo, M. and Di Prisco, M. Long-term aging effects on tensile characterization of steel fibre reinforced concrete. fib Structural Concrete, 2016.] on SFRC show, in a 10-year period, an increase of more than 30% in the compressive strength and an increase of approximately 50% in the flexural strength, measured in four-point bending tests.
In contrast, according to [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], UHPFRC has a fast mechanical properties evolution in time, reaching high early age strength and stiffness, and a short-term hydration regime, which is virtually completed after 90 days. Experimental tests on UHPFRC performed by [11[11] Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.] demonstrated a pronounced increase of both the compressive and flexural strengths. In this case, the incorporation of 2.5% of steel fibers led to an increase of approximately 50% on the compressive strength and in a flexural strength twice the one observed in the specimen without fibers.
According to [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.], for structural applications, achieving a strain at peak stress higher than 0.3% (beyond steel onset of yielding) is important to guarantee fibers full contribution up to and beyond steel bars yielding and a perfect bond between rebars and matrix.
Despite that, design guidelines and specifications should be assigned to link the material properties to structural applications. One possible solution is to review the current parameters and models specified for FRC and HPFRC in order to better represent UHPFRC specifications. In this section, UHPFRC mechanical properties and some design procedures are discussed.
3.1 Size effect
The size effect on UHPC beams was observed in [30[30] Leutbecher, T. and Fehling, E. Structural Behaviour of UHPC under Tensile Stress and Biaxial Loading. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, p. 435-448.] experimental tests. The highest compressive and flexural strength capacities were obtained in slender prismatic specimens [31[31] Orgass, M. and Klug, Y. Fibre Reinforced Ultra-High Strength Concretes. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, p. 637-648.].
According to [32[32] Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.], structural members subjected to bending, without reinforcement, are prone to the size effect, both in terms of resistance and ductility. In contrast, UHPFRC is less susceptible to the size effect due to its dense microstructure (high fiber-matrix bond strength) and the addition of fibers in a volume higher than 2% [32[32] Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.]. In agreement with that, three-point bending tests performed by [33[33] Mahmud, G. H.; Yang, Z. and Hassan, A. M. T. Experimental and numerical studies of size effects of Ultra High Performance Steel Fibre Reinforced Concrete (UHPFRC) beams. Construction and Building Materials, n. 48, p. 1027-1034, 2013.] on UHPFRC notched beams with steel fibers, considering different heights (from 30 mm to 150 mm), demonstrated that the size effect in terms of nominal stress is negligible. Numerical simulations of beams with a depth up to 300 mm confirmed the experimental results.
According to [32[32] Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.], in quasi-fragile materials, characterized by a post-cracking pseudo-plastic zone, the size effect is negligible and lower than the dispersion (scattering) of the experimental results. This is because the flexural strength capacity is mostly activated during the pseudo-plastic zone, where the material behavior is independent of the size of the specimen. In this case, the size effect is directly related to the extension of the pseudo-plastic zone: increasing its limit, reduces the size effect. Besides, due to [32[32] Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.], in very thin members (25 mm to 75 mm) the size effect is negligible.
As a result, as stated by [32[32] Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.], for members with a large pseudo-plastic zone, it is possible to adopt in design procedures, constitutive models based on the continuum mechanics and stress-strain relationships.
3.2 Compressive strength
In design, simplified constitutive models for the compressive strength are established, based on both the characteristic value (statistical distribution, considering a 95% confidence interval) and the modulus of elasticity (linear-elastic relation). For UHPFRC, AFGC-SETRA [34[34] AFCG and SETRA. Ultra-High Performance Fibre Reinforced Concrete-Interim Reccomendations. France, 2013.] establishes the beginning of the yield plateau (liner-elastic phase) according to Eq. 5, where: α is equal to 0.85; fck is the cylindrical compressive characteristic strength; θ is the coefficient for transient loads; Yb is the safety factor.
Design recommendations from [35[35] Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.], establishes an UHPFRC design compressive strength with a factor of safety () equal to 1.4 and is the coefficient to take into account the load duration, normally assumed as 1.0; is the coefficient to take into account UHPFRC limited deformation in compression, being equal to 0.85; is the coefficient for considering the structural behavior of UHPFRC, being equal to 0.67. In this case, the coefficient for transient loads () is not considered.
In the design of a UHPC precast/prestressed bridge girder, [36[36] Almansour, H. and Lounis, Z. Innovative Design of Precast/Prestressed Girder Bridge Superstructures using Ultra High Performance Concrete. Annual Conference of the transportation Association of Canada, 2008.] assumed an elastic-perfectly plastic stress-strain relation, with an ultimate compressive strength limited to 65% of the strength capacity ().
According to [37[37] Graybeal, B. and Davis, M. Cylinder or Cube: Strength Testing of 80 to 200 MPa (11.6 to 29 ksi) Ultra-High-Performance Fiber-Reinforced Concrete. ACI Materials Journal, vol. 105, p. 603-609, 2008.], the compressive strength measured in cubes is about 5% higher than cylinders. In this case, the smaller the specimen, the higher is the standard deviation. The specimens tested (76 mm x 152 mm) were within the interval of 8% of the control specimen, which is lower than the limit recommended by [34[34] AFCG and SETRA. Ultra-High Performance Fibre Reinforced Concrete-Interim Reccomendations. France, 2013.]: standard deviation (S) .
From regression analysis, [37[37] Graybeal, B. and Davis, M. Cylinder or Cube: Strength Testing of 80 to 200 MPa (11.6 to 29 ksi) Ultra-High-Performance Fiber-Reinforced Concrete. ACI Materials Journal, vol. 105, p. 603-609, 2008.] determined an exponential equation (Eq. 6) for UHPC compressive strength evolution in time under standard laboratory curing regime.
where: is the compressive strength at 28 days; t is the time after casting in days.
3.3 Flexural capacity
Experimental results of UHPFRC from [38[38] Kang, S.-T.; Lee, Y.; Park, Y.-D. and Kim, J.-K. Tensile fracture properties of an Ultra High Performance Fiber Reinforced Concrete (UHPFRC) with steel fiber. Composite Structures, vol. 92, p. 61-71, 2010.] demonstrated that the increase of fiber volume, on one hand, does not change the initial stiffness. On the other hand, it increases both the flexural strength and structural ductility (higher deformability).
An equation to predict FRC flexural strength (rule of mixture) was described in [39[39] Naaman, A. E. High Performance Fiber Cement Composites. High-performance Construction Materials: Science and Applications, World Scientific Publishing Company , 2008, pp. 448.], as is shown in Eq. 7, where: .is FRC flexural strength; 0 is the flexural strength of plain concrete; Vf is the fiber volume ratio; lf is the fiber length; df is the fiber diameter; A and B are empirical constants.
Experimental tests on UHPFRC carried out by [38[38] Kang, S.-T.; Lee, Y.; Park, Y.-D. and Kim, J.-K. Tensile fracture properties of an Ultra High Performance Fiber Reinforced Concrete (UHPFRC) with steel fiber. Composite Structures, vol. 92, p. 61-71, 2010.], considering different fiber volume (1% to 5%), show a linear relationship between fiber volume and flexural strength, as predicted by [40[40] Naaman, A. E. A statistical theory of strength for fiber reinforced concrete. PhD thesis, Massachusetts Intitute of Technology, 1972.], with a high coefficient of determination (R2=0.97). For the same fiber geometry (lf/df=13/0.2), [31[31] Orgass, M. and Klug, Y. Fibre Reinforced Ultra-High Strength Concretes. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, p. 637-648.] found the following values for the empirical constants (Eq. 5): A = 1 and B = 0.307. In conclusion, [38[38] Kang, S.-T.; Lee, Y.; Park, Y.-D. and Kim, J.-K. Tensile fracture properties of an Ultra High Performance Fiber Reinforced Concrete (UHPFRC) with steel fiber. Composite Structures, vol. 92, p. 61-71, 2010.] affirm that the rule of mixture can be also applied to UHPFRC with satisfactory confidence.
3.4 Tensile stress-strain capacity
Experimental tests carried out by [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.] on UHPFRC, using high strength smooth steel fibers, show that an increase in the amount of fibers from 1.5% to 2.5% (+67%) led to an increase of the tensile strength from 8 MPa to 14 MPa (+75%), as well as an increase in the maximum post-cracking tensile strain from 0.17% to 0.24% (+41%). Test results of UHPFRC using hooked end steel fibers from [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.] demonstrated that the variation on the fiber volume fraction from 1% to 2% (+100%) was followed by an increase on the tensile strength from 9 MPa to 14 MPa (+55%), while the maximum tensile strain remained at 0.46%. Moreover, the change in fiber volume fraction from 1% to 2% (100%) in a UHPFRC reinforced with twisted fibers ([24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.]) indicated an increase on the tensile strength from 8 MPa to 15 MPa (87.5%) as well as an increase in the ultimate tensile strain from 0.33% to 0.61% (+85%). According to [24[24] K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.], the results demonstrated that UHPFRC performance can be enhanced by the incorporation of deformed (twisted) steel fibers instead of smooth fibers, especially the ultimate tensile strain capacity.
UHPFRC design tensile strength () can be determined from [35[35] Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.], according to Eq. 8, where: is the tensile characteristic strength; is the factor of safety taken as 1.4 for UHPFRC without reinforcement or 1.3 for reinforced UHPFRC; is the coefficient to take into account the load duration, normally assumed as 1.0; is the coefficient to take into account UHPFRC thickness and fabrication process, varying from 1.0 to 0.8; is the coefficient related to fiber orientation (irregular distribution), being equal to 1.0 in case of global behavior (Bernoulli principle is applied) or equal to 0.85 in case of local behavior (D-regions).
In the design of a UHPC precast/prestressed bridge girder, [36[36] Almansour, H. and Lounis, Z. Innovative Design of Precast/Prestressed Girder Bridge Superstructures using Ultra High Performance Concrete. Annual Conference of the transportation Association of Canada, 2008.] assumed an allowable tensile strength equal to 0.4, where the maximum tensile strength was assumed to be equal to the first cracking strength. During construction, the tensile strength was limited to 60% of the allowable tensile value. Moreover, [36[36] Almansour, H. and Lounis, Z. Innovative Design of Precast/Prestressed Girder Bridge Superstructures using Ultra High Performance Concrete. Annual Conference of the transportation Association of Canada, 2008.] defined an elastic-perfectly plastic stress-strain relation, with an ultimate limit strain equal to 0.003.
UHPFRC tensile constitutive law can be determined by means of inverse analysis from bending tests, using both the uncracked beam analysis, based on standard continuum mechanics (differential equations), and the strain compatibility approach, with the following assumptions: constant (average) shear stress distribution; plane section approach; constitutive laws (stress-strain relations in compression and tension).
3.5 Shear strength
A shear design model is proposed in [27[27] Wipf, T. J.; Phares, B. M.; Sritharan, S.; Degen B. E. and Giesmann, M. T. Design and Evaluation of a Single-Span Bridge Using Ultra-High Performance Concrete. Iowa Department of Transportation, IHRB Project TR-529, 2009.] for I-shaped UHPC prestressed beams, based on the Modified Compression Field Theory (MCFT) analytical procedure from [41[41] Collins, M. P. and Mitchell, D. Prestressed Concrete Structures. Prentice Hall, 1991.]. The recommendations are made for both SLS and ULS. According to [27[27] Wipf, T. J.; Phares, B. M.; Sritharan, S.; Degen B. E. and Giesmann, M. T. Design and Evaluation of a Single-Span Bridge Using Ultra-High Performance Concrete. Iowa Department of Transportation, IHRB Project TR-529, 2009.], UHPC shear service strength can be accurately calculated following the uncracked beam analysis based on continuum mechanics. The ultimate shear capacity can be determined by means of MCFT approach, which combines equilibrium, compatibility and constitutive laws of the materials into an analysis based on average strains and stresses.
The design of shear capacity in UHPFRC reinforced with steel bars and in composite members are described in [34[34] AFCG and SETRA. Ultra-High Performance Fibre Reinforced Concrete-Interim Reccomendations. France, 2013.] and [35[35] Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.], assuming the superposition of effects (concrete + steel bars + fibers contributions).
The shear capacity in regions with discontinuities (D-regions), where the Bernoulli law is not applicable, can be determined by a truss model as is described in [27[27] Wipf, T. J.; Phares, B. M.; Sritharan, S.; Degen B. E. and Giesmann, M. T. Design and Evaluation of a Single-Span Bridge Using Ultra-High Performance Concrete. Iowa Department of Transportation, IHRB Project TR-529, 2009.] and [42[42] Pansuk, W. Shear capacity of RC and ultra high strength fiber reinforced concrete flanged beams. phD thesis, Hokkaido University, Japan, 2007.]. According to [42[42] Pansuk, W. Shear capacity of RC and ultra high strength fiber reinforced concrete flanged beams. phD thesis, Hokkaido University, Japan, 2007.], a perfectly plastic behavior (constant stress distribution) in the post-cracking phase can be assumed along the full depth of the beam (homogeneous distribution of the fibers through the beam depth). Moreover, due to fibers contribution to the redistribution capacity, the limits of the strut rotation can be widened to the interval: .
3.6 Punching shear
Punching shear capacity is significantly improved in UHPC members due to the material high tensile strength. According to [43[43] Harris, D. K. Characterizaion of Punching Shear Capacity of Thin UHPC Plates. Master Dissertation, Virginia Polytechnic Institute and State University, 2004.], a small loading area is able to induce a punching shear failure in UHPC slabs. Nevertheless, a 63.5 mm thickness slab can provide enough shear strength capacity [36[36] Almansour, H. and Lounis, Z. Innovative Design of Precast/Prestressed Girder Bridge Superstructures using Ultra High Performance Concrete. Annual Conference of the transportation Association of Canada, 2008.].
ACI 318 [44[44] American Concrete Institute. Building Code Requirements for Structural Concrete and Commentary (ACI 318R-08). ACI Committee 318, Farmington Hills, MI, 2008.] punching shear provisions can predict with reasonable accuracy UHPC punching shear force resistance ([43[43] Harris, D. K. Characterizaion of Punching Shear Capacity of Thin UHPC Plates. Master Dissertation, Virginia Polytechnic Institute and State University, 2004.], [45[45] Joh, C.; Hwang, H. and Kim, B. Punching shear and flexural strengths of ultra high performance concrete slabs. High Performance Structures and Materials IV, vol. 97, p. 97-106, 2008.]).
3.7 Creep and shrinkage
According to [14[14] Toutlemonde, F. and Resplendino, J. (eds.). Designing and Building with UHPFRC: State-of-the-Art and Development, John Wiley and Sons, 2011. ], UHPFRC creep coefficient is around 1.0, decreasing after a heat treatment to a value within 0.2 and 0.5. This is similar to UHPC creep coefficient (0.8) obtained in [5[5] Sritharan, S. Design of UHPC Structural Members: Lessons Learned and ASTM Test Requirements. Advances in Civil Engineering Materials, vol. 4, p. 113-131, 2015.].
Tensile creep and relaxation tests on UHPFRC at 3 days age were carried out by [46[46] Switek, A.; Denarié, E. and Bruhwiler, E. Modeling of viscoelastic properties of Ultra High Performance Fiber Reinforced Concrete (UHPFRC) under low to high tensile stresses. Symposium on Concrete Modelling, 22-25 June 2010.]. The results indicate a non-linear behavior for all the load levels (0.3fc, 0.6fc, 0.9fc). Moreover, a perfect correlation between the prediction of the relaxation curve (using creep experimental values), using [47[47] Bazant, Z. P. Numerical determination of long-range stress history from strain history in concrete. Materials and Structures , vol. 5, p. 135-141, 1972.] numerical algorithm, and [46[46] Switek, A.; Denarié, E. and Bruhwiler, E. Modeling of viscoelastic properties of Ultra High Performance Fiber Reinforced Concrete (UHPFRC) under low to high tensile stresses. Symposium on Concrete Modelling, 22-25 June 2010.] experimental values, for a stress level of 0.3fc, was achieved.
UHPC shrinkage strain values obtained in [48[48] Flietstra, J. C. Creep and shrinkage behavior of ultra-high performance concrete under compressive loading with varying curing regimes. Master Dissertation, Michigan Technological University, 2011.] and [49[49] Kamen, A. Time dependent behaviour of ultra high performance fibre reinforced concrete (UHPFRC). 6th International PhD Symposium in Civil Engineering, Zurich, 2006.] (between 3.10-6 to 4.10-6) are similar to the ones of conventional concrete. Due to UHPFRC very low porosity and high amount of cement, autogenous shrinkage developed during hydration can lead to microcracks and macrocrack propagation as a result of the development of high induced tensile stresses (self-equilibrated stresses).
UHPFRC total shrinkage can be calculated according to [35[35] Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.], as is shown in Eq. 9, where: is the shrinkage asymptotic value within the range 0.6‰ to 0.8‰; c and d are constants dependent on the type of cement; t is the time in days.
3.8 Fracture energy
Experimental results from [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.] and [50[50] Macá, P.; Sovják, R. and Vavriník, T. Experimental Investigation of Mechanical Properties of UHPFRC. Precedia Engineering, vol. 65, p. 14-19, 2013.] have shown that UHPFRC fracture energy is about five times greater compared to FRC. According to [6[6] Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cement and Concrete Research, p. 1362-1370, 2006.], this difference regards the level of densification of the microstructure.
UHPFRC remarkable material properties lead to high tensile strain (> 0.3) and strength (> 8 MPa) capacities, and the development of a pseudo-plastic phase (strain hardening) prior to concrete softening, which is responsible to high energy absorption (toughness) before fracturing.
3.9 Steel bars
Based on preliminary tests, [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.] observed that 14 mm diameter steel bars yielded for an anchorage length higher than 150 mm (10). This threshold is much smaller than the one established in design codes for conventional concrete (40). This variation can be attributed to the higher bond strength developed in UHPC due to its dense microstructure, which guarantee a lower porosity in the ITZ zone and a higher matrix tensile strength capacity. Besides, according to [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.], a perfect bond between concrete and rebars can be assumed both at the elastic limit and pseudo-plastic phase.
A limitation of the stresses in steel bars (Es = 200 GPa), respectively to 300 MPa in the multicracking phase and 500 MPa during crack localization, is recommended by [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.].
According to [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.], in case of harmless exposure (no crack width limitation), steel bars with yielding strength of 500 MPa are not recommended, since they limit UHPFRC optimum utilization (steel bars yielding point is achieved before concrete reaches the maximum tensile strength). In this case, high performance steels can be adopted to take full advantage of UHPFRC ductile behavior, which is characterized by a large plastic deformation.
3.10 Crack width limitations
According to [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], the presence of through cracks is the main cause of steel bars severe corrosion in RC structures. In contrast, in non-through cracks, limited to 0.4 mm, the corrosion starts at the crack tip and depends on concrete permeability to develop. If concrete cover permeability is low, the ingress of water and oxygen is slow, delaying the corrosion process. As a result, concrete cover and transport properties (associated with permeability) are the two most important parameters for the durability of concrete structures in aggressive environments [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.].
According to [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.], crack localization () should be avoided since it compromises structural durability due to the considerable increase of permeability.
An expression to determine the maximum crack opening for reinforced HPFRC was derived in [3[3] Walraven, J. C. High performance fiber reinforced concrete: progress in knowledge and design codes. Materials and Structures, vol. 42, p. 1247-1260, 2009.], based on the Model Code 90 original formulation for reinforced plain concrete. The constitutive law in tension is simplified by a trilinear model assuming an initial linear-elastic phase, followed by a perfect plastic () and softening behavior. The expression is shown in Eq. 10, where: is the mean tensile strength; is the mean bond strength; is the steel bars diameter; is the reinforcing ratio of steel bars; , assuming that is the post-cracking “plastic” stress; N is the normal tensile force; is the steel elastic modulus; is the area of the reinforcement; , where is the HPFRC elastic modulus.
3.10.1 Limitations due to cyclic loads
Due to [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.], finer cracks and multiple microcracks lead to higher water absorption, which are amplified under cyclic load, being more detrimental compared to large crack openings. Thus, limiting the crack width in structures subjected to transient and dynamic forces, for example in bridges design, is not a suitable way to prevent water penetration [1[1] Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization. Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.].
3.10.2 Limitations due to severe loads
Based on UHPFRC permeability tests, [4[4] Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses. Materials and Structures , vol. 40, p. 269-277, 2007.] recommends, for structural applications subjected to severe loads, a limitation of the tensile deformation of 0.15%, which corresponds to the multicracking phase. It was observed that, before this limit, the permeability of cracked and uncracked materials are similar.
4. Mechanical characterization
The constitutive law of UHPFRC in tension can be obtained straightforwardly by standard uniaxial direct tensile tests. However, tensile tests are affected by the eccentricity both of the load and the specimen, the boundary conditions (fixed-end and rotating-end conditions) and stress concentrations. As a result, design procedures recommend indirect tensile tests such as three-point bending tests (EN-14651 [51[51] EN 14651. Test method for metallic fibered concrete - Measuring the flexural tensile strength (limit of proportionality (LOP), residual). European Comettee for Standardization, 2005.]) or four-point bending tests (UNI 11039 [52[52] UNI11039. Concrete Renforced with Steel Fibres. Part II: Test Method for the Determination of First Cracking Strength and Ductility Indexes. 2003.]). The great disadvantage of flexural tests is that an inverse analysis is required to determine the constitutive law of the material in tension.
According to [53[53] Lopez, J. A.; Serna, P.; Navarro-Gregori, J. and Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Materials and Structures , vol. 48, p. 3703-3718, 2015.], due to UHPFRC strain-hardening response (high strain capacity before crack localization), the characterization of the material by means of the tensile stress-strain curve is more appropriate than the stress - crack opening displacement (COD) approach adopted for FRC.
An inverse analysis methodology for UHPFRC, based on four-point bending tests, is proposed in [54[54] Baby, F.; Graybeal, B.; Marchand, P. and Toutlemonde, F. UHPFRC tensile behavior characterization: inverse analysis of four-point bending test results. Materials and Structures , vol. 46, p. 1337-1354, 2013.]. The model assumes a two-step solution, with a preliminary inverse analysis to convert the load versus deflection (P-δ) curve into bending moment versus curvature (M-θ). The equation is based on the linear-elasticity approach and does not consider shear contribution. Due to the non-linear behavior, a double integration of the curvature over the length of the beam, by means of the trapezoidal rule, is carried out adopting an iteration process to minimize the error. A second inverse analysis is performed in order to convert the bending moment versus curvature (M-χ) into stress-strain curve (point-by-point process). This process is based on the cross-sectional equilibrium, assuming a linear strain distribution (plane section approach).
A comparison of [54[54] Baby, F.; Graybeal, B.; Marchand, P. and Toutlemonde, F. UHPFRC tensile behavior characterization: inverse analysis of four-point bending test results. Materials and Structures , vol. 46, p. 1337-1354, 2013.] model with direct tensile tests has shown a good agreement between the results, with a slightly overestimation of both the strength and strain capacities. A simplified characteristic bilinear curve is also proposed from [54[54] Baby, F.; Graybeal, B.; Marchand, P. and Toutlemonde, F. UHPFRC tensile behavior characterization: inverse analysis of four-point bending test results. Materials and Structures , vol. 46, p. 1337-1354, 2013.] original model. The results were compared with characteristic bilinear curves obtained from direct tensile tests, showing a tendency of the simplified model to underestimate the strength at the post-cracking regime. This was attributed to the fact that, for bending tests, the tensile area is smaller (the highest tensile stress is concentrated at the lowest fiber). As a result, the tensile behavior is more susceptible to be affected to eventual concrete flaws, which lead to an increase of the standard deviation and a reduction of the characteristic value.
Unnotched four-point bending tests were performed by [53[53] Lopez, J. A.; Serna, P.; Navarro-Gregori, J. and Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Materials and Structures , vol. 48, p. 3703-3718, 2015.] to determine UHPFRC stress-strain response by means of a load-curvature method. In compression, a linear stress evolution is assumed. In tension, a trilinear curve is adopted, taking into account the initial linear-elastic phase, the pseudo-strain hardening phase (multicracking) and the softening behavior (crack localization and progressive fiber debonding). A closed-form solution for M-χ relationship is defined from the stress-strain law at the cross-sectional level, assuming a plane section approach and equilibrium equations. Moreover, a constant shear stress contribution in the curvature integral is assumed. The solution is based on an iterative process, with error minimization by the sum of the residual squares. The model gives the average curvature at the central one-third length.
The integration procedure in [53[53] Lopez, J. A.; Serna, P.; Navarro-Gregori, J. and Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Materials and Structures , vol. 48, p. 3703-3718, 2015.] model is simplified by assuming a linear curvature distribution, up to matrix cracking strength (approximately 70% of the peak load), and a natural logarithm curve at the post-cracking regime. During softening, an average curvature is assumed, where the cracked area often coincides with the beam depth (smeared over a crack bandwidth into a stress-strain relationship). In this case, the tensile law should be defined in terms of , based on the fracture mechanics approach (discrete crack formulation). If the UHPFRC exhibits a strain hardening response before localization, the average space between cracks can be considered to be the link between strain and crack opening before localization (see also [55[55] Di Prisco, M.; Colombo, M. and Dozio, D. Fibre-reinforced concrete in fib Model Code 2010: principles, models and test validation. Structural Concrete, vol. 14, p. 342-361, 2013.]).
A simplified inverse analysis method is also proposed in [35[35] Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.], based on four-point bending tests.
An important aspect brought to light by [53[53] Lopez, J. A.; Serna, P.; Navarro-Gregori, J. and Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC. Materials and Structures , vol. 48, p. 3703-3718, 2015.] is the fact that the degree of correspondence between direct tensile tests and inverse analyses are the result of several factors that are not related to the back analysis procedure, such as the specimen size, way of casting and fiber distribution.
5. UHPC behavior at high temperature
Concrete exposed to high temperatures is prone to chemical and physical transformations. In microscopic scale, concrete is subjected to drying (free water evaporation), dehydration (CSH physical and chemical bound water loss) and pore-pressure build-up (due to moisture diffusion). In mesoscopic level, strain incompatibilities between aggregates expansion and cement paste shrinkage are developed. At the macroscopic level, concrete is susceptible to thermal expansion, cracking formation and spalling activation. These thermo-hygro-chemical phenomena are responsible for concrete damage and degradation and are influenced by the temperature history (previous fire exposure, maximum temperature reached, heating rate). The type of load applied (compression, tension, bending) during heating influences concrete creep behavior, which is accelerated at high temperatures.
Among all thermochemical reactions, CSH chemistry is very important to understand concrete physical microstructure properties evolution during heating and cooling, since it occupies around 50% of the cement paste volume. According to [56[56] Allen, A. J.; Thomas, J. J. and Jennings, H. M. Composition and density of nanoscale calcium-silicate-hydrate in cement. Nature materials, vol. 6, p. 311-316, 2007.], concrete behavior is largely related to the CSH gel viscoelastic response, stress level and relative humidity changes. This is because creep is directly related to the long-term relaxation of self-equilibrated micro-stresses in the CSH nano-porous microstructure [57[57] Bazant, Z. P.; Hauggaard, A. B.; Baweja, S. and Ulm, F.-J. Microprestress-Solidification Theory for Concrete Creep. I:Aging and Drying Effects. Journal of Engineering Mechanics, n. November, p. 1188-1194, 1997.].
The CSH gel is formed due to the expansion reaction of both cement constituent minerals larnite (C2S) and alite (C3S) in contact with water (concrete hydration and short-term aging). This expansion is not followed by concrete volume change and, as a result, causes a reduction in the capillary pore system and in the concrete permeability. The interconnected gel creates a continuous phase, isolating free water within its nanostructure interlayer. Moreover, CSH strong van der Walls force leads to high water adsorption on its surface.
According to [58[58] Alonso, C. and Fernandez, L. Dehydration and rehydration processes of cement paste exposed to high temperature environments. Journal of Materials Science , n. 39, p. 3015-3024, 2004.], concrete drying, due to heating, up to 250ºC, removes most of the CSH physically bound water (dehydrated CSH). Above 200ºC, CSH is progressively decomposed into new calcium silicates (C2S and C3S), releasing the chemically bound water and reducing concrete binding properties. Beyond 750ºC, there is a complete disintegration of the CSH gel.
As a result, concrete thermochemical transformations during heating are directly related to dehydration due to the loss of physically and chemically bound water. These transformations are responsible for matrix microprestress relaxation (time-dependent deformation), concrete strength reduction and material increasingly ductility.
Moreover, the vaporization process (moisture diffusion due to free water evaporation at 100ºC) leads to an increase of the pore-pressure that could lead to violent spalling. This phenomenon is especially important in UHPC due to its very low porosity and dense microstructure, which favors the moisture clog. The latter is defined as the dilatation and vaporization of moisture content, which obstructs the interconnected porous network, leading to pore-pressure build-up.
5.1 Spalling and pore pressure
At 100ºC vaporization process starts combined with pore-pressure increase, resulting in free water loss. High values of pore-pressure are achieved at 180ºC, from which point a progressive decline is observed. Beyond 220ºC, a drastic pore-pressure reduction occurs. The thermo-hygro process, describing the flow of a fluid in a porous medium, can be expressed both by Darcy’s Law of pressure gradient and by Fick’s Law of diffusion and molar concentration.
The increase in pore pressure occurs due to the flow of fluids to inner parts of the bulk matrix, where they are condensed, creating a region with high water content (saturated zone) which imposes a barrier to the natural fluid flow (moisture clog). As a result, there is an increase in pore-pressure near the concrete surface, which pushes the liquid water out of the specimen, causing water exudation. Due to the pore-pressure increase near the surface, violent spalling could occur.
UHPC is especially susceptible to violent spalling because of its very dense matrix. In order to control and avoid spalling triggering, polypropylene (PP) fibers should be incorporated in UHPC mix design. In this case, fibers melting, around 180ºC, on one hand, increases matrix permeability and, on the other hand, releases matrix steam pressure [60[60] Zeiml, M.; Leithner, D.; Lackner, R. and Mang, H. A. How do polypropylene fibers improve the spalling behaviorof in-situ concrete?. Cement and Concrete Research , vol. 36, p. 929-942, 2006.].
Experimental tests on UHPC carried out by [61[61] Xiong, M.-X. and Liew, J. Y. R. Spalling behavior and residual resistance of fibre reinforced Ultra-High performance concrete after exposure to high temperatures. Materiales de Construcción, vol. 65, 2015.], demonstrated that even a small amount of PP fiber incorporation (0.1% by volume) can prevent spalling. Similarly, tests results from [62[62] Diederichs, U. and Mertzsch, O. Behavior of Ultra High Strength Concrete at High Temperatures. Ultra High Performance Concrete (UHPC): Proceedings of the Second international Symposium on Ultra High Performance Concrete, Kassel , Kassel university Press, 2008, p. 347-354.] demonstrated no evidence of spalling on UHPC reinforced with PP fibers. In contrast, steel fibers are not effective to prevent spalling, even in quantities of 1% by volume.
UHPC tests at high temperature performed by [63[63] Heinz, D.; Dehn, F. and Urbonas, L. Fire Resistance of Ultra High Performance Concrete (UHPC) - Testing of Laboratory Samples and Columns under Load. Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004.] on specimens with 3.5% by volume of steel fibers and 0.66% by volume of PP fibers showed no sign of spalling. Moreover, tests on concrete samples with 0.3% by volume of PP fibers show only small signs of spalling activation.
5.2 Transient creep
Due to concrete complex behavior and the coupling effects of the different strain components at high temperature, it is rather a very difficult task to uncouple transient creep from other thermomechanical strain sources (recoverable and irrecoverable mechanical strains). For practical purposes, transient creep can be described accurately enough by concrete overall behavior. In this case, the concept of LITS (Load Induced Thermal Strain) defined in [64[64] Khoury, G. A. Strain of heated concrete during two thermal cycles. Part 1: strain over two cycles, during first heating and at subsequent constant temperature. Magazine of Concrete Research, n. 6, p. 367-385, 2006.], can be adopted. It includes both transient creep and mechanical strain components (plastic strains and changes in the elastic strain due to concrete softening behavior).
LITS is equal to the difference between the total strain (), measured on a preloaded specimen, and the free thermal strain (), measured on an unloaded specimen, subtracting the initial elastic deformation () at 20°C, as is shown in Eq. 11, where: is the total strain; is the recoverable (elastic) mechanical strain at 20°C; is the thermal strain. It includes changes in the elastic strain due to concrete heating (concrete loss of stiffness) and irrecoverable (plastic) mechanical strains (irreversible strains due to the material strength decay at high temperature).
Free thermal strain is measured experimentally during concrete first heating, being equal to the sum of concrete shrinkage and the recoverable and irrecoverable thermal strains, as is shown in Eq. 12, where: is the recoverable thermal strain; is the irrecoverable thermal strain; is concrete shrinkage. Alternatively, in the lack of experimental results, the free thermal strain can be calculated according to the coefficient of linear thermal expansion, which assumes concrete thermal strain as fully recoverable.
A LITS semi-empirical model is proposed in [65[65] Buttignol, T. E. T. On the Load Induced Thermal Strain for Plain and Steel Fiber Reinforced Concrete Subjected to Uniaxial Loading. PhD thesis, Politecnico di Milano, 2016.]. Its main advantage in relation to other empirical models is the fact that it was calibrated with several experimental results obtained in literature for plain concrete (conventional, high strength and ultra-high performance) subjected to a uniaxial compressive load. Moreover, the model recognizes concrete as a heterogeneous 2-phase material (aggregates + matrix). A comparison of the model with experimental results from literature demonstrated, in the validity range, its reliability.
The semi-empirical model [65[65] Buttignol, T. E. T. On the Load Induced Thermal Strain for Plain and Steel Fiber Reinforced Concrete Subjected to Uniaxial Loading. PhD thesis, Politecnico di Milano, 2016.] is a good solution for design engineers to obtain a preliminary and straightforward quantification of the total strain without the necessity of performing complex numerical analyses, which requires to take into account the heterogeneity (2-phase material), the boundary conditions, the thermal gradient and concrete thermomechanical properties.
In the semi-empirical model, LITS is equal to the sum of thermomechanical (microcracking, aggregate degradation and thermal expansion restraint) and thermochemical (drying and dehydration creep) strain contributions. LITS thermomechanical strain is originated from coarse aggregates inclusions in the matrix, which lead to microcracking (thermal mismatch), concrete thermal expansion restraint imposed by the sustained compressive load and LITS acceleration due to aggregates degradation.
LITS thermochemical strain (matrix-dependent) occurs due to both concrete free water loss (drying creep) and CSH dehydration. It occurs in the cement paste and, thus, it is insensitive to the aggregate type. As a result, an UHPC will develop only thermochemical strains due to the absence of coarse aggregates.
The semi-empirical model is defined in terms of a compliance function (), as is shown in Eq. 13, where: is the thermomechanical compliance function in 10-3 1/MPa for siliceous, calcareous and basalt aggregate types (Eq. 14); is the thermochemical compliance function in 10-3 1/MPa (Eq. 15); is the variable dependent of the aggregate content (Eq. 16); is a variable dependent of the binder (Eq. 17). Temperature is given in ºC, while the quantities of the binder and aggregates are given in kg.
Total LITS (in mm/m), for a specified load level, is calculated according to Eq. 18 and LITS coefficient () is obtained from Eq. 19.
Two examples of validation of the model with experimental results are shown in Figures 3 and 4, considering tests results from [62[62] Diederichs, U. and Mertzsch, O. Behavior of Ultra High Strength Concrete at High Temperatures. Ultra High Performance Concrete (UHPC): Proceedings of the Second international Symposium on Ultra High Performance Concrete, Kassel , Kassel university Press, 2008, p. 347-354.] and [66[66] Huismann, S.; et al. Transient strain of high strength concrete at elevated temperatures and the impact of polypropylene fibers. Materials and Structures , n. 45, p. 793-801, 2012.], respectively on UHPC and HSC specimens. From the comparison, one can observe a good approximation between the proposed model and the experimental curves.
Comparison between LITS model [65[65] Buttignol, T. E. T. On the Load Induced Thermal Strain for Plain and Steel Fiber Reinforced Concrete Subjected to Uniaxial Loading. PhD thesis, Politecnico di Milano, 2016.] and UHPC experimental results [62[62] Diederichs, U. and Mertzsch, O. Behavior of Ultra High Strength Concrete at High Temperatures. Ultra High Performance Concrete (UHPC): Proceedings of the Second international Symposium on Ultra High Performance Concrete, Kassel , Kassel university Press, 2008, p. 347-354.]
Comparison between LITS model [65[65] Buttignol, T. E. T. On the Load Induced Thermal Strain for Plain and Steel Fiber Reinforced Concrete Subjected to Uniaxial Loading. PhD thesis, Politecnico di Milano, 2016.] and HSC experimental results [66[66] Huismann, S.; et al. Transient strain of high strength concrete at elevated temperatures and the impact of polypropylene fibers. Materials and Structures , n. 45, p. 793-801, 2012.]
6. Conclusions
In this paper, a literature survey was performed in order to examine UHPFRC material and mechanical properties, together with some design recommendations. Besides, concrete behavior at high temperature, specifically spalling and transient creep phenomena, were described. The main conclusions are summarized below.
-
A great variability of UHPFRC mixes is found in literature. In some mixtures, more than 1000 kg/m3 of binder is incorporated, increasing the production cost and the mixing procedures. An optimization process can reduce the amount of cement without weakening the material.
-
In contrast to conventional concrete, UHPFRC fresh state properties are characterized by a short period of hydration (≈90 days), an initial long period of dormant (≈24 hours) and a relatively low degree of hydration (). The high amount of binder can lead to mixture overheating, self-desiccation and the formation of balls of cement.
-
The hydrated cement grains create a dense and interconnected microstructure, leading to a very low permeability and improving substantially the mechanical properties, which are characterized by a very high compressive strength capacity, high ductility, enhanced toughness and better bond properties. In order to fully profit from the superior UHPFRC properties, current design codes recommendations should be verified. For example, design tensile constitutive laws should be defined assuming a bilinear (elastic-perfectly plastic regime) or trilinear model to take into account the linear-elastic branch of the curve, the pseudo-plastic phase (multicracking) and the softening behavior (crack localization). Moreover, shear design should include fiber contribution; reinforcing steel bars anchorage length can be limited to 10; and a perfect bond between matrix and rebars can be assumed both at the elastic and pseudo-plastic phases. Besides, due to the high ductility, crack localization can occur after a deformation equal to 0.2%, beyond steel bar yielding point.
-
The mechanical characterization of the material can be carried out by means of bending tests, followed by inverse analysis, to determine the tensile constitutive law. In this case, models based on continuum mechanics, assuming a cross-sectional equilibrium and Bernoulli principle (plane section), can be applied. The characteristic length (crack-opening-strain relationship) can be taken as the average space between cracks during strain hardening and as function of the beam depth during crack localization.
-
The exposure to high temperature leads to a pronounced decrease of the mechanical properties of UHPC due to physical-chemical transformations (free water evaporation, CSH dehydration and microcracking). Moreover, UHPC is prone to violent spalling due to its dense microstructure. Researches on this area demonstrated that a small amount of PP fibers incorporated in the mix can reduce and even avoid spalling triggering.
-
A LITS semi-empirical model [65] that could be adopted for UHPC was described. A comparison of the model with experimental tests obtained in literature demonstrated a good approximation of the model. Despite that, more tests should be carried out in order to reassert the validity of the model.
7. Acknowledgements
The authors would like to acknowledge the support of CNPq through a post-doctoral scholarship granted to the first author.
8. References
-
[1]Denarié, E and Bruhwiler, E. Strain-hardening Ultra-high Performance Fibre Reinforced Concrete: Deformability versus Strength Optimization Proceedings of an ASMES International Workshop, Freiburg, Germany, 2011.
-
[2]Oesterlee, C.; Sadouki, H. and Brühwiler, E. Structural analysis of a composite bridge girder combining UHPFRC and reinforced concrete UHPC-2008: The Second International Symposium on Ultra High Performance Concrete, March 2008.
-
[3]Walraven, J. C. High performance fiber reinforced concrete: progress in knowledge and design codes Materials and Structures, vol. 42, p. 1247-1260, 2009.
-
[4]Charron, J.-P.; Denarié, E. and Bruhwiler, E. Permeability of ultra high performance fiber reinforced concretes (UHPFRC) under high stresses Materials and Structures , vol. 40, p. 269-277, 2007.
-
[5]Sritharan, S. Design of UHPC Structural Members: Lessons Learned and ASTM Test Requirements Advances in Civil Engineering Materials, vol. 4, p. 113-131, 2015.
-
[6]Habel, K.; Viviani, M.; Denarié, E. and Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC) Cement and Concrete Research, p. 1362-1370, 2006.
-
[7]Habel, K. Structural behaviour of elements combining ultra-high performance fibre-reinforced concretes (UHPFRC) and concrete PhD thesis, The Ecole Polytechnique Fédérale de Lausanne, 2004.
-
[8]Waller, V. Relations entre composition des bétons, exothermie en cours de prise et résistance à la compression PhD thesis, Laboratoire Central des Ponst et Chaussées Nantes (LCPC), 2002.
-
[9]van Breugel, K.; Jensen, O. M. and Lura, P. Autogenous shrinkage in high performance cement paste. An evaluation of basic mechanisms Cement and Concrete Research , vol. 33, p. 223-232, 2003.
-
[10]Kamen, A.; Denarié, E.; Sadouki, H. and Bruhwiler, E. Evaluation of UHPFRC activation energy using empirical models Materials and Structures , vol. 42, p. 527-537, 2009.
-
[11]Yu, R.; Spiesz, P. and Brouwers, H. J. H. Mix design and properties assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Cement and Concrete Research , vol. 56, p. 29-39, 2014.
-
[12]Russell H. G. and Graybeal B. A. Ultra-High Performance Concrete: A State-of-the-Art Report for the Bridge Community Report FHWA-HRT-13-060, Jun, 2013.
-
[13]Moser, B. and Pfeifer, C. Microstructure and Durability of Ultra-High Performance Concrete UHPC-2008: The Second International Symposium on Ultra High Performance Concrete, March 2008, pp. 417-424.
-
[14]Toutlemonde, F. and Resplendino, J. (eds.). Designing and Building with UHPFRC: State-of-the-Art and Development, John Wiley and Sons, 2011.
-
[15]Resplendino, J. First recommendations for Ultra-High-Performance Concretes and examples of application Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, pp. 79-90.
-
[16]Carsten, V.; Matthias, G. and Bernhard, M. Seeing at the nanoscale: Hydration of pozzolanic and cementitious materials Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, pp. 143-152.
-
[17]Rossi, P.; Arca, A.; Parant; E. and Fakhria, P. Bending and compressive behaviours of a new cement composite Cement and Concrete Research , vol. 35, p. 27-33, 2005.
-
[18]Andreasen, A. and Andersen, J. Ueber die Beziehung zwischen Kornabstufung und Zwischenraum in Produkten aus losen Körnern (mit einigen Experimenten) Kolloid-Zeitschrift, vol. 50, p. 217-228, 1930.
-
[19]Brouwers, H. J. H. and Hadix, H. J. Self-compacting concrete: the role of the particle size distribution First International Symposium on Design, Performance and Use of Self-Consolidating Concrete, Changsha, Hunan, China, 2005.
-
[20]Fuller, W.B. and Thompson, S.E. The laws of proportioning concrete Transactions of the ASCE, vol. 159, 1907.
-
[21]Funk, J. E. and Dinger, D.R. Particle Packing, Part VI - Applications of Particle Size Distribution Concepts Interceram, vol. 43, pp. 350-3, 1994.
-
[22]Chan, Y.-W. and Li, V. C. Age effect on the characteristics of fibre/cement interfacial properties Journal of Materials Science, n. 32, p. 5287-5292, 1997.
-
[23]Buttignol, T. E. T.; Colombo, M. and Di Prisco, M. Long-term aging effects on tensile characterization of steel fibre reinforced concrete fib Structural Concrete, 2016.
-
[24]K. Wille, D.-J. Kim e A. E. Naaman , «Strain-hardening UHP-FRC with low fiber contents,» Materials and Structures , vol. 44, p. 583-598, 2011.
-
[25]Markovic, I. High-performance hybrid-fibre concrete-development and utilisation phD thesis, Technische Universitat Delft.
-
[26]Naaman, A. E. and Wille, K. Some correlation between high packing density, ultra-high performance, flow ability, and fiber reinforcement of a concrete matrix 2nd Iberian congress on self compacting concrete - BAC2010 , University of Minho-Guimaraes, Portugal, 2010.
-
[27]Wipf, T. J.; Phares, B. M.; Sritharan, S.; Degen B. E. and Giesmann, M. T. Design and Evaluation of a Single-Span Bridge Using Ultra-High Performance Concrete Iowa Department of Transportation, IHRB Project TR-529, 2009.
-
[28]Barnett, S. J.; Lataste, J.-F.; Parry, T.; Millard, S. G. and Soutsos, M. N. Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength Materials and Structures , vol. 43, p. 1009-1023, 2010.
-
[29]Naaman, A. E. and Reinhardt, H. W. Proposed classification of HPFRC composites based on their tensile response Materials and Structures , vol. 39, p. 547-555, 2006.
-
[30]Leutbecher, T. and Fehling, E. Structural Behaviour of UHPC under Tensile Stress and Biaxial Loading Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, p. 435-448.
-
[31]Orgass, M. and Klug, Y. Fibre Reinforced Ultra-High Strength Concretes Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004, p. 637-648.
-
[32]Jungwirth, J. an Muttoni, A. Structural Behavior of Tension Members in UHPC Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2008, p. 533-546.
-
[33]Mahmud, G. H.; Yang, Z. and Hassan, A. M. T. Experimental and numerical studies of size effects of Ultra High Performance Steel Fibre Reinforced Concrete (UHPFRC) beams Construction and Building Materials, n. 48, p. 1027-1034, 2013.
-
[34]AFCG and SETRA. Ultra-High Performance Fibre Reinforced Concrete-Interim Reccomendations France, 2013.
-
[35]Brühwiler, E. (ed.). Recommendation:Ultra-High Performance Fibre Reinforced Cement-based composites (UHPFRC). Construction material, dimensioning und application. Lausanne, Switzerland, 2016.
-
[36]Almansour, H. and Lounis, Z. Innovative Design of Precast/Prestressed Girder Bridge Superstructures using Ultra High Performance Concrete Annual Conference of the transportation Association of Canada, 2008.
-
[37]Graybeal, B. and Davis, M. Cylinder or Cube: Strength Testing of 80 to 200 MPa (11.6 to 29 ksi) Ultra-High-Performance Fiber-Reinforced Concrete ACI Materials Journal, vol. 105, p. 603-609, 2008.
-
[38]Kang, S.-T.; Lee, Y.; Park, Y.-D. and Kim, J.-K. Tensile fracture properties of an Ultra High Performance Fiber Reinforced Concrete (UHPFRC) with steel fiber Composite Structures, vol. 92, p. 61-71, 2010.
-
[39]Naaman, A. E. High Performance Fiber Cement Composites High-performance Construction Materials: Science and Applications, World Scientific Publishing Company , 2008, pp. 448.
-
[40]Naaman, A. E. A statistical theory of strength for fiber reinforced concrete PhD thesis, Massachusetts Intitute of Technology, 1972.
-
[41]Collins, M. P. and Mitchell, D. Prestressed Concrete Structures Prentice Hall, 1991.
-
[42]Pansuk, W. Shear capacity of RC and ultra high strength fiber reinforced concrete flanged beams. phD thesis, Hokkaido University, Japan, 2007.
-
[43]Harris, D. K. Characterizaion of Punching Shear Capacity of Thin UHPC Plates Master Dissertation, Virginia Polytechnic Institute and State University, 2004.
-
[44]American Concrete Institute. Building Code Requirements for Structural Concrete and Commentary (ACI 318R-08). ACI Committee 318, Farmington Hills, MI, 2008.
-
[45]Joh, C.; Hwang, H. and Kim, B. Punching shear and flexural strengths of ultra high performance concrete slabs High Performance Structures and Materials IV, vol. 97, p. 97-106, 2008.
-
[46]Switek, A.; Denarié, E. and Bruhwiler, E. Modeling of viscoelastic properties of Ultra High Performance Fiber Reinforced Concrete (UHPFRC) under low to high tensile stresses Symposium on Concrete Modelling, 22-25 June 2010.
-
[47]Bazant, Z. P. Numerical determination of long-range stress history from strain history in concrete Materials and Structures , vol. 5, p. 135-141, 1972.
-
[48]Flietstra, J. C. Creep and shrinkage behavior of ultra-high performance concrete under compressive loading with varying curing regimes Master Dissertation, Michigan Technological University, 2011.
-
[49]Kamen, A. Time dependent behaviour of ultra high performance fibre reinforced concrete (UHPFRC) 6th International PhD Symposium in Civil Engineering, Zurich, 2006.
-
[50]Macá, P.; Sovják, R. and Vavriník, T. Experimental Investigation of Mechanical Properties of UHPFRC Precedia Engineering, vol. 65, p. 14-19, 2013.
-
[51]EN 14651. Test method for metallic fibered concrete - Measuring the flexural tensile strength (limit of proportionality (LOP), residual) European Comettee for Standardization, 2005.
-
[52]UNI11039. Concrete Renforced with Steel Fibres. Part II: Test Method for the Determination of First Cracking Strength and Ductility Indexes 2003.
-
[53]Lopez, J. A.; Serna, P.; Navarro-Gregori, J. and Camacho, E. An inverse analysis method based on deflection to curvature transformation to determine the tensile properties of UHPFRC Materials and Structures , vol. 48, p. 3703-3718, 2015.
-
[54]Baby, F.; Graybeal, B.; Marchand, P. and Toutlemonde, F. UHPFRC tensile behavior characterization: inverse analysis of four-point bending test results Materials and Structures , vol. 46, p. 1337-1354, 2013.
-
[55]Di Prisco, M.; Colombo, M. and Dozio, D. Fibre-reinforced concrete in fib Model Code 2010: principles, models and test validation Structural Concrete, vol. 14, p. 342-361, 2013.
-
[56]Allen, A. J.; Thomas, J. J. and Jennings, H. M. Composition and density of nanoscale calcium-silicate-hydrate in cement Nature materials, vol. 6, p. 311-316, 2007.
-
[57]Bazant, Z. P.; Hauggaard, A. B.; Baweja, S. and Ulm, F.-J. Microprestress-Solidification Theory for Concrete Creep. I:Aging and Drying Effects Journal of Engineering Mechanics, n. November, p. 1188-1194, 1997.
-
[58]Alonso, C. and Fernandez, L. Dehydration and rehydration processes of cement paste exposed to high temperature environments Journal of Materials Science , n. 39, p. 3015-3024, 2004.
-
[59]Fu, Y. and Li, L. Study on mechanism of thermal spalling in concrete exposed to elevated temperatures Materials and Structures , vol. n. 44, p. 361-376, 2011.
-
[60]Zeiml, M.; Leithner, D.; Lackner, R. and Mang, H. A. How do polypropylene fibers improve the spalling behaviorof in-situ concrete? Cement and Concrete Research , vol. 36, p. 929-942, 2006.
-
[61]Xiong, M.-X. and Liew, J. Y. R. Spalling behavior and residual resistance of fibre reinforced Ultra-High performance concrete after exposure to high temperatures Materiales de Construcción, vol. 65, 2015.
-
[62]Diederichs, U. and Mertzsch, O. Behavior of Ultra High Strength Concrete at High Temperatures Ultra High Performance Concrete (UHPC): Proceedings of the Second international Symposium on Ultra High Performance Concrete, Kassel , Kassel university Press, 2008, p. 347-354.
-
[63]Heinz, D.; Dehn, F. and Urbonas, L. Fire Resistance of Ultra High Performance Concrete (UHPC) - Testing of Laboratory Samples and Columns under Load Proceedings of the International Symposium on Ultra High Performance Concrete, Kassel, Germany, 2004.
-
[64]Khoury, G. A. Strain of heated concrete during two thermal cycles. Part 1: strain over two cycles, during first heating and at subsequent constant temperature Magazine of Concrete Research, n. 6, p. 367-385, 2006.
-
[65]Buttignol, T. E. T. On the Load Induced Thermal Strain for Plain and Steel Fiber Reinforced Concrete Subjected to Uniaxial Loading PhD thesis, Politecnico di Milano, 2016.
-
[66]Huismann, S.; et al. Transient strain of high strength concrete at elevated temperatures and the impact of polypropylene fibers Materials and Structures , n. 45, p. 793-801, 2012.
Publication Dates
-
Publication in this collection
Aug 2017
History
-
Received
20 Nov 2016 -
Accepted
22 June 2017