Abstract
This paper presents results of a time-domain spherical-multipole near-to-far-field transformation together with a moment expansion applied to antenna radiation patterns. The equivalence principle is applied to the tangential fields all over the FDTD/WP-PML spatial grid and the use of the spherical-multipole expansion leads to the near-to-far-field transformation, and energy and power norms of temporal signals are used to obtain the antenna radiation patterns for transient and steady-state responses. Such approach is employed to obtain UWB antenna radiated fields and radiation patterns directly in time-domain, it being more convenient to perform an unified characterization in time and frequency domains.
Finite-difference time-domain method; time-domain spherical multipole; time-domain moment expansion
IFederal University of São João del-Rei, Department of Telecommunications and Mechatronics Engineering, Ouro Branco, MG, glaucio@ufsj.edu.br and Graduate Program in Electrical Engineering - Federal University of Minas Gerais
IIFederal University of Minas Gerais, Department of Electronic Engineering, Belo Horizonte, MG, cassio@cpdee.ufmg.br
IIIFederal University of Vales do Jequitinhonha e Mucuri, Department of Computing, Diamantina, MG, arfonseca@ufvjm.edu.br
ABSTRACT
This paper presents results of a time-domain spherical-multipole near-to-far-field transformation together with a moment expansion applied to antenna radiation patterns. The equivalence principle is applied to the tangential fields all over the FDTD/WP-PML spatial grid and the use of the spherical-multipole expansion leads to the near-to-far-field transformation, and energy and power norms of temporal signals are used to obtain the antenna radiation patterns for transient and steady-state responses. Such approach is employed to obtain UWB antenna radiated fields and radiation patterns directly in time-domain, it being more convenient to perform an unified characterization in time and frequency domains.
Index Terms: Finite-difference time-domain method, time-domain spherical multipole, time-domain moment expansion.
I. INTRODUCTION
The finite-difference time-domain (FDTD) method in addition to absorbing boundary conditions and perfect matched layers (PML) has been successfully used in analysis of radiation and scattering problems. FDTD is very efficient when making near-field calculations, while for the far field it is necessary to implement an additional method to perform a near-to-far-field (NF-FF) transformation. The first technique used to perform the NF-FF transformation could only be applied for a single frequency analysis [1], [2]. In order to obtain a larger frequency bandwidth response, a broadband excitation followed by discrete Fourier transform was performed [1], [3].
Recently, methods involving a recursive addition of tangential fields contribution over a virtual equivalence surface have been used to perform the same task [4]-[7]. Conventional time-domain NF-FF transformation techniques [1], [3], where time-domain far fields can be directly obtained, are based on the retarded potential method and as a consequence, a new integration over the near-field is necessary for each observation point [5], [9]. Therefore, when broadband results are required at a large number of observation angles, as is the case with radiation patterns, these techniques require a large number of computational resources [3]. Recently a time-domain spherical- multipole near-to-far- field was proposed where once multipole amplitudes were obtained, the time-domain multipole expansion is valid at any arbitrary point in the far field [8]-[10].
In this paper we propose the use of a moment expansion together with a time-domain spherical-multipole NF-FF. The main advantage of a time domain multipole approach is that the radiated fields can be obtained for an antenna excited by any sources with pulsed temporal behavior and thus it allows the characterization of its radiation pattern in time and frequency domains. Such approach is very useful in the unified characterization of UWB antennas. The definition of gain and radiation pattern in time-domain based on the concept of norms applied to temporal signals is very important as it allows the comparison between the energy (or power) of the radiated field and that of the antenna driving source [12].
This letter is organized as follows: Section II gives a brief description of the time-domain spherical-multipole near-to-far-field transformation. In Section III, the proposed code is applied to obtain a radiation pattern of an IR-UWB antenna and results compared with those previously obtained by measurements [11].
II. TIME-DOMAIN SPHERICAL-MULTIPOLE NEAR-TO-FAR-FIELD EXPANSION
Using a spherical-multipole expansion, the electromagnetic field can be expanded as [8]-[10]
where  and
and  denotes the frequency-domain spherical-multipole amplitudes [8],
denotes the frequency-domain spherical-multipole amplitudes [8],  is the intrinsic impedance with
is the intrinsic impedance with  and
and  denoting the permittivity and permeability, respectively.
denoting the permittivity and permeability, respectively.
The set of vector spherical-multipole functions are defined as [10]
where  is a spherical Hankel function of the second kind and
is a spherical Hankel function of the second kind and  denoting the wavenumber.
denoting the wavenumber.
The set of vector functions with respect to the transverse fields on a spherical surface are defined as [10]
where  denotes the normalized surface spherical-harmonics defined as
denotes the normalized surface spherical-harmonics defined as
where  denotes an associated Legendre function of the first kind,
denotes an associated Legendre function of the first kind,  . and
. and  . It is important to mention that the maximum order of n has been empirically found to be
. It is important to mention that the maximum order of n has been empirically found to be  [8], when considering a d-digit accuracy and r0 denoting the radius of the minimum sphere which contains all the physical sources.
[8], when considering a d-digit accuracy and r0 denoting the radius of the minimum sphere which contains all the physical sources.
Considering that FDTD near-field components on a Huygens surface can be replaced by equivalent electric and magnetic dipoles, the far field can be obtained in time-domain by a near-to-far-field transformation as [10]
where is the velocity of light in vacuum,
is the velocity of light in vacuum,  and
and  are the time-domain spherical-multipole amplitudes [8] and r,
are the time-domain spherical-multipole amplitudes [8] and r,  and
and  denote the spherical coordinates of the far-field point.
denote the spherical coordinates of the far-field point.
For frequency-domain radiation patterns, applying a modified Fourier transform to the time-domain multipole amplitudes, the multipole amplitudes are obtained in frequency-domain and the power radiation pattern of the antenna can be obtained by [9]
For antennas with narrowband operation it is enough to analyze their characteristics in frequency-domain. However, with the beginning of antenna operation with pulsed signals, which requires a wider bandwidth, it is necessary to make a redefinition on antenna parameter analysis, and it is very useful to define a time-domain radiation pattern, based on the energy of radiated fields. The norm of a time-dependent signal is a way to quantify the energy contained in a signal. For the time-domain radiation pattern, the time-domain electric far field calculated by the near-to-far-field transformation can be used and the time-domain patterns is defined as [12]
where
and  is a norm of a time-dependent signal [12], which can be evaluated for energy and power signals.
is a norm of a time-dependent signal [12], which can be evaluated for energy and power signals.
III. MOMENT EXPANSION OF TIME FUNCTIONS AND IMPULSE RESPONSE
The impulse response of an antenna can be obtained by an inverse Fourier transform in a deconvolution process. It can be also be obtained directly from an arbitrary time response of the antenna under analysis, by a moment expansion of a signal in the time domain [13]. Considering a circuit excited at a port i with a signal  and the associated response,
and the associated response,  , at a port k, the followed relation is valid
, at a port k, the followed relation is valid
where  is the impulse response between k and i ports written as
is the impulse response between k and i ports written as
with  being the inverse Fourier transform,
being the inverse Fourier transform,  . The impulse response
. The impulse response  can be obtained by FDTD using a Fourier process for the samples
can be obtained by FDTD using a Fourier process for the samples  and
and  , or, the integral equation as in (10).
, or, the integral equation as in (10).
A deconvolution with less computational effort can be obtained using the expansion as in [13]
where  and the coefficients
and the coefficients  are obtained by the moments
are obtained by the moments  of the time signal
of the time signal  :
:
with
and
The moment expansion as in (11) can be used to obtain the impulse response:
or, for  with non-zero average:
with non-zero average:
or, for the zero average case:
In this work the input signal for the antenna under analysis was the gaussian pulse in the form of
Using the FDTD time increment , and for a Gaussian pulse excitation in the form of (20) we can use a fourth order approximation for the input i and output port k leading to an impulse response between these ports hik as [13]
, and for a Gaussian pulse excitation in the form of (20) we can use a fourth order approximation for the input i and output port k leading to an impulse response between these ports hik as [13]
where the parameters a0, a2, a4 and n0 are
and the shift parameter , with
, with  , is chosen in order to put the center of gravity of the input signal at
, is chosen in order to put the center of gravity of the input signal at  [13].
[13].
IV. NUMERICAL RESULTS
Here we suggest an alternative approach to perform the spherical-multipole near-to-far-field transformation together with a moment expansion process in order to obtain the time-domain radiation pattern of an UWB antenna.
Once the far fields are obtained by the time-domain spherical-multipole transformation, for each coordinate θ and φ, we can use these values as outputs for the moment expansion technique, vk, and derive their correspondent impulse response. From the impulse response each far field component obtained from a sinusoidal source could be directly estimated by means of a convolution process and the time-domain radiation pattern could be directly obtained, without the need to perform a Fourier transform.
As a Gaussian pulse is band-limited, the computation of the frequency-domain far fields on the FDTD solver is less accurate outside a frequency band depending on the chosen computational parameters [16]. As a consequence, the moment expansion technique with fourth-order truncation has shown to improve accuracy and computational efficiency when using Gaussian pulse excitation when compared with the Fourier transform, especially when the upper frequency of the impulse response is greater than its upper (10% amplitude) frequency [13]-[15]. The used parameters for the impulse response retrieval via FDTD and ME deconvolution moment expansion technique may be  , where
, where  , where n may be in the range [8-10], Δ is the largest FDTD cell size and fM is the highest frequency to be computed. The Gaussian-pulse parameters may be also such that its 10% amplitude upper frequency fG may be in the range
, where n may be in the range [8-10], Δ is the largest FDTD cell size and fM is the highest frequency to be computed. The Gaussian-pulse parameters may be also such that its 10% amplitude upper frequency fG may be in the range  [13].
[13].
In order to validate the proposed method the time and frequency-domain radiation pattern of a half wavelength dipole at 10 GHz, fed by a Gaussian source in form of (20) was simulated and compared with the analytical frequency-domain solution [17]. The FDTD grid are 101 Δx × 101 Δy × 101 Δz with Δx = Δy = Δz = 0.484 mm, Δt = 0.6415 ps, and 6 PML cells. The Huygens surface was chosen to located 10 cells away from the dipole and the upper limit nmax = 12 [8] was also used. Fig. 1 depicts the vertical time and frequency-domain radiation pattern radiation patterns obtained from the spherical-multipole together with the moment expansion proposed technique, TD(ME) and FD(ME), and the frequency-domain radiation pattern analytical solution used as reference [17], illustrating the accuracy of the technique proposed here, especially when obtaining time-domain radiation patterns.
The spherical-multipole time-domain near-to-far-field technique together with moment expansion are applied to an UWB patch antenna [11] in order to obtain its far field and radiation pattern at 4, 7 and 10 GHz. Figure 2 shows the geometry of the UWB antenna under analysis. The patch antenna dimensions are Lsub = 35 mm, Wsub = 30 mm, Lf = 12.5 mm, Wf = 3.2 mm, Lp = 14.5 mm, Wp = 15 mm, Wc = 1 mm, Lst1 = 1 mm, Wst1 = 1.5 mm, Lst2 = 1.5 mm, Wst2 = 1.5 mm, Lsl1 = 5 mm, Lsl2 = 7 mm and Wsl = 0.5 mm. This UWB antenna has also a 1.6 mm thick FR4 dielectric substrate, on z-plane, with a relative permittivity of εr = 4.4. The antenna dimensions corresponds to 120 Δx × 140 Δy × 6 Δz FDTD cells, at x, y and z direction, respectively.
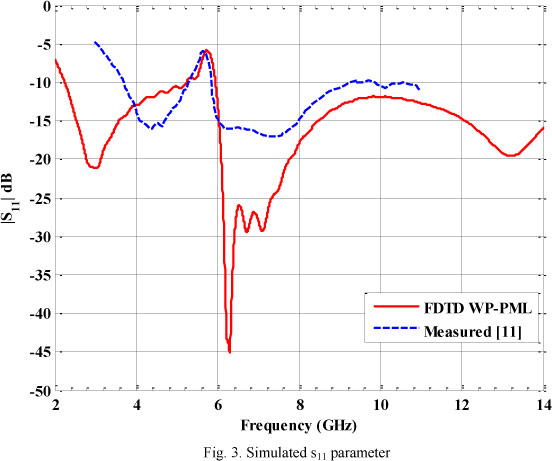
The full domain of the FDTD solver was 180 Δx × 200 Δy × 63 Δz cells with 5 PML cells in each direction and the antenna feed was driven by a Gaussian pulse in the form of (20), with T0 = 15 ps and τ0 = 3T0 , and the simulation time was  . An excitation plane was defined at FDTD code where a vertical electrical field was imposed at a rectangular region below the structure of the UWB antenna. Figure 3 shows the simulated antenna reflection s11 parameter, obtained from the developed FDTD/WP-PML Fortran code, where the effect of the U-slotted filter to reject frequencies between 5.15 GHz and 5.825 GHz can be cleared observed. A good agreement could be observed between the simulation and measurements previously obtained [11].
. An excitation plane was defined at FDTD code where a vertical electrical field was imposed at a rectangular region below the structure of the UWB antenna. Figure 3 shows the simulated antenna reflection s11 parameter, obtained from the developed FDTD/WP-PML Fortran code, where the effect of the U-slotted filter to reject frequencies between 5.15 GHz and 5.825 GHz can be cleared observed. A good agreement could be observed between the simulation and measurements previously obtained [11].
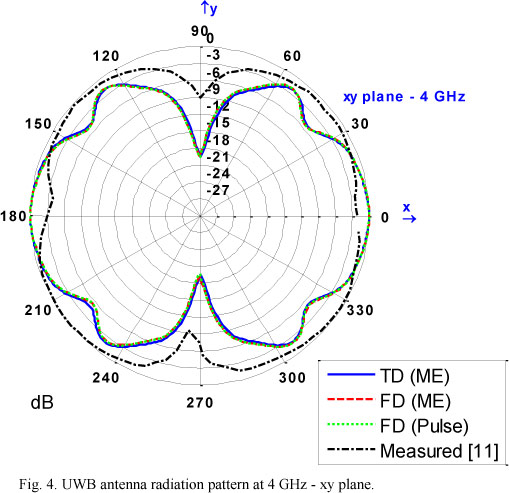
Simulated frequency and time-domain radiation patterns are shown on Figures 4-12 on the x-y, x-z and y-z plane at 4, 7, and 10 GHz. Frequency-domain radiation patterns followed by a moment expansion technique were obtained using Eq. 6 and results are referenced as FD (ME). Time-domain radiation patterns followed by a moment expansion technique were obtained using Eq. 7 and results are referenced as TD (ME). A conventional frequency-domain radiation pattern obtained from a Fourier transform was also obtained in order the compare and validate results of the proposed technique and results are referenced as FD(Pulse). A good agreement could also be observed between the simulation using the proposed technique and results previously obtained from measurements [11].
The differences between simulation and measurements can be explained by the specific modeling of the source used in this research, which can be different from the used reference [11], and by the use of a maximum empirically order of n, nmax, for the specified accuracy of the multipole model, as well as the truncation on the simulation time when time-domain multipoles amplitudes are calculated. The electric and magnetic dipoles obtained on the Huygens surface are not obtained from a perfect sphere with constant radium, as the FDTD use cube Yee cells, and this approximation can also contribute to the differences observed. It is also important to mention that similar differences were found when comparing the measurements and the simulation obtained by commercial software [11].
As the spherical-multipole near-to-far-field is a time-domain technique these results showed that the use of the proposed moment expansion together with the NF2FF transform allows the radiation pattern to be evaluated directly in time-domain with good agreement with measurements as well as with conventional frequency-domain radiation patterns.
V. CONCLUSION
In this work a time-domain spherical-multipole together with a moment expansion of time signals was proposed to characterize the radiation pattern of an IR-UWB antenna at three different frequency bands. Time and frequency-domain radiation patterns were obtained for the frequency bands under analysis and results were compared with measurements results previously obtained. Good agreements could be observed, validating the proposed use of moment expansion together with time-domain spherical-multipole NF-FF transformation and also validating the use of the time-domain radiation pattern. The importance of time-domain radiation patterns relies in the fact that energy and power norms of temporal signals can be used to obtain the antenna radiation patterns for transient and steady-state responses, from any arbitrary source feeding the antenna, which is very important specially for UWB antennas. Better results are expected to be obtained by adding a technique that permits the extension of simulation time without significantly increasing of the computational effort.
ACKNOWLEDGMENTS
This work was partially supported by CNPq, under Covenant 573939/2008-0 (INCT-CSF) and Project 471430/2011-0, and Fapemig, under Projeto do Pesquisador Mineiro.
Received 21 Oct 2012
For review 7 Dec 2012
Accepted 8 July 2013
- [1] A. Taflove and S. C. Hagness, Computation Electrodynamics: The Finite-Difference Time-Domain Method, Artech House, Boston, MA, 1995.
- [2] A. Taflove, "Application of the finite-difference time-domain method to sinusoidal steady state electromagnetic penetration problems," IEEE Transactions on Electromagnetic Compability, vol. 22, no. 3, pp. 191 - 202, August 1980.
- [3] A. Elsherbeni and V. Demir, The Finite-Difference Time-Domain Method for Electromagnetics with MATLAB Simulations, Scitech Publishing, Raleigh, NC, 2009.
- [4] K. Yee, D. Inghmam and K. Shlager, "Time Domain extrapolation to the far field based on FDTD calculations," IEEE Transactions on Antennas and Propagation, vol. 39, no. 3, pp. 410 - 413, March 1991.
- [5] R. Luebbers, K. Kunz, M. Schneider and F. Hunsberger, "A finite-difference time-domain near zone to far zone transformation," IEEE Transactions on Antennas and Propagation, vol. 39, no. 3, pp. 429 - 433, March 1991.
- [6] M. Barth, R. McLeod and R. Ziolkowski, "A near and far field projection algorithm for finite-difference time-domain codes," Journal of Electromagnetic Waves and Applications, vol. 6, no. 1 - 6, pp. 5 - 18, March 1992.
- [7] D. Sullivan and J. L. Young, "Far-field time-domain calculation from aperture radiators using the FDTD method," IEEE Transactions on Antennas and Propagation, vol. 4, no. 3, pp. 464 - 469, March 2001.
- [8] C. Oetting and L. Klinkenbusch, "Near-to-Far-Field Transformation by a Time-Domain Spherical-Multipole Analysis," IEEE Transactions on Antennas and Propagation, vol. 53, no. 6, pp. 2054 - 2063, June 2005.
- [9] J. Adam and L. Klinkenbusch, "Efficient evaluation of antenna fields by a time-domain multipole analysis," Advances in Radio Science, vol. 7, pp. 43 - 48, May 2009.
- [10] J. Adam, L. Kinkenbusch, H. Mextorf and R. H. Knöchel, "Numerical Multipole Analysis of Ultrawideband Antennas," IEEE Transactions on Antennas and Propagation, vol. 58, no. 12, pp. 3847 - 3855, December 2010.
- [11] T. Vuong, A. Ghiotto, Y. Duroc and S. Tedjini, "Design and characteristics of a small u-slotted planar antenna for IR-UWB," Microwave and Optical Technology Letters , vol. 49, no. 7, pp. 1727 - 1731, July 2007.
- [12] C. G. Rego, S. T. M. Gonçalves and F. J. S. Moreira, "High-frequency asymptotic for prompt response of parabolic reflector antennas," Int. J. Electron. Commun., vol. 64, pp. 36 - 46, 2010.
- [13] G. Marroco and F. Bardati, "Time-domain macromodel of planar microwave devices by FDTD and moment expansion," IEEE Transactions on Microwave Theory and Techniques, vol. 49, pp. 1321 - 1328, July 2001.
- [14] G. Marroco and F. Bardati, "FDTD computation of microwave device impulse response," Electronics Letters, vol. 35, no. 3, pp. 223 - 224, February 1999.
- [15] G. Talenti, "Recovering a function from a finite number of moments," Inverse Problems, vol. 3, pp. 501 - 517, 1987.
- [16] G. L. Ramos and C. G. Rego, "Time-Domain Spherical Multipoles Applied to Radiation Pattern Characterization," 15º SBMO Simpósio Brasileiro de Micro-ondas e Optoeletrônica e o 10º CBMag Congresso Brasileiro de Eletromagnetismo, August 2012.
- [17] C. A. Balanis, Antenna Theory: Analysis and Design, Wiley-Interscience, 2nd ed., 2005.
Characterization of the radiation pattern of antennas using time-domain spherical-multipole and moment expansion
Publication Dates
-
Publication in this collection
10 Feb 2014 -
Date of issue
Dec 2013
History
-
Received
21 Oct 2012 -
Accepted
08 July 2013 -
Reviewed
07 Dec 2012