Abstract
In this work, we investigate the effects of estimation uncertainties in the optimization of the optical signal-to-noise ratio (OSNR) at the wavelength division multiplexing (WDM) optical networks. The OSNR optimization increases the network throughput and energy efficiency and it enables to minimize the number of retransmissions by higher layers. The OSNR optimization algorithms are related to the optical channel estimation performed by the combinations of optical performance monitors (OPM) measurements, analytical models and numerical simulations. Furthermore, the estimation uncertainties are introduced by several factors such as the availability of monitoring information, monitoring accuracy, imperfection of physical layer and dynamic of channel allocation. Our numerical results have demonstrated the relation between the uncertainties in the channel error estimation, normalized mean squared error (NMSE) and power penalty. The developed methodology can be utilized to determinate the maxim level of acceptable uncertainties in the channel error estimation according the power penalty permitted in the OSNR optimization.
optical networks; optical signal noise ratio; uncertainties; optimization algorithm
I. introduction
The continuous increase of Internet traffic and others applications such as high-definition video communications, e-learning and cloud computing results in the high bandwidth request in the optical core networks. Because of this rapid increase in traffic demands, optical transmission and networking technologies are moving toward more efficient, flexible and scalable solutions [11 D. Kilper, K. Bergman, V. W. S. Chen, I. Monga, G. Porter, and K. Rauschenbach, "Optical Networks Come of Age," OSA Optics and Photonics News, pp. 50-57, Sep. 2014.]. The dynamic adaptation of the network resources such as bandwidth, lightpaths, rate and power is necessary to build flexible networks that simultaneously support legacy and new services [11 D. Kilper, K. Bergman, V. W. S. Chen, I. Monga, G. Porter, and K. Rauschenbach, "Optical Networks Come of Age," OSA Optics and Photonics News, pp. 50-57, Sep. 2014.][22 B. Birand, H. Wang, K. Bergman, D. Kilper, T. Nandagopal, G. Zussman, "Real-time power control for dynamic optical networks - algorithms and experimentation," IEEE Journal on Selected Areas in Communications, vol. 32, no. 8, pp. 1615 – 1628, Aug. 2014.]. These networks must provide maximum reuse of existing optical infrastructure, flexible bandwidth upgradeability and management, apart from capability to provide higher capacity [33 R. Doverspike and J. Yates, “Optical network management and control,” Proc.IEEE, vol. 100, no. 5, pp. 1092–1104, May 2012.]. In addition, it is mandatory to the next generation of optical systems to increase energy efficiency, since the increase of the power consumption in Information and Communication Technology (ICT) has been continuously observed considering the traffic increasing [44 Rodney S. Tucker, "Green Optical Communications - Part II: Energy Limitations in Networks", IEEE J Selected Topics in Quantum Electronics, vol. 17, no. 2, pp. 261 – 274, March-April 2011.].
The evolution of optical network layer equipment has provided flexibility with respect to the adjustment of the network link conditions and traffic demands, however optical networks are mostly static yet owing to potential impairments that are hard to forecast or model [22 B. Birand, H. Wang, K. Bergman, D. Kilper, T. Nandagopal, G. Zussman, "Real-time power control for dynamic optical networks - algorithms and experimentation," IEEE Journal on Selected Areas in Communications, vol. 32, no. 8, pp. 1615 – 1628, Aug. 2014.][55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.]. These impairments are composed by the linear and nonlinear physical effects [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. The linear impairments include amplified spontaneous emission (ASE), polarization mode dispersion (PMD) and group velocity dispersion (GVD) or chromatic dispersion (CD) effects [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. Besides, the nonlinear impairments include self-phase modulation (SPM), cross-phase modulation (XPM) and four-wave mixing (FWM) [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. In this scenario, the lightpaths are exceptionally modified, as soon as assigned due to these impairments [22 B. Birand, H. Wang, K. Bergman, D. Kilper, T. Nandagopal, G. Zussman, "Real-time power control for dynamic optical networks - algorithms and experimentation," IEEE Journal on Selected Areas in Communications, vol. 32, no. 8, pp. 1615 – 1628, Aug. 2014.][55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.]. Furthermore, algorithms of resource allocation such as routing and wavelength allocation (RWA) and power allocation (PA) are done mainly at the planning step, with significant over-provisioning. In the RWA, given a set of connection requests that represents a traffic matrix, the problem consists of selecting a lightpath, that is, an appropriate path and a wavelength on the links of that path, for each requested connection [33 R. Doverspike and J. Yates, “Optical network management and control,” Proc.IEEE, vol. 100, no. 5, pp. 1092–1104, May 2012.][55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.]. On the other hand, the PA consists in the determination of the appropriated value of the transmitted power for each lightpath according to the adequate optical signal-to-noise ratio (OSNR) level [22 B. Birand, H. Wang, K. Bergman, D. Kilper, T. Nandagopal, G. Zussman, "Real-time power control for dynamic optical networks - algorithms and experimentation," IEEE Journal on Selected Areas in Communications, vol. 32, no. 8, pp. 1615 – 1628, Aug. 2014.]. However, any changes are executed manually using offline algorithms, which is expensive and time demanding [33 R. Doverspike and J. Yates, “Optical network management and control,” Proc.IEEE, vol. 100, no. 5, pp. 1092–1104, May 2012.]. In this work, the PA problem applied to the OSNR optimization is investigated considering the computational complexity to the integration with RWA optimization problem.
The establishment of lightpaths with a higher OSNR enables us to minimize the number of retransmissions by higher layers, thus increasing network throughput and energy efficiency [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.][88 F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683]. For a dynamic traffic requests the objective is to minimize the blocking probability of the lightpaths established by routing, assigning channels while maintain an acceptable level of optical power and suitable OSNR all over the network [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.][99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014]. Furthermore, different lightpaths can travel via different routes and presents different requirements of quality of service (QoS). The QoS is related to the OSNR, dispersion, and nonlinear effects those are represented by the quality-of-transmission (QoT) [55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.][77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. Therefore, it is desirable to adjust network parameters such as optical transmitted power, amplifier gain, OADMs/OXCs power losses in an optimal way, based on online decentralized iterative algorithms, to accomplish such adjustment [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]-[99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014][1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.]. The OSNR optimization could be integrated with RWA, considering the OSNR optimization procedure implemented after the routing step and the lightpath assignment have been established [1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.]. This approach is conveyed to the generalized multiprotocol label switching (GMPLS) signaling protocol in order to allocate the available power resources if and only if the connection meets OSNR constraints. Otherwise, the request is blocked.
The OSNR optimization algorithms are related to the optical channel estimation in the lighpath route or in the receiver node [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]-[1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.]. The estimation process is based on combinations and interpolations of optical performance monitors (OPM) measurements, as well as in analytical models and numerical simulations [1111 Z. Pan, C. Yu, and A. Willner, “Optical performance monitoring for the next generation optical communication networks,” Opt. Fiber Technol., vol. 16, no. 1, pp. 20–45, 2010.]-[1313 S. Pachnicke, T. Gravemann, M. Windmann, and E. Voges, “Physically constrained routing in 10-Gb/s DWDM networks including fiber nonlinearities and polarization effects,” J. Lightwave Technol., vol. 24, n. 9, pp. 3418–3426, Sep. 2006.]. The main figures of merit of QoT are the OSNR and the bit error rate (BER) [55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.]. The estimation of QoT at each node is affected directly by the transmitted pulse shape, filter types and bandwidth. These elements will compromise some parameters of the received signal samples utilized in the estimation processes. In addition, the estimation processes is affected by the channel impairments, mainly GVD and PMD, and on the noise power spectral density (PSD) [1414 S. Azodolmolky et al., “A novel impairment aware RWA algorithm with consideration of QoT estimation inaccuracy,” J. Opt. Commun. Netw., vol. 3, pp. 290–299, Apr. 2011.]. The dispersive effects, such as GVD and PMD are signal degradation mechanism that significantly affects the overall performance of optical communication systems, as well as the degradation of the measurements performed by OPM [1212 D. Kilper, R. Bach, D. Blumenthal, D. Einstein, T. Landolsi, L. Ostar, M. Preiss, and A. Willner, “Optical performance monitoring,” J. Lightw. Technol., vol. 22, no. 1, pp. 294–304, Jan. 2004.] [1414 S. Azodolmolky et al., “A novel impairment aware RWA algorithm with consideration of QoT estimation inaccuracy,” J. Opt. Commun. Netw., vol. 3, pp. 290–299, Apr. 2011.]. The effects of PMD is one major physical impairment that must be considered in high capacity optical networks which can hardly be controlled due its dynamic and stochastic nature [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. In addition, the GVD causes the temporal spreading of optical pulses that limits the product line rate and link length [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. On the other hand, the OSNR measurements techniques could be affected by these dispersion effects in the transmission link [1111 Z. Pan, C. Yu, and A. Willner, “Optical performance monitoring for the next generation optical communication networks,” Opt. Fiber Technol., vol. 16, no. 1, pp. 20–45, 2010.]. Therefore, the measured information about the channel gain utilized by the OSNR optimization algorithm could be deteriorated by the uncertainties caused by the effects of CD and PMD. The power uncertainties of 1dB could results in 20% of further regenerators in the optical network [1515 T. Zami, A. Morea, F. Leplingard, and N. Brogard, “The relevant impact of the physical parameters uncertainties when dimensioning an optical core transparent network,” in Proc. European Conf. Optical Communications (ECOC), 2008.].
In this context, the contribution of this work lies in the modeling and evaluation of the effects of estimation uncertainties in the OSNR optimization applied to the context of optical networks. The estimation uncertainties depends on the several factors such as the availability of monitoring information, monitoring accuracy, imperfection of physical layer and dynamic of channel allocation [1414 S. Azodolmolky et al., “A novel impairment aware RWA algorithm with consideration of QoT estimation inaccuracy,” J. Opt. Commun. Netw., vol. 3, pp. 290–299, Apr. 2011.][1515 T. Zami, A. Morea, F. Leplingard, and N. Brogard, “The relevant impact of the physical parameters uncertainties when dimensioning an optical core transparent network,” in Proc. European Conf. Optical Communications (ECOC), 2008.]. Hence, specifically, our contribution in the OSNR optimization modeling is based on the analytical-iterative algorithm for adjusting the transmitted power levels according the OSNR target [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. The proposed algorithm is distributed and autonomous, i.e., it deploys decentralized feedback while it needs only the estimation of local QoT parameters for the algorithm updating [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.][99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014]. In this sense, in the previous works the perfect channel estimation hypothesis were considered while herein, differently, we adopt the channel estimation based on availability of monitoring information, monitoring accuracy and imperfection of physical layer.
The remainder of this paper is described as follows. In Section II, the network architecture, the transmission system and the OSNR optimization algorithm are described. In Section III, the system model with the aim to obtain the estimation uncertainties is formulated. In Section IV, the main results are analyzed, and finally, the relevant conclusions are presented in Section V.
II. Wavelength Division Multiplexing Optical Network
This section illustrates the WDM network architecture, as well as the OSNR model for considering intensity modulated wavelengths channels.
A. Network Architecture
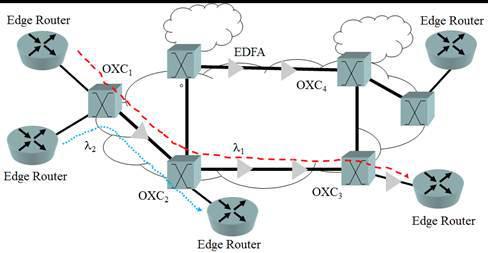
The WDM network considered in this work is formed by nodes that have optical switching nodes interconnected by WDM links with lightpaths defined by virtual paths based in wavelengths as depicted in Fig. 1. The WDM optical switching nodes consist of optical line terminals (OLTs), optical add/drop multiplexers (OADMs) and optical cross-connects (OXCs). Optical amplifiers (OAs) are utilized in the fiber link to compensate the optical fiber losses. The WDM networks present the advantage of the transparency to protocols and to the bit-rates. In addition, the channels can be added or dropped in optical domain. However, there is an interaction between network and physical layers that requires further considerations on the impairments and degradations in the network management and control [33 R. Doverspike and J. Yates, “Optical network management and control,” Proc.IEEE, vol. 100, no. 5, pp. 1092–1104, May 2012.].
B. Optical Signal Noise Ratio Model
Each link in an optical network is represented by the ensemble of N spans that include one optical amplifier per span. Hence, in each link, a group of M = {1, …, m} intensity modulated wavelengths channels are multiplexed together and transmitted across the link. The OSNR for the ith channel is given by [99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014]:
where piis the transmitted power of the ith channel, pjis the transmitted power of the interfering channels in the same route, Aj is the channel transmission matrix and ni is the spontaneous amplified emission (ASE) noise power accumulation in chains of optical amplifiers for the ith channel. The noise modeling for ni is obtained according to the recursively model detailed in the Appendix [1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.]; the noise contribution of each amplifier (NASE) is given by
where nsp is the spontaneous emission factor, typically around 2 − 5, h is Planck’s constant, f is the carrier frequency, Gamp is the amplifier gain and B is the optical bandwidth. m x m) system matrix with non-zero diagonal elements, while the off diagonal elements are dependent on specific optical network parameters such as link and span gains [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. The elements of system matrix can be calculated by [99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014], is the (
is the (
where Gi and Gj are ith channel gain and the jth interfering channel gain, respectively. In these channel gain elements were considered combining the gain of each amplifier in the link and optical fiber losses. In this sense, the channel gain is represented by kth amplifier gain operating in automatic power control (APC) mode, considering wavelength dependent and lth optical fiber loss typically channel independent. P0 is the total power allowed in each optical fiber established by the APC; this control mode operates scaling the gain such that the same total power is established at the output of each amplifier [99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014]. Therefore, the power scaling introduces coupling between channel powers, and channel OSNR is no longer independent of other channels’ powers as illustrated in previous OSNR formalism, eq. (1). is the
is the  is the
is the  , where
, where
C. Optical Signal Noise Ratio Optimization
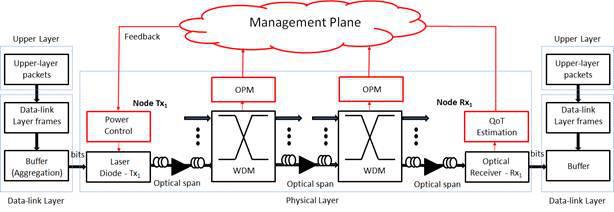
The distributed power control analytical-iterative algorithm (DPCA) adopted for the OSNR optimization presents a geometric rate of convergence regarding the optimal solution of transmitted power according the target OSNR [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. Furthermore, the DPCA utilizes only the estimation of local QoT parameters for the algorithm update, for each (ith) channel as illustrated in Fig. 2.
In dynamical WDM optical networks, there are modifications of system parameters at network reconfiguration level and updates that need to be performed after network topology changing has been propagated [66 G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.]. In this context, in the DPCA scheme it is assumed that system parameters, including channel gains and interference between channels are stationary between any updates. Such characteristics of on the system parameters stationary are standard assumption in adaptive control [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.].
The optimal transmitted power adjustment aiming to determine the instantaneous OSNR is based on the follow iterative DPCA power-updating equation [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.],
where ith channel, n is the number of iterations. In this work, the estimated OSNR is obtained by eq. (1), but considering the estimation uncertainties described in the Section III. Moreover, Fig. 3 illustrates the OSNR optimization procedure based on the power control considering the OSNR estimation integrated to the RWA processing. For more mathematical formalism details and discussion related to the utilized DPCA, please see Section IV of [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. is the adjustment parameter,
is the adjustment parameter, is the estimated OSNR and
is the estimated OSNR and  is the target OSNR of the
is the target OSNR of the
OSNR optimization based on the power control considering the OSNR estimation integrated to the RWA processing.
The quality of solution achieved by any iterative resource allocation procedure could be measured by how close to the optimum solution the found solution is, and can be quantified by the normalized mean squared error (NMSE) when equilibrium is reached after n iterations. For power allocation problem, the NMSE definition is given by [88 F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683],
where p* is the optimized (minimum) power vector solution obtained through matrix inversion I is an identity matrix, H is the normalized interference matrix, whose elements can be evaluated by i 1 j and zero for other case [88 F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683]. The matrix inversion is equivalent to a centralized power control strategy, i.e. the existence of a central node able to proceed with power control calculation. The central node storages information about all physical network architecture like link length between nodes and regular update about link establishment and dynamic of traffic [88 F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683]. These observations justify the need for on-line OSNR optimization algorithms, which have provable convergence properties for general network configurations [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.], [99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014]. , where
, where  the expectation operator. The vector
the expectation operator. The vector  denotes the squared Euclidean distance to the origin, and
denotes the squared Euclidean distance to the origin, and  for
for
Another figure of merit suitable to evaluate the effects of estimation uncertainties is the power penalty associated to the ith lightpath (PPi). In this work the parameter PPi is defined as the ratio between the transmitted power obtained by the optimization algorithm (pi) and the optimal transmitted power obtained by the centralized matrix inversion (ith node after n iterations is given by ) calculation. The power penalty in dB for the
) calculation. The power penalty in dB for the
D. Lightpath Setup Time
In this subsection, the time of convergence for the jointly power control and OSNR estimation procedures is evaluated considering the lightpath setup time. For this goal, the power control algorithm is considered integrated to the distributed routing strategy. Thus, to assess the lightpath setup time it is applied the methodology similar to that one presented in [1616 L. Velasco, F. Agraz, R. Martínez, R. Casellas, S. Spadaro, R. Muñoz, and G. Junyent, “GMPLS-based multi-domain restoration: Analysis, strategies, policies and experimental assessment,” J. Opt. Commun. Netw., vol. 2, pp. 427–441, 2010.][1717 L. Velasco, A. Jirattigalachote, M. Ruiz, P. Monti, L. Wosinska, and G. Junyent, “Statistical Approach for Fast Impairment-Aware Provisioning in Dynamic All-Optical Networks”, J. Opt. Commun. Netw.,, vol. 4, no. 2, pp. 130-141, 2012.], but adding the computation time of power control algorithm and OSNR estimation.
where tRWA is the computation time of the RWA algorithm, tOCC is the processing time in each controller in the control plane, tlink is the propagation delay in each network link, tconfig is the software configuration time of an optical node, tswitch is the time to perform the optical switching, d represents the number of nodes traversed by the lightpath and tOSNR is the joint computational time to execute the power control algorithm and OSNR estimation procedures.
III. Estimation Uncertainties Model
In the estimation uncertainties model we have considered the uncertainty in the QoT estimation parameters in each iteration/updating of the DPCA. The uncertainties occur in the QoT estimation process, which is related to optical channel error estimation in the receiver node or in the lightpath route. The reasons for the error in the estimation process were described in the introductory section.
In our model, the values obtained from the QoT estimation process present a random error characteristic represented herein by the random variable called the channel error estimation (ε). Furthermore, this random variable depends on what monitoring information is available in the network to perform the estimation, for instance, OSNR monitor, PMD monitor, residual chromatic dispersion monitor, and power channel monitor [1515 T. Zami, A. Morea, F. Leplingard, and N. Brogard, “The relevant impact of the physical parameters uncertainties when dimensioning an optical core transparent network,” in Proc. European Conf. Optical Communications (ECOC), 2008.]. In this context, ε quantity is affected by the availability of monitoring information, monitoring accuracy and imperfection of physical layers for each lightpath. Hence, the channel error estimation is modeled as:
where uth monitor for U monitors available in each link. The entire lightpath is composed by a set of L links. In this work, this parameter is assumed to be the precisions of the OPMs, such as the accuracy of the equipment of power meter ΔP , the OSNR monitoring ΔOSNR , the PMD monitoring ΔPMD , and the chromatic dispersion monitoring ΔCDθu defines the binary variable optical monitor availability, where we can assume θu =1 for the presence and θu = 0 for the absence of the optical monitor. . The parameter
. The parameter  is the parameter that determine the accuracy of the information of the
is the parameter that determine the accuracy of the information of the
The error in the channel estimation is expeditiously incorporated adding random error to the each channel (Gi), and, as a consequence, in the calculated OSNR, considering regular iteration basis. The ratio of the estimated channel vector (1 x m) values is given by (1 + ε); hence, the estimated channel vector  ) with dimension (
) with dimension ( on each iteration is given by:
on each iteration is given by: ) and the true channel vector (
) and the true channel vector (
For an illustrative case, the error in the channel estimation could be considered as a random variable with a uniform distribution within the range 1414 S. Azodolmolky et al., “A novel impairment aware RWA algorithm with consideration of QoT estimation inaccuracy,” J. Opt. Commun. Netw., vol. 3, pp. 290–299, Apr. 2011.]. Herein, the assumption of ε = 0 corresponding to the case where we have full confidence in channel estimation and assume that it returns the true channel matrix. On the other hand, ε = 1 corresponding to the case with maximum inaccuracy. [
[
IV. Numerical Results
In this section we discuss the validity of the proposed optical network model by exploring a typical optical network example. Indeed, for numerical example evaluation, we have chosen the Southern Finland network topology illustrated in Fig. 3. This topology consists of 12 nodes and 19 bi-directional links. Furthermore, Table I summarizes the optical fiber link parameters deployed with their respective entry values. Notice that for the numerical results discussed in this section, typical values of parameters of devices, components and equipment have been assumed. For simplicity we adopt m = 8 channels uniformly distributed from 1554 nm to 1561 nm with channel separation of 1 nm. Each optical amplifier has a parabolic spectral gain profile of 15 - 4 x 1016(λ - 1555 X 10-9)2 and a total output power of 8 dBm. It is worth noting that aiming to obtain diversity in distance and number of hops, the routes were not necessarily chosen by shortest path. The routes considered for OSNR optimization is illustrated in Table II and will be utilized in the remainder of this work.
It is assumed the continuous monitoring of QoT metrics by the establishment of a supervisor lightpaths entity, while the physical layer impairments performance of each supervised lightpath is tracked by a monitor placed at the receiving lightpath end. This kind of monitoring presents lower cost compared with others approaches to perform the monitoring processes [55 J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.]. Table III shows the required accuracy of the monitoring parameters [1818 D. Dahan et al.: Optical performance monitoring for translucent/transparent optical networks, IET Optoelectr., vol. 5, n. 1, pp. 1-18, Feb. 2011.]. In all numerical results considered in this section, the adjustment parameter of the DPCA a = 0.4 has value been adopted; thus, a trade-off between the quality of the solutions and velocity of convergence in the DPCA of (4) can be reached [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.]. The increase of a arises from the increment of the DPCA convergence velocity, although the quality of the answer found is affected.
Fig. 4 depicts the transmitted power evolution for de number of iterations considering perfect channel estimation hypothesis, i.e. without channel estimation uncertainties. The optimized transmitted power vector in dBm for routes R1, R2, …, R6 of Table II, obtained via matrix inversion, is represented by horizontal lines (dot lines).
Transmitted power evolution as a function of the number of iterations for routes illustrated in Table II. The optimized transmitted power obtained with matrix inversion is represented by horizontal dot lines.
It can be seen from Fig. 4 that the transmitted powers obtained by DPCA reach the convergence to the optimal values as obtained with matrix inversion when the number of iterations increases for each transmitted node, i.e., the node from which the lightpaths were originated. The transmitted power obtained by DPCA represents the methodology previously proposed in [77 L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.][99 Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014] and with the transmitted power obtained via matrix inversion will be utilized to evaluate the next results. The target OSNR for all the nodes is equal and the variation of the transmitted power is related to three factors, e.g., distance, accumulated ASE and the interference between the wavelengths in the same link. If no power control has been utilized the transmitted power of each node will be 1 mW and the total transmitted power will be 6 mW. On the other hand, the total optimized transmitted power, i.e. the sum of transmitted power illustrated in Fig.4 is substantially reduced to approximately 4.03 mW (6.05 dBm). Furthermore, the power penalty is PP ≈ 1.76 dB when any transmitted power is utilized.
Fig. 5 shows the NMSE evolution as a function of the channel estimation error, i.e. when there are uncertainties in the OSNR estimation. The vertical dash line represents the channel error estimation when there are OPMs installed in all the established lightpahts. The available OPMs are able to perform OSNR, Power, CD and PMD measurements and the accuracy of the monitoring parameters considered are the same required accuracy described in Table III.
NMSE evolution as a function of the channel error estimation for routes illustrated in Table II.
From Fig. 5, as expected, one can observe the increasing of the NMSE when the channel error estimation increases. The increasing in the channel error estimation is related with the availability of OPMs in each link and their accuracy. Moreover, the value of zero for the channel error estimation is obtained when there are OPMs available in all links of the lightpath and there are not uncertainties in the OPMs measurements. On the other hand, the value of one for the channel error estimation is obtained when there aren’t OPMs available in any link of the lightpath and/or the measurements of the OPMs do not present high level of confidence [1818 D. Dahan et al.: Optical performance monitoring for translucent/transparent optical networks, IET Optoelectr., vol. 5, n. 1, pp. 1-18, Feb. 2011.]. The channel error estimation of ε =0.2 represents the maximum uncertainty when there are OPMs of OSNR, power, CD and PMD measurements in all links with acceptable accuracy of the measurements. For this case, the NMSE is approximately 10-2, which is adequate to the dynamical adjustment of the transmitted power [88 F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683]. However, if there are available only the OPM of power meter in all links of the lightpath, the channel error estimation will increase to 0.4 and the NMSE is approximately 6 ´ 10-2. For this case, it is necessary the evaluation of the transmitted power level aiming to reach the target OSNR with this level of uncertainty.
The power penalty evolution for the number of iterations is illustrated in Fig. 6, considering the routes of Table II and two level of channel error estimation of (a) ε = 0.2 and (b) ε = 0.4. It can be seen the magnitude of the power penalty in the transmitted power for each route to reach the target OSNR. The variation of the power penalty for different routes is affected by the same elements that affect the variation of transmitted power, i.e. distance, accumulated ASE and the interference between the wavelengths in the same links. Moreover, the power penalty is defined by eq. (6), which defines the relation between the instantaneous DPCA iterative-based transmitted power pi[n] given by eq. (4) and the optimal transmitted power  obtained via the centralized matrix inversion. Therefore, the instantaneous transmitted power presents some variation during the evolution of the power control algorithm before reach the steady state value.
obtained via the centralized matrix inversion. Therefore, the instantaneous transmitted power presents some variation during the evolution of the power control algorithm before reach the steady state value.
Power penalty evolution as a function of the number of iterations for routes of Table II; channel error estimation of: (a) 0.2 and (b) 0.4.
When the power penalty curves from Fig. 6 (a) and (b) are compared one can observe that increasing values in the mean value of the power penalty when the channel error estimation grows from 0.2 to 0.4. On the other hand, one can observe that for some routes, for example R4, there is a decrease of the power penalty, but the mean value of the power penalty increase. This effect occurs because when the channel error estimation is added to the algorithm optimization process, the better solution for each transmitted power is reached when the target OSNR is established.
The effect of different channel error estimation over the power penalty of transmitted power for the routes of Table II is illustrated in Fig. 7; indeed, it is shown the mean power penalty for the channel error estimation considering the routes R1 to R6 of Table II. It can be seen clearly the intensification of the power penalty with the deterioration of the channel estimation. Accordingly, the optimization algorithm works to achieve the target OSNR at expense of the transmitted power increase in the scenario with channel error estimation. The impact of the channel error estimation is related with the necessity of the increase in the number of regenerators in the optical network. The channel error estimation of ε =0.2 and ε =0.4 results in the power penalty of PP ≈ 0.68 and 1.14 dB, respectively. For comparison, the power uncertainties of 1 dB could results in an increasing of 20% in further regenerators along the optical network routes [1515 T. Zami, A. Morea, F. Leplingard, and N. Brogard, “The relevant impact of the physical parameters uncertainties when dimensioning an optical core transparent network,” in Proc. European Conf. Optical Communications (ECOC), 2008.]. Besides, Fig. 7 reveals that for the power penalty of 1.76 dB, which is obtained when any OSNR optimization algorithm is utilized, the channel error estimation is about 0.52. In other words, for our typical numerical example with the level of uncertainties in the channel error estimation lower than 0.52 the utilization of OSNR optimization algorithm can be advantageously implemented and justified.
Mean power penalty evolution as a function of the channel error estimation for routes illustrated in Table II.
In order to evaluate the impact of the convergence of the distributed power control, in the next it is discussed the lightpath setup time for the longest lightpath. There is an increase in the lightpath setup time when others aspects such as power control algorithm and OSNR estimation are adopted. In this context, Fig. 8 shows the lightpath setup time versus the computational time of the OSNR optimization considering the cases without power control and with power control. The time of the OSNR optimization is composed by the power control algorithm and OSNR estimation. The adopted mean time parameters for the power control algorithm integrated with a distributed routing strategy is depicted in Table IV. These parameters were previously defined in [1616 L. Velasco, F. Agraz, R. Martínez, R. Casellas, S. Spadaro, R. Muñoz, and G. Junyent, “GMPLS-based multi-domain restoration: Analysis, strategies, policies and experimental assessment,” J. Opt. Commun. Netw., vol. 2, pp. 427–441, 2010.][1717 L. Velasco, A. Jirattigalachote, M. Ruiz, P. Monti, L. Wosinska, and G. Junyent, “Statistical Approach for Fast Impairment-Aware Provisioning in Dynamic All-Optical Networks”, J. Opt. Commun. Netw.,, vol. 4, no. 2, pp. 130-141, 2012.].
The lightpath setup time for a computational time of the OSNR optimization considering cases without power control and with power control.
The increasing of the computational time of the OSNR optimization causes the increases of the lightpath setup time for the case with power control. In order to evaluate the accepted level of the increase in the lightpath setup time, we compare the distributed routing strategy with QoT assessment where the lightpath setup time could presents an increase of almost 97 % for the distributed RWA (without power control algorithm) for 1000 ms of QoT computational time [1717 L. Velasco, A. Jirattigalachote, M. Ruiz, P. Monti, L. Wosinska, and G. Junyent, “Statistical Approach for Fast Impairment-Aware Provisioning in Dynamic All-Optical Networks”, J. Opt. Commun. Netw.,, vol. 4, no. 2, pp. 130-141, 2012.], i.e. the doubling of lightpath setup time. This order of time variation is considered acceptable. From Fig. 8, the variation of the lightpath setup time for 1000 ms of OSNR optimization computational time is approximately 96% when the power control algorithm is considered. Furthermore, the power control algorithm will not affect the overall network performance. The power control algorithm depends heavily on the hardware and software deployed, furthermore in the optical nodes the power control algorithm could be performed in hardware-accelerated computation or via software. In this context, considering the simulations performed with MATLAB (version 7.1) in a personal computer with 4 GB of RAM and processor Intel Core i5@ 1.6 GHz, the computational time needed for the convergence of the power control algorithm is approximately 275 ms.
V. Conclusions
In this work, we have investigated the effects of estimation uncertainties in the optimization of the optical signal-to-noise ratio (OSNR) at the wavelength division multiplexing (WDM) optical networks. The OSNR optimization algorithms are related to the optical channel estimation performed by the combinations of optical performance monitors (OPM) measurements, analytical models and simulations. Furthermore, the estimation uncertainties are introduced by several factors such as the availability of monitoring information, monitoring accuracy, imperfection of physical layer and dynamic of channel allocation. As a proof of concept, a numerical example was evaluated and the normalized mean squared error (NMSE) and power penalty (PP) for different levels of uncertainties in the channel error estimation were analyzed; hence, an introduction of a channel error estimation of ε = 0.2 and ε = 0.4 has resulted in a power penalty of PP ≈ 0.68 and 1.14 dB, respectively. For comparison, the power penalty without any OSNR optimization procedure has increased to PP ≈ 1.76 dB, resulting in an augmented channel error estimation of 0.52. As a consequence, this value represents the maximum level of uncertainty allowed for the utilization of any OSNR optimization algorithm. Finally, analyses of the power control algorithm integrated with routing and wavelength allocation (RWA) procedures will not affect the overall network performance considering the lightpath setup time.
Appendix - Optical Amplifier Noise Modelling
The ASE at cascaded amplified spans is given by model developed by Fig. 9 from [1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.].
This model considers that the receiver Rx receives the signal from a link with cascading amplifiers, numbered as 1, 2, . . starting from the receiver. The pre-amplifier can be considered as the amplifier number 0 of the cascade. Let k and Nsp-k its spontaneous emission factor. The span between the k-th and the (k − 1)th amplifier has attenuation Lk. The equivalent spontaneous emission factor is given by [1010 G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.]. be the gain of amplifier
be the gain of amplifier
Calculating recursively nione can find the noise at cascading amplifiers.
In this work, the optical amplifiers operate in APC model, where a constant total power, or a constant total launching power after each span, compensates variations in fiber-span loss across a link. The amplifier gain with wavelength dependency is given by:
where l is the wavelength in nm.
ACKNOWLEDGMENT
This work was supported in part by the Araucaria Foundation, PR, Brazil under grant 668/2014, National Council for Scientific and Technological Development (CNPq) of Brazil under Grant 202340/ 2011-2, 446995/2014-2, and State University of Londrina-Paraná State Government (UEL).
REFERENCES
-
1D. Kilper, K. Bergman, V. W. S. Chen, I. Monga, G. Porter, and K. Rauschenbach, "Optical Networks Come of Age," OSA Optics and Photonics News, pp. 50-57, Sep. 2014.
-
2B. Birand, H. Wang, K. Bergman, D. Kilper, T. Nandagopal, G. Zussman, "Real-time power control for dynamic optical networks - algorithms and experimentation," IEEE Journal on Selected Areas in Communications, vol. 32, no. 8, pp. 1615 – 1628, Aug. 2014.
-
3R. Doverspike and J. Yates, “Optical network management and control,” Proc.IEEE, vol. 100, no. 5, pp. 1092–1104, May 2012.
-
4Rodney S. Tucker, "Green Optical Communications - Part II: Energy Limitations in Networks", IEEE J Selected Topics in Quantum Electronics, vol. 17, no. 2, pp. 261 – 274, March-April 2011.
-
5J. Sole-Pareta, S. Subramaniam, D. Careglio, and S. Spadaro, “Cross-layer approaches for planning and operating impairment-aware optical networks,” Proc. IEEE, vol. 100, no. 5, pp. 1118–1129, May 2012.
-
6G. P. Agrawal, Fiber-optic communication systems, John Wiley & Sons, 2002.
-
7L. Pavel, “OSNR optimization in optical networks: Modeling and distributed algorithms via a central cost approach,” IEEE J. Sel. Areas Commun., vol. 24, no. 4, pp. 54–65, Apr. 2006.
-
8F. R. Durand and T. Abrão, “Distributed SNIR Optimization Based on the Verhulst Model in Optical Code Path Routed Networks With Physical Constraints”, J. Opt. Commun. Netw., vol. 3, no. 9, pp. 683–691, Sep. 2011. doi:10.1364/JOCN.3.000683
-
9Y. Pan, and L. Pavel, “OSNR Game Optimization with Link Capacity Constraints in General Topology WDM Networks, ” Optical Switching and Networking, vol. 11, Part A, pp. 1-15, Jan. 2014
-
10G. Pavani, L. Zuliani, H. Waldman and M. Magalhães, “Distributed approaches for impairment-aware routing and wavelength assignment algorithms in GMPLS networks”, Computer Networks, vol. 52, no. 10, pp. 1905–1915, July 2008.
-
11Z. Pan, C. Yu, and A. Willner, “Optical performance monitoring for the next generation optical communication networks,” Opt. Fiber Technol., vol. 16, no. 1, pp. 20–45, 2010.
-
12D. Kilper, R. Bach, D. Blumenthal, D. Einstein, T. Landolsi, L. Ostar, M. Preiss, and A. Willner, “Optical performance monitoring,” J. Lightw. Technol., vol. 22, no. 1, pp. 294–304, Jan. 2004.
-
13S. Pachnicke, T. Gravemann, M. Windmann, and E. Voges, “Physically constrained routing in 10-Gb/s DWDM networks including fiber nonlinearities and polarization effects,” J. Lightwave Technol., vol. 24, n. 9, pp. 3418–3426, Sep. 2006.
-
14S. Azodolmolky et al., “A novel impairment aware RWA algorithm with consideration of QoT estimation inaccuracy,” J. Opt. Commun. Netw., vol. 3, pp. 290–299, Apr. 2011.
-
15T. Zami, A. Morea, F. Leplingard, and N. Brogard, “The relevant impact of the physical parameters uncertainties when dimensioning an optical core transparent network,” in Proc. European Conf. Optical Communications (ECOC), 2008.
-
16L. Velasco, F. Agraz, R. Martínez, R. Casellas, S. Spadaro, R. Muñoz, and G. Junyent, “GMPLS-based multi-domain restoration: Analysis, strategies, policies and experimental assessment,” J. Opt. Commun. Netw., vol. 2, pp. 427–441, 2010.
-
17L. Velasco, A. Jirattigalachote, M. Ruiz, P. Monti, L. Wosinska, and G. Junyent, “Statistical Approach for Fast Impairment-Aware Provisioning in Dynamic All-Optical Networks”, J. Opt. Commun. Netw.,, vol. 4, no. 2, pp. 130-141, 2012.
-
18D. Dahan et al.: Optical performance monitoring for translucent/transparent optical networks, IET Optoelectr., vol. 5, n. 1, pp. 1-18, Feb. 2011.
Publication Dates
-
Publication in this collection
Mar 2016