Abstract
Introduction
Cardiovascular diseases represent a major cause of death world-wide and one of their greatest complications is the development of cardiac arrhythmias, in which ventricular fibrillation (VF) stands out as the most severe one. The only therapy that reverses VF is defibrillation. However defibrillatory shock is capable of killing heart cells and it is known that the orientation of the cell major axis with respect to the electrical field (E) direction is a determining factor for cellular excitation and injury, which is leading to the development of new defibrillation protocols. The aim of this work is to fill the gap in information about cell lethality for intermediate cell orientation angles.
Methods
Ventricular myocytes were extracted from adult male Wistar rats and the cells were plated in a chamber for perfusion and stimulation with bipolar voltage pulses to determine the stimulation threshold (ET). Then, monopolar stimulus was applied and amplitude was increased until cell lethal injury. This protocol was performed on four experimental groups: cells oriented at 0°, 30°, 60° and 90°, with respect to E direction.
Results
87 cells were analyzed and an increase in amplitude of E associated with 50% lethality (E50) was verified as the direction of E application and cell major axis orientation departed.
Conclusion
Taken the same probability of lethality, our data suggest a nonlinear increase of E amplitude from 0° to 90° similar to that of ET. These in-between data had not yet been shown and are important for service-based future defibrillation protocols.
Keywords
Defibrillation; Cell electrical stimulation; Probability of cellular lethality
Introduction
Despite the significant reduction of 25.3% in the mortality rate associated with cardiovascular diseases between 2004 and 2014, it remains as the leading cause of death worldwide, accounting for the death of 17.3 million people out of 54 million of all deaths in 2013 ( Benjamin et al., 2017 Benjamin EJ, Blaha MJ, Chiuve SE, Cushman M, Das SR, Deo R, de Ferranti SD, Floyd J, Fornage M, Gillespie C, Isasi CR, Jiménez MC, Jordan LC, Judd SE, Lackland D, Lichtman JH, Lisabeth L, Liu S, Longenecker CT, Mackey RH, Matsushita K, Mozaffarian D, Mussolino ME, Nasir K, Neumar RW, Palaniappan L, Pandey DK, Thiagarajan RR, Reeves MJ, Ritchey M, Rodriguez CJ, Roth GA, Rosamond WD, Sasson C, Towfighi A, Tsao CW, Turner MB, Virani SS, Voeks JH, Willey JZ, Wilkins JT, Wu JH, Alger HM, Wong SS, Muntner P. Heart disease and stroke statistics-2017 update: a report from the American Heart Association. Circulation. 2017; 135(10):e146-603. http://dx.doi.org/10.1161/CIR.0000000000000485. PMid:28122885.
http://dx.doi.org/10.1161/CIR.000000000...
). One of the major complications resulting from cardiovascular diseases is the development of cardiac arrhythmias, in which ventricular fibrillation (VF) stands out as the most severe and life-threatening arrhythmia, being able to quickly lead to the development of cardiac arrest and even death.
The only available therapy capable of terminating VF is defibrillation ( Weisz, 2009 Weisz MT. Physical principles of defibrillators. Anaesth Intensive Care Med. 2009; 10(8):367-9. http://dx.doi.org/10.1016/j.mpaic.2009.05.002.
http://dx.doi.org/10.1016/j.mpaic.2009....
; Zipes et al., 2006 Zipes DP, Camm AJ, Borggrefe M, Buxton AE, Chaitman B, Fromer M, Gregoratos G, Klein G, Moss AJ, Myerburg RJ, Priori SG, Quinones MA, Roden DM, Silka MJ, Tracy C, Smith SC Jr, Jacobs AK, Adams CD, Antman EM, Anderson JL, Hunt SA, Halperin JL, Nishimura R, Ornato JP, Page RL, Riegel B, Priori SG, Blanc JJ, Budaj A, Camm AJ, Dean V, Deckers JW, Despres C, Dickstein K, Lekakis J, McGregor K, Metra M, Morais J, Osterspey A, Tamargo JL, Zamorano JL. ACC/AHA/ESC 2006 guidelines for management of patients with ventricular arrhythmias and the prevention of sudden cardiac death: a report of the American College of Cardiology/American Heart Association Task Force and the European Society of Cardiology Committee for Practice Guidelines (Writing Committee to Develop Guidelines for Management of Patients With Ventricular Arrhythmias and the Prevention of Sudden Cardiac Death). J Am Coll Cardiol. 2006; 48(5):e247-346. http://dx.doi.org/10.1016/j.jacc.2006.07.010. PMid:16949478.
http://dx.doi.org/10.1016/j.jacc.2006.0...
), which consists on the application of high intensity electrical fields (HEF) in the heart. Although the electrical field intensity threshold required for heart defibrillation is 6 V/cm ( Ideker et al., 1995 Ideker RE, Zhou X, Knisley SB. Correlation among fibrillation, defibrillation, and cardiac pacing. Pacing Clin Electrophysiol. 1995; 18(3 Pt 2):512-25. http://dx.doi.org/10.1111/j.1540-8159.1995.tb02562.x. PMid:7777416.
http://dx.doi.org/10.1111/j.1540-8159.1...
), this field magnitude needs to be achievable throughout the myocardium, implying that high-intensity shocks are necessary to obtain successful defibrillation. Due to the anisotropic nature of the heart tissue, non-uniform potential gradients are generated, which may expose some regions of the heart to an electrical field (E) as large as 100 V/cm ( Yabe et al., 1990 Yabe S, Smith WM, Daubert JP, Wolf PD, Rollins DL, Ideker RE. Conduction disturbances caused by high current density electric fields. Circ Res. 1990; 66(5):1190-203. PMID:2335021. ). This can lead to depression of electrical and contractile cell functions and even cell death ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
; Prado et al., 2016 Prado LN, Goulart JT, Zoccoler M, Oliveira PX. Ventricular myocyte injury by high-intensity electric field: Effect of pulse duration. Gen Physiol Biophys. 2016; 35(2):121-30. http://dx.doi.org/10.4149/gpb_2015047. PMid:26830130.
http://dx.doi.org/10.4149/gpb_2015047 ...
).
It is believed that cell injuries associated with defibrillation process are probably caused by the electroporation phenomenon: the opening of non-selective pores in the cell membrane by the application of HEF, allowing the unrestrained exchange of water and ions ( Miklavcic et al., 2010 Miklavcic D, Pucihar G, Macek Lebar A, Krmelj J, Towhidi L. The pulse intensity-duration dependency for cell membrane electroporation. In: Pakhomov AG, Miklavicic D, Markov MS, editors. Advanced electroporation techniques in biology and medicine. Boca Raton: CRC Press, 2010. p. 246-59. https://doi.org/10.1201/EBK1439819067-17.
https://doi.org/10.1201/EBK1439819067-1...
; Ivorra, 2010 Ivorra A. Tissue electroporation as a bioelectric phenomenon: Basic concepts. Berlin: Springer; 2010, p. 23-61. https://doi.org/10.1007/978-3-642-05420-4_2.
https://doi.org/10.1007/978-3-642-05420...
; Jones et al., 1987 Jones JL, Jones RE, Balasky G. Microlesion formation in myocardial cells by high-intensity electric field stimulation. Am J Physiol. 1987; 253(2 Pt 2):H480-6. PMid:2441612. ; Klauke et al., 2010 Klauke N, Smith G, Cooper JM. Regional electroporation of single cardiac myocytes in a focused electric field. Anal Chem. 2010; 82(2):585-92. http://dx.doi.org/10.1021/ac901886j. PMid:20020746.
http://dx.doi.org/10.1021/ac901886j ...
; Kotnik et al., 2003 Kotnik T, Pucihar G, Reberšek M, Miklavčič D, Mir LM. Role of pulse shape in cell membrane electropermeabilization. Biochim Biophys Acta - Biomembr. 2003; 1614(2):193-200. http://dx.doi.org/10.1016/S0005-2736(03)00173-1.
http://dx.doi.org/10.1016/S0005-2736(03...
; Krauthamer and Jones, 1997 Krauthamer V, Jones JL. Calcium dynamics in cultured heart cells exposed to defibrillator-type electric shocks. Life Sci. 1997; 60(2):1977-85. http://dx.doi.org/10.1016/S0024-3205(97)00162-8.
http://dx.doi.org/10.1016/S0024-3205(97...
; Nikolski and Efimov, 2005 Nikolski V, Efimov I. Electroporation of the heart. Europace. 2005; 7:S146-54. http://dx.doi.org/10.1016/j.eupc.2005.04.011.
http://dx.doi.org/10.1016/j.eupc.2005.0...
; Tsong, 1991 Tsong TY. Electroporation of cell membranes. Biophys J. 1991; 60(2):297-306. http://dx.doi.org/10.1016/S0006-3495(91)82054-9. PMid:1912274.
http://dx.doi.org/10.1016/S0006-3495(91...
; Weaver, 1994 Weaver JC. Molecular basis for cell membrane electroporationa. Ann N Y Acad Sci. 1994; 720(1):141-52. http://dx.doi.org/10.1111/j.1749-6632.1994.tb30442.x. PMid:8010633.
http://dx.doi.org/10.1111/j.1749-6632.1...
). When E is sufficiently high, it can cause cell irreversible hypercontracture, by the excessive increase of the intracellular calcium concentration, as well as the loss of its physical integrity ( Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
; Knisley and Grant, 1995 Knisley SB, Grant AO. Asymmetrical electrically induced injury of rabbit ventricular myocytes. J Mol Cell Cardiol. 1995; 27(5):1111-22. http://dx.doi.org/10.1016/0022-2828(95)90047-0. PMid:7473769.
http://dx.doi.org/10.1016/0022-2828(95)...
; Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). The electroporation phenomenon depends on the transmembrane potential (Vm ) exceeding a certain threshold ( Fedorov et al., 2008 Fedorov VV, Nikolski VP, Efimov IR. Effect of electroporation on cardiac electrophysiology. USA: Humana Press; 2008, p. 433-48. https://doi.org/10.1007/978-1-59745-194-9_34.
https://doi.org/10.1007/978-1-59745-194...
; Ivorra, 2010 Ivorra A. Tissue electroporation as a bioelectric phenomenon: Basic concepts. Berlin: Springer; 2010, p. 23-61. https://doi.org/10.1007/978-3-642-05420-4_2.
https://doi.org/10.1007/978-3-642-05420...
; Kotnik et al., 2003 Kotnik T, Pucihar G, Reberšek M, Miklavčič D, Mir LM. Role of pulse shape in cell membrane electropermeabilization. Biochim Biophys Acta - Biomembr. 2003; 1614(2):193-200. http://dx.doi.org/10.1016/S0005-2736(03)00173-1.
http://dx.doi.org/10.1016/S0005-2736(03...
; Prado et al., 2016 Prado LN, Goulart JT, Zoccoler M, Oliveira PX. Ventricular myocyte injury by high-intensity electric field: Effect of pulse duration. Gen Physiol Biophys. 2016; 35(2):121-30. http://dx.doi.org/10.4149/gpb_2015047. PMid:26830130.
http://dx.doi.org/10.4149/gpb_2015047 ...
) and the maximum Vm variation depends directly on the magnitude of the applied E, cell geometry (cell width and length) and also on the E orientation with respect to the cell major axis, as described by the electromagnetic model proposed by Klee and Plonsey ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
).
The response of cardiac cells to E application has been receiving much attention from the literature, from the point of view of both physiological aspects involved and for possible clinical applications. Every cell in the heart is independently excitable and capable of triggering its contractile mechanism and understanding how they individually respond to E may aid understanding the heart response as a whole ( Bardou et al., 1990 Bardou AL, Chesnais JM, Birkui PJ, Govaere MC, Auger PM, Von Euw D, Degonde J. Directional variability of stimulation threshold measurements in isolated guinea pig cardiomyocytes: Relationship with orthogonal sequential defibrillating pulses. Pacing Clin Electrophysiol. 1990; 13(12 Pt 1):1590-5. http://dx.doi.org/10.1111/j.1540-8159.1990.tb06859.x. PMid:1704510.
http://dx.doi.org/10.1111/j.1540-8159.1...
; Penna and Bassani, 2010 Penna LB, Bassani RA. Increased spontaneous activity and reduced inotropic response to catecholamines in ventricular myocytes from footshock-stressed rats. Stress. 2010; 13(1):73-82. http://dx.doi.org/10.3109/10253890902951778. PMid:19697264.
http://dx.doi.org/10.3109/1025389090295...
; Tung et al., 1991 Tung L, Sliz N, Mulligan MR. Influence of electrical axis of stimulation on excitation of cardiac muscle cells. Circ Res. 1991; 69(3):722-30. http://dx.doi.org/10.1161/01.RES.69.3.722. PMid:1873867.
http://dx.doi.org/10.1161/01.RES.69.3.7...
).
It has already been reported that stimulus orientation influences the E excitation threshold (ET) and that there is a non-linear increase in ET for angles between 0º and 90º, as the angle between E direction and cell orientation increases ( Bassani et al., 2006 Bassani RA, Lima KA, Gomes PAP, Oliveira PX, Bassani JWM. Combining stimulus direction and waveform for optimization of threshold stimulation of isolated ventricular myocytes. Physiol Meas. 2006; 27(9):851-63. http://dx.doi.org/10.1088/0967-3334/27/9/008. PMid:16868351.
http://dx.doi.org/10.1088/0967-3334/27/...
). Thus, ET for a cell oriented at 90º is about two times greater than that for another oriented at 0º. Studies were also performed to investigate whether E magnitude for a same probability of lethality (lethal E) would also increase if cell orientation was changed from 0º to 90º and, indeed, it was found that, E needed to cause lethal injury to 50% of the cells oriented at 90º was twice as large for cells oriented at 0º ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). Although the authors have obtained information regarding the angles displaying the highest E variation ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
), only these two values are still a weak evidence to describe cell lethality behavior, especially because the phenomenon by which cell death is believed to occur (electroporation) is still not fully understood. Therefore, direct interpolation might be an oversimplification and novel data in this gray region would be a more reliable approach. The aim of this work is to supply data in between these angles that display the highest E variation in order to clarify how the increase steps in.
Considering that heart cells receiving a defibrillation shock are oriented in different directions with respect to that electric field, it is important to be aware of the values of fields that are lethal to the myocardial cells in different orientations, in order to optimize the defibrillatory protocols so they may cause the least possible lesions to the patients.
Methods
Isolated rat myocytes
Left ventricular myocytes were isolated from hearts of adult (4-6 months-old) male Wistar rats. The cardiac myocytes were isolated from 32 rats by coronary perfusion with collagenase I at 37oC, as described by Penna and Bassani ( Penna and Bassani, 2010 Penna LB, Bassani RA. Increased spontaneous activity and reduced inotropic response to catecholamines in ventricular myocytes from footshock-stressed rats. Stress. 2010; 13(1):73-82. http://dx.doi.org/10.3109/10253890902951778. PMid:19697264.
http://dx.doi.org/10.3109/1025389090295...
). The experimental protocol was approved by the Institutional Committee for Ethics in Animal Research (CEUA/IB/UNICAMP, protocol 4093-1(K)).
Experimental protocol
The schematic representation of the experimental setup is shown in Figure 1 . After treatment with collagen to support cell adhesion, 20 minutes were waited and then approximately 150 µl of cells in solution were inserted in the perfusion chamber ( Figure 1 , developed by CEB/UNICAMP; Campinas, SP, Brazil) for perfusion and stimulation, whose walls were made of acrylic and the bottom was a glass coverslip. For cell stimulation, a pair of platinum electrodes were placed along the lateral inner walls, 0.75 cm apart, parallel to the solution flow direction, allowing a laminar flow of solution in a constant volume and an approximately constant E ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). Another 20 minutes were waited for cell adhesion onto the coverslip and the chamber was placed on an inverted microscope (developed by CEB/UNICAMP; Campinas, SP, Brazil - Figure 1 ) and cells were perfused (~3 mL/min) with Tyrode's solution (composition in mM): 140 NaCl, 6 KCl, 1.5 MgCl2.6H2O, 5 HEPES, 1 CaCl2.2H2 O, 11 glucose, pH 7.4) at 23°C.
Schematic representation of the experimental setup. A Computer is connected to a webcam to allow visualization of the myocytes plated on the perfusion chamber. Cells could be stimulated by the LIS or by the HIS, depending on the position of the switch. Oscilloscope was used for voltage measurements during the experiment.
A suitable cell was searched in the perfusion chamber, i.e., a rod-shaped cell, distant at least 2 mm from the electrodes ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
), that had clear cross striations and responded to electrical stimulation by performing contractions. The experimental groups were defined as group 0º, group 30º, group 60º and group 90º, in which the cell major axis was oriented at 0º, 30º, 60º or 90º, respectively, with respect to E direction. This way, in each experiment, it was obligatory that the angle between the cell and E direction belonged to one of the experimental groups. Measurements of cell length and width were taken with an image editing software (Adobe Photoshop). Only one cell per chamber was studied.
A low-intensity voltage stimulator (LIS, 0 – 45 V, developed by CEB/UNICAMP; Campinas, SP, Brazil - Figure 1 ) and a high-intensity voltage stimulator (HIS, 0 – 135 V, developed by CEB/UNICAMP; Campinas, SP, Brazil - Figure 1 )) were connected to a switch box ( Figure 1 ) and its output was connected to the perfusion chamber, i.e., cells could be stimulated by LIS or HIS, depending on the switch position. An oscilloscope was used to measure the voltage output from each stimulator.
The following step consisted in determining ET for the chosen cell. LIS was used to apply 0.5 Hz biphasic square pulses above threshold and 10 ms total duration (5 ms per phase). ET was determined by decreasing the pulse intensity until the cell stopped contracting. Then the stimulation was resumed with an amplitude 20% higher than ET, in order to assure that the cell would keep performing contractions in response to low intensity stimulation.
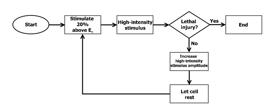
Next, the HIS, synchronized with LIS, was adjusted to produce monophasic pulses with 5 ms total duration. A high-intensity stimulus, with initial amplitude of 8xET (i.e. 8 times the stimulation threshold), was applied to the cell two seconds after the last low-intensity pulse. We let the cell rest for shock recovery, usually a time of few minutes. This protocol was repeated, as can be seen in the flowchart shown in Figure 2 , with an increased stimulus amplitude (12xET, 16xET, 20xE T, 25xET, 30xET) until lethal injury was induced. Cell death was identified as the development of sustained hypercontracture accompanied by irreversible loss of responsiveness to electrical stimulation ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
).
Electrical field and maximum variation of the membrane potential estimation
The intensity of the electrical field was calculated as in the case of a parallel plate capacitor ( Gomes et al., 2001 Gomes PAP, Bassani RA, Bassani JWM. Electric field stimulation of cardiac myocytes during postnatal development. IEEE Trans Biomed Eng. 2001; 48(6):630-6. http://dx.doi.org/10.1109/10.923781. PMid:11396593.
http://dx.doi.org/10.1109/10.923781 ...
; Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
) given by Equation 1:
where v is the stimulus voltage and d is the distance between the electrodes (0.75cm). In order to guarantee the accuracy of the calculated electrical field, an electrical potential mapping was performed inside the perfusion chamber and showed an error < 2% for measurements made distant at least 2 mm from the electrodes ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
).
The model proposed by Klee and Plonsey ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
) was used to estimate the maximum variation in transmembrane electrical potential at threshold (ΔVT), assuming the myocyte as a prolate spheroid and that the cellular membrane has a dielectric behavior. Hence, the ΔV T induced by an E applied at an angle θ with respect to the cell major axis is given by Equation 2:
Where a and c are half of the cell length and width, respectively, and A and C are constants that depends only on the cell’s geometry, as shown below:
Statistical analysis
Data were analyzed with Prism 5.03 (GraphPad Software, San Diego, USA). Eighty-seven cells were used in this study, arranged in the 4 experimental groups.
The obtained data from cell length, cell width, ET and ∆V T are shown as means accompanied by the standard errors of the mean. The values for each group were analyzed by three normality tests (Kolmogorov-Smirnov, D’Agostino & Pearson e Shapiro-Wilk) and means were compared using one-way analysis of variance followed by Bonferroni´s multiple comparisons test. Values of p < 0.05 were considered as indicative of statistically significant difference.
For each group, the lethal and the maximum non-lethal E were used as inputs for survival analysis fitted by a non-linear regression in order to determine the lethality curves. The data was modeled by the following function:
where P(E) is the probability of cell death when subjected to E, E50 is the amplitude of E related to a probability of lethality of 50% and h is the Hill coefficient. The parameters calculated by fitting are shown accompanied by their 99% confidence interval (CI99), and non-overlapping intervals were considered as indicative of statistically significant difference.
Results
Comparison between cell experimental groups
Means accompanied by the standard errors of the mean of ET, ∆V T, cell length and cell width can be seen in Table 1 . Values of ∆VT, cell length and cell width were not statistically different among the experimental groups.
The only parameter that showed dependence on the angle between cell orientation and E direction was ET ( Table 1 ), being statistically different in all groups, except between 0º and 30º.
Lethality
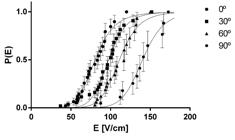
Lethality curves for each experimental group are shown in Figure 3 . E50 and h means and CI99 are shown in Table 2 .
Curves describing the probability of lethality as a function of the applied electrical field (E) generated from non-linear fit for each studied group. Symbols represent means and vertical bars represent standard errors of the means from survival analysis.
Significant differences were noted among all groups in terms of E50, as can be seen by CI99 non-overlapping, indicating that there is dependence of the probability of lethality on the orientation of the cell in relation to the E direction. In terms of h, there was no significant difference among the experimental groups.
We normalized E by ET ( Figure 4 ), which allowed us to verify that the normalized E50 shows statistical difference only for the 90º group compared to the 0º and 30º groups (non-overlapping CI99s), as can be seen in Table 3 . With respect to h, there was no statistically significant difference among any of the groups.
Curves describing the probability of lethality as a function of the applied electrical field (E). In these curves E was expressed as a multiple of the threshold electrical field (XET). Symbols represent means and vertical bars represent standard errors of the means from survival analysis.
Threshold E versus lethal E
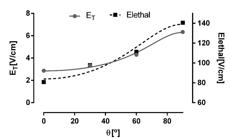
In order to compare the way ET and lethal E was increasing, we plot their mean values versus angle for four different cell orientations: 0º, 30º, 60º and 90º. That allowed us to verify a non-linear increase in ET, which is similar to that of lethal E.
Discussion
Values found for ∆VT, cell length and cell width were similar to those previously found in the literature ( Bassani et al., 2006 Bassani RA, Lima KA, Gomes PAP, Oliveira PX, Bassani JWM. Combining stimulus direction and waveform for optimization of threshold stimulation of isolated ventricular myocytes. Physiol Meas. 2006; 27(9):851-63. http://dx.doi.org/10.1088/0967-3334/27/9/008. PMid:16868351.
http://dx.doi.org/10.1088/0967-3334/27/...
; Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
; Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). It was not verified statistical difference among the experimental groups, which is important to ensure homogeneity of the cell samples used since it has already been shown that different cell sizes may influence ET and lethal E ( Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
).
On the other hand, there is a non-linear increase in ET as the angle between cell orientation and E direction increases ( Figure 5 ). This is in accordance with Klee and Plonsey model ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
) and with values already reported in the literature ( Bassani et al., 2006 Bassani RA, Lima KA, Gomes PAP, Oliveira PX, Bassani JWM. Combining stimulus direction and waveform for optimization of threshold stimulation of isolated ventricular myocytes. Physiol Meas. 2006; 27(9):851-63. http://dx.doi.org/10.1088/0967-3334/27/9/008. PMid:16868351.
http://dx.doi.org/10.1088/0967-3334/27/...
; DeBruin and Krassowska, 1999 DeBruin KA, Krassowska W. Modeling Electroporation in a Single Cell. I. Effects of field strength and rest potential. Biophys J. 1999; 77(3):1213-24. http://dx.doi.org/10.1016/S0006-3495(99)76973-0. PMid:10465736.
http://dx.doi.org/10.1016/S0006-3495(99...
; Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
; Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
; Prado et al., 2016 Prado LN, Goulart JT, Zoccoler M, Oliveira PX. Ventricular myocyte injury by high-intensity electric field: Effect of pulse duration. Gen Physiol Biophys. 2016; 35(2):121-30. http://dx.doi.org/10.4149/gpb_2015047. PMid:26830130.
http://dx.doi.org/10.4149/gpb_2015047 ...
).
Plot of threshold E and lethal E mean values versus angle for four different cell orientations: 0º, 30º, 60º and 90º, fitted by the Klee and Plonsey model ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324... ).
Regarding the lethal E, for the 0° group, E50 of 80.82V/cm was obtained, being close to the values already reported in the literature (E50 = 68V/cm ( Tung, 1996 Tung L. Detrimental effects of electrical fields on cardiac muscle. Proc IEEE. 1996; 84(3):366-78. http://dx.doi.org/10.1109/5.486740.
http://dx.doi.org/10.1109/5.486740 ...
); E50 = 90.73V/cm ( Neunlist and Tung, 1997 Neunlist M, Tung L. Dose-dependent reduction of cardiac transmembrane potential by high-intensity electrical shocks. Am J Physiol Circ Physiol. 1997; 273(6 Pt 2):H2817-25. http://dx.doi.org/10.1152/ajpheart.1997.273.6.H2817. PMid:9435619.
http://dx.doi.org/10.1152/ajpheart.1997...
)). Similarly, the value of E50 for the 90º group (140.7V/cm) is also close to what have been reported so far (E50 = 136.6V/cm ( Tung, 1996 Tung L. Detrimental effects of electrical fields on cardiac muscle. Proc IEEE. 1996; 84(3):366-78. http://dx.doi.org/10.1109/5.486740.
http://dx.doi.org/10.1109/5.486740 ...
)). The approximately 2-fold ratio between E50 of 90º oriented cells was again observed when compared to cells that were oriented at 0º.
The present study shows that there is a non-linear increase in E associated with cell lethal injury as the angle between cell orientation and E direction is increased, for angles between 0º and 90º, similar to that observed for ET. Thus, as can be seen in Figure 3 , given the same probability of lethality, cells oriented at 0º with respect to E have greater sensitivity to E than those oriented at 30º. Likewise, cells at 30º are more sensitive to E when compared to those oriented at 60º. Finally, we verified that cells oriented at 90º were the least sensitive to E (the E necessary to cause a lethal effect is greater) ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). This is to our knowledge the first time that lethality probability curves and lethal E values for cells oriented at 30º and 60º have been reported.
The results previously shown can be justified by assuming that the most likely phenomenon responsible for cell death is electroporation ( Weaver, 1994 Weaver JC. Molecular basis for cell membrane electroporationa. Ann N Y Acad Sci. 1994; 720(1):141-52. http://dx.doi.org/10.1111/j.1749-6632.1994.tb30442.x. PMid:8010633.
http://dx.doi.org/10.1111/j.1749-6632.1...
). Electroporation manifestation depends on Vm exceeding a certain threshold value and the maximum variation of this potential, ΔVm, depends on the intensity of the applied E, the cell geometry (width and length) and the angle between the cell orientation and E direction. Thus, assuming that the membrane is a perfect dielectric, a possible explanation for the non-linear increase observed for E50 values for cell orientations between 0º and 90º can be obtained by calculating the ΔVm induced by fixed E in a cell with average dimensions (length equal to 130 μm and width equal to 30 μm) in different orientations. The effect in a cell oriented at 30° is a ΔVm equivalent to 89% of that caused to a cell oriented at 0º ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
). For the 60° oriented cell, the ΔVm caused is equivalent to 63% of that at 0°. ΔVm is even smaller if the cell is oriented at 90º with respect to the E, being approximately 45%. Therefore, it can be seen that as we increase the angle between the cell major axis and the direction of the applied E, ΔVm for a same E magnitude decreases, which would reduce the probability of pore and, consequently, the likelihood of lethality. However, because the membrane is not a perfect dielectric, these percentage values found above are not totally accurate, being overestimated, since the model proposed by Klee & Plonsey ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
) does not take into account pores opening in the membrane. Nonetheless, the model is useful to qualitatively verify the need for an increase in the external E as cell orientation with respect to the E is increased to reach a given variation in transmembrane potential capable of causing electroporation (and consequently cell lethal injury).
From Figure 5 , we can draw a similarity, although in different magnitudes, in the behavior of E50 and E T as θ increases. And although the processes of cellular excitability and electroporation of the cell membrane are considered different phenomena – since the former is a self-stimulatory process, where the opening of a certain amount of ion selective voltage-dependent channels increases membrane depolarization and, consequently, increases the probability for more channels opening, leading to the firing of action potentials, and the latter is a self-limiting phenomenon, as the ion fluxes that flow through the pores curtail membrane polarization due to the electrical field ( Cheek and Fast, 2004 Cheek ER, Fast VG. Nonlinear changes of transmembrane potential during electrical shocks: role of membrane electroporation. Circ Res. 2004; 94(2):208-14. http://dx.doi.org/10.1161/01.RES.0000111526.69133.DE. PMid:14670844.
http://dx.doi.org/10.1161/01.RES.000011...
; Neunlist and Tung, 1997 Neunlist M, Tung L. Dose-dependent reduction of cardiac transmembrane potential by high-intensity electrical shocks. Am J Physiol Circ Physiol. 1997; 273(6 Pt 2):H2817-25. http://dx.doi.org/10.1152/ajpheart.1997.273.6.H2817. PMid:9435619.
http://dx.doi.org/10.1152/ajpheart.1997...
) – when we expressed values of lethal E as multiples of ET ( Table 3 ), we verified that the direction-dependent difference of E50 was greatly diminished (showing that ET might be a reasonable predictor of lethal E-values). Furthermore, Figure 4 displays an inverted relation: the E/ET ratio for 50% lethality was 20% lower for cells oriented at 90º than for cells at 0º. A possible explanation for this is due to the fact that, for cells oriented at 90º, the area of the membrane exposed to the maximum ΔVm is 2.5-fold larger when compared to cells oriented at 0º, which implies that a larger membrane area reaches supracritical V m values and undergoes permeabilization ( Oliveira et al., 2008 Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
http://dx.doi.org/10.1109/TBME.2008.200...
). This type of analysis allowed us to infer that an E of about 26 times the threshold corresponds to a probability of lethality of at least 50% of the cells, regardless of their orientation.
A significant limitation to be considered in this study was the progressive increase of the HEF intensity applied during the experimental protocol, since it was a function of ET . This is done with a cell carrying several shocks before dying, which activates cell repair mechanisms, reducing cell vulnerability to subsequent shocks ( Spaeth et al., 2010 Spaeth CS, Boydston EA, Figard LR, Zuzek A, Bittner GD. A model for sealing plasmalemmal damage in neurons and other eukaryotic cells. J Neurosci. 2010; 30(47):15790-800. http://dx.doi.org/10.1523/JNEUROSCI.4155-10.2010. PMid:21106818.
http://dx.doi.org/10.1523/JNEUROSCI.415...
; Steinhardt et al., 1994 Steinhardt RA, Bi G, Alderton JM. Cell membrane resealing by a vesicular mechanism similar to neurotransmitter release. Science. 1994; 263(5145):390-3. http://dx.doi.org/10.1126/science.7904084. PMid:7904084.
http://dx.doi.org/10.1126/science.79040...
; Togo et al., 1999 Togo T, Alderton JM, Bi GQ, Steinhardt RA. The mechanism of facilitated cell membrane resealing. J Cell Sci. 1999; 112(Pt 5):719-31. PMid:9973606. ). It was observed during the experiments that damage was caused to cells, promoting reductions in cell length and reversible hypercontracture. It has already been shown that a reduction in cell length increases E50 ( Goulart et al., 2012 Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
http://dx.doi.org/10.4322/rbeb.2012.040...
). Thus, the cumulative effect of shocks should not be overlooked and values found for lethal E (and cell probability of lethality) may be overestimated.
Also, we should emphasize that experiments were performed with isolated cells that were oriented at 0º, 30º, 60º or 90º with respect to the E direction. It is very difficult to directly extrapolate the results found in this work for clinical applications, since the heart has several cells of different sizes, oriented in the most diverse directions and connected through gap-junctions, in a way that each cell responds quite differently to the applied external E. It has already been shown that in heart tissue this difference in E response depends not only on the orientation of the cell with respect to E and cellular geometry, but also on the fact that the cardiac tissue is heterogeneous, resulting in the formation of virtual electrodes that modify E amplitudes and directions ( Coster and Zimmermann, 1975 Coster HG, Zimmermann U. The mechanism of electrical breakdown in the membranes ofValonia utricularis. J Membr Biol. 1975; 22(1):73-90. http://dx.doi.org/10.1007/BF01868164. PMid:1127686.
http://dx.doi.org/10.1007/BF01868164 ...
; Knisley et al., 1994 Knisley SB, Hill BC, Ideker RE. Virtual electrode effects in myocardial fibers. Biophys J. 1994; 66(3 Pt 1):719-28. http://dx.doi.org/10.1016/S0006-3495(94)80846-X. PMid:8011903.
http://dx.doi.org/10.1016/S0006-3495(94...
; Roth, 1995 Roth BJ. A mathematical model of make and break electrical stimulation of cardiac tissue by a unipolar anode or cathode. IEEE Trans Biomed Eng. 1995; 42(12):1174-84. http://dx.doi.org/10.1109/10.476124. PMid:8550059.
http://dx.doi.org/10.1109/10.476124 ...
), while the results shown in this work were obtained in a controlled and homogenous environment.
From the present results, it is possible to conclude that cell orientation with respect to E direction directly influences the probability of lethality of isolated myocytes in response to the application of HEF and that this probability of lethality, given a same E, is greater when E is applied at 0º with the cell orientation and decreases non-linearly as E is applied closer to the 90º. These results are in line with what was theoretically predicted by the Klee and Plonsey model ( Klee and Plonsey, 1976 Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
http://dx.doi.org/10.1109/TBME.1976.324...
).
Our work was able to provide information about the behavior of cell lethality as a function of E direction and cell orientation, not only by showing that there is an increase in the probability of cell lethality, but also how this increase is happening. Results showing how cell lethality is affected by HEF for directions other than 0º and 90º were absent in the literature and could contribute for the design of new defibrillation protocols ( Viana et al., 2016 Viana MA, Bassani RA, Petrucci O, Marques DA, Bassani JWM, Viana MA, Bassani RA, Petrucci O, Marques DA, Bassani JWM. System for open-chest, multidirectional electrical defibrillation. Res Biomed Eng. 2016; 32(1):74-84. http://dx.doi.org/10.1590/2446-4740.02015.
http://dx.doi.org/10.1590/2446-4740.020...
), by providing data on an E upper limit for cell survival, and also support further works in areas related to electropermeabilization and cell/tissue stimulation. Furthermore, these data could be used as adjusting or comparing parameters for computational models and simulations.
Acknowledgements
The authors are grateful to the team of R&D staff at CEB/UNICAMP for the technical support and also to Dr. Jair Goulart and MSc. Marcelo Zoccoler for scientific support during the development of this work. This study was supported by CAPES (Coordination of Improvement of Higher Education Personnel, scholarship to FSCL).
-
How to cite this article: Leomil FSC, Oliveira PX. New insight on the relationship between lethal electrical fields versus cardiomyocyte orientation. Res Biomed Eng. 2018; 34(3):. DOI: 10.1590/2446-4740.180023.
References
- Bardou AL, Chesnais JM, Birkui PJ, Govaere MC, Auger PM, Von Euw D, Degonde J. Directional variability of stimulation threshold measurements in isolated guinea pig cardiomyocytes: Relationship with orthogonal sequential defibrillating pulses. Pacing Clin Electrophysiol. 1990; 13(12 Pt 1):1590-5. http://dx.doi.org/10.1111/j.1540-8159.1990.tb06859.x. PMid:1704510.
» http://dx.doi.org/10.1111/j.1540-8159.1990.tb06859.x - Bassani RA, Lima KA, Gomes PAP, Oliveira PX, Bassani JWM. Combining stimulus direction and waveform for optimization of threshold stimulation of isolated ventricular myocytes. Physiol Meas. 2006; 27(9):851-63. http://dx.doi.org/10.1088/0967-3334/27/9/008. PMid:16868351.
» http://dx.doi.org/10.1088/0967-3334/27/9/008 - Benjamin EJ, Blaha MJ, Chiuve SE, Cushman M, Das SR, Deo R, de Ferranti SD, Floyd J, Fornage M, Gillespie C, Isasi CR, Jiménez MC, Jordan LC, Judd SE, Lackland D, Lichtman JH, Lisabeth L, Liu S, Longenecker CT, Mackey RH, Matsushita K, Mozaffarian D, Mussolino ME, Nasir K, Neumar RW, Palaniappan L, Pandey DK, Thiagarajan RR, Reeves MJ, Ritchey M, Rodriguez CJ, Roth GA, Rosamond WD, Sasson C, Towfighi A, Tsao CW, Turner MB, Virani SS, Voeks JH, Willey JZ, Wilkins JT, Wu JH, Alger HM, Wong SS, Muntner P. Heart disease and stroke statistics-2017 update: a report from the American Heart Association. Circulation. 2017; 135(10):e146-603. http://dx.doi.org/10.1161/CIR.0000000000000485. PMid:28122885.
» http://dx.doi.org/10.1161/CIR.0000000000000485 - Cheek ER, Fast VG. Nonlinear changes of transmembrane potential during electrical shocks: role of membrane electroporation. Circ Res. 2004; 94(2):208-14. http://dx.doi.org/10.1161/01.RES.0000111526.69133.DE. PMid:14670844.
» http://dx.doi.org/10.1161/01.RES.0000111526.69133.DE - Coster HG, Zimmermann U. The mechanism of electrical breakdown in the membranes ofValonia utricularis. J Membr Biol. 1975; 22(1):73-90. http://dx.doi.org/10.1007/BF01868164. PMid:1127686.
» http://dx.doi.org/10.1007/BF01868164 - DeBruin KA, Krassowska W. Modeling Electroporation in a Single Cell. I. Effects of field strength and rest potential. Biophys J. 1999; 77(3):1213-24. http://dx.doi.org/10.1016/S0006-3495(99)76973-0. PMid:10465736.
» http://dx.doi.org/10.1016/S0006-3495(99)76973-0 - Fedorov VV, Nikolski VP, Efimov IR. Effect of electroporation on cardiac electrophysiology. USA: Humana Press; 2008, p. 433-48. https://doi.org/10.1007/978-1-59745-194-9_34.
» https://doi.org/10.1007/978-1-59745-194-9_34 - Gomes PAP, Bassani RA, Bassani JWM. Electric field stimulation of cardiac myocytes during postnatal development. IEEE Trans Biomed Eng. 2001; 48(6):630-6. http://dx.doi.org/10.1109/10.923781. PMid:11396593.
» http://dx.doi.org/10.1109/10.923781 - Goulart JT, de Oliveira PX, Bassani JWM, Bassani RA. The influence of cell dimensions on the vulnerability of ventricular myocytes to lethal injury by high-intensity electrical fields. Rev Bras Eng Bioméd. 2012; 28(4):337-45. http://dx.doi.org/10.4322/rbeb.2012.040.
» http://dx.doi.org/10.4322/rbeb.2012.040 - Ideker RE, Zhou X, Knisley SB. Correlation among fibrillation, defibrillation, and cardiac pacing. Pacing Clin Electrophysiol. 1995; 18(3 Pt 2):512-25. http://dx.doi.org/10.1111/j.1540-8159.1995.tb02562.x. PMid:7777416.
» http://dx.doi.org/10.1111/j.1540-8159.1995.tb02562.x - Ivorra A. Tissue electroporation as a bioelectric phenomenon: Basic concepts. Berlin: Springer; 2010, p. 23-61. https://doi.org/10.1007/978-3-642-05420-4_2.
» https://doi.org/10.1007/978-3-642-05420-4_2 - Jones JL, Jones RE, Balasky G. Microlesion formation in myocardial cells by high-intensity electric field stimulation. Am J Physiol. 1987; 253(2 Pt 2):H480-6. PMid:2441612.
- Klauke N, Smith G, Cooper JM. Regional electroporation of single cardiac myocytes in a focused electric field. Anal Chem. 2010; 82(2):585-92. http://dx.doi.org/10.1021/ac901886j. PMid:20020746.
» http://dx.doi.org/10.1021/ac901886j - Klee M, Plonsey R. Stimulation of spheroidal cells - The role of cell shape. IEEE Trans Biomed Eng. 1976; BME-23(4):347-54. http://dx.doi.org/10.1109/TBME.1976.324597. PMid:1278928.
» http://dx.doi.org/10.1109/TBME.1976.324597 - Knisley SB, Grant AO. Asymmetrical electrically induced injury of rabbit ventricular myocytes. J Mol Cell Cardiol. 1995; 27(5):1111-22. http://dx.doi.org/10.1016/0022-2828(95)90047-0. PMid:7473769.
» http://dx.doi.org/10.1016/0022-2828(95)90047-0 - Knisley SB, Hill BC, Ideker RE. Virtual electrode effects in myocardial fibers. Biophys J. 1994; 66(3 Pt 1):719-28. http://dx.doi.org/10.1016/S0006-3495(94)80846-X. PMid:8011903.
» http://dx.doi.org/10.1016/S0006-3495(94)80846-X - Kotnik T, Pucihar G, Reberšek M, Miklavčič D, Mir LM. Role of pulse shape in cell membrane electropermeabilization. Biochim Biophys Acta - Biomembr. 2003; 1614(2):193-200. http://dx.doi.org/10.1016/S0005-2736(03)00173-1.
» http://dx.doi.org/10.1016/S0005-2736(03)00173-1 - Krauthamer V, Jones JL. Calcium dynamics in cultured heart cells exposed to defibrillator-type electric shocks. Life Sci. 1997; 60(2):1977-85. http://dx.doi.org/10.1016/S0024-3205(97)00162-8.
» http://dx.doi.org/10.1016/S0024-3205(97)00162-8 - Miklavcic D, Pucihar G, Macek Lebar A, Krmelj J, Towhidi L. The pulse intensity-duration dependency for cell membrane electroporation. In: Pakhomov AG, Miklavicic D, Markov MS, editors. Advanced electroporation techniques in biology and medicine. Boca Raton: CRC Press, 2010. p. 246-59. https://doi.org/10.1201/EBK1439819067-17.
» https://doi.org/10.1201/EBK1439819067-17 - Neunlist M, Tung L. Dose-dependent reduction of cardiac transmembrane potential by high-intensity electrical shocks. Am J Physiol Circ Physiol. 1997; 273(6 Pt 2):H2817-25. http://dx.doi.org/10.1152/ajpheart.1997.273.6.H2817. PMid:9435619.
» http://dx.doi.org/10.1152/ajpheart.1997.273.6.H2817 - Nikolski V, Efimov I. Electroporation of the heart. Europace. 2005; 7:S146-54. http://dx.doi.org/10.1016/j.eupc.2005.04.011.
» http://dx.doi.org/10.1016/j.eupc.2005.04.011 - Oliveira PX, Bassani RA, Bassani JWM. Lethal effect of electric fields on isolated ventricular myocytes. IEEE Trans Biomed Eng. 2008; 55(11):2635-42. http://dx.doi.org/10.1109/TBME.2008.2001135. PMid:18990634.
» http://dx.doi.org/10.1109/TBME.2008.2001135 - Penna LB, Bassani RA. Increased spontaneous activity and reduced inotropic response to catecholamines in ventricular myocytes from footshock-stressed rats. Stress. 2010; 13(1):73-82. http://dx.doi.org/10.3109/10253890902951778. PMid:19697264.
» http://dx.doi.org/10.3109/10253890902951778 - Prado LN, Goulart JT, Zoccoler M, Oliveira PX. Ventricular myocyte injury by high-intensity electric field: Effect of pulse duration. Gen Physiol Biophys. 2016; 35(2):121-30. http://dx.doi.org/10.4149/gpb_2015047. PMid:26830130.
» http://dx.doi.org/10.4149/gpb_2015047 - Roth BJ. A mathematical model of make and break electrical stimulation of cardiac tissue by a unipolar anode or cathode. IEEE Trans Biomed Eng. 1995; 42(12):1174-84. http://dx.doi.org/10.1109/10.476124. PMid:8550059.
» http://dx.doi.org/10.1109/10.476124 - Spaeth CS, Boydston EA, Figard LR, Zuzek A, Bittner GD. A model for sealing plasmalemmal damage in neurons and other eukaryotic cells. J Neurosci. 2010; 30(47):15790-800. http://dx.doi.org/10.1523/JNEUROSCI.4155-10.2010. PMid:21106818.
» http://dx.doi.org/10.1523/JNEUROSCI.4155-10.2010 - Steinhardt RA, Bi G, Alderton JM. Cell membrane resealing by a vesicular mechanism similar to neurotransmitter release. Science. 1994; 263(5145):390-3. http://dx.doi.org/10.1126/science.7904084. PMid:7904084.
» http://dx.doi.org/10.1126/science.7904084 - Togo T, Alderton JM, Bi GQ, Steinhardt RA. The mechanism of facilitated cell membrane resealing. J Cell Sci. 1999; 112(Pt 5):719-31. PMid:9973606.
- Tsong TY. Electroporation of cell membranes. Biophys J. 1991; 60(2):297-306. http://dx.doi.org/10.1016/S0006-3495(91)82054-9. PMid:1912274.
» http://dx.doi.org/10.1016/S0006-3495(91)82054-9 - Tung L, Sliz N, Mulligan MR. Influence of electrical axis of stimulation on excitation of cardiac muscle cells. Circ Res. 1991; 69(3):722-30. http://dx.doi.org/10.1161/01.RES.69.3.722. PMid:1873867.
» http://dx.doi.org/10.1161/01.RES.69.3.722 - Tung L. Detrimental effects of electrical fields on cardiac muscle. Proc IEEE. 1996; 84(3):366-78. http://dx.doi.org/10.1109/5.486740.
» http://dx.doi.org/10.1109/5.486740 - Viana MA, Bassani RA, Petrucci O, Marques DA, Bassani JWM, Viana MA, Bassani RA, Petrucci O, Marques DA, Bassani JWM. System for open-chest, multidirectional electrical defibrillation. Res Biomed Eng. 2016; 32(1):74-84. http://dx.doi.org/10.1590/2446-4740.02015.
» http://dx.doi.org/10.1590/2446-4740.02015 - Weaver JC. Molecular basis for cell membrane electroporationa. Ann N Y Acad Sci. 1994; 720(1):141-52. http://dx.doi.org/10.1111/j.1749-6632.1994.tb30442.x. PMid:8010633.
» http://dx.doi.org/10.1111/j.1749-6632.1994.tb30442.x - Weisz MT. Physical principles of defibrillators. Anaesth Intensive Care Med. 2009; 10(8):367-9. http://dx.doi.org/10.1016/j.mpaic.2009.05.002.
» http://dx.doi.org/10.1016/j.mpaic.2009.05.002 - Yabe S, Smith WM, Daubert JP, Wolf PD, Rollins DL, Ideker RE. Conduction disturbances caused by high current density electric fields. Circ Res. 1990; 66(5):1190-203. PMID:2335021.
- Zipes DP, Camm AJ, Borggrefe M, Buxton AE, Chaitman B, Fromer M, Gregoratos G, Klein G, Moss AJ, Myerburg RJ, Priori SG, Quinones MA, Roden DM, Silka MJ, Tracy C, Smith SC Jr, Jacobs AK, Adams CD, Antman EM, Anderson JL, Hunt SA, Halperin JL, Nishimura R, Ornato JP, Page RL, Riegel B, Priori SG, Blanc JJ, Budaj A, Camm AJ, Dean V, Deckers JW, Despres C, Dickstein K, Lekakis J, McGregor K, Metra M, Morais J, Osterspey A, Tamargo JL, Zamorano JL. ACC/AHA/ESC 2006 guidelines for management of patients with ventricular arrhythmias and the prevention of sudden cardiac death: a report of the American College of Cardiology/American Heart Association Task Force and the European Society of Cardiology Committee for Practice Guidelines (Writing Committee to Develop Guidelines for Management of Patients With Ventricular Arrhythmias and the Prevention of Sudden Cardiac Death). J Am Coll Cardiol. 2006; 48(5):e247-346. http://dx.doi.org/10.1016/j.jacc.2006.07.010. PMid:16949478.
» http://dx.doi.org/10.1016/j.jacc.2006.07.010
Publication Dates
-
Publication in this collection
13 Sept 2018Jul-Sep 2018 -
Date of issue
Sept 2018
History
-
Received
16 Apr 2018 -
Accepted
29 June 2018