Creep of a C-S-H gel: a micromechanical approach

PHYSICAL SCIENCES

Creep of a C-S-H gel: a micromechanical approach

Julien Sanahuja^I,*; Luc Dormieux^II

^ILafarge Centre de Recherche, 95 rue du Montmurier, BP 15, 38291 Saint-Quentin Fallavier cedex, France

^IIÉcole Nationale des Ponts et Chaussées, Institut Navier, 6 et 8 avenue Blaise Pascal, 77455 Marne-la-Vallée, France

^{Correspondence to}

ABSTRACT

Both clays and calcium silicate hydrates(the main hydration products of Portland cements) exhibit a microstructure made up of lamellar particles. The microscopic mechanism responsible for the macroscopic creep of such materials is often described as the relative sliding of the sheets. This paper proposes a micromechanical approach to estimate the macroscopic creep behavior rising from this microscopic mechanism. The asymptotic evolution of creep at both short- and long-term is especially investigated. More precisely, a non-vanishing initial elastic strain is retrieved. At long-term, a threshold on porosity appears. At lower porosities, the creep evolution admits an asymptotic strain. At higher porosities, it admits an asymptotic strain rate.

Key words: homogenization, creep, cement paste, C-S-H gel.

RESUMO

Argilas e hidratos de cálcio (principal produto de cimentos) ambos exibem microestrutura composta por partículas em forma de lamelas. O principal mecanismo responsável pelo fenômeno de fluência macroscópico é frequentemente descrito pelo deslizamento entre as lamelas. O artigo propõe uma abordagem micromecânica para estimar a fluência macroscópica que surge a partir do mecanismo microscópico. A evolução assintótica da fluência para tempos curtos e longos é especialmente investigada. Mais precisamente uma tensão inicial não nula é derivada. Para tempos longos um limiar de porosidade surge da modelagem. Na faixa de porosidades mais baixas a evolução da fluência admite deformação assintótica. Para porosidades altas o problema admite taxa de deformação assintótica.

Palavras-chave: homogeneização, fluência, pasta de cimento, C-S-H gel.

INTRODUCTION

Concrete is a complex multi-scale composite involving multi-physics processes. As it is the only evolving component of concrete, the cement paste has a major influence on the mechanical properties of concrete. As the aggregates do not exhibit significant creep, the first step is to investigate the creep of the cement paste. Moreover, nanoindentation tests have shown that, in the cement paste, only (calcium silicate hydrates) exhibit non-negligible creep (Acker 2001).

The growth of C-S-H on the surface of a C₃S (tricalcium sulfate) grain wetted by a drop of lime saturated solution has been observed by AFM (Garrault et al. 2005). C-S-H seem to grow by the aggregation of small flattened particles whose largest face is parallel to the surface of the grain. The size of these particles has been measured: 60*30 nm by 5 nm thick. The model of Courault and Nonat (Courault 2001, Nonat et al. 2001) describes these particles as the superposition of a few sheets (see Fig. 1).

The starting point of the micromechanical model is a hypothesis on the mechanism, occuring at the nano-scale, responsible for the macroscopic creep. We assume that this mechanism is a relative sliding of the sheets in the solid particles of C-S-H. This hypothesis, even if still in debate, has been suggested by several authors (Lohtia 1970, Ruetz 1968, Wittmann 1982, Benboudjema 2002, Gmira 2003, Nonat 2004, Jennings et al. 2005, Tamtsia and Beaudoin 2000).

This paper is, thus, devoted to the micromechanical modelling of creep of porous polycrystals made up of lamellar grains. This model seems reasonable as a first approach to investigate creep of a C-S-H gel. It may also be applicable to clays. In the micromechanical model of the elasticity of a cement paste proposed and validated with respect to stiffness experimental data in (Sanahuja et al. 2007), the behavior of the solid particles of C-S-H is regarded as isotropic elastic, characterized by the Young's modulus E_s = 71.6 GPa and the Poisson's ratio ν_s = 0.27. The model developed here enriches this elastic behavior incorporating the viscoelastic relative sliding of the sheets, considered as the main mechanism responsible for macroscopic creep. Its derivation is based on the homogenization techniques developed in (Dormieux et al. 2006), and on approaches commonly used to deal with viscoelastic behaviors in micromechanics.

The model is developed considering spherical shapes to represent the solid particles in order to keep closed form expressions. The orientation distribution of the grains is isotropic. In Section 2, the viscoelastic behavior of the elementary particle is modelled, considering both the microstructural description of the particle (Fig. 1) and the hypothesis of relative sliding of the sheets. Then, the correspondence principle is introduced and the behavior of the elementary particle is written in the Carson domain. The technical part of the homogenization process is presented in Appendix A. In short, particles (with an uniform distribution of orientation) are homogenized with pores in the framework of elasticity. Due to the random nature of the morphology, a self-consistent scheme is used. To keep expressions in a closed form, spherical shapes are used for both the solid phase and the pore space. Useful truncated series expansions are derived in Appendix A.2.2. Section 3 focuses on the results of the model. First, a systematic investigation of the creep behavior at both short- (Section 3.1) and long-term (Section 3.2) is performed, taking advantage of the aforementioned truncated series expansions. Second, numerical simulations of the creep function over the whole time range are performed. Section 4 paves the way towards a creep model of cement paste. In particular, the case of oblate particles (flattened spheroids), whose axis of revolution is perpendicular to the sheets, is a straightforward generalization of the model presented in this paper.

NOMENCLATURE

first-order tensor

A second-order tensor

fourth-order tensor

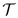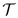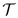₁ ⊥ ₂ tensorial product of the tensors ₁ and ₂

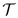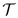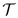₁ .₂ contraction of the tensors ₁ and ₂

₁ : 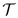₂ double contraction of the tensors 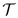₁ and 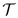₂

^-1 inverse of the tensor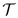

1 second-order unit tensor

fourth-order unit tensor

: S = S, where S is a symmetrical tensor

projector extracting the spherical part of a second-order tensor ( = 1/31 ⊥ 1)

: S = 1/3 (trS)1, where S is a symmetrical tensor

projector extracting the deviatoric part of a second-order tensor ( = - )

: S = S^dev, where S is a symmetrical tensor

trA trace of A

A^dev deviator of A, A^dev = A - 1/3(trA)1

(e₁, e₂, e₃) reference base

r, θ, spherical coordinates

(e_r, e_θ , e_ø) spherical base

H(x) Heaviside function, H(x) = 1 if x > 0 and H(x) = 0 if x < 0

t time

p complex variable in the Laplace domain

f (p) Laplace-Carson transform of the function

j being a particular phase of the REV:

f_j volume fraction of phase j

a

_j average of the field a over the domain occupied by phase j

_j stiffness tensor of phase j

j compliance tensor of phase j, _j =

if phase j is isotropic, 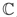_j = 3k_j + 2g_j:

k_j bulk modulus of phase j

g_j shear modulus of phase j

E_j Young's modulus of phase j

ν_j Poisson's ratio of phase j

with the classical relations:

ε, E microscopic and macroscopic strain tensors

σ, Σ microscopic and macroscopic stress tensors

φ porosity

r_s aspect-ratio of a spheroid (< 1 for oblates, = 1 for a sphere, > 1 for prolates)

usual cement's chemistry abbreviations:

C CaO

S SiO₂

H H₂O

MICROMECHANICAL MODELLING

BEHAVIOR OF THE PARTICLES

The isotropic elastic behavior of the solid particles (characterized by the bulk and shear moduli k_s and g_s) is modified to incorporate the relative sliding mechanism of the sheets. The latter only affects the shear strains onto (e₁, e₃) and (e₂, e₃), where e₃ is perpendicular to the sheets. The elastic behavior, thus, has to be replaced by a viscoelastic one that keeps the initial elastic strain (when t → 0⁺) during a creep experiment. The simplest rheological model fulfilling this condition is the Maxwell model (Fig. 2). The viscosity of the dashpot is denoted by η_s. The behavior of the solid particles, as a strain-stress relationship, is, thus, modified as follows:

As far as the shear strain onto (e₁, e₂) and the extension strains in the e₁, e₂ and e₃ directions are concerned, the behavior remains elastic.

The variable relative orientation of the particles couples these strain modes in quite a complicated way. The macroscopic viscoelastic behavior rises from these couplings. Homogenization of random media and the Laplace-Carson transform allow to estimate these couplings, considering a random distribution of the particles and an isotropic distribution of their orientation.

The Laplace-Carson transform is indeed classically used in order to transform, from a formal point of view, a non-aging linear viscoelastic problem into a linear elastic one. The effective behavior in the Carson domain can be estimated resorting to classical homogenization techniques in the framework of linear elasticity. The last step consists in inverting the Laplace-Carson transform to get the effective viscoelastic behavior, equivalently characterized by the creep or relaxation function. This is often the most mathematically involved step, as the inverses of only a few simple functions are analytically known. Numerical inversion is required in the case of more complicated functions. The Laplace and Laplace-Carson transforms are respectively defined as:

The viscoelastic behavior of the particle whose sheets are perpendicular to e_r (orientation described by θ and ), thus, becomes in the Carson domain:

with the isotropic elastic part:

and the viscous part that depends on the particle orientation, using Voigt notation:

HOMOGENIZATION

In the Carson domain, the compliance of the particles is found to have exactly the pattern of the compliance dealt with in Appendix A.2, provided that k,g and c_s are respectively substituted by k(p) = k_s, g(p) = g_s and c_s(p) = η_sp. Pores are found inbetween the particules. The porosity is denoted by φ. The results derived in Appendix A.2 can, then, be reused to get the effective moduli k^SCS(p) and g^SCS(p) of the porous polycrystal in the Carson domain (as described by (33)). The last step is to perform an inverse Laplace-Carson transform to obtain the spherical and deviatoric effective creep functions.

EFFECTIVE CREEP FUNCTIONS

Let us first consider a creep experiment under a spherical macroscopic stress of the form Σ(t) = Σ₀H(t)1, which corresponds to Σ(p) = Σ₀1 in the Carson domain. The macroscopic strain in the Carson domain is, then, E(p) = E^sph(p)1, with:

The following normalized variables can be defined:

Taking advantage of the time-frequency scaling of the Laplace transform, which yields g(t) = f(αt) ⇒ g(p) = f(p/α) as far as the Laplace-Carson transform is concerned, the normalized creep strain t_n → (t_n) is the inverse Laplace-Carson transform of:

Finally, the spherical creep strain reads:

In a similar way, let us now consider a creep experiment under a deviatoric macroscopic stress of the form Σ(t) = Σ₀H(t)T^dev, which corresponds to Σ(p) = Σ₀T^dev in the Carson domain. The deviatoric creep strain, then, reads E^dev(t) = E^dev(t)T^dev, with:

where is the inverse Laplace-Carson transform of:

Only numerical computations of f_k(φ, ν_s, p_n) and f_g(φ, ν_s, p_n) are available (calculated from (34) and (35)). The Laplace-Carson transform, therefore, cannot be analytically inverted. However, taking advantage of the truncated series expansions derived in Appendix A.2.2, the creep response at both short- (t_n → 0) and long-term (t_n → ∞) can be investigated.

RESULTS

CREEP AT SHORT-TERM

We first consider the case t_n → 0, obtained when p_n → ∞ . We recall the truncated series expansion (50), which is valid for 0 < φ < 1/2:

The normalized spherical creep strain, thus, reads asymptotically:

where and are respectively given by (55) and (56). And the normalized deviatoric creep strain reads asymptotically:

where and are respectively given by (52) and (53). An initial elastic strain is, thus, observed on the whole range of porosities, from 0 to 1/2. The instantaneous stiffness corresponds exactly to the stiffness obtained by the self-consistent scheme with an elastic solid phase whose moduli are k_s and g_s. This was the purpose of the present model, developed as an extension of the elastic model. Figure 3 depicts the elastic part and the initial slope of the spherical and deviatoric creep strains. Note that the elastic strain and the initial slope are both higher in the case of deviatoric creep than in the case of spherical creep.

CREEP AT LONG-TERM

Let us now consider the case t_n → ∞, obtained from p_n → 0. When 0 < φ < 1/4, we recall the truncated series expansion (36):

The normalized asymptotic spherical creep strain, thus, reads:

where is given by (41). And the normalized asymptotic deviatoric creep strain reads:

where is given by (38). The creep strain reaches an asymptotic level, which depends on the porosity (see Fig. 4).

When 1/4 < φ < 1/2, we recall the truncated series expansionn (44):

The normalized spherical and deviatoric creep strain, then, read:

where and are respectively given by (48) and (46). Within this range of porosities (1/4 - 1/2), the asymptotic creep strain grows at a constant rate. This rate is represented as a function of porosity on Figure 5.

These results on creep at long-term, sketched on Figure 6, can be commented out:

• at long-term (t_n → ∞), the dashpot can be considered as free (non-zero strain at vanishing stress);

• when porosity is higher than 1/4, the polycrystals are of sufficient low density so that the sheets can slide freely, without being restrained by neighboring particles (that may have a different orientation): the macroscopic strain grows indefinitely;

• when porosity is lower than 1/4, the polycrystals are compact: the neighboring particles restrict the relative sliding of the sheets, activating their elastic compliance; the asymptotic macroscopic behavior is, therefore, elastic.

NUMERICAL SIMULATION OF THE CREEP STRAIN OVER THE WHOLE TIME RANGE

The complete evolution of the creep strain with respect to time can only be obtained by the numerical inversion of the Laplace-Carson transform. The Gaver-Stehfest algorithm (Abate and Whitt 2006, Gaver 1966, Stehfest 1970) is used. Basically, the inverse function is approximated by a finite linear combination of values of the function in the Carson space, based on the sequence of Gaver approximants (Gaver 1966). The spherical and deviatoric creep strains are plotted with respect to time on Figure 7, for five different porosities.

The asymptotic evolutions depicted in Section 3.1 at t_n → 0, and in Section 3.2 at t_n → ∞ are retrieved. Moreover, the deviatoric creep strain is always higher than the spherical one.

CONCLUSION AND PROSPECTS

The micromechanical model of cement paste developed and validated with respect to elastic measurements in (Sanahuja et al. 2007) distinguished two types of C-S-H. In this model, high density (HD) C-S-H is viewed as a porous polycrystal made up of particles of the same shape as the elementary brick represented on Figure 1, whereas low density (LD) C-S-H is made up of more flattened particles (which can be viewed as a juxtaposition of several elementary bricks). This porosity and the aspect-ratio are, thus, two morphological parameters of the microstructure. Table 1 gathers the typical values of these morphological parameters for the two model materials (porosity of LD C-S-H is provided as the range reached at the end of hydration when 0.2 < w/c < 0.6).

This model being successfully validated with respect to elastic measurements, the morphology can be tentatively reused as an input to investigate other mechanical behaviors including creep, which is the subject of the present paper. However, the developments presented here need to be reworked to consider flattened solid particles (oblate shape) instead of spheres.

Thus, the next step would be to revisit the model described in (Sanahuja et al. 2007) to deal with creep. C-S-H creep would be dealt with the use of the model developed in the present paper, modified to take into account the flattened shape of the C-S-H solid particles. This may help to investigate one main question about the creep strain evolution of concrete at long-term, namely whether it reaches a stable value or grows at a constant rate.

EFFECTIVE STIFFNESS OF POROUS POLYCRYSTALS MADE UP OF LAMELLAR PARTICLES

We consider a porous polycrystal. The solid grains are made up of stacked planar sheets. The porosity is denoted by φ. This section is devoted to the estimation of the effective stiffness of such material. The micromechanical modelling of the behavior of polycrystals made up of lamellar particles, in the framework of homogenization of random media, was initiated in (Dormieux et al. 2006). At the polycrystal scale, the effective behavior of the grains is modelled by a transversely isotropic stiffness tensor.

THE MOST GENERAL CASE: UNSPECIFIED TRANSVERSELY ISOTROPIC STIFFNESS TENSOR

In this first part, the stiffness of the solid grains is a transversely isotropic stiffness tensor with unspecified components. In an orthonormal base whose third vector is perpendicular to the sheets, the stiffness tensor of each grain is supposed to have the same components. Using Voigt notation, and the vector e_r being perpendicular to the sheets, this transversely isotropic tensor reads:

where (e_r, e_θ, e_ø) is the spherical base. The stiffness of a grain, thus, only depends on its orientation, described by the two Euler angles (θ, ), and on the five components c₁₁₁₁, c₁₁₂₂, c₁₁₃₃, c₃₃₃₃ and c₂₃₂₃.

The morphology being random and polycrystalline, it seems natural to resort to a self-consistent scheme to model the elasticity of such a porous material. For simplicity, the grains are represented by spherical shapes (Fig. 8). Note that the derivation is feasible with spheroids whose axis of revolution is perpendicular to the sheets, but the expressions involved are much lengthier. The orientation distribution of the particles is supposed to be isotropic. Thus, the effective stiffness is also isotropic. The self-consistent estimate of the latter is denoted by 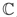^SCS= 3k^SCS + 2g^SCS, where k^SCS and g^SCS are the estimates of the effective bulk and shear moduli.

The derivation of the homogenization scheme requires, for uniform strain boundary conditions (E) on the REV, estimates of the average strain in the pore space and in the solid domain, and of the average stress in the solid domain.

The average strain in the pore space is estimated by the uniform strain that rises in a spherical pore embedded into an infinite reference medium, whose stiffness is the sought homogenized one, and with an uniform strain E^∞ at infinity (the latter will be linked to the strain E applied at the boundary of the REV using the average law (27)):

being the Eshelby tensor (Eshelby 1957) of a sphere in a reference medium whose stiffness is 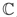^SCS. This reference medium being isotropic, the expression of this Eshelby tensor is simple:

The average strain in the set of grains whose vector perpendicular to the sheets is e_r (parametrized by θ , ) is estimated by the uniform strain that rises in a sphere made up of the same material than these grains, embedded into the infinite effective medium, and with the uniform strain E^∞ at infinity (Eshelby 1957):

being the Hill tensor of a sphere in a medium whose stiffness is 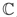^SCS; it is related to the corresponding Eshelby tensor (23) by = : 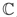^SCS.

The average strain over the whole solid domain is, then, obtained as an angular average, e_r following an isotropic orientation distribution:

The average stress over the whole solid domain is estimated in the same way, from (24):

The uniform strain E at the boundary of the REV is, then, related to the reference strain E^∞ using (22), (25) and the average rule:

The macroscopic stress is Σ = (1- φ)σ

_s. The effective stiffness tensor is, then, defined as the tensor relating the macroscopic strain and stress: Σ 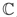= ^SCS : E. Taking into account (22), (25) and (26), the latter reads:

This tensorial equation reduces to two scalar equations since all the tensors involved and resulting from the integrations are isotropic. The self-consistent estimates k^SCS and g^SCS of the effective bulk and shear moduli are the positive solutions of these two nonlinear equations.

ISOTROPIC COMPLIANCE ADDED TO A COMPLIANCE MODELLING THE SLIDING OF THE SHEETS

The compliance of the grains is now supposed to be the sum of:

• an isotropic compliance (bulk and shear moduli denoted by k and g);

• a compliance (characterized by the modulus c_s) that only allows the simple shear activated by relative sliding of the sheets: ε₁₃ = σ₁₃ /2/ c_s and ε₂₃ = σ₂₃ /2/ c_s (e₃ being perpendicular to the sheets).

The total compliance of the grain whose vector perpendicular to the sheets is e_r, thus, reads:

with:

and, using Voigt notation:

Effective moduli

The stiffness of the grains being transversely isotropic, we take advantage of the results established in the Section A.1, introducing the five components:

The effective moduli, normalized by k, appear as functions of the porosity φ, the Poisson's ratio ν = (3k - 2g)/(6k + 2g) and the ratio χ = c_s/g:

For φ > 1/2, f_k(φ, ν, χ) and f_g( φ , ν , χ ) vanish. The equations to be solved to get f_k and f_g are sought for φ < 1/2. The tensorial equation (28) yields, on one hand, the expression of f_k as a function of f_g:

hiding the dependency of f_k and f_g with respect to (φ, ν, χ), and, on the other hand, a fourth order polynomial equation in f_g:

Only a numerical resolution can provide f_k(φ, ν, χ) and f_g(φ, ν, χ) (see Fig. 9). However, some truncated series expansions of f_k(φ, ν, χ) and f_g(φ, ν, χ) can be derived when χ → 0 or ∞ . These ones are used in Sections 3.1 and 3.2.

Truncated series expansions

When χ → 0 and 0 < φ < 1/4, the truncated series expansions of f_k and f_g read:

with:

with

and with:

Note that the effective moduli tend towards 0 when φ → 1/4^-.

When χ → 0 and 1/4 < φ < 1/2, the truncated series expansions of f_k and f_g read:

with:

and with:

The effective moduli are of the same order as χ, which is compatible with the fact that they tend towards 0 when φ → 1/4^-.

When χ → ∞ and 0 < φ < 1/2, the truncated series expansions of f_k and f_g read:

with:

and with:

Note that is the effective shear modulus obtained by the usual self-consistent scheme (isotropic solid phase). Indeed, when χ → ∞ , the compliance _g(θ, ), added to the isotropic compliance _iso, vanishes. This remark is also valid for the bulk modulus.

Manuscript received on June 16, 2008; accepted for publication on April 27, 2009

Selected paper presented at the IUTAM Symposium on Swelling and Shrinking of Porous Materials: From Colloid Science to Poromechanics - August 06-10 2007, LNCC/MCT.

• ABATE J AND WHITT W. 2006. A unified framework for numerically inverting Laplace transforms. INFORMS J Comput 18: 408421.
• ACKER P. 2001. Micromechanical analysis of creep and shrinkage mechanisms. In: Creep, shrinkage and durability mechanics of concrete and other quasi-brittle materials. Proceedings of the sixth international conference concreep6.
• BARBARULO R. 2002. Comportement des matériaux cimentaires: actions des sulfates et de la température. PhD thesis, École nationale supérieure de Cachan.
• BENBOUDJEMA F. 2002. Modélisation des déformations différées du béton sous sollicitations biaxiales. Application aux enceintes de confinement de bâtiments réacteurs des centrales nucléaires. PhD thesis, Université de Marne-la-Vallée.
• COURAULT A-C. 2001. Stoechiométrie des C-S-H et propriétés dans différents environnements chimiques. Modélisation expérimentale. PhD thesis, Université de Bourgogne, Dijon, France.
• DORMIEUX L, LEMARCHAND E AND SANAHUJA J. 2006. Comportement macroscopique des matériaux poreux à microstructure en feuillets. CR Mécanique 334: 304310.
• ESHELBY J. 1957. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond A 241: 376396.
• GARRAULT S, FINOT E, LESNIEWSKA E AND NONAT A. 2005. Study of C-S-H growth on C3S surface during its early hydration. Mater Struct 38: 435442.
• GAVER D. 1966. Observing stochastic processes and approximate transform inversion. Oper Res 14: 444459.
• GMIRA A. 2003. Etude texturale et thermodynamique d'hydrates modèles du ciment. PhD thesis, Univ. Orléans.
• JENNINGS H, THOMAS J, GEVRENOV J, CONSTANTINIDES G AND ULM F. 2005. Nanostructure of C-S-H gel in cement paste as a function of curing conditions and relative humidity. In: Creep, shrinkage and durability of concrete and concrete structures. Proceeding of Concreep 7 IA-Concreep, Nantes, France, p. 1937.
• LOHTIA R. 1970. Mechanism of creep in concrete. Roorkee University Research Journal 12(1-2): 3747.
• NONAT A. 2004. The structure and stoichiometry of the C-S-H. Cem Concr Res 34: 15211528.
• NONAT A, COURAULT A-C AND DAMIDOT D. 2001. A new model describing the variation of Ca/Si ratio with lime concentration in solution. Cement wapno beton 8: 184191.
• RUETZ W. 1968. An hypothesis for the creep of the hardened cement paste and the influence of simultaneous shrinkage. In: Proceedings of the Structure of Concrete and its Behavior under Load, p. 365387.
• SANAHUJA J, DORMIEUX L AND CHANVILLARD G. 2007. Modelling elasticity of a hydrating cement paste. Cem Concr Res 37(10): 14271439.
• STEHFEST H. 1970. Algorithm 368: numerical inversion of Laplace transforms. Commun. ACM 13(624): 4749.
• TAMTSIA B AND BEAUDOIN J. 2000. Basic creep of hardened cement paste, a re-examination of the role of water. Cem Concr Res 30: 14651475.
• WITTMANN F. 1982. Creep and shrinkage mechanisms. In: BAZANT P AND WITTMANN FH (Eds), Creep and shrinkage in concrete structures, J Wiley & Sons, p. 129161.

Correspondence to:

Julien Sanahuja

Publication Dates

• Publication in this collection
  25 Feb 2010
• Date of issue
  Mar 2010

History

• Received
  16 June 2008
• Accepted
  27 Apr 2009