Abstracts
We describe the group structure of monomial Cremona transformations. It follows that every element of this group is a product of quadratic monomial transformations, and geometric descriptions in terms of fans.
monomial birational maps; toric varieties
Descrevemos a estrutura do grupo das transformações de Cremona monomiais. Concluímos que todo elemento deste grupo é um produto de aplicações monomiais quadráticas e damos descrições geométricas em termos de leques.
aplicações birracionais monomiais; variedades tóricas
On the Monomial Birational Maps of the Projective Space
Gérard Gonzalez-SprinbergI; Ivan PanII
IInstitut Fourier, Université de Grenoble I UMR 5582 CNRS-UJF 38402 Saint-Martin-d'Hères, France
IIInstituto de Matemática, Universidade Federal do Rio Grande do Sul, 91501-970 Porto Alegre, Brasil
Correspondence Correspondence to: Ivan Pan E-mail: pan@mat.ufrgs.br/ gonsprin@ujf-grenoble.fr
ABSTRACT
We describe the group structure of monomial Cremona transformations. It follows that every element of this group is a product of quadratic monomial transformations, and geometric descriptions in terms of fans.
Keywords: monomial birational maps, toric varieties.
RESUMO
Descrevemos a estrutura do grupo das transformações de Cremona monomiais. Concluímos que todo elemento deste grupo é um produto de aplicações monomiais quadráticas e damos descrições geométricas em termos de leques.
Palavras-chave: aplicações birracionais monomiais, variedades tóricas.
1. INTRODUCTION
The best known birational map of
r is maybe the standard Cremona transformation Sr :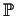 rr defined by Sr = (X0-1 : ... : Xr-1). For r = 2 there is a geometric description in the classic references on this subject; moreover a Max Noether's famous theorem shows that every birational map of
rr defined by Sr = (X0-1 : ... : Xr-1). For r = 2 there is a geometric description in the classic references on this subject; moreover a Max Noether's famous theorem shows that every birational map of 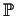 2 is a composition of automorphisms and S2, and then that every Cremona transformation is a composition of quadratic ones. If r > 2 there is no analogous to Noether's theorem (Hudson 1927, Katz 1992, Pan 1999). In this note we consider birational maps generalizing Sr. Our approach is based in a toric point of view and the property that Sr stabilizes the open set X0...Xr
2 is a composition of automorphisms and S2, and then that every Cremona transformation is a composition of quadratic ones. If r > 2 there is no analogous to Noether's theorem (Hudson 1927, Katz 1992, Pan 1999). In this note we consider birational maps generalizing Sr. Our approach is based in a toric point of view and the property that Sr stabilizes the open set X0...Xr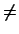 0. We consider birational maps of
0. We consider birational maps of 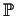 r with this property. In the second paragraph of (Russo and Simis 2001) the birationality of these maps is characterized in terms of certain syzygies as an application of a more general criterion; see also (Simis and Villarreal 2002): compare their Proposition 1.1 with our Proposition 3.1.
r with this property. In the second paragraph of (Russo and Simis 2001) the birationality of these maps is characterized in terms of certain syzygies as an application of a more general criterion; see also (Simis and Villarreal 2002): compare their Proposition 1.1 with our Proposition 3.1.
2. MONOMIAL CREMONA TRANSFORMATIONS
Let N be a rank r free 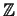 -module,
-module, 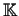 an algebraically closed field,
an algebraically closed field, 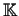 * : =
* : = 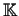 \{0}. Let
\{0}. Let  =
=  N : = N
N : = N 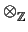
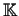 . The action of
. The action of  on itself induces a natural inclusion
on itself induces a natural inclusion 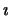 of the torus in the group
of the torus in the group  Aut(
Aut( ) of the algebraic variety's automorphisms of
) of the algebraic variety's automorphisms of  ; we consider the subgroup G
; we consider the subgroup G of
of  Aut(
Aut( ) given by the algebraic group's automorphisms of
) given by the algebraic group's automorphisms of  . Note that, with an appropriate choice of a basis of N, we may identify
. Note that, with an appropriate choice of a basis of N, we may identify  to (
to (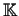 *)r. Since
*)r. Since 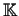 is algebraically closed an automorphism in
is algebraically closed an automorphism in  Aut(
Aut( ) may be written in the form F = (F1,..., Fr) with
) may be written in the form F = (F1,..., Fr) with

(1)
where li
*, aij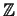 , 1
, 1 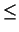 i, j
i, j 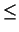 r.
r.
LEMMA 2.1. There is a split exact sequence of groups
where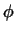 (F) : =
(F) : = 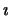 (F(1
(F(1 )-1) o F, for F
)-1) o F, for F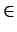 Aut(
Aut( ).
).
PROOF. One has 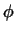 (F)
(F) 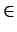 G
G , because
, because  Fi is a character of the torus, 1
Fi is a character of the torus, 1 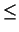 i
i 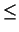 r; it is easily seen that the sequence is exact. The inclusion of G
r; it is easily seen that the sequence is exact. The inclusion of G in
in  Aut(
Aut( ) is a section of
) is a section of 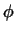 , hence the sequence splits.
, hence the sequence splits. 
In the following we consider the projective space
r over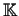 as a toric variety, e.g., a compactification of the torus
as a toric variety, e.g., a compactification of the torus  =
=  N associated to a complete regular fan of N
N associated to a complete regular fan of N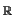 : = N
: = N 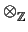
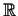 with (r + 1) cones of dimension 1. (One standard reference for toric varieties is (Oda 1988)).
with (r + 1) cones of dimension 1. (One standard reference for toric varieties is (Oda 1988)).
DEFINITION 2.2. A monomial Cremona transformation is a birational map F :
rr defined on and such that F(
and such that F( )
) 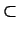
 .
.
We note
Bir (
(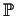 r) the group of these transformations; there is a natural isomorphism
r) the group of these transformations; there is a natural isomorphism  Bir
Bir (
(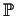 r)
r) 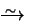 Aut(
Aut( ).
).
PROPOSITION 2.3. Fixing a basis of the lattice N, there exists an isomorphism
PROOF. It follows from Lemma 2.1. Given F 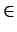
 (
(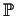 r), we associate (F(1
r), we associate (F(1 ),(aij)), where (aij) is the r × r-matrix corresponding to
),(aij)), where (aij) is the r × r-matrix corresponding to 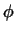 (F)
(F) 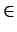 G
G via the equality (1) and the isomorphism GGLr(
via the equality (1) and the isomorphism GGLr(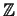 ) induced by the choice of the basis of N.
) induced by the choice of the basis of N. 
REMARK 2.4. The action of
GLr(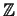 ) on
) on  corresponding to the semidirect product in the proposition is
corresponding to the semidirect product in the proposition is
(aij) . ( ,...,
,..., ) =
) = 
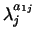 ,...,
,...,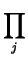
 .
.
COROLLARY 2.5. The center of  Bir
Bir (
(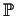 r) is trivial. The center of the subgroup {F : F(1
r) is trivial. The center of the subgroup {F : F(1 ) = 1
) = 1 } is
} is  Sr
Sr .
.
As a consequence of Proposition 2.3 we obtain an analogous to the M. Noether's theorem (on the generators of the Cremona group of
2) in arbitrary dimension for the monomial case. THEOREM 2.6. The group  Bir
Bir (
(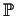 r) is generated by a quadratic transformation and the linear monomial automorphisms. Consequently, every birational map is a product of quadratic transformations.
r) is generated by a quadratic transformation and the linear monomial automorphisms. Consequently, every birational map is a product of quadratic transformations.
PROOF. It follows from Proposition 2.3 and the fact that
GLr(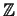 ) is generated by a transvection and two permutations (Coxeter and Moser 1957, Trott 1962) which induce respectively a quadratic transformation and two linear maps in
) is generated by a transvection and two permutations (Coxeter and Moser 1957, Trott 1962) which induce respectively a quadratic transformation and two linear maps in  Bir
Bir (
(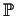 r).
r). 
3. DEGREES AND MATRICES
Let X0,..., Xr be homogeneous coordinates in 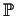 r, xi : = Xi/X0, 1
r, xi : = Xi/X0, 1 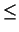 i
i 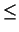 r, the affine coordinates corresponding to the canonical basis of N =
r, the affine coordinates corresponding to the canonical basis of N = 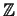 r. Every non-constant monomial rational map F :
r. Every non-constant monomial rational map F : 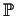 r
r
 ) = 1
) = 1 may be written uniquely in the form
may be written uniquely in the form
 ...
...
(2)
such that:
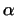 (ej)
(ej) 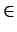
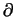 C+, 0
C+, 0 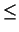 j
j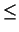 r,
r,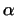 (e) = deg(F)e, where
(e) = deg(F)e, where 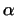 =
= 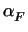 = (
= (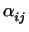 ), ej, 0
), ej, 0 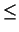 j
j 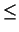 r, is the canonical basis of
r, is the canonical basis of 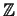 r+1 , e =
r+1 , e = 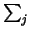 ej , C+ is the cone
ej , C+ is the cone 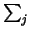
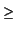 0ej and
0ej and 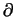 C+ its boundary. The positive integer deg(F) is the degree of F, e.g. deg(F) =
C+ its boundary. The positive integer deg(F) is the degree of F, e.g. deg(F) = 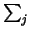
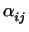 ,
,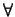 i.
i.
The map F is birational if and only if there exists an integer (r + 1) × (r + 1)- matrix 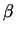 , satisfying (i), (ii), and v
, satisfying (i), (ii), and v 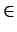
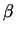 = Id + e . tv.
= Id + e . tv.
In the affine open set X0...Xr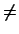 0 one may write F as
0 one may write F as
The matrix A : = (aij) is the matrix of exponents of (1).
PROPOSITION 3.1. Let F
 Bir
Bir (
(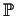 r) be such that F(1
r) be such that F(1 ) = 1
) = 1 ,
, 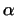 =
= 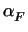 , d = deg(F). There exists a unique isomorphism
, d = deg(F). There exists a unique isomorphism 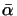 such that the following diagram is commutative and with exact lines.
such that the following diagram is commutative and with exact lines.
One has d = | det(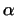 )| and A is the matrix of
)| and A is the matrix of 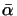 in the basis
in the basis  ,...,
,..., .
.
PROOF. It follows from properties (ii) and (iii) of 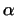 and the form in which
and the form in which 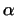 is written in the basis e, e1,..., er because (2) and (3) imply aij =
is written in the basis e, e1,..., er because (2) and (3) imply aij = 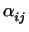 -
-  , 1
, 1 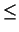 i, j
i, j 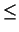 r.
r. 
REMARK 3.2.
(a)
r+1/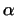 (
(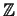 r+1) is cyclic of order d.
r+1) is cyclic of order d.
(b) We obtain 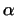 from A as follows:
from A as follows:
EXAMPLE 3.3. Let A be the matrix whose lines are (1, 0, 0),(a, 1, 0),(0, a, 1), a 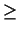 1. Then
1. Then
FA = (X0a+1 : X0aX1 : X1aX2 : X2aX3)
and
FA-1 = (X0a2-a+1X1aX2a : X0a2-aX1a+1X2a : X0a2X2a+1 : X1a2+aX3).
EXAMPLE 3.4. Finite subgroup of
Bir (
(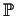 r) are obtained by this method. For example the Weyl's group of type W(Dr), r
r) are obtained by this method. For example the Weyl's group of type W(Dr), r 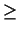 3, and order 2r-1r!, as a Cremona subgroup may be represented as the subgroup generated by an involution of degree 3
3, and order 2r-1r!, as a Cremona subgroup may be represented as the subgroup generated by an involution of degree 3
F = (X0Xr-1Xr : X1Xr-1Xr : ... : Xr-2Xr-1Xr : X02Xr-1 : X02Xr)
= (X0Xr-1Xr : X1Xr-1Xr : ... : Xr-2Xr-1Xr : X02Xr-1 : X02Xr)
and the linear automorphisms F permuting Xi with Xi+1, 1
permuting Xi with Xi+1, 1 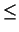 i < r. In an analogous form one obtains a representation of the group W(Br), r
i < r. In an analogous form one obtains a representation of the group W(Br), r 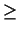 2, of order 2rr!, generated by an involution of degree 2
2, of order 2rr!, generated by an involution of degree 2
F = (X0Xr : X1Xr : ... : Xr-1Xr : X02)
= (X0Xr : X1Xr : ... : Xr-1Xr : X02)
and the preceding r 1 permutations.
4. GEOMETRIC DESCRIPTION, EXAMPLES
Let F 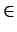
 (
(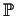 r); we denote by BF its base-scheme. By composing F with an automorphism induced by an element of the torus we may assume that F(1
r); we denote by BF its base-scheme. By composing F with an automorphism induced by an element of the torus we may assume that F(1 ) = 1
) = 1 . e.g. F = (1
. e.g. F = (1 , A)
, A) 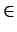 GLr(
GLr(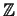 ), we note FA = F; the base-scheme is not changed.
), we note FA = F; the base-scheme is not changed.
The union of the fundamental hyperplanes
r\ contains the base-points set.
contains the base-points set.
Let e1,..., er the canonical basis for N = 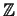 r, e : = e1 + ... + er,
r, e : = e1 + ... + er, 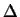 the fan associated to the faces of the simplex
the fan associated to the faces of the simplex  = [e1,..., er, - e] and A(
= [e1,..., er, - e] and A(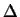 ) the same with respect to the simplex A(
) the same with respect to the simplex A( ). We consider
). We consider 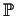 r defined by
r defined by 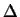 ; let
; let 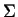 be a fan that is a common subdivision for
be a fan that is a common subdivision for 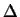 and A(
and A(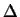 ).
).
PROPOSITION 4.1. One has a commutative diagram
where X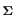 is the toric variety associated to
is the toric variety associated to 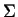 ,
,  is equivariant and
is equivariant and  is equivariant relatively to the automorphism of the torus induced by A.
is equivariant relatively to the automorphism of the torus induced by A.
PROOF. From (3), il follows that F induce F* : 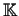 [
[ ] ®
] ® 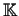 [
[ ] which corresponds, by duality, to the lattice's automorphism A : N ® N.
] which corresponds, by duality, to the lattice's automorphism A : N ® N. 
EXAMPLE 4.2. Let  be, FA = (X02, X0X1, X1X2). One obtains a (regular) fan
be, FA = (X02, X0X1, X1X2). One obtains a (regular) fan 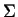 that is a subdivision of
that is a subdivision of 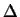 and A(
and A(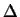 ) by blowing-up the closed orbits associated to the cones
) by blowing-up the closed orbits associated to the cones  e1, e2
e1, e2 and
and  e1, - e
e1, - e and then
and then  - e2, - e
- e2, - e .
.
EXAMPLE 4.3. Let A = - Id, then FA = Sr. One obtains a (regular) fan 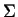 by the elementary subdivisions of
by the elementary subdivisions of 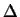 (resp. of -
(resp. of - 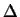 ), successively, of the cones of decreasing dimensions from r to 2. For example, if r = 3, let
), successively, of the cones of decreasing dimensions from r to 2. For example, if r = 3, let  (resp.
(resp.  ) be the fan obtained by the elementary subdivisions of the 4 maximal cones of
) be the fan obtained by the elementary subdivisions of the 4 maximal cones of 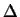 (resp. -
(resp. - 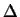 ), and
), and  (resp.
(resp.  ), and the following subdivisions corresponding to the 6 cones of dimension 2 of
), and the following subdivisions corresponding to the 6 cones of dimension 2 of 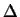 (resp. -
(resp. - 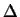 ). One has
). One has 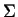 =
=  =
=  . The toric variety V
. The toric variety V (resp. V
(resp. V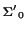 ) is the blowing-up of
) is the blowing-up of 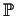 3 in 4 points and V
3 in 4 points and V (resp. V
(resp. V ) is the blowing-up of these in the strict transforms of the 6 lines. The induced birational map V
) is the blowing-up of these in the strict transforms of the 6 lines. The induced birational map V
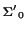 is composition of 6 flops, e.g., corresponding to small resolutions of singularities of type an affine cone over a smooth quadric, associated to the 6 faces of the convex polyhedron P
is composition of 6 flops, e.g., corresponding to small resolutions of singularities of type an affine cone over a smooth quadric, associated to the 6 faces of the convex polyhedron P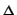 : = Conv(
: = Conv(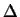
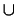 (-
(- 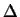 )).
)).
On the other hand, the (normalized) blowing-up of the base-scheme B is the toric variety associated to the fan 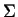 (B) defined by the faces of the polyhedron P(B) = Conv(P
(B) defined by the faces of the polyhedron P(B) = Conv(P
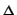 . The toric variety V
. The toric variety V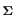 (B) has 12 singular points of type an affine cone over a smooth quadric. Finally, the fan
(B) has 12 singular points of type an affine cone over a smooth quadric. Finally, the fan 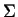 is a regular subdivision of
is a regular subdivision of 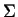 (B) and the induced morphism V
(B) and the induced morphism V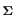 ® V
® V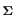 (B) is a minimal resolution of V
(B) is a minimal resolution of V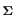 (B).
(B).
ACKNOWLEDGMENTS
The second author was a visiting Professor at Institut Fourier and also partially supported by the Cooperação Franco-Brasileira.
Manuscript received on December 18, 2002; accepted for publication on April 30, 2003;
presented by ARON SIMIS
Mathematics Subject Classification: 14E07, 14M25.
- COXETER H AND MOSER W. 1957. Generators and relations for Discrete Groups. Springer-Verlag.
- HUDSON HP. 1927. Cremona Transformations in Plane and Space. Cambridge at the University Press.
- KATZ S. 1992. Recent works on Cremona Transformations. Research Notes in Math. 2: 109-119, Sundance 90.
- ODA T. 1988. Convex Bodies and Algebraic Geometry. Springer-Verlag.
- PAN I. 1999. Une remarque sur la génération du groupe de Cremona. Bol Soc Bras Mat 30: 95-98.
- RUSSO F AND SIMIS A. 2001. On birational maps and Jacobian matrices. Compositio Math 126: 335-358.
- SIMIS A AND VILLARREAL R. 2002. Constraints for the Normality of Monomial Subrings and birationality, to appear in Proc. of the A.M.S.
- TROTT S. 1962. A pair of generators for the unimodular group. Can Math Bull 5: 245-252.
Correspondence to:
Publication Dates
-
Publication in this collection
31 July 2003 -
Date of issue
June 2003
History
-
Accepted
30 Apr 2003 -
Received
18 Dec 2002









