Multiphysical modelling of fluid transport through osteo-articular media

BIOMEDICAL AND MEDICAL SCIENCES

Multiphysical modelling of fluid transport through osteo-articular media

Thibault Lemaire; Salah Naili; Vittorio Sansalone

Laboratoire de Modélisation et Simulation Multi-Echelle, Biomécanique, CNRS 3160 MSME, Université Paris Est, 61, Avenue du Général de Gaulle, 94010 Créteil Cédex, France

^{Correspondence to}

ABSTRACT

In this study, a multiphysical description of fluid transport through osteo-articular porous media is presented. Adapted from the model of Moyne and Murad, which is intended to describe clayey materials behaviour, this multiscale modelling allows for the derivation of the macroscopic response of the tissue from microscopical information. First the model is described. At the pore scale, electrohydrodynamics equations governing the electrolyte movement are coupled with local electrostatics (Gauss-Poisson equation), and ionic transport equations. Using a change of variables and an asymptotic expansion method, the macroscopic description is carried out. Results of this model are used to show the importance of couplings effects on the mechanotransduction of compact bone remodelling.

Key words: biomechanics, multi-scale, homogenization, osteo-articular tissues, coupling effects.

RESUMO

Neste estudo uma descrição multifísica do transporte de fluidos em meios porosos osteo articulares é apresentada. Adaptado a partir do modelo de Moyne e Murad proposto para descrever o comportamento de materiais argilosos a modelagem multiescala permite a derivação da resposta macroscópica do tecido a partir da informação microscópica. Na primeira parte o modelo é apresentado. Na escala do poro as equações da eletro-hidrodinâmica governantes do movimento dos eletrolitos são acopladas com a eletrostática local (equação de Gauss-Poisson) e as equações de transporte iônico. Usando uma mudança de variáveis e o método de expansão assintótica a derivação macroscópica é conduzida. Resultados do modelo proposto são usados para salientar a importância dos efeitos de acoplamento sobre a transdução mecânica da remodelagem de ossos compactados.

Palavras-chave: biomecânica, multiescala, homogeneização, tecidos osteo articulares, efeitos de acoplamento.

1 INTRODUCTION

Osteo-articular media, such as bone tissues or cartilage, are complex saturated porous tissues composed of a solid matrix, cells and a fluid phase. The movement of the fluid phase within the spaces of the solid matrix is referred to as interstitial fluid flow. Although much is suspected about the role of fluid movement on biological activities such as growth, adaptation and repair mechanisms, relatively little is known about flow characteristics under in vivo conditions. The behaviour of osteo-articular tissue is governed by different effects due to many driving forces (hydraulic, biochemical, electrical, mechanical, etc.). For instance, the measurements of streaming potentials are commonly used to validate poroelastic models of bone (Salzstein et al. 1987, Salzstein and Pollack 1987, Cowin et al. 1995). In parallel, the role of electro-chemical phenomena in tissue remodelling and growth has been put into relief (Frank and Grodzinsky 1987a, b, Pollack 2001, Knothe Tate 2003, Sharma et al. 2007, Lemaire et al. 2008).

In this study, a multiphysical description of fluid transport through compact bone tissue is presented. Thanks to this modelling, it is possible to estimate the in vivo electro-chemical part of the fluid stimulation of the cells. Our approach is based on several previous works carried out under the aegis of Moyne and Murad (2002, 2006, Murad and Moyne 2006, 2008) and Lemaire et al. (2002, 2007, Lemaire 2004). All of these works aim at studying the hydro-mechanical behaviour of expansive clayey materials. Since the solid-fluid interface of these media presents a negative surface charge, many electro-physical phenomena, such as osmotic swelling, streaming potentials or electro-osmosis, may occur. Osteo-articular tissues present the same kind of electrical property. Indeed, bone matrix and cell membranes present negative surface potentials because of the presence of fatty acids and adsorbed species. In this paper, we intend to use the approach of Moyne and Murad to study interstitial fluid velocities in compact bone as it was done a few years ago (Lemaire et al. 2006). Nevertheless, we recently pointed out the necessity to improve the microscopical description of the living tissue (Lemaire et al. 2008) and proposed to add a parameter to describe the influence of a sub-microscopical structure corresponding to the fiber matrix surrounding the cells.

First the model is carried out. The two-scale saturated porous medium is composed by fluid and solid phases. This solid phase includes the cells and the bone matrix, whereas the fluid phase corresponds to the interstitial fluids. Typically, in compact bone, the microscale refers to the size of the micropores (the canaliculi, whose radius is ~ 10^-8 m), whereas the macroscale corresponds to the osteon radius (10^-4 m). The multiscale structure of compact bone is detailed in Section 4.1.

At the pore scale, electro-hydrodynamics equations governing the electrolyte movement are coupled with local electrostatics (Gauss-Poisson equation) and ionic transport equations. In particular, the fluid movement at the microscale is described thanks to a Brinkman equation. Indeed, in living tissues, the micropores that contain the cells are partially filled by a pericellular fibrous network. This network generates supplementary viscous effects. Thus, since a classical Stokesian approach cannot take into account this sub-microscopical friction effect, a Brinkman-like term is added thanks to a permeability parameter K_f. Using the change of variables proposed by Moyne and Murad (2002) and an asymptotic expansion method (Auriault 1991b), a macroscopic description of the fluid flow is derived.

The efficiency of this model is, then, presented in a biological application dealing with the mechanotransduction of bone remodelling. Indeed, after having briefly introduced the multi-scale structure of compact bone, the key role of interstitial fluid movements in the vicinity of the mechano-sensitive cells of bone is discussed, and the importance of osmotic and electro-osmotic coupled phenomena at this scale is clearly demonstrated.

2 MICROSCOPICAL EQUATIONS IN THE FLUID PHASE

The material is seen as an uniformly negatively charged porous medium that can be represented by a periodic cell (representative elementary volume). This medium is saturated by a continuum dielectric aqueous solution with binary monovalent symmetric electrolytes. Obviously, the chemical species of osteo-articular fluids are not only monovalent ions. For instance, the presence of proteins and the special role of calcium in bone activity could be taken into account with a more detailed chemical description. Nevertheless, the scope of this work is focused on studying electro-chemical effects governing fluid transport within the framework of continuum mechanics. Thus, the nature of the ionic species does not matter too much since the steric and hydration effects are neglected and ions are treated as point charges. Moreover, to simplify the approach, the chemical exchanges among the different phases of the medium are not taken into account. Hence, the surface charge of the medium remains constant. In what follows, we begin by presenting the microscopic phenomena that govern electric potential distribution, ion transport and fluid flow.

2.1 ELETROSTATICS

Neglecting magnetic effects, the electric potential 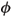in the fluid satisfies the Gauss-Poisson equation:

where ∇ · is the divergence operator, ∇ the gradient operator, F the Faraday's constant, ε₀ the vacuum permittivity, e the relative dielectric constant of the solvent, and, n⁺ and n^- the cationic and anionic molar concentrations, respectively.

Boundary conditions are obtained by writing the electric flux continuity at the pore's walls. Noting σ the surface charge density and n the normal unit vector exterior to the the fluid domain, we have:

2.2 IONS TRANSPORT

The convection-diffusion equations of Nernst-Planck that governs the ion transport are:

where t is the time, D₊ and D_- are the water-ions diffusion coefficients for cations and anions, respectively. The vector v is the fluid velocity. The reduced electric potential 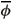= F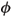/RT is introduced with the help of absolute temperature T and ideal gas constant R.

Boundary conditions are written considering the impervious property of the pore's walls. Noting n the normal unit vector exterior to the the fluid domain, we have:

2.3 MODIFIED BRINKMAN EQUATION

In all the studies cited in the introduction, the movement of the incompressible and Newtonian electrolyte solution was described by a modified Stokes equation treating electro-viscous effects due to Coulombic forces and neglecting inertial terms. In order to model living materials, this description has to be improved. Indeed, electron photomicrographs of the compact bone volume presented by You et al. (2004) showed the presence of micro-elements forming a fibrous pericellular matrix partially occupying the pore space. The purely Stokesian treatment of the fluid movement within the pore is then inadequate, since it does not take into account the friction effect generated by the fibers. These elements, which belong to a lower structural level, are known to slow down the fluid flow at a macroscopic scale (Gururaja et al. 2005). Our microscopical modelling of the electrolyte solution movement has then to be changed to express the action of this supplementary damping force. Following the arguments of Brinkman (1947), a dissipative new term is added to the modified Stokes equation:

where p is the hydraulic pressure, µ_f is the fluid dynamic viscosity and K_f is an intrinsic permeability parameter quantifying the damping effect due to the fibrous matrix.

Although the Brinkman equation is semi-empirical in nature, it has been validated by detailed numerical tests of the Stokes equation in regions near the interface among dissimilar regions (Martys et al. 1994).

Furthermore mass conservation equation is written as:

Boundary conditions at the interface are no-slip conditions:

2.4 AN ALTERNATIVE FORMULATION IN THE FLUID PHASE

An original approach of this multiphysical treatment of interstitial fluid flow within charged porous media consists in introducing a change of variables to separate microscopic variables that may vary at the pore's scale, and macroscopic variables that only vary at the macroscopic scale. This change of variables is detailed elsewhere (Moyne and Murad 2003, Lemaire et al. 2002, 2006). Its principle consists in building at each location of the fluid phase an equivalent virtual bulk (bulk's fields are indexed b) which is at thermodynamical equilibrium (in terms of electro-chemical potentials µ), and conserves the electro-neutrality condition:

Consequently, bulk's and real fields are linked as follows:

where π is Donnan osmotic pressure.

The electric potential is, thus, decomposed into a bulk electric potential γ_b playing a similar role as the streaming potential, and another potential φ corresponding to the double-layer potential (see Eq. (10)). When the quantity φ is reduced to = Fφ/RT, this later potential rules the Boltzmann distributions of the ionic species given by (11). The bulk concentration, which verifies the electro-neutrality condition (9), also appears in these ionic distributions. Finally, the bulk pressure can be expressed by subtracting the Donnan osmotic pressure π from the hydraulic pressure p (see Eq. (12)).

As a consequence, the problem can be reformulated in terms of bulk variables. Equation (1) is rephrased to obtain the Poisson-Boltzmann equation:

where the streaming potential has been reduced

_b = Fψ_b/RT.

The Debye length , which characterizes the thickness of the diffuse double layers, is here introduced. Furthermore, the new form of the Nernst-Planck equation (3) is:

Finally, the modified Brinkman equation (5) is reformulated:

In this expression, the different terms governing the fluid transport can be identified: i) the effect of the viscous shearing stresses acting on a volume element of fluid; ii) the effect of the damping force of the fibrous matrix; iii) the hydraulic driving effect due to the gradient of bulk pressure; iv) the osmotic driving effect due to the gradient of bulk concentration; v) the electro-osmotic driving effect due to the gradient of bulk electric potential. We can notice that the change of variables does not change the mass conservation equation (6).

The boundary conditions (2) and (4) are finally reformulated in terms of bulk variables:

No-slip conditions for the velocity (7) are not modified by the change of variables.

3 HOMOGENIZATION PROCEDURE

The aim of this section is to propagate the microscopic phenomena presented in term of bulk variables to the upper scale. This change of scale is carried out within the general framework of periodic homogenization (Auriault 1991a). Thus, the bounded macroscopic medium is assumed to be made by a repeated microscopic cell. The microscopic length ℓ characterizing the cell defines the length-scale for which the microscopic heterogeneities are relevant. At the macroscopic length-scale L of the porous medium, these heterogeneities are no more significant. The ratio η = ℓ/L corresponds to the perturbation parameter. To obtain a macroscopic equivalent description, the influence of the inhomogeneities of the microscopic scale has to decay asymptotically as the ratio η decreases. As a consequence, this ratio has to be very small when compared with one.

3.1 NON-DIMENSIONAL WRITING OF THE MICROSCOPIC PROBLEM

The first step of the periodic homogenization procedure consists in writing the microscopic equations in a non-dimensional fashion. Thus, we have to divide all the quantities q appearing in equations describing the microscale by reference values:

The subscript "r" and the prime are respectively assigned to the reference values that are used to normalize each quantity and to the resulting non-dimensional quantity. For instance, the reference length L_r is chosen to be on the order of the macroscopic medium length, i.e., L_r ≡ L. In compact bone, this macroscopic length corresponds typically to the osteon radius (10^-4 m). This reference length is used to obtain the non-dimensional writing of spatial derivative operators. Moreover, the reference values corresponding to constant quantities are these quantities themselves.

3.1.1 Micro/macro coordinates and spatial operator

Microscopic and macroscopic coordinates x and X respectively associated with the microscopic cell and the overall dimension of the medium are introduced. The associated reference lengths are x_r ≡ ℓ and X_r≡ L (Lemaire et al. 2006). As a consequence, choosing the reference characteristic length L_r on the order of the macroscopic medium length, i.e. L_r ≡ L, the spatial differential operator ∇ is transformed as:

where ∇_x and ∇_X are the differential operators referring to the microscopic and macroscopic coordinates, respectively. Thus, we have finally:

3.1.2 Poisson-Boltzmann equation

To transform Eq. (13), the chosen reference electric potential

_r corresponds to the surface potential of the pore walls. For instance, in bone tissues, this electric potential can be approximated by the values of the zeta potential measured in bone tissue by Berreta and Pollack (1986):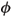 _r = -3.55 mV. As a consequence, the non-dimensional number representing the reduced reference potential 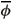_r = Q = F

_r/RT is scaled to O(η⁰), where O(•) is big-oh notation that is used to describe the asymptotic behaviour of the function. This implies that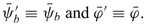

Moreover, the bulk concentration plays a role in the definition of the Debye length. It is, then, necessary to propose a reference value for this concentration. Following Moyne and Murad's arguments (Moyne and Murad 2002), local electroneutrality leads to a 1/ℓ faster variation of the ionic concentrations, in comparison with the changes of the pore's surface charge density σ. Thus, these authors proposed to express thereference concentration as n_r ≡ σ/Fℓ. Moreover, the condition of electrical flux continuity at the interface provides that σ ≡ εε₀

_r/ℓ and reference concentration is rewritten as n_r ≡ εε₀

_r/Fℓ². According to these scaling laws, we have L_Dr ≡ ℓ. As a consequence, the Poisson-Boltzmann Eq. (13) is rephrased in:

Furthermore, the electrical flux continuity condition (16) is transformed in:

Using local electro-neutrality, this number can be interpreted as the ratio between the electrical and thermal energies Q = Fσℓ/εε₀RT.

3.1.3 Nernst-Planck equations

The temporal differential-operator is scaled thanks to the reference time t_r = L²/D_r, where D_r = max(D₊,D_-) and max is the function that returns the maximum value. Thus, the Nernst-Planck Eq. (14) is rewritten as:

where the Péclet number is defined by P_e = v_rL/D_r. The quantity v_r is a reference velocity.

Different cases can be viewed depending on the nature of the main driving effect (Auriault and Adler 1995). If diffusion is predominant, the Péclet number is small P_e = O( h ). If convection at the large scale is predominant, the Péclet number is important P_e = O(η^-1). Finally, if convection and diffusion are equivalent, we have P_e = O(1).

The impervious condition (17) is also rephrased:

3.1.4 Modified Brinkman equation

We introduce the Reynolds number R_e = p_r L/µ_fv_i and the number D_e = RTn_r/p_r, which measures the importance of the osmotic effects related to the pressure effects. The intrinsic permeability K_f, which quantifies the friction effect generated by the fibers, has to be reduced by a squared length. The order of magnitude of this permeability can be calculated thanks to the model of Tsay and Weinbaum (1991) adapted by Weinbaum et al. (1994). Thus, physiologically significant values of this parameter lay between 5.9 ×10^-18 m² and 2.0×10^-17 m² (Lemaire et al. 2008). Consequently, we choose to reduce the permeability parameter with the squared microscopic length ℓ². The modified Brinkman equation is, then, rewritten in its non-dimensional form:

Moreover, the mass conservation equation (6) is written in its non-dimensional form:

Finally, the no-slip condition (7) at the solid-fluid interface is rephrased:

3.2 ASYMPTOTIC EXPANSIONS

Each quantity q is expressed as a function depending on both the scales q = q(x,X). Moreover, it is written in terms of asymptotic expansion of the small parameter η:

For constant quantities, we can notice that q_[i](x,X) = 0 for i > 0 and, thus, q(x,X) = q_[0] = q. These asymptotic expansions are introduced in the previous equations. Using the decomposition of the spatial derivative operator (see Eq. (20)) in the previous equations, we collect the different powers of η.

3.2.1 Developments of the Boltzmann terms

Combining the asymptotic expansion of the double-layer potential with a Taylor development at the origin of the exponential function, the Boltzmann term exp() is expanded at the second order:

Hence, the expansions of hyperbolic cosine and sine functions at the first order are, respectively:

3.2.2 Poisson-Boltzmann equation

At the zeroth order, the Poisson-Boltzmann equation gives:

The corresponding boundary condition at the zeroth order is obtained from the equation (22):

3.2.3 Nernst-Planck equation

To study the Nernst-Planck equations, the Péclet's number has to be scaled in regards to the transport process. For the case of transport within cortical bone's lacuno-canalicular system, the reference length corresponds to the osteon's radius and typical values of velocities have been calculated by Rémond et al. (2008). Comparing to the order of magnitude of classical diffusion coefficients in water, the main part of ionic transport is diffusive and the Péclet's number is small. Thus, P_e = O(η) and the asymptotic expansion of the Nernst-Planck equation is carried out. Collecting the terms at the second order, we have:

At the first order, we obtain:

Finally, the ionic transport gives at the zeroth order:

Moreover, the impervious boundary condition (24) gives, respectively, at the first and zeroth orders:

3.2.4 Brinkman equation

Two non-dimensional numbers have been introduced in the Brinkman equation (25). It is, then, necessary to estimate their order of magnitude. On the one hand, the Reynolds number R_e = p_r L/µ_f v_r, which compares inertial and viscous effects, is quantified using the scaling law proposed by Auriault (1991a). The orders of magnitude of the reference velocity v_r and pressure p_r of the fluid are based on classical dimensional analysis of Darcy law, which leads to v_r ≡ ℓ²p_r/µ_fL. Consequently, we have the order of magnitude of the Reynolds number R_e ≡ O(η^-2). On the other hand, according to Derjaguin et al. (1987), electrical stresses counterbalance the osmotic pressure effects. This argument leads to an estimation of the non-dimensional number D_e. Indeed, since electrical and pressure effects have the same order of magnitude, we have D_e ≡ O(1). Using these scaling laws in the Brinkman problem, the collection of terms at the first and zeroth orders gives:

The corresponding no-slip boundary condition (27) gives that all the terms in the asymptotic expansion of the velocity are zero at the wall. Finally, the asymptotic expansion of the continuity equation (26) gives at the first and zeroth orders:

3.3 SLOW VARIABLES OF THE PROBLEM

The set of previous equations is used to separate variables that only vary at the macroscopic scale (slow variables) from those which possibly vary at the microscopic scale (fast variables).

For frequent geometries of pores such as parallel platelets (clayey materials, gels) or parallel cylindric channels (filters, bones, Kozeny-Carman materials), it is possible to make the cartesian or cylindric coordinates correspond to the macro and microscopic coordinates. The example of the tubular geometry of the canaliculi is used hereafter (see Section 4.1). When considering such a situation, the slow variables useful for the model can be easily deduced. First, using the impervious condition (37) in equation (34), we show that the zeroth order terms of bulk concentration and potential do not vary at the microscopic scale. Taking into account this result in the first order of the Brinkman equation (39), we also obtain that the zeroth order term of the bulk pressure is a slow variable. Finally, bulk variables are only slow ones:

This result shows the interest of working with bulk variables, since they only depend on themacroscopic coordinate.

To obtain this result for any geometry of the porous network, it is necessary to adopt another approach as proposed by Moyne and Murad (2002) to avoid the miscomprehension that appears by combining equations (34) and (37).

3.4 CONSEQUENCES ON PREVIOUS EQUATIONS

Considering that the slow variables do not vary at the microscale through equality (43), equations (32) to (40) can be simplified as follows:

3.5 CLOSURE PROBLEMS

The next step consists in deriving the macroscopic description from the previous equations. If the Poisson-Boltzmann and the ionic transport equations can be treated similarly as proposed by Moyne and Murad (2002), the derivation of the macroscopic Darcy law is slightly different.

3.5.1 Local Poisson-Boltzmann equation

Because of the scaling factor in the Poisson-Boltzmann equation, this equation is purely expressed at the microscopical scale. If the Debye length is small compared to the pore size, this equation can, thus, be linearized thanks to the Debye-Hueckel approximation:

3.5.2 Ionic transport

The macroscopic transport equations can be obtained by solving the closure problems of Nernst-Planck equations. To apply the homogenization procedure of the Taylor dispersion problem proposed by Auriault and Adler (1995), the change of variables proposed by Moyne and Murad (2002) is used to rephrase equations (46), (47) and (48). Indeed, to avoid working with the electro-migration term in the Nernst-Planck model, these authors proposed to consider auxiliary concentrations to recover classical convection-diffusion equations, and suggested the following change of variables using the streaming potential ψ that coincides with our bulk potential ψ_b:

The expansion of these auxiliary concentrations can be obtained from the development (29):

As a consequence, equation (46) becomes:

with the associated boundary condition derived from equation (48):

These two last equations form the closure problem for as obtained by Moyne and Murad (2002), whose solution is presented by Auriault and Adler (1995).

Moreover, when rephrasing equation (47) in terms of fictitious concentrations and using the mass conservation equation (41), we have:

Again, this equation is similar to the one treated by Moyne and Murad (2002) and can be rewritten as proposed by these authors.

3.5.3 Derivation of a macroscopic Darcy law

To rewrite the Brinkman equation (49), its linearity property is used. Thus, the fluid velocity is splitted into three terms: v' = v'_P +v'_C + v'_E, where v'_P, v'_C and v'_E are respectively associated with the Poiseuille, osmotic and electro-osmotic flows. Brinkman equation is, then, decomposed into three independent equations with similar no-slip conditions at the canaliculus wall and cell membrane:

where the subscript α = P, C or E stands respectively for the Poiseuille, osmotic and electro-osmotic effects. The quantities G_α and F_α are expressed for α = P, C, E by:

Following the linearity arguments of Auriault and Adler (1995), the velocity has the form:

where is the second order tensor associated with the permeability at the pore's scale corresponding to the α driving gradient.

Introducing this expression of into equation (56) yields in the form:

where is an arbitrary function of the macroscopic variable X and is an auxiliary ℓ-periodical vector-valued function satisfying the cell problem:

where I is the second order identity tensor.

Noting < . > the average over the representative unit cell, the seepage velocity due to the α driving effect is given by:

where the second order permeability tensor = < > is introduced. Moreover, integrating over the unit cell the continuity equation (42), we finally obtain the upscaled version of the Brinkman equation:

Thus, for each of the three driving effects, equation (62) has to be solved to determine the permeability . In parallel, the macroscopic flow can be determined from equation (64).

Hence, the averaged macroscopic fluid flow can be described through a modified Darcy law of the form:

4 APPLICATION OF THE MODEL TO COMPACT BONE

In this section, we propose to illustrate the interest of this model in the scope of bone remodelling.

4.1 THE STRUCTURE OF COMPACT BONE

Compact bone presents a well organised structure composed of mineralized cylinders called osteons. These osteons, which are a few hundred micrometers in diameter, are centered on Haversian canals whose diameters are on the order of 40-100 µm (Cowin 2001). Osteons run primarily in the longitudinal axis of the bone. These macrochannels contain the vasculature, the nerves and interstitial fluid.

Moreover, there are other extravascular pores in the solid matrix of the bone. For instance, lacunæ are ellipsoidal cavities with diameters of 10-30 µm occupied by osteocyte cells. The canaliculi are small cylindric channels whose diameter is on the order of 0.1 µm. They form a network connecting lacunæ and the Haversian vascular canals. Cytoplasmic osteocyte cell process occupies the central zone of each canaliculus, so that the interstitial fluid pathway corresponds to an annular geometry. As introduced in Figure 1, the canaliculus scale will be referred to as the microscale hereafter, whereas the macroscopic length will correspond to the osteon. We introduce a cylindrical coordinate system to describe the geometry of the annular space perfused by the fluid in the canaliculi. The radial and longitudinal coordinates r and z are, thus, identified with the microscopic and macroscopic coordinates x and X, respectively. Since canaliculi are mainly oriented in the radial direction of the osteon, the longitudinal coordinate z at the canalicular scale corresponds to the radial direction at the osteon scale.

Furthermore, electron photomicrographs of the lacuno-canalicular system presented by You et al. (2004) showed the presence of nano-elements forming a fibrous pericellular matrix in the annular space of the canaliculi. Even if this fibrous matrix obviously disturbs the interstitial fluid movement, its influence on the tissue behaviour is not yet well understood. According to physiological arguments, Lemaire et al. (2008) quantified its friction effect thanks to a very low permeability parameter K_f laying between 5×10^-18 m² and 5 ×10^-17 m².

4.2 DEBYE-HUECKEL APPROXIMATION

To solve the local electrical problem, the Debye-Hueckel approximation (see Eq. (50)) is used since the surface potential remains small (less than 25mV) and the pores are large enough in comparison with the Debye length. The analytical solution of this equation in a cylindrical geometry is given by Lemaire et al. (2006).

4.3 COUPLED PERMEABILITY PARAMETERS AT THE PORE SCALE

The coupled Darcy law is now derived in the context of compact bone. Considering that the fluid velocity develops in the longitudinal direction of the pores and only depends on the canalicular radial coordinate r, we have three problems to solve, after projecting equation (56) on z-axis:

where u is the longitudinal component of the fluid velocity. From these equations, the permeability at the pore scale k_α(r) can be calculated.

The spatial variation of the three velocities at the pore scale is shown in Figure 2 through plotting the permeability parameters at the pore scale k_α(r) for α = P, E,C. The model parameters used to plot these graphs are presented in Table I. To underline the effect of the fibers, the Stokesian case (K_f → ∞) is also plotted.

Quantitatively, the presence of the pericellular matrix does slow down the fluid flow. Within the realistic range of pericellular permeability values, the fluid velocity is scaled down by a factor of 1 000 (K_f = 5×10^-18 m²) to 100 (K_f = 5×10^-17 m²) in comparison with the one associated with a clear fluid-filled canaliculus.

Nevertheless, the decreases in velocity are not the same when comparing hydraulic and electro-chemical effects. Near the walls of the pore, the action of the negative double layer potential tends to maintain the electro-chemical effects. In the central zone, this electric potential action disappears and these effects are less significant. In parallel, the hydraulic local permeability k _P, which only depends on the geometry and the fluid viscosity, is not affected by these local electric fluctuations.

4.4 CONSEQUENCES FOR THE MECHANOTRANSDUCTION

Mechanotransduction signals for bone remodelling are linked to fluid flow (Weinbaum et al. 1994, Jacobs et al. 1998, Burger et al. 2003). In particular, cells buried in the lacuno-canalicular porosity of the bone matrix are sensitive to shear stresses induced by fluid flow. In classical model, the only considered fluid shear effect is that due to the hydraulic driving force. Therefore, it would be interesting to quantify the coupled fluid shear stresses acting on the cell process membrane. Typically, the in vivo shear stress values that initiate endothelial cell response are of a one or two Pascals. The order of magnitude of the shear stress calculated by Weinbaum et al. (1994) in cortical bone fits well with this value.

In order to evaluate this physical parameter, we approximate the macroscopic driving gradients thanks to literature values of Table I. With our model, the shear effect τ_P generated by Poiseuille effect is similar to the one generated by electro-osmosis τ_E (around 0.5 Pa) and is three times lower than the chemical shear stress τ_C (around 1.5 Pa).

As a result, it is worth considering the coupled effects in the description of the fluid movement at the canaliculus scale. It is all the more true when studying the mechanotransduction of bone remodelling.

CONCLUSION

Following the Moyne and Murad approach, a two-scale modelling of coupled phenomena governing osteo-articular materials has been carried out. The difficulty to propose suitable in vivo experimental studies explains the strong need for sophisticated theoretical models that can describe the behaviour of living media. Through the results of our model, we propose a possible way to understand how the electro-chemical phenomena play a key role in the mechanotransduction of the bone remodelling. Contrary to classical models describing fluid flows in the bones, the coupled Darcy law developed in this study is able to quantify appreciable electrokinetics phenomena. This study has to be continued by introducing possible exchanges of ionic species between the fluid and cells to better describe cell activity.

ACKNOWLEDGMENTS

The authors thank Dr. Marcio Murad from the "Laboratório Nacional de Computação Científica" (Petrópolis, Brazil) and Dr. Christian Moyne from the "Laboratoire d'Energétique et de Mécanique Théorique et Appliquée" (Nancy, France) for helpful discussions and their reception in Brazil.

Manuscript received on June 6, 2008; accepted for publication on November 5, 2008

Selected paper presented at the IUTAM Symposium on Swelling and Shrinking of Porous Materials: From Colloid Science to Poromechanics – August 06-10 2007, LNCC/MCT.

• AURIAULT JL. 1991a. Dynamic behaviour of porous media. In: BEAR J AND CORAPCIOGLU MY (Eds), Transport processes in Porous Media: Kluwer Academic Publishers. Appl Sci 202: 471-519.
• AURIAULT JL. 1991b. Heterogeneous medium. Is an equivalent macroscopic description possible? Int J Eng Sci 29: 785-795.
• AURIAULT JL AND ADLER PM. 1995. Taylor dispersion in porous media: analysis by multiple scale expansions. Adv Water Resour 18: 217-226.
• BERRETA D AND POLLACK S. 1986. Ion concentration effects on the zeta potential of bone. J Orthop Res 4: 337-341.
• BRINKMAN HC. 1947. A calculation of the viscous forces exerted by a flowing fluid on a dense swarm of particles. Appl Sci Res A1: 27-34.
• BURGER EH, KLEIN-NULEND J AND SMIT TH. 2003, Strain-derived canalicular fluid flow regulates osteoclast activity in a remodelling osteon-a proposal. J Biomech 36: 1453-1459.
• COWIN SC. 2001. Bone mechanics handbook, 2^nd ed., CRC Press, Boca Raton, FL.
• COWIN SC, WEINBAUM S AND ZENG Y. 1995. A case for bone canaliculi as the anatomical site of strain generated potentials. J Biomech 28: 1281-1297.
• DERJAGUIN B, CHURAEV N AND MULLER V. 1987. Surface forces, Plenum Press, New York.
• FRANK EH AND GRODZINSKY AJ. 1987a. Cartilage electromechanics. I. Electrokinetic transduction and the effects of electrolyte ph and ionic strength. J Biomech 20: 615-627.
• FRANK EH AND GRODZINSKY AJ. 1987b. Cartilage electromechanics. II. A continuum model of cartilage electrokinetics and correlation with experiments. J Biomech 20: 629-639.
• GURURAJA S, KIM HJ, SWAN CC, BRAND RA AND LAKES RS. 2005. Modeling deformation-induced fluidflow in cortical bone's lacunar-canalicular system. Ann Biomed Eng 33: 7-25.
• JACOBS CR, YELLOWLEY CE, DAVIS BR, ZHOU Z, CIMBALA JM AND DONAHUE HJ. 1998. Differential effect of steady versus oscillating flow on bone cells. J Biomech 31: 969-976.
• KNOTHE TATE ML. 2003. "Whither flows the fluid in bone?" An osteocyte's perspective. J Biomech 36: 1409-1424.
• LEMAIRE T. 2004. Couplages électro-chimio-hydro-mécaniques dans les milieux argileux, PhD thesis, Institut National Polytechnique de Lorraine, Nancy, France.
• LEMAIRE T, MOYNE C, STEMMELEN D AND MURAD M. 2002. Electro-chemo-mechanical couplings in swelling clays derived by homogenization : electroviscous effects and onsager's relations. In: AURIAULT J, GEINDREAU C, ROYER P, BLOCH J-F, BOUTIN C AND LEWANDOWSKA J (Eds), 'Poromechanics II', Balkema Publishers, Lisse, p. 489-500.
• LEMAIRE T, NAILI S AND RÉMOND A. 2006. Multi-scale analysis of the coupled effects governing the movement of interstitial fluid in cortical bone. Biomechan Model Mechanobiol 5: 39-52.
• LEMAIRE T, MOYNE C AND STEMMELEN D. 2007. Modelling of electro-osmosis in clayey materials includingph effects. Phys Chem Earth 32: 441-452.
• LEMAIRE T, NAILI S AND RÉMOND A. 2008. Study of the influence of fibrous pericellular matrix in the cortical interstitial fluid movement. J Biomech Eng 130: 1-11.
• MARTYS N, BENTZ D AND GARBOCZI E. 1994. Computer simulation study of the effective viscosity in Brinkman's equation. Phys Fluids 6: 1434.
• MOYNE C AND MURAD MA. 2002. Electro-chemo-mechanical couplings in swelling clays derived from a micro/macro-homogenization procedure. Int J Sol Struct 39: 6159-6190.
• MOYNE C AND MURAD MA. 2003. Macroscopic behavior of swelling porous media derived from micromechanical analysis. Transp Porous Med 50: 127-151.
• MOYNE C AND MURAD MA. 2006. A two-scale model for coupled electro-chemo-mechanical phenomena and Onsager's reciprocity relations in expasive clays: II computational validation. Transp Porous Med 63: 13-56.
• MURAD MA AND MOYNE C. 2006. Two-scale model for coupled electro-chemo-mechanical phenomena and Onsager's reciprocity relations in expansive clays: I homogenization analysis. Transp Porous Med 62: 333-380.
• MURAD MA AND MOYNE C. 2008. A dual-porosity model for ionic solute transport in expansive clays. Comput Geosci 12: 47-82.
• POLLACK S. 2001. Streaming potentials in bone. In: Cowin S (Ed), Bone Mechanics Handbook, 2^nd ed., CRC Press, Boca Raton, FL.
• RÉMOND A, NAILI S AND LEMAIRE T. 2008. Interstitial fluid flow in the osteon with spatial gradients ofmechanical properties: a finite element study. Biomech Modeling Mechanobiol 7: 487-495.
• SALZSTEIN RA AND POLLACK SR. 1987. Electromechanical potentials in cortical bone. II. Experimental analysis. J Biomech 20: 271-280.
• SALZSTEIN RA, POLLACK SR, MAK AFT AND PETROV N. 1987. Electromechanical potentials in cortical bone. I. A continuum approach. J Biomech 20: 261-270.
• SHARMA U, MIKOS AG AND COWIN SC. 2007. Mechanosensory mechanisms in bone. In: Princ Tissue Eng, Elsevier, p. 919-933.
• TSAY R-Y AND WEINBAUM S. 1991. Viscous flow in a channel with periodic cross-bridging fibers: exact solutions and brinkman approximation. J Fluid Mech 226: 125-148.
• WEINBAUM S, COWIN SC AND ZENG Y. 1994. A model for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J Biomech 27: 339-360.
• YOU LD, WEINBAUM S, COWIN SC AND SCHAFFLER MB. 2004. Ultrastructure of the osteocyte process and its pericellular matrix. Anat Rec 278A: 505-513.

Publication Dates

• Publication in this collection
  25 Feb 2010
• Date of issue
  Mar 2010

History

• Received
  06 June 2008
• Accepted
  05 Nov 2008