Incorporating electrokinetic effects in the porochemoelastic inclined wellbore formulation and solution

ENGINEERING SCIENCES

Incorporating electrokinetic effects in the porochemoelastic inclined wellbore formulation and solution

Vinh X. Nguyen^I; Youname N. Abousleiman^II

^IMewbourne School of Petroleum and Geological Engineering, Poromechanics Institute, The University of Oklahoma Sarkeys Energy Center, Suite P119, 100 East Boyd Street, Norman, Oklahoma 73019 USA

^IIMewbourne School of Petroleum and Geological Engineering, ConocoPhillips School of Geology and Geophysics School of Civil Engineering and Environmental Science, Poromechanics Institute, The University of Oklahoma Sarkeys Energy Center, Suite P119, 100 East Boyd Street, Norman, Oklahoma 73019 USA

^{Correspondence to}

ABSTRACT

The porochemoelectroelastic analytical models and solutions have been used to describe the response of chemically active and electrically charged saturated porous media such as clays, shales, and biological tissues. However, these attempts have been restricted to one-dimensional consolidation problems, which are very limited in practice and not general enough to serve as benchmark solutions for numerical validation. This work summarizes the general linear porochemoelectroelastic formulation and presents the solution of an inclined wellbore drilled in a fluid-saturated chemically active and ionized formation, such as shale, and subjected to a three-dimensional in-situ state of stress. The analytical solution to this geometry incorporates the coupled solid deformation and simultaneous fluid/ion flows induced by the combined influences of pore pressure, chemical potential, and electrical potential gradients under isothermal conditions. The formation pore fluid is modeled as an electrolyte solution comprised of a solvent and one type of dissolved cation and anion. The analytical approach also integrates into the solution the quantitative use of the cation exchange capacity (CEC) commonly obtained from laboratory measurements on shale samples. The results for stresses and pore pressure distributions due to the coupled electrochemical effects are illustrated and plotted in the vicinity of the inclined wellbore and compared with the classical porochemoelastic and poroelastic solutions.

Key words: drilling, electrokinetic, inclined wellbore, osmotic, poromechanics, stability.

RESUMO

Modelos analíticos poroelásticos incluindo acoplamento químico e elétrico e soluções têm sido utilizados paradescrever a resposta de meios porosos saturados ativos química e eletricamente tais como argilas, folhelhos e tecidos biológicos. Entretanto tais tentativas têm sido restritas a problemas de consolidação unidimensional os quais exibem limitações na prática não constituindo exemplos realistas para validação de soluções numéricas. Este trabalho apresenta formulações gerais dos modelos poroelásticos lineares incluindo acoplamento químico e elétrico e apresenta a solução de um problema de estabilidade de um poço perfurado através de uma formação saturada quimicamente ativa e ionizada tal como um folhelho submetido a um estado tridimensional de tensão. A solução analítica para esta geometria incorpora o acoplamento entre a deformação do sólido e o fluxo simultâneo de fluido e íons induzido pelos gradientes de poro pressão, potencial químico e potencial elétrico sob condições isotérmicas. O fluido residente na formação é modelado como uma solução eletrolítica composta de um solvente e cátions e anions dissolvidos. A abordagem analítica integra na solução o uso quantitativo da capacidade de troca catiônica (CTC) comumente obtida por medidas experimentais em amostras de folhelhos. Os resultados obtidos para as distribuições de tensões e poro pressão devido ao acoplamento eletroquímico são ilustrados e plotados na vizinhança do poço inclinado e comparados com as soluções clássicas poroelásticas com acoplamento químico.

Palavras-chave: perfuração, eletrocinética, poço inclinado, osmose, poromecânica, estabilidade.

INTRODUCTION

It has long been known that chemically active porous media exhibit swelling and shrinking when brought in contact with aqueous solutions. This phenomenon observed in clays, shales, and biological tissues is generally termed osmosis, which is the non-hydraulically driven fluid flow. As such, the coupled fluid flows driven by gradients of chemical and electrical potentials are called chemico-osmosis and electro-osmosis, respectively. Indeed, osmosis through clays and argillaceous rocks has been invoked to explain such observed phenomena as breaching of clay barriers in waste treatment systems (Hudec 1980) and high over pressures in subsurface aquifers (Neuzil 2000). Similarly, osmotic effect is also associated with swelling phenomena observed in charged hydrated biological tissues (Ehlers and Markert 2001). Therefore, the nature of these complex physicochemical interactions requires proper quantification of their effects on the mechanical response of the system.

Of particular interest is the electrochemical effect on the stress and pore pressure distribution in sedimentary subsurface where oil and gas exploration activities are being conducted. Osmotic effects may be important in oil fields where clays and shales separate fluid of different salinity and/or electrical potential, especially in wellbore drilling. The electrochemical interactions between the invading drilling fluid with formation pore fluid species and the solid matrix result in changes of pore pressure distribution. Simultaneously, the effective stress is also modified, which could be detrimental to the formation integrity. Hence, quantitative evaluation and prediction of the overall response require that these coupled interactions be accounted for appropriately.

There is extensive evidence that clay-rich porous formations behave like a semi-permeable membrane, which can restrict solute transport of certain pore fluid species (Young and Low 1965, Olsen 1969, Neuzil 2000). A membrane reflects solutes on the basis of particle size and/or electrical repulsion (Gregor and Gregor 1978). The low permeability and charged surfaces on the constituent clays of shale contribute to its salt rejecting membrane behavior. Differences in chemical potentials of the fluid’s components separated by shale layers cause fluxes of water and solute/ions. Furthermore, when the porous medium, saturated with electrolyte solution, is subjected to an electrical potential gradient, additional electrokinetic effects are introduced. Such electrokinetic effects are associated with the flow of charged particles/ions (streaming currents) and flow of solvent (electro-osmosis) of the pore fluid. In general, these processes involve the coupled and simultaneous flow of fluid, electricity, and chemical species under the influences of mechanical pressure, chemical potential, and electrical potential gradients. Macroscopic transport formulations for these flow phenomena have been derived based on non-equilibrium thermodynamics for irreversible processes (Katchalsky and Curran 1967, Yeung and Mitchell 1993, Malusis and Shackelford 2002, Rosanne et al. 2005).

Early analyses addressing chemical interactions in reactive porous media were presented by lumping the activity-generated osmotic pressure and pore pressure into a chemical potential term, ignoring the solute transport effect (Yew et al. 1990). This chemical potential is treated as a modified pressure, which is used in the evaluation of effective stresses. In other simple approaches, the fluid pressure and solute diffusion effect are taken into account, but ignore the transient coupled deformation-diffusion process (Van Oort 1994).

Recently, the extension of Biot’s original theory of poromechanics (Biot 1941) to include coupled chemical and electrokinetic effects has been the subject of extensive research. Biot’s theory is reformulated for a porous system saturated with several species of the pore fluid based on the mixture theory and non-equilibrium thermodynamics (Sachs and Grodzinsky 1987, Corapcioglu 1991, Sherwood 1993, Heidug and Wong 1996, Huyghe and Janssen 1999). However, general analytical solutions to these formulations for engineering problems are very limited. Sherwood and Bailey (1994) provided an isotropic solution ofa plane strain cylindrical wellbore by simplifying the porochemoelastic formulation using the lumped chemical potential mentioned above and ignoring solute transport and electrokinetic effects. Ekbote and Abousleiman (2006) generalized to the fully coupled anisotropic formulation for a chemically active formation, and published the analytical solution for the inclined wellbore subjected to in-situ state of stress in isotropic and transversely isotropic formations; however, also neglecting electrical coupling.

Analytical solutions accounting for electrokinetic effects have been limited to the one-dimensional consolidation problem. Esrig (1968) derived such a solution for consolidation with radial drainage due to an electrokinetic application, and pointed out that the rate of pore pressure diffusion was determinedby the hydraulic permeability and not by the electrokinetic permeability. His solution, however, employed many simplified assumptions and ignored the ion transport effect. Recently, the full porochemoelectroelastic one-dimension analytical solutions have been published (Gu et al. 1999, Van Meerveld et al. 2003). These solutions can be applied to limited laboratory and field testing conditions, yet are very restrictedand fall short from serving as bench marks for the validation of numerical schemes.

This work presents the analytical porochemoelectroelastic solution to one of the practical field problems: the drilling of an inclined wellbore in a chemically active and ionized shale formation subjected to three-dimensional in-situ state of stress. First, the general isotropic porochemoelastic governing equations extended to incorporate electrokinetic effects are formulated. The inclined wellbore solution is systematically derived in the Laplace transform domain using matrix diagonalization techniques to obtain uncoupled formulations. The obtained solution is used to simulate and study the effects of the coupled electrochemical phenomena on stresses and pore pressure distributions in the vicinity of an inclined wellbore, and the subsequent impact on borehole stability.

POROCHEMOELECTROELASTIC GOVERNING EQUATIONS

In a chemically active porous medium, the driving force for the flow of pore fluid and its dissolving species is the chemical potential comprised of the mechanical pressure and osmotic pressure accounting for the chemical activity of pore fluid components. However, the saturating pore fluid is more often an electrolyte solution, which contains solutes that dissolve into electrically charged ions that are sensitive to an electrical potential gradient. On the other hand, many porous media exhibit some degree of ionization, i.e., thesolid matrix is electrically charged. For example, the abundant presence of clay minerals such as montmorillonite, illite, etc., usually renders the shale surface negatively charged due to isomorphic substitution of lower-valence cations for higher valence-cations in the clay structures (Grim 1968). The electrically charged nature of the porous medium generates an electrostatic potential field and, as a result, the movement of ionic species is no longer controlled by the chemical potential alone. Incorporating the electrical effect, the total driving force (termed the electrochemical potential) for fluid components r under isothermal condition is expressed as (Katchalsky and Curran 1967)

where µ^r is the electrochemical potential of the r^th fluid species (r = solvent, cation and anion), V^r is the partial molar volume, p is the thermodynamic pressure, R is the universal gas constant, T is the temperature, a^r = ζ ^rm^r is the chemical activity, ζ ^r is the chemical activity coefficient, m^r is the mole fraction where Σ_r m^r = 1, z^r is the valence of ionic species, F is Faraday constant and ψ is the electrical potential. In an ideal or dilute solution, the activity coefficient has the property that ζ ^r→ 1 as m^r → 0, so that a^r m^r. For simplicity, the pore fluid is modeled as an electrolyte solution comprised of a solvent (f) and one type of dissolved cation (c) and anion (a). The porous solid matrix could be ionized or electrically neutral, but the whole fluid-saturated porous medium is electrically neutral.

TRANSPORT EQUATIONS

Eq. 1 shows that the electrochemical potential difference can be caused by imbalances in the pore pressure, in the chemical composition, or in the electrical potential. The presence of the electrochemical gradient results in simultaneous fluxes of the pore fluid species. For an isothermal aqueous pore solution containing one type of cation and anion, the set of linear phenomenological equations relating the flows and the driving forces in index notation is (Yeung and Mitchell 1993)

where x_i represents the spatial coordinates, the subscript o denotes initial condition, q_i is the total volumetric fluid flow vector through the porous medium per unit time (m·s^-1), I_i is the electrical current density (A·m^-2·s^-1),

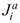- mªq_i/ 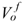and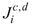

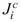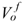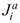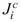-m^cq_i/ are the diffusion mass fluxes (mol·m^-2·s^-1) of the ion species relative to that of the water solvent in which and are the absolute mass fluxes of the anion and cation relative to the solid framework, respectively.

L_mn are phenomenological coefficients representing various transport processes such as hydraulic conduction (Darcy’s law), electro-osmosis, chemico-osmosis, electrical conduction (Ohm’s law), solute/ion diffusion (Fick’s first law), streaming current and potential, electrophoresis, etc. According to the Onsager principle, these coefficients are related as L_mn = L_nm (m ≠ n), which results in only ten independent transport coefficients. These transport coefficients have been well identified in the literature, and can be expressed in terms of familiar field and/or laboratory measurable parameters such as permeability, electro-osmotic permeability, formation resistivity, membrane reflection coefficient, and solute diffusion coefficients as summarized in Table I (Katchalsky and Curran 1967, Yeung and Mitchell 1993, Malusis and Shackelford 2002). The transport coefficients as presented in Table I are modified from parameters as derived by Yeung and Mitchell (1993) to account for the limiting behavior of the effective ion diffusion when the clay membrane behavior is ideal, i.e., the absolute ion fluxes vanish, 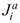= = 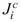0, for perfect membrane efficiency, χ = 1. Generally, the transport coefficients L_mn are functions of ion concentration. When the system is not too far from equilibrium, i.e., when the macroscopic gradients are sufficiently small, these coefficients can be assumed to be constants. From Table I, modeling of the coupled transport processes requires measurements of only six independent transport parameters {k, χ, k_eo, k_e, , }.

CONSTITUTIVE EQUATIONS

In the porochemoelectroelastic constitutive approach, the original Biot’s poroelastic constitutive relations must be extended to account for the electrochemical potentials of all pore fluid solvent and ion species. On a thermodynamic basis, the change in free energy density for a porous medium completely saturated with an electrolyte solution can be expressed as (Coussy 2004)

where σ_ij is the total stress tensor, ε_ij is the linearized strain tensor, and M^r is the mass content of the pore fluid species in mole per unit reference bulk volume. The above expression is written assuming infinitesimal deformation and isothermal condition. The electrochemical potentials of all pore fluid components are not independent, but related by the Gibbs-Duhem equation as (Katchalsky and Curran 1967)

In writing the above equation, it has been assumed that the pore space is completely saturated such that = Σ_{r = a,c,f} V^rM^rwhere is the porosity. Application of the Gibbs-Duhem equation into the freeenergy density leads to

It is obvious that the free energy W admits ε_ij and p as state variables instead of the electrochemical potentials of all pore fluid components. As such, the linearized isotropic constitutive equations follow naturally as (Coussy 2004)

where ε_kk = ε₁₁ + ε₂₂ + ε₃₃ is the volumetric strain, G and ν are the shear modulus and Poisson ratio, α is the pore pressure coefficient (PPC), represents the pore compressibility, δ_ij is the Kronecker delta (δ_ij = 1 for i = j and δ_ij = 0 for i ≠ j), compression is positive, and repeated index indicates summation. The porosity in Eq. 10 can be replaced in favor of the total fluid content ζ using the complete saturation condition and isothermal fluid state equation

in which M^sol = Σ_{r = a,c,f} M^r is the total fluid mass content (moles) and ρ^sol is the fluid mass density (mole/m³); 1/K_f is the isothermal fluid compressibility. Using Eq. 10 and Eq. 12 into Eq. 11 yields

where 1/M = + _o/K_f is the familiar storage coefficient in ground water literature. It is also necessary to obtain the variation of individual fluid component contents by linearizing the relation

in which m^r = M^r/M^sol is the mole fraction of fluid species and the initial porosity is related to the initial fluid mass content and density as Substituting Eq. 13 into Eq. 14 gives the constitutive relations for solute content as

In summary, the constitutive equations for chemically active and charged saturated porous medium are

Eqs. 16-19 are the same as the original Biot’s poroelastic constitutive formulation without electrochemical interactions. It can be observed that the pore pressure, not the electrochemical potentials, is important; and changing the fluid composition (chemical activity) of the pore fluid and/or electrical potential at constant pressure will not affect the stress, strain and/or total fluid content in the medium. The electrochemical effect, however, enters through the transient nature of the fluid and ion flows due to differences in the electrochemical potentials across the porous medium as shown previously in the transport Eqs. 2-5.

OTHER GOVERNING EQUATIONS

Other governing equations are the strain-displacement relations (Eq. 20) and conservation equations, which include the quasi-static stress equilibrium equation (Eq. 21), mass balance equations (Eqs. 22-24), and electrical charge conservation equation (Eq. 25) written in index notation as

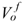
in which u_i is the displacement vector. In the ion mass conservation Eqs. 23-24, the first equality is written by defining the ion volumetric fluxes as = (r = a,c) to be consistent with the previously defined ion content ζ ^r = M ^r/≈ M ^r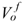. The second equality in Eqs. 23-24 expands the absolute fluxes, 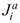and 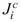, in terms of the relative diffusion fluxes accounting for the advection contributions, mªq_i and m^cq_i.

In the charge conservation Eq. 25, ρ_e is the total charge density in the porous medium. It is reasonable to assume an electrostatic condition ∂ ρ_e/∂t = 0, i.e., any electrical charge build-up is instantly equilibrated/neutralized (Sachs and Grodzinsky 1987, Corapcioglu 1991). The charge conservation reduces to (recall Eq. 3)

where ∇² is the Laplacian operator. The constitutive Eqs. 16-19, the transport Eqs. 2-5, the strain-displacement Eq. 20, and the conservation Eqs. 21-26 complete the governing equations for the responses of chemically active and electrically charged porous media saturated with electrolyte pore fluid consisting of two ion species. The porochemoelectroelastic model requires a set of ten independent parameters as opposed to seven by the porochemolelastic and five by the poroelastic models. Table II summarizes and compares the required material coefficients for these models.

FIELD AND DIFFUSION EQUATIONS

The governing equations are combined to yield the field and diffusion equations that are used to solve for the coupled stress and pore pressure responses. First, the equilibrium Eq. 21 combined with the stress-strain-pressure Eq. 16 and leads to

Differentiating with respect to x_j gives

Taking into account the strain-displacement Eq. 20, the following relation can be derived

Using Eq. 29, Eq. 28 is simplified to the field compatibility equation in poroelasticity (Rice and Cleary 1976)

where η is a lumped poroelastic coefficient defined as η = α(1 - 2ν)/[2(1 - ν)].

The diffusion equations are derived by substituting the fluid/ion content constitutive Eqs. 17-19 and the transport Eqs. 2-5 into the mass balance equations Eqs. 22-24 as

The last terms on the right-hand side of Eqs. 32-33 correspond to ion transport by advection. When the hydraulic diffusion (k) is smaller than the effective ion diffusion (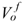/RT), the ion transport process is dominated by the diffusion mechanism (Yeung and Datla 1995). As a result, the advection q_i(∂m^r/ ∂x_i) terms in Eqs. 32-33 can be neglected, leading to complete linearization of the ion transport equations. Furthermore, the assumption of electrostatic condition allows us to conveniently uncouple the pressure and ion concentrations from the electrical potential field. Application of the Poisson-type Eq. 26 into the diffusion Eqs. 31-33 to eliminate the electrical potential and grouping like terms yields

where pª = (RT/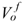)mª and p^c = (RT/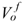)m^c are pressure equivalent terms and D_kl is a non symmetric lumped coefficient matrix defined in terms of the original transport coefficients L_mn and is given as

Note that there are no electrical transport coefficients such as the electro-osmotic permeability, k_eo, and/or electrical conductivity, k_e, appearing in the lumped transport coefficients, D_kl. Consequently, the assumptions of electrostatic condition and negligible advection effect result in a system of diffusion equations uncoupled from the electrical potential field, and the rate/speed of diffusion are controlled only by the hydraulic permeability, effective diffusion coefficients, and membrane reflection coefficient; not by the electro-osmotic permeability and electrical conductivity. The effective transport coefficients D_kl are, however, dependent upon the electrostatic potential field internal to the charged shale, i.e., function of fixed charge density in the shale solid matrix and ion concentration in the shale pore fluid. Thus, the significant contribution of an externally applied electrical field may only manifest as possible boundary condition effect, e.g., flux boundary condition. The electrical transport coefficients do come into play when calculating the flux or the streaming potential field established under perturbed conditions. This observation has been confirmed by laboratory and field data as reported by Esrig (1968). In the following section, the set of governing field Eqs. 30 and 34-36 will be applied to model the drilling of an inclined wellbore through a chemically active and ionized shale formation.

INCLINED WELLBORE SOLUTION

The inclined wellbore problem assumes that the wellbore axis generator is deviated with respect to the far field in-situ state of stresses, S_H, S_h, and S_V as shown in Fig. 1(a). The deviation is defined by theinclination angle, φ_z, formed with the vertical direction, and the azimuth angle, φ_y, formed with maximum horizontal in-situ stress. The porochemoelastic analytical solution for an inclined wellbore drilled inchemically active rock formations has been published by Ekbote and Abousleiman (2006). Their solution approach follows the loading decomposition scheme as in Cui et al. (1997) to arrive at the final three-dimension solution. By the same token, the approach is applicable to the current linear porochemoelectroelastic model with the relevant initial and boundary conditions for the stress, pore pressure, ion concentrations, and electrical potential.

INITIAL EQUILIBRIUM CONDITIONS

Before drilling, the undisturbed formation is saturated with a pore fluid having initial pore pressure, p_o, and ions with mole fractions, and . Estimation of the initial formation ion mole fractions, however, is not trivial. As discussed above, the pore surfaces of clay-rich sedimentary formations are negatively charged. These negative fixed charges must be balanced by either increasing the pore fluid mobile/exchangeable cations or expelling some of the pore fluid anions. As a result, the equilibrium pore fluid in these rock formations, e.g., shale, is not electrically neutral as depicted in Fig. 2(a). It contains excess exchangeable cation concentration to counter-balance the negative fixed charges on the shale layers according to the electrical neutrality requirement as

where z^c > 0 and zª, z^fc < 0 are the valences of the cation, anion and shale fixed charge, respectively, and m^fc is the concentration of these fixed charges on the surface of the solid shale matrix expressed in terms of mole fraction. Calculation of the initial ion concentration in the pore fluid requires knowledge of the pore water activity of the formation, e.g., measured by an osmometer. The measured pore water activity is actually the water activity of a free outer solution that is in thermodynamic equilibrium with the formation initial state which requires equality of individual electrochemical potentials (Overbeek 1956)

For a solution containing electro neutral salt, C_xA_y, which dissociates into x cations of type C having valence z^c and y anions of type A having valence zª, the measured water activity can be used to estimate the equilibrium outer salt concentration, , through the relation assuming dilute solution ( 1). On the basis of Eqs. 1 and 39, we may write for the equilibrium case

Making use of the electro neutrality condition, xz^c + yzª = 0, for the outer solution, the electrical potential term is eliminated by multiplying Eq. 41 with x and Eq. 42 with y, and adding the resultant equations together to arrive at

In the above, the exponential of the pressure term has been neglected since

(p_eq - p_o) in normal field conditions. For example, considering NaCl salt solution at T = 30ºC, R = 8.314 J/mol-ºK, 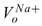= 2.33e-6 m³/mol, and 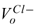= 15.17e-6 m³/mol, then, the term 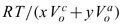is approximately 146 MPa, which is usually two orders of magnitude greater than the pressure difference. For brevity, only the results for x : y ≡ 1 : 1 salts such as NaCl and KCl are presented in the following. Derivation for salt solution of different x : y can be carried out analogously. Eq. 43 simplifies to

Solving Eq. 44 together with the electro neutrality requirement inside the formation (Eq. 38) for the initial ion concentrations gives

To complete the calculation of initial ion mole fraction, the amount of negative fixed charge must be estimated. The fixed charge mole fraction is related to the formation Cation Exchange Capacity (CEC) measured in milli-equivalent of cations per 100 grams of dry clay by

in which ρ_s is the average grain density in g/cc and 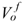is the water molar volume in liter/mol. Assuming z^c = 1 and zª = z^fc = -1, and expressing the fixed charge concentration in terms of CEC and the equilibrium salt salinity in terms of measured water activity, the initial anion concentration in the formation is (Hanshaw 1964)

Examination of Eq. 48 shows that, for two formations of the same porosity, the one with the higher surface charge density or CEC will accommodate fewer anions and, thus, expulse more free salt. Hence, a smectite abundant formation (CEC ~ 80-120 meq./100gr) exhibits more reactivity and more idealmembrane behavior with aqueous solution than an illite formation (CEC ~ 20-30 meq./100gr). Meanwhile, as the porosity tends toward zero, vanishes, implying that the more compacted the formation,the more efficient is the shale’s ion exclusion behavior. It is also interesting to see that when the measured pore water activity is high, e.g., → 1, approaches zero. However, this does not necessarily mean that all the anions are excluded from the formation since the pore fluid could simply be just water ( = 1).

BOUNDARY CONDITIONS

After wellbore drilling, the borehole is filled with a drilling fluid having pressure p_mud and solute mole fraction corresponding to a fluid mud activity . For 1:1 salts, the solute in the mud dissociatesinto cations and anions with equal mole fraction = = . As depicted in Fig. 2(b), thedrilling mud of equal ion concentration is in contact with a formation pore fluid having excess cation concentration. At the mud/shale interface, the electrochemical potentials of all fluid species must be continuous or else there would be infinite fluxes across the boundary. This leads to similar thermodynamic requirements as in Eq. 39

where R_w is the wellbore radius. Following a similar procedure and replacing the corresponding subscripts "eq" and "o" with "mud" and "r = R_w", the ion concentrations in the shale at the wellbore wall are determined as

Eqs. 50-51 reveal that the total ion mole fraction in the formation at the boundary is larger than or equal to the outer mud ion concentration of 2. Consequently, there exists a fixed-charge-induced osmotic pressure differential at the wellbore mud/shale interface according to

The above induced osmotic pressure is calculated based on the requirement of continuous electrochemical potential of the electrically neutral water at the borehole wall, in Eq. 49. Additionally, Eq. 52 shows that for the same drilling mud salinity, the higher the CEC of the formation, the larger the osmotic pressure differential developed at the wellbore wall. When the formation is free of fixed charge, i.e., CEC, m^fc → 0, the pressure and ion concentrations are indeed continuous at the boundary: The discontinuities of ion concentrations and pore pressure at the mud/shale interface are well known in chemistry as the Donnan equilibrium effect (Overbeek 1956).

Accordingly, the boundary conditions to be imposed at the wellbore wall, r = R_w, are

And at the far field, r → ∞

In the above, σ_m, σ_d, θ_r are parts of the stress boundary condition and rotation angle in polar coordinate for a circular borehole as defined in Cui et al. (1997)

where t is time and H[t] is the Heaviside unit step function (H[t < 0] = 0 and H[t > 0] = 1). S_x, S_y, S_z, S_xy, S_xz, and S_yz are far-field in-situ stresses transformed into the local wellbore coordinate (x,y,z) as depicted in Fig. 1(b). Δp_mud/shale, and are the pressure and ion concentration differential at the mud/shale boundary defined as

where are defined in Eqs. 50-52. It should be noted here that since the governing field and diffusion equations are uncoupled with the electrical potential field and the boundary conditions are of Dirichlet’s type, i.e., the values of the variables are specified on the problem’s boundaries, it is not necessary to specify the boundary condition for the electrical potential field, unless we want to solve for the fluxes and/or streaming electrical potential field.

THE PROBLEM SOLUTIONS

Following Cui et al. (1997), the problem can be solved by the superposition of three sub-problems. The three sub-problems are described as the modified plane strain problem, the uniaxial problem, and an anti-plane shear problem. It was shown that, of the three problems, solutions for the uniaxial and anti-plane shear problems are purely elastic since they do not generate excess pore pressure (Cui et al. 1997). The solutions to the individual problems are presented here.

Problem 1: plane strain problem

The boundary conditions for this problem are as follow.

At the far field (r → ∞)

At the wellbore wall (r = R_w)

The boundary conditions of this problem are designed such that a plane strain solution can be used. First, a reduced set of the governing Eq. 30 and Eqs. 34-36 is derived to obtain the time-dependent solutions for a plane strain condition. Specifically, the field Eq. 30 is rewritten in polar coordinate (r, θ) as

Based on the boundary loading conditions Eqs. 71-75, the various variables can be decomposed as (Carter and Booker 1982)

where P, Pª, P^c, E_kk, S_kk, S_rr, S_θθ, and T_rθ are functions of time and radial distance only, and n is an integer number depending on loading conditions. To facilitate the Laplace transform technique, we solve for the perturbations/changes with respect to the initial reference state, so that the initial conditions and far field boundary conditions for all variables vanish identically.

Incorporating Eq. 77 into Eq. 76 to eliminate θ dependency and seeking bounded solutions gives

where C_o = C_o[s] is a constant to be determined from boundary conditions, the tilde sign ~ denotes Laplace transform solution and s is the Laplace variable. Utilizing Eq. 79 to replace the volumetric strain in the diffusion Eqs. 34-36 leads to

where = ∂²/∂r² + (1/r)(∂/∂r) - n²/r². The above system of differential equations only yieldsrealistic solutions if the 3×3 coefficient matrix [Z] = [Y]^-1[D] is positive definite. It is easy to verify that [Z] is positive definite since all determinants of [Z] and its leading principal sub matrices are positive (Johnson 1970).

The solution to this coupled system can be found by uncoupling the diffusion equations using matrix diagonalization techniques (Farlow 1993). Here, the general solutions are straightforward and given by superimposing the homogenous solution and the particular solution as

where C_i = C_i[s] are constants to be determined from the boundary condition, K_n[ξ_ir] is the modified Bessel function of the second kind of order n, ξ_i = , in which λ_i is the eigenvalue of [Z] with {m_1i, m_2i, m_3i} as its corresponding eigenvector, and f_i = α[Y]^-1 for i = 1,2,3.

Once the pressure solutions are obtained, the general solutions for stress, strain, and displacement are straightforward to obtain using the constitutive equations (Eq. 16) and strain-displacement relations (Eq. 20). For brevity, these derivations are not presented here. To determine the constants C_i, the boundary conditions for this problem are further decomposed into three loading cases namely: elastic radialloading, diffusion, and a poroelastic deviatoric stress loading case.

• Case 1

The boundary conditions at the wellbore wall are

and the solution is purely elastic as given by the classical Lamé solution

where the superscript (1) denotes the loading case and only the non-zero solutions are listed.

• Case 2

The boundary conditions at the wellbore wall are

The solution is transient and given in Laplace transform domain, which could be inverted to the time domain using the Stehfest’s algorithm (Stehfest 1970) as presented in ^{Appendix A}

where the tilde ~ denotes the quantities in the Laplace transform domain. In the above

Φ and Ξ are functions defined as

• Case 3

The boundary conditions at the wellbore wall are

and the solutions in Laplace transform domain are

where the constants h, D₁, D₂, D₃, D₄, and D₅ are given as

Θ, Π , and Ω are functions defined as

Problem 2: uniaxial stress problem

At the far field (r → ∞)

At the wellbore wall (r = R_w)

The solution is stress and pore pressure free, and is given by a constant stress everywhere as

Problem 3: anti-plane shear problem

At the far field (r → ∞)

At the wellbore wall (r = R_w)

The solution is an elastic one and given as

COMPLETE INCLINED WELLBORE SOLUTIONS

The complete solutions for stresses and pore pressures are obtained by superimposing the non-zerosolutions of the three sub-problems as

RESULTS AND APPLICATIONS

The solutions developed in the previous section are applied to simulate and assess the electrokinetic effect in a chemically active and ionized rock formation on the stress and pore pressure distribution in the vicinity of a wellbore.

A wellbore of radius 0.1 m is assumed to be drilled in a shale formation characterized by in-situ stress and pore pressure given as: S_V = 73.5 MPa, S_H = S_h= 58.8 MPa, and p_o = 29.4 MPa at a depth of 2940 meters. The formation pore fluid is assumed to be a NaCl salt solution with activity . For simplicity, the wellbore is assumed to be vertical, φ_y = φ_z = 0º. The formation material properties are those of an offshore West Africa shale with moderate clay content (~ 60%) retrieved at the above true vertical depth where the formation temperature is taken to be T = 100ºC.

The electrokinetic effect on the response of a chemically active formation is investigated in conjunction with the corresponding poroelastic and porochemoelastic counterparts for the case of high ( > ) and low mud activity ( < ). The wellbore is assumed to be filled with a drilling fluid maintained at density of 1.07 SG (Specific Gravity - the ratio of fluid density to the density of water) leading to a wellbore mud pressure of p_mud = 30.87 MPa. All of the material properties, pore-fluid properties, and mud properties as well as resulting calculated parameters for use in the solution, are tabulated in Table III.

Figure 3 shows the pore pressure profile at time t = 0.01 day ( ~ 15 minutes) into drilling for the case of high mud activity ( = 0.93 > = 0.90) using the complete solutions in Eq. 129 by combining the Laplace transform time inversion of Eqs. 88 and 103. Compared with the poroelastic and porochemoelastic response, it is obvious that there is a pressure increase at the wellbore wall due to the electrokinetic equilibrium requirement. This pressure discontinuity is not generated due to the chemical activity/salinity gradient between the mud and the formation as shown in the lumped chemical potential model (ignoring ion transport), but is a consequence of the electrostatic restriction of the negative fixed charge present on the shale pore surface. The chemical osmotic effect is to increase the near wellbore response of pore pressure in the shale formation. This makes sense since high mud activity induces additional osmotic flow into the formation. Figure 4 shows time evolution of the pore pressure profile for the porochemoelectroelastic solution along with the porochemoelastic solution in dashed lines. As time elapses, the initial osmotic pore pressure peak inside the formation decreases due to subsequent diffusion of solvent and ions. However, the fixed-charge induced pore pressure jump at the mud/shale interface stays constant through the course of time.

Figures 5 and 6 show, respectively, the corresponding effective radial and tangential stresses at t = 0.01 day (15 minutes). Negative values denote tensile stress. As seen in Figure 5, the effective radial stress attains less compressive value with respect to the regular porochemoelastic solution due to the jump in pore pressure at the borehole wall as shown previously. As a result, a tensile region is developed in the near wellbore region, which causes spalling failure of the formation. Similarly, Figure 6 shows that the electrokinetic effect weakens the compressive effective tangential stress close to the borehole wall, which promotes tensile fracturing failure in the formation. Unlike the porochemoelastic response, the tensile region for porochemoelectroelastic model does not vanish as time evolves, but enlarges as illustrated in Figures 7 and 8.

Figure 9 shows the pore pressure response for the case of low mud activity ( = 0.87 < = 0.90). Since the mud salinity is higher than the formation salinity, there will be an induced osmotic back flow of water from the formation toward the wellbore and solute migration into the formation. As a result, the near wellbore pore pressure will be depressed accordingly as illustrated in Figure 9. Meanwhile, the redistribution of the ion at the mud/shale interface still enforces a pressure jump at the borehole wall.In other words, the electrical effect is to always impose a pressure increase across the mud/shale interface if the formation is negatively charged. Figures 10 and 11 show the corresponding effective radial and tangential stresses for this case. Although the chemical osmosis does enhance the effective stresses, the electrokinetic enforcement of higher wall pressure leads to weaker compressive stresses in the nearwellbore region. In this case, the electrokinetic effect counteracts chemical osmosis.

It should be noted that the lumped chemical potential model (ignoring ion transport) does not provide bounds on the responses of the stress and pore pressure since it does not account for the electrokinetic restriction. Depending on the relative magnitudes of the chemical osmotic and electrokinetic effect, the contribution of one effect to the overall response can overshadow the other one. In the porochemoelectroelastic model, the electrokinetic effects are manifested as a pressure discontinuity at the mud/shaleboundary. This pressure difference is a direct function of the shale cation exchange capacity (CEC). Figures 12 and 13 illustrate the effects of CEC on the pressure redistribution in the formation for high and low mud activity, respectively. It is observed that the higher the shale CEC, the higher the pressure increases at the mud/shale boundary. When the CEC is large enough, the resulting electrically induced pore pressure will eclipse the chemical osmotic effect.

CONCLUSIONS

A general isotropic porochemoelectroelastic formulation has been presented to account for electro-chemical effect in the overall response of chemically active porous media. Based on this formulation, a set of field and diffusion equations was developed to solve for the stress and pore pressure distribution. The corresponding analytical solution for the inclined wellbore problem in chemically active formations subjected to thethree-dimensional in-situ state of stress has been derived and presented in this paper.

From the present solutions, it is observed that the rate of diffusion is affected not only by the hydraulic Darcy’s permeability, Fick’s solute diffusion coefficient, and the membrane reflection coefficient, but with the electrokinetic contribution that manifests itself as a boundary effect at the borehole wall. Proper modeling of the electrokinetic contribution requires the use of the commonly measured shale parameters - Cation Exchange Capacity.

Via the inclined wellbore solution, effective stress and pore pressure analyses were carried out to study the electrokinetic and chemical effects on the overall poromechanic responses of the chemically active formations. Effective stress calculations show that the porochemoelectroelastic solution predictions differ substantially from the normal porochemoelastic and poroelastic approaches. Since wellbore stability analyses are usually performed based on effective stresses, ignoring the electrokinetic effects will mislead the predictions and assessment of potential problems in the field.

ACKNOWLEDGMENTS

Partial funds for this work were provided by the PoroMechanics Institute at the University of Oklahoma through the Rock Mechanics Consortium industry members.

Manuscript received on May 2, 2008; accepted for publication on September 10, 2008

Selected paper presented at the IUTAM Symposium on Swelling and Shrinking of Porous Materials: From Colloid Science to Poromechanics - August 06-10 2007, LNCC/MCT.

with the coefficient A_n given by

where the symbol ! denotes factorial operation, "Floor(x)" gives the greatest integer less than or equal to x, and "Min" means picking the minimum values. The number of term N in the series summation is an even integer number between 2 and 20. It has been shown that a selection of N = 8 generally gives satisfactory results (Cheng et al. 1994).

• BIOT MA. 1941. General theory of three dimensional consolidation. J Appl Physics 12(2): 155164.
• CARTER JP AND BOOKER JR. 1982. Elastic consolidation around a deep circular tunnel. Int J Solids Struct 18(12): 10591074.
• CHENG AH-D, SIDAURUK P AND ABOUSLEIMAN Y. 1994. Approximate inversion of Laplace transform. Mathematica Journal 4(2): 7682.
• CORAPCIOGLU YM. 1991. Formulation of electro-chemico-osmotic process in soils. Transp Porous Media 6: 435444.
• COUSSY O. 2004. Poromechanics, Chichester: J Wiley & Sons, England, 298 p.
• CUI L, CHENG AH-D AND ABOUSLEIMAN Y. 1997. Poroelastic solution of an inclined borehole. ASME J Appl Mech 64: 3238.
• EHLERS W AND MARKERT B. 2001. A linear viscoelastic biphasic model for soft tissues based on the Theory of Porous Media. ASEM J BioMech Engrg 123: 418424.
• EKBOTE S AND ABOUSLEIMAN Y. 2006. Porochemoelastic solution for an inclined borehole in a transversely isotropic formation. J Engng Mech 132(7): 754763.
• ESRIG MI. 1968. Pore pressure, consolidation, and electrokinetics. J Soil Mech Found Div, Proceedings ASME 94(SM4): 899921.
• FARLOW SJ. 1993. Partial differential equations for scientists and engineers. New York, Dover Publications Inc., USA, p. 223231.
• GREGOR HP AND GREGOR CD. 1978. Synthetic membrane technology. Sci Amer 239: 112128.
• GRIM RE. 1968. Clay Mineralogy. New York, McGraw-Hill Book Co 2^nd ed.
• GU WY, LAI WM AND MOW VC.1999. Transport of multi-electrolytes in charged hydrated biological soft tissues. Transp Porous Media 34(1-2): 143157.
• HANSHAW BB. 1964. Clays and Clay minerals. In: BRADLEY WF (Ed), National Conference. Proceedings of the 12^th National Conference, Atlanta Georgia, 1963, Pergamon Press, New York, USA, p. 397421.
• HEIDUG WK AND WONG SW. 1996. Hydration swelling of water absorbing rocks: A constitutive model. Intl J Numer Analyt Meth Geomech 20: 403430.
• HUDEC PP. 1980. Hypersaline brine and clay liner interactions. Proceedings 3^rd Int Symp Water-Rock Interaction, Edmonton, Alberta, Alberta Research Council, Edmonton, Alberta, p. 153154.
• HUYGHE JM AND JANSSEN JD. 1999. Thermo-chemo-electro-mechanical formulation of saturated charged porous solids. Transp Porous Media 24: 129141.
• JOHNSON CR. 1970. Positive definite matrices. Amer Math Monthly 77(3): 259264.
• KATCHALSKY A AND CURRAN PF. 1967. Nonequilibrium thermodynamics in biophysics, Cambridge, MA: Harvard University Press, p. 95123.
• MALUSIS MA AND SHACKELFORD CD. 2002. Theory for reactive solute transport through clay membrane barriers. J Cont Hydro 59(3-4): 291316.
• NEUZIL CE. 2000. Osmotic generation of anomalous fluid pressures in geological environments. Nature 403: 182184.
• OLSEN HW. 1969. Simultaneous fluxes of liquid and charge in saturated kaolinite. Soil Sci Soc Am Proceedings 33: 338344.
• OVERBEEK JTHG. 1956. The Donnan equilibrium. Prog Biophys 6: 5784.
• RICE JR AND CLEARY MP. 1976. Some basic stress diffusion solutions for fluid saturated elastic porous media with compressible constituents. Rev Geophys Space Phys 14: 227241.
• ROSANNE M, PASZKUTA M AND ADLER PM. 2005. Electrokinetic phenomena in saturated compact clays. J Colloid Interface Sci 297: 353364.
• SACHS JR AND GRODZINSKY AJ. 1987. An electromechanically coupled poroelastic medium driven by an applied electrical current: surface detection of bulk material parameters. Phys Chem Hydrodynamics 11: 585614.
• SHERWOOD JD. 1993. Biot poroelasticity of a chemically active shale. Proc Royal Soc Lond A 440: 365377.
• SHERWOOD JD AND BAILEY L. 1994. Swelling shale around a cylindrical wellbore. Proc Royal Soc Lond A 444: 161184.
• STEHFEST H. 1970. Numerical inversion of Laplace transforms. Comm ACM 13: 4749.
• VAN MEERVELD J, MOLENAAR MM, HUYGHE JMRJ AND BAAIJENS FPT. 2003. Analytical solution of compression, free swelling and electrical loading of saturated charged porous media. Transp Porous Media 50(1-2): 111126.
• VAN OORT E. 1994. A novel technique for the investigation of drilling fluid induced borehole instability in shales. SPE/ISRM 28064 presented at the 1994 SPE/ISRM Rock Mechanics in Petroleum Engineering Conf, Delft.
• YEUNG AT AND DATLA S. 1995. Fundamental formulation of electrokinetic extraction of contaminants from soil. Can Geotech J 32(4): 569583.
• YEUNG AT AND MITCHELL JK. 1993. Coupled fluid, electrical and chemical flows in soil. Geotechnique 43(1): 121134.
• YEW CH, CHENEVERT ME, WANG CL AND OSISANYA SO. 1990. Wellbore stress distribution produced by moisture adsorption. SPE Drilling Engng 5: 311316.
• YOUNG A AND LOW PF. 1965. Osmosis in argillaceous rocks. Bull Amer Assoc Petrol Geol 49: 10041008.

APPENDIX A  - STEHFEST'S ALGORITHM

[

Given 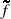[s] as the Laplace transform of the function f[t] and a value of time t, the following equation implements Stehfest's algorithm and allows the calculation for the numerical value of f[t] (Stehfest 1970)

Publication Dates

• Publication in this collection
  25 Feb 2010
• Date of issue
  Mar 2010

History

• Received
  02 May 2008
• Accepted
  10 Sept 2008