MODELLING AND PARAMETER ESTIMATION IN REACTIVE CONTINUOUS MIXTURES: THE CATALYTIC CRACKING OF ALKANES. PART I

MODELLING AND PARAMETER ESTIMATION IN REACTIVE CONTINUOUS MIXTURES: THE CATALYTIC CRACKING OF ALKANES. PART I

¹²

¹ Instituto de Pesquisa e Desenvolvimento (IPD), Av. das Américas, n° 28705, Guaratiba - Rio de Janeiro – RJ – Brasil, E-mail: [e-mail]

² Universidade Federal do Rio de Janeiro, Depto. de Eng. Química , Escola de Química , Bl. E, Centro de Tecnologia, Cidade Universitária, Rio de Janeiro - RJ , Brasil, 21949-900 Phone: (+55) [phone], E-mail: [e-mail]

(Received: June 4, 1998; Accepted: March 3, 1999)

Abstract - Fragmentation kinetics is employed to model a continuous reactive mixture. An explicit solution is found and experimental data on the catalytic cracking of a mixture of alkanes are used for deactivation and kinetic parameter estimation.

Keywords: modelling, catalytic cracking, mixture.

INTRODUCTION

The concept of continuity in a mixture applies whenever the mixture is so complex that it is no longer worthwhile to distinguish among individual chemical species; instead, an index (such as number of carbon atoms, boiling point or chromatographic retention time) is chosen to characterize each component and the continuity of this index is assumed. Concentration c_i of species A_i is replaced by f(x)dx, the element of concentration of material with an index in the (x, x + dx) interval. Function f(x) is known as the concentration distribution function of the mixture (in units of concentration if x is dimensionless), where x is the continuous index of the mixture. In this work, x represents the (continuous) number of carbon atoms in a molecule.

Catalytic cracking of gasoil has been modeled by non-continuous second order models with lumped components (Weekman, 1979; Abbot et al., 1985). In this context, kinetic data fitting is easily achieved, but some problems appear when mixture properties, such as density, viscosity or distillation curve need to be predicted. This occurs as a consequence of the limitations of the lump approach with regard to physical characterization of the mixture, especially in the cases where the number of lumps is small.

On the other hand, use of the continuous concept, while increasing the mathematical complexity of the kinetic modelling, makes the thermodynamic description of the mixture viable by means of well-established group contribution methods (Reid et al., 1987). In addition, the continuity hypothesis of the reactive mixture may explain how a so typically first-order reaction, as in the case of hydrocarbon catalytic cracking, can be better adjusted by discrete second-order models.

In the field of reactive continuous mixtures without catalyst deactivation, attention must be drawn to Aris’ work (1989). In this work the author analyses overall (lumped) reaction kinetics for many initial distributions of reactants and, vice-versa, finds out which initial distribution produces a given overall reaction kinetics. In the former case, the most frequently used distribution is the following one-parameter gamma distribution:

(1)

where f0 is a concentration distribution function and C0 is the total concentration of the mixture in gmoles per volume. The f0/C0 ratio or g0(x) is a dimensionless concentration distribution function (DCDF).

Another feature of Aris’ work is that the main focus is on the case of a reactive continuous family forming another continuous family. This can be seen in the following sequential reaction scheme, where index x spans all families:

(2)

Aris’ work also treats the doubly distributed continuum (2 indices), which was first employed by Prasad, Wittman, Agnew and Sridhar (1986). These authors developed a model with production within the reactant family, which generates an even more exciting challenge. A family is defined as a set of substances that have a common functional group in their molecular structure and differ from each other only in their index number. This hypothesis, which assumes the existence of only one family, is the essence of the work of Prasad et al., where the generic chemical reaction is:

A(x1,x2) ® A(y1,y2) + A(x1-y1,x2-y2) (3)

This model of chemical transformation leads to material balances in the form of integral-differential equations of the anti-Volterra kind. Prasad et al. (1986) solved this problem with bicubic quadratures after making some appropriate simplifications of the initial reactant distribution and imposing restrictions on the index domain. Simplifications of the stoichiometric coefficient distribution function and/or of the kinetic constant distribution function are also found in other works (for example, McCoy and Wang, 1994) and provide semi-analytical solutions. In fact, research using semi-empirical or analytical approaches to continuous kinetics for complex reactive mixtures is very prolific and it seems that there is room enough in the field to accommodate numerous new applications – as in many new processes in the oil, coal and polymer industries – or new strategies for mathematical solution.

Within this context, the present work aims at analyzing the continuous kinetics of the catalytic cracking of a single-indexed family – a reactant family which requires only one index for the complete characterization of its components. More specifically, this paper explores theoretical approaches to the catalytic cracking of linear alkanes. The resulting kinetic model is similar to the one shown in Equation 3, which has been called fragmentation kinetics (McCoy, 1994) or distributed cracking (Peixoto, 1997). Concluding the paper, experimentation with explicit solutions to the model is conducted.

KINETIC MODELLING AND MATERIAL BALANCE

In the present approach, the catalytic cracking of a continuous mixture can be investigated under the assumption of the following distributed first-order fragmentation:

(4)

After division by C0 (the initial total concentration in gmoles per volume unit), the material balance applied to a mixture element with an index between x and x + dx, in a fluid element V traveling along an isothermal heterogeneous plug-flow reactor (IHPFR) is (McCoy and Wang, 1994):

(5)

Since the previous equation is valid for any V and any range of index x, the kinetic equation for fragmentation without growth (which would be required in a microbiological population balance, for instance) results in:

(6)

with the following initial condition:

(7)

where g0(x) and g(x,t ) are the initial dimensionless concentration distribution function (DCDF) and this same function after time contact t with the catalyst, respectively. The catalyst is supposed to be uniformly distributed throughout the reactor and to have constant properties. In the present context, g0(x) represents the mixture inlet condition in the reactor.

Some restrictions apply to function v(x,y), the stoichiometric coefficient distribution function (SCDF). Since the SCDF is a distribution function of fractions, the condition concerned with its integration within the feasible index range, after the breakage of a y-indexed molecule, is

(8)

since two molecules must replace a broken one (Prasad et al., 1986). Furthermore, this function must exhibit an obvious symmetry (Prasad et al., 1986), as follows:

v(x,y) = v(y-x,y) (9)

It is assumed that function K(x,t), the kinetic constant distribution function (KCDF), is a separable function of x and t (Peixoto, 1996; Peixoto, 1997) and of other variables such as temperature and catalyst configuration, as follows:

(10)

where K(x) is now a new dimensionless kinetic constant distribution function (DKCDF), k0 is constant or a term that is, at most, dependent on temperature and catalyst configuration and has the dimensions of time^-1, and D(t) is the fraction of active catalytic sites after reactor run time (or catalyst age) t, described by:

(11)

with the following initial condition:

D(0) = 1 (12)

where the only restriction imposed upon operator Á is such that Á (D(t),t)<0, " t. Since t <<t in a typical run, D(t) is approximately constant in the (0,t ) interval, entailing a change in variables that warps the time scale to a dimensionless "crazy clock" scale in order to take into account the following effects of catalyst deactivation:

(13)

with the following initial condition:

q = 0 for t = 0 (14)

In this new time scale, the first-order kinetic equation for fragmentation of McCoy and Wang (1994), applied to a steady-state IHPFR, becomes:

(15)

with the following initial condition:

(16)

where:

(17)

It can be seen that Equation 15 becomes the continuous kinetic model for production outside the reactant family (PORF) (Aris, 1989) whenever v(x,y) = 0.

PERTURBATION SOLUTION

A perturbation solution (Nayfeh, 1981) to the integral equation of fragmentation 15 was sought. The following scheme is used :

(18)

This form also encompasses production outside the reactant family (Aris, 1989) requiring only that g_n(x) = 0 (n > 0). It will be shown that this occurs naturally when v(x,y) = 0. In other words, the perturbation approach is flexible enough to recover the case of PORF as a limiting condition.

Equation 18 is substituted into Equation 15, giving:

(19)

Expanding the exponential term in its power series:

(20)

Equating the coefficients of q :

® ® (21)

gives

(22)

Finally, defining m = j + 1, we obtain

(23)

which is the recurrence formula for g_n(x) functions. As mentioned above, it can be seen that v(x,y) = 0 implies g_n(x) = 0, recovering the case of PORF. The flexibility of the recurrence formula 23 with regard to any g0(x), K(x) and v(x,y) models can also be seen, since, up to this point, no restrictions were made on them.

NUMERICAL IMPLEMENTATION OF THE PERTURBATION SERIES

In order to make the calculation of g(x,q ) operational, the series in Equation 18 is truncated after term g_m(x) and each coefficient function is expanded in a finite basis of orthonormal functions in the (0,¥ ) domain, as follows:

(24)

where

(25)

or

(26)

The basis functions are Laguerre polynomials, which have been normalized and weighted by the exp(-x/2) function, as follows:

(27)

where Pl_i(x) is the normalized Laguerre polynomial of order i obtained from the classic Laguerre polynomial of order i, L_i(x), given by the following recurrence formulae:

(28)

and

(29)

Coefficient matrix , perturbation function vector and orthonormal basis vector are defined as:

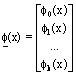(30)

such that

(31)

Examining recurrence formula 23, it can be seen that every g_n(x) function has a known term depending only on integration of g0(x), and another term depending on integration of the sum of all functions with an index between 1 and . This can be written as:

(32)

where

(33)

and

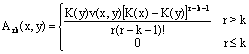
Substituting into Equation 32 gives:

(35)

As a consequence of truncation, Equation 35 is no longer an equality, with a residual vector, as follows:

(36)

In order to establish a process to generate , we use the Galerkin method which is a general approach to the asymptotically correct solution of functional problems in inner product spaces where a complete orthogonal basis can be found (Kreyszig, 1978). In the present case, the Galerkin framework implies that the basis functions and the residual vector are orthogonal, i.e.,

(37)

resulting in

(38)

With the orthonormal behavior of the f _i(x) basis functions, a successive substitution scheme to find is:

(39)

After convergence of this process, we may write

(40)

where

(41)

The algorithm is initialized with the choice of m and k. Matrix is then calculated by successive iterations on Equation 39. Sizes m and k may be sequentially increased, enlarging matrix until there is no significant difference between two consecutive sets of model outputs for given parameter values.

In order to depict the implementation of this procedure, the following two-parameter gamma distribution is employed as an initial distribution (DCDF):

(42)

The model for the SCDF is an adaptation of Prasad’s (1986) doubly distributed empirical SCDF. According to the authors, the SCDF must exhibit a maximum value in an intermediate index value, with a fast decay to zero at both ends, besides the requisites of integral value and symmetry (Equations 8 and 9). So, the SCDF model is (Peixoto, 1996; McCoy and Wang, 1994)

(43)

Following a common procedure employed in the literature (Aris, 1989), it was used the following linear model in the dimensionless kinetic constant distribution function (DKCDF):

K(x) = x (44)

For evaluation and numerical comparison purposes, the following residue norm is defined:

(45)

Table 1 shows the behavior of this norm as dimension k of the functional basis and perturbation order m are increased. Figures 1 and 2 present, in graphical form, the dependence of the residual vector on index x for two sets of values of m and k. As shown in Table 1 and Figures 1 and 2, the method decreases the residual vector asymptotically. It must also be said that the above results were obtained by fixing the gamma parameters of g0(x) arbitrarily at h = 10 and e = 1 for illustrative purposes only.

Table 1:
1: Decay of the residue of Equation 36 with the size of matrix

size (): m x k

m = k = 3

2.3075

m = k = 5

1.6763

m = k = 7

1.5616

Figure 1:
Graphic representation of R(x)^tR(x) with m = k = 3.

Figure 2:
Graphic representation of R(x)^tR(x) with m = k = 7.

MODEL TUNING AND DATA FITTING

Recently Kobolakis and Wojciechowski (1985) carried out an experimental study on the catalytic cracking of a 99% paraffinic oil (composed predominantly of linear alkanes in the C5 to C30 range) with zeolitic catalysts. The products generated in their experiments were lighter paraffins and small quantities of deposited carbon and of olefins. So, it has been considered that these data are appropriate for testing the model, whose key point is the existence of only one continuous family embracing reactants and products. A statistical procedure may then be established to adjust the model, via data fitting standard techniques, to the experimental information generously provided to this work by Dr. Wojciechowski in a personal communication (1996).

Indeed, the inexact or approximate points in this procedure are the consequence of assuming that: (i) the initial oil contains only linear alkanes; (ii) the basic cracking reaction generates only lighter linear alkanes, which would be the case if cracking occurred in the presence of an excess of hydrogen (in other words, it is neglected the differences between an olefin and the corresponding linear alkane with the same number of carbon atoms); and (iii) the model is unable to "see" stoichiometrically the deposition of carbon; nevertheless, the catalyst deactivation phenomenon is taken into account by the empirical procedure shown above, which resulted in the time-scale transformation t ® q .

The data fitting procedure is applied in two subsequent phases. Firstly an initial and analytic DCDF, g0, is generated by adjusting the two parameters (e , h ) of a gamma distribution function to the discrete composition of fresh oil from Wojciechowski’s data. Secondly, model parameters, including deactivation parameters, are estimated with the corresponding cracked oil data.

In a typical experiment an IHPFR reactor is filled with a given mass of fresh catalyst. After controlled conditions of temperature and pressure are met, a given mass of fresh oil is continuously pumped through the reactor during the time of experiment (see tf below). The cracked oil is collected in a single vessel and analyzed after the run. Detailed information concerning the experimental equipment and procedure can be found in Kobolakis and Wojciechowski (1985) and Peixoto (1996).

In order to adapt the model to the experiment, the following quantities (Kobolakis and Wojciechowski, 1985; Peixoto, 1996) are defined: g - catalyst/oil mass ratio (kg cat/kg oil); j - catalyst porosity; tf - time (sec) of continuous operation of the reactor; b - dimensionless constant given by (j r _v/r _cat); kcin - kinetic parameter (sec^-1) given by k0 b. With these terms it can be shown (Peixoto, 1996) that

t = g b tf (46)

The following Wojciechowski deactivation model is also employed:

(47)

giving

(48)

with Equations 13 and 46, after regrouping of parameters and .

Since the model response depends only on q and x (Equation 18), it can be seen that all relevant parameters (kcin, Gd, Nd) influence the model only through q . It must also be noted that (g , tf) are independent experimental coordinates and (t, x) are independent model variables.

Parameter Estimation for Initial Distribution

Table 2

N° of carbonsMass fractions (% w/w)60.750072.930086.6400910.04001011.62001112.19001211.20001310.0300148.5500157.4000166.1100174.9900183.7300192.5000201.2700

N° of carbons	Mass fractions (% w/w)
6	0.7500
7	2.9300
8	6.6400
9	10.0400
10	11.6200
11	12.1900
12	11.2000
13	10.0300
14	8.5500
15	7.4000
16	6.1100
17	4.9900
18	3.7300
19	2.5000
20	1.2700

Table 2: Kobolakis and Wojciechowski's fresh oil data.

A standard maximum likelihood procedure (Peixoto, 1996) was established for the estimation of gamma parameters (e , h ) in the tuning of the fresh oil DCDF (g0). Numerical nonlinear optimization was conduced on the appropriate objective function with a BFGS algorithm (Edgar and Himmelblau, 1988). Table 3 below presents the relevant statistical entities (with their symbols) and their relationship to parameters, experimental data and coordinates. In this Table, the initial mass fraction distribution function X0(x), is defined by:

(49)

where g0(x) is given by Equation 42 and mm(x) = 14x + 2 is the molecular weight of species with index x.

- lumped mass fraction around index x with D x=0.5) }Parameters (b )e , h Independent Variable (molecule size)xEstimated Dependent Variable ( - lumped mass fraction around index x with D x=0.5) Replications (pi) 1 Scale Factor (ri) 10% of Z0(xi) (experimental) Weight Matrix (W) Diag (p1/r1 ... pn/rn) Fundamental Variance Estimator (S2y) (n: number of experiments)Confidence Region (p: number of parameters)Objective Function (F ) Min{}

Parameters (b )	e , h
Independent Variable (molecule size)	x
Estimated Dependent Variable ( - lumped mass fraction around index x with D x=0.5)
Replications (pi)	1
Scale Factor (ri)	10% of Z0(xi) (experimental)
Weight Matrix (W)	Diag (p1/r1 ... pn/rn)
Fundamental Variance Estimator (S2y) (n: number of experiments)
Confidence Region (p: number of parameters)
Objective Function (F )	Min {}

Table 3: Statistical entities in the fresh oil DCDF tuning.

Table 4 presents general results from the fitting process: the estimated parameters, the intrinsic variance estimator and the estimated parameter variance-covariance matrix. In Figure 3 the experimental compositional histogram for fresh oil is plotted against the estimated Z0(x). Figure 4 presents the parameter confidence region (for a confidence level of 99%) with dimensionless percentage scales.

Table 4: Statistical results in the fresh oil DCDF tuning.

1.0744	11.5212
	S2y = 0.0132

Figure 3:
Experimental compositional histogram versus estimated distribution (Z0(x)).

Figure 4:

Model Parameter Estimation

Model tuning via estimation of the three parameters (kcin, Gd, Nd) was accomplished with another maximum likelihood application (Peixoto, 1997). With the values of these parameters and with the fresh oil DCDF obtained in the previous fitting, the cracked oil DCDF can be generated at any (x, tf, g ) condition by Equations 18 and 48, allowing the subsequent estimation of any oil property. From Wojciechowski’s cracking data, the information for g = 0.0011 was selected as shown in Table 5.

tf (min)2.042.053.354.969.5617.9530.90N° of carbonsMass fractions (% w/w)60.87000.89000.95000.94001.18001.18001.320073.29003.27003.50003.82003.82003.66004.150087.01007.12007.85007.70007.81008.03008.6300910.730010.230010.800010.280010.650010.500010.62001012.120011.720012.110011.830012.170011.990012.01001111.950011.950012.050011.930012.070011.950011.92001211.060011.190011.050011.160011.230010.980010.9600139.77009.99009.71009.88009.88009.70009.5800148.29008.53008.26008.39008.37008.28008.1700157.12007.25006.97007.04007.03006.96006.9300165.92005.91005.85005.90005.77005.79005.6600174.90004.90004.79004.76004.64004.79004.6300183.56003.61003.40003.46003.27003.40003.2400192.35002.38002.15002.21001.99002.17001.9900201.13001.15000.90000.97000.70000.93000.7400

tf (min)	2.04	2.05	3.35	4.96	9.56	17.95	30.90
N° of carbons	Mass fractions (% w/w)
6	0.8700	0.8900	0.9500	0.9400	1.1800	1.1800	1.3200
7	3.2900	3.2700	3.5000	3.8200	3.8200	3.6600	4.1500
8	7.0100	7.1200	7.8500	7.7000	7.8100	8.0300	8.6300
9	10.7300	10.2300	10.8000	10.2800	10.6500	10.5000	10.6200
10	12.1200	11.7200	12.1100	11.8300	12.1700	11.9900	12.0100
11	11.9500	11.9500	12.0500	11.9300	12.0700	11.9500	11.9200
12	11.0600	11.1900	11.0500	11.1600	11.2300	10.9800	10.9600
13	9.7700	9.9900	9.7100	9.8800	9.8800	9.7000	9.5800
14	8.2900	8.5300	8.2600	8.3900	8.3700	8.2800	8.1700
15	7.1200	7.2500	6.9700	7.0400	7.0300	6.9600	6.9300
16	5.9200	5.9100	5.8500	5.9000	5.7700	5.7900	5.6600
17	4.9000	4.9000	4.7900	4.7600	4.6400	4.7900	4.6300
18	3.5600	3.6100	3.4000	3.4600	3.2700	3.4000	3.2400
19	2.3500	2.3800	2.1500	2.2100	1.9900	2.1700	1.9900
20	1.1300	1.1500	0.9000	0.9700	0.7000	0.9300	0.7400

Table 5: Kobolakis and Wojciechowski's cracked oil data for g = 0.0011.

Again, numerical nonlinear optimization was appropriately handled by using an objective function with a BFGS algorithm (Edgar and Himmelblau, 1988). Table 6 below presents the relevant statistical entities (with their symbols) and their relationship to model parameters, experimental data and coordinates. In this Table, the mass fraction distribution function after transformed time q , X(x,q (t)), is defined by:

(50)

Table 6: Statistical entities for model tuning.

Parameters (b )	kcin, Gd, Nd
Independent Variable	tf, g , x
Estimated Dependent Variable ( - lumped mass fraction around index x with D x=0.5, after reaction time tf)
Replications (pi)	1
Scale Factor (ri)	10% of (experimental)
Weight Matrix (W)	Diag (p1/r1 ... pn/rn)
Fundamental Variance Estimator (S2y) (n: number of experiments)
Confidence Region (p: number of parameters)
Objective Function (F )	Min {}

Table 7 presents general results from the fitting process: the estimated parameters, the intrinsic variance estimator, the converged matrix and the estimated parameter variance-covariance matrix. In Figures 5 and 6 the experimental compositional histogram (for tf = 2.04 min and tf = 30.90 min, respectively) is plotted versus the estimated Figures 7, 8 and 9 present bidimensional projections of the parameter hyperellipsoidal confidence region (for a confidence level of 99%) with dimensionless percentage scales.

Table 7: Statistical results for model tuning.

= 0.0051 kg cat/(kg oil-sec)					= 4.4140.10-4 seg-1
= 2.1742					S2y = 0.0153
H =	2.7355	-5.2357	3.3899	-0.7014		-0.3687	0.1160	0.0875	0.0071
	23.4661	-19.5005	-5.1492	1.6845		0.4420	-0.3896	-0.2228	-0.0832
	1.8761	32.3961	-10.2372	-11.9353		-4.5583	-1.2111	-0.6328	-0.3220
	-23.8678	-26.6629	34.1358	22.0223		4.6287	-0.9839	-0.7475	-0.4170
	57.8383	5.2951	-59.0711	-30.7419		-0.0740	7.3352	3.6625	1.5871
	-118.5952	53.7782	75.1490	43.7424		-8.0628	-17.5540	-8.6564	-2.5965
	242.3835	-228.9712	-27.8408	-79.9112		24.5924	28.4299	19.3452	3.3452

Figure 5:

Figure 6:

Figure 7:

Figure 8:

Figure 9:

As the reader can easily see upon inspection of Figures 7 to 9, the parameter confidence region has a very unfavorable nature due to its very large size (in percentage scales). This would mean that model parameters are statistically poorly defined as a consequence of the kind of data used and/or limitations in the underlying theory. Nevertheless, in the work of Kobolakis and Wojciechowski (1985) a classic kinetic lumped model had its parameters adjusted to similar experimental data and the authors observed an analogous lack of parameter definition, which made them state that "this is due to the fact that the functional relationships involved tend to have flat regions about the minimum." As occurred in the present work, the authors’ lumped model had also predicted the experimental results accurately, despite large uncertainties in the estimated parameter values.

SIMULATIONS

Catalytic cracking simulations may be carried out employing the estimated parameters and the results obtained with the model of this work. However, before that, the concept of cracking conversion must be introduced. This concept was defined by Kobolakis and Wojciechowski (1985) as the relative mass reduction of oil boiling above a given temperature. This is illustrated in Figure 10 where the conversion of oil with more than 15 carbon atoms is given by:

(51)

The time evolution of this conversion may also be depicted as a consequence of the time evolution of X(x,q (t)). Figure 11 illustrates the time behavior of conversion obtained with the estimated parameters. Figures 12 and 13 present graphic information for X(x,q ) model using the estimated information generated in this work.

Figure 10:

Figure 11:

Figure 12:

Figure 13:

RESULTS AND DISCUSSION

The model described exhibits a desirable algebraic flexibility with respect to the proposed KCDF and SCDF. It must be said, however, that numerical aspects were not taken into account in this analysis, but are addressed in Part II of this work. The qualitative analysis of model behavior by simulation was also satisfactory. The model can also predict typical experimental data accurately, even with great uncertainty in the estimated parameters. Considerations on this behavior were made in the regression section. The numerical scheme employed was also successful, decreasing asymptotically the residue generated as a consequence of series truncation.

NOMENCLATURE

B dimensionless constant (j r _v/r _cat) D(t) fraction of active catalytic sites g_n(x) perturbation function g(x,t) and g0(x) DCDF H coefficient matrix J Jacobian matrix of model response with respect to parameters k0 kinetic parameter kcin kinetic parameter (k0 b) kcin, Gd, Nd, md, kd model parameters K(x) DKCDF K(x,t) KCDF L_i(x) Laguerre polynomial n number of experiments p number of parameters p_I replications Pl_i(x) normalized Laguerre polynomial r_I scale factor R(x) residual vector S²_y fundamental variance estimator t catalyst age tf time on stream tf time of reactor operation ~ estimate of something v(x,y) SCDF W weight matrix Z0(x), Z(x) fraction of species near index x

Greek Letters

b parameters e , h gamma distribution parameters F objective function F _1-a Fisher coordinate at level (1 - a ) 100% and appropriate number of degrees of freedon f _i(x) orthonormal functions g catalyst/oil mass ratio G (x) gamma function j catalyst porosity q "crazy clock" time scale r _v, r _cat vapor and catalyst densities

REFERENCES

Aris, R., Reaction in Continuous Mixtures, AIChE J., 35, 539 (1989).

Astarita, G., and Ocone, R., Chemical Reaction Engineering of Complex Mixtures, AIChE J., 34, 1299 (1988).

Edgar, T. F. and Himmelblau, D. M., Optimization of Chemical Processes, McGraw Hill, Inc., New York (1988).

Himmelblau, D., Process Analysis by Statistical Methods, John Wiley, New York (1970).

Ho, T. C. and Aris, R., On Apparent Second-Order Kinetics, AIChE J., 33, 1050 (1987).

Jacob, S. M.; Gross, B.; Voltz, S. E. and Weekman, V. W., A Lumping and Reaction Scheme for Catalytic Cracking, AIChE J., 22, 701 (1976).

Kobolakis, I. and Wojciechowski, B. W., The Catalytic Cracking of a Fisher-Tropsch Synthesis Product, The Can. Jour. of Chem. Eng., 63, 269-287 (1985).

Kreyszig, E., Introductory Functional Analysis with Applications , John Wiley, New York (1978).

Laxminarasimhan, C. S.; Verma, R. P. and Ramachandran, P. A., Continuous Lumping Model for Simulation of Hydrocracking, AIChE J., 42, 2645 (1996).

Madras, G.; Chung, G. Y.; Smith, J. M. and McCoy, B. J., Molecular Weight Effect on the Dynamics of Polystyrene Degradation, Ind. Eng. Chem. Res., 36, 2019 (1997).

McCoy, B. J. and Wang, M., Continuous-Mixture Fragmentation Kinetics: Particle Size Reduction and Molecular Cracking, Chem. Eng. Sci., 49, 3773 (1994).

McCoy, B. J., Continuous Kinetics of Cracking Reactions: Thermolysis and Pyrolisis, Chem. Eng. Sci., 51, 2903 (1996).

Nace, D. M.; Voltz, S. E. and Weekman, V. W., Application of a Kinetic Model for Catalytic Cracking, Ind. Eng. Chem. Proc. Des. Develop., 10, 530 (1971).

Nayfeh, A. H., Introduction to Perturbation Techniques , John Wiley & Sons, New York (1981).

Prasad, G. N.; Wittman, C. V.; Agnew, J. B. and Sridhar, T., Continuous Reaction Mixture Model for Coal Liquefaction, AIChE J., 32, 1277 (1986).

Peixoto, F. C., Modelagem Contínua para Craqueamento Catalítico de Frações de Petróleo , D.Sc. qualifying, Escola de Química, Universidade Federal do Rio de Janeiro (UFRJ), (1997).

Peixoto, F. C., Modelagem e Estimação de Parâmetros em Misturas Contínuas com Reações Químicas, M.Sc. thesis, Escola de Química, Universidade Federal do Rio de Janeiro (UFRJ), (1996).

Wang, J. M. M. and McCoy, B. J., Continuous Kinetics for Thermal Degradation of Polymer in Solution, AIChE J., 41, 1521 (1995).

Weekman, V. W., Lumps, Models and Kinetics in Practice, Chem. Eng. Prog. Monogr. Ser., 75(11) (1979).

Wojciechowski, B. W., Experimental Data for the Catalytic Cracking of a Fisher-Tropsch Synthesis Product, personal communication (1996).

Wylie, C. R. and Barrett, L. C., Advanced Engineering Mathematics, 6th ed., McGraw Hill, Inc., New York (1985).

Publication Dates

• Publication in this collection
  23 Apr 1999
• Date of issue
  Mar 1999

History

• Accepted
  03 Mar 1999
• Received
  04 June 1998