Abstract
It is suggested a general mechanism through which a lambda-type behavior is produced in the specific heat of a Bose gas near the critical temperature Tc . It is essential that the quasiparticle spectra have a gap proportional to the condensate. It works for a general class of quasiparticle spectra, and in particular, for the weakly interacting Bose gas. The introduction of a chemical potential in the theory is briefly discussed.
l - type phase transition for a weakly interacting bose gas
I. Cabreraa,b, D. Olivaa,b and H. Pérez Rojasa,b,c
aInternational Centre for Theoretical Physics,
P.O. Box 586 34100 Trieste, Italy
b Grupo de Fisica Teórica, ICIMAF,
Calle E No. 309, Vedado, La Habana 4, Cuba
c Helsinki Institute of Physics,
P.O. Box 9 (Siltavuorenpenger 20C), FIN-00014, University of Helsinki, Finland
Received on 22 November, 1999
It is suggested a general mechanism through which a l-type behavior is produced in the specific heat of a Bose gas near the critical temperature Tc . It is essential that the quasiparticle spectra have a gap proportional to the condensate. It works for a general class of quasiparticle spectra, and in particular, for the weakly interacting Bose gas. The introduction of a chemical potential in the theory is briefly discussed.
I Introduction
In his book on Statistical Mechanics, [1] Feynman refers to the l point behavior and expresses his view that perhaps part of the explanation of the l transition involves Bose condensation. One interesting model of the l behavior is the one presented by Ceperley [2], but in it the boson system is simulated by means of Monte Carlo techniques using path integrals. However, although the analytic behavior of the specific heat in a neighborhood of the critical temperature is provided by renormalization group methods, which gives an accurate description of the l behavior (see i.e. [3]), we are not aware of any model exhibiting the mechanism through which the condensate induces the divergence of the specific heat cv at Tc. There are two phenomena which are expected to be explained by a satisfactory model of the weakly interacting bose gas: 1) the existence of a gapless mode, which is more manifest at T = 0, and 2) the l behavior, which would appear at finite temperatures. In our opinion both phenomena must be manifest even at the one-loop level, as it is in the relativistic models we mention below, but which is not the case in the usual non-relativistic model, i.e., the l behavior cannot be found by using the Bogoliubov's spectrum [4] for the weakly interacting Bose gas near T = 0 by taking it as valid at temperatures near the critical point.
Our aim is to show that if the bosonic quasiparticle spectra has a gap proportional to the condensate, a divergence in cv appears at the transition temperature, and that this is the case for the weakly interacting Bose gas near the critical temperature.
First of all, we wish to remind the simple model of the temperature self-interacting scalar one-component field f with Z2 symmetry breaking x = áfñ in relativistic quantum statistics [5]. Here the symmetry breaking parameter plays the role of a field condensate. The effective potential is V(x, T) =  + V1(T, x), where l
+ V1(T, x), where l is the coupling constant, -a2 is the negative mass term and V1(T, x) is the sum of T-dependent tadpole diagrams. On the mass shell V(xc, T) =W is the thermodynamical potential, xc being the extremum of V(x, T), where the spectrum is
is the coupling constant, -a2 is the negative mass term and V1(T, x) is the sum of T-dependent tadpole diagrams. On the mass shell V(xc, T) =W is the thermodynamical potential, xc being the extremum of V(x, T), where the spectrum is  (p) =
(p) =  , M = 2l1xc.
, M = 2l1xc.
In the high temperature limit one has V1(T, x) = l T2x2/8, the extremum of V(x, T) leading for T < Tc to a temperature-dependent mass M(T) = l1
T2x2/8, the extremum of V(x, T) leading for T < Tc to a temperature-dependent mass M(T) = l1 , Tc = 4a2/l
, Tc = 4a2/l being the critical temperature for symmetry restoration. The infrared contribution to the thermodynamical potential in the limit T
being the critical temperature for symmetry restoration. The infrared contribution to the thermodynamical potential in the limit T 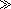 M(T) is DW
M(T) is DW 
 . One obtains then a specific heat Dcv = -T
. One obtains then a specific heat Dcv = -T
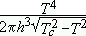 which diverges as t-1/2, t = |1 - T/Tc|, for T ® Tc, showing a l-type behavior. This expression shows that the divergence appears already at the one-loop approximation of cv, although it is quantitatively satisfactory for t
which diverges as t-1/2, t = |1 - T/Tc|, for T ® Tc, showing a l-type behavior. This expression shows that the divergence appears already at the one-loop approximation of cv, although it is quantitatively satisfactory for t 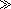 l1 [6], since in the region closer to Tc, the contribution from higher loops must be considered. In that region, renormalization group techniques gives an universal expression for the divergence as t-a, where a < 1/2 .
l1 [6], since in the region closer to Tc, the contribution from higher loops must be considered. In that region, renormalization group techniques gives an universal expression for the divergence as t-a, where a < 1/2 .
In the two component scalar field case, having U(1) symmetry, two modes appear after the symmetry breaking, the massive  1(p) = c
1(p) = c , M = 2l1xc, and the massless
, M = 2l1xc, and the massless  2(p) = pc. The contribution to the thermodynamic potential infrared term is the same as in the previous case (the massless term does not contribute), and cv diverges as t-1/2.
2(p) = pc. The contribution to the thermodynamic potential infrared term is the same as in the previous case (the massless term does not contribute), and cv diverges as t-1/2.
Actually, both in the relativistic and non-relativistic cases, with spectra
r =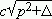 , and n = p2/2m + D, respectively. By taking some characteristic small momentum p0 and introducing x = cp/T, calling h = cp0/T, it is easy to see that there is a common infrared contribution to W ~ -AT5/2ò
, and n = p2/2m + D, respectively. By taking some characteristic small momentum p0 and introducing x = cp/T, calling h = cp0/T, it is easy to see that there is a common infrared contribution to W ~ -AT5/2ò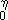 x4dx/[x2 + DT-1] ~ A¢TD3/2, where the mass (gap) D ~ b[1 - (T/Tc)g ], g > 1, and A, A¢, b being constants. Then one can state as a theorem that for T ® Tc , the one-loop thermodynamic potential obtained from such spectra leads to a divergent cv behavior as ~ D-1/2.
x4dx/[x2 + DT-1] ~ A¢TD3/2, where the mass (gap) D ~ b[1 - (T/Tc)g ], g > 1, and A, A¢, b being constants. Then one can state as a theorem that for T ® Tc , the one-loop thermodynamic potential obtained from such spectra leads to a divergent cv behavior as ~ D-1/2.
In the relativistic limit this comes from (A contains a factor  -3 ):
-3 ):
The the infrared limit of the last expression is
This means that near Tc
From cV = -T , we get that cV diverges as D-1/2.
, we get that cV diverges as D-1/2.
In the non-relativistic case we have a similar formula, by taking x = p/ , since
, since
from which we get the same behavior near Tc.
It is expected that any system having a spectrum of similar infrared properties than the previous ones, would have also a specific heat having an infinite behavior at the critical point. We would like to show that such is the case of the Bogoliubov model of the weakly interacting Bose gas near the critical point. It contains a gap due to the condensate, which leads to a divergence in the specific heat (in the region T/Tc < 1), already at the one-loop approximation.
II Bogoliubov Hamiltonian near the critical point
We will start from the quantized Hamiltonian for a weakly interacting Bose gas expanded in terms of the elementary creation and annihilation operators for spinless boson fields, we shall assume momentum conservation in the interactions and call U(r) the repulsive potential of the two body interaction, U = òòd3re
= òòd3re U(r). For p = 0 (zero momentum transfer in the collision) Uo = òd3rU(r). In the temperature interval we are considering the momenta are very small and we can assume that the momentum transfer in each collision is almost zero, p
U(r). For p = 0 (zero momentum transfer in the collision) Uo = òd3rU(r). In the temperature interval we are considering the momenta are very small and we can assume that the momentum transfer in each collision is almost zero, p  0. For that reason it is possible to express approximately the matrix elements by using Uo. The scattering length can be written then as a =
0. For that reason it is possible to express approximately the matrix elements by using Uo. The scattering length can be written then as a =  U0, and a > 0 since the potential is repulsive.
U0, and a > 0 since the potential is repulsive.
We shall assume the conditions a/l  1 and ra3
1 and ra3 1 where l is the thermal de Broglie wavelength and r = N/V the particle density. Then, by starting from the fact that the occupation number of the ground state n0 is a large number, we will write ao =
1 where l is the thermal de Broglie wavelength and r = N/V the particle density. Then, by starting from the fact that the occupation number of the ground state n0 is a large number, we will write ao =  eiq, a
eiq, a =
=  e-iq. From this we would get an infinite set of (non-equivalent) representations as a consequence of breaking the first order gauge symmetry [7] y(x) ® eiay(x) (y(x) = V-1/2åeikxak), and we take the physical representation as the one with q = 0 which leads to,
e-iq. From this we would get an infinite set of (non-equivalent) representations as a consequence of breaking the first order gauge symmetry [7] y(x) ® eiay(x) (y(x) = V-1/2åeikxak), and we take the physical representation as the one with q = 0 which leads to,
We assume conservation of the total number of particles N and then åp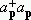 + n0 = N. The usual procedure for T® 0, by following Bogoliubov [8] [9] (see also [10]), assuming that å
+ n0 = N. The usual procedure for T® 0, by following Bogoliubov [8] [9] (see also [10]), assuming that å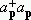 = ånp
= ånp
 by [N - å
by [N - å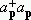 ]2 in the first and n0 by N in the third term, which leads to the cancellation of a term
]2 in the first and n0 by N in the third term, which leads to the cancellation of a term 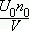 å
å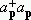 in the last term in curly brackets of (5). This means to neglect one term of second order in ånp, the number of excited particles. But if ånp» N, one cannot neglect the term (ånp)2 = å
in the last term in curly brackets of (5). This means to neglect one term of second order in ånp, the number of excited particles. But if ånp» N, one cannot neglect the term (ånp)2 = å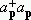
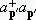 . This is the case for temperatures near and below the transition point, and even for very low temperatures; e.g., as in the case n0N/2, ånpN/2. Thus, we keep n0(T) explicit in our formulae as a quantity decreasing with increasing temperature. We conclude that Bogoliubov' gapless spectrum is an approximation valid actually for T = 0 , for almost all the system in the condensate.
. This is the case for temperatures near and below the transition point, and even for very low temperatures; e.g., as in the case n0N/2, ånpN/2. Thus, we keep n0(T) explicit in our formulae as a quantity decreasing with increasing temperature. We conclude that Bogoliubov' gapless spectrum is an approximation valid actually for T = 0 , for almost all the system in the condensate.
In our present approach the last term in (5) accounts for the energy due to the interactions of particles with momenta p ¹ 0. Since we are considering an interval of temperatures very near (but below) the transition temperature, we assume that such term is approximately constant and take it as EN=O(U0N2/2V). Then the problem we are left with is the diagonalization of the sum of the second and third terms in (5). Our assumptions are valid for a wide range of values of n0 (if N  1023 our approximation is good up to, say, n0
1023 our approximation is good up to, say, n0 1021). Thus, we keep our calculations in the one-loop approximation and in terms of n0 and when compared with the standard Bogoliubov's model [8] it differs in the coefficient of the last term in curly brackets, which is changed from 2 to 4. The next step is to make the usual Bogoliubov's canonical transformation ap = (bp - apb
1021). Thus, we keep our calculations in the one-loop approximation and in terms of n0 and when compared with the standard Bogoliubov's model [8] it differs in the coefficient of the last term in curly brackets, which is changed from 2 to 4. The next step is to make the usual Bogoliubov's canonical transformation ap = (bp - apb
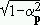 and a
and a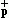 =(b
=(b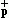 -apb-p)/
-apb-p)/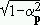 as a result of which we obtain the diagonalized Hamiltonian,
as a result of which we obtain the diagonalized Hamiltonian,
where Eo =  [no2 - no] -
[no2 - no] - 
 ap and ap =
ap and ap =  [4
[4 +
+  - e(p)], and if we denote by K =
- e(p)], and if we denote by K =  , then
, then
is the spectrum of the new Bose quasiparticles representing the elementary excitations of the system, where b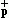 ,bp are their creation and annihilation operators. The limit T® 0 does not lead to Bogoliubov's spectrum, in which the gap term 2
,bp are their creation and annihilation operators. The limit T® 0 does not lead to Bogoliubov's spectrum, in which the gap term 2 K is absent, since both models correspond to different approximations. Actually, having only one mode, the present model bears in this respect more resemblance with the Z2 case than with the U(1) one. In our model the long wavelength limit is obviously not linear in p, as it is usually. We may argue that our limit is not T ® 0 and also that its small value probably makes difficult to identify it among the experimental errors for p ® 0 near Tc. Actually, as K
K is absent, since both models correspond to different approximations. Actually, having only one mode, the present model bears in this respect more resemblance with the Z2 case than with the U(1) one. In our model the long wavelength limit is obviously not linear in p, as it is usually. We may argue that our limit is not T ® 0 and also that its small value probably makes difficult to identify it among the experimental errors for p ® 0 near Tc. Actually, as K  kT is very small (for n0
kT is very small (for n0 1020, K
1020, K  10-12 eV) it can be usually neglected, but it is able to produce the macroscopic effect of a typical l-type divergent specific heat near Tc. As limp® 0 e(p)=2
10-12 eV) it can be usually neglected, but it is able to produce the macroscopic effect of a typical l-type divergent specific heat near Tc. As limp® 0 e(p)=2 K, the gap parameter K formally behaves as the analog of a rest energy in relativistic dynamics. This gap has the property that it decreases with temperature and goes to zero, as well as E0, ap, for T ® Tc.
K, the gap parameter K formally behaves as the analog of a rest energy in relativistic dynamics. This gap has the property that it decreases with temperature and goes to zero, as well as E0, ap, for T ® Tc.
Below we will calculate the thermodynamic potential by taking the chemical potential m = 0 by assuming that the number of quasiparticles nq = åpb
bp is not conserved (See, however, next section). The term K is proportional to n0, the eigenvalue of a0 with regard to the coherent ground state. In our present approximation, the quasi-particles are actually massive since their effective mass is m* = [¶2e(p)/¶p2]-1|p=0 =  m/4. An explicit computation of cv showing the divergent behavior close to the critical temperature is easily done by doing first the temperature expansion of the thermodynamic potential of the quasiparticles by taking the spectrum (7).
m/4. An explicit computation of cv showing the divergent behavior close to the critical temperature is easily done by doing first the temperature expansion of the thermodynamic potential of the quasiparticles by taking the spectrum (7).
Due to the interaction term, the ground state energy E0 is different from zero,
where E, F are the usual elliptic integrals.
III The specific heat
We will calculate the thermodynamical potential of the quasiparticles W . The total energy is then U = E0 + EN - T(¶W/¶T) + W. We will do also the asymptotic expansion of W close to Tc for T < Tc. By changing to the variable x =  it reads W =
it reads W = 
 dxx2 ln[1-e-
dxx2 ln[1-e- ], where M = Kb
], where M = Kb  1 and we obtain an expansion in terms of it, in the same way done in the case of the effective potential in the temperature scalar model [5]. After some calculations which we outline in the appendix (these are given in detail in [11]), the perturbative expansion of W in powers of K is obtained, and from it the specific heat is given by cv =
1 and we obtain an expansion in terms of it, in the same way done in the case of the effective potential in the temperature scalar model [5]. After some calculations which we outline in the appendix (these are given in detail in [11]), the perturbative expansion of W in powers of K is obtained, and from it the specific heat is given by cv =  - T
- T as,
as,
Here a = ( )(
)( ). The last term diverges at Tc. We shall write no = Nf(T) where f(T) = (1 - Ne/N) and Ne is the density of particles not in the ground state. By starting from Np = nq(1 + a
). The last term diverges at Tc. We shall write no = Nf(T) where f(T) = (1 - Ne/N) and Ne is the density of particles not in the ground state. By starting from Np = nq(1 + a )/(1 - a
)/(1 - a ) + a
) + a /1 - a
/1 - a , [12] the expression for Ne =
, [12] the expression for Ne =  -3ò d3pNpis given in the Appendix as an expansion similar to the one for W. Under the assumption Kb
-3ò d3pNpis given in the Appendix as an expansion similar to the one for W. Under the assumption Kb  1, the leading terms are
1, the leading terms are
where Ne0 = AT3/2 and A = (2pmk/h2)3/2z(3/2), C = p1/2( )AK1/2/k1/2z(3/2). This equation for Ne is to be solved by iteration, by taking in M as a first approximation f(T) = [1 - Ne0/N]. It must be observed that as T decreases, the rate of condensation in (10) is stronger than for the ideal gas. We will take N = ATc3/2. By evaluating (9) with helium parameters and taking the scattering length as a = 10-10 cm, the curve for cv(T) defined in the region T £ Tc is depicted in Fig. 1. Then an infinite l-type behavior of cv(T) similar to the scalar field case results. Such a behavior cannot be obtained by using the usual Bogoliubov's spectrum [4].
)AK1/2/k1/2z(3/2). This equation for Ne is to be solved by iteration, by taking in M as a first approximation f(T) = [1 - Ne0/N]. It must be observed that as T decreases, the rate of condensation in (10) is stronger than for the ideal gas. We will take N = ATc3/2. By evaluating (9) with helium parameters and taking the scattering length as a = 10-10 cm, the curve for cv(T) defined in the region T £ Tc is depicted in Fig. 1. Then an infinite l-type behavior of cv(T) similar to the scalar field case results. Such a behavior cannot be obtained by using the usual Bogoliubov's spectrum [4].
cv/Nk-curve obtained from our model, where the l shape is shown. For T > Tc the ideal gas curve has been drawn for comparison.
The more exact part of the cv curve lies in the region near and below Tc since we assumed EN constant and Kb  1. But the last condition is valid even for very low T and EN decreases to small values as T ® 0. Thus, the cv curve drawn is approximately valid even in that region. The behavior of cv for T > Tc is beyond the scope of the present letter. Such problem must be investigated by starting from an adequate model of imperfect gas in the region T ³ Tc[13].
1. But the last condition is valid even for very low T and EN decreases to small values as T ® 0. Thus, the cv curve drawn is approximately valid even in that region. The behavior of cv for T > Tc is beyond the scope of the present letter. Such problem must be investigated by starting from an adequate model of imperfect gas in the region T ³ Tc[13].
IV The introduction of a chemical potential
The absence of a second (gapless) Goldstone mode does not mean an incompleteness of our model, since although we are dealing with a two-dimensional problem, the present representation behaves as similar to the one-dimensional scalar case seen in the Introduction, whose spectrum bears a gap. On the other hand, an investigation of the Bose gas by using the Green's function method made by Beliaev [14] leads to the usual Bogoliubov spectrum in terms of n0 at strictly T = 0. However, this is made by introducing a chemical potential m, which loses its usual meaning, since the calculation of the Green functions by starting from a density matrix, demands commutation between the Hamiltonian H and the number N of excited particles, which is not the case since the quasiparticle number is not conserved. If m = 0 in [14] our spectrum is reproduced, and the gap cannot be erased in higher loop calculations.
The papers [14] were written before the formulation of Goldstone theorem [15], which lead to a better understanding of the theory of spontaneous symmetry breaking. Actually, Beliaev results are based in the same operator algebra representation used by Bogoliubov, and describe the existence of only one mode, which is gapless. It misses a second mode having a gap, which is expected to appear in usual U(1) gauge invariant models with spontaneous symmetry breaking, as was pointed out in the Introduction. If the chemical potential is understood not in the usual sense, but as a parameter introduced before the breaking of the symmetry, one finds that the representation used by Beliaev is not the unique one: there is a set of infinite unequivalent ones, which is typical of the spontaneously broken symmetry case [7]. One of these is being investigated by two of the present authors (D.O. and H.P.R.) for the temperature case. In it, as in the U(1) scalar relativistic model considered in the introduction, a two mode spectrum is found. One of them is a gapless Goldstone mode and the other one has a gap, the later producing a lambda behavior in the specific heat. Work in this problem is in progress.
V Conclusions
In relativistic models of a scalar bose gas with symmetry breaking, it is found a divergent behavior of the specific heat at the one loop level of the thermodynamic potential, which comes from the temperature dependent mass (gap) in the spectrum, which is consistent qualitatively with renormalization group predictions. By analogy, we consider the usual Bogoliubov model near the critical temperature for the phase transition, and a gap is shown to be present, leading to a divergence in the specific heat. We discussed briefly the introduction of a chemical potential in the model, as done in Beliaev procedure [14], and the absence of a Goldstone mode. We conclude that the model we have discussed, although not being perhaps the final one, is an step towards it, since it is able to describe the property of lambda behavior in the non-ideal Bose gas.
Acknowledgments
The authors would like to thank Professor M. Virasoro, IAEA and UNESCO for hospitality at the International Centre of Theoretical Physics. All authors thank A. Amezaga, A. Cabo, S. Fantoni, S. Giovannazi, F. Hussain, G. A. Mezincescu, C. Montonen, K. Narain A. Polls, A. Smierzi and R. Sorkin for valuable comments and suggestions. H.P.R. would like to thank his former student R. Torres Rivero for having called his attention to the possible relation of the l -type spectrum with some temperature-dependent mass model, and M. Chaichian for several illuminating discussions and hospitality in the High Energy Physics Division, Department of Physics, University of Helsinki. The partial support of the Academy of Finland under Project No. 163394 is greatly acknowledged.
VI Appendix
To make an asymptotic expansion of W in terms of M = Kb, we write W = W(0) +  |M=0M + R(M) , where we stop our expansion in the first-order term and R(M) is certain function of M which we are going to find out by using R(M) = W(M) - W(0) -
|M=0M + R(M) , where we stop our expansion in the first-order term and R(M) is certain function of M which we are going to find out by using R(M) = W(M) - W(0) -  |M=0M and
|M=0M and  =
=  -
-  |M=0. Then
|M=0. Then
from which  |M=0 = 4(2m)3/2VG(3/2)z(3/2)/b5/2
|M=0 = 4(2m)3/2VG(3/2)z(3/2)/b5/2
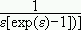 =
= 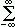
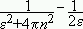 , and performing the adequate regularizations, we get finally (see also [11]),
, and performing the adequate regularizations, we get finally (see also [11]),
By a similar procedure,we get,
References
[1] R.P. Feynman, Statistical Mechanics Benjamin, Reading, Mass. (1982).
[2] D.M. Ceperley, Rev. Mod. Phys. 67, 2 (1995).
[3] J.A. Lipa, D.R. Swanson, J.A. Nissen, T. P. Chuy and U.E. Israelsson, Phys. Rev. Lett. 76, 944 (1996).
[4] K. Huang, in Bose-Einstein Condensation, Edited by A. Griffin, D.W. Snoke and S. Stringari, Cambridge University Press (1995).
[5] L. Dolan and R. Jackiw, Phys. Rev. D9, 3320 (1974).
[6] D.A. Kirzhnits and A.D. Linde, Ann. Phys. 101, 195 (1976).
[7] F. Strocchi, Elements of Quantum Mechanics of Infinite Degrees of Freedom, World Scientific, Singapore (1985).
[8] R. K. Pathria, Statistical Mechanics, Pergamon Press (1972).
[9] N. N. Bogoliubov, J. Phys. USSR 11, 23 (1947).
[10] K.A. Brueckner and K. Sawada, it Phys. Rev. 106, 1117 (1957)
[11] I. Cabrera and H. Perez Rojas, Cond-mat 9797044
[12] L.D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press (1966).
[13] A.L. Fetter and J.D. Walecka,Quantum Theory of Many Particle Systems, Mc Graw Hill Book Co, (1972).
[14] S.T. Beliaev, JETP 34 , 289 (1958); JETP 34 , 299 (1958).
[15] J. Goldstone, Nuovo Cimento 25, 154 (1961).
- [1] R.P. Feynman, Statistical Mechanics Benjamin, Reading, Mass. (1982).
- [2] D.M. Ceperley, Rev. Mod. Phys. 67, 2 (1995).
- [3] J.A. Lipa, D.R. Swanson, J.A. Nissen, T. P. Chuy and U.E. Israelsson, Phys. Rev. Lett. 76, 944 (1996).
- [4] K. Huang, in Bose-Einstein Condensation, Edited by A. Griffin, D.W. Snoke and S. Stringari, Cambridge University Press (1995).
- [5] L. Dolan and R. Jackiw, Phys. Rev. D9, 3320 (1974).
- [6] D.A. Kirzhnits and A.D. Linde, Ann. Phys. 101, 195 (1976).
- [7] F. Strocchi, Elements of Quantum Mechanics of Infinite Degrees of Freedom, World Scientific, Singapore (1985).
- [8] R. K. Pathria, Statistical Mechanics, Pergamon Press (1972).
- [9] N. N. Bogoliubov, J. Phys. USSR 11, 23 (1947).
- [10] K.A. Brueckner and K. Sawada, it Phys. Rev. 106, 1117 (1957)
- [12] L.D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press (1966).
- [13] A.L. Fetter and J.D. Walecka,Quantum Theory of Many Particle Systems, Mc Graw Hill Book Co, (1972).
- [14] S.T. Beliaev, JETP 34 , 289 (1958);
- JETP 34 , 299 (1958).
- [15] J. Goldstone, Nuovo Cimento 25, 154 (1961).
Publication Dates
-
Publication in this collection
23 Apr 2002 -
Date of issue
Dec 2001
History
-
Received
22 Nov 1999
















