Some unusual algebraic structures and their applications in many-body problems

Some unusual algebraic structures and their applications in many-body problems

S. S. Avancini^*

Departamento de Física, Universidade Federal de Santa Catarina Campus Trindade, C.P. 476, Florianópolis, SC, Brazil, CEP 88.040-900

ABSTRACT

In this paper, we introduce the q-deformed and quon algebras formalism. Some applications of these algebraic structures are considered. A possible connection of the quon algebra with composite particle systems is discussed and perspectives on using such mathematical objects in the Bose-Einstein condensation is presented.

I Introduction

The identification of algebraic structures in quantum physical systems has been an important tool for their understanding. Concepts of symmetry, invariance and group theory have shown to be of great utility from the beginning of quantum mechanics[1]. In a more recent context some unusual algebraic structures related to quantum inverse scattering methods and statistical mechanics models have appeared[2]. These algebraic structures are usually called q-algebras, q-deformed algebras or quantum groups. In current theoretical investigations there have been extensive applications of q-algebras to many branches of physics[3,4,5]. In a sense, many successful standard applications of group theory in the past may be extended to a quantum group symmetry. The aim of this paper is to discuss the use of q-algebras in the framework of many-body problems. We introduce the mathematical fundamentals as simply as possible and consider applications to q-deformed pseudo-spin models. These models can be considered as convenient theoretical laboratories where one can test the properties of these algebraic structures. We also show that the q-algebra formalism may be useful in the context of boson mappings,i. e., when the substitution of fermion pairs by bosons is convenient. A q-deformed algebra has a closely related algebraic structure which is called the quon algebra[6,7]. Such algebra was proposed to describe particles that violate statistics by a small amount. We consider the applications of quon algebras in boson mappings and nuclear models. We also show that they may be relevant in the study of composite bosonic particles (particles composed by fermion pairs), since deviations of a true bosonic particle could be accommodated in a natural way through the quon algebra. This formalism can also be applied to the study of Bose-Einstein condensation in trapped atoms[8]. This paper is organized as follows: In Sec.II quantum groups or q-algebras are defined and some of their properties and applications are analysed, in Sec.III the quon algebra formalism is considered and ,finally, in Sec.IV we present our conclusions.

II q-deformed algebras or quantum groups

The q-algebras or quantum groups are generalizations of classical Lie groups and Lie algebras and involve two fundamental ideas: Deformation and Non-commutative co-multiplication[5]. Next, these two concepts will be discussed in detail.

A. q-deformed objects

A q-boson algebra[9,10] (deformed harmonic oscillator) is a set of elements called q-boson operators: a (annihilation), a^† (creation), N (number), which satisfy the following commutation relations:

Note that the first and second commutation relations are equal to the common harmonic oscillator, however, the third depends on the parameter q and only when q = 1 we recover the ordinary harmonic oscillator algebra. Above, we have defined the q-commutator as

This definition will be often used in this work. Although eq. (2) is valid for any q, we consider only q real or q a root of unit, in order for the following hermitian conjugation to hold:

a^†= a, N^†= N.

Let us see now the consequences of the q-commutation relation. It follows from the q-commutation between a and a^† given in eq.(1) that:

and also:

where we have defined the very important object q-number or q-square brackets as:

Note that N differs from a^†a and [x]_q goes to x when q goes to 1. It is useful to notice that the the q-boson operators can be expressed in terms of ordinary boson operators[4]. If b and b^† are ordinary boson operators, where [b,b^†] = b b^†-b^†b = 1 and N = b^†b, then one can show that a and a^† can be written in terms of b and b^† through the relations:

The Fock space is constructed by allowing polynomials in the creation operator to act on the vacuum:

One can show that the action of the operators on the basis is given by

We remark that these equations are very similar to the ones of the ordinary case, the only difference being the q-number appearing under the square roots instead of common numbers.

B. q-Deformed harmonic oscillator

Analogously to the ordinary oscillator, the Hamiltonian of the q-deformed harmonic oscillator is defined as:

In this last equality, we have used the expressions for aa^† and a^† a given in eqs.(3,4). Since this Hamiltonian operator is diagonal in the basis |nñ, the spectrum can be easily found:

In eq.(9), we had only to substitute the operators N and N+1 in square brackets by the q-numbers [n] and [n+1] respectivelly.

We will show now the physical meaning of the deformation of the oscillator.

In Fig.1, we can see that for the ordinary oscillator (q = 1) the spectrum is evenly spaced, however, for the deformed one (q ¹ 1) the spectrum has different spacings, being uncompressed for real q and having the opposite behavior for q a root of unity. To understand this behavior, we take q as being equal to e^t and we assume that t is small, so up to the first order in the t parameter: q = e^t @ 1+t. Firstly substituting in the oscillator energy, eq.(10), the q numbers n and n+1 by their explicit expressions, results in

and secondly substituting q by 1+t and keeping only terms up to the second order in t we arrive at:

These expressions show that the deformed oscillator is not harmonic and the frequency in not w₀. Notice that the effect of deformation is to produce:

• Anharmonic Spectrum (nonlinear oscillator)

• Shift in Frequency

This can be useful in applications. Now we will define another example of a q-deformed algebra.

C. The quantum group su_q(2) or the deformed angular momentum algebra

It is generated by the operators J_±, J₀ satisfying the commutation relations:

[J₀ ,J_±] = ±J_±

and

One can define analogously to the ordinary case, the Casimir Invariant as:

This operator commutes with all the generators of the algebra,

[J²,J_±] = [J²,J₀] = 0 .

Of course, when q® 1 Þ su_q(2)®su(2), i. e., we recover the ordinary su(2) algebra. We can construct the irreducible representations of su_q(2) using a method very similar to the commonly used for su(2)[3,10,9]. Denoting the basis states by {|jmñ}, where m runs from j up to -j, the matrix elements of the generators are given by following expressions:

These expressions are very similar to those commonly used, the only difference is the presence of q numbers. Until now we have been discussing deformation. Next we will turn to the second important concept of the quantum algebra formalism, The co-multiplication concept. We will introduce the co-multiplication through the q-deformed angular momentum algebra addition.

D. q-deformed angular momentum addition

In ordinary quantum mechanics when we add angular momenta we use an action on product kets. If

_total =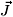 (1,2) = 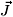(1)+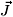(2) stands for the total angular momenta of two independent systems, thus its action on the ket |yñ = |yñ₍₁₎Ä|yñ₍₂₎ may be written more precisely as

this defines a commutative co-multiplication D:

Of course,

_total, also generates an su(2) algebra.

Let us consider the generalization for quantum groups.

If we calculate the commutator between J₀(1,2) and J_±(1,2) then

[J₀(1,2) ,J_±(1,2)] = J_±(1,2).

Therefore everything is fine, but calculating the commutator between J₊(1,2) and J–(1,2),

So, the commutator [J₊(1,2),J–(1,2)] differs from [2J₀(1,2)]. This is due to the following property of q numbers: [x]+[y] ¹ [x+y]. Hence, the J₀(1,2) , J_±(1,2) above defined do not satisfy the commutation relations of su_q(2). The correct q-deformed total angular momenta operators have to be equal to these:

the main difference compared to the usual case, is the non-commutative co-multiplication, defined through the formula:

D(J_± ) = J_±Äq^J0 + q^-J0ÄJ_± .

This is an essential feature of q-angular momenta. It means that the addition of q-angular momenta depends on the order. So we have to deal with q-deformed Clebsh-Gordan Coefficients[11,12]:

Next, we will discuss briefly some possible applications

E. Applications

a) Rotational spectra of pair-pair Nuclei

One can use the q-rotor to describe the rotational nuclear spectra of pair-pair nuclei[4]. The following expression defines the q-rotor:

The spectrum follows on from the previous expressions noticing that the q-rotor hamiltonian is determined by the su_q(2) Casimir invariant. From eqs.(13-14) it follows:

The above expression differs from the pure rotor through the q-numbers [j] and [j+1] instead of j and j+1. One can compare the q-rotor with the Variable Moment of Inertia Model (VMI) model[13]. In the VMI the energy is given through the expression:

where K and q₀ are free parameters and q(j) is determined from:

Note that in the VMI the moment of inertia is not rigid. It is given as a function of the angular momentum j and the spectrum is determined minimizing the energy as a function of q. An important point to stress is that: for the q-rotor and VMI we obtain similar expansions in terms of j:

E_j = E₀+Aj(j+1) + B(j(j+1))² + C(j(j+1))³ + ... .

So stretching effects can be taken into account by the deformation[4].

b) Vibrational and Rotational Spectra of Molecules

The q-deformed rotor and oscillator can be used in the description of the energy spectrum of atoms and molecules. Details can be found in [4]

c) Pseudo-Spin Models: Lipkin, Pairing, Moszkowski, etc

In order to understand the physical meaning of the q-deformation the deformed Lipkin model has been proposed in ref.[14]. In general, pseudo-spin models can be considered as laboratories where the properties of q-deformed models can be studied since they can be exactly solved. The behavior of phase transition, correlations studies in the q-deformed time-dependent Hartree-Fock approximation, boson expansions, etc, have been studied[15, 16, 17, 18]. Details can be found in the cited references and therein.

d) Quantum Optics, Hydrogen Atom, Quantum Field Theory, etc. There are many applications of q-algebras to all branches of physics. They are discussed in details in the books[11,5] and references therein.

III The quon algebra

So far in this work we have concentrated on the q-algebras properties. In what follows we will present the second main topic of this work, the quons. The quons are particles which obey q-mutation relations that interpolate between the ordinary boson and fermion commutation relations. They were introduced by Greenberg[6] in 1991 to describe particles that violate the boson and fermion statistics by a small amount. Let us stress that the quons are equivalent to q-algebras only in the one degree of freedom case. We define the q-mutation relation by the expression:

note that when q goes to 1 we recover the bose statistics and when q goes to -1 we recover the fermi statistics. One can define a quon Fock space analog, through polynomials in the quon creation operators, a, acting on the vacuum:

as always the annihilation operators acting on the vacuum yields zero, a_jk |0ñ = 0. Here, we have an important difference between quons and q-algebras. Note that no commutation relation between two a^†¢s and two a¢s can be given. To see this, assume that for an arbitrary we set:

Then, acting with the annihilation operators on this state, of course, results in the null vector (a₁ |sñ = 0 and a₂ |sñ = 0 ). However, we also obtain that q is equal to one or minus one, that is, a boson or a fermion algebra. Notice that no commutation relation among creations operators or annihilation operators are necessary to calculate matrix elements of any physical operator. Let us see now how to construct many quons states.

A. Many-quon states

As an example, we can consider a two quon system occupying the arbitrary states 1 and 2 :

Notice that these states are not independent(non-orthogonal). To see this we have only to calculate the overlap matrix of these states. The overlap matrix results in:

One can easily show that the basis that diagonalizes this overlap matrix is :

where |Sñ is a symmetric state and |Añ is an antisymmetric one. In order to understand the structure of these states aiming at generalizations, let us consider the 3-quon states. Now, the non-orthogonal basis will contain the six independent states,

and the orthonormal basis may be obtained by classifying these states according to the irreducible representations of the permutation group of three elements, S₃. Adopting for short the convention

So, all the normalized 3-quon basis states are given by:

We have one symmetric, one anti-symmetric and four mixed-symmetry states according to the irreducible representations of S₃[7,19]. So, the procedure which was used to construct these states can be extended to any number of quons. However, it becomes very difficult in practical terms to apply this procedure when the number of quons increases, except for the symmetric and anti-symmetric states that we are going to consider next:

B. Quon Restricted to the Symmetric and Anti-symmetric Subspaces

1. Restriction to the Symmetric Space

Here, we will show that restricted to the symmetric subspace, the action of the creation operator on an arbitrary N-quon state is simple and similar to the ordinary case. One can show that the most general orthonormalized symmetric state for a system of N quons can be written as[19]:

where

_N is a convenient symmetrizer operator, n_a,n_b,... are the occupation number of the states a, b,... and the factor in front of S_N is a normalization factor. The sum of n_a +n_b +n_g +... is equal to the total number of quons, N, and note that in the denominator appears the q-factorial of the q-number N. Here, the q-number is given by:

The q-factorial is defined in close analogy to the commonly used factorial:

A very important result for applications of the quon algebra, that we are going to use next, is the following[19]:

We see that the action of the annihilation operator is very similar to the ordinary case, the only difference is the square root of [N]/N. Let us see now what happens in the anti-symmetric subspace.

2. Restriction to the Anti-Symmetric Space

We can proceed by analogy to the symmetric case. When restricted to the antisymmetric space one can find that the most general orthonormalized antisymmetric state for a system of N quons can be written as:

with being a convenient anti-symmetrizer operator and i_a stands for an occupied state. Now, we define the anti-deformed quantum number N through the expression:

One can show[20] the important result on the action of the annihilation operator on the anti-symmetric N-quon state:

Notice that we have obtained again expressions which are very similar to the ordinary ones, the only difference is the presence of the square root of { N } /N. In the following section we are going to consider applications of the quon algebra in boson expansions.

C. Boson expansions

More specifically let us consider the generalized Marumori Boson Mapping[21]. If Ô symbolizes a Fermionic Operator acting on the fermionic Hilbert space spanned by a finite basis of states, { |nñ}, n = 0,1,2,...,N, then the operator Ô can be exactly represented in this basis as:

We will map a Fermion operator Ô onto a corresponding boson operator Ô_B through the expression,

where the round kets |n) form an infinity basis for the boson Fock space,

By choosing the boson physical subspace in one-to-one correspondence with the original fermion subspace, it follows that the mapping preserves all matrix elements in the physical subspace.

So, the Marumori mapping is an exact one[21]. Note that explicit expressions for the mapped operators are obtained, by using the expression for the vacuum Boson projector[22]:

So, one can develop the boson image of the fermionic operator as an infinite normal ordered expansion, called Marumori expansion. We will show now an application.

it 1. The Pairing Model

The two level pairing model consists of two N-fold degenerate levels, whose energy difference is e. We denote |j₁m₁ñ as the lower level and |j₂m₂ñ as the upper level. The hamiltonian consists in a one-body term which is related to the number of excited particle-hole pairs(half the difference between occupied states in the upper and lower levels) and an interaction term:

where = (-1)^j-mb_j-m. If the interaction strength g is equal to zero the ground state consists of the lower level completely occupied. Once the interaction is turned on the ground state become a mixture of configurations. By introducing the quasi-spin su(2) generators:

One can rewrite the pairing Hamiltonian as

So, since L_± and L_z and S_± and S_z generate su(2) algebras, one can see that the pairing interaction has an underlying su(2)Äsu(2) algebra which allows one to obtain an exact pairing model solution. In particular, we take the fermion number of the system, N º 2W, to be even simulating a closed shell nucleus and the degeneracy of each level J to be N=(2J+1). The basis of states used for the numerical diagonalization of the pairing Hamiltonian is given by the following product states:

2. Mapped Pairing Hamiltonian

Here, we will show the result of mapping the operators entering in the pairing Hamiltonian, eq.(43), keeping only terms up to the fourth order[23]:

Diagonalizing the above equation is a simple task by using the basis

the matrix elements of H_q can be easily obtained from these expressions:

with similar expressions for the a₂ and a operators.

To calculate the energy we adopt a criterion for fixing the q parameter. We fix q eliminating all fourth order non-diagonal terms in the Hamiltonian, yielding the value for q:

So, the Hamiltonian becomes:

Some Remarks

a)For a large number of particles (W®¥) , q = 1 is recovered.

b) We have substituted the diagonal terms coming from the quonic image of S_z and L_z by their corresponding number operators.

c)A small term proportional to g a

a

a₂a₂ has been neglected.

In fig.2 we show our ground state energy results for the pairing hamiltonian. It is compared in this figure, the second order bosonic Hamiltonian (SBE) result, the q-RPA result, the SCRPA(self consistent randon phase approximation)result and the exact result. We remind that the second order boson expansion Hamiltonian gives the RPA solution if we diagonalize it in an unrestricted basis. It is clearly seen from this figure the advantages of the quonic bosonic expansion when compared with the usual one.

IV Quon as su(2) Irreducible Tensor Operators

In this section we will show that it is possible to define ordinary angular momentum tensors in terms of quons[24]. Differently from the q-deformed algebra, quons support su(2) tensor operators. This is a very important result for possible applications. We assume that a_m, a, m = -j,...,+j are (2j+1) operators which satisfy the q-mutation relations (or the quon algebra):

For future convenience, we will introduce here the transition number operator, N_ab, as follows:

where

This operator has commutation relations similar to the ordinary case, but now it is given by an infinity series in terms of a and a^† . One can show that the transition number operator N_ab satisfies the important commutation relation:

The above commutation relation shows that the transition number operators are the generators of an su(2j+1) algebra. Thus, we may define the su(2) generators as:

where J₀,J_± are ordinary su(2) generators satisfying the commutation relations,

One can now verify that the a operators satisfy the equations below:

Therefore, a, a_m form genuine irreducible tensor operators of the su(2) algebra.

The above expressions can be easily proved from the properties of the transition number operators.

Remarks

i) - Note that the above equations define a mapping (analogous to the Holstein-Primakoff mapping) between the su(2) generators and the quon operators.

ii) - This mapping can be the departure point for the treatment of pseudo-spin models within the quonic frame.

iii) - Once it is known how the angular momentum of the deformed bosons involved have to be coupled, boson expansions normally used in the literature can now be studied within the quon algebra framework .

iv) - In the quantum algebra framework the coupling rules do not obey regular angular momentum coupling rules.

Some applications of the quon algebra and its su(2) tensor structure have been done in the context of the Dyson and Marumori boson mapping for the pairing plus quadrupole-quadrupole Hamiltonian. More details can be found in the references[16,25,26]

A. Composite Particles

Next, we will present another possible application of the quon algebra. We assume a system composed of non-point-like particles, that is, where each particle is itself a bound system of several fundamental particles(bosons or fermions). As an example, we consider a composite boson formed from a bound state of two distinct fermions. A is a creation operator of a composite boson,

In this expression stands for the bound-state wave-function and the quantum number a stands for the center of mass momentum, internal energy, spin, etc.

Here, are creation and annihilation operators of 2 ordinary distinct fermions. So, as always they obey the fermion commutation relations:

From the definition of A^†, eq.(55), its conjugate hermitian A and the fermion commutation relations, eq.(56), we can show that:

where D_abis given by

We interpret A^†_a (A_a) as creation (annihilation) composite boson operators. Now, we will try to relate the composite Bosons and the quon algebra. We start with the quon algebra: . If we take q = 1-x then the commutator between a_a and a can be written as

comparing this result with our previous expression for the commutation relation between the composite boson annihilation and creation operators, eq.(58), we may identify:

For composite bosons we have previously obtained that any pair of composite annihilation(creation) operators commute with each other. So, restricting the physical sub-space to totally symmetric states, |y,Sñ, the following commutation relations are now valid also for quons

Then, the analogy between a composite particle and the quon algebra is complete[27]. Here, it will be discussed the physical meaning of the deformation parameter in the present context. We will consider a system of N composite bosons, at T=0, occupying a volume V and we will take the ground state of the system to be the condensate state:

this is performed in close analogy with the ideal bose gas. In this expression, A creates a composite boson in its ground state with center of mass momentum zero. Note that now the condensate state |Nñ incorporates kinematical correlations due composite nature of the bosons. (Pauli exclusion principle operates on the constituent fermions) We will take the analog to the boson occupation number operator to be A

A:

So, for a spin zero boson with its spatial part, F, having a gaussian form(rms = r₀), the average number of composite bosons occupying the ground state, N₀, is to lowest order in the density (n = N/V) given by :

where g is a parameter that depends on the wave function form[29]. If we look at the limits here, we see that when the size of the composite boson goes to zero, r₀® 0, (infinite tight binding) we recover the Bose-Einstein condensation and at the other extremum, r₀ ~ n^-1/3(mean separation of the bosons in the medium) when the size of the composite is large, the depletion is almost total.

Next, we will compare the composite gas system with a quon gas. Again, we consider a system of N quons, at T=0, occupying a volume V. As in the previous case, we take as the closest analog of the ideal boson gas ground state the N quon state:

Now we calculate the expectation value of a

a₀, which is not the number operator, in the state |Nñ. Making use of the results given earlier:

Using the above result one obtains to the lowest order in x,

Comparing this result with

it is clear that the effect of the deformation is such that

that is, the effect of the deformation parameter is proportional to the ratio of the volume occupied by the bosons to the volume of the system. It is also clear that when this ratio is small, meaning that there is no considerable overlap of the boson internal wave functions, the system behaves as a normal boson gas[27].

B. Perspectives

In the previous subsection, we have discussed the connection between the quon algebra formalism and composite particle systems. We believe that the quons can be an efficient tool in the description of the Bose-Einstein condensates(BEC) in trapped gases[8]. Especially because, first, in recent experiments it has been possible to achieve atomic densities in the trap where the compositeness character of the atoms may be observable and second the effects beyond mean-field can be taken into account through a generalized Gross-Pitaeviskii equation based on quon degrees of freedom[28].

Also it is promising the applications of the quon formalism in exciton states in semiconductors. We remind that excitons are formed by a bound electron-hole pair[29] and the departure from a true boson particle can be investigated within the quon formalism.

V Conclusions

We have shown that the q-deformed objects (q-algebra or quons) may be useful in the study of many physical systems. They may reveal new hidden symmetries in physical problems. The q-Deformation may be useful for phenomenological models (q-rotor, q-oscillator, etc) where, stretching and anharmonic effects can be taken into account through the deformation. In many physical problems the q-deformation may incorporate in an effective and elegant framework the interaction of the constituents of physical system.

We have also shown that the use of quons in boson expansion techniques, incorporates correlations in an effective way. So, the convergence of the expansion is increased. (For example, in the pairing model the expansion up to the second order is already very close to the exact result). An important point is that the quon boson expansion does not imply any increase in the complexity of the commonly used formalism. Finally we have discussed applications of the quon algebra in composite particle systems. Compositeness effects in systems formed by non-fundamental particles may be modelled by the quon algebra. Quons can be applied in the study of high density BEC in harmonic traps. Works on BEC and excitons are now under consideration.

Acknowledgments

I would like to thank firstly the organizing committee of the XXV Reunião de Trabalho Sobre Física Nuclear no Brasil for kindly inviting me to give a talk which resulted in this paper and secondly Dr. D. P. Menezes, Dr. F. F. de Souza Cruz, Dr. J. R. Marinelli and Dr. M. M. W. de Moraes my colleagues of the Physics Department of the Federal University of Santa Catarina who have contributed to most of my work on q-deformation.

References

[1] M. Hamermesh, Group Theory and its Application to Physical Problems, Dover Pub.(1989); W. Greiner, B. Müller, Quantum Mechanics Symmetries, Second Edition, Springer(1994).

[2] Mo-Lin Ge(Ed.), Quantum Group and Quantum Integrable Systems, Nankai Lectures on Mathemathical Physics, World Scientific Pub. Co., 1992.

[3] M.R. Kibler, Introduction to Quantum Algebras, Second International School on Theoretical Physics, Poland (1992), World Scientific.

[4] Bonatsos et al, Prog. Part. Nucl. Phys. 43, 537 (1999).

[5] M. Chaichian and A. Demichev, Quantum Groups, World Scientific Pub. Co., 1996.

[6] O.W. Greenberg, Phys. Rev. D 43, 4111 (1991).

[7] O.W. Greenberg, Physica A180, 419 (1992).

[8] F. Dalfovo, S. Giorgini, L. Pitaevskii, and S. Stringari, Rev. Mod. Phys. 71, 463 (1999).

[9] A.J. Macfarlane, J. Phys. A 22, 4581 (1989).

[10] L.C. Biedenharn, J. Phys. A 22, L873 (1989).

[11] L. C. Biedenharn and M. A. Lohe, Quantum Group Symmetry and q-Tensor Algebras, World Scientific Pub. Co., 1995.

[12] S.S. Avancini and D. P. Menezes, J. Phys. A 26, 1139 (1993).

[13] M. A. Mariscotti, G. Scharff-Goldhaber, and B. Buck, Phys. Rev. 178, 1864 (1969).

[14] D. Galetti and B. M. Pimentel, An. Acad. Bras. Ci. 7, 1 (1995).

[15] S. S. Avancini, A. Eiras, D. Galetti, B. M. Pimentel, and C. Lima, J. Phys. A 28, 4915 (1995).

[16] S. S. Avancini, D. P. Menezes, F. F. de Souza Cruz, and M.M. W. de Moraes, Int. J. Mod. Phys. E5, 403 (1996).

[17] S. S. Avancini and J. C. Brunelli, Phys. Lett. A174, 358 (1993).

[18] S.S. Avancini, F.F. de Souza Cruz, D. P. Menezes, and M.M. W. de Moraes, J. Phys. A28, 701 (1995).

[19] S. S. Avancini, J. R. Marinelli, and C. E. de O. Rodrigues, Phys. Lett. A 297, 137 (2002).

[20] S. S. Avancini, F. F. de Souza Cruz, J. R. Marinelli, D. P. Menezes, and M. M. Watanabe de Moraes, arXiv:nucl-th/0207088, to be published in Phys. Lett. A.

[21] A. Klein and E. R. Marshalek, Rev. Mod. Phys. 63, 375 (1991).

[22] S.S. Avancini, F.F. de Souza Cruz, J. R. Marinelli, D. P. Menezes, and M.M. W. de Moraes, J. Phys. A29, 5559 (1996).

[23] S.S. Avancini, F.F. de Souza Cruz, J. R. Marinelli, and D. P. Menezes, Phys. Rev. C62, (2000) art. 024312.

[24] S.S. Avancini, F. F. de Souza Cruz, J. R. Marinelli, and D. P. Menezes, Phys. Lett. A276, 109 (2000).

[25] S.S. Avancini, F. F. de Souza-Cruz, J. R. Marinelli, D. P. Menezes, and M. M. W. de Moraes, J. Phys. G: Nucl. Part. Phys. 25, 525 (1999).

[26] S.S. Avancini, J. R. Marinelli, and D. P. Menezes, J. Phys. G: Nucl. Part. Phys. 25, 1829 (1999).

[27] S.S. Avancini and G. Krein, J. Phys. A 28, 685 (1995).

[28] S. S. Avancini, J. R. Marinelli, and G. Krein, Compositeness effects in the Bose-Einstein Condensation, arXiv:cond-mat/0210310

[29] M. Combescot and C. Tinguy, Eur. Phys. Lett. 55(2001)390; M. Combescot and O. Betbeder-Matibet, arXiv:cond-mat/0204079.

Received on 30 October, 2002

Publication Dates

• Publication in this collection
  25 Aug 2003
• Date of issue
  June 2003

History

• Accepted
  30 Oct 2002
• Received
  30 Oct 2002