Rotational dynamics of the magnetic moments in ferrofluids

Rotational dynamics of the magnetic moments in ferrofluids

Claudio Scherer and Trieste F. Ricci

Institute of Physics, Federal University of Rio Grande do Sul

91501-970 Porto Alegre, RS - Brazil

Received on 19 January, 2001

We present a set of six non-linear stochastic diffferential equations for the six variables which are relevant for the dynamical behavior of the magnetic moments in ferrofluids, namely, the three Euler angles of the magnetic particle, the two polar angles of the magnetic moment relative to the particle and the modulus of the magnetic moment. The interaction between the magnetic particle and the solvent fluid is modeled by dissipative and random noise torques, and so is the interaction between the particle and its magnetic moment, treated as an independent physical entity. In the appropriate limits, the model system reduces to the cases of super-paramagnetic or of non-super-paramagnetic (blocked magnetic moments) particles. Numerical results show that for non-zero moment of inertia the precession of the magnetic moment around the magnetic field is accompanied by "nutation". It is also indicated how the dynamic complex susceptibility may be calculated from the equations of motion and the numerical results show that the nutation leads to a second resonance peak.

I Introduction

The rotational dynamics of the magnetic moments in ferrofluids is the essential phenomenon to explain the frequency dependent magnetic susceptibility of these materials. Two distinct rotational relaxation mechanisms may coexist in ferrofluids: the Néel relaxation, by which the magnetic moment moves with respect to the mechanical particle, and the Brownian, or Debye relaxation, corresponding to the particle's rotation inside the fluid. In most experimental situations one of these mechanisms is dominant, and this may be the reason why there is not, up to now, that we know, a satisfactory theory, sufficiently general to be applied for all situations, from the pure Néel to the pure Brownian relaxation, passing by all possible combinations of those mechanisms. In this respect the model of "two spheres", by Fannin and Coffey[14] should be mentioned as a first effort. The non-inertial limit, i.e., when the contribution of the moments of inertia of the particle to the equations of motion is negligible, in comparison to the other forces involved, has been treated by Shliomis and Stepanov [3], where they introduce the egg model. There they compare the magnetic particle with an egg, the yolk corresponding to the magnetic moment, and show that in the non-inertial limit and for weak applied field the equations of motion decouple, so allowing one to simultaneously account for the combined motion of the magnetic moment and the particle.

The purpose of the present paper is to present a general set of equations of motion for the combined system of magnetic moment plus mechanical particle, inside a fluid. The main limitation of our approach is that we deal only with axially symmetric particles, with easy axis of magnetization parallel to the symmetry axis. However, the magnetic moment is allowed to rotate inside the particle, as well as to have an oscillating modulus, and the particle is allowed to rotate with respect to the solvent, which is immobile with respect to the laboratory. The suspension is considered sufficiently dilute for the particle-particle interaction to be negligible, so that we deal only with single particle dynamics.

In contradistinction to most existing theories, our approach includes in the equations of motion the particle's moment of inertia. To neglect inertia may be a good approximation for many ferrofluids, because of the smallness of the particles, but we are presenting a theory which intends to be sufficiently general to include non-stable suspensions, for which the particles may be considerably bigger. In the case of super-paramagnetic particles, an aspect which distinguishes our theory from the usual approaches is that the rotation of the potential gradient on the magnetic moment, accompanying the Brownian rotation of the particle, is taken into account.

In section II we write the equations of the rotational motion of an axially symmetric particle inside a fluid (Langevin-type equations), based on the generalized Euler-Lagrange equations. In section III we obtain, from the equations of section II, in a convenient limit, the equations of motion for the magnetic moment m, which reduce, in the case of constant modulus of m, to the Gilbert's equation. In section IV we arrive at the set of six coupled equations, for the six degrees of freedom, the three Euler angles of the particle's rotations, the two polar angles of m and its modulus. In section V we indicate, briefly, how to calculate, by numerical simulation of the equations of motion, the dynamic magnetic susceptibility, a procedure which was more carefully explained in a previous paper [22]. Some less general situations are considered in section VI as particular cases and numerical results are given.

II Rotational Dynamics of a Particle in a Fluid

Consider a particle of axially symmetric shape in suspension in a fluid. The principal moments of inertia will be denoted by I₁ = I₂ and I₃. Disregarding translational degrees of freedom, its Lagrangian may be written in terms of the Euler angles q, f and y (in the notation of Goldstein [16]), taken as generalized coordinates, as

where V(q, f) is some orientation dependent potential. It cannot depend on y because of the axial symmetry of the particle.

The interaction forces (torques) between the particle and the fluid are of the dissipative and noise types. Therefore, they are not included in the Lagrangian, but instead, we have to use the "generalized Euler-Lagrange equations", with the corresponding torques, represented by Q_i, at the right hand side:

where q_i = q, f or y.

We write the non-conservative torques Q_i as sums of dissipative and noise terms, in the form

where is the following Rayleigh dissipation function [16],

and G_i(t) are the noise torques. The dissipation constants l and l¢ may be different because l¢ is associated with the particle rotation around the symmetry axis, while l is associated with the rotations perpendicular to it. Substituting Eqs. (1), (3) and (4) into Eq. (2) we obtain the following system of equations for the particle's rotation:

where V_q = ¶V / ¶q and V_f = ¶V / ¶f. The expression ( + cosq) was left unbroken wherever it appears in the above equations because it represents the component of the angular velocity vector w along the symmetry axis and we make use of this fact in the interpretation of the dissipative torques in terms of the components of w, as follows.

Let us define the following four unit vectors: z, along the laboratory z-axis, c, along the particle's symmetry axis, a, perpendicular to the plane containing c and z (-plane) and b, perpendicular to the -plane, namely,

As a notation to be used throughout this work, subscripts z, c, a or b on a vector indicate its orthogonal projection on the z, c, a or b directions and subscript indicates the vector's projection on the plane perpendicular to c .

The particle's angular velocity vector w may be decomposed into a sum of two vectors, perpendicular and parallel to c, respectively,

with

and

The orthogonal projection of w

on the z-axis is

and the orthogonal projection of w (or of w) on the direction perpendicular to the plane is

Thus we see that the dissipative torques present in Eqs. (5a), (5b) and (5c) are given by w

_a, w

_z and w

_c, respectively, times the dissipation parameters l or l¢.

The noise torques will be treated along these same lines. We start by defining the noise torque vector by its orthogonal components,

The noise becomes completely defined by stating the statistics of its three components. The usual procedure is to consider them as statistically independent, Gaussian white noise. This is, however, not a necessary assumption and we leave it open for future modeling. What we need now is to know how the three components come into Eqs. (5). Guided by the above decomposition of the dissipative torque, we are led to identify

Before we proceed to deduce the equations of motion for the general case of magnetic particles in suspensions we show, in the next section, how to obtain, from Eqs. (5), the equations of motion for the spherical coordinates of a mono-domain magnetic moment.

III Equations of Motion for a Magnetic Moment

The magnetic moment m of a mono-domain particle is related to its internal angular momentum S by m = gS, where g is the gyro-magnetic factor. Although the modulus S of S is taken as constant in most works on super-paramagnetism and magnetic fluids, for very small particles its oscillation may be significant and we prefer to allow it to be time dependent. The modern technology allows the preparation of samples with magnetic particles whose diameters are smaller than 20Å [17] and super-paramagnetic clusters containing only 12 magnetic atoms have also been reported [18]. We can model the magnetic moment by a rotating charged particle, in the limit of zero moments of inertia, I₁® 0, I₃® 0, and ® ¥ so that I₃ = S. Because in the next section we will work with the joint system, a particle and its fluctuating magnetic moment, we write the generalized coordinates, potential energy, dissipative and noise torques, with a notation distinct from that corresponding to the particle. Namely, we make the following substitutions: q ® J, f ® j, I₃® S, V ® W, l® x, l¢® x¢ and G® 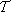. We also introduce two modifications in the equation corresponding to Eq. (5c), namely, we write S-S₀ instead of S in the dissipative term and introduce a torque W_s, whose origin will be explained below. In the said limit and with the new notation the system of Eqs. (5) becomes:

Here we have written S - S₀, instead of S, in the dissipation term of Eq. (7c) to account for the fact that the relaxation of the fluctuations of S is towards a most probable (equilibrium) value S₀ and not towards 0. It may appear strange that, even though we have derived the equations of motion for S from the equations of motion for a symmetric particle, in a convenient limit, we have now to add a term "ad hoc" (S₀), which does not have an equivalent in the particle's equations. This is so because in classical physics the equilibrium magnetization is always zero. Non-zero equilibrium magnetic moments can only exist because of the quantum mechanical nature of matter and, therefore, cannot be deduced from a pure classical approach. The torque W_s was introduced because a crystal field may have an effective interaction with m, with origin in an orbital contribution to S [29], with a possible torque component parallel to S. There is not an equivalent term in Eq. (5c) because of the assumed axial symmetry of the particle.

It is interesting to study the behavior of Eqs. (7) in the absence of noise,

_i=0 and with W_s=0. Eq. (7c) has then the trivial stationary solution S=S₀. Assuming this constant value for S in Eqs. (7a) and (7b) they reduce to

The conservative torques, -W_J and -W_j, have, usually, contributions from two different origins, the interaction of S with a crystalline, anisotropy field and/or with a magnetic field, which can also be of several different origins. In the case of magnetic field, H, the potential energy is W = -m · H. With a little of algebraic work one can show, in this case, that the set of Eqs. (8) is equivalent to the well known Gilbert's equation [10],

for m = gS and S = S₀. This equation was used by W. F. Brown [12] as a starting point for his stochastic theory of super-paramagnetism, where he assumed the magnetic field H to contain a noise term. A more general theory for super-paramagnetism, which allows also for oscillations on the modulus m = gS of the magnetic moment, was worked out by Ricci and Scherer [20, 21, 22], based on the set of Eqs. (7). For this reason we will not continue to explore the consequences of Eqs. (7) in the present paper, turning, instead, to the more general approach, where the rotations of the mechanical particle are taken into account, in addition to the motion of S relative to the particle.

IV Equations of Motion for a Small Magnetic Particle in Suspension

In recent years several researchers [1, 4, 14, 23] have drawn attention to the importance of the motion of the magnetic particle, its inertia and viscous interaction with the fluid, to the dynamic magnetic susceptibility of ferrofluids. A theoretical treatment of this problem, which is both, more fundamental and more general than those previously published, follows naturally from the context described above.

Taken together, the systems of Eqs. (5) and (7) contain all the degrees of freedom relevant to the problem. To the potential energy terms, V in Eqs. (5) and W in Eqs. (7), the interaction energy between the magnetic moment and the particle, which we will denote by U , has to be added. Due to the particle's symmetry, this term can only depend on S and on the angle between S and the symmetry axis, c. It is convenient to define another orthogonal set of unit vectors, related to the direction of the magnetic moment, namely, s, in the S direction, u, perpendicular to the -plane and v, perpendicular to the -plane,

The interaction energy U can then be written as U(S, s · c). In principle the particle can interact also with other fields, besides H, as is the case if it has an electric dipole and an electric field is present. For this reason we keep also the potential energy V(q, f) in the new set of equations.

The dissipative interaction associated with the rotation of S relative to the particle will be written in terms of the relative angular velocity vector. Since only rotations perpendicular to S can lead to a meaningful interaction torque with origin on the relative motion, we define the relative angular velocity w_r as

where

is the angular velocity of rotation of the magnetic moment with respect to the laboratory and

is the orthogonal projection of the particle's angular velocity w on the plane perpendicular to S. The dissipative interaction torque on the particle is then +x w_r. The plus sign is because of the way we defined w_r, where the particle's angular velocity appears with a minus sign. Guided by the interpretation of the dissipative torque terms of Eqs. (5) in terms of angular velocity components, as explained bellow the said equations, we write down immediately the dissipative torque terms to be added to the left-hand sides (therefore, with a - sign) of Eqs. (5), namely

Of course, all this scalar products, as well as those which follow, in the next equations, may be easily written as functions of the four angles q, f, J and j and their time derivatives, by using Eqs. (6) and (10). However, because scalar products are very easily handled in numerical procedures, we prefer to leave them in this form.

Clearly, the torque on the magnetic moment, due to the relative motion, is the "reaction" to the torque on the particle, i.e., it is equal to -xw_r, and, in place of x and x sin²J in Eqs. (7) we shall use (remembering that w_r = w_r)

No term coming from the relative angular velocity w_r has to be added to Eq. (7c) because w_r is perpendicular to S. However, there is the term x¢ (S - S₀) already present in that equation, with origin in the (quantum) fluctuations of S, and this term will be kept. Since angular momentum has to be conserved, its reaction counterpart on the particle has to be added to Eqs. (5). Calling

the terms to be added to the left-hand sides of Eqs. (5) are

The noise torques of interaction between the particle and the magnetic moment can be written down along the same lines of procedure as done for the noise torques of the fluid on the particle, at the end of section II. We assume three orthogonal, independent, noise torque vectors, along the unit vectors defined with respect to the direction of the magnetic moment:

Being 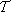the torque on the magnetic moment, then the torque on the particle is -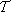. Following the same line of reasoning as done before, we identify the torques in Eqs. (7):

Correspondingly, the following terms have to be added to the right-hand-sides of Eqs. (5):

Therefore, the state of the composed system, the particle and its magnetic moment, is described by the 6 generalized coordinates, q, f, y, J, j and S, whose dynamical behavior is governed by the following set of coupled differential equations:

This set of six equations is of very general applicability on magnetic suspensions. It allows for a large variety of modeling: There are three independent conservative interaction potentials, V, U and W, four dissipative parameters, l, l¢, x, and x¢, and also the noise torques G and 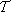, whose statistical properties are open for modeling. Particle-particle interaction was not explicitly taken into account.

V Dynamic Susceptibility

To calculate, from the set of Eqs.(12) the dynamic magnetic susceptibility, and therefore the absorption lines of magnetic resonance, it is better to transform them into the usual form of first order differential Langevin equations [19]. Noting that the first three equations are second order, we introduce new variables,

and transform Eqs.(12), so that, together with Eqs.(13), we have a set of nine first order equations. For example, Eq.(12a) becomes

We use also the Wiener processes W_j(t), which are related to the white noise components G_j (or whatever appears at the right hand side of Eqs.(12)) by

and make the usual substitutions G

_j(

t)

dt®

dW

_j(

t) to write the set of stochastic differential equations in the form

where

X

_i(

t) are the dependent variables h, n, r, q, f, y, J, j,

S and

A

_i(

X(

t),

t) and

B

_ij(

X(

t)) are obtained by comparison between Eq.(14) and those from the set of first order equations mentioned above, after the expressions for

V,

U and

W have been introduced. In the typical case of magnetic resonance, with a strong constant magnetic field

H

₀ parallel to the

z-axis and a periodic weak field

F(

t) perpendicular to it, the

A

_i(

X(

t),

t) turn out to be written in the form

Following the procedure of reference [22], the response functions are then given by

The symbol

X

_i(

t |

x) means the stochastic variable

X

_i at time

t, given that the "vector" of stochastic variables

X had the value

x at the initial time

t = 0, á

X

_i(

t |

x)ñ

₀ means average over many realizations of

X

_i, from 0 to

t, in abscence of the perturbing field

F(

t), starting from the point

x, ¶

_k means derivative with respect to the

k component of the initial "point"

x and á¼ñ

_eq means average over the equilibrium distribution of initial points. This equilibrium average may include average over the distribution of particle's characteristics, if polydispersity is to be considered. For example, if the particles are all made of the same material and have the same shape, varying only in size, assuming some given distribution of a linear dimension,

r, then the other particle's parameters shell be scaled accordingly. For example,

As was shown in reference [22], Eq. (16) may be evaluated from numerical simulations of Eq. (14). From the results obtained for F_ij(t) we can then calculate the susceptibility c_ij(w) by numerical Fourier-Laplace transform.

VI Some Limit Cases and Results of the Simulation

Several interesting limit situations are readily obtained from Eqs.(12). The "super-paramagnetic" limit, for which the particle's coordinates, q, f, and y, are taken as constants, so that the system reduces to the last three equations, or, equivalently, to Eqs. (7), has been treated in three previous papers by Ricci and Scherer [20, 21, 22]. A further simplification, in this limit, which is appropriate for most cases of practical interest, follows by assuming S = S₀ = constant. In this case the only relevant equations are Eq. (12d) and Eq. (12e), and, moreover, the term in also vanishes. The noise torques 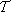_u and

_z may then be written in terms of a stochastic magnetic field, rendering our set of equations in a form equivalent to Brown's generalization [12] of Gilbert's equation, Eq. (9). This case has been treated by several authors, of which a very interesting account is given in a recent paper by Garcia-Palacios and Lázaro [15], where much numerical work is presented.

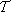
The "blocked" limit (also called "Brownian" limit [24] or "inertial limit"[2]), corresponds to the case when the magnetic moment is blocked along the particle's symmetry direction, i.e., J = q and j = f. This may happen because the sample is kept below the "blocking temperature" T_B [28] or because the material is so highly anisotropic that the magnetic moments only exists parallel to the easy axis [18]. The particle is still immersed in a fluid carrier, being able to rotate, together with its magnetic moment.

In terms of the set of Eqs.(12), the blocked limit is obtained by assuming an interaction potential U of the form -U₀d(s - c), with U₀® ¥, so that the only states energetically possible are those with s = c, i.e., J = q and j = f. By summing Eq. (12a) with Eq. (12d) and Eq. (12b) with Eq. (12e) the interaction terms U_q and U_J as well as U_f and U_j cancel out. The terms containing w_ra, w_{r z}, _a,

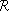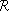
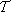_z, _a, and

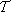_z become identically zero, and 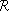_c becomes (S - S₀). Choosing q and f to denote the common polar angles, the system of equations, in the notation of the previous section, becomes:

This is still a rather general set of equations. A first obvious simplification occurs, in most cases of interest, when S = S₀. Then also = 0 and 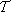_c = 0 and the system is reduced to three equations. Much work has been done in this case, mainly in the context of electric dipolar molecules, for which S = S₀ = 0. For example, McConnell [25], Coffey et al.[26], and Gaiduk and McConnell [27] describe dielectric relaxation and dynamics of polar molecules in great detail.

As a simple illustration we will assume a constant modulus for the magnetic moment, i.e., S = S₀, and for the interaction potential we consider only W = -m · H = -gS₀s · H, where H = H₀z is a constant field. The interaction energy between the magnetic moment and the field is then

With this simplifications, the system of Eqs. (18) becomes

We will consider in this simple illustration only the limit of very weak noise. Then Eq.(19c) has the approximate stationary solution r @ 0. We, therefore, neglect r in Eqs.(19a) and (19b), which become

which, together with the definition of h and n in Eqs.(13), form a set of four first order Langevin equations.

The simulations, of which we present some results in the figures, have been developed along the following procedure: An ensemble of 500 particles were initially put on the equator, i.e., q = 0 and with f = h = n = 0 and the equations of motion, with a different realization of the noise for each particle, were solved for some time, long enough for the ensemble to acquire a stationary distribution. Along this period the average value of S_z = cos(q) (we choose S₀ = 1) was calculated. The result is shown in Fig.1, for several values of the "moment of inertia", I/I^*, where I is I₁ and I^* is an arbitrary reference value. We see that for very low I, < S_z > increases monotonically to its stationary value (which is very close to 1 because the noise is very low), like in the super-paramagnetic case, when the magnetic moment precesses around the magnetic field following a spiral path. For bigger values of the inertia, q does not behave monotonically, but shows oscilations, a phenomenon known as "nutation".

In order to calculate the response functions, the new state of each particle was taken as the initial state for 500 independent realizations of the noise. Average values of these 250000 realizations have been calculated along the time, according to Eq. (16). By numerical Fourier-Laplace transform of the response functions we obtain the dynamic susceptibilities, c_ij(w). The imaginary part of the diagonal component, Im c_xx(w), is directly related to the magnetic resonance line. We show it, for several values of the moment of inertia, in Fig.2. For small I ( » super-paramagnetic limit) there is only one resonance peak (-w is physically equivalent to +w). For bigger values of I e second peak becomes apparent, which corresponds to the phenomenon of nutation, seen in Fig.1. We note that the frequency units, in Fig.2, are different for the different plots, and, therefore, the absolute values of the frequencies should not be used for comparison between the different plots.

References

[2] W.T. Coffey and Yu.P. Kalmykov, J. Magn. Magn. Mater. 164, 133 (1996).

[3] M.I. Shliomis and V.I. Stepanov, Theory of the Dynamic Susceptibility of Magnetic Fluids, in Relaxation Phenomena in Condensed Matter, Adv. Chem. Phys. Series, 87, 1 (1994).

[4] P.C. Morais, A.L. Tronconi, F.A. Tourinho and F. Pelegrini, Solid State Communications 101, 693 (1997).

[5] P.C. Fannin, S.W. Charles and T. Relihan, J. Magn. Magn. Mater. 162, 319 (1996). See also P. C. Fannin, D. Vincent, G. Massart, P. Perov, S. Neveu, Eur. Phys. Jour.-Appl.Phys. 8, 247 (1999); P. C. Fannin, P. A. Perov, S. W. Charles, Jour. Phys. D - Appl. Phys. 32, 2367 (1999).

[6] D. Vincent, S. Neveu, L. Jorat and G. Noyel, J. Magn. Magn. Mater. 163, 216 (1996).

[7] R. V. Upadhyay, D. Srinivas, R. V. Mehta, J. Magn. Magn. Mater., 214, 105 (2000).

[8] P.C. Fannin, L. Kinsella and S.W. Charles, J. Phys. D: Appl. Phys. 30, 533 (1997).

[9] K. Raj, B. Moskowitz and R. Casciari, J. Magn. Magn. Mater. 149, 174 (1995).

[10] T.L. Gilbert, Phys. Rev. 100, 1243 (1955).

[11] L. Landau and E. Lifshitz, Phys. Z. Sowjetunion 8, 153 (1935).

[12] W.F. Brown, Phys. Rev. 130, 1677 (1963).

[13] P. Debye, Polar Molecules (Chemical Catalog, New York, 1929).

[14] P.C. Fannin and W.T. Coffey, Phys. Rev. E 52, 6129 (1995).

[15] J.L. Garcia-Palacios and F.J. Lazaro, Phys. Rev. B 58, 14937 (1998).

[16] H. Goldstein, Classical Mechanics, Addison-Wesley, second ed. (1980).

[17] J.P.Chen, C.M.Sorensen, K.J. Klabunde and G.C. Hadjipanayis, Phys. Rev. B 51, 11527 (1995).

[18] M.A. Novak, R. Sessoli, A. Caneschi and D. Gatteschi, J. Magn. Magn. Mater. 146, 211 (1995).

[19] C.W. Gardiner, Handbook of Stochastic Methods, Springer, Berlin (1989).

[20] T.F. Ricci and C. Scherer, Braz. J. Phys. 21, 172 (1991).

[21] T.F. Ricci and C. Scherer, J. Stat. Phys. 67 1201 (1992).

[22] T.F. Ricci and C. Scherer, J. Stat. Phys. 86, 803 (1997).

[23] P.C. Fannin, S.W. Charles and T. Relihan, J. Phys. D: Appl. Phys. 28, 1765 (1995).

[24] M.I. Shliomis, Sov. Phys. Usp. 17, 153 (1974).

[25] J.R. McConnell, Rotational Brownian Motion and Dielectric Theory, Academic Press, London (1980).

[26] W.T. Coffey, Yu.P. Kalmikov and J.T. Waldron, The Langevin Equation, World Scientific, London (1998).

[27] V.J. Gaiduk and J.R. McConnell, Dielectric Relaxation and Dynamics of Polar Molecules (Series in Contemporary Physics, vol. 8), World Scientific, London (1999).

[28] D.D. Awschalom and D.P. DiVincenzo, Physics Today (April 1995) 43.

[29] R.M. White, Quantum Theory of Magnetism, Springer, Berlin (1983). File translated from T_EX by T_TH, version 3.01.On 4 Dec 2001, 21:27.

• [1] Y.L. Raikher and V.V. Rusakov, Phys. Rev. E 54, 3846 (1996).
• [2] W.T. Coffey and Yu.P. Kalmykov, J. Magn. Magn. Mater. 164, 133 (1996).
• [3] M.I. Shliomis and V.I. Stepanov, Theory of the Dynamic Susceptibility of Magnetic Fluids, in Relaxation Phenomena in Condensed Matter, Adv. Chem. Phys. Series, 87, 1 (1994).
• [4] P.C. Morais, A.L. Tronconi, F.A. Tourinho and F. Pelegrini, Solid State Communications 101, 693 (1997).
• [5] P.C. Fannin, S.W. Charles and T. Relihan, J. Magn. Magn. Mater. 162, 319 (1996).
• See also P. C. Fannin, D. Vincent, G. Massart, P. Perov, S. Neveu, Eur. Phys. Jour.-Appl.Phys. 8, 247 (1999);
• P. C. Fannin, P. A. Perov, S. W. Charles, Jour. Phys. D - Appl. Phys. 32, 2367 (1999).
• [6] D. Vincent, S. Neveu, L. Jorat and G. Noyel, J. Magn. Magn. Mater. 163, 216 (1996).
• [7] R. V. Upadhyay, D. Srinivas, R. V. Mehta, J. Magn. Magn. Mater., 214, 105 (2000).
• [8] P.C. Fannin, L. Kinsella and S.W. Charles, J. Phys. D: Appl. Phys. 30, 533 (1997).
• [9] K. Raj, B. Moskowitz and R. Casciari, J. Magn. Magn. Mater. 149, 174 (1995).
• [10] T.L. Gilbert, Phys. Rev. 100, 1243 (1955).
• [11] L. Landau and E. Lifshitz, Phys. Z. Sowjetunion 8, 153 (1935).
• [12] W.F. Brown, Phys. Rev. 130, 1677 (1963).
• [13] P. Debye, Polar Molecules (Chemical Catalog, New York, 1929).
• [14] P.C. Fannin and W.T. Coffey, Phys. Rev. E 52, 6129 (1995).
• [15] J.L. Garcia-Palacios and F.J. Lazaro, Phys. Rev. B 58, 14937 (1998).
• [16] H. Goldstein, Classical Mechanics, Addison-Wesley, second ed. (1980).
• [17] J.P.Chen, C.M.Sorensen, K.J. Klabunde and G.C. Hadjipanayis, Phys. Rev. B 51, 11527 (1995).
• [18] M.A. Novak, R. Sessoli, A. Caneschi and D. Gatteschi, J. Magn. Magn. Mater. 146, 211 (1995).
• [19] C.W. Gardiner, Handbook of Stochastic Methods, Springer, Berlin (1989).
• [20] T.F. Ricci and C. Scherer, Braz. J. Phys. 21, 172 (1991).
• [21] T.F. Ricci and C. Scherer, J. Stat. Phys. 67 1201 (1992).
• [22] T.F. Ricci and C. Scherer, J. Stat. Phys. 86, 803 (1997).
• [23] P.C. Fannin, S.W. Charles and T. Relihan, J. Phys. D: Appl. Phys. 28, 1765 (1995).
• [24] M.I. Shliomis, Sov. Phys. Usp. 17, 153 (1974).
• [25] J.R. McConnell, Rotational Brownian Motion and Dielectric Theory, Academic Press, London (1980).
• [26] W.T. Coffey, Yu.P. Kalmikov and J.T. Waldron, The Langevin Equation, World Scientific, London (1998).
• [27] V.J. Gaiduk and J.R. McConnell, Dielectric Relaxation and Dynamics of Polar Molecules (Series in Contemporary Physics, vol. 8), World Scientific, London (1999).
• [28] D.D. Awschalom and D.P. DiVincenzo, Physics Today (April 1995) 43.
• [29] R.M. White, Quantum Theory of Magnetism, Springer, Berlin (1983). File translated from T_EX by T_TH, version 3.01.On 4 Dec 2001, 21:27.

Publication Dates

• Publication in this collection
  26 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  19 Jan 2001