Viscoelastic ferrogel: dynamic magnetic susceptibilities

Viscoelastic ferrogel: dynamic magnetic susceptibilities

Yu. L. Raikher and V. V. Rusakov

Laboratory of Complex Fluids, Institute of Continuous Media Mechanics

Ural Division of RAS, 614013, Perm, Russia

Received on 16 December, 2000

Theoretical model to describe magnetodynamics of a ferrogel, i.e., an assembly of ferromagnetic nanoparticles embedded in a gel, is proposed. The reorientations of the particles are determined by the influence of the elastic matrix and the rotational Brownian motion. The set of essential parameters, on which the components of the dynamic magnetic susceptibility tensor depend, is discussed. In the framework of the model, absorption of the energy of an ac field is studied. With allowance for the interaction of elastic and Brownian forces, the effective relaxation times and eigenfrequencies for the longitudinal and transverse components of the ferrogel magnetization are evaluated.

I Introduction

Properties of complex magnetic fluids-this is the name for composite materials produced in result of embedding magnetic nanoparticles in easily deformable substances (soft matter)-are interesting from numerous viewpoints. On the one hand, magnetic particles by integration in supramolecular structures can give birth to new magnetically-controlled intellectual materials as, e.g. ferroliquid crystals [1, 2, 3] or ferrogels [4, 5]. On the other hand, having been admixed to the matrix in small amounts, the same particles will work as magnetic-field controlled micro-rotors that probe the rheology of the carrier fluid at the scale comparable with the particle size, i.e., 10 nm [6]. Indeed, in single-domain particles the specific magnetic moments are high, and accurate measurements of their response to an ac field (it causes rotational swings of the grains) are quite feasible. However, to rely on such magnetorheological intrascopy, besides solving technical problems of measurement, one faces the necessity to adequately interpret the collected data. Therefore, a theory specializing in magnetic spectra of soft ferrodispersions is required. A good particular example yield Refs. [7, 8, 9, 10], where the experimental technique and theoretical treatment concerning magnetic paints (ferrolaquers) are described. In the systems studied the magnetic particles were aluminum-covered iron needles about 150 nm in length with the aspect ratio about 1:8 suspended in a resin-containing fluid matrix subjected to subsequent crosslinking.

In a sufficiently diluted disperse system, the limit that one has to consider if the attention is focused on the properties of the matrix, the main contribution to the system response goes from individual particles. Unlike the case of coarse suspensions, in a nanodispersion the orientational dynamics of the particles is always an interplay between the force (applied field, elasticity and viscosity of the environment) and noise (Brownian diffusion) factors. For understanding of the magnetic spectra of complex magnetic fluids it is equally necessary to account for both factors [6, 11].

In Ref. [12] the system under study was a weak ferrogel modeled by a dilute suspension of magnetically hard nanoparticles in an elastic matrix. All the particles were assumed to be spherical and of equal size. The coupling of an individual particle to its environment was described according to the following scheme:

- the dissipative part was taken in the Stokes approximation so that the friction force imposed by the matrix is proportional to the product of the particle velocity and the viscosity of the fluid;

- the equilibrium thermal fluctuations were introduced in the dynamic equations of the particle as a white noise by means of the fluctuation-dissipation theorem.

The afore-mentioned rotary (torsional) oscillator model is well-known as one of the main theoretical tools in the statistical mechanics of suspensions and in molecular spectroscopy [13, 14, 15]. For example, in Ref. [13] it was used to explain the details of the high-frequency absorption in polar liquids. The interpretation was based on the calculation of the longitudinal (the subscript indicates the orientation of the probing field with respect to the equilibrium direction of the particle axis ) dynamic susceptibility in an assembly of electric dipoles subjected to the Brownian rotary motion. Note that due to some purposes (the results [13] are reproduced in the book [14]) only the longitudinal, and not transverse, susceptibility was taken into account. Meanwhile, as is shown below, under strong elasticity the longitudinal dynamic polarization "freezes" and becomes rather small in comparison with the transverse one. Due to that, in an elastic material with the chaotic distribution of the particle axes it is, first place, the transverse component that plays the dominating rôle in formation of the observed (macroscopic) susceptibility.

In Ref. [12] we adapted the model of a torsional oscillator surrounded by a Newtonian fluid for the case of ferrogel and determined the principal values of the magnetic susceptibility tensor: c_|| and c_^. As it was expected, our results confirmed that with the elasticity growth the main part in the response signal belongs to the transverse susceptibility. However, the most essential result of the work [12] was the conclusion that in the studied model within the whole physically relevant material parameter range the magnetic as well as orientational relaxation of ferrogel is monotonic. In other words, the system is unable for oscillations and no resonances could be excited in it.

In the present paper we modify the model [12] just in one aspect. Namely, not changing the part concerning the equilibrium elasticity, we assume that the dissipative mechanism that couples a particle with the matrix is viscoelasticity. This means that the time, during which stress relaxation in the matrix takes place, is admitted to be finite. This property to a smaller or greater extent is inherent to any fluid [16]; the more so-to soft systems like polymeric gels [17, 18]. As it turned out, as soon as the matrix is taken to be not just viscous but viscoelastic, the magnetic spectrum of such a ferrogel changes drastically. In particular, oscillatory damping regimes become possible that means that under external excitation the system is capable of a resonance behavior.

It is noteworthy to recall in this connection the spectra of magnetic nanosuspensions with viscoelastic but fluid matrices. As far as we know, the studies of this type of complex fluid suspensions were begun by the works [19, 20], where the kinetic equations describing the translational motion of the particles were derived and the corresponding coordinate and velocity correlation functions were found. In Refs. [6, 11] the said approach was extended for the case of rotary Brownian motion. In the studies of the dynamic magnetic susceptibility the possibility of a resonance behavior was demonstrated. Since the system under discussion does not possess an equilibrium elasticity so that the restoring torque is solely due to the retarded stress in the matrix, the found resonances turned out to be located at sufficiently high frequencies.

II Model

Consider an assembly of single-domain particles suspended in a gel. The particles are assumed to be magnetically hard so that inside each of them the magnetic moment m is completely "frozen-in" in the particle body. Incorporation of the particles in the structure of the gel is modeled by an elastic harmonic potential. By this, some preferred orientation of the particle axis is imposed. If this direction is the same for all the particles (e.g. the oligomer matrix was crosslinked in the presence of an external field), then the system is characterized by the macroscopic longitudinal (c_||) and transverse (c_^) susceptibilities, which take the form of the sums of the corresponding contributions of individual particles. If, on the contrary, the equilibrium direction of the particle magnetic moment does exist only microscopically whilst the system as a whole is isotropic, then the macroscopic susceptibility is determined as a weighted average = (c_|| + 2c_^), see [21], for example. In this connection, note the above remark on the dielectric susceptibility theory for polar fluids given in [13].

As the mechanism of the particle / matrix dissipative interaction, here we employ the rheological Maxwell model with a single relaxation time. This assumption is similar to those of Refs. [6, 11, 22]. To simplify the mathematical work, the particles are taken to be flat rotators so that each of them has just one degree of freedom that is the angle J between its magnetic moment m and the direction of the equilibrium orientation. Under those conditions, the equation of rotational motion for a particle with the moment of inertia I writes

Here the first term in the right-hand side (rhs) has the dynamic origin: the regular torque due to the elastic environment of the particle and the external magnetic field H. The second term is the friction torque owing to the dissipative interaction. Assuming the elastic potential of the matrix to be harmonic, one has

where the subscripts that mark the field components correspond to the directions J = 0 (longitudinal) and J = p/2 (transverse) with respect to the symmetry (easy) axis of the elastic potential.

In the Maxwell model of a viscoelastic fluid, the torque exerted by the matrix on the particle is characterized by the reference stress retardation time t_M and is described by the equation

The first term in rhs of Eq. (3) renders the regular component of the dissipative torque (the Stokes friction) while the second one is the random component, i.e., the noise. The latter is associated with a thermal bath at the temperature Q; hereafter we set the Boltzmann constant to unity. It is the noise that induces the Brownian motion of the particle. By the order of magnitude we set the friction coefficient to be z = 6h

V that corresponds to a spherical particle of the volume

V embedded in a fluid with the viscosity h. It is easy to show, see [6, 11], that the random torque correlator at equilibrium is

so that the noise in Eq. (3) is white and the fluctuation-dissipation theorem holds.

Eliminating the dissipative torque Q(t) from Eq. (1) with the aid of Eq. (3), at H = 0 we arrive at the Langevin equation for a Brownian oscillator in a viscoelastic fluid:

In the limit of a medium that is purely viscous (t_M®0) equation (5) reduces to the previously-studied model of a torsional oscillator that is characterized by three relaxation times: t_I, t_K and t_D [12]. Let us recall their meanings. From comparison of the inertial I and Stokes friction z torques there follows the definition for the so-called inertial time

that yields the reference time lapse, after which the particle angular velocity equalizes with that of the surrounding medium provided that the latter is viscous with the viscosity coefficient h.

Since it is assumed that the carrier medium of the suspension possesses also some equilibrium elasticity, then in a natural way one introduces the reference frequency w_K of rotational swings of the particles and the coupled to it (by means of t_I) orientational time:

The interval t

_K having passed, the particle axis settles to the equilibrium direction with respect to the elastic potential

U.

From the fact that the Brownian particle is in thermal equilibrium with its environment (thermal bath) follows the existence of one more time scale: the thermal frequency w_Q. The latter (once again by means of t_I) is linked to the well-known Debye time t_D of thermal orientational relaxation:

When passing to the case of a viscoelastic medium, the set of reference times is extended by adding the retardation time t_M. As one can see from Eq. (4), at t_M¹ 0 the problem acquires one more reference frequency that owes to the dynamic (non-equilibrium) elasticity of the matrix:

It is worth a note that it is right this frequency that determines the resonance behavior of the particle response in a viscoelastic medium with zero equilibrium elasticity present [6, 11].

Insofar we have found that the system under study has four independent parameters with the dimensions of time. In below we show that in a typical suspension they differ considerably from one another. This means that the system response to a probing field H(t) strongly depends upon the relation between the field period and the reference times of the problem. However, prior to get to analyzing the modes of the response to a weak field, let us check the compatibility of our model with the Stokes approximation. As known (see, for example, Ref. [23])) the Stokes limit means that the Reynolds number is small. When applied to a particle with the linear size a that rotates with the angular velocity (frequency) w, this condition takes the form

where we set that the fluid and particle densities (r

_f and r

_p, respectively) are of the same order of magnitude. Substituting into Eq. (10) the reference frequencies-elastic w

_K from Eq. (7), thermal w

_Q from Eq. (8) and Maxwellian w

_M from Eq. (9)-one finds that the Stokes approximation (10) remains valid as long as

In other words, the inertial time should be the shortest of the reference times of the system.

It is convenient to introduce the dimensionless times of the elastic, Debye (thermal) and Maxwellian relaxation defined through the scale t_I as

so that condition (11) takes the form T_K, T_D, T_M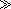 1. Estimation of T_D for suspensions had been done many times (see Refs. [6, 12]) and it may be written as T_D ~ ah²/Q. Thence, condition T_D 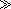1 at Q 10³ K and h 10^-2 P holds starting from a 10^-9 cm, i.e., always.

To make an assessment for the parameter T_K, we remark the following. The elasticity modulus E of a polymeric gel is of the high-elasticity (entropy) origin so that by the order of magnitude E ~ nQ, where n is the number of links in a unit volume. From dimensionality considerations, it follows that a particle embedded in a polymeric network will arise an additional energy K ~ EV ~ nQV. Therefore, the elastic constant by the order of magnitude equals temperature times the number of the gel links forced out by the particle. We assume that the particle "senses" the matrix elasticity if, when embedded, it ousts out at least one link. This implies K Q, so that T_K is of the same order as T_D, for which inequality (9) is valid virtually always. For the particles of the size a ~ 10 nm the condition nV ~ 1 yields E ~ 10⁴ Pa ~ 0.1 atm., so that the value of the link concentration n ~ 10¹⁸ cm^-3 occurs to be close to the real threshold of gel formation in polymers [17].

III Angle Correlation Function

In the equilibrium state, the angle correlation function depends only on the time lapse between the initial and final moments and is determined by all the reference times of the problem. In this section we shall derive the general formula for the angle correlator but first let us consider its limiting behavior at t®0. For this case the phase lag is given by

hereafter the starting moment is chosen at

t = 0. We multiply Eq. (13) by the initial value J = J(0) and make the ensemble average. For ergodic systems it is equivalent to the time average, so with allowance for the equipartition theorem one has

In result, for the short-time (ballistic) asymptotics of the orientation correlator we find

To obtain the equilibrium angle correlator at arbitrary times, one has to use the Langevin equation (5). The general solution of the homogeneous linear equation corresponding to Eq. (5), we seek in the form J µ exp(

t). Substitution in Eq. (5) yields the characteristic equation

In the previous works, the particular cases of this dispersion relation have been investigated to a detail: for

K = 0 (a free Brownian particle) in [6, 19], and for t

_M = 0 (torsional oscillator in a viscous medium) in [12, 13, 14].

For the analysis of the roots of the cubic equation (16) it is convenient to cast it in a dimensionless form. Scaling the decrements in the units of the Maxwell time, i.e., denoting l = t_M, we reduce Eq. (16) to

From here one clearly sees that for t

_M¹ 0 the eigenfrequencies and decrements of the system depend of two dimensionless parameters:

m and

T

_M. Since all the coefficients of Eq. (17) are real, complex roots that correspond to the case of oscillatory relaxation, may emerge only in pairs, and the Vièta theorem takes the form

First we evaluate the real root of Eq. (17) that exists at any values of the material parameters and describes the monotonic relaxation regime; in below we call this solution the r-branch. For that, we rewrite Eq. (17) in the form

As is noted above, the validity range of the model under study is

T

_M

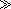
1. Thence the decrement of the

r-branch follows immediately on iterating rhs of Eq. (19). In the first order in 1/

T

_M, it writes

Now we look for at the complex-conjugated roots

of Eq. (17). Substituting Eq. (21) in Eq. (17) and setting the real and imaginary parts of the emerging equation to zero gives

From this set, once again, one sees that the real solution (

r-branch) is ever-existing whereas the complex roots (

q-branch) are possible only under condition

Let us demonstrate that at T_M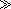 1 condition (23) holds under any circumstances. Substitution of expression (23) into the first of Eqs. (22) transforms it to

The sought for solution is obtained on iterating the rhs of Eq. (24), so that for the decrement of the oscillatory mode one gets

In turn, substitution of Eq. (25) in Eq. (23) yields the frequency of a torsional oscillator embedded in a viscoelastic environment:

The last form of expression (26) clearly indicates that both elastic mechanisms-the equilibrium and dynamic-on equal basis contribute to the eigenfrequency. To avoid any confusion, we remind that in formulas (17)-(26) the decrements l, g and the frequency W_q are dimensionless, scaled with t_M.

Relations (25) and (26) establish that g_q» q < and W_q/g_q ~ (1 + m)^3/2 that entails that at T_M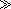 1 inequality (23) certainly holds. This leads, in turn, to a fundamental conclusion that in the physically relevant range of material parameters, in the spectrum of the system under study, besides the monotonic mode, there necessarily exists an oscillatory one with a fairly high quality factor: W_q/g_q 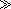1.

Now, having found the roots of the characteristic equation, let us proceed to evaluation of the angle correlator proper. We write the general solution of the homogeneous equation (5) as

Taking into account the initial conditions, one arrives at the set of linear algebraic equations

with respect to the coefficients

C

_i. Solution by a standard method gives

Here D

_kjº l

_k - l

_j and

By multiplying the phase evolution equation (29) by the initial value of the angle J and taking the equilibrium ensemble average with allowance for Eqs. (14), one arrives at the expression

In the framework of the studied model this formula is the exact result. It determines the angle correlation function for arbitrary values of the material parameters. For example, assuming t small and expanding Eq. (31) in a series, after simple although tedious calculations one recovers the short-time limit (15).

As stated in above, for the physics of nanoparticle dispersions in fluids and gels the most interesting time domain is T_M, T_D, T_K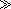 1. In this limit, relation (31) may be simplified considerably. Let us first transform it in such a way that the coefficient alongside each eigenfunction would depend only on the respective eigenvalue. For example, from Eq. (31) it follows that the coefficient in front of exp(l₁t) is the fraction

Eliminating from it l

₂ and l

₃ with the aid of the Vièta theorem (18), one gets

Since all the eigenvalues enter the correlator in a symmetrical way, with the aid of the scheme (33) it can be presented in the form

A merit of this expression is that it explicitly incorporates the large parameter

T

_M. Expanding the correlator with respect to 1/

T

_M << 1 with allowance for relationships (20), (25) and (26) one finds in the leading order:

Note that in Eq. (35) we have returned to the dimensional form so that

Formulas (35) shows clearly that the parameter that controls the contribution of the oscillatory mechanism in the orientational relaxation has the form of the ratio of two reference times: m = t_M/t_K = K/K_M. As it should have been expected, in the case where the viscoelasticity of the system is low (t_M << t_K) the orientational relaxation of the particles is monotonic; this process was studied to a detail in Ref. [12].

IV Equilibrium Distribution Function. Static susceptibility

Generally speaking, to obtain the equilibrium orientational distribution of the particles in a viscoelastic environment and in an arbitrary axially-symmetric potential U(J), one has to solve the corresponding kinetic equation, see, for example, Refs. [11, 24]. However, for the case of a harmonic potential, studied here, the result is easily achieved by the following procedure [19]. According to constitutive equations (1) and (3) of the model, its natural phase variables are the angle J, angular velocity and torque Q. A reasonable assumption is that the sought for distribution is the function of all those quantities. Moreover, the angular part of the equilibrium distribution function should be, of course, determined by the Boltzmann formula

The equilibrium correlators, i.e., the mean squares of the angular variables are given by relations (14). Now we need the cross-correlators between the angular variables and the torque. Multiplying Eq. (1) by W º dJ/dt we get

After ensemble averaging and substitution of equilibrium correlators this yields

Multiplying Eq. (3) by J and, once again, averaging one finds

Since the correlator á J

y(

t) ñ turns to zero due to d-correlation of the noise

y(

t) and á JW ñ vanishes because of the equipartition theorem, Eq. (39) yields

This relationship ends up the proof of the fact that in equilibrium all the cross-correlations are zero, i.e., different phase variables are statistically independent.

Let us find the equilibrium fluctuation of the torque under assumption that there is no correlation between Q and the orientational potential that is expressed by an arbitrary angular function U(J). This hypothesis finds its justification in the structure of Eq. (3) that does not bear any sign of angular dependence. Multiplying Eq. (1) by Q and then using Eq. (3) and relations (14), we get

From the above given consideration it follows that the equilibrium distribution function is completely determined by the second diagonal statistical moments of the phase variables W and Q. Adding this part to the Boltzmann expression (37), one gets the equilibrium distribution [11, 24] in the form

here

Z is the partition function determined by the normalizing condition. It is seen clearly from Eq. (42) that for the case of a Newtonian liquid (t

_M ® 0) Eq. (42) reduces to the classical Maxwell-Boltzmann distribution. Indeed, the angle part of

W

_s according to the fundamental rules of the equilibrium statistical mechanics is determined only by the form of the potential function and cannot depend on the dissipative characteristics of the system. This means, in particular, that the expressions for the static susceptibilities

found in Ref. [12] for a torsional oscillator in a viscous fluid, equally hold for the considered here more general case: a torsional oscillator in a viscoelastic fluid.

The equilibrium moments entering Eq. (43) at H = 0 are calculated with the aid of the formula

In result, relations (43) transform to

For the limiting cases of weak and strong rigidity one finds, respectively,

V Dynamic Susceptibility

The dynamic susceptibility of the system with respect to the probing field H(t) µ exp(-iwt) is evaluated in the framework of the linear response theory, see Ref. [15], for example. The general expression is taken in the normalized form

where the equilibrium correlation functions of the dipolar moment are given by the relations

We need these functions for the case

H = 0. In this limit, the dynamic equations (1) and (3) turn out to be linear with respect to the angle variable J. Since in Eq. (3) the term

y(

t) is a white noise, i.e., a Gaussian random process, function J acquires the same statistical properties. This allows to transform formulas (48) by means of the relationship

that holds for the functions of Gaussian variables. In result, the dipolar correlation functions (48) assume the form

Substituting the explicit angle correlation function (35) in the dipolar correlators (50) and then the results formulas into Eq. (47), we get the principal components of the magnetic susceptibility as integral expressions. Although those integrals cannot be taken exactly, it is possible to present them in a form that is rather convenient for both analytical treatment and numeric calculations of the functions c_a(w).

Let us expand the transverse dipolar correlator (50) in a Taylor series with respect to its angular argument:

and then twice use the binomial expansion: first for the powers of the angle correlator (35) and then for the powers of cosine. This gives

here we denote

Substituting expansion (52) in Eq. (47) and integrating it term-by-term, we arrive at the series representation:

where formula (14) for the equilibrium angle fluctuation is taken into account.

Repeating similar calculational procedure for the longitudinal susceptibility, we get

where we use the notation

= (2

n -

k) g

_r +

k g

_q, cf. (53).

Formulas (54) and (55) are rather convenient to analyze the functions c_a(w) in the low-temperature limit and as well for numerical calculations in a wide temperature range. However, to reveal their dispersion structure, it is useful to regroup the series (54) and (55). We make the rearrangement in such a way that each term of a new series would incorporate all the contributions to the susceptibility at the given frequency. For the transverse case from Eq. (54) one finds

where

For the longitudinal case from formula (55) it follows

with the notation

The quantities, which enter formulas (56), are expressed through the material parameters of the problem as

So, the frequency dependence of the spectra is determined by the dispersion factors that in formulas (56) and (57) stand in the rear positions. Each susceptibility is presented as a set of equidistant resonance lines (lorentzians) at the frequencies that are the multiples of the basic eigenfrequency W_q.

VI Dynamic Susceptibility. High-Rigidity Limit

Here we consider the case K > Q, i.e., w_K > w_Q that is natural to term a high rigidity limit. According to the above-given estimates, it corresponds to strong interaction between the embedded particle and the gel matrix, i.e., a pronounced macroscopic anisotropy caused by the elasticity of the molecular network. The approximate formula for the transverse susceptibility follows from summation of series (56) truncated at n = 1. This leads to

with the notation

From formula (59) one sees that the absorption spectrum (the imaginary part of the complex susceptibility) of a relatively rigid gel incorporates both athermic and temperature-dependent components. The former comprises a low-frequency relaxation line and a resonance one at the frequency W_q. The amplitude of the relaxational line turns out to be (1 + m) times smaller than that of a usual Debye one. The resonance line has the width g_q and the maximum that reaches as high as

This means that the oscillatory mode plays a considerable part in the relaxation of the transverse magnetization of the system at

m

} > 1.

The presence of athermic lines implies that the corresponding contributions to the susceptibility can be calculated directly from the dynamic equations, thermal fluctuations being completely neglected. For the transverse probing field taking into account that the angle deviations J are small, from Eqs. (1)-(3) we get

Substituting in Eq. (62) a harmonic probing field, from the definition of a susceptibility one finds

This expression leads, in particular, to a correct form of the static susceptibility (46). With allowance for the conditions t

_M, t

_K

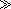
t

_I, one can split Eq. (63) into the relaxational (low-frequency) and resonance (high-frequency) contributions and write

Using definitions (36) for the decrements g, one finds that formula (64) coincides with the first three (athermic) terms of expansion (59), which presents the susceptibility c_^ in the high-rigidity limit.

All the other terms of the sum (59) incorporate the coefficient (Q/K)² that is the sign of their thermofluctuational origin. We remark the frequency dependence of those terms: there are present dispersion factors with the second and third overtones of the basic frequency W_q. The appearance of multiple frequencies in the spectrum of c_^(w) is a fundamental feature in the dynamics of systems with fluctuations. Namely, in the presence of a noise (thermal or whatever), the linear response of the system is multi-frequency and comprises the eigenfrequency overtones. As it follows from Eq. (59), this effect disappears tracelessly when one passes to the athermic conditions, where the higher harmonics might be generated only in result of nonlinear mechanisms.

From (59) it follows that the absorption maximum at the double frequency has the order

where the amplitude of the first peak is estimated by formula (61). Therefore, in the high rigidity limit the second absorption peak is much lower than the first one. For the third harmonic peak from Eq. (59) one finds

The comparison shows that at

m < 2 the relation

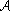
₃ <

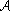
₂ takes place so that the heights of the absorption peaks form a monotonically decreasing sequence.

The situation changes to the opposite as soon as the factor m exceeds 2. Taking for estimates the case m 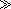1, from Eq. (65) one finds that the second harmonic amplitude goes down to zero as ₂ ~ m^-2

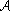₁ whereas that of the third harmonic tends to a finite value ₃ ~ (1-m^-1)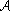₁. Hence, the relationship between the amplitudes is

It indicates an interesting effect: suppression of even harmonics in the spectrum of the transverse susceptibility with the growth of viscoelasticity of the system. To get an explanation for this, one has to take two circumstances into account. First, as formula (35) shows, with the growth of the parameter

m, the rôle of the oscillatory mode in the angular correlator becomes more important. Second, the transverse dipolar correlator (50) is an odd function of the angular correlator á J

_tJ ñ. Given that, the even harmonics appear in the relevant spectral expansion multiplied by a small parameter ~

m

^-2, and the higher

m the more the odd ones dominate. However, in the high-rigidity limit (w

_K > w

_Q), this comb-like spectrum is enveloped by a decreasing curve since at w > w

_Q the susceptibility tends to zero. This is the universal feature of the linear-response theory. Indeed, in this approach one assumes that the equilibrium of the system is not disturbed, so that overpowering majority of the particles in the system has the kinetic energy close to Q. At higher energies, the system becomes "transparent" to the excitation due to the exponentially small population of the corresponding states.

This behavior is illustrated by Figs. 1 and 2. In the first one the stress retardation time t_M changes (grows top to bottom) whilst all the other reference times are fixed. Therefore, the parameter m = t_M/t_K grows top to bottom, equalling 2 in Fig. 1b, where 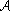₂ = 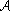₃. It is to be compared to the situation 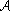₂ > 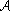₃ in Fig. 1a corresponding to m = 0.8 and to that in Fig. 1c, where 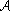₂ < 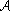₃ at m = 4. In Fig. 2, the Maxwellian time is fixed and we vary the elastic restoration time t_K. From top to bottom one has m » 3 (a), 2 (b) and 1 (c), and the interplay of the second and third peaks is in full agreement with the estimates (65)-(67).

Low-temperature behavior (the high-rigidity limit) of the longitudinal susceptibility c_|| is essentially different from c_^ since there is no athermic limit for c_||. Indeed, under diminution of fluctuations the magnetic material saturates, and its susceptibility along the direction of its magnetization tends to zero as c_||(0) (Q/K)(nm²/2K), see Eq. (46). For the dynamic susceptibility, in linear in Q/K approximation, from expansion (55) one finds

The same result can be obtained more directly from the general formula (47), if to substitute there the longitudinal correlation function by the leading term

of its low-temperature expansion.

From Eq. (68) it follows that in a rigid gel the absorption spectrum for the probing field directed along the particle orientation axis comprises a low-frequency (relaxational) line and two resonance ones-at the basic and doubled frequencies. Performing the analysis similar to that done for the transverse case, one finds that for the longitudinal spectra the critical value of the parameter m is m_* = ( - 1)/4 » 1.19. At m < m_* the energy is absorbed mostly at the basic frequency W_q, whereas at m > m_* the main rôle passes to the second harmonic. In other words, in the longitudinal absorption spectrum suppression of odd harmonics takes place. The cause of this effect is, once again, the presence of the oscillatory mode in the angular correlator (35). This time, however, the longitudinal dipolar correlator is even with respect to á J_tJ ñ, so that the even harmonics are favored.

Figs. 3 and 4 make those qualitative considerations more vivid. In Fig. 3 the stress retardation time t_M changes (grows top to bottom) whilst all the other ones are fixed. This means that the parameter m = t_M/t_K grows top to bottom, equalling » 1.19 in Fig.3b, where 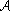₁ = 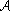₂. One can clearly see the difference between Fig. 3a, where m = 0.8 and 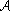₁ > 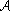₂, and Fig. 3c, where m = 1.4 thus ensuring 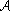₁ < 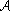₂. In Fig. 4, the stress relaxation time is fixed and we change the elastic restoration time t_K. From top to bottom one has m » 1.4 (a), 1.2 (b) and 0.7 (c). The data of Fig. 2 was obtained numerically; they fall in full agreement with the estimates of Eq. (68).

VII Conclusions

In the above-presented consideration, when considering a ferrogel, we assume that the dissipative mechanism that couples the nanoparticles and the matrix is of the viscoelastic type. This assumption seems to be more realistic than formerly used hypothesis that presents the said interaction as just a simple viscous friction.

The viscoelastic mechanism imparts novel essential features to the dynamic magnetic response of a ferrogel. Unlike the purely viscous case, here the oscillatory regime is possible that means that under appropriate conditions the magnetic spectrum of a ferrogel comprises a number of equidistant resonance lines. To the eigenfrequency both elastic forces-equilibrium and dynamic (Maxwell)-contribute on the equal basis. Due to the inherent mesoscopic anisotropy of the gel system, the spectra of response to the probing field directed either along or across the easy axis of the particle orientation, differ considerably. There are two main aspects of those differences. First, the transverse susceptibility has a finite zero-temperature (athermic) limit whereas the longitudinal one turns to zero with temperature. Second, due to the parity properties of the respective dipolar correlators, in the spectrum of the linear response signal there may occur a selective suppression of the amplitudes of the higher harmonics. This effect takes place under sufficiently strong viscoelasticity. Depending on the type of the signal that one analyzes, either even (in the transverse response) or odd (in the longitudinal one) higher harmonics are suppressed.

Acknowledgements

Support of this work by the International Association for the Promotion of Co-operation with Scientists from the New Independent States of the Former Soviet Union Grant No. INTAS 97-31311.

References

[1] L. Liebert and A. Martinet, J. Phys. Lett. (France) 40, L363 (1979).

[2] P. Fabre, C. Cassagrande, M. Veyssie, V. Cabuil, and R. Massart, Phys. Rev. Lett. 64, 539 (1990).

[3] V.V. Berejnov, J.-C. Bacri, V. Cabuil, R. Perzynski, and Yu.L. Raikher, Europhys. Lett. 41, 507 (1998).

[4] J. Dumas and J.-C. Bacri, J. Phys. Lett. (France) 41, L279 (1980).

[5] M. Zrínyi, L. Barsi, and A. Büki, J. Chem. Phys. 104, 8750 (1996); M. Zrínyi, L. Barsi, D. Szabo, and H.-G. Kilian, ibid. 106, 5685 (1997).

[6] Yu.L. Raikher and V.V. Rusakov, Phys. Rev. E 54, 3846 (1996).

[7] A.A. Potanin, R.J. Hirko, V.T. Peikov, and A.M. Lane, J. Rheology 42, 1249 (1998).

[8] V.T. Peikov and A.M. Lane, J. Colloid & Interface Sci. 206, 350 (1998).

[9] V.T. Peikov, K.S. Jeon and A.M. Lane, J. Magn. Magn. Mater. 193, 307, 311 (1999).

[10] M. Benakli, P.B. Visscher, B.S. Chae, and A.M. Lane, J. Appl. Phys. 87, 5657 (2000).

[11] J.-L. Dejardin, Phys. Rev. E 58, 2808 (1998).

[12] Yu.L. Raikher, V.V. Rusakov, W.T. Coffey, and Yu.P. Kalmykov, Phys. Rev. E 63, 031402 (2001).

[13] J.H. Calderwood, W.T. Coffey, A. Morita, and S. Walker, Proc. Roy. Soc. London A352, 275 (1976).

[14] W.T. Coffey, M.W. Evans and P. Grigolini, Molecular Diffusion and Spectra, Wiley-Interscience, New York, 1984.

[15] W.T. Coffey, Yu.P. Kalmykov, and J.T. Waldron, The Langevin Equation. World Scientific, Singapore, 1996.

[16] R. Zwanzig and M. Bixon, Phys. Rev. A2, 2005 (1970).

[17] P.G. de Gennes, Scaling Concepts in Polymer Physics, Cornell Univ. Press, Itaka, 1979.

[18] M. Doi and S.F. Edwards, The Theory of Polymer Dynamics, Oxford Univ. Press, Oxford, 1986.

[19] V.S. Volkov, Sov. Phys. JETP 71, 93 (1990).

[20] V.S. Volkov and A.I. Leonov, J. Chem. Phys. 104, 5922 (1996).

[21] L.D. Landau and E.M. Lifshitz, Electrodynamics of Continuous Media, Pergamon Press, Oxford, 1960.

[22] J.H. van Zanten and K.P. Rufener, Phys. Rev. E 62, 5389 (2000).

[23] L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Pergamon Press, Oxford, 1959.

[24] Yu.L. Raikher and V.V. Rusakov, J. Mol. Liquids 71, 81 (1997).

Publication Dates

• Publication in this collection
  26 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  16 Dec 2000