Interfacial instabilities in confined ferrofluids

Interfacial instabilities in confined ferrofluids

José A. Miranda^*

Laboratório de Física Teórica e Computacional, Departamento de Física,

Universidade Federal de Pernambuco, Recife, PE 50670-901 Brazil

Received on 7 November, 2000

We investigate the flow of two immiscible, viscous fluids in the confined geometry of a Hele-Shaw cell. We consider that one of the fluids is a ferrofluid and that an external magnetic field is applied. The interfacial instabilities which arise between the fluids are studied for various situations: (a) different cell geometries (radial, rectangular); (b) frontal and parallel flows; (c) distinct applied field configurations (tangential, perpendicular, normal) and (d) motionless and rotating cells. The interplay between applied magnetic field and several other destabilizing/stabilizing factors in determining the interface behavior is analyzed. Stability analysis and numerical simulations are used to describe linear and nonlinear stages of the interface evolution.

I Introduction

The formation of patterns and shapes in the natural world has long been a source of fascination for both scientists and laymen [1, 2]. Nature provides an endless array of patterns formed by diverse physical, chemical and biological systems. The scales of such patterns range from the growth of bacterial colonies [3] to the large-scale structure of the universe [4]. This enormous range of scales over which pattern formation occurs and the intriguing fact that they emerge spontaneously from an orderless and homogeneous environment captivate our imagination.

Interface dynamics plays a major role in pattern formation. It determines the shapes of objects, and therefore, it has important applications in a wide range of interdisciplinary fields: hydrodynamics [5] (convection patterns and shapes of boundaries between fluids), metallurgy [6] (dendritic shapes of crystals), and biology [3, 7] (shapes of plants, cells, etc.). Despite the great variety and richness of this immense set of pattern formation systems, in this work we focus on a few specific examples of interfacial patterns, which arise at the interface separating two viscous fluids, when they flow in very narrow, quasi-two-dimensional passages.

The outline of the work is the following: section II introduces the Saffman-Taylor problem, which addresses fluid flow in a confined device called Hele-Shaw cell. Flow of both nonmagnetic and magnetic fluids (ferrofluids) are discussed. Section III considers flow of ferrofluids in rotating Hele-Shaw cells. The combined effects of external, applied magnetic field and rotation on the shape of the interfacial patterns are analyzed. It is shown, through a linear stability study, that an in-plane, azimuthal magnetic field is able to stabilize the fluid-fluid interface. Numerical simulations are used to examine interface behavior under perpendicular applied field. Section IV studies the situation in which the fluids flow parallel to each other, for various magnetic field configurations. We show that depending on the field direction it can stabilize or destabilize the interface. For such parallel flows, solitons arise at the interface. We suggest magnetic forces may introduce new and interesting behaviors related to soliton interations. Finally, section V presents our concluding remarks and perspectives.

II Fluid flow in confined geometry

A. The Saffman-Taylor problem and the Hele-Shaw cell

The Saffman-Taylor problem [8, 9] addresses motion of two viscous immiscible fluids in the narrow space between two plates, known as a Hele-Shaw cell [10]. When a fluid of low viscosity displaces a fluid of higher viscosity, the interface between them becomes unstable and starts to deform. Dynamic competition in such confined environment leads ultimately to the formation of beautiful fingering patterns [9].

The original Hele-Shaw cell (that has little to do with the current version) was first utilized about a century ago by a British naval architect of that name [10]. A long and narrow channel containing a fluid was used to study the flow of water around the hull of a ship. The cell made its reappearance in the 1950's [8, 11, 12], in the study of the problem of oil recovery from porous media. The process involved pumping water down an oil well in order to push trapped oil into surrounding wells where it could be recovered. It turned out to be a quite frustrating experience, as the water would tend to propagate via a branching type of deformation, leaving a substantial fraction of the oil behind. The viscous fingering instability made oil recovery inefficient. The Hele-Shaw cell was modified to study this kind of instability: a top plate was added to the channel and two fluids were introduced.

To this day, investigations of the viscous fingering instability have found the Hele-Shaw cell to be a simple yet elegant device in the study of interfacial pattern formation. Nowadays experiments and theory focus on two basic Hele-Shaw flow geometries (i) rectangular [8] and (ii) radial [13]. In rectangular geometry cells the less viscous fluid is pumped against the more viscous one along the direction of the plates. A gravity-driven flow is also possible, if we tilt the cell and allow gravity to act. Meanwhile, in the radial geometry case, the less viscous fluid is injected to invade the more viscous one, through an inlet located on the top glass plate. Typical examples of viscous fingering patterns can be seen in reference [9]: rectangular cells produce patterns showing "fingers" of the less viscous fluid inside the more viscous one, while radial cells lead to the formation of "fan-like", branched structures.

For both geometries, the initial developments of the interface instability track the predictions of linear stability theory [8, 9]. After the initial surface deformation, as the unstable modes of perturbation grow, they become coupled in a weakly nonlinear stage of evolution [14, 15]. Finally, the system evolves to a complicated late stage, characterized by formation of fingering structures, in which nonlinear effects dominate [9].

The fluids are driven by pressure gradient or gravity, and it is a simplifying feature of the Hele-Shaw geometry that the fluid velocity is simply proportional to the pressure gradient [8, 9]. In this case, the Laplace equation applies. At first glance, it may seem very simple to solve Laplace equation. The basic equations for the Hele-Shaw system are indeed simple. However, their solutions are definitely not so simple. The difficulty of solving the Laplace's equation lies in the existence of moving boundary conditions, which involve a functional of the unknown interface shape. This is what is called a free boundary problem, which is in general not possible to be solved analytically in a closed form.

The basic physical aspects leading to viscous fingers can be summarized as follows: in the Saffman-Taylor problem, if a forward bump is formed on the interface between the fluids, it enhances the pressure gradient and the local interface velocity. Because the velocity of a point on the interface is proportional to the local pressure gradient, the bump grows faster than other parts on the interface. On the other hand, the effect of surface tension competes with this diffusive instability. Surface tension acts to reduce the pressure at highly curved parts of an interface, and sharp bumps are forced back. As a result we have the formation of the fingering patterns mentioned above.

B. Confined ferrofluids

An interesting variation of the traditional Saffman-Taylor problem is to consider the situation in which one of the fluids in the Hele-Shaw cell is magnetic. Magnetic fluids are also known as ferrofluids [16]. Roughly speaking, a ferrofluid can be defined as a colloidal suspension of tiny magnetic particles in a nonmagnetic solvent. It is composed of 3-15 nm particles of solid, magnetic, single-domain material particles coated with a monolayer of surfactant molecules and suspended in a fluid carrier. Although the solid particles are ferromagnetic, a ferrofluid is actually paramagnetic because the individual particle magnetizations are randomly oriented. Thermal agitation keeps the particles suspended because of Brownian motion, and the coating prevents the particles from sticking to each other. In ionic ferrofluids coating is replaced by electrostatic repulsion. Since the magnetic particles are much smaller than the Hele-Shaw cell thickness, we neglect their particulate nature and consider a continuous paramagnetic fluid. For the present work, we will be interested solely in describing the general mechanisms leading to the very nice labyrinthine structures in ferrofluids. The reader can find much more information about these fascinating complex fluids in Rosensweig's classic book [16].

We proceed by discussing the flow of ferrofluids in the confined Hele-Shaw geometry for both rectangular and radial setups.First, suppose we have a vertical, rectangular Hele-Shaw cell, in which the upper less dense and less viscous fluid is nonmagnetic, while the lower, more dense and more viscous one is a ferrofluid. Instead of pumping the less viscous fluid against the more viscous one by applying an external pressure gradient, lets us consider the situation in which we apply a uniform magnetic field, perpendicular to the cell plates. In the absence of an applied magnetic field, the interface is flat and gravitationally stable. When we turn on the uniform magnetic field, interesting things begin to happen. The externally applied field tends to align the tiny magnetic moments in a direction normal to the plates. Consequently, these magnetic moments start to repel each other within the plane of the Hele-Shaw cell and the interface begins to deform. The surface tension between the two fluids tries to stabilize the interface. Gravity is also stabilizing if the more dense fluid is on the bottom. If the field intensity is increased, fingers start to develop and begin to split at their tips. Finally, by increasing the field even further, a labyrinth-type pattern is formed [17, 16]. These patterns are quite different from those that arise when nonmagnetic fluids flow in rectangular Hele-Shaw cells.

Similar branching labyrinth patterns occur in a radial geometry setup, in which an initially circular ferrofluid droplet is surrounded by a nonmagnetic fluid [18, 19, 20, 21, 22, 23]. In the absence of an applied magnetic field, the equilibrium ferrofluid shape is determined by surface tension, resulting in a circular droplet. Interfacial instability is driven by the competition between capillary and magnetic forces. Surface tension acts to minimize the length of the interface between the fluids and favors compact domain shapes. In contrast, the repulsive dipole-dipole interaction tends to maximize the distance between dipoles and favors extended domain shapes. Eventually, as a result of the competition, multiply bifurcated labyrinthine patterns are formed. The branched patterns are quite distinct from the "fan-like" patterns obtained for radial flow with nonmagnetic fluids. So, for both rectangular and radial geometries, as a result of the ferrofluid interaction with the external field, the usual viscous fingering instability [8, 9] is supplemented by a magnetic fluid instability [16], resulting in a variety of new interfacial behaviors.

In the following sections we revisit the tradicional radial and rectangular magnetic liquid setups discussed above, by adding modifications into the system: (a) in the radial case, instead of considering the cell at rest (motionless Hele-Shaw cell), we assume that it is under rotation around the axis passing through the center of the cell (rotating Hele-Shaw cell); (b) in the rectangular case, instead of analyzing the situation in which one fluid is pushed by the other (frontal flow), we investigate the case in which the fluids flow side by side, with their flow velocities pointing along the initially unperturbed, flat interface separating them (parallel flow). For these two new situations we examine the relevant effects acting on the interface, due to applied magnetic field, by employing linear stability theory and numerical methods.

III Ferrofluid flow in rotating Hele-Shaw cells

In recent years, reseachers have been studying a number of modifications of the classic Saffman-Taylor setup [9]. An interesting variation of the traditional viscosity-driven fingering instability is the investigation of radial Hele-Shaw flows in the presence of centrifugal driving. The inclusion of centrifugal forces can be considered by rotating the cell, with constant angular velocity, around an axis perpendicular to the plane of the flow. In this case, the interface instability can also be driven by the density difference between the fluids [24, 25]. In contrast to the "fan-like" patterns obtained in motionless Hele-Shaw cells, which show fingers that split at their tips, rotating cell effects make the initial circular droplet to throw out attached droplets, which subsequently throw out fingers that form a set of new droplets [25], leading to what we could call a "hammerhead shark" pattern.

In this section we analyze the situation in which one of the fluids is a ferrofluids and study the effects on the fluid-fluid interface when magnetic field and rotation are simultaneously present [26]. We consider the situation in which a non-uniform, azimuthal, in-plane field is applied. The competition between rotation and magnetic field is analyzed. We show the azimuthal magnetic field provides a new mechanism for stabilizing the interface. The destabilizing effect of perpendicular applied field is studied through numerical methods.

Consider a Hele-Shaw cell of thickness b containing two immiscible, incompressible, viscous fluids (see Fig. 1). We assume that b is smaller than any other length scale in the problem, and therefore the system is considered to be effectively two-dimensional. Denote the densities and viscosities of the inner and outer fluids, respectively as r₁, h₁ and r₂, h₂. The flows in fluids 1 and 2 are assumed to be irrotational. Between the two fluids there exists a surface tension s. We assume that the inner fluid is the ferrofluid (magnetization ), while the outer fluid is nonmagnetic. During the flow, the fluid-fluid interface has a perturbed shape described as  = R + z(q, t), where q represents the polar angle, and R is the radius of the initially unperturbed interface.

Figure 1.
Schematic configuration of the rotating Hele-Shaw cell with ferrofluid.

The cell rotates, with constant angular velocity W, about an axis perpendicular to the plane of the flow (Fig. 1). An external magnetic field , produced by a long, straight wire carrying a current I, is directed along the axis of rotation. Current I produces an azimuthal magnetic field external to the wire = (I/2 pr) , where r is the distance from the wire, and is the unit vector pointing in the direction of increase of q.

Following the standard approximations used by Rosensweig [16] and others [19, 22, 23] we assume that the ferrofluid magnetization is collinear with the external field and that the influence of the demagnetizing field is neglected. It is also assumed that the ferrofluid is electrically nonconducting and that the displacement current is negligible. For the quasi two-dimensional geometry of a Hele-Shaw cell, the three dimensional flow may be replaced with an equivalent two-dimensional flow (x, y) by averaging over the z direction perpendicular to the plane of the Hele-Shaw cell. Imposing no-slip boundary conditions and a parabolic velocity profile one derives Darcy's law for ferrofluids in a Hele-Shaw cell [23, 27], which must be augmented by including centrifugal forces,

where p is the hydrodynamic pressure, m₀ is the free-space permeability, and denotes a unit vector pointing radially outward. Equation (1) describes nonmagnetic fluids by simply dropping the terms involving magnetization.

It is convenient to rewrite equation (1) in terms of velocity potentials, since the velocity field is irrotational. We write = -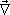f, where f defines the velocity potential. Similarly, we rewrite the magnetic body force in equation (1) as m₀( · 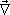) = m₀M

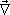H = Y, where we have introduced the scalar potential

with M = M(H) = cH, c being a constant magnetic susceptibility.

With the definitions of f and Y we notice that both sides of equation (1) are recognized as gradients of scalar fields. After integrating both sides of equation (1), we evaluate it for each of the fluids on the interface. Then, we subtract the resulting equations from each other, and divide by the sum of the two fluids' viscosities to get the equation of motion

To obtain (3) we have used the pressure boundary condition p₁- p₂ = sk at the interface, where k denotes the interfacial curvature in the planeof the Hele-Shaw cell [26]. The sign convention for the curvature k is such that a circular interface has positive curvature. The dimensionless parameter A = (h₂-h₁)/(h₂ + h₁) is the viscosity contrast.

In the framework of our linear analysis, we assume a small perturbation of the initially circular interface of the form z(q, t) = z_n(t) exp(inq) with n = 0, 1, 2,..., to derive the linear dispersion relation l(n) defined by dz/dt = l(n) z_n. Knowing that f obeys Laplace's equation and expressing it in terms of z through the kinematic boundary condition [16], equation of motion (3) leads to [26]

We define the dimensionless parameters N_W = [R³(r₁ - r₂)W²]/s and N_B = m₀cI²/(4p²sR) as the rotational and magnetic Bond numbers, respectively.

Inspecting equation (4) we observe the interplay of rotation, magnetic field and surface tension in determining the interface instability. If l(n) > 0 the disturbance grows, indicating instability. The contribution coming from the surface tension term has a stabilizing nature. N_W may be either positive or negative, depending on the relative values of the densities. If r₁ > r₂, N_W > 0 and rotation plays a destabilizing role. In contrast, N_B always tends to stabilize the interface. This indicates that the rotation-driven instability could be delayed or even prevented if a sufficiently strong magnetic field is applied.

The stabilizing role of the magnetic field can be explained by its symmetry properties and non-uniform character. Notice that such a field possesses a radial gradient. The magnetic field influence is manifested as the existence of a body force due to field non-uniformity. The field produces a force directed radially inward, that tends to move the ferrofluid toward the current-carrying wire (regions of higher magnetic field). This force opposes the centrifugal force and favors interface stabilization. This effect is similar to the gradient-field stabilization mechanism discussed by Rosensweig [16].

A quantity of importance can be extracted from l(n): the fastest growing mode n^*, given by the closest integer to the maximum of equation (4) with respect to n

n^* is strongly correlated to the number of ripples present in the early stages of pattern formation. By equation (5) we verify that, for positive N_W, increasingly larger values of N_B tend to decrease the number of interface ripples. The azimuthal magnetic field can be seen as a control parameter to discipline the number of interface undulations. This fact is illustrated in Fig. 2.

Figure 2.
Plot of n_max as a function of N_B for increasing values of N_W. These curves are obtained using equation (5).

The effect of a uniform magnetic field applied perpendicular to the rotating cell is worth investigating as well. Linear stability analysis of the perpendicular field configuration has been carried out in reference [26]. As expected, the perpendicular field has a destabilizing role. It is of interest to study the combined role of rotation and perpendicular field in more advanced stages of the interface evolution. Intensive numerical simulations, based on conformal mapping techniques [23], have been performed by Jackson and Miranda [28] in order to investigate rotating cell ferrofluid patterns, under perpendicular field, in the fully nonlinear regime. Representative examples of such numerical simulations are shown in Fig. 3.

Figure 3.
Numerical simulations showing the interfacial instability of an initially, nearly circular ferrofluid droplet in a Hele-Shaw cell, in the presence of a perpendicular magnetic field: (a) and (b) motionless cell; (c) and (d) rotating cell. Figures (b) and (d) depict the resulting droplet shape obtained in time evolution (a) and (c), respectively. The physical parameters are given in the text.

Fig. 3(a) depicts the interface evolution of an initially, nearly circular ferrofluid droplet of radius R = 2 cm, under the influence of a perpendicular field (N_B = 0.575), in a motionless Hele-Shaw cell of thickness b = 0.4 cm. The overlaid contours shown in Fig. 3(a) have approximately equal time steps and the total "numerical experiment" time t=5 s . We used a random initial condition [23]: we splinkled a small amount of random noise (amplitude < 0.05 R) in the first four Fourier modes as an initial condition. Fig. 3(b) shows the ferrofluid droplet shape at t = 5 s, when the droplet comes to rest. The dumbbell-shaped structure shown in Fig. 3(b) is similar to the one simulated numerically by Tsebers and Zemitis [29], who used boundary integral equation techniques. Related numerical studies for droplets in motionless cells have been carried out in references [30, 31].

Figs. 3(c) and 3(d) are obtained using the same physical parameters as those used in 3(a) and 3(b), but now rotation is added (N_W = 0.6) and the total numerical experiment time t = 2 s. The ferrofluid droplet now evolves, under perpendicular field, in a rotating Hele-Shaw cell. Fig. 3(d) shows the droplet shape at t = 2 s. This shorter evolution time is expected since both rotation and applied field are destabilizing effects. In contrast to Fig. 3(c), the droplet in 3(d) is not at rest. The interface configuration in 3(d) corresponds to some intermediate state for the motion of the droplet due to centrifugal forces acting on its periphery.

We summarize our preliminary numerical results [28] as follows: (i) without rotation, the droplet comes to rest in a final fingered stage. With rotation included, there is no final stage. This is an unstable situation and the droplet ends up shooting off to one side or the other after enough time. A possible explanation to such behaviors is the fact that the Fourier mode n=1, that corresponds to a translation of the circle, is unstable (stable) for rotating (motionless) cells; (ii) rotation leads to more bulbous ends and to a thinner (although reasonably constant thickness) connecting arm.

IV Parallel flow with confined ferrofluids

Most of experimental and theoretical investigations of the Saffman-Taylor problem in the literature consider fluid motion in confined Hele-Shaw cells under frontal flow. In contrast, we consider the so-called parallel flow which occurs when the fluids flow parallel to the initially unperturbed interface separating them.

Recent studies [32, 33, 34] examined the dynamics of fluid interfaces under parallel flow in Hele-Shaw cells. Zeybek and Yortsos [32, 33] studied, both theoretically and experimentally, parallel flow in a horizontal Hele-Shaw cell in the large capillary number limit. For finite capillary number and wavelength, linear stability analysis indicates that small perturbations decay, but the rate of decay vanished in the limit of large capillary numbers and large wavelength. Furthermore, a weakly nonlinear analysis of the problem found Korteweg-de Vries (KdV) dynamics leading to stable finite amplitude soliton solutions. Solitons were indeed observed experimentally. Gondret and Rabaud [34] incorporated inertial terms into the equation of motion in a Hele-Shaw cell and found a Kelvin-Helmholtz instability for inviscid fluids. For viscous fluids they derived a Kelvin-Helmholtz-Darcy equation and found the threshold for instability was governed by inertial effects, while the wave velocity was governed by the Darcy's law flow of viscous fluids. Their experimental results supported their theoretical analysis.

Here we perform the linear stability analysis for parallel flow in which one fluid is a ferrofluid and a magnetic field is applied [35]. We consider three separate field configurations: (a) tangential, for in-plane fields tangent to the unperturbed interface; (b) normal, for in-plane applied fields normal to the unperturbed interface; (c) perpendicular, when the field is perpendicular to the plane defined by the Hele-Shaw cell plates. We show the magnetic field provides additional mechanisms for destabilizing the interface, and we analyze qualitatively the interactions between solitons caused by the magnetic field. We neglect inertial terms because they are not needed to understand the interfacial instability.

As we did in section III let us briefly describe the physical system of interest. Consider two semi-infinite immiscible viscous fluids, flowing with velocities U₁ and U₂, along the x direction, in a rectangular Hele-Shaw cell (see Fig. 4). To achieve steady-state parallel flow

Figure 4.
Schematic configuration of the parallel flow geometry. The lower fluid is a ferrofluid, and the upper one nonmagnetic. The external magnetic field may be oriented along the x, y or z axis.

the velocities and viscosities must obey the condition h₁U₁ = h₂U₂. We assume that the lower fluid is the ferrofluid (magnetization ), while the upper fluid is nonmagnetic. In order to include the acceleration of gravity , we tilt the cell so that the y axis lies at angle b from the vertical direction. To include magnetic forces, we apply a uniform magnetic field ₀, which may point along the x, y or z axis. During the flow, the fluid-fluid interface has a perturbed shape described as y=z(x, t) (solid curve in Fig. 4).

As was the case for the rotating cell case studied in section 3 the starting point of our analysis is the generalized Darcy's law [23, 27]. By applying similar conditions as those used in section 3 we end up getting the equation of motion

we have introduced the scalar magnetic potential

and the local field = - 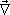j. Demagnetizing effects are neglected. The unprimed coordinates denote arbitrary points in space. The primed coordinates ¢ are integration variables within the magnetic domain , and d²r¢ denotes the infinitesimal area element. The vector ¢ represents the unit normal to the magnetic domain inconsideration.

We perturb the interface with a single Fourier mode z(x, t)=z_k exp[i(wt - kx)], where k denotes a wave number. Following linear stability analysis standard procedures, we first consider that the velocity potential for fluid i, f_i, obeys Laplace's equation Ѳf_i=0 and vanishes as y ® ±¥. Then, we use the kinematic boundary condition [16] to express f_i in terms of the perturbation amplitudes to obtain the dispersion relation for growth of the perturbation z(x, t)

where N_B = 2M²b/s is the magnetic Bond number and k₀ = . The real part of w is k times the phase velocity, and is the viscosity-weighted average of the two fluid velocities. Note that the magnetic field does not alter the phase velocity of the waves. The imaginary part of w, which governs the exponential growth or decay of the wave amplitude, does include effects of the magnetic field. Exponential (unstable) growth occurs when the imaginary part of w is negative.

Terms containing I_j(k) originate from the Fourier transforms of

the magnetic contribution to equation (6). The subscript

j =

x,

y,

z indicates the tangential, normal and perpendicular magnetic field configurations, respectively. After some algebra we find relatively simple integral expressions for the magnetic terms

I

_j(

k) [35]

and

Consider the stability of the fluid-fluid interface for the different field configurations. The initially flat interface is unstable to perturbations with wave number k when N_BI_j(k)-(k b)²-(k₀b)²is positive. If the heavier fluid is below the lighter fluid,(r₁ > r₂), then both gravity and surface tension stabilize the system and k₀ is real. Therefore, in the absence of applied magnetic field (N_B=0), the temporal growth rate of any perturbation is negative and waves are damped. On the other hand, if the external magnetic field is nonzero, the stability of the interface will depend on the field's direction. Fig. 5 illustrates how the magnetic terms (10), (11) and (12) vary with reduced wave number kb. Inspecting Fig. 5 and the imaginary part of the dispersion relation (8) we note that a tangent field configuration (I_x(k) < 0), makes the growth rate even more negative than when the field is absent. So a tangent external field has a stabilizing nature, reinforcing the effects of gravity and surface tension. In contrast, since I_y(k) and I_z(k) are both positive quantities, if a sufficiently strong magnetic field is applied normal to the fluid-fluid interface, or perpendicular to the cell plates, the growth rate may become positive, leading to a possible destabilization of the interface. We conclude that the magnetic field can destabilize the interface even in the absence of inertial effects. These effects can be explained very simply: for normal and perpendicular fields, the ferrofluid spreads out in the Hele-Shaw plane due to magnetic repulsion, leading to interface deformation. In contrast, for a tangent field, any interface perturbation tends to be stabilized, due to magnetic attraction.

Figure 5.
Plot of I_j(k) as a function of kb for (a) tangential, (b) normal, and (c) perpendicular magnetic field configurations.

In addition to the interface stability issue discussed above, it is of interest to study the action of the applied magnetic field on the solitons that appear in parallel flow in Hele-Shaw cells. We suggest that the solitons may be considered as localized perturbations on the flat interface. When magnetic fields are present the solitons acquire net dipole moments equal to the magnetization of the fluid multiplied by the integrated area of the soliton. Dipole interactions are long-ranged, falling off as 1/x³ for moments separated by a distance x. This contrasts with the fluid-dynamic interaction of solitons which decays exponentially with separation. An interesting additional feature of the dipole-dipole interaction is its variation with the relative orientation of dipole moments and the vector joining them. In the case of solitons with parallel moments ₁ and ₂ displaced from each other along the x axis, the interactions will be attracting, with strength 2m₁m₂, when the magnetizations lie along the x axis (tangetial) but will be repelling, with strength m₁m₂ when the magnetizations lie along the y (normal) or z (perpendicular) axes. In this sense parallel flow with ferrofluids could be used as a novel system to investigate soliton interactions.

V Concluding remarks and perspectives

In this work we reviewed the basic aspects related to interfacial pattern formation in Hele-Shaw flows, and discussed modifications regarding flow of ferrofluids in such confined geometry: free boundary motion in rotating radial cells and the interface behavior under parallel flow in rectangular cells with ferrofluids.

First, we addressed the interplay between centrifugal and magnetic forces in determining the instability of the fluid-fluid interface in rotating cells. The linear stability analysis of the problem shows that a non-uniform, azimuthal magnetic field, applied tangential to the cell, tends to stabilize the interface. We verified that maximum growth rate selection of initial patterns is influenced by the applied field, which tends to decrease the number of interface ripples. Numerical simulations were presented in relation to the case in which a uniform magnetic field is applied normally to the plane defined by the rotating Hele-Shaw cell. In a future work we plan to investigate numerically the dynamical competition between rotation (which push the fingers "sideways") and magnetic field (which tends to bifurcate the finger tips) in the highly nonlinear pattern formation stage. We point out that, to date, there are no experiments on rotating cells with ferrofluids. Since the experimental Hele-Shaw setup is relatively simple, it would be of considerable interest to perform such experiments which are likely to lead to new and exciting interfacial patterns in the highly nonlinear regime. It would be nice to compare numerical simulations with real experiments.

Finally, we presented the linear stability analysis for parallel flow in a Hele-Shaw cell when one of the fluids is a ferrofluid. We showed that the dispersion relation governing mode growth is modified so that the magnetic field can destabilize the interface even in the absence of inertial effects. However, we found that the magnetic field does not affect the speed of wave propogation for a given wave number. We pointed out that magnetic field creates an effective interaction between the solitons. M. Widom and I plan to investigate the influence of the magnetic field on the shape of the solitons in a more quantitative fashion, by performing the weakly nonlinear analysis of the system.

Acknowledgements

It is a pleasure to thank R. Perzynski and F. Tourinho for inviting me to give a talk related to this work at the International Workshop on Magnetic Fluids (Brasília - DF, 2000). I thank H. Nazareno (director of ICCMP-Unb, Brasília - DF) for his kind hospitality. I also thank M. Widom and D. P. Jackson for ongoing collaborations. This work was partially supported by CNPq and FINEP (Brazilian Agencies).

References

[1] D'Arcy W. Thompson, On Growth and Form (Cambridge University Press, Cambridge, 1944).

[2] P. S. Stevens, Patterns in Nature (Little Brown, Boston, 1974).

[3] H. Meinhardt, Models of Biological Pattern Formation (Academic Press, New York, 1982).

[4] J. Binney and S. Tremaine, Galactic Dynamics (Princeton University Press, Princeton, 1987).

[5] S. Chandrasekhar, Hydrodynamic and Hydromagnetic Stability (Oxford University, London, 1961).

[6] B. Chalmers, Principles of Solidification (Wiley, New York, 1964).

[7] L. A. Segel, Mathematical Models of Molecular and Cellular Biology (Cambridge University Press, Cambridge, 1980).

[8] P. G. Saffman and G. I. Taylor, Proc. R. Soc. LondonSer. A 245, 312 (1958).

[9] For review articles on this subject, see D. Bensimon,L. P. Kadanoff, S. Liang, B. I. Shraiman, and C. Tang, Rev. Mod.Phys. 58, 977 (1986); G. Homsy, Ann. Rev. Fluid Mech.19, 271 (1987); K. V. McCloud and J. V. Maher, Phys. Rep. 260, 139 (1995).

[10] H. S. Hele-Shaw, Trans. Inst. Naval Arch. 40, 21 (1898).

[11] R. L. Chuoke, P. van Meurs and C. van der Poel, J. Pet. Technol.11, 64 (1959).

[12] R. L. Chuoke, P. van Meurs and C. van der Poel, Petrol. Trans. AIME 216, 188 (1959).

[13] L. Paterson, J. Fluid Mech. 113, 513 (1981).

[14] J. A. Miranda and M. Widom, Int. J. Mod. Phys. B 12, 931 (1998).

[15] J. A. Miranda and M. Widom, Physica D 120, 315 (1998).

[16] R. E. Rosensweig, Ferrohydrodynamics (Cambridge University Press, Cambridge, 1985), and references therein.

[17] A. O. Tsebers and M. M. Maiorov, Magnetohydrodynamics 16, 126 (1980).

[18] A. O. Tsebers and M. M. Maiorov, Magnetohydrodynamics 16, 231 (1980).

[19] A. O. Tsebers and M. M. Maiorov, Magnetohydrodynamics 16, 21 (1980).

[20] A. G. Boudouvis, J. L. Puchalla, L. E. Scriven, J. Colloid Interface Sci. 124, 688 (1988).

[21] A. J. Dickstein, S. Erramilli, R. E. Goldstein, D. P. Jackson and S. A. Langer, Science 261, 1012 (1993).

[22] S. A. Langer, R.E. Goldstein and D. P. Jackson, Phys. Rev. A. 46, 4894 (1992).

[23] D. P. Jackson, R. E. Goldstein and A. O. Cebers, Phys. Rev. E 50, 298 (1994).

[24] L. W. Schwartz, Phys. Fluids A 1, 167 (1989).

[25] Ll. Carrillo, F. X. Magdaleno, J. Casademunt and J. Ortín, Phys. Rev. E 54, 6260 (1996).

[26] J. A. Miranda, Phys. Rev. E 62, 2985 (2000).

[27] A. O. Tsebers, Magnetohydrodynamics 17, 113 (1981).

[28] D. P. Jackson and J. A. Miranda, unpublished (2000).

[29] A. O. Tsebers and A. A. Zemitis, Magnetohydrodynamics 19, 360 (1983).

[30] A. Cebers and I. Drikis, Magnetohydrodynamics 32, 11 (1996).

[31] A. G. Papathanassiou and A. G. Boudouvis, Magnetohydrodynamics 35, 314 (1999).

[32] M. Zeybek and Y. C. Yortsos, Phys. Rev. Lett. 67, 1430(1991).

[33] M. Zeybek and Y. C. Yortsos, J. Fluid Mech. 241, 421 (1992).

[34] P. Gondret and M. Rabaud, Phys. Fluids 9, 3267 (1997).

[35] J. A. Miranda and M. Widom, Phys. Rev. E 61, 2114 (2000).

Publication Dates

• Publication in this collection
  26 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  07 Nov 2000