Mössbauer spectroscopy, superparamagnetism and ferrofluids

Mössbauer spectroscopy, superparamagnetism and ferrofluids

H.-D. Pfannes, J. H. Dias Filho, R. Magalhães-Paniago,

J. L. López, and R. Paniago

Laboratory for Hyperfine Spectroscopy and Surface Physics

Departamento de Física, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil

Received on 21 December, 2000

Some fundamentals of Mössbauer spectroscopy and of fluctuating magnetic hyperfine interactions are reviewed. An expression for calculation of spin-phonon interaction transition probabilities on the ground of a Debye model is given. Basic ideas of superparamagnetism and classical results for low-temperature relaxation rates are presented. A theory of superparamagnetism based on spin-phonon interaction is introduced. It is shown how to calculate from this Mössbauer spectra taking all spin-levels into account. Experimental spectra of ferrofluids are compared with simulated spectra and found in good accordance.

I Introduction

The Mössbauer effect is based on the "recoilless" absorption and emission of low energy (E₀=10-100keV) g-photons in solids [1, 2]. A simple explanation for this effect relies on the Heisenberg uncertainty relation: the uncertainty in momentum Dp » /Dx of bound atoms is of the order of 10^-23 kgms^-1 (Dx = 0.1Å) but the recoil moment of e.g. a g-photon with energy E₀=10keV is smaller (» 5 · 10^-24 kgms^-1), i.e. the recoil which eventually can excite vibrations (phonons) of the emitting atom sometimes may not be measurable. The recoil is then transmitted to the crystal as a whole and since the mass of the crystal is much greater than the atomic mass it does not alter the g-energy ("recoilless" emission). The Mössbauer radiation emitted from a Mössbauer source has therefore the exact resonance energy necessary for absorption in an absorber containing the same material as the source. Moreover, when the lifetime t of the excited Mössbauer energy level is longer (e.g. t = 10^-7s) than the inverse vibration (phonon) frequency of the emitting or absorbing atom (e.g. 10^-13s) the atom carries out many cycles during the lifetime and the Doppler broadening of the emitted radiation averages out. As a result a sharp line with the natural linewidth G = /t at the position E₀ is emitted from the source and nuclear resonance absorption with an energetic resolution G/E₀ = 10^-13, sufficient to resolve hyperfine interactions, is possible [2]. The above mentioned conditions for recoilless emission limits the Mössbauer isotopes to those isotopes which possess low energy nuclear g-transitions (small recoil moment), long lifetimes of the excited state (hyperfine resolution), high Debye temperature (small Dx) and solid sources and absorbers. These conditions are ideally fulfilled for ⁵⁷Fe which is indeed the most popular Mössbauer isotope. Fig. 1 shows schematically the decay scheme of ⁵⁷Co, which is used as parent for a ⁵⁷Fe Mössbauer source. The Mössbauer resonant absorption and varios re-emissions are also indicated in Fig.1. In order to vary the energy of the Mössbauer radiation emitted by the source in the range of hyperfine energies and thus render possible Mössbauer spectroscopy it is sufficient to move the source with some mm/s. The intensity of the Mössbauer photons behind the absorber as function of the relative velocity between source and absorber represents a Mössbauer (transmission) spectrum as shown schematically in the insert of Fig.1.

I.2 Hyperfine Interactions

The interaction of the extended nuclear charge with electrons present in the nuclear volume leads to a shift of the center of the spectrum (isomer shift) and provides information on the valence state of the Mössbauer atom.

An electric field gradient present at the nucleus' site interacts with the nuclear electric quadrupole moment and results in a (quadrupole) splitting of a single Mössbauer line (into two lines for nuclei with nuclear spin of the ground and excited states, I_g,e = 1/2, 3/2, respectively). This nuclear quadrupole interaction allows conclusions on the valence, bonding properties and symmetry of the vicinity of the Mössbauer atom.

The magnetic hyperfine interaction is especially important in our context. The main part of it stems from the Fermi contact interaction which is the interaction of the nuclear magnetic dipole moment with a net spin-up or down s-electron density at the nucleus. It can be represented by a spin-Hamiltonian [2]

where

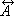
is the hyperfine tensor. When the hyperfine tensor is isotropic, i.e.

H

_mhf =

AS

_z

I

_z with the hyperfine interaction constant

A, we can interpret it as a nuclear Zeeman effect due to the field

B

_n at the nucleus' site (inner field)

For a Mössbauer isotope with I_g,e=1/2, 3/2 a six-line spectrum with relative intensities depending on the angle between the g-direction and the z-axis results. The presence of six lines in a ⁵⁷Fe Mössbauer spectrum thus indicates the presence of a (static) magnetic field at the nucleus which may be caused by long range order magnetism.

I.3 Fluctuating hyperfine fields

Fluctuations of the hyperfine interactions can alter the spectra. E.g. when B_n changes it's direction many times during the lifetime of the excited state the nucleus "sees" only an average zero field and the splitting collapses.

It can be shown that the Mössbauer absorption spectrum I(w) observed in the energy (frequency) domain, i. e. the number of counts in transmission direction behind the absorber as function of the source velocity v, is given by the real part of the trace of the spectrum of the temporal correlation function of the Mössbauer radiation operator A (e.g. magnetic dipole radiation) as [3, 4]

where

p = G/2 -

iw(

E

₀ =

w =

E

₀

v/

c) and r is the density operator of the whole system. It is advantageous here to use superoperators and Hamilton superoperators

H

^x (Liouville operators) in order to avoid time ordering problems when

H(

t) is not commuting with itself at different times as is the case when combined nuclear quadrupole and (non-diagonal) magnetic hyperfine interaction is present. A superoperator

A

^x acts on another operator

B in the form

A

^x

B =

A

⁺

B -

BA which is equal to the commutator [

A,

B] when the operator

A is hermitian. The Liouville operators can be represented in a projector base |

ij) = |

i > <

j| of the Hamiltonian eigenstates |

i > and |

j > and the eigenvalues of

H

^x are the spectroscopic important differences (

E

_i-

E

_j). The product (

B|

A) is given by (

B|

A) =

Tr(

B +

A) and the time evolution

A(

t) of an operator

A can be written exp(

iHt)

Aexp(-

iAt) = exp(

i

H

^x

t)

A(0). We can then write [4]

Here a practical difficulty arises: H^x comprises the entire solid (nucleus-electrons-phonons- photons and interactions) and the calculation of I(w) involves the inversion of matrices with huge dimensions. Two simplifying approaches have been used: the stochastic and ab initio models. We present here some ideas on the latter model.

The Hamiltonian of the system is subdivided

One shows then that under the assumptions

H

^x

_Bath-Ion <<

H

_Ion,

H

_Bath (convergency of approximation solution) and r = r

_Ion·r

_Bath (irreversible Bath-Ion interaction) the Mössbauer spectrum is given by [4, 5]

where the relaxation superoperator

R contains matrix elements of the spin-operator

S

_q and bath correlation spectral densities which depend on bath-operators

F

_q. Here the ion-bath interaction was described by a

dynamical spin Hamiltonian

H

_Ion-Bath = å

_q

S

_q

F

_q.

E.

g. in 2

^nd order of

H

^x

_Ion-Bath after some tedious calculation one obtains as relaxation supermatrix elements [5]

with the reservoir correlation spectral densities

where the bath operators F are in the interaction representation. When I and I" _q¢q are independent of w ("white noise approximation", normally valid in the case of spin-phonon relaxation), the matrix elements (eg|R|eg) are transition probabilities W between the states |e > and |g >.

I.4 Spin-phonon interaction

Simplifying, we start with a dynamical spin-Hamiltonian which represents the spin-phonon interaction in 2^nd order perturbation theory (B are coupling constants) [6,7]

with the averaged strain operator

The equivalent operators O contain the ladder operators S. We take only direct processes into account (see Fig.2) where the absorption (annihilation) or emission (creation) of a phonon leads to a spin transition.

The spectral bath correlation density can then be calculated in the harmonic approximation by introducing the Debye model. In the long-wavelength limit (w = vk) we obtain (r = M/V = density, v = averaged sound velocity)

and the spin-phonon transition probabilities (cf.

Fig.2) are

With these relations paramagnetic spin-phonon relaxation spectra of e.g. Fe(III) impurities (S = 5/2) can be calculated, eventually using effective spins - [5] because the supermatrix for S = 5/2 has already a rank of (2I_g + 1)(2I_e + 1)(2S + 1)² = 288 for ⁵⁷Fe and is not hermitian. An example for Fe(III) impurities in monocrystals of LiNbO₃ is given in [8]. For bigger spins like that corresponding to the total magnetic moment of magnetic nanoparticles (S = 1000-10000) the rank of the supermatrix involved would be of the order of 10⁸, without any possibility of numerical treatment. But it is yet possible to realize calculations for big spins when only diagonal interaction is present and thus no superoperator formalism is needed for the combined stochastic-quantum mechanical problem (see be below in section II.4).

II Superparamagnetism

Superparamagnetism has to do with the thermally induced inversion of the magnetization of small (nano-sized) magnetic particles. This is an important phenomenon since ultra-fine magnetic particles are important in many systems, e.g. in soils, rocks, argiles, ceramics, paintings, living organisms (ferritin, magnetic bacteria, magnetically based navigation of animals), recording media (what is the ultimate magnetic storage density?), catalysts, etc. and ferrofluids.

II.1 Basic ideas of superparamagnetism

When the dimensions of a small magnetic particle are of the order of the width of a Bloch wall the particle will be a single domain particle. At low temperatures the spin waves are frozen and thus the magnetization is equal to the spontaneous magnetization M_s. Since the exchange (or superexchange) interaction is predominant compared to anisotropy interactions |M| may be regarded as constant so that the only degree of freedom of the magnetization would be it’s orientation q relative to some (uniaxial) anisotropy axis. When measuring a property related to the magnetization at T > 0 it may happen that the magnetization fluctuates (thermally activated) between easy directions and the characteristic time of measurement is greater than the (overbarrier) fluctuation time of the magnetization. In this case we say that superparamagnetic behavior is measured (the measurement method "sees" only the time-averaged value). From now on we will use the following simplifications: only an uniaxial symmetry of the form [9-12]

is present (

K = anisotropy constant,

V = volume of the particle), the external field

B is parallel to the positive

z-direction, all particles are identical in material, form and spatial orientation and are uniform (no surface effects) and isolated (no particle-particle interaction) and the rotation of the magnetization happens by coherent rotation of the spins ("unison"). Under these circumstances various authors deduced expressions for the relaxation time t of reversions of the magnetization between the easy ±

z-directions.

Néel [11] relates the vibrational strain energy of the particles to it’s thermal energy and calculates the magnetic energy caused by the deformation. At low temperature he obtains

where G is Young's modulus, g₀ = gm_B/» ge/m is the gyromagnetic ratio, a = KV/k_BT and h = BM_s/2K is the reduced external field (0 £ h £ 1).

Brown [12] considers a random walk of the magnetization on a sphere similar to Brownian motion. In the classical equation of motion of the magnetization (Gilbert's equation) a dissipative and random field term h(t) is introduced. A Fokker-Planck equation is obtained which is approximately solved. The result for low temperature (a << 1) is

This expression is widely used in the literature but it's not valid for high temperatures and h » 1.

Bessais, Ben-Jaffel, Dormann [13] find more exact solutions of the Fokker-Planck equation by using Fourier and Chebyshev series and deduce

Villain et al. [14] analyze paramagnetic like relaxation in magnetic molecules with S = 10 due to spin-phonon interaction. The corresponding relaxation rate was calculated to

Jones, Srivastava [15] introduce the "many states model" in order to calculate Mössbauer spectra (see below in section II.4). For a large (classical) spin (continuum limit) they also deduce from this model a Fokker-Planck like equation and solve it in the low temperature regime and obtain (R µ square of a random field)

One observes that all these expressions contain the same Arrhenius-like exponential factor but various prefactors. In principle they are only valid in the low temperature regime. No microscopic, non-phenomenological explanation of the superparamagnetic mechanism is given by the above authors.

II.2 Superparamagnetism by spin-phonon relaxation

Recently a mechanism for superparamagnetic relaxation based on spin-phonon interaction was suggested [16]. We shortly repeat here the main ideas and results of this work.

The supposed unison rotation of the spins suggests the attribution of a large spin to the magnetization defined by M_sV = gm_BS. Relating Scosq to the spin operator S_z and suppressing a constant term KV, the anisotropy energy (13) corresponds to a spin-Hamiltonian

where g is the electronic g-factor, m_B the Bohr magneton and AS² = KV (height of the barrier for B = 0). The superparamagnetic relaxation of the particles is assumed to be induced by interaction of the large spin S with the phonons of the particle (or of a bath). In order to turn over between opposite easy directions the spin S must pass through intermediate levels characterized by S_z. Eigenvectors of (19) are |S_z > = |m > , with eigenvalues E_m = -AS- 2AhSS_z for S_z = -S, -S+1, ..., S-1, S. Fig. 3 shows a graph of E_m vs. m and a possible phonon induced spin transition between the lowest levels of both sides of the barrier.

Figure 3.
Anisotropy energy vs. eigenvalues with applied magnetic field. Spin transitions from |-S > to |S > with Dm = Dn = 2 are indicated.

II.3 Calculation of a relaxation time for |S > « | -S >

The spin transition rate induced by phonons is given in (12). Considering only the relaxation |S > « |-S > under the condition that the occupation of all intermediate levels remains constant (pseudo two level system) and assuming detailed balance, a rate equations system (master equations) can be established and solved for a relaxation time t_± [16]. In the case of spin jumps with Dm = Dn = 2 we obtain (C¢ = (3(B₁p)²/2p⁴rv⁵)(AS²)³, a_± = a(1 ± h)²)

with

A good approximation up to

h » 0.95 is

Here S = 3222, r = 5000kgm^-3, v = 3000ms^-1 and KV = AS² = 2.67·10^-20J was assumed, which are typical values for a 90Å MnFe₂O₄-particle with 5 spins per unit cell of 8.4Å lattice constant [16, 17]. For the only free parameter, the coupling parameter B, a value of 13cm^-1 was chosen, which results in relaxation rates in accordance with the experiments.

The functional dependence on the anisotropy energy KV, temperature T and external field (h) in the expressions (14)-(18) and (21) is similar. They contain the same Arrhenius-like factor and differ only slightly in the field dependence of the pre-factor, which is proportional to (1 - h²)(1 ± h) in (15) and (18) instead of (1 - h²)(1 + h)(1 - h) in (21). In view of the completely different physical approach used this may be remarkable. Of course all the expressions differ in the other factors which appear in the pre-factor since they depend on the parameters involved in the specific model. We conclude that our model adequately describes superparamagnetism.

On the basis of (21) Mössbauer spectra can be calculated using an effective spin. At low temperature experimental spectra can be reproduced [17]. Spectra at somewhat higher temperature can approximately reproduced taking collective excitations, i. e. a thermally averaged inner field, into account. However for higher temperatures this method fails and calculations based on the method presented in the following are indicated.

II.4 Multi-level calculation of Mössbauer spectra

In the case of isotropic magnetic hyperfine interaction and diagonal nuclear Hamiltonian (nuclear quadrupole interaction << magnetic hyperfine interaction) the expression (6) and (7) can be simplified so that no superoperators are needed. Furthermore one can simulate a Mössbauer spectrum by summing up three separately calculated spectra consisting of the pairs of lines (1-6), (2-5), (3-4) in the six-lines spectrum. The simplified expression [15] for one pair of lines reads

where

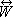
is a row vector consisting of probabilities (Boltzmann factors) of the (2

S+1) states and

M contains the static line positions w

_i, given by the splitting (1-6), which is assumed to be proportional to

S

_z. The relaxation matrix

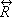
has as elements transition probabilities

r

_ij =

W

_ij between the states |

i > ® |

j > (

i ¹

j) and

r

_ii = -å

_j

W

(

i ¹

j). The total Mössbauer spectrum is obtained by summing up the three calculated two-lines spectra (1-6), (2-5) and (3-4), where in the calculation of the w

_i adequately reduced splittings (2-5) and (3-4), still proportional to

S

_z, and the same transition probabilities as in the calculation of (1-6) are used.

As before, for the spin-transitions DS_z = 2 is presumed. We take therefore only spin-matrix elements, that contain S, into account, which results in transition probabilities

The Boltzmann factors contained in 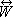are

Introducing these expressions in (22) one can simulate Mössbauer spectra. The inverse of is required for each value of w (256 Mössbauer velocities), involving a order of 256 times N³ operations for a matrix of rank N. In our case is tridiagonal and thus only of the order of 256N² operations are necessary for inversion. A further significant saving in computer time is obtained by observing that in (22) in fact not the inverse ^-1 but only ^-1 is needed. Writing ^-1 = or the = 1 problem is reduced to solve a set of simultaneous linear equations for which requires only an order of 256N operations [15, 18]. This method allows one to simulate spectra for spins S up to several thousand, corresponding to spins found in real systems, on a modest computer in a few minutes.

Fig. 4 shows some simulations of spectra using this multi-level relaxation method for a spin S = 3222 at different temperatures and several external magnetic fields. The parameters used in the calculations of the transition probabilities are that of eq. (21).

Figure 4.
Simulated Mössbauer spectra at different temperatures and zero external field (left) and different fields at 600K (right). See text.

Despite the above described possibility of rapid simulation of spectra for a large spin it may sometimes be necessary to use a smaller (reduced) spin in order to calculate real spectra. E. g., if the simulation of powder spectra is desired, one has to effect an average over the different orientations of the crystallites relative to the external field- and g-direction. This implies in the presence of a field component perpendicular to the z-axis, which results in a mixture of the spin levels, so that is no longer tridiagonal. Furthermore, when size-dispersion is present, as is always the case in real samples, one has also to sum up sufficiently spectra corresponding to different volumes (and anisotropy constant values K, which often depend on the crystallite size).

We compared therefore spectra simulations for different values S_red of reduced spins at different temperatures. The result is shown in Fig. 5. It can be seen that practically identical spectra are obtained for different spins when the temperature is reduced by a factor of approximately S/S_red. One can therefore use a smaller spin S_red in practical simulations.

Figure 5.
Variation of S, S = 3222, 322, 32 (simulation time = 5min, 20s, 3s).

III Application to ferrofluids

Many ferrofluids are based on nano-sized particles of ferrites. Static Mössbauer spectra of ferrites can normally be satisfactorily fitted by two sextets with relative total area corresponding to the ratio of ⁵⁷Fe atoms on octahedral and tetrahedral substitutional sites (Néel model [19]). However, for simplification of the calculations, we use in the following simulations only one single sextet with larger (~ 0.4mms^-1) linewidth and suppress also the quadrupole splitting. In the calculations also the size distribution (log-normal distribution with mean diameter d₀ and width s) as deduced from the sample synthesis and electron microscopy has been taken into account by summing up spectra (sample synthesis by F.A. Tourinho, UnB, Brasilia). The random orientation of the nanoparticles has been counted for by using relative line intensities in the sextets of 3:2:1. Fig. 6 shows experimental spectra of a NiFe₂O₄ based frozen ferrofluid in the temperature range T = 90...4.2K. In the corresponding simulations a reduced spin S_red depending on the crystallite diameter d (size distribution) defined by S_red(d) = S(d₀)(d/d₀)³ with S(d₀) = 32 and reduced temperatures T_red = T(S_red/3222) were used.

Figure 6.
Spectra of frozen NiFe₂O₄-ferrofluid, d₀ = 10nm (left) and simulations with S_red(d₀) = 32 and reduced temperatures, log-normal size distribution (s = 0.1, d₀6 = 10 nm), K = 4 · 10⁴Jm^-3, no quadrupole interaction.

Similarly, Fig.7 shows experimental spectra and simulations of a powder of CoFe₂O₄, precursor of a cobaltferrite based ferrofluid. The simulations have been done analogously to those of Fig.6. Considering the various simplifications made the coincidence of experimental and simulated spectra is satisfactory.

IV Conclusion

Experimental superparamagnetic Mössbauer line patterns are reproduced by ab-initio simulations based on a spin-phonon interaction model and taking intermediate spin levels into account, without using a thermallly averaged hyperfine field due to collective excitations. We use spin-transitions probabilities per time W_i^j derived from a dynamic spin-Hamiltonian (weak spin-bath interaction) that induces transitions in the spin and phonon subsystems and adopt the Debye model in the long wavelength limit.

With this method one is able to calculate Mössbauer spectra for S=3222 within several minutes (provided that the relaxation matrix R is tridiagonal) on a small personal computer. Comparison of spectra calculated with a smaller spin exhibit similar shapes than that of the "real" spin S, provided the temperature is adequately reduced. Simulations of Mössbauer spectra of ferrofluids-ferrites are compared with real spectra and show good correspondence.

References

[1] R.L. Mössbauer, Z. Physik 151, 124 (1958); Naturwissenschaften 45, 538 (1958); Z. Naturforsch. 14a, 211 (1959).

[2] V.I. Goldanskii, R.H. Heber, Chemical applications of Mössbauer Spectroscopy, Academic Press, New York, 1968.

[3] S. Dattagupta, G.K. Shenoy, B.D. Dunlap and L. Asch, Phys. Rev. B16, 3893 (1977).

[4] L. Cianchi, P. Moretti, M. Mancini and G. Spina , Rep. Progr. Phys. 49, 1243 (1986).

[5] H.D. Pfannes, Hyp. Interact. 110, 127 (1997).

[6] R. Orbach, H.J. Stapleton, in: Electron Paramagnetic Resonance, ed. S. Geschwind (Plenum Press, New York, 1972).

[7] K.K.P. Srivastava, S.N. Mishra, Phys. Stat. Sol. (b) 100, 65 (1980).

[8] H.-D Pfannes, R. Magalhães-Paniago, E. Bill, A. X. Trautwein, Hyp. Interact. 94, 2005 (1994).

[9] S. Mfrup, J. A. Dumesic, H. Topsfe, in:Applications of Mössbauer Spectroscopy, Vol. II, ed. R. L. Cohen (Academic Press, New York, 1980).

[10] J. L. Dormann, Revue Phys. Appl. 16, 275 (1981).

[11] L. Néel, Ann. Geophys. 5, 99 (1949).

[12] W.F. Brown, Jr., Phys. Rev. 130, 1677 (1963).

[13] L. Bessais, L. Ben Jaffel, J. L. Dormann, Phys. Rev. B45, 7805 (1992).

[14] J. Villain, F. Hartmann-Boutron, R. Sessoli, A. Rettori, Europhys. Lett. 27, 159 (1994).

[15] D.H. Jones, K.K.P. Srivastava, J. Mag. Magn. Mat. 78, 320 (1989).

[16] H.-D. Pfannes, A. Mijovilovich, R. Magalhães-Paniago and R. Paniago, Phys. Rev. B 62, 3372 (2000).

[17] H.D. Pfannes, J.H. Dias Filho, J.L. López, S.L. Pereira, P.C. Morais, F.A. Tourinho, Hyp. Interact. 113, 507 (1998).

[18] H.-D. Pfannes, J. H. Dias Filho, R. Magalhães-Paniago and R. Paniago, J. Mag. Magn. Mat. (2001) in the press.

[19] L. Néel, Ann. Phys. 3, 137 (1948).

Publication Dates

• Publication in this collection
  26 Mar 2002
• Date of issue
  Sept 2001

History

• Received
  21 Dec 2000