Abstract
Following up the detailed three-dimensional analysis of the particle dynamics in a free electron laser with a helical wiggler and a uniform axial guide magnetic field, achieved by Rhimi et al. [1], we study the motion of the electrons in the neighborhood of the ideal trajectory. The normal modes <img src="http:/img/fbpe/bjp/v31n3/shace.gif">± of the quadratic Hamiltonian are analyzed numerically in both the normal and reversed-field configurations for different values of the ratio <img src="http:/img/fbpe/bjp/v31n3/20eq01.gif">w/<img src="http:/img/fbpe/bjp/v31n3/20eq01.gif">0. The electron trajectories are thus discussed. It is found that pseudo-circular and elliptic trajectories are characterizing both group-I and reversed-field group-II modes while the motion in the normal group-II mode is much more complicated.
Normal modes propagation in a helical free-electron laser with an axial guide field
Riadh El-Bahi, Mohamed Nazih Rhimi, and Abdel Wahab Cheikhrouhou
Department of Physics, Faculty of Sciences,
University of Sfax,
B.P 802, Sfax 3018, Tunisia
Received on 5 January, 2001
Following up the detailed three-dimensional analysis of the particle dynamics in a free electron laser with a helical wiggler and a uniform axial guide magnetic field, achieved by Rhimi et al. [1], we study the motion of the electrons in the neighborhood of the ideal trajectory. The normal modes
± of the quadratic Hamiltonian are analyzed numerically in both the normal and reversed-field configurations for different values of the ratio
w/
0. The electron trajectories are thus discussed. It is found that pseudo-circular and elliptic trajectories are characterizing both group-I and reversed-field group-II modes while the motion in the normal group-II mode is much more complicated.
I Introduction
The electron dynamics in a Free Electron Laser (FEL) with a helical wiggler field and a uniform axial guide field has been the subject of many researches [1-10], in particular when the spatial dependence of the wiggler field is included. It was established in early works that a particular case of steady motion exists, in which the electrons follow an axially centered helical path with constant axial velocity in such a way that the transverse velocity vector of the electron is parallel or anti-parallel to the transverse magnetic field at each point. Of course, now electron is likely to follow this ideal trajectory, and the question of what the non- ideal trajectories look like arises. Freund and Ganguly [3] have studied the equations of motion in the neighborhood of the ideal trajectory, and have obtained two squared frequencies, which characterize the oscillations of the electrons about it. Rhimi et al. [1] have extended this work by using guiding centers coordinates to show that the key quantity (called  z¢) is a combination of linear and orbital momentum which is conserved along any trajectory as a consequence of the screw-displacement symmetry of the magnetic field. For a given electron, one determines the value of
z¢) is a combination of linear and orbital momentum which is conserved along any trajectory as a consequence of the screw-displacement symmetry of the magnetic field. For a given electron, one determines the value of  z¢ from the initial conditions, and provided certain conditions are met, a fixed point of the Hamiltonian exists. The Hamiltonian is then expanded about the fixed point, and its quadratic term may be reduced by the use of the properties of the "rotational" variable
z¢ from the initial conditions, and provided certain conditions are met, a fixed point of the Hamiltonian exists. The Hamiltonian is then expanded about the fixed point, and its quadratic term may be reduced by the use of the properties of the "rotational" variable  to two uncoupled harmonic oscillators of characteristic frequencies
to two uncoupled harmonic oscillators of characteristic frequencies  ±, and amplitudes |
±, and amplitudes | ± (
± ( = 0)|2 that are constants of motion.
= 0)|2 that are constants of motion.
In this paper, we continue the work of ref. [1] with the study of the trajectories described by those harmonic oscillators. The general behavior of the rotational variable
± as a function of the normalized radius has been investigated for the values 0.05 and 0.3 of the ratio w/
w/ 0. Provided that the magnitudes of the oscillator amplitudes are not too large, the electron dynamics in the neighborhood of the steady-state trajectories can be described accurately using our method. It is the behavior of those amplitudes with right to the beam radius that is one of the most important tasks of our work. As a matter of fact, it is through the extension of of the canonical transformation of Chen and Davidson[5] and the definition of the rotational variable
0. Provided that the magnitudes of the oscillator amplitudes are not too large, the electron dynamics in the neighborhood of the steady-state trajectories can be described accurately using our method. It is the behavior of those amplitudes with right to the beam radius that is one of the most important tasks of our work. As a matter of fact, it is through the extension of of the canonical transformation of Chen and Davidson[5] and the definition of the rotational variable  that our formalism showed to be efficient to deal with the physical insight of the problem.
that our formalism showed to be efficient to deal with the physical insight of the problem.
The organization of the paper is as follows: The problem formulation is given in section II. Section III is devoted to the quadratic approximation to the Hamiltonian and the investigation of normal modes. We end by the conclusions.
II Problem formulation
The physical configuration we employ is that of a relativistic electron beam propagating through an ambient magnetic field composed of a helically symmetric and periodic helical wiggler field, and a uniform guide field
where
B
0 denotes the magnitude of the guide field, and the wiggler field
B
w is taken to be that generated by a bifilar helix [11]
represents the wiggler field in cylindrical coordinates. In Eq. (2),
B
w describes the wiggler amplitude,
k
w=2p/l
w is the wiggler wave number, l
w is the wiggler period, and
I
n(
k
w
r) and
I¢
n(
k
w
r) represent the modified Bessel function of order
n and its derivative, respectively.
The self-electric and self-magnetic fields are neglected within the neutral electron beam. Then it follows from the steady-state Maxwell equation that B=Ñ×A and the vector potential can be written as
The Hamiltonian that governs the motion of an electron within the beam is:
where
P is the canonical momentum,
c is the velocity of light, -
e and
m are the charge and the mass of the electron, respectively; and g is the relativistic mass factor
and the mechanical momentum
p is related to the canonical momentum
P by
III Hamiltonian quadratic approximation and normal modes
In addition to the energy, the second constant of motion
z¢ is given by [1]
where
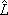
z is the
z-component of the angular momentum,

f =
 exp(
exp(
if) and

y =
 exp(
exp(
iy) are the rotational variables corresponding to the angles f and y, respectively
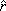
c = (2
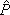
f/

0)
1/2 is the gyroradius and
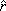
c = (2
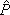
y/

0)
1/2 is the guiding radius [8].
Introducing dimensionless parameters and variables defined by
the Hamiltonian given by Eq.(4) is then expressed in the dimensionless form as
where  0w = eB0,w/mc2kw are the dimensionless non-relativistic frequencies and the complex quantity K is
0w = eB0,w/mc2kw are the dimensionless non-relativistic frequencies and the complex quantity K is
The complex quantity
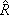
in the last equation is given by
The one-dimensional case corresponding to K = 1 has been studied extensively in the litterature [2, 5-9]. The three-dimensional case was undertaken by Freund et al. [3] and Rhimi et al. [1] in different manners. Provided a fixed point exists and after expanding the Hamiltonian in a Taylor series about it, and retaining only the lowest order terms, we obtain [1]
where
0 is the steady state Hamiltonian evaluated at the fixed points (exactly helical trajectories) and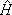 Q is the quadratic part of the Hamiltonian. Treating
Q is the quadratic part of the Hamiltonian. Treating 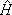 Q yielded two uncoupled harmonic oscillators whose characteristic frequencies and amplitude are
Q yielded two uncoupled harmonic oscillators whose characteristic frequencies and amplitude are  + and
+ and  -, and
-, and  + and
+ and  - respectively. The quadratic piece of the Hamiltonian is thus written as:
- respectively. The quadratic piece of the Hamiltonian is thus written as:
and the solution to Hamiltons equations are simply
giving two obvious constants of motion

±(
t = 0). The complete solution to the problem, in the quadratic approximations, has thus been found.
Expressing the oscillator rotational variables
± as a linear combination of the different actions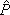 f and
f and 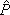 y, and corresponding angles f and y
y, and corresponding angles f and y
The normalization of the rotational variable
± is obtained by requiring that the Poisson bracket of ± with its complex conjugate
± with its complex conjugate 
 be
be
which is equivalent to imposing
The investigation of these coefficients that depend only on the ratio

w/

0 and the normalized radius
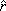
0, will allow the study the different modes of propagation and to identify, and then avoid the problematic operating conditions of the concerned FEL.
The general behavior of these coefficients as functions of
0 and w/
w/ 0 is shown in Figs. 1-4. The range of
0 is shown in Figs. 1-4. The range of 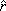 0 in each figure has been limited to values such that the lower characteristic frequency
0 in each figure has been limited to values such that the lower characteristic frequency  - is real. Both group I (
- is real. Both group I (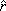 0 < 0) and group II (
0 < 0) and group II (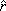 0 > 0) are represented in Figs. 1 and 3
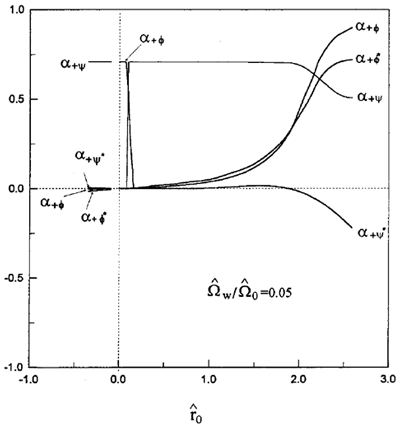
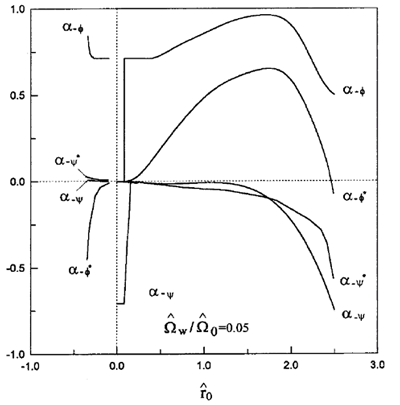
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
for
0 > 0) are represented in Figs. 1 and 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
for  w/
w/ 0 = 0.05 and in Figs. 2 and 4
Figure 4. Same as in Fig. 3, for w/0 = 030.
The behavior of the group-II motion is much more complicated, as is apparent in Figs. 1-4. First, in group-II reversed-field characterized by small positive values of 0 (0 < - w/0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/, respectively and all others are much smaller in magnitude. The rotational variable + may thus be identified with (f- f0- if) (constant gyroradius trajectory) while - is described by (y- y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2f0/0)1/2 and (2y0/0)1/2 swept out with frequencies + and -, respectively. For group-II reversed field where 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
for
0 = 0.05 and in Figs. 2 and 4
Figure 4. Same as in Fig. 3, for w/0 = 030.
The behavior of the group-II motion is much more complicated, as is apparent in Figs. 1-4. First, in group-II reversed-field characterized by small positive values of 0 (0 < - w/0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/, respectively and all others are much smaller in magnitude. The rotational variable + may thus be identified with (f- f0- if) (constant gyroradius trajectory) while - is described by (y- y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2f0/0)1/2 and (2y0/0)1/2 swept out with frequencies + and -, respectively. For group-II reversed field where 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
for  w/
w/ 0=0.3. First, we see in both Figs. 1 and 2, that for group I, the coefficient a+y» 1/
0=0.3. First, we see in both Figs. 1 and 2, that for group I, the coefficient a+y» 1/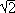 , while a+f, a+f* and a+y are much smaller in magnitude. This implies that the rotational variable
, while a+f, a+f* and a+y are much smaller in magnitude. This implies that the rotational variable  + is quasi-identical with (-(
+ is quasi-identical with (-(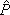 y-
y-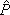 y0)-i(y-p/2)). We can expect that the rotational variable
y0)-i(y-p/2)). We can expect that the rotational variable  - should predominantly entail (
- should predominantly entail (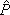 f-
f- 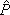 f0+if) and (
f0+if) and (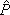 f-
f- 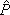 f0- if). Looking at Figs 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
and 4
Figure 4. Same as in Fig. 3, for w/0 = 030.
The behavior of the group-II motion is much more complicated, as is apparent in Figs. 1-4. First, in group-II reversed-field characterized by small positive values of 0 (0 < - w/0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/, respectively and all others are much smaller in magnitude. The rotational variable + may thus be identified with (f- f0- if) (constant gyroradius trajectory) while - is described by (y- y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2f0/0)1/2 and (2y0/0)1/2 swept out with frequencies + and -, respectively. For group-II reversed field where 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
for group I shows that the coefficients a-y and a-y* are indeed small, while at the vicinity of the stability limits (where the frequency
f0- if). Looking at Figs 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
and 4
Figure 4. Same as in Fig. 3, for w/0 = 030.
The behavior of the group-II motion is much more complicated, as is apparent in Figs. 1-4. First, in group-II reversed-field characterized by small positive values of 0 (0 < - w/0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/, respectively and all others are much smaller in magnitude. The rotational variable + may thus be identified with (f- f0- if) (constant gyroradius trajectory) while - is described by (y- y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2f0/0)1/2 and (2y0/0)1/2 swept out with frequencies + and -, respectively. For group-II reversed field where 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
for group I shows that the coefficients a-y and a-y* are indeed small, while at the vicinity of the stability limits (where the frequency  - becomes imaginary), both coefficients a-f and a-f* diverge. This divergence is accompanied by a vanishing of the frequency, so that the quadratic Hamiltonian remains finite. For smaller values of |
- becomes imaginary), both coefficients a-f and a-f* diverge. This divergence is accompanied by a vanishing of the frequency, so that the quadratic Hamiltonian remains finite. For smaller values of |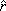 0|, a-f» 1/
0|, a-f» 1/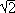 with a-f*» 0 and consequently
with a-f*» 0 and consequently  - should mainly involve (
- should mainly involve (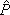 f-
f- 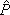 f0+ if). This advantageous situation (quazi- constant gyroradius) requires either high energy or small axial fields [1]. The contribution of the conjugate (
f0+ if). This advantageous situation (quazi- constant gyroradius) requires either high energy or small axial fields [1]. The contribution of the conjugate (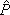 f-
f- 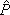 f0- if) increases with increasing |
f0- if) increases with increasing |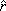 0|, making the gyroradius trajectory elliptic rather than circular. Quasi-circular transverse motion is preferable, since the trajectory is close to the steady-state orbits and the axial velocity has less ripple. Hence, on the basis of the above stated explanation, we deduce that group-I motion is lucid provided one stays far away from the stability limits.
0|, making the gyroradius trajectory elliptic rather than circular. Quasi-circular transverse motion is preferable, since the trajectory is close to the steady-state orbits and the axial velocity has less ripple. Hence, on the basis of the above stated explanation, we deduce that group-I motion is lucid provided one stays far away from the stability limits.
 + as a function of
+ as a function of  0 with
0 with  w/
w/ 0 = 0.05.
0 = 0.05. 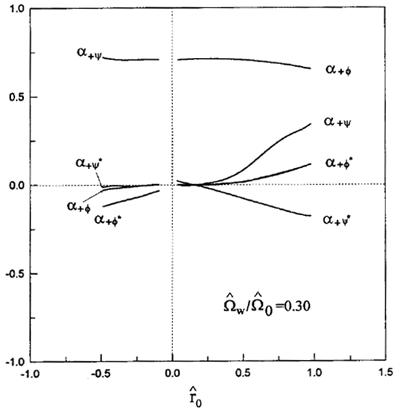
 w/
w/ 0 = 0.30.
0 = 0.30.
For the normal group-II motion, the situation remains the same up to the region of closest approach where the frequencies repel each other (
0» 0.1). In Figs. 1 and 3 Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05. , it is clear that this frequency crossing is behind the abrupt rise of the coefficients a-f and a+y to the value of 1/ and the accompanying fall of a+f and a-y to zero (
and the accompanying fall of a+f and a-y to zero (  + is converted to
+ is converted to  - and vice-versa). In this case for
- and vice-versa). In this case for 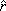 0£ 0.01,
0£ 0.01,  + describes a circle of constant gyroradius at frequency
+ describes a circle of constant gyroradius at frequency  +, while for
+, while for 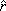 0³ 0.05,
0³ 0.05,  + , it traces out a circle of constant guiding center radius at the same frequency. On the other hand,
+ , it traces out a circle of constant guiding center radius at the same frequency. On the other hand,  - moves from a circular motion of constant guiding center radius to a circular motion of constant gyroradius but with a frequency
- moves from a circular motion of constant guiding center radius to a circular motion of constant gyroradius but with a frequency  -. Beyond
-. Beyond 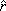 0» 0.015, as is apparent in Fig. 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
, a-f* becomes non-negligible leading to complicated trajectories. For larger values of
0» 0.015, as is apparent in Fig. 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
, a-f* becomes non-negligible leading to complicated trajectories. For larger values of 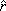 0, all coefficients become significant, and the simple behavior of the oscillator amplitudes
0, all coefficients become significant, and the simple behavior of the oscillator amplitudes  + and
+ and  - is no longer easy to touch (see Figs. 1 and 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
).
- is no longer easy to touch (see Figs. 1 and 3
Figure 3. The coefficients of the normal mode - as a function of 0 with w/0 = 0.05.
).
As seen in Figs. 2 and 4
Figure 4. Same as in Fig. 3, for w/0 = 030.
The behavior of the group-II motion is much more complicated, as is apparent in Figs. 1-4. First, in group-II reversed-field characterized by small positive values of 0 (0 < - w/0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/, respectively and all others are much smaller in magnitude. The rotational variable + may thus be identified with (f- f0- if) (constant gyroradius trajectory) while - is described by (y- y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2f0/0)1/2 and (2y0/0)1/2 swept out with frequencies + and -, respectively. For group-II reversed field where 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
and for the larger value of  w/
w/ 0 =0.3, the transition region being much larger in the variable hat r0 reaches the stability limits before being complete. All the coefficients are almost divergent and do contribute to the oscillator rotational variables
0 =0.3, the transition region being much larger in the variable hat r0 reaches the stability limits before being complete. All the coefficients are almost divergent and do contribute to the oscillator rotational variables  ± on the same feet, the thing that complicates the trajectories beyond the value of
± on the same feet, the thing that complicates the trajectories beyond the value of  0» 0.25. Obviously, such a situation worsens with increasing
0» 0.25. Obviously, such a situation worsens with increasing  w/
w/ 0.
0.
IV Conclusions
In this work, we are following up the detailed three-dimensional analysis of the particle dynamics in a Free electron laser with a helical wiggler and a uniform axial guide magnetic field, achieved by Rhimi et al. [1]. Using Eq. (12), the general behavior of the rotational variable  ± as a function of the normalized radius has been investigated for the values 0.05 and 0.3 of the ratio
± as a function of the normalized radius has been investigated for the values 0.05 and 0.3 of the ratio  w/
w/ 0. Provided that the magnitudes of the oscillator amplitudes are not too large, the electron dynamics in the neighborhood of the steady-state trajectories can be described accurately using our method. It is the behavior of those amplitudes with right to the beam radius that is one of the most important tasks of our work. A uniformly reversed guide field can present a better quality of trajectories for an electron beam drifting through the wiggler field. In fact, we observe that in the limit of intense axial guide fields the elliptic motion reduces to a circular one in which the radial displacement of the guiding-center from the axis of symmetry is constant. This simple and favorable situation persists into the normal group-II region, but for small field for the radius
0. Provided that the magnitudes of the oscillator amplitudes are not too large, the electron dynamics in the neighborhood of the steady-state trajectories can be described accurately using our method. It is the behavior of those amplitudes with right to the beam radius that is one of the most important tasks of our work. A uniformly reversed guide field can present a better quality of trajectories for an electron beam drifting through the wiggler field. In fact, we observe that in the limit of intense axial guide fields the elliptic motion reduces to a circular one in which the radial displacement of the guiding-center from the axis of symmetry is constant. This simple and favorable situation persists into the normal group-II region, but for small field for the radius  0. As the limits of stability (where one of our oscillator frequencies vanish) are approached, certain normal mode coefficients become large, and the corresponding movement unpredictable. Pseudo-circular and elliptic trajectories are characterizing both group-I and reversed-field group-II while the motion in the normal group-II is found to be much more complicated. Under certain conditions, the simple picture of the transverse motion as a superposition of the ideal helical motion and the parasitic cyclotron motion is identified.
0. As the limits of stability (where one of our oscillator frequencies vanish) are approached, certain normal mode coefficients become large, and the corresponding movement unpredictable. Pseudo-circular and elliptic trajectories are characterizing both group-I and reversed-field group-II while the motion in the normal group-II is found to be much more complicated. Under certain conditions, the simple picture of the transverse motion as a superposition of the ideal helical motion and the parasitic cyclotron motion is identified.
The explicit calculation of the orbits followed by a particle for which the present formalism is adequate, is under way and the results are postponed to a subsequent publication.
- [1] M.N. Rhimi, R. El-Bahi, and A. W. Cheikhrouhou, "Classical Harmonic Oscillator Approach of a Helical-Wiggler Free-Electron Laser with Axial Guide Field," Can. J. Phys., to appear.
- [2] R.E. Aamodt, Phys. Rev. A 28, 2895 (1983).
- [3] H.P. Freund and A.K. Ganguly, IEEE J. Quant. Electr. 7, 1073 (1985).
- [4] J. Fajans, D.A. Kirkpatrick, and G. Bekefi, Phys. Rev. A 32, 3448 (1985).
- [5] C. Chen and R.C. Davidson, Phys. Fluids B 2, 171 (1990).
- [6] C. Chen and R.C. Davidson, Phys. Rev. A 43, 5541 (1991).
- [7] L. Wang. D.L. Bosley and J. Kevorkian, Physica D 88, 87 (1995).
- [8] L. Wang and J. Kevorkian, Phys. Plasmas 3, 1162 (1996).
- [9] V.L.B. de Jesus, A.P. Guimarães, and I. S. Oliveira, Braz. J. Phys. 29, 541 (1999).
- [10] P.W. Milloni and J.H. Eberly, Lasers (Wiley, New York, 1998).
- [11] J.P. Blewett and R. Chasman, J. Appl. Phys. 48, 2692 (1977).
- [12] W. Dittrich and M. Reuter, Classical and Quantum Dynamics: from Classical Paths to Path Integrals (Springer, New York, 1994) Second ed.
 - as a function of
- as a function of  0 with
0 with  w/
w/ 0 = 0.05.
0 = 0.05.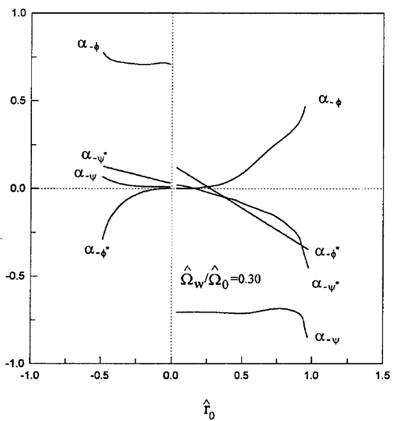
 w/
w/ 0 = 030.
0 = 030. 0 (
0 ( 0 < -
0 < -  w/
w/ 0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/
0) and where the beam and the axial fields are anti-parallel, the curves are self- explanatory. The coefficients a+f and a-y are very close to 1/ and -1/
and -1/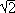 , respectively and all others are much smaller in magnitude. The rotational variable
, respectively and all others are much smaller in magnitude. The rotational variable  + may thus be identified with (
+ may thus be identified with (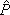 f-
f- 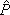 f0- if) (constant gyroradius trajectory) while
f0- if) (constant gyroradius trajectory) while  - is described by (
- is described by (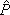 y-
y- 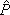 y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2
y0- i(y-p/2)) (constant guiding center radius trajectory). The trajectories of the gyroradius and the guiding center radius in the complex plane are thus circles centered at (2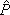 f0/
f0/ 0)1/2 and (2
0)1/2 and (2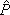 y0/
y0/ 0)1/2 swept out with frequencies
0)1/2 swept out with frequencies  + and
+ and  -, respectively. For group-II reversed field where
-, respectively. For group-II reversed field where 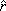 0 is very close to zero, the situation is completely comparable to the one-dimensional case [8].
0 is very close to zero, the situation is completely comparable to the one-dimensional case [8]. Publication Dates
-
Publication in this collection
27 Mar 2002 -
Date of issue
Sept 2001
History
-
Received
05 Jan 2001


















