Uma heurística baseada em geração sequencial de padrões para o problema de corte de estoque unidimensional com um número reduzido de padrões

A heuristic based on sequential pattern generation for the one-dimensional cutting stock problem with a reduced number of patterns

Uma heurística baseada em geração sequencial de padrões para o problema de corte de estoque unidimensional com um número reduzido de padrões

A heuristic based on sequential pattern generation for the one-dimensional cutting stock problem with a reduced number of patterns

Horacio Hideki Yanasse^I; Gonçalo Renildo Lima Cerqueira^II

^IInstituto Nacional de Pesquisas Espaciais - INPE CEP 12227-010, São José dos Campos - SP, Brasil e-mail: [e-mail]

^IIUniversidade Estadual do Sudoeste da Bahia - UESB CEP 50000-010, Vitória da Conquista - BA, Brasil e-mail: [e-mail]

RESUMO

Apresentamos neste trabalho uma heurística que procura determinar uma solução para o problema de corte de estoques unidimensional com um número reduzido de padrões. A heurística é composta de 3 fases. Na primeira geram-se padrões sucessivamente que são aceitos caso tenham desperdício limitado. Cada padrão aceito é repetido o máximo possível, sem que itens sejam cortados além da demanda. Neste processo de geração de padrões priorizam-se itens grandes e itens com demandas grandes. Na segunda fase, o problema residual é resolvido e, na terceira fase, uma técnica de redução de padrões da literatura é utilizada. Os testes computacionais realizados mostram que o método proposto não é dominado pelos algoritmos existentes na literatura.

Palavras-chave: Redução de padrões. Padrões de corte. Heurística.

ABSTRACT

In this work we present a heuristic that tries to determine a solution for the one-dimensional cutting stock problem with a reduced number of patterns. The heuristic is composed of 3 phases. In the first, patterns are generated successively, and they will be accepted if they have limited waste. Each accepted pattern is repeated as many times as possible avoiding cutting items in order to keep the demand. In this pattern, the generation process priority is given to large items and items with large demands. In the second phase, the residual problem is solved and, in the third phase, a pattern reduction technique reported in the literature is used. The computational tests performed show that the proposed method is not dominated by the existing algorithms in the literature.

Keywords: Pattern reduction. Cutting patterns. Heuristic.

1 Introdução

O Problema de Corte de Estoque Unidimensional - PCEU consiste em cortar a partir de objetos em estoque, uma certa quantidade demandada de itens menores de modo a otimizar uma função objetivo que pode ser, por exemplo, a minimização da quantidade de objetos processados ou dos custos da produção (DYCKHOFF, 1990; HINXMAN, 1980). A soma dos comprimentos dos itens cortados de um objeto não deve ultrapassar o seu tamanho, portanto, é preciso encontrar a maneira como tais objetos serão cortados, ou seja, estabelecer quais padrões de corte utilizar para resolver o problema. Em algumas empresas em que o problema aparece, existe também uma preocupação para que a quantidade de padrões distintos seja a menor possível, uma vez que, cada novo padrão a ser utilizado, necessita de preparação do equipamento de corte, consumindo recursos como mão de obra e tempo, que influenciam os custos de produção.

Na literatura, o PCEU aparece com diferentes objetivos como a minimização de perdas, a minimização de custos, a minimização da quantidade de objetos utilizados, etc. Existem casos em que outros custos também são considerados como os referentes à troca de padrões distintos. Um compromisso entre a quantidade de objetos e um número reduzido de padrões pode levar à aceitação de uma solução com uma quantidade ligeiramente maior de objetos cortados desde que se tenha uma menor quantidade de diferentes padrões.

Neste trabalho propomos uma heurística para resolver o PCEU com um número reduzido de padrões distintos.

Gilmore e Gomory (1961) formularam o Problema de Corte de Estoques como um problema de programação linear inteira. Para resolvê-lo, Gilmore e Gomory (1963) propuseram a aplicação do método simplex com geração de colunas, após relaxar as condições de integralidade das variáveis de decisão. Colunas são geradas na medida necessária e uma solução para o problema inteiro pode ser obtida arredondando-se a solução encontrada no problema relaxado.

Suponhamos que objetos de comprimento L em estoque existam em quantidade suficiente para produzir d_i itens menores de comprimento l_i para i

I. Um modelo matemático para o problema de corte de estoques unidimensional é o seguinte (Equações 1 a 5):

Sujeito a

em que:

• a_ij é uma variável de decisão que indica a quantidade de itens tipo i no padrão j;

• M é o conjunto de índices de todos os padrões viáveis;

• I é o conjunto de índices dos diferentes itens;

• x_j é uma variável de decisão que representa a frequência do padrão de corte j; e

• c_j é o custo do padrão de corte j.

A função objetivo (1) minimiza os custos dos padrões utilizados. O conjunto de restrições (2) impõe que a quantidade cortada de cada item deve atender exatamente a sua demanda; as restrições (3) exigem que o comprimento total de itens cortados não ultrapasse o comprimento do objeto e, (4)-(5) são restrições de não negatividade e integralidade da quantidade de vezes que cada item deve ser cortado em cada padrão e do número de vezes que cada padrão deve ser cortado.

O modelo (1)-(5) é não linear devido à restrição (2). Para evitar a não linearidade, pode-se enumerar todos os padrões de corte que satisfazem as restrições (3) e (4) e o problema linear inteiro passa a ser composto por (1), (2) e (5). A dificuldade desta formulação está no fato do número de padrões a explicitar (|M |) aumentar muito à medida que aumenta o número de diferentes itens e suas demandas.

2 Revisão da literatura

Entre os trabalhos encontrados na literatura para a resolução do PCEU e que levam em consideração também os custos relativos ao número de diferentes padrões, o único método exato de resolução do qual temos conhecimento, foi proposto por Vanderbeck (2000). Uma das explicações possíveis para isso é devido à dificuldade de sua resolução. De fato, Mcdiarmid (1999) mostrou que o problema de minimização de padrões é NP-árduo. Vanderbeck (2000) formulou o problema como um problema de programação linear quadrática inteira que é resolvido com um algoritmo tipo branch-and-bound associado a uma técnica de geração de colunas. Testes computacionais realizados mostraram que o algoritmo só é viável para aplicação prática na resolução de problemas pequenos.

Walker (1976) utilizou um procedimento baseado em uma modificação das regras do método simplex na tentativa de controlar quais variáveis poderiam entrar na base e, com isso, reduzir o número de padrões na solução.

Yanasse e Limeira (2006) propuseram um procedimento híbrido para obter um número reduzido de padrões no PCEU. A heurística por eles proposta gera padrões de corte com desperdício limitado, em que cada padrão quando repetido num número máximo de vezes, sem que haja excesso na produção dos itens, deve completar a demanda de pelo menos dois dos itens contidos nele. Se nenhum dos padrões gerados satisfaz mais os níveis de aspiração desejados, o processo de geração de padrões é interrompido e, se ainda houver itens com demandas não nulas, um problema residual é resolvido e técnicas de redução de padrões são aplicadas à solução encontrada. Segundo Yanasse e Limeira (2006), o método proposto consegue obter boas soluções para o problema quando comparado com outros métodos sugeridos na literatura.

Haessler (1975) propôs uma heurística com custos associados à mudança de padrões e perdas e níveis de aspiração para a entrada de um padrão na solução. Tais níveis são estabelecidos segundo alguns critérios como máxima perda permissível; número máximo e mínimo de itens no padrão; e número mínimo de objetos a serem cortados de acordo com o padrão. Seus valores dependem da demanda remanescente de cada item e podem variar ao longo do processo de busca por um bom padrão, no sentido de que podem ser reduzidos até que um padrão seja determinado dentro dos níveis de aspiração aceitáveis. Segundo o autor, a heurística proposta limita o número de mudanças de padrões e a quantidade de desperdício na solução.

Farley e Richardson (1984) utilizaram programação linear para resolver o problema de minimização de padrões com único objetivo composto pela soma dos custos dos padrões e do custo de preparação associado a cada padrão.

Diegel et al. (1993) propuseram um método baseado em combinação de padrões para tentar reduzir o número de padrões de corte distintos. Eles apresentaram um procedimento para identificar um par de padrões num plano de corte que pode ser substituído por um único padrão (combinação 2 para 1). Dados dois padrões quaisquer 1 e 2 com suas respectivas frequências x₁ e x₂ para cada item de comprimento l_i a soma s_i= a_i1x₁+ a_i2x₂, 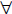i 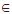I representa o número de itens do tipo i fornecido pelos dois padrões, enquanto que x_p= x₁ + x₂ é o número total de objetos a serem usados pelos padrões 1 e 2. Os dois padrões podem ser substituídos por um único p = (a_1p,..., a_np) com a_ip= s_i /x_p 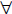i 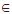I se todas as razões s_i /x_p são números inteiros e o padrão p é viável. Aplicando o novo padrão x_p vezes teremos o mesmo número de itens de cada tamanho conforme os dois padrões originais.

Foerster e Wascher (2000) estenderam o método de Diegel et al. (1993) para um número maior de combinação de padrões que foi denominado genericamente de KOMBI. Tal procedimento também mantém constante o número de objetos cortados.

Umetami, Yagiura, Ibaraki (2003) propuseram o Iterated Local SearchAlgorithm (ILS), que fixa o número de diferentes padrões e busca uma solução que minimiza o desvio quadrático dos itens produzidos em relação à demanda. O algoritmo gera uma solução na vizinhança de uma solução inicial pela perturbação de um dos padrões contido nela. A frequência dos novos padrões é obtida pela resolução de um problema auxiliar de programação linear.

Cui et al. (2008) apresentaram um método de redução de padrões para o PCEU baseado em ideias similares àquelas propostas por Haessler (1975), com níveis de aspiração para o desperdício e número de diferentes itens por padrão. No método proposto por eles, geram-se vários planos de corte para o PCEU e aquele com menor perda e menor número de padrões distintos é selecionado como a solução do problema. Segundo os autores, o algoritmo proposto apresenta vantagens em relação a outros encontrados na literatura, como a simplicidade de implementação do código e a independência de planos de corte gerados por outros algoritmos.

Em muitos dos trabalhos da literatura não é definida uma função objetivo que considera conjuntamente os custos relativos ao problema básico de corte de estoque e os custos referentes à redução do número de padrões distintos. O problema é tratado como se fosse multiobjetivo e, neste caso, as soluções são comparadas e ditas dominadas ou não. A heurística proposta neste trabalho segue esta mesma linha.

3 O algoritmo proposto

A heurística proposta é composta de 3 fases. Na primeira fase geram-se padrões levando-se em consideração a demanda média dos itens remanescentes. Apenas itens cujas demandas são iguais ou superiores a esta média podem aparecer mais de uma vez no padrão. Além disso, um padrão é construído valorizando os itens maiores, começando com itens maiores que L/2 e, caso não seja aceito como parte da solução por não apresentar os níveis toleráveis de desperdício, estes valores são reduzidos, permitindo que sejam colocados itens menores de modo a favorecer a aceitação de um padrão de corte gerado. A frequência do padrão é determinada de maneira que este possa ser utilizado o máximo possível sem que nenhum item tenha sua demanda ultrapassada. Nesta primeira fase do algoritmo, o processo é repetido até que os padrões de corte gerados não sejam mais aceitos por não apresentarem o nível aceitável de desperdício estabelecido previamente. Na segunda fase, o problema residual (problema com itens cujas demandas não foram ainda atendidas) é resolvido e, na terceira fase, aplica-se a técnica de redução de padrões proposta por Foerster e Wascher (2000) à solução obtida.

a) Fase 1: processo inicial de geração de padrões

Seja d_m = (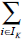d_i)/K a demanda média dos itens, em que K > 0 é a quantidade de itens com demanda não nula ainda existente; I_K é conjunto de índices destes itens; I_K I e |I_K| = K. Inicialmente K = n. Um item i é candidato a estar no próximo padrão se l_i > 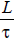, iniciando-se com um valor para τ igual a 2. Caso o valor corrente de τ leve à geração de um padrão que não satisfaça os níveis de aspiração para o desperdício, seu valor é atualizado para τ τ + 1 e um novo padrão de corte é determinado, com maior possibilidade de ser aceito, visto que quanto maior o valor de τ, maior o número de itens candidatos.

Almejamos uma solução com um número reduzido de padrões, assim, impomos um limitante para a quantidade máxima de itens tipo i permitida no padrão calculada por meio da relação q_i = [d_i/d_m], 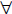i 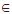I e l_i > 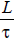, e q_i é igual a 0 para os demais itens. O padrão de corte é obtido resolvendo o seguinte problema da mochila limitada (Equações 6 a 8):

Sujeito a

em que v_i é o valor de utilidade do item 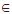i I.

Para que os itens maiores que L/2 sejam preferidos em comparação aos menores na determinação do padrão, define-se (Equação 9):

Na heurística proposta tem-se este cuidado especial para itens maiores que L/2, pois itens deste tamanho aparecem necessariamente uma única vez nos padrões que os contêm e, geralmente, são difíceis de serem combinados com os demais itens na formação de padrões com perdas pequenas. Para tentar manter um número reduzido de padrões e gerar bons padrões que os contêm, é interessante considerar estes itens no início, quando ainda se tem um número maior de itens a combinar.

Após gerar o padrão, ele será aceito se o seu desperdício é limitado, ou seja, se ΔL = (L - 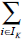l_iy_i) < µL em que µ é uma taxa de desperdício tolerável para o problema previamente estabelecida. Caso o padrão gerado seja aceito, sua frequência é dada por ƒ_P = mínimo [d_i /y_i] com 0 < y_i < d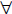_i, i 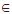I_K. Dada a restrição imposta ao tamanho dos itens no problema da mochila, este processo de geração de padrões pode levar a sobras reaproveitáveis do objeto cortado. Enquanto existirem itens com demandas maiores ou iguais à frequência do padrão corrente, isto é, d_i> ƒ_P para algum i

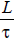I_K tal que ΔL >l_i e l_i > , então, para completar o padrão corrente faz-se y_i = 1 e ΔL = ΔL - l_i. Finalmente, a demanda dos itens é atualizada por meio da relação d_i= d_i 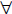- ƒ_Py_i, i 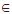I e o processo de geração de padrões é repetido enquanto existirem itens com demandas não nulas e padrões com desperdício limitado possam ser determinados.

b) Fase 2 - resolução do problema residual

Nesta fase resolvemos um problema residual para completar as demandas não nulas de alguns itens, se ainda existirem.

Para tentar gerar padrões de qualidade, com os níveis de aspiração originalmente estabelecidos, a frequência do próximo padrão é determinada a partir da maior demanda existente para o problema residual. Seja dr_i a demanda residual do item i

I e D= max {dr_i }. Determinamos o maior valor inteiro k, k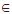 [1,..., D] tal que (L - 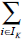l_iq_i) < µL em que q_i = [dr_i /k] é a quantidade máxima de itens tipo i permitida em cada padrão. Resolvemos o problema da mochila limitada, o padrão P = [y₁, ...,y_n] gerado é aceito e sua frequência é dada por ƒ_P = k. Este processo é repetido até terminar com toda a demanda.

Para estabelecer o nível de aspiração µ de um padrão a compor a solução do problema, utilizamos como referência o número de objetos de uma solução inteira obtida da seguinte forma: utilizamos a formulação proposta por Gilmore e Gomory (1961) para o problema de corte de estoques, relaxamos as condições de integralidade das variáveis de decisão, resolvemos o problema linear pelo método simplex com geração de colunas e arredondamos para baixo (Stadtler, 1990; Gau; Wascher, 1995) as variáveis não inteiras da solução. A base inicial utilizada na geração de colunas é formada por padrões homogêneos, ou seja, padrões formados com apenas um tipo de item. Para satisfazer as demandas remanescentes, aplicamos a heurística FFD, encontrada em Johnson (1973). O plano de corte encontrado fornece uma quantidade de objetos N_obj de uma solução para o problema, que é utilizado como referência neste trabalho.

A partir de N_obj, diferentes porcentagens de perda µ são utilizadas como níveis de aspiração para o desperdício variando-se para mais e para menos esta quantidade de objetos N_obj obtida. São considerados no máximo 11 possíveis valores diferentes, variando-se o número de objetos no intervalo [0,95 N_obj, 1,05 N_obj]. Estes valores são escolhidos de modo a tentar manter intervalos iguais, se possível. Por exemplo, se 0,05 N_obj for maior do que 3, o tamanho do passo Δs = [0,05N_obj /5], e Δs = 1 caso contrário. A melhor solução obtida é mantida.

c) Fase 3 - aplicação de um método de redução de padrões

Nesta fase, aplicamos o método KOMBI de redução de padrões sugerido por Foerster e Wascher (2000) à melhor solução encontrada na fase 2.

A heurística completa pode ser esquematizada como se segue:

AlgoritmoHeurística de Redução de Padrões - HRP

Início

Entrada: objetos de comprimento L, n-itens de comprimento l_i e demanda d_i, i

I.

Saída: solução do problema de corte com número reduzido de padrões.

(Primeira fase)

Resolver o Problema de Corte e determinar N_obj, a quantidade de objetos de referência para o desperdício.

Faça: Per_otm= 1; Pad_otm= M (M é um número grande)

Se 0,05N_obj > 3 então passo Δs = [0,05N_obj /5], senão Δs = 1

Passo 1:

Para β = -0,05N_obj,..., + 0,05 N_obj, com passo Δs faça

(percentual de referência para a perda máxima)

Faça dr_i= d_i (dr_i é a demanda residual i

I) e I_k = I.

Faça PARE = Falso

Faça SAIR = Falso

Passo 2:

Enquanto (PARE = Falso e SAIR = Falso) faça: τ = 2

Compute K para os itens l_i i

I_K. Inicie com K = n.

Compute a demanda média d_m = (dr_i)/K.

Passo 3:

Se τ > 20 então SAIR = Verdadeiro

Faça q_i = 0 para todo i

I.

Para os itens l_i tal que l_i > L / τ, i

I_K, faça q_i = [dr_i /d_m]

Gere o padrão de corte resolvendo o problema da mochila limitada.

Se o padrão obedece ao nível de aspiração então o aceite, senão faça τ = τ + 1 e volte ao passo 3

Determine a frequência máxima para que não ocorra superprodução de nenhum item, em que y_i > 0 é a quantidade de itens tipo i no padrão.

Faça ΔL = (L - l_iy_i).

Para i

I_K tal que l_i > , d_i > ƒ_P , ΔL > l_i, faça y_i = 1 e ΔL = ΔL - l_i.

Atualize a demanda por meio da relação:

dr_i = dr_i - ƒ_P y_i, i

I_k.

Se dr_i = 0 i

I então faça |I_K| = 0 e PARE = Verdadeiro

(Fim do Enquanto)

(Segunda Fase)

Passo 4:

Se SAIR = Verdadeiro então

Compute D = .

Determine o maior valor inteiro k, k [1,..., D] tal que (L - l_iq_i) < µL, e q_i = [dr_i /k].

Resolva o problema da mochila limitada, determine o padrão P = [y₁,..., y_n].

Aceite-o, e atualize a demanda.

Passo 5:

Se toda demanda foi satisfeita então

Estabeleça a solução do problema original.

(Terceira Fase)

Aplique o método KOMBI de redução de padrões.

Compute a perda (Per) e o número de padrões (Pad) da solução corrente.

Se Per < Per_otme Pad < Pad_otm então

Per_otm= Per, Pad_otm = Pad e o parâmetro corrente β fornece a melhor solução para o problema.

Atualize β e volte ao Passo 1

Senão volte ao Passo 4

Fim.

Como já relatado na seção 2, o método KOMBI estende o procedimento sugerido por Diegel et al. (1993) de combinar 3 padrões em 2 e de 2 padrões em 1 para p padrões em q em que p > q e inteiros. A aplicação do KOMBI na terceira fase do algoritmo proposto se dá para valores inteiros de p e q de modo que o esforço computacional exigido esteja dentro do tolerado pelo decisor.

Ilustramos a seguir um exemplo do método KOMBI12 para redução do número de padrões.

Considere um exemplar do problema apresentado na Tabela 1. São considerados 10 diferentes itens e o tamanho do objeto em estoque é L = 1000. Resolvendo o problema com aplicação da primeira e segunda fases da heurística de redução de padrões (HRP), obtém-se uma solução com 37 objetos e 9 diferentes padrões, apresentado na Tabela 2.

Apliquemos à solução o KOMBI12 que tenta combinar dois padrões em um. Considere os dois últimos padrões da solução gerada por HRP, p₁ = ( 0 0 0 0 0 0 2 0 1 1) e p₂ = ( 0 0 0 0 0 0 0 0 1 3), com frequências x₁ = 1 e x₂ = 1, respectivamente. O número de itens do tipo i fornecido pelos dois padrões é obtido pela soma s_i = a_i1x₁+a_i2x₂, 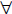i 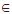I. Note que os dois padrões juntos produzem somente itens do tipo 7, 9 e 10, em quantidades s₇ = 2, s₉ = 2 e s₁₀ = 4, respectivamente. A frequência do novo padrão p = (a_1p, ...., a_np) é a soma das frequências dos padrões combinados x_p = x₁ + x₂ = 2. A quantidade de itens do tipo i no padrão p é dada por a_ip= s_i/x_p, 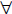i 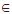I. Portanto, a_7p = 1, a_9p = 1 e a_10p = 2. Como os valores obtidos são inteiros, o padrão p = (0 0 0 0 0 0 1 0 1 2) é viável e, cortado 2 vezes, fornece o mesmo número de itens dos dois padrões originais. A aplicação do KOMBI12 reduziu o número de padrões na solução de 9 para 8 mantendo constante o número de objetos como mostra a Tabela 3.

Observa-se que a combinação de padrões obtidos na fase 1 com padrões obtidos na fase 2 é possível, apesar dos itens a serem combinados, dos padrões das duas fases, poderem apresentar diferenças significativas. Embora na fase 1 seja dada prioridade aos itens maiores e, na fase 2, aos itens de maior demanda, os padrões obtidos não se limitam a itens com tais características.

Observa-se ainda que a eficiência global em termos de perdas é preservada, pois o número de objetos resultantes é mantido e os itens produzidos são os mesmos.

4 Experimentos computacionais

A implementação da heurística foi feita em C++ e os testes computacionais foram realizados em um computador Intel Core 2 Duo, 1.50GHz com 2GB de memória (RAM). O CPLEX 10 foi utilizado para resolução dos problemas de corte de estoques e determinação da quantidade de objetos N_obj.

Os problemas testes foram obtidos por intermédio do CUTGEN1, um gerador aleatório de problemas de corte de estoque unidimensional desenvolvido por Gau e Wascher (1995). Consideramos as mesmas 18 classes testadas por Foerster e Wascher (2000), Yanasse e Limeira (2006) e Cui et al. (2008), cada uma com 100 instâncias e adotamos no CUTGEN1 a mesma semente, 1994. As classes estão divididas conforme a quantidade de itens n, a média d_m das demandas d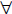_i, i 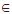I e combinações diferentes de valores ν₁ e ν₂ para determinação do comprimento dos itens que são gerados no intervalo [ν₁L, ν₂L], como mostrado na Tabela 4. O comprimento do objeto em estoque é L = 1000 para todas as instâncias testadas.

Na Tabela 5, apresentamos os resultados dos testes computacionais realizados com a heurística, coluna HRP, e reproduzimos de Cui et al. (2008) os resultados de Yanasse e Limeira (2006) e Foerster e Wascher (2000), colunas YL e FW, respectivamente, bem como os resultados por eles obtidos. A coluna "perda" indica a taxa média de desperdício na solução, enquanto que a coluna "padrões" é a média do número de padrões na solução. Em seu trabalho, Cui et al. (2008) apresentaram duas soluções diferentes para o problema. Na primeira (coluna Cui 1) tem-se seu melhor resultado para a perda média que foi comparada apenas com o procedimento de Foerster e Wascher (2000) que priorizaram a minimização do desperdício. Na segunda (coluna Cui 2), são soluções com vistas a reduzir a média do número de padrões, que foi comparada com o procedimento de Yanasse e Limeira (2006). Os valores em destaque na Tabela 5 indicam soluções não dominadas em cada linha. Podemos observar na Tabela 5 que HRP não é dominada por nenhum dos outros procedimentos em 12 das 18 classes, e quando se exclui o procedimento de Cui et al.(2008), HRP não é dominada em nenhuma das 18 classes.

Na Tabela 6 apresentamos os resultados de testes computacionais realizados com a heurística HRP para três valores diferentes do parâmetro β que regula o valor de µ . O primeiro, quando o parâmetro (ver pseudocódigo de HRP) β = -0,05N_obj; o segundo, quando β = 0.0; e o terceiro, quando β = + 0,05N_obj, em que N_obj é a quantidade de objetos de uma solução para o problema de corte obtida com a aplicação do simplex com geração de colunas. Estes valores representam uma variação com relação à perda gerada ao se resolver o problema de corte por meio do CPLEX de -5%, 0% e +5%, respectivamente.

Analisando os resultados obtidos e comparando-os entre si, nota-se um "equilíbrio" na quantidade de soluções não dominadas para os 3 diferentes valores do parâmetro β (e, consequentemente, de µ ), totalizando 9 soluções não dominadas quando há um decréscimo de 5%, 11 quando se usa o valor sem acréscimos, e 11 quando ocorre um acréscimo de +5%. Devido a este "equilíbrio" observado, a heurística utiliza diferentes valores de µ e guarda a melhor solução obtida. Para os 3 valores considerados do parâmetro β, a melhor solução obtida para as classes 3 e 5 ocorre quando o decréscimo é de 5% no total de objetos; para as classes 4, 8, 10, 14 e 15, quando o acréscimo é de +5% no total de objetos; e para a classe 7, quando não se varia o total de objetos. Nas demais classes, obtiveram-se soluções não dominadas com 2 ou mais valores diferentes para β.

Na Tabela 7 apresentam-se os tempos computacionais dos trabalhos de Yanasse e Limeira (2006) e Foerster e Wascher (2000) reproduzidos de Cui et al. (2008) além dos tempos observados com a heurística HRP. Observamos que estes valores não são diretamente comparáveis, pois foram executados em máquinas diferentes e por versões diferentes de otimizadores. Podemos apenas dizer que os tempos de execução da heurística HRP são aceitáveis para sua aplicação prática.

5 Conclusões

Apresentamos uma Heurística de Redução de Padrões (HRP) que pela geração de padrões com desperdício limitado busca encontrar soluções alternativas para o Problema de Corte de Estoque com um menor número possível de padrões. Os testes computacionais realizados mostram que o desempenho de (HRP) é melhor que o de Yanasse e Limeira (2006) e Foerster e Wascher (2000) e não é dominada pelas soluções obtidas por eles em nenhuma das 18 classes e que (HRP) é dominada pelo procedimento de Cui et al. (2008) nas classes 4, 8, 10, 14, 16 e 18. Buscamos, com o algoritmo HRP, contribuir para o avanço das pesquisas que visam gerar boas heurísticas para o Problema de Corte de Estoque Unidimensional com redução do número de padrões.

Agradecimentos. Os autores agradecem o apoio financeiro às instituições CAPES, UESB, FAPESP e CNPq, sem o qual não seria possível o desenvolvimento deste trabalho. Os autores agradecem também os comentários dos revisores anônimos que contribuíram para a melhora deste trabalho.

Recebido: 26/11/2008

Aceito: 12/5/2009

• CUI, Y. et al. A heuristic for the one dimensional cutting stock problem with pattern reduction. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, v. 222, n. 6, p. 677-685, 2008.
• DIEGEL, A. et al. Setup combining in the trim loss problem - 3-to-2 & 2-to-1 Durban: Business Administration; University of Natal, 1993. Working Paper. First Draft.
• DYCKHOFF, H. A typology of cutting and packing problems. European Journal of Operational Research, v. 44, p. 145-159, 1990.
• FARLEY, A. A.; RICHARDSON, K. V. Fixed charge problems with identical fixed charges. European Journal of Operational Research, v. 18, p. 245-249, 1984.
• FOERSTER, H.; WÄSCHER, G. Pattern reduction in one-dimensional cutting stock problem. International Journal of Production Research, v. 38, n. 7, p. 1657-1676, 2000.
• GILMORE, P.; GOMORY, R. A linear programming approach to the cutting-stock problem. Operations Research, v. 9, p. 849-859, 1961.
• GILMORE, P.; GOMORY, R. A linear programming approach to the cutting-stock problem II. Operations Research, v. 11, n. 6, p. 863-888, 1963.
• GAU, T.; WÄSCHER, G. CUTGEN1: a problem generator for the standard one-dimensional cutting stock problem. European Journal of Operational Research, v. 84, p. 572-579, 1995.
• HAESSLER, R. W. Controlling cutting pattern changes in one-dimensional trim problems. Operations Research, v. 23, n. 3, p. 483-493, 1975.
• HINXMAN, A. I. The trim loss and assortment problem: a survey. European Journal of Operational Research, v. 5, p. 8-18, 1980.
• JOHNSON, D. S. Near-optimal bin packing algorithms Cambridge: Massachusetts Institute of Technology, 1973. Tecnical Report MAC TR-109, Project MAC.
• McDIARMID, C. Pattern minimisation in cutting stock problems. Discrete Applied Mathematics, v. 98, p. 121-130, 1999.
• STADTLER, H. A one-dimensional cutting stock problem in the aluminm industry and its solution. European Journal of Operational Research, v. 44, p. 209-223, 1990.
• UMETAMI, S.; YAGIURA, M.; IBARAKI, T. One-dimensional cutting stock problem to minimize the number of different patterns. European Journal of Operational Research, v. 146, p. 388-402, 2003.
• VANDERBECK, F. Exact algorithm for minimizing the number of setups in the one-dimensional cutting stock problem. Operations Research, v. 48, n. 6, p. 915-926, 2000.
• YANASSE, H. H.; LIMEIRA, M. S. A hybrid heuristic to reduce the number of different patterns in cutting stock problems. Computers and Operations Research, v. 33, p. 2744-2756, 2006.
• WALKER, W. E. A heuristic adjacent extreme point algorithm for the fixed charge problem. Management Science, v. 22, n. 5, p. 87-596, 1976.

Datas de Publicação

• Publicação nesta coleção
  03 Ago 2009
• Data do Fascículo
  Jun 2009

Histórico

• Aceito
  12 Maio 2009
• Recebido
  26 Nov 2008