An Improved Method for Acquisition of the Parameters of Jiles-Atherton Hysteresis Scalar Model Using Integral Calculus

Abstract

An accurate modeling of materials is essential to obtain reliable results in fields calculation. The Jiles-Atherton approach is widely used for modeling the magnetic hysteresis and depends on its set of five parameters to properly represent material. In this article is proposed an original methodology for obtaining this set of parameters avoiding the derivatives rough calculation and using the calculation of integrals. From the model equations, a new methodology with two nonlinear algebraic systems of five equations in five unknowns is obtained. The initial magnetization curve, the anhysteretic curve and filtering data are not necessary. The proposed methodology also does not restrict the search space of parameters. The parameters assume values in the interval (0,∞). Calculated data were compared with experimental data to validate the methodology. The simulations showed that the proposed method can obtain an accurate set of parameters from a single experimental hysteresis loop and with low computational effort.

Index Terms
Cauchy problem; Maclaurin's series; Magnetic hysteresis; magnetic materials

I. INTRODUCTION

Several models for scalar modeling of magnetic hysteresis are found in the literature but the Jiles- Atherton approach has been widely used [¹]-[⁹]. To completely characterize a given material the Jiles-Atherton model requires the determination of five parameters: m_s(A/m), α, a (A/m), k, and c [¹⁰]-[¹²]. The calculation of these parameters has been performed through different methods stochastic and deterministic.

Recent research developed by the authors of this article resulted in three different methodologies to calculate the parameters of the Jiles-Atherton model, based on the knowledge of only one experimental B-H curve of the material. The three methodologies have the same origin (the equations of Jiles-Atherton); they use the same method (non-linear least squares) to solve an equations system of infinitely many solutions where the solution is the set of parameters to be calculated; and they were applied to characterize the same material. The differences between the methodologies will be highlighted. In the first method, after algebraic manipulation of the Jiles-Atherton equations one obtains M_irr = M_irr (H_e (H, B)), and reaches to a nonlinear ordinary differential equation dB / dH = f₁ (H, B). The derivative is calculated roughly. The system of equations is written with this last equation. The derivative of a function B (H) at the point H₁ is defined by the limit, $B\text{'}(H_1)=\underset{\mathrm{\Delta }H\to 0}{\lim }\left[B(H_1+\mathrm{\Delta }H)-B(H_1)\right]/\mathrm{\Delta }H$, when this limit exists. Thus, to improve the first method, in the case of noisy loops, it is necessary to avoid the derivative calculation. In the second method (which avoids the derivative calculus) proposed in this paper, after algebraic manipulation of the Jiles-Atherton equations, one obtains M_an = M_an (H_e) and dM_an / dH_e = f₂ (H_e) allowing write a linear ordinary differential equation ODE. The Cauchy problem associated with ODE is solved and its initial value is an experimental magnetic field and magnetic induction. This allows writing a nonlinear algebraic equation B/μ₀-H = f₃ (H, B). The integral involved in this algebraic equation is solved roughly using Maclaurin series. To improve the accuracy are considered the first ten terms of the series. The equations system is written with this algebraic equation. In order to improve the second methodology is necessary to avoid rough calculation of integrals. Therefore, the third methodology was developed. In the third method, after algebraic manipulation of Jiles-Atherton equations, are obtained directly (without using rough calculations of derivative and integrals) B = B (H_e, H). A nonlinear algebraic equation f₄ (H, B) is written and used to construct the system of equations.

For the same material, the different methodologies do not provide, as a result, equal sets of parameters. It is true that the proposed methodologies have the same origin, but the methodologies identify the set of parameters by solving different equations systems. The first methodology calculates parameters based on derivatives rough calculation; the second method calculates parameters based on power series approximation to solve the integral; the third method is simpler and does not use derivative or integral to identify the parameters.

Each of the equations systems analyzed in the three methodologies has infinitely many solutions. Although there are infinitely many solutions, only some of them can be calculated because the main equations in each methodologies have a division operator (which is inherited from Jiles-Atherton equations) and hence indeterminate forms can happen avoiding the calculation of all existing solutions.

In addition, there are five parameters, which can also be seen as five degrees of freedom. Depending on the value assumed by one of the parameters, the other can be set according to assumed already value.

The Jiles-Atherton equations originate three methodologies, this is fact, and cannot be seen as a drawback because the three methodologies give opportunity to calculate several sets of parameters which are then analyzed based on criteria that facilitate the selection of the set that best represents the experimental behavior of the material.

In this article, a new and original method to determine the five parameters of Jiles-Atherton hysteresis scalar model is proposed. Reference [¹³] proposes an original method to determine the five parameters of the model. In that study an implicit formula was developed and the magnetic induction B was written in function of magnetic field H and in terms of the derivative of B with respect to the magnetic field. If there are numerical noises added to the measured experimental data then the calculation of the derivative may be difficult. Despite this, the approach has been used to characterize different materials and the results show good agreement of measured data and calculated data.

The main contribution of this paper is to improve the method for obtaining the parameters of Jiles- Atherton model using an inverse model, where the magnetic induction is the independent variable, and, unlike the previous work, avoiding the use of derivatives calculus in the characterization method.

In summary, the proposed approach can be described as follows. First, the model Jiles-Atherton is written as a linear ordinary differential equation. Then, the Cauchy problem associated with this differential form is considered [¹⁴]. The initial value of the Cauchy problem is an arbitrary data point (H₀, B₀). Then the Cauchy problem is solved using the method of integrating factor [¹⁵] and integration by parts. Finally, the definite integral obtained is solved numerically by Maclaurin series [¹⁶]. The proposed method is simple because the integrand can be represented by polynomial functions facilitating their integration.

II. MATHEMATICAL MODELING

To determine the model parameters a single main equation is obtained (as one can see in ^appendix) based on the five equations of Jiles-Atherton and on a constitutive relation [¹²]. This equation is given by (1).

The equation (1) is a function of B, H, in that also appear the five parameters of the Jiles-Atherton model. The equation implicitly relating magnetic field and magnetic induction. Knowing the coordinates of points, magnetic field and magnetic induction, using equation is possible to identify the five parameters of the model. Another advantage of (1) is the derivative absence.

(1) $$\begin{array}{l}(B/{\mu }_0)-H=[(B_0/{\mu }_0)-H_0]\times e^{[(\alpha B_0/{\mu }_0)-(\alpha -1)H_0-(\alpha B/{\mu }_0)+(\alpha -1)H]/(k\delta )}+\\ (1-c)(m_s/(k\delta ))e^{[-(\alpha B/{\mu }_0)+(\alpha -1)H]/(k\delta )}\times {\displaystyle \sum _{n=0}^{\infty }\{\left[c_n/(n+1)\right][{\left(\left(\alpha B/{\mu }_0\right)-\left(\alpha -1\right)H\right)}^{n+1}-}\\ {\left(\left(\alpha B_0/{\mu }_0\right)-(\alpha -1)H_0\right)}^{n+1}]\}+c{m}_s[\cot h\left(\left[\left(\alpha B/{\mu }_0\right)-(\alpha -1)H\right]/a\right)-\\ a/\left[\left(\alpha B/{\mu }_0\right)-(\alpha -1)H\right]]-c{m}_s[\cot h\left(\left[\left(\alpha B_0/{\mu }_0\right)-(\alpha -1)H_0\right]/a\right)-\\ a/\left[\left(\alpha B_0/{\mu }_0\right)-(\alpha -1)H_0\right]]e^{\left[\left(\alpha B_0/{\mu }_0\right)-(\alpha -1)H_0-(\alpha B/{\mu }_0)+(\alpha -1)H\right]/(k\delta )}\end{array}$$

Where: m_s (A/m), α, a (A/m), k, and c are the five material parameters; δ takes the value 1 for the ascending branch of the hysteresis loop, and the value −1 for the descending branch of the hysteresis loop; H is the magnetic field; B is the magnetic induction; and μ₀ is the magnetic permeability of vacuum.

III. SOLVING SYSTEM OF EQUATIONS

Equation (1) can be used to obtain the five parameters of Jiles-Atherton model when an experimental B-H loop is used as a reference. Initially, do (1) equal to zero and 0 = f (H, B) denote this operation. Then, 0 = f(H, B) was used to write two systems of non-linear algebraic equations, as can be seen in Fig. 1. The first system represents the ascending branch of the hysteresis loop (Asc.) when δ = +1. The second system represents the descending branch of the hysteresis loop (Desc.) when δ = −1. Then points (H₀, B₀) belonging to the experimental curve are selected. Each system has five equations in five unknowns. The unknowns are the five parameters of the Jiles-Atherton model. Finally, each system of equations is solved using the nonlinear least squares method. The parameter set that represents the material, which corresponds to the experimental hysteresis loop, is the solution of the equation system.

Fig. 1
System of equations for each branch of the experimental hysteresis loop.

Consider a system of five nonlinear equations given by F_i (x) = f (H_i, B_i) where x = [m_s α a k c] are the five unknowns, i = 1, …, 5. The aim is to find a vector x such that F_i (x) = 0. To solve this system of equations is necessary minimizing the sum of squares. If the sum of the squares is null then the system of equations is solved. To solve the system was used the Trust-Region-Dogleg algorithm (TRD) or Trust-Region-Reflective algorithm (TRR) [¹⁷], [¹⁸] belonging to the nonlinear least squares method.

The system has infinitely many solutions and is solved by the following method: first, is assigned an arbitrary initial value for the set of parameters x₀ = [m_s0 α₀ a₀ k₀ c₀]. To the descending branch of the hysteresis loop select a point with coordinate (H₀, B₀) belonging to the experimental curve. Five points with coordinates (H, B) positioned in this branch as can be seen in Fig. 1 are selected. The five points are not positioned considering the most relevant slopes of the branch because (1) does not have the term dB/dH. The proposed equation f (H, B) evaluated in each selected point (H, B) is writen (this allows to obtain a five-equation system). By solving this system of equations (using the TRD algorithm or TRR algorithm), a candidate to solution (cs) is obtained.

The candidate to solution above now is used as initial value for the current set of parameters, x₀ = cs. Repeat the procedure for the ascending branch of the experimental hysteresis loop. The point of coordinates (H₀, B₀) and the five points of coordinates (H, B) belong to the ascending branch. This new system of equations is solved (by the TRD algorithm or TRR algorithm) and new candidate to solution is obtained and used as a set of initial parameters for the system.

This procedure is repeated until a certain error criterion is obeyed by candidate to solution, or until the maximum number of iterations is reached. When a solution is found the simulated hysteresis loop is calculated and the curve obtained is compared with the measured data. For the set of parameters representing the material, corresponding to the experimental hysteresis loop, are calculated: mean squared error (MSE); total accumulated distance calculated considering measured points and calculated points; and percentage error calculated considering the measured magnetic loss and calculated magnetic loss.

If the algorithm does not converge, then the initial set of parameters should be changed as well as the points with coordinates (H₀, B₀), the error criterion and the maximum number of iterations.

The main steps of the numerical procedure to calculate the parameters of the Jiles-Atherton hysteresis scalar model are shown in Fig. 2.

Fig. 2
Numerical procedure to calculate parameters.

IV. APPLICATION RESULTS OF PROPOSED METHODOLOGY

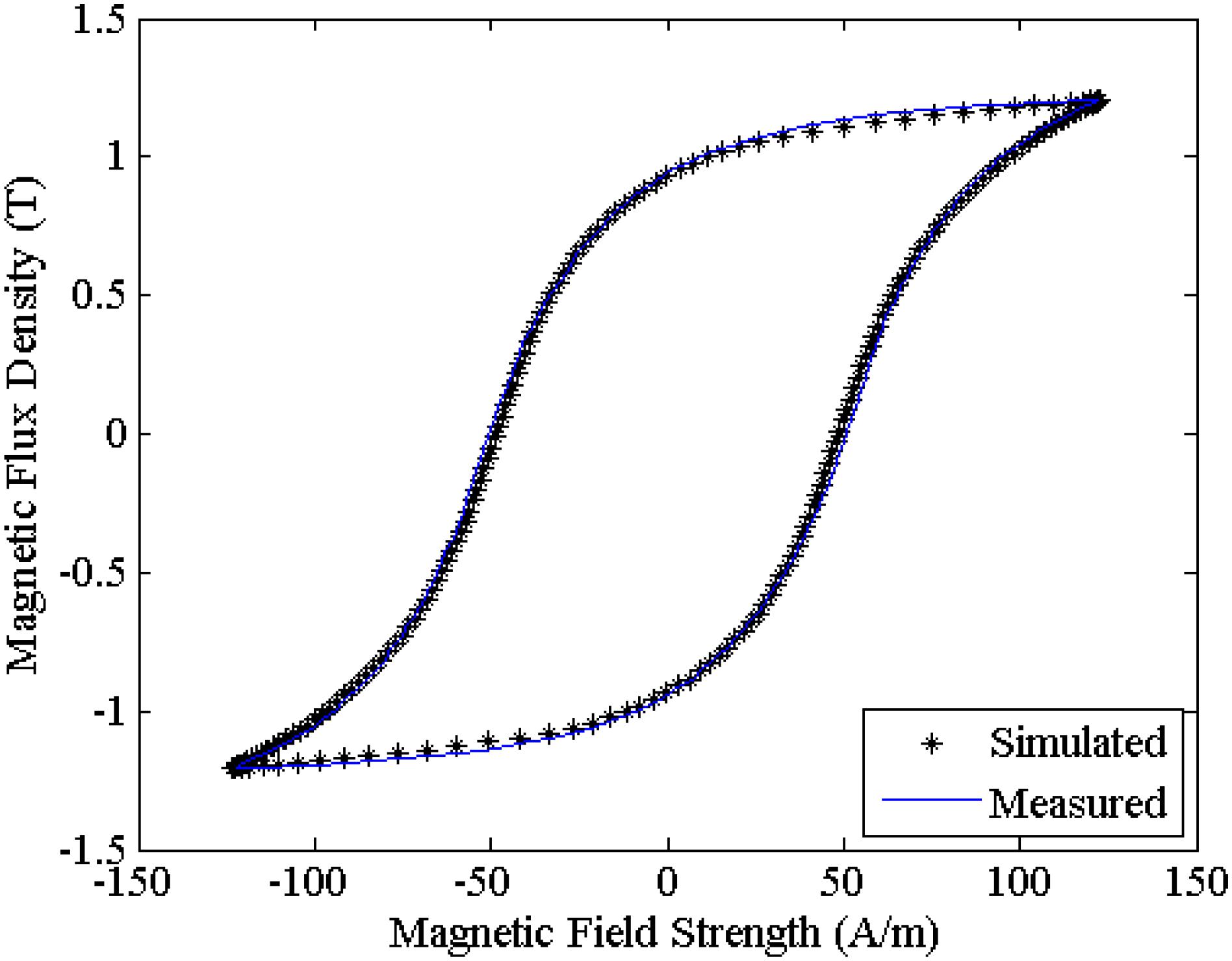
In this section, calculated hysteresis loops are compared to measured hysteresis loops to validate the proposed methodology. The results were obtained using the proposed methodology and the equations were solved using the TRD algorithm or TRR algorithm. The experimental data were obtained using an Epstein frame with closed loop control [¹⁹], sinusoidal magnetic induction with frequency of 1 Hz. Three materials of grain oriented silicon steel cut in the rolling direction were considered, as shown in Fig. 3-5. A material of grain non-oriented silicon steel cut in the transverse direction was characterized as can be seen in Fig. 6. A material of non-oriented steel silicon cut in the direction of 45 degrees was analyzed as can be seen in Fig. 7. The corresponding values of the model parameters (solution) are shown in table I. In the same table the simulation time (t) for obtaining the parameters with a PC i5, 2.67 GHz is given as well as the number of iterations (NI) for each output, the initial set of parameters used (initial), and initial value used for the Cauchy problem (H₀, B₀). The parameters are rapidly obtained and the proposed methodology can be used for fast characterization of materials. This reduced time brings advantages to the next procedures.

Fig. 3
Calculated results and measured results for material 1: soft loop (TRD).

Fig. 4
Calculated results and measured results for material 2: first case (TRD).

Fig. 5
Calculated results and measured results for material 3: third case (TRD).

Fig. 6
Calculated results and measured results for material 4: fourth case (TRD).

Fig. 7
Calculated results and measured results for material 5: fifth case (TRR).

TABLE I
RESULTS

Case	Description	Parameters of Material
		ms	α	a	k	c
Soft	Initial	1.72×106	1.7×10−4	129.8	195	0.47
	Solution	1.67×106	2.38×10−4	129.5	89.13	0.51
	t (s)	4.31	NI	3
	H0, B0	Desc.	19, 1	Asc.	−19, −1.1
1°	Initial	1.5×106	4×10−4	200	200	3.12
	Solution	1.78×106	1.54×10−4	101.5	81.22	0.34
	t (s)	2.56	NI	3
	H0,B0	Desc.	−15, 0.8	Asc.	14, −0.8
3°	Initial	1×106	5.0×10−4	500	300	0
	Solution	1.47×106	1.36×10−4	69.69	48.06	0.16
	t (s)	1.97	NI	4
	H0,B0	Desc.	−13, 0.9	Asc.	15, −0.9
4°	Initial	1.55×106	200×10−4	519	460	0.3
	Solution	1.55×106	1.07×10−3	518.4	459.9	0.3
	t (s)	2.53	NI	3
	H0,B0	Desc.	−6, 1.03	Asc.	6, −1.01
5°	Initial	1.3×107	18×10−4	154	195	0.08
	Solution	1.33×106	7.88×10−4	363.71	330.27	0.45
	t (s)	2.58	NI	4
	H0,B0	Desc.	71, 0.8	Asc.	−71, −0.8

The hysteresis sigmoid soft loop simulated agrees with the experimental data as shown in Fig. 3. As one can see in Fig. 4-7 the simulated loops also show good agreement with the measured hysteresis loops.

Table II shows indicators of the solution quality: mean square error (MSE); calculated distance considering measured points and calculated points (Dist.); and percentage error calculated considering the measured magnetic loss and calculated magnetic loss (Error%).

TABLE II
SOLUTION QUALITY INDICATORS

Case	Solution Quality Indicators
	Total Dist.	Minimum Dist.	Maximum Dist.	MSE	Error%
Soft	4155	1.89×10−3	31.23	10.43	7.11
1°	1111.7	5×10−3	17.86	7.68	3.86
3°	6342.5	3.13×10−3	22.29	4.59	1.53
4°	15581.1	1.94×10−3	73.33	19.00	1.95
5°	15521.4	5.13×10−3	60.89	22.80	0.74

The two systems of nonlinear equations presented in the proposed methodology can be solved using the method of nonlinear least squares (used in adjustment nonlinear curves).

From the equations of Jiles-Atherton hysteresis scalar model and a constitutive relationship were written two systems of nonlinear equations. The aim is to compute the parameters of Jiles-Atherton model of the curve that best fits the experimental data of magnetic induction and magnetic field for a given material. These parameters, which fit (by the nonlinear least squares technique) the nonlinear function (obtained from the proposed methodology) to a set of experimental points of magnetic induction and magnetic field, can be identified for example by Trust-Region-Dogleg algorithm or Trust-Region-Refective algorithm [¹⁷].

With characteristic of avoid the derivative calculus, this methodology shows great potential for reliable and fast identification of the parameters of the Jiles-Atherton model. Although the aim of this work is the parameters identification of the Jiles-Atherton scalar hysteresis model the method proposed here can also be used to determine the parameters of the Jiles-Atherton vector model. In this case the methodology can be used for each main direction of magnetization: longitudinal direction and transverse direction.

In [²⁰] - [²⁸], one can see methodologies to determine the parameters of Jiles-Atherton hysteresis scalar model using algebraic manipulation of the model equations and the application of nonlinear least squares method to solve the system of equations obtained.

V. CONCLUSION

In this article, a modeling of magnetic hysteresis is presented using the Jiles-Atherton model. A mathematical model and a new methodology, which requires few experimental data from the hysteresis loop, are used to evaluate the model parameters. The proposed approach improves the way in which these parameters are determined avoiding the calculus of derivatives. To our knowledge, this model which implicitly relates the magnetic field and the magnetic induction has never been proposed in the literature. Despite the complexity involved in the derivation of the algebraic system and in the integral calculus by unconventional methods, the final results allows fast computational method providing reliable hysteresis loop when compared with experimental loops.

ACKNOWLEDGMENT

This work has been supported by UTFPR, Fundação Araucária, SETI, CAPES, and CNPq.

APPENDIX

The equations that allows identifying the model parameters are the equations of the Jiles-Atherton scalar hysteresis model and a constitutive relationship. According to [¹²] are considered the following equations:

(2) $$M=M_{irr}+M_{rev}$$

(3) $$M_{rev}=c\left(M_{an}-M_{irr}\right)$$

(4) $$M_{an}=m_s\left[\coth \left(\frac{H_e}{a}\right)-\frac{a}{H_e}\right]$$

(5) $$\frac{d{M}_{irr}}{d{H}_e}=\frac{M_{an}-M_{irr}}{k\delta }$$

(6) $$H_e=H+\alpha M$$

(7) $$B={\mu }_0(H+M)$$

A. Cauchy Problem Associate

Keeping in mind that the purpose of this section is to find the five parameters of the Jiles-Atherton hysteresis scalar model without using the derived calculation, the mathematical modeling begins combining (3) and (2): M = M_irr+c(M_an-M_irr) that is

(8) $$M=(1-c)M_{irr}+c{M}_{an}$$

Furthermore, considering (6) we have αM = H_e-H, that is, M = (H_e-H)/α which combined with (7) allows to write B = μ₀[H+((H_e-H)/α)]. From this last equation one obtains:

(9) $$B={\mu }_0\left(1+\frac{1}{\alpha }\right)H+\frac{{\mu }_0}{\alpha }{H}_e$$

From (9) we then get μ₀H_e/α = B-μ₀H(1-1/α) which also means:

(10) $$H_e=\frac{\alpha }{{\mu }_0}B-(\alpha -1)H$$

On the other hand, equation (8) allows calculating the derivative of magnetization with respect to the effective magnetic field:

(11) $$\frac{dM}{d{H}_e}=(1-c)\frac{d{M}_{irr}}{d{H}_e}+c\frac{d{M}_{an}}{d{H}_e}$$

This way, combining (5) and (11) this gives us:

(12) $$\frac{dM}{d{H}_e}=\frac{(1-c)}{k\delta }{M}_{an}-\frac{(1-c)}{k\delta }{M}_{irr}+c\frac{d{M}_{an}}{d{H}_e}$$

By multiplying (8) by 1/(kδ) it is also true that:

(13) $$\frac{M}{k\delta }=\frac{(1-c)}{k\delta }{M}_{irr}+\frac{c}{k\delta }{M}_{an}$$

After that, (12) added to (13) allows write: $\frac{dM}{d{H}_e}+\frac{M}{k\delta }=\frac{(1-c)}{k\delta }{M}_{an}+c\frac{d{M}_{an}}{d{H}_e}+\frac{c}{k\delta }{M}_{an}$, or $\frac{dM}{d{H}_e}+\frac{M}{k\delta }=\frac{M_{an}}{k\delta }-\frac{c{M}_{an}}{k\delta }+c\frac{d{M}_{an}}{d{H}_e}+\frac{c}{k\delta }{M}_{an}$ that is

(14) $$\frac{dM}{d{H}_e}+\frac{M}{k\delta }=\frac{M_{an}}{k\delta }+c\frac{d{M}_{an}}{d{H}_e}$$

Taking into account (4), one can see that M_an = M_an(H_e) and dM_an/dH_e = f(H_e) that is M_an and dM_an/dH_e both depend of H_e, as a result it is stated that (14) is a linear ordinary differential equation of the first order, with dependent variable M and independent variable H_e.

Consider the Cauchy problem associated with (14). A Cauchy problem is defined by an equation or systems of first order equations and an initial condition. From (7)B/μ₀ = H+M or M = (B/μ₀)-H, as a result the initial condition will be: M(H_e0) = M₀ = (B₀/μ₀)-H₀.

Concerning (10)H_e0 = (α/μ₀)B₀-(α-1)H₀ and consequently

(15) $$M(H_{e0})=M\left(\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0\right)=M_0=\frac{B_0}{{\mu }_0}-H_0$$

The following Cauchy problem is established:

$$\{\begin{array}{l}\frac{dM}{d{H}_e}+\frac{M}{k\delta }=\frac{M_{an}}{k\delta }+c\frac{d{M}_{an}}{d{H}_e}\hfill \\ M(M_{e0})=M\left(\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0\right)=M_0=\frac{B_0}{{\mu }_0}-H_0\hfill \end{array}$$

B. Solving Cauchy Problem

The method of integrating factor will be used in solving the Cauchy problem. The integrating factor is determined assuming that there is a function u(H_e) such that:

$$\begin{array}{l}u(H_e)\frac{dM}{d{H}_e}+u(H_e)\frac{M}{k\delta }=u(H_e)\frac{M_{an}}{k\delta }+u(H_e)c\frac{d{M}_{an}}{d{H}_e}\text{and}\\ u(H_e)\frac{dM}{d{H}_e}+u(H_e)\frac{M}{k\delta }=\frac{d}{d{H}_e}\left(u\left(H_e\right)M\right)\\ \text{As}u(H_e)\ne 0\text{and}M(H_e)\ne 0\text{then}\\ {\text{u(H}}_e\text{)}\frac{dM}{d{H}_e}+H(H_e)\frac{M}{k\delta }=M\frac{du}{d{H}_e}+\frac{dM}{d{H}_e}u(H_e)\end{array}$$

In the above equation the terms on the right side are compared with those terms on the left side and one can conclude that:

$$\frac{du}{d{H}_e}=\frac{u(H_e)}{k\delta }\text{that is}\frac{u\text{'}(H_e)}{u(H_e)}=\frac{1}{k\delta }$$

As d(ln[u(H_e)])/dH_e = u'(H_e)/u(H_e) then d(ln[u(H_e)])/dH_e = 1/(kδ). Separating the variables in the equation above and integrating we then get $\int d\ln (u(H_e))=\int [1/(k\delta )d{H}_e]$, as a result ln(u(H_e)) = [H_e/(kδ)]+cte. Especially for cte = 0 this give us ln(u(H_e)) = H_e/(kδ) which also means $u(H_e)=e^{He/(k\delta )}$. The integrating factor is $e^{He/(k\delta )}$.

Equation (14)) is multiplied by the integrating factor and this gives us:

(16) $$e^{\frac{H_e}{k\delta }}\frac{dM}{d{H}_e}+e^{\frac{H_e}{k\delta }}\frac{M}{k\delta }=e^{\frac{H_e}{k\delta }}\frac{M_{an}}{k\delta }+c{e}^{\frac{H_e}{k\delta }}\frac{d{M}_{an}}{d{H}_e}$$

As $e^{\frac{H_e}{k\delta }}\frac{dM}{d{H}_e}+e^{\frac{H_e}{k\delta }}\frac{M}{k\delta }=\frac{d}{d{H}_e}\left(e^{\frac{H_e}{k\delta }}M\right)$ then we can rewrite (16) as

$$\frac{d}{d{H}_e}\left(e^{\frac{H_e}{k\delta }}M\right)=e^{\frac{H_e}{k\delta }}\frac{M_{an}}{k\delta }+c{e}^{\frac{H_e}{k\delta }}\frac{d{M}_{an}}{d{H}_e}$$

Integrating the above equation that gives us:

$\int d\left(e^{\frac{H_e}{e^{k\delta }}}M\right)=\int e^{\frac{H_e}{k\delta }}\frac{M_{an}}{k\delta }d{H}_e+c\int e^{\frac{H_e}{k\delta }}\frac{d{M}_{an}}{d{H}_e}d{H}_e$ which also means

(17) $$M{e}^{\frac{H_e}{k\delta }}-M_0{e}^{\frac{H_{e0}}{k\delta }}=\frac{1}{k\delta }{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{M}_{an}{e}^{\frac{x}{k\delta }}dx+c{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{e}^{\frac{x}{k\delta }}\frac{d{M}_{an}}{dx}dx}}$$

In the second term on right side of (17) is applied integration by parts given by $\int UdV=UV-\int VdU$. For $U=e^{x/(k\delta )}$ this gives us $dU=(1/(k\delta )e^{x/(k\delta )})dx$. For $dV=(d{M}_{an}/dx)dx$ then $\int dV=\int (d{M}_{an}/dx)dx$ that is V=M_an. It is also true that:

(18) $$c{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{e}^{\frac{x}{k\delta }}\frac{d{M}_{an}}{dx}dx=c\left\{{\left(M_{an}{e}^{\frac{x}{k\delta }}\right)}_{H_{e0}}^{H_e}-\frac{1}{k\delta }{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{e}^{\frac{x}{k\delta }}{M}_{an}(x)dx}\right\}}$$

Combining (18) and (17) one obtains:

(19) $$\begin{array}{l}\begin{array}{ll}M{e}^{\frac{H_e}{k\delta }}-M_0{e}^{\frac{H_{e0}}{k\delta }}=\frac{1}{k\delta }{{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{M}_{an}{e}^{\frac{x}{k\delta }}dx+c\left(M_{an}{e}^{\frac{x}{k\delta }}\right)}}_{H_{e0}}^{H_e}-\frac{c}{k\delta }{\displaystyle {\int }_{H_{e0}}^{H_e}{e}^{\frac{x}{k\delta }}{M}_{an}(x)dx}\hfill & \text{or}\hfill \end{array}\\ M{e}^{\frac{H_e}{k\delta }}-M_0{e}^{\frac{H_{e0}}{k\delta }}=\left(\frac{1}{k\delta }-\frac{c}{k\delta }\right){\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{e}^{\frac{x}{k\delta }}{M}_{an}(x)dx+c{M}_{an}(H_e)}{e}^{\frac{H_e}{k\delta }}-c{M}_{an}(H_{e0})e^{\frac{H{}_{e0}}{k\delta }}\\ M{e}^{\frac{H_e}{k\delta }}-M_0{e}^{\frac{H_{e0}}{k\delta }}=\left(1-c\right)\frac{1}{k\delta }{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{M}_{an}(x)e^{\frac{x}{k\delta }}dx+c{M}_{an}(H_e)}{e}^{\frac{H_e}{k\delta }}-c{M}_{an}(H_{e0})e^{\frac{H{}_{e0}}{k\delta }}\end{array}$$

Both members of equation (19)) are multiplied by $e^{-He/(k\delta )}$, we then get:

$$M-M_0{e}^{\frac{H_{e0}-H_e}{k\delta }}=(1-c)\frac{1}{k\delta }{e}^{\frac{-H_e}{k\delta }}{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{M}_{an}(x)e^{\frac{x}{k\delta }}dx+c{M}_{an}(H_e)-c{M}_{an}(H_{e0})e^{\frac{H_{e0}-H_e}{k\delta }}}.$$

The total magnetization is isolated of the other variables in the equation above, this gives us:

$$M-M_0{e}^{\frac{H_{e0}-H_e}{k\delta }}+(1-c)\frac{1}{k\delta }{e}^{\frac{-H_e}{k\delta }}{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{M}_{an}(x)e^{\frac{x}{k\delta }}dx+c{M}_{an}(H_e)-c{M}_{an}(H_{e0})e^{\frac{H_{e0}-H_e}{k\delta }}}.$$

Considering the above equation and (4) one can write:

(20) $$\begin{array}{l}M=M_0{e}^{\frac{H_{e0}-H_e}{k\delta }}+(1-c)\frac{1}{k\delta }{e}^{\frac{-H_e}{k\delta }}{\displaystyle \underset{H_{e0}}{\overset{H_e}{\int }}{m}_s\left[\coth \left(\frac{x}{a}\right)-\frac{a}{x}\right]e^{\frac{x}{k\delta }}}dx+\\ c{m}_s\left[\coth \left(\frac{H_e}{a}\right)-\frac{a}{H_e}\right]-c{m}_s\left[\coth \left(\frac{H_{e0}}{a}\right)-\frac{a}{H_{e0}}\right]e^{\frac{H_{e0}-H_e}{k\delta }}\end{array}$$

C. Proposal Relation: Magnetic Induction with Magnetic Field

Once solved the associated Cauchy problem it is important to note that: one can return to original equations of the model to write an equation that relates the magnetic induction with the magnetic field, where also appear the parameters of the material. Taking this into account, from equality (7)M = (B/μ₀)-H which together with (10) are moved to (20) allowing to say that:

(21) $$\begin{array}{l}\frac{B}{{\mu }_0}-H=\left[\frac{B_0}{{\mu }_0}-H_0\right]e^{\frac{\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0-\frac{\alpha }{{\mu }_0}B+(\alpha -1)H}{k\delta }}+\\ (1-c)\frac{m_s}{k\delta }{e}^{\frac{\frac{\alpha }{{\mu }_0}B+(\alpha -1)H}{k\delta }}{\displaystyle \underset{\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0}{\overset{\frac{\alpha }{{\mu }_0}B-(\alpha -1)H}{\int }}\left[\coth \left(\frac{x}{a}\right)-\frac{a}{x}\right]e^{\frac{x}{k\delta }}dx+}\\ c{m}_s\left[\coth \left(\frac{\frac{\alpha }{{\mu }_0}B-(\alpha -1)H}{a}\right)-\frac{a}{\frac{\alpha }{{\mu }_0}B-(\alpha -1)H}\right]-\\ c{m}_s\left[\coth \left(\frac{\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0}{a}\right)-\frac{a}{\frac{\alpha }{{\mu }_0}{B}_0-(\alpha -1)H_0}\right]\\ e^{\frac{\frac{\alpha }{{\mu }_0}{B}_0(\alpha -1)H_0-\frac{\alpha }{{\mu }_0}B+(\alpha -1)H}{k\delta }}\end{array}$$

The definite integral in (21) is solved by Maclaurin series and one can obtain (1).

REFERENCES

• ^[1]
  J. V. Leite, N. Sadowski, P. Kuo-Peng, N. J. Batistela, and J. P. A. Bastos, “The inverse Jiles-Atherton model parameters identification,” IEEE Trans. Magn., vol. 39, pp. 1397-1400, May 2003.
• ^[2]
  J. V. Leite, N. Sadowski, P. Kuo-Peng, N. J. Batistela, J. P. A. Bastos, and A. A. de Espíndola, “Inverse Jiles-Atherton vector hysteresis model,” IEEE Trans. Magn., vol. 40, no. 4, pp. 1769-1775, Jul. 2004.
• ^[3]
  D. Lederer, H. Igarashit, A. Kost, and T. Honma, “On the parameter identification and application of the Jiles-Atherton hysteresis model for numerical modelling of measured characteristic,” IEEE Trans. Magn, vol. 35, no. 3, pp. 1211–1214, May 1999.
• ^[4]
  P. R. Wilson, J. N. Ross, and A. D. Brown, “Optimizing the Jiles-Atherton model of hysteresis by a genetic algorithm,” IEEE Trans. Magn, vol. 37, no. 2, pp. 989-993, Mar. 2001.
• ^[5]
  J. V. Leite, S. L. Avila, N. J. Batistela, W. P. Carpes Jr., N. Sadowski, P. Kuo-Peng, and J. P. A. Bastos, “Real coded genetic algorithm for Jiles-Atherton model parameters identification,” IEEE Trans. Magn, vol. 40, no. 2, pp. 888-891, Mar. 2004.
• ^[6]
  S. Cao, B. Wang, R. Yan, W. Huang, and Q. Yang, “Optimization of hysteresis parameters for the Jiles-Atherton model using a genetic algorithm,” IEEE Trans. App. Supercond, vol. 14, no. 2, pp. 1157-1160, Jun. 2004.
• ^[7]
  F. R. Fulginei and A. Salvini, “Softcomputing for the identification of the Jiles-Atherton model parameters,” IEEE Trans. Magn, vol. 41, no. 3, pp. 1100-1108, Mar. 2005.
• ^[8]
  M. Toman, G. Stumberger, and D. Dolinar, “Parameter identification of the Jiles-Atherton hysteresis model using differential evolution,” IEEE Trans. Magn, vol. 44, no. 6, pp. 1098-1101, Jun. 2008.
• ^[9]
  A. Corana, M. Marchesi, C. Martini, and S. Ridella, “Minimizing multimodal functions of continuous variables with the 'simulated annealing' algorithm,” ACM Transactions on Mathematical Software, vol. 13, pp. 262-280, Sept. 1987.
• ^[10]
  D. C. Jiles and D. L. Atherton, “Theory of ferromagnetic hysteresis,” Journal of Magnetism and Magnetic Materials,vol. 61, pp. 48-60, 1986.
• ^[11]
  D. C. Jiles, J. B. Thoelke, and M. K. Devine, “Numerical determination of hysteresis parameters for the modeling of magnetic properties using the theory of ferromagnetic hysteresis,” IEEE Trans. Magn, vol. 28, pp. 27-35, Jan. 1992.
• ^[12]
  N. Sadowski, N. J. Batistela, J. P. A. Bastos, and M. Lajoie- Mazenc, “An inverse Jiles-Atherton model to take into account hysteresis in time stepping finite element calculations,” IEEE Trans. Magn, vol. 38, no. 2, 2002.
• ^[13]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “A new methodology to obtain the parameters of the scalar Jiles-Atherton hysteresis model,” in CEFC 2012 Proceedings, Annecy, 2012.
• ^[14]
  J. Manuel Sotomayor Tello, “Lições de equações diferenciais ordinárias,” Rio de Janeiro: Instituto de Matemática Pura e Aplicada, Projeto Euclides, 1979, pp. 5-7.
• ^[15]
  Jaime E. Munoz Rivera, “Cálculo diferencial II & equações diferenciais,” Textos de graduação. Petrópolis. Editora Gráfica Rondon Ltda, 2007, pp. 35-36.
• ^[16]
  Norman B. Haaser, Joseph P. Lasalle, and Joseph A. Sullivan, “Análisis matemático 2,” Curso Intermedio, vol. 2. México. Editoral Trillas, 1970, pp. 517.
• ^[17]
  [Online]. Available: http://www.mathworks.com/help/optim/ug/equation-solving-algorithms.html
  » http://www.mathworks.com/help/optim/ug/equation-solving-algorithms.html
• ^[18]
  Rodrigo M. Rosa, “Estudo e implementação do método dogleg para programação não linear,” Trabalho de conclusão de curso Bacharelado Matemática, UFSC, Florianópolis, SC, 2005.
• ^[19]
  N. J. Batistela, “Caracterização e modelagem eletromagnética de lâminas de aço ao silício,” Tese Doutor em Engenharia Elétrica, CTC, UFSC, Florianópolis, SC, 2001.
• ^[20]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Uma nova metodologia para obtenção de parâmetros do modelo de histerese de Jiles-Atherton,” in MOMAG 2012 Anais de evento, João Pessoa, 2012.
• ^[21]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “An improved methodology for obtaining Jiles-Atherton hysteresis model parameters,” in COMPUMAG 2015 Proceedings, Montréal, 2015.
• ^[22]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Uma nova metodologia para obtenção dos parâmetros do modelo escalar de histerese de Jiles-Atherton,” in MOMAG 2016 Anais de evento, Porto Alegre, 2016.
• ^[23]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Uma metodologia aprimorada para obtenção dos parâmetros do modelo escalar de histerese de Jiles-Atherton,” in MOMAG 2016 Anais de evento, Porto Alegre, 2016.
• ^[24]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Uma metodologia simplificada para a obtenção dos parâmetros do modelo escalar de histerese de Jiles-Atherton,” in MOMAG 2016 Anais de evento, Porto Alegre, 2016.
• ^[25]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Inserção do sexto parâmetro no modelo escalar de histerese de Jiles-Atherton e metodologia para identificação dos parâmetros,” in MOMAG 2016 Anais de evento, Porto Alegre, 2016.
• ^[26]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “A new method for parameters obtaining of Jiles-Atherton hysteresis scalar model,” in CEFC 2016 Proceedings, Miami, 2016.
• ^[27]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “A simplified method for acquisition of the parameters of Jiles-Atherton hysteresis scalar model without use of derivatives,” in CEFC 2016 Proceedings, Miami, 2016.
• ^[28]
  F. B. R. Mendes, J. V. Leite, N. J. Batistela, N. Sadowski, and F. M. S. Suárez, “Insertion of a sixth parameter in Jiles- Atherton hysteresis scalar model and the method for parameters identification,” in CEFC 2016 Proceedings, Miami, 2016.

Publication Dates

• Publication in this collection
  Jan-Mar 2017

History

• Received
  30 Oct 2016
• Reviewed
  03 Nov 2016
• Accepted
  28 Dec 2016