Study of reflection and transmission of plane waves at thermoelastic-diffusive solid/liquid interface

Study of reflection and transmission of plane waves at thermoelastic-diffusive solid/liquid interface

J.N. Sharma ; R. Kaur

Department of Mathematics, National Institute of Technology Hamirpur-177005, India [e-mail], [e-mail]

ABSTRACT

The paper concentrates on the study of reflection and transmission characteristics of waves at the interface of a thermoelastic-diffusive solid half-space underlying an inviscid liquid. The analytic expressions for amplitude ratios, reflection and transmission coefficients, in terms of incident angles and material parameters have been obtained for quasi-longitudinal (qP) and quasi-transverse (qSV) wave incidence. The normal and grazing incidence cases have also been derived and discussed. The total reflection phenomenon has also been discussed. The energy law has been shown to be obeyed by the incidence, reflected and transmitted waves by deriving energy equation and its simulation. The numerical computations of reflection and transmission coefficients have been carried out for copper material half-space in contact with water at the interface by using MATLAB software. The computer simulated results have been presented graphically in order to bring out clear comparison of various situations.

Keywords: Thermoelastic Diffusion, Inviscid fluid, Reflection, Transmission, Energy Ratios, Critical angle.

1 INTRODUCTION

Diffusion is defined as a movement of the particles from a region of high concentration to the low concentration. Thermal diffusion utilizes the transfer of heat across a thin liquid or gas to accomplish isotope separation. Today, the study of thermal diffusion phenomenon got a great deal of interest due to its wide ranging applications in geophysics and industrial applications. The concentration obeys the famous Fick's law, which does not take into consideration the mutual interaction between the solvent and the solute or the effect of temperature on this interaction. However, there is a certain degree of coupling with temperature and temperature gradients as temperature speeds up the diffusion process. The thermo-diffusion in elastic solids is due to coupling of temperature, mass diffusion and strain fields addition to heat and mass exchange with the environment. Nowacki (1974, 1976) developed the theory of coupled thermoelastic diffusion. The recent development of generalized theory of thermoelastic diffusion by Sherief et al. (2004) allows the finite speed of propagation of thermo-diffusive waves. Sharma (2007) discussed the propagation of plane harmonic waves in generalized thermo-elasto-diffusive solid. Kumar et al. (2014) studied the propagation of Rayleigh waves in a homogeneous isotropic micro-stretch generalized thermoelastic diffusion solid half-space.

The phenomenon of wave reflection and refraction is a fundamental topic in many fields such as seismology, geophysics, earthquake engineering, non-destructive evaluation, etc. Jeffreys (1930) and Gutenberg (1944) considered the reflection of elastic plane waves at a solid half space. Knott (1899) derived the general equations for reflection and refraction of waves at plane boundaries. Singh (2005) discussed the reflection of P and SV waves from the free surface of an elastic solid with generalized thermo-diffusion. Singh (2006) studied the reflection of SV waves from the free surface of an elastic solid in generalized thermo-elastic diffusion. Sharma and Sharma (2010) investigated the reflection characteristics of acousto-diffusive waves from the surface of a semiconductor half-space which is subjected to stress free, isoconcentrated and stress free, impermeable conditions. Kumar and Kansal (2012) considered the reflection and refraction of plane waves at the interface of an elastic solid half-space and a thermoelastic diffusive solid half-space. Bijarnia and Singh (2012) investigated the propagation of plane waves in a transversely isotropic generalized thermoelastic solid half-space with diffusion and they also studied the reflection of these plane waves from a thermally insulated free surface. Kumar et al. (2013) studied the reflection and refraction phenomenon due to plane wave's incident obliquely at a plane interface between uniform elastic solid half-space and microstretch thermoelastic diffusion solid half-space.

Wu, et al. (1990) investigated the reflection and transmission of elastic waves from the boundary of a fluid-saturated porous solid. Lin, et al. (2005) studied the reflection of plane waves in a poroelastic half-space saturated with inviscid fluid. Deresiewicz (1960) studied the reflection of plane waves from a plane stress-free boundary in the coupled theory of thermoelasticity. Sharma, et al. (2003) studied the reflection of generalized thermoelastic from the boundary of a half space. Sinha and Sinha (1974) and Sinha and Elsibai (1996, 1997) investigated the reflection of thermoelastic waves from the free surface of a solid half-space and at the interface of two semi-infinite media in welded contact, in the context of generalized thermoelasticity. Das, et al. (2008) explored the reflection of generalized thermoelastic waves from isothermal and insulated boundaries of a half space. Sharma, et al. (2008) studied the reflection of piezo-thermoelastic waves from the charge free and stress free boundary of transversely isotropic half space. Abd-Alla and Al-Dawy (2000) discussed the reflection of thermoelastic plane wave at a generalized thermoelastic half space with one and two relaxation times. Singh (2010) applied the LS and GL theories of generalized thermoelasticity to study the reflection from a thermally insulated stress-free thermoelastic solid half-space of monoclinic type. Sharma et al. (2012) studied the reflection and transmission characteristics of acoustic waves at an interface of a semiconductor half-space underlying an inviscid liquid. Sharma and Bhargava (2014) investigated the reflection and transmission of thermoelastic plane waves at an imperfect interface between a thermal conducting viscous-liquid and generalized thermoelastic solid half-space. Sharma, et al. (2008) studied the generalized Rayleigh waves in thermoelastic solids under viscous fluid loading.

Keeping in view the above state facts and applications of reflection/transmission phenomenon in thermoelastic-diffusive solid under the interaction of fluid, the present paper is devoted to discuss the reflection and transmission of plane waves at the interface between such continua. The effects of incident angles, material parameters and fluid loading on reflection and transmission coefficients of various possible waves due to the incident P and SV waves have been considered. The analytical results so obtained have been verified numerically and are illustrated graphically.

2 FORMULATION OF THE PROBLEM

We consider a homogeneous isotropic, thermoelastic-diffusive solid in the undeformed state initially at uniform temperature T₀, underlying an inviscid liquid half-space. We take origin of the rectangular Cartesian co-ordinate system Oxyzat any point on the plane surface (interface) with z-axis directed normally into the solid half-space, which is thus represented by as shown in Figure 1.

We choose the x-axis along the direction of propagation of waves in such a way that all the particles on the line parallel to the y-axis are equally displaced. Therefore, all the field quantities are independent of y-co-ordinate. Further, the disturbances are assumed to be confined to the neighborhood of the interface Z= 0 and hence vanish as

.

The basic governing field equations of motion, heat conduction equation, mass equation and constitutive relations for a solid medium, in the absence of heat sources and body forces, are given by Sherief et al. (2004)

where

Here are the displacement vector, temperature change and mass concentration respectively. Here are coefficients of linear thermal expansion and linear diffusion expansion; λ, μ are Lame's parameters; ρ is the mass density; K is the thermal conductivity; D is the mass diffusion coefficient; a and b are thermo-diffusive and diffusive constants; are thermal and mass flux relaxation times and C_e is the specific heat at constant strain. The quantity δ_iji the Kronecker's delta with j = 1 for Lord and Shulman (LS) theory (1967) and j = 2 for Green and Lindsay (GL) theory (1972). The superposed dot notation is used for time differentiation.

The basic governing equations for inviscid fluid (liquid) medium are given by

where and are the density and coefficient of volume thermal expansion; is the velocity vector and T_L is the temperature deviation in the liquid temperature from its ambient temperature .

In order to facilitate the analysis, we define the following dimensionless quantities

Here is the characteristic frequency,are thermo-mechanical coupling constant and mass concentration of the solid respectively, C₁, C₂ are respectively the longitudinal and shear wave velocities in the solid half-space, is the thermomechanical coupling and C_L is the velocity of sound in the fluid.

Upon using quantities (8) in equations (1)-(7), we obtain

where

are again designated to have their usual meaning in the changed variables

The scalar point potential functions and vector point potential functions have been defined through the relations given below:

where

In case

the above equations provide us

Upon introducing expressions (17) in equations (9)-(15), and noting that

for inviscid fluid, one obtains

The equation (18) corresponds to decoupled shear motion which remains independent of temperature and mass concentration changes.

3 BOUNDARY CONDITIONS

The boundary conditions to be satisfied at the solid-liquid interface (Z = 0) are given by

where corresponds to the thermally insulated boundary and refers to the isothermal one and the pressure (p) of the liquid is given

4 SOLUTION OF THE PROBLEM

We assume wave solutions of the form

where

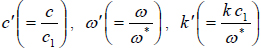are the non-dimensional phase velocity, frequency and wave number of waves respectively. The primes have been suppressed for convenience.

Upon using solution (27) in equations (18)-(23), one obtains a system of algebraic equations in unknowns A, B, C, D and E. The condition for the existence of non-trivial solution of this system of equations on simplification, provides us

where

In the absence of mass diffusion , the quantitiesdefined in equation (29) become

In case elastic and thermal fields are uncoupled

to each other, the equation (30) reduces to

The equation (30) and (31) will be used for reductions in the following analysis.

5 REFLECTION AND TRANSMISSION AT SOLID-LIQUID INTERFACE

In this section we shall discuss reflection and transmission of waves at the interface of thermo-elasto-diffusive solid and inviscid fluid for (qP)-wave and (qSV)-wave incidence cases.

5.1. Quasi longitudinal (qP)-wave incidence

Suppose that a (qP) -wave is incident at the interface from the solid half-space. Then the total wave fields after reflection and transmission of waves from the interface are given by

In the absence of mass diffusion

, we have

In the absence of mass diffusion and thermal variations

, we have

Upon using equations (32)-(37) and employing the boundary conditions (24)-(26), one obtains a system of five coupled algebraic equations (A.1)-(A.5) given in the Appendix. Since all the waves, incident, reflected or transmitted must be in phase at the interface Z = 0 for all values of X and τ, therefore the equations (A.1)-(A.5), lead to

The equation (41) with the help of equation (28) implies that

This is the modified form of the Snell's law, which in the absence of thermal, mass diffusion, viscosity and fluid field

, becomes

This implies that

which is the Snell's law as stated in Achenbach [33].

The system of equations (A.1)-(A.5) with the help of equation (41) can be expressed as

where A,Zp and B are defined in the Appendix.

Solving the system of equations (44), the amplitude ratios

are obtained as

where has been defined in equation (A.9) of Appendix and can be obtained from by replacing first, second, third, fourth and fifth column by, respectively.

For the normal and grazing incidence, the relation (45) reduces to

respectively. The quantities

have been defined in equation (A.9) of Appendix.

Thus for the grazing incidence, the reflected qP wave annihilates the incident qP wave and there is no reflection or transmission of other waves through the interface.

In the absence of mass diffusion

, the non vanishing amplitude ratios are

Here the quantities

are defined by equation (A.9) in the Appendix.

In the absence of mass diffusion and thermal fields , the non vanishing amplitude ratios at normal and grazing incidence of qP wave, are given by

and

respectively. The relations (48) are in complete agreement with the corresponding equations of Achenbach (1973). Clearly qP wave is reflected as well as transmitted in case of normal incidence, however, for grazing incidence the reflected qP-wave annihilates the incident one.

5.1.1 Quasi longitudinal ( qP )-wave incidence at free surface

In case the liquid media is absent

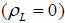, the amplitude ratios for stress free, insulated and stress free, isothermal thermoelastic half-space are, respectively, given by

In the absence of mass diffusion, fluid and thermal fields

, the non-vanishing amplitude ratios are

Relations (53) are in complete agreement with the corresponding equations as in Achenbach (1973). In case of both normal

incidence, the relations (53) provide us

Thus, the incident qP-wave is reflected as qP-wave without change in phase in case of normal incidence and the reflected qP -wave annihilates the incident qP-wave for grazing incidence one. It may be noted from the above analytical expressions for the reflection/transmission coefficients that the characteristics of reflected and transmitted waves depends on material parameters and incidence angle in addition to thermal variation and fluid loading effects.

5.2 Quasi transverse ( qSV )-wave incidence

Now consider the reflection and transmission of a plane qSV-wave for similar conditions on the boundary as in Section 5.1 above. The total displacement field in this case is given by

where

are defined in equations (32)-(37).

Upon using expressions (55) in the boundary conditions (24)-(26), at the surface Z= 0 and assuming that all the incident, reflected or transmitted waves are in phase at this surface for all values of X and τ, so that

we obtain a system of five coupled algebraic equations given as

Where

Upon solving system of equations (57), the amplitude ratios can be obtained as

whereare amplitude ratios of the reflected and transmitted waves. Here, the quantities used in equation (58) can be obtained from by replacing first, second, third, fourth and fifth column byrespectively.

In case of both normal

incidence, the relation (58) reduces to

Thus the shear (qSV) wave is reflected as qSV-wave in case of normal incidence and the reflected (qSV) wave annihilates the incident wave for grazing incidence.

In the absence of mass diffusion

, the non vanishing amplitude ratios are

Here, the quantities used in equation (60) can be obtained from by replacing first, second, third and fourth column byrespectively.

In the absence of mass diffusion and thermal fields, the amplitude ratios at norma lincidence of qSV wave, are given by

Thus only shear (qSV) wave is reflected as qSV-wave in case of normal incidence and the reflected (qSV) wave annihilates the incident wave for grazing incidence case. The other waves do not reflect or transmit in either case.

5.2.1 Quasi transverse (qSV )-wave incidence at the free surface

In case

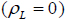, the amplitude ratios for stress free, insulated and stress free, isothermal thermoelastic half-space are, respectively, given by

and

where

are defined in equations (51) and (52) respectively.

In the absence of mass diffusion, fluid and thermal fields

, the non vanishing amplitude ratios are

Equations (64) are in agreement with the corresponding equations as in Achenbach (1973). In case of both normal incidence of qSV wave, the expressions for reflection coefficients in equation (63) provide us

Thus only shear wave is reflected as qSV wave without any change of phase in case of normal incidence and reflected qSV-wave annihilates the incident qSV wave in case of grazing incidence. It is noticed that the reflection/transmission characteristics of waves depends upon material parameters and incidence angle in this case too.

6 TOTAL REFLECTION

In this section, the case of total reflection beyond critical angle has been discussed. We consider the equation (56) which implies that

Here the quantities are complex and so does at the wave numbersare also complex. Thus the phase velocitiesof these waves are complex and the waves becomes attenuated in space. If we take

whereare real quantities. Then respectively represent phase speed and attenuation coefficients of these waves.

Upon using relations (67) in equation (66), we get

Because

, therefore

Now upon using equations (66)-(68), the potential function

given in equation (32) can be rewritten as

Now for and θ increases to the value first for then is called critical angle. Forthe factor becomes purely imaginary. In the absence of thermal field the critical angle for elastic wave is obtained when . Thus in the presence of thermal field, the value of critical angle increases as . we have

Thus the thermal part and elastic part of reflected P-wave propagates horizontally in X-direction and these quantities decay exponentially with depth.

Moreover, we have also considered the relation , which shows that is real only if this equals to in the absence of mass diffusion. In the presence of mass diffusion for qPwave, the critical angle is (see numerical results later on) and beyond this cutoff point maximum incident shear wave power is converted to reflected shear wave.

7 ENERGY EQUATIONS

From the principle of energy, the energy carried to the boundary by the incident wave must be equal to the energy carried away from the boundary by the reflected and transmitted waves. For the incident qP waves the particle velocities are

For the reflected qP waves

For the reflected qP waves

For the transmitted qP waves

If we take the kinetic energy per unit volume , then the energy flux for the waves mentioned above may be computed by multiplying the total energy per unit volume by the velocity of propagation and the area of the wave front involved. Here the cross-sectional areas of the incident, reflected and transmitted waves are proportional to the cosines of the angles made by the ray directions of the waves with the normal to the interface. Thus, we may write the equality between the incident, reflected and transmitted waves in case of qP waves for the unit area on the interface as

In the absence of mass diffusion

, the energy equation is given by

In the absence of mass diffusion and thermal fields

, the energy equation is given by

For the incident qSV waves the particle velocities are

In this case, the energy equation may be obtained by writing the equality between the incident qSV wave and the sum of the reflected qP wave, reflected qSVwave and transmitted qP wave energies for the unit area on the interface as

In the absence of mass diffusion

, the energy equation is given by

In the absence of diffusion and thermal fields

, the energy equation is given

Here TED stands for thermoelastic-diffusion, TE for thermoelasticity and E for elastic one. It is shown with the help of numerical results in the following section that the energy equation is satisfied in each case.

8 NUMERICAL RESULTS AND DISCUSSIONS

In this section the reflection and transmission coefficients for qP and qSV wave incidences at an interface between thermoelastic-diffusive solid and inviscid fluid have been computed numerically. The material chosen for this purpose is Copper, the physical data for which is given as in Sherief et al. (2004)

The liquid chosen for the purpose of numerical calculations is water, the velocity of sound in which is given b . The values of specific heat of water at different temperatures have been given in Table 1 below: The values of the reflectioncoefficients for incident qP and qSV waves have been computed from equations (45), (47), (49), (50), (58), (60), (62) and (63) for various values of the angle of incidence lying between . The numerical computations have been carried out with the help of MATLAB software. The computed results have been presented graphically in Figures 2-¹¹, and the satisfaction of energy equations at different angles of incidence is given in Table 2.

Here, TED refers to thermoelastic diffusion case, ED to elastic-diffusive case and TE to thermo-elastic one.

Figures 2-⁴, show the energy distribution of reflection and transmission coefficients in case of qPwave incidence at the interface, for thermoelastic diffusion, elastic diffusive and thermoelastic solids, respectively.

It is noticed that the transmitted longitudinal wave losses energy with increasing angle of incidence. A significant effect of diffusion is noticed on the transmitted longitudinal wave between the range. The presence of diffusive field significantly affected the reflected longitudinal wave in the range, after which the behavior of reflected longitudinal wave is almost similar for each case. The effect of thermal and diffusive fields on the reflected thermal wave is noticed in the range. In the absence of diffusive field only a meager amount of energy is associated with the reflected thermal wave except in the range. A significant effect of diffusion and thermal fields has been noticed on the reflected shear wave. From figures 2 and 3, it is noticed that the reflected diffusive wave increases to attain its maximum value at and decreases formeaning that diffusive wave get sufficient amount of energy before it dies out at .

The transmitted wave also gets affected due to thermoelastic diffusion and mass diffusion for via-a'-vis thermal variations as evident from Figures 2 to ⁴.

Figures 5 and 6, present the energy distribution of reflection coefficients in case of qP wave incidence at stress free surface for thermoelastic diffusion and thermoelastic solids respectively.

The effect of diffusion on reflected longitudinal wave is significantly noticed at the normal incidence . In the presence of mass diffusion and thermal fields, the reflected thermal field decreases with increasing angle of incidence except at , where no reflection of thermal wave is noticed. The reflected diffusive wave decreases with increasing angle of incidence and between and it loses energy. In the absence of thermal field only a meager amount of energy is associated with the thermal wave except in the range . From Figures 2-6, it is revealed that at grazing incidence, the reflected and transmitted waves of incident qP wave vanishes except reflected longitudinal wave, thereby meaning that reflected longitudinal wave annihilates the incident longitudinal wave. It is noticed that in the absence of mass diffusion and thermal variations, the trend and nature of reflection and transmitted waves almost agrees with those presented in Achenbach (1973) and Kino (1987).

Figures 7-¹¹, shows the energy distribution of reflection coefficients in case of qSV wave incidence at the interface and stress free surfaces.

It is noticed that for shear wave incidence, there exists two critical angles in case of TED and TE: for transmitted longitudinal wave () and for reflected shear wave beyond which it becomes evanescent in Z -direction and whole of the incident shear wave power is converted to the reflected shear wave. It is also noticed that the reflected longitudinal wave increases to attain its maximum value at due to high stresses generated in the material at this angle of incidence and after that it decreases sharply to become zero at . Beyond this longitudinal wave cutoff, only the decaying fields are associated with the longitudinal wave components and it propagates parallel to the surface and a large amount of energy dissipation has been noticed near. It is observed that the reflected thermal wave and transmitted longitudinal wave are significantly affected due to the presence of thermal and diffusive fields. From figures 7, 8 and ¹⁰, it is noticed that at is quite close to zero though not exactly zero, a phenomenon closely analogous to Brewster angle in optics [Kino, (1987)] has been observed.

This may be used to convert a shear wave to longitudinal wave.

From Table 2, it is inferred that in case of qPwave incidence energy equation is approximately satisfied at all the incidence angles though it exactly holds near the normal and grazing incident angles. Therefore, there is a slight dissipation of energy at the other angles of incidence. In case of qSV wave incidence, the energy equation holds approximately everywhere except in the neighborhoods of critical angle and where large amount of energy dissipation has been noticed. These conclusions are in agreement with Mott (1971).

9 CONCLUDING REMARKS

1. The analytic expressions for reflection and transmission coefficients for qP and qSV wave incident obliquely at the interface between thermoelastic-diffusive solid and inviscid fluid media have been derived.

2. For qP wave incidence at the surface, the significant amount of energy is carried out by transmitted longitudinal wave in the presence of liquid, however the maximum amount of energy is carried out by reflected longitudinal wave in the absence of liquid.

3. For qSV wave incidence at the surface, the maximum amount of energy is carried out by reflected longitudinal wave before the critical angle occurs and there after reflected shear wave becomes prominent.

4. It is observed that the distribution of energy through the reflected and transmitted waves obey energy equations in the respective cases of wave incidence with some exceptions in the neighbourhood of critical angle.

5. The reflection and transmission coefficients have been observed to depend on the material parameters and angle of incidence.

6. Significant effect of mass diffusion and thermal variations has been noticed on the reflection/transmision characteristics of waves.

7. The phenomenon of total reflection reveals that the thermal and elastic parts of reflected qPwave propagate horizontally but decay exponentially with depth.

8. The study may find applications in semiconductor, seismology and signal processing.

Received 15.05.2014

In revised form 29.06.2014

Accepted 18.08.2014

Available online 26.09.2014

Appendix

Upon employing the boundary conditions (24)-(26) at the solid-liquid interface, following system of equations is obtained

Where

The quantities A, Z_p and B used in equation (44) are given by

Hereare amplitude ratios of the reflected and transmitted wave. The quantities are given by

Also the quantities , and used in equations (45), (46) and (47) are given by

can be written from by replacing first, second, third, fourth and fifth column by can be obtained from by replacing first, second, third and fourth column by respectively.

• Abd-Alla, A.N. and Al-Dawy, Amira A.S., (2000). The reflection phenomena of SV-waves in generalized thermoelastic medium, International Journal of Mathematics and Mathematical Sciences 23:529-546.
• Achenbach, J.D., (1973). Wave propagation in elastic solids, North Holland, Amsterdam.
• Bijarnia R. and Singh, B., (2012). Propagation of plane waves in an anisotropic generalized thermoelastic solid with diffusion. Journal of Engineering Physics and Thermophysics, 85:478-486.
• Das, N.C., Lahiri, A., Sarkar, S. and Basu, S., (2008). Reflection of generalized thermoelastic surface waves from isothermal and insulated boundaries of a half-space Computers and Mathematics with Applications, 56:2795-2805.
• Deresiewicz, H., (1960). Effect of boundaries on waves in thermoelastic solids: reflection of plane waves from a plane stress free boundary, Journal of Mechanics and Physics of Solids, 8:164-185.
• Green, A.E. and Lindsay, K.A., (1972). Thermoelasticity. Journal of Elasticity 2:1-7.
• Gutenberg, B., (1944). Relation of reflected and refracted seismic waves, Bulletin of Seismological Society of America,     34:85-102.
• Jeffreys, H., (1930). The thermodynamics of an elastic solids, Proceeding of the Cambridge Philosophical Society, 26:101- 106.
• Kino, G.S., (1987). Acoustic waves: Devices, imaging and analog signal processing, Prentice Hall, Englewood Cliffs, New Jersey.
• Knott, C.G., (1899). Reflection and refraction of elastic waves with seismological applications, Philosophical Magazine, 48:64-97.
• Kumar, R., Ahuja, S. and Garg, S.K., (2014). Rayleigh waves in isotropic microstretch thermoelastic diffusion solid half-space, Latin American Journal of Solids and Structures, 11:299-319.
• Kumar, R., Garg, S.K. and Ahuja, S., (2013). Propagation of plane waves at the interface of an elastic solid half-space and a microstretch thermoelastic diffusion solid half-space, Latin American Journal of Solids and Structures, 10:1081-1108.
• Kumar R. and Kansal, T., (2012). Reflection and refraction of plane waves at the interface of an elastic solid half-space and a thermoelastic diffusive solid half-space. Archives of Mechanics, 64:293-317.
• Lin, C.H., Lee, V.W. and Trifunac, M.D., (2005). The reflection of poroelastic half-space saturated with inviscid fluid, Soil Dynamics and Earthquake Engineering, 25:205-223.
• Lord, H.W. and Shulman, Y., (1967). A generalized dynamical theory of thermoelasticity, Journal of Mechanics and Physics of Solids, 15: 299-309.
• Mott, G., (1971). Reflection and refraction coefficients at a Fluid-Solid interface, Journal of Acoustical Society of America, 50 (3):819-829.
• Nowacki, W. (a), (1974). Dynamical problems of thermo-diffusion in solids-I, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22:55-64.
• Nowacki, W. (b), (1974). Dynamic problems of thermo-diffusion in solids-II, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22:129-135.
• Nowacki, W. (c), (1974). Dynamic problems of thermo-diffusion in solids-III, Bulletin of Polish Academy of Sciences Series, Science and Technology, 22:275-276.
• Nowacki, W., (1976). Dynamic problems of thermo-diffusion in solids, Engineering Fracture Mechanics, 8:261-266.
• Sinha, A.N. and Sinha, S.B., (1974) Reflection of thermoelastic waves at a solid half-space with thermal relaxation, Journal of Physics of the Earth, 22:237-244.
• Sinha S.B. and Elsibai, K.A., (1996). Reflection of thermoelastic waves at a solid half-space with two thermal relaxation times, Journal of Thermal Stresses, 19:763-777.
• Sinha S.B. and Elsibai, K.A., (1997). Reflection and refraction of thermoelastic waves at an interface of two semi infinite media with two thermal relaxation times, Journal of Thermal Stresses, 20:129-146.
• Singh, B., (2005). Reflection of P and SV waves from free surface of an elastic solid with generalized thermo-diffusion, Journal of Earth System Science, 114:159-168.
• Singh, B., (2006). Reflection of SV waves from the free surface of an elastic solid in generalized thermo-elastic diffusion, Journal of Sound and Vibration, 291:764-778.
• Singh, B., (2010). Reflection of plane waves at the free surface of a monoclinic thermoelastic solid half-space, European Journal of Mechanics A/Solids, 29:911-916.
• Sherief, H.H., Hamza, F. and Saleh, H., (2004). The theory of generalized thermoelastic diffusion, International Journal of  Engineering Science, 42:591-608.
• Sharma, A., Sharma, J.N. and Sharma, Y.D., (2012). Modelling Reflection and Transmission of Acoustic Waves at a Semiconductor: Fluid Interface, Advances in Acoustics and Vibrations, 2012:1-10.
• Sharma, J.N., (2007). Generalized thermoelastic diffusive waves in heat conducting materials, Journal of Sound and Vibration, 301:979-993.
• Sharma, J.N., Kumar, V. and Chand, D., (2003). Reflection of generalized thermoelastic waves from the boundary of a half-space, Journal of Thermal Stresses, 26:925-942.
• Sharma, J.N. and Sharma, A., (2010). Reflection of acousto-diffusive waves from the boundary of a semiconductor half-space, Journal of Applied Physics, 108:033712-033724.
• Sharma, J.N., Sharma, R. and Sharma, Y.D., (2008). Generalized Rayleigh waves in thermoelastic solids under viscous fluid loading, International Journal of Applied Mechanics and Engineering, 13:217-238.
• Sharma, J.N., Walia, V. and Gupta, S.K., (2008). Reflection of piezothermoelastic waves from the charge and stress free boundary of a transversely isotropic half-space, International Journal of Engineering Science, 46:131-146.
• Sharma, K. and Bhargava, R.R. (2014). Propagation of thermoelastic plane waves at an imperfect boundary of thermal conducting viscous liquid/generalized thermoelastic solid, Afrika Matematica, 25:81-102.
• Wu, K.Y., Xue, Q. and Adler, L., (1990). Reflection and transmission of elastic waves from a fluid-saturated porous solid boundary, Journal of Acoustical Society of America, 87:2349-2358.

Publication Dates

• Publication in this collection
  08 Dec 2014
• Date of issue
  2014

History

• Accepted
  18 Aug 2014
• Reviewed
  29 June 2014
• Received
  15 May 2014