Abstract
The kinetic model for change of phases developed by M. Avrami at the end of the thirties has been used to describe the temporal behavior of phase changes. Until today this model is studied and adapted to include broader hypotheses. However, the mathematical format presented by M. Avrami is difficult to be understood by beginners. The purpose of this work is to clarify the mathematical treatment of Avrami's work, going straightforward to the arguments that led to his main results.
Avrami; phase change; kinetic model
Review Article
Kinetics of Phase Change
A.C. Faleirosa, T.N. Rabeloa, G.P. Thimb, M.A.S. Oliveirab
aDepartamento de Matemática, Instituto Tecnológico de Aeronáutica,
12228-900 São José dos Campos - SP, Brazil
bDepartamento de Química, Instituto Tecnológico de Aeronáutica,
12228-900 São José dos Campos - SP, Brazil
e-mail: faleiros@ief.ita.cta.br
Received: March 30, 2000; Revised: August 17, 2000
The kinetic model for change of phases developed by M. Avrami at the end of the thirties has been used to describe the temporal behavior of phase changes. Until today this model is studied and adapted to include broader hypotheses. However, the mathematical format presented by M. Avrami is difficult to be understood by beginners. The purpose of this work is to clarify the mathematical treatment of Avrami's work, going straightforward to the arguments that led to his main results.
Keywords: Avrami, phase change, kinetic model
1. Introduction
Sixty years has passed since a theory about the kinetic of the phase change was proposed by Melvin Avrami at the end of the thirties1,2. Despite of all this elapsed time, it is still used to describe the nucleation and growth of new phases3-8 and new improvements have been suggested to make its hypothesis as broad and flexible as possible9-13.
Avrami's model assumes that the system subjected to the phase change is composed by germs of the new phase. These germs are transitory molecule arranges randomly distributed that are similar to those existent in the new forming phase. According to the statistical fluctuation, these arrangements form and disappear, but some remain in latent state without growing. When, for some reason, the phase change begins, some of these primordial germs start growing, reaching a critical size and become stable. From this point on, they are called grains of the new phase. They will suffer an expansion process, at which the number of essential germs decreases with time. This decrease occurs by two mechanisms: germ transforms into grains, or growing grains swallow some of the existent germs. Avrami developed his theory making these physical assumptions and doing a mathematical treatment, which considers the functional relation between the number of germs and the volume of the new growing phase.
The goal of this work is to clarify the mathematical arguments used by Avrami in his original papers, going directly to the arguments that lead us into the main results of his theory.
2. Germs, Grains and Transformed Volume
In this section the notation and the basic principles of Avrami's model will be established.
Consider a metastable material that starts changing phase at some moment. Let N0 be the number of essential germs of the new phase per unit volume at the beginning of the phase change process. Germs form and disappear but it can be supposed that their density remains constant during the phase change process.
Two mechanisms can be considered to explain the temporal variation of the number of germs. In the first one, germs start growing and become grains of the new phase. In the second one, germs are swallowed by the growing grains, which occupy the places before occupied by the swallowed germs. In the following paragraphs the kinetic of these two mechanisms will be described.
For the first mechanism, let N = N(t) be the number of germs for the new phase per unit volume at the instant t Suppose uniform distribution of the germs in the entire volume of the previous phase. At the initial time, N(0) = N0. Let N' = N'(T) be the number of grains of the new phase, at the instant t per unit volume. The probability n of a germ to transform into grain, per unit of time, is given by the equation14-19
Here, Q is the activation energy per mol, T is the absolute temperature, R is the universal constant of the gases, and A(T) is the necessary work to form a mol of grain at the temperature T. Therefore, the variation of the number of germs that transform into grain per unit volume at the time period dt is given by
For the second mechanism, the variation in the number of germs is due to the new phase growth that, by expansion, swallows the germs and occupies the places before occupied by the swallowed germs. Let N = N(t) be the number of swallowed germs per unit volume at the instant t. The variation of the number of swallowed germs per unit volume at the time period dt is given by
here, dV is the volume variation per unit volume of the new phase during the time period dt. However, this is an roughly estimated relation, which is applied when the number of grains is small in relation to the number of germs. In a future section we will present the exact relation for the swallowed germs.
The variation of the number of germs per unit volume at the time period is given by
The negative sign is justified by the fact that an increase of N' and N produces a decrease of N. Therefore, the derivatives of N, N' and N, per unit volume at the instant t are
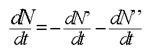
(1)
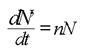
(2)
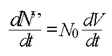
(3)
One important particular case for the Eq. 1 happens when n is so big that almost all germs transform into grains before any ingestion has the chance to occur. In this case, the term dN/dt can be ignored in comparison with the term dN'/dt and Eq. 1 reduces to

(4)
If the temperature and the essential germ concentration remain constant, n can be considered constant during the entire process and, under these conditions, Eq. 4 becomes a separable differential equation. Dividing (4) by N it follows
or
Integrating it from the initial time to the time t,
or
and, explicitting N(t),

(5)
Taking the above equation to Eq. (4), and integrating it, follows
or
where N' ® N0 when t ® ¥. Figure 1 shows the curves for
with n = 1, 2, and 5 and N0 = 1.
Curves for N' = N 0 (1 - e -nt) , with n = 1, 2, and 5 and N0 = 1. The continuous line corresponds to n = 5, the dashed line to n = 2 and the dotted line to n = 1.
3. Characteristic Time Scale
Going back to the general case, to simplify Eqs. 1, 2 and 3, another time scale t = t(t) defined by
will be used. Its derivation in the variable t produces

(6)
The relation between the time scale t and t will be uniform only if n is constant during the entire process. This new time scale is called characteristic time scale. From this point on, unless opposite mention, the characteristic time t will be used. As n > 0 the derivative dt/dt = n will be positive, assuring that t = t(t) is strictly increasing having, in this way, an inverse t = t(t) The derivative of this inverse is
Substituting Eqs.(2) and (3) in Eq. (1), the following is obtained:
and, changing it to the variable t,
or
Integrating the above equation from 0 to t, follows
and, since N(0) = N0 and V(0) = 0,

(7)
To solve this integral equation, it is necessary to obtain the functional relation V(t), which is a composite function similar to j(t(t)) that can be rewritten as
when t = t (t). The chain rule applied to this function can be written in the following way

(8)
Applying the Chain rule (8) to Eq. (2), follows

(9)
which can be integrated. As N'(0) = 0, this integration results in

(10)
Equation (7) is valid only during the time that there are germs to be consumed or to be transformed into grains. Let t =  or t =
or t =  be the instant in which all germs were consumed. From this time on, the number of grains remain constant. While the numbers N and N' and remain constant, the volume of the new phase keeps growing.
be the instant in which all germs were consumed. From this time on, the number of grains remain constant. While the numbers N and N' and remain constant, the volume of the new phase keeps growing.
4. Exact Relationship for the Swallowed Germs
In this section we will improve the description for the N'(t) behavior.
We must observe that Eq. (3) is valid when the number of grains is small in comparison with the number of germs. Otherwise, the density found by the new phase progressive front is N/(1 - V) where (1 - V) is the volume fraction per unit volume that was not transformed. Thus, when the number of grains is not small compared with the number of germs, Eq. 3 must be substituted by

(11)
which taken to Eq. (1) gives
or, in the t variable
Dividing the above equation by nN follows
or
whose integral from 0 to t leads to
that can be solved in the variable N producing

(12)
Substituting Eq. (12) in (10) results into

(13)
According to Eq. (12), N decreases asymptotically to zero but doesn't vanish. However, experiments show that at certain instant  the germs exhaust. To describe this experimental fact, it must be observed that Eq. (13) is valid only until the instant t. In order to have agreement between experimental results and theory, it is necessary to attribute a defined value to
the germs exhaust. To describe this experimental fact, it must be observed that Eq. (13) is valid only until the instant t. In order to have agreement between experimental results and theory, it is necessary to attribute a defined value to  for small values of N. We can arbitrarily make
for small values of N. We can arbitrarily make  equal to the instant in which N = 1 and take this value to Eq. (12), which follows
equal to the instant in which N = 1 and take this value to Eq. (12), which follows
This is a transcendental equation defining
For t bigger than  , N is practically null, while N' remains constant with values given by Eq. 13
, N is practically null, while N' remains constant with values given by Eq. 13
5. Extended Volume
In this section, to obtain the functional relation V[N(t)] between the transformed volume and the number of grains, it is developed the concepts of averaged radius and volume of the grain. From these concepts the extended volume of the new phase is obtained. This relation is necessary in order to integrate Eq. (7).
Not all grains start growing at the same instant. When a grain touches another one, there is an interruption in its growth at the interface. The volume that a grain would have if its growth were not interrupted by the contact with another grain is called extended volume. The grain that was born at instant z has, at the moment t, an extended volume represented by vex(t, z). Both instants are referred to the characteristic time scale.
Generally, the grains are not perfectly spherical. Therefore, when one refers to the radius r of a grain, in fact, we are referring to the averaged radius of the grains. The radius that a grain would have if there were not contact among the grains is called extended averaged radius. Let G(t) be the averaged rate of growth of a grain. At an instant t the extended averaged radius of a grain, which was born at the instant t = y is given by
In the characteristic time scale, this extended radius of the averaged grain is
or

(14)
where
Here, t = z is the instant that a grain appeared. The extended volume of the grain is

(15)
where s is a shape factor, equal to 4p/3 for spherical grains.
Let dN'(z) be the variation of the number of germs that transform into grains between the instants t = z and t = z + dz. According to Eq. 9, dN'(z) = N(z)dz. If the volume of each grain were added, supposing that the growing of each grain is not hinder by other grains, we obtain the total extended volume per unit volume at the instant t

(16)
6. Characteristic Phenomena at the Isokinetic Phase
The factors that control n must control G and it might be expected similarities between the variation of these parameters with the external conditions. Keeping this in mind, one can infer that n and G are approximately proportional at a large range of concentration and temperature. This range will be called isokinetic range. If one admit that the relation
is constant for a given substance at the isokinetic range, from Eqs. (14) and (15) we obtain

(17)

(18)
and from Eq. (16),

(19)
If a is independent of the temperature and concentration at the isokinetic range, the transformation story and the kinetic description of the process at the time scale t will also be independent of the temperature and concentration. Therefore, for a given substance, there is an isokinetic range of temperature and concentration, at which the characteristic kinetic of a phase change remains unaltered at the characteristic time scale. Thus, to establish the kinetics of a reaction in a concentration and temperature range at the isokinetic range, it is enough to solve just one problem at the time scale t.
Equations (15), (18) and (19) apply to pseudo-spherical or polyhedral grain growth. If the grain grows along two or one dimension (plate or needle like), Eq. (19) must be substituted by

(20)
and

(21)
where s' = p and s = 1. Equation (19) applies only to isokinetic domains, i.e., in the situations that a = G/n is constant.
7. Evolution of the Extended Volume
In this section Avrami's main argument is developed.
Let z be the instant in which the grain appears and t the actual time of the phase change, both in the characteristic time scale. Consider a grain, selected arbitrarily, and let v' = v'(t, z) be the volume part of this grain that is not superimposed to other grains and vex = vex(t, z) be the extended volume of this grain, i.e., the volume that it would have if its growth were not obstructed due to the contact with other grains. If this grain were taken off from its place, leaving behind the overlapped parts, v' would be the fraction matter not transformed, which during the phase change contributed exclusively for this grain growth. Therefore, v'/vex is equal to the volume fraction of matter that remains in the old phase. Remembering that 1 - V(t) is the volume fraction that was not transformed, it follows that, on average,

(22)
Another way to justify this equation is the following: If, for example, 30% of the initial volume is transformed, it follows that (1 - V) = (1 - 0,3) = 0.7. Analyzing a grain in this medium, on average, 30% of it will be superimposed to other grains. Since vex is the extended volume of the grain, the part v' that is not superimposed to other grains must be equal to 70% of the extended volume and v'/vex must be equal to 0.7. Figure 2 depicts a grain with extended volume vex and its part with volume v'.
A grain in a process of phase change. The biggest disk represents a generic grain whose volume is vex. The white parts represent other grains that are in touch with or were swallowed by it. The black part is not superimposed to other grains and has volume v'.
Admitting grains randomly distributed, Eq. (22) can be used as an average. However, the grains are randomly distributed only in the region that was not transformed. In the transformed region, there are only grains of the new phase and all germs were swallowed. Therefore, the assumption that the grains are randomly distributed is true only for grains that, at the time z of its appearance, were outside of the transformed volume V(z). There are two ways to overcome this situation and obtain the same final result.
The first way to overcame the situation mentioned above is to consider all germs, including those that, at the instant z, are located inside of the grains, which will be called ghost germs. The number of these germs, in the characteristic time scale, is given by Eq. (5)
In this case, the random situation can be reestablished if we associate ghost grains to those germs that would be transformed into grains if they had not been absorbed by the other grains that grew up. During the time interval from z to (z + dz), the variation of the number of new grains per unit volume, including the ghost grains, is dN'(z) = N(z)dz, where N(z) = N0e-z. If vex(t, z) is the extended volume of one grain, at the instant t, that started growing up at the instant z then the extended volume Vex(t) of all grains in the new phase is

(23)
Consider the following property of real numbers: if
then
Taking into account this property, and adding the numerators and denominators of Eq. (22) over all grains, we obtain
where V' is the overall grain addition of v' while Vex is the overall grain addition of vex
From the above equation and Eq. (23),

(24)
The second way to arrive at the above result is to assume random distribution of the germs only in the volume 1 - V(z) that was not transformed at the instant z, and consider that the number of germs in this region is expressed by Eq. (12)
In this case, when ghost grains are not considered, the Vex value is still given by
At the instant z, the volume that was not transformed is 1 - V(z) The germs that started growing at z were randomly distributed in this volume. At the instant t the volume in the old phase is 1 - V(t). The ratio
is the fraction of volume that was not transformed at the instant t in relation to the volume that was not transformed at the instant z. Since the ghost grains are not considered in this case, one can consider that z is the initial instant of the transformation and that the initial volume of the material that did not suffer any change is 1 - V(z). Like before, in average, the ratio between v' and vex is equal to the volumetric fraction of matter that was not transformed. Now, this fraction is equal to [1 - V(t)]/[1 - V(z)] and, therefore,
or
Multiplying both sides of this equation by the number of grains dN'(z) = N(z)dz formed during the time interval dz, follows
or using Eq. (12)
which integrated from 0 to t gives
But,  is exactly V'(t) and hence,
is exactly V'(t) and hence,
which coincides precisely with Eq. (24).
When the new phase is composed of thin grains, the grains superimpose very little and we can assume that V(t) = V'(t) which combined with Eq. (24) gives

(25)
Under isothermal conditions and uniform concentrations, n can be considered constant. Considering polyhedral growth, at the time scale t the extended radius rex of grains that appeared at the instant y is proportional to t - y. That is rex = G(t - y), where the constant of proportionality G is the radial growth rate. In the characteristic time scale, t = nt and z = ny thus, rex = (G/n)(t - z) = a(t - z), with a = G/n. Therefore,
where s = 4p/3 for spherical grains. From Eq. (25),
or

(26)
with

(27)
and
When t << 1 one obtains
That way,
and, therefore,
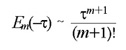
(28)
When t >> 1, the e-t value becomes very small, i.e., this value is much smaller than any entire power of t. In this case, who dictates the asymptotic behavior is the biggest t power and hence
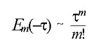
(29)
Using the Eqs. (28) and (29) asymptotic developments in Eq. (26), one obtain
when t << 1 and
when t >> 1.
Both of the equations have the Btk format, with B and k constants. Substituting these equations in Eq. (25), follows

(30)
which is the empirical expression obtained by J.B. Austin and R.L. Rickett20 for the isothermal transformation of super-cooled austenite into bainite.
Equation (26) is valid until total germs consumption, which occurs at the instant  . From this instant on, the superior limit of the integral must be substituted by
. From this instant on, the superior limit of the integral must be substituted by  . In this case Eq. (26) transforms into
. In this case Eq. (26) transforms into
Although germs do not exist anymore, the grains keep growing. This explains the appearance of t and t in this integral. Applying the property  to the above equation, one obtain
to the above equation, one obtain
and making x = z -  ,
,
From the E3(-t) definition, one can write
In order to obtain the needle and planar growth expression, it is enough substitute E3 for E1 and E2 and b will be now N0(G/n) and 2pN0(G/n)2, respectively. Defining
it is possible to unify the previous expressions and write, for the three growth types,

(31)
Infinitesinal volume increment of a grain during the process of phase change. The ring around de disk, with volume dvex, is the result of the growth of the grain during a small time interval. The black parts, with volume dv', are the one that is not superimposed to any other grain.
8. Relation between Real and Extended Volume
Applying the same logic used in the previous section to the volume increment of only one grain in a small time interval, one obtain for the averaged grain
Figure 3 depicts the meaning of the differential volumes dv' and dvex. Here, as we are dealing with infinitesimal increments, dv' = dv. Multiplying and dividing the previous ratio by the number of grains per volume, we obtain

(32)
which is a separable differential equation. Rearranging this equation and integrating it, it comes
or
where C is the integration constant. Considering that Vex = 0 when V = 0, we get C = 1 so that

(33)
This is the fundamental relation, applicable to every case in which there is a randomly thin grain distribution. This deduction was made independently of isothermal or isokinetic assumptions. Using Eq. (33) into Eqs. (12) and (13), we obtain

(34)

(35)
9. Isokinetic domain transformation
The phase change kinetics is totally determined by Eqs. (33), (34) and (35). For the isokinetic case, Vex is given by Eq. (26), which applied to Eqs. (33), (34) and (35), produces

(36)

(37)

(38)
remembering that E(t) = Em(-t).
Equation (37) shows that the number of germs decreases exponentially, but never vanishes. However, it is observed experimentally that they become equal to zero at some time  . This time is considered the one when N = 1 This unit value is negligible in comparison with the initial particles number and can be considered the actual zero point. Assuming N(
. This time is considered the one when N = 1 This unit value is negligible in comparison with the initial particles number and can be considered the actual zero point. Assuming N( ) = 1 in Eq. (37), it follows
) = 1 in Eq. (37), it follows

(39)
When t >  , the number of germs are exhausted. Using Eq. (31) in Eqs. (33) and (38), one obtain
, the number of germs are exhausted. Using Eq. (31) in Eqs. (33) and (38), one obtain

(40)

(41)
10. Beginning of the Transformation
For polyhedral growth and t << 1 from Eqs. (28) and (36), one obtain
or

(42)
where b = 8pG3N0/n3 and t = nt.
Taking into account that
when t << 1, Eq. (38) reduces to

(43)
Equation (43) shows that, at the initial instants of the transformation, the number of grains present is proportional to the time, while Eq. (42) shows that the transformed volume is proportional to t4.
Equation (42) shows that the transformation begins when bt4/4! is significantly different from zero. For usual values of b, this occurs when t is around 1. Let t = tb be the instant at which the transformation starts. As t = nt, we obtain ntb = tb @ 1 or tb = 1/n. This result was empirically obtained by H. Krainer21 in his experiments for the decomposition of austenite in steels.
11. Temporal Evolution of the Transformation
In this section we will be concerned with obtaining relations valid during almost the entire isokinetic transformation.
From the expressions (36) and (40), valid for t <  and t ³
and t ³  , respectively, which we reproduce again:
, respectively, which we reproduce again:
and
one obtain the following estimations:
1. If N0 >> 1 (situation in which the germs do not vanish) and n << 1 (case in which t << 1 during almost the entire transformation), Eq. (42) will be a good approximation during the entire transformation, and one obtain the situation studied by Mehl-Johson22.
2. If N0 >> 1 (situation in which the germs do not vanish) and n >> 1 (case in which t >> 1 during almost the entire transformation), Equations (36) and (29), give us

(44)
3. If N0 is small (the number of germs become equal to zero at the beginning of the transformation, so that  << 1), Eq. (39) together with the asymptotic development Eq. (28), give us
<< 1), Eq. (39) together with the asymptotic development Eq. (28), give us

(45)
where m = 1, 2, or 3, respectively, for needle, planar and volumetric growing. As  is small, t >
is small, t >  during almost the entire transformation. In this way, almost the entire transformation can be described by Eq. (40). The asymptotic relation Eq. 29, valid for t >> 1, gives
during almost the entire transformation. In this way, almost the entire transformation can be described by Eq. (40). The asymptotic relation Eq. 29, valid for t >> 1, gives

(46)
Taking the asymptotic relations (45) and (46) to (40), and considering that (t -  ) is almost equal to t since
) is almost equal to t since  can be considered small, follows
can be considered small, follows
Here, the identity exp(-ln N0) = 1/N0 was used. After simplifications,

(47)
which is very similar to Eq. (44). The occurrence of N0 - 1 instead of N0 as in Eq. (44), is due to the fact that the ultimate germ per unit volume was neglected to deduce this last equation.
Similar deductions can be done for phase changes with planar and needle growth.
For planar growth,

(48)
valid when n << 1 and

(49)
valid when n >> 1.
For needle growth,

(50)
valid when n << 1 and

(51)
valid when n >> 1
All the above expressions have the same format of the Austin-Rickett20 formula

(52)
The t value for certain level of transformation, for example 25%, or 50% or 75%, is always the same for a big range of temperature, concentration, etc. Using Eq. (36), one obtain the ratio
From the asymptotic relations (28) and (29), it follows

for t << 1
and

for t >> 1
where m = 1, 2, or 3 for needle, planar or volumetric growing, respectively. From these relations it comes for t << 1,

(53)
and, for t >> 1,

(54)
The asymptotic relations (53) and (54) furnish the extreme values between which t0.75/t0.25 is situated. Making m = 3, 2, and 1, the extreme values between which the ratio t0.75/t0.25 is located, for polyhedral, planar and needle growth are, respectively,
Here, the approximations (4.82)1/4 = 1.48, (4.82)1/3 = 1.69 and (4.82)1/2 = 2.2 were used.
Several experimental results fall inside the above intervals23. Some discrepancies were observed and need to be analyzed to obtain better understanding of the factors that provoked these deviations.
12. Conclusion
The analysis done in this work shows, step by step, the kinetic model proposed by M. Avrami to describe the kinetics of phase change.
A different model to visualize de most important part of Avrami's arguments is proposed (Evolution of the extended volume), which we consider easier to understand than the ones proposed before.
The final result of the model is the fundamental relation:
which is applicable to every isokinetic and isothermal phase change transformation. Fitting experimental results with this expression, one determine the values of B and k for the kinetic law of a phase change.
The model also makes possible to determine the dimension of the grain. This can be done utilizing the ratio between two growth time. For example, take the spent time to 75% of a new phase grow in relation to the one necessary to 25% of the new phase grow. After that, compare the value for this ratio with the ones predictable by the asymptotic relations (53) and (54), which furnish the extreme values for t0.75/t0.25 for polyhedral, planar and linear growth, respectively.
- 1. Avrami, M. J. Chem. Phys., v. 7, p. 1103, 1939.
- 2. Avrami, M. J. Chem. Phys., v. 8, p. 212, 1940.
- 3. Weiberg, M.C.; Birnie, D.P.; Shneidman, V.A. J. Non-Crystalline Solids, v. 219, p. 89, 1997.
- 4. Malek, J.; Mitsuhashi, T.; Ramirez-Castellanos, J.; Matsui, Y. J. Mat. Res., v. 14 n. 5, p. 1834, 1999.
- 5. Jean, J.H.; Lin, S.C. J. Mat. Res., v. 14, n.7, p. 2922 1999.
- 6. Zhong, Z.K.; Guo, Q.P. J. Polimer Science Part B - Polymer Physics, v. 37, n. 19, p. 2726, 1999.
- 7. Li, W.Y.; Mitchell, B.S. J. Non-Crystalline Solids, v. 255, n. 2-3, p. 199, 1999.
- 8. Di Lorenzo, M.L.; Silvestre, C. Progress in Polymer Science, v. 24, n. 6, p. 917, 1999.
- 9. Kong, L.X.; Hodgson, P.D.; Wang, B. J. Mat. Proc. Tech., v. 90, p. 44, 1999.
- 10. Volpe, M.; Tomellini, M.; Fanfoni, M. Surf. Sci., v. 423, n. 2-3, p. 1258, 1999.
- 11. Jouppila, K.; Kansikas, J.; Roos ,Y.H. Carbohydrate Polymers, v. 36, n. 2-3, p. 143, 1998.
- 12. Meier, A.; Chidambaram, P.R.; Edwards, G.R. Acta Materialia, v. 46, n. 12, p. 4453, 1998.
- 13. Yavari, A.R.; Negri, D. Nanostructured Materials, v. 8, n. 8, p. 969, 1997.
- 14. Volmer, M.; Weber, A. Zeits. F. Physik. Chemie, v. 119, p. 277, 1926.
- 15. Volmer, M.; Marder, M. Zeits. F. Physik. Chemie, v. A154, p. 97, 1931.
- 16. Stranski, N.; Kaischew R. Zeits. F. Physik. Chemie, v. B26, p. 317, 1934.
- 17. Stranski, N.; Kaischew, R. Zeits. F. Physik. Chemie, v. 36, p. 393, 1935.
- 18. Borelius, G. Ann. Physik, v. 33, p. 517, 1938.
- 19. Becker, R. Ann. Physik, v. 32, p. 128, 1938.
- 20. Austin, J.B.; Rickett R.L. Metals Technology, p. 964, 1938.
- 21. Krainer, H. Archiv F. Eisenhuttenwesen, v. 9, p. 619, 1936.
- 22. Mehl, R.F. Johnson W. Metals Technology, p. 1089, 1939.
- 23. Davemport, B. Trans. A.I.M.E., v. 90, p. 117, 1930 and v. 100, p.13, 1932.
Publication Dates
-
Publication in this collection
17 Nov 2000 -
Date of issue
July 2000
History
-
Accepted
17 Aug 2000 -
Received
30 Mar 2000





































































