Classical charge oscillations in nanoscopic systems

Oscilações de carga clássicas em sistemas nanoscópicos

ARTIGOS GERAIS

Classical charge oscillations in nanoscopic systems

Oscilações de carga clássicas em sistemas nanoscópicos

R. De Luca¹; S. Ganci

Dipartimento di Matematica e Informatica, Università degli Studi di Salerno, Fisciano, SA, Italy. Studio di Catalogazione e Conservazione Strumenti Scientifici, Casarza Ligure, GE, Italy

ABSTRACT

A single charge confined on the axis of a nanocylinder, carrying a charge of opposite sign, and two equal free classical charges on a conducting thin nanoring are two systems which can oscillate with frequencies in the THz domain. The potential energy obtained for the latter case can be generalized to n equal charges (n > 2). It can be shown that the n charges occupy positions on the ring corresponding to the n roots of unity at equilibrium.

Keywords: charge oscillations, THz domain, nanoscopic system.

RESUMO

Uma única carga confinada ao longo do eixo de um nanocilindro, que possui uma carga de sinal contrário, e duas cargas iguais livres em um fino nano-anel condutor são exemplos de sistemas que podem oscilar com frequências na região de THz. A energia potencial obtida para o último caso pode ser generalizado para n cargas iguais (n > 2). Mostra-se que as n cargas ocupam posições sobre o anel que correspondem no equilíbrio às n raízes da unidade.

Palavras-chave: oscilações de carga, região de THz, sistemas nanoscópicos.

1. Introduction

The problem of oscillating charges in the THz domain is a rather interesting topic, since the study of these systems may be used to develop security detectors [1], which are now of importance to allow safe mobility by public transportation. Indeed, terahertz radiation can be easily transmitted through commonly used non-metallic covers, which might hide potentially dangerous materials as, for example explosives. Furthermore, most of these mediums have characteristic responses in the terahertz domain. The resulting spectra in this domain can thus be used to identify hidden potentially dangerous materials, otherwise not detectable, such as explosives carried by terrorists under their clothes. Therefore, the terahertz radiation emitted by an oscillator (or a collection of those) could be used to device new types of detectors to allow safe public transportation. These characteristic frequencies appear, typically, in nanoscopic systems. Being these systems analyzed by means of elementary classical electrodynamics concepts, their study can link the actual research on nanoscale systems [2] to physics teaching. When dealing with nanocylinders (or nanorings), however, the detailed structure of these materials needs to be considered. Indeed, the interatomic distances of the molecules constituting the cylinder (or ring) are of the order of 10^-10 m (1 Å), so that the charge distribution in space is far from uniform over the characteristic length of the system, which may be only ten times larger than the interatomic distance. A complete quantum mechanical description of the system, however, goes beyond the scope of the present work.

In the present work we shall first give a classical example of a single charge oscillating on a conducting wire placed on the axis of a charged nanocylinder, noticing that these oscillations are indeed in the terahertz domain. Subsequently, after having introduced the problem of two point charges in a conducting nanoring, we study the oscillation mode of this system by Lagrangian methods. We generalize, in the static case, the result found for two point charges to n of such entities. An analytic solution of the equilibrium equations for n=3 is given in the Appendix as a mathematical endeavour.

2. A single charge inside a uniformly charged nanocylinder

The system we consider in the present section consists of a single charge q on a finite conducting wire placed along the axis of a uniformly charged cylinder of radius R and height a. The charge must be confined within the wire, since we would like it to oscillate on the cylinder axis, in the proximity of its equilibrium point. The confinement of the charge is necessary since, by Earnshaw theorem [3], no stable equilibrium point may be found for a free charge in space in the presence an electric field generated by any charge distribution. The total charge on the cylinder is Q, whose sign is opposite to the sign of q, and, as shown in Fig. 1, the displacement of the charge q from its equilibrium point O, placed at the midpoint of the cylinder axis, corresponding, on its turn, to the midpoint of the conducting wire, is denoted by x. The centre of a thin portion of the cylinder, of height dξ is at distance ξ from point O. Therefore, the electrostatic potential dV at x, generated by the charge distributed on the thin ring is given by

where k = and dQ = 2πRσdξ, σ = being the charge density on the cylinder.

Therefore, the electrostatic potential V at x is given by

By setting η = x - ξ, we have dη= -dξ, so that

and finally

where we have expressed the arguments of the logarithm function in terms of normalized quantities.

Therefore, the potential energy U (x) can be written as follows

whose graph is shown in Fig. 2, along with the series expansion to second order in

The series expansion of U (x) suggests that the charge q, if slightly displaced from its equilibrium position at x = 0, is subject to small oscillations about this point, the frequency of oscillation υ being

where m is the mass of the charged particle. We notice that, for >> 1, i.e., in the case of a thin ring, the expression for υ becomes the following

By setting a = 2R in Eq. (6), we may estimate the dimensions of the cylinder, if the desired frequency is taken to be of the order of 1 THz. In order to do this, we further assume that Q = -100q, and that the particle be an electron, so that a ≅ 122 nm and R ≅ 61 nm. For thin rings, on the other hand, by again taking a proton as the oscillating charge and Q =-100e, the radius R of the ring needs to be of about 86 nm, in order to obtain frequency oscillations of 1 THz. We thus see that, in these types of problems, oscillation frequencies in the THz domain can be obtained in nanoscopic systems.

Notice that nothing has been said about the electromagnetic friction force due to the interaction of the accelerated charge with the ions within the conductor or on its radiation emission [4], since we have only considered the natural frequency of the system. While electromagnetic friction force effects will be taken into account in the following section, here we would like to briefly mention how to calculate the radiation power emitted by the oscillating charge. We thus consider a charge q oscillating with angular frequency ω = 2πυ and a maximum excursion x₀≅ 10 nm about its equilibrium position. The mean square acceleration of the charge will be . If we apply the classical Larmor formula [4], we may find the power emitted by the charge to be

where ε₀ is the dielectric constant of vacuum and c is the speed of light. If we take q = e and set υ = 1.0 THz, we obtain P = 4.45 × 10^-19Watt = 2.78 eV/s.

3. Two charges on a nanoring

In the present section we consider a similar problem leading to oscillations of point particles in the THz domain. The second system we would like to study consists of two point particles carrying charges q1 and q₂, respectively, confined to move on a thin conducting ring of radius R, as shown in Fig. 3.

In this case we shall adopt a Lagragian approach to determine the oscillating frequency of the two point particles, both of mass m and charge q. By taking the angles the charges make with the horizontal as generalized coordinates, we may write the Lagrangian L of the system as follows

We may assume that the effect of the friction force, due to the motion within the conductor, on the i-th particle can be schematized by means of the viscous force Qi = -γ_i [4]. Therefore, Langrage's equations can be written as follows

At equilibrium θ₂-θ₁ =π. Therefore, by defining θ=θ₂-θ₁=π + ξ, we can recast the above equations in terms of the sole variable ξ in the following way

where = . For small oscillations of the charges about their equilibrium position, we can set

sin ≈ and cos ≈ 1, so that Eq. (11) becomes

which is the dynamical equation of a damped oscillator, whose natural frequency is υ = If the frequency is assumed to be of the order of 1 THz, by setting q = -e, taking the particles to be electrons, we have R ≅ 3 nm.

4. Static solution for n charges on a thin ring

In the present section we study the static conditions for a system of

n > 2 equal point charges

q on a conducting thin ring. By extending the analysis of the previous section to an arbitrary number of charges at equilibrium, the equilibrium conditions are analytically solved for

n = 3 in the

^Appendix.

In general, we may state that, given n (n > 2) equal free point charges q, confined on a circumference of radius R, the equilibrium positions of these charges correspond to the vertices of a regular polygon, having exactly n sides, inscribed in the circumference itself.

In order to prove what stated above, let us consider a coordinate system Oxy, with origin O in the centre of the ring. Let us also consider a charge at point A (R, 0). Being the charge at equilibrium, there could not exist a component of the electric field tangential to the circumference of radius R at A. In order to satisfy this condition, we distinguish two cases: odd and even number of charges n.

If n is odd, we find that the remaining couples of charges, different from the charge in A, are formed each by two charges which are positioned symmetrically with respect to the diameter AA', A' (-R, 0) being the opposite point to A on the circumference. This is so because the y-component ( y being the direction tangent to the circumference at A) of the electric field generated by the two charge in the couple considered must be zero (see Fig. 4). From this follows that, for each couple, the distance of each of the two point charges in the couple from A is the same. Since the same reasoning can be carried out by isolating a charge placed in the nearest neighbour point B to A, and by considering couples of charges which are symmetrically placed with respect to BB', whereB' is a point opposite to B on the circumference, we can argue that the distance between any two adjacent charges must be constant, if we extend the same argument to a nearest neighbour charge to B, and so on. In this way, we can conclude that the n charges need to be necessarily placed at the vertices of a regular polygon with n sides inscribed in the circumference.

On the other hand, if n is even, and if we start by considering a first charge is place in A (R, 0), there must exist, necessarily, a second charge in A^' (-R, 0). The remaining couples of charges are placed, as before, in such a way that the positions of the two charges in each couple are symmetric with respect to the diameter AA . It follows that, for each couple, the distance of each of the two point charges from A is the same. However, we could start by considering a first charge being placed in a nearest neighbour point B to A, so that a second charge needs to placed in B^', opposite to B on the circumference. The remaining couples of charges are placed in such a way that the positions of the two charges in each couple are symmetric with respect to the diameter BB'. From this point on, we adopt the same reasoning as before to conclude that, even in this case, the n charges need to be necessarily placed at the vertices of a regular polygon with n sides inscribed in the circumference.

5. Conclusions

Two different systems, showing charge oscillation, have been analyzed by means of classical mechanics and basic electrodynamics concepts. It is noted that, when the characteristic dimensions of these systems are of the order of 1 nm, the natural oscillation frequencies of the moving charges are in the THz regime.

In particular, the system consisting of a uniformly charged nanocylinder of radius R and length a and a conducting nanorod, placed along the cylinder axis and carrying a charge q, is first considered. It is noted that the nanocylinder can generate an electric field on its axis such that the charge q can oscillate about the axis midpoint along the nanorod. Frequencies of the order of 1 THz are obtained for an oscillating electron (q = -e), and for Q =-100q, a ≅ 122 nm and R ≅ 61 nm. The oscillations of a point charge about the centre of a nanoring on a conducting nanorod placed along its axis are studied by taking the limiting condition a = 0.

As a second example, the case of a nanoring of radius R with two equal free charges confined to move along its circumference is studied. By adopting a La-grangian approach, the classical equations of the motion of the system are solved for small oscillations of the charges about their equilibrium positions. It is found that, by taking the oscillating particles to be electrons, we need to have R ≅ 3 nm, in order to have frequencies in the THz domain. The static solutions for these systems are studied for n > 2, finding that the n charges attain equilibrium positions corresponding to the vertices of a regular polygon with n sides inscribed in the ring.

We may consider this classical analysis useful for didactical purposes, since it proposes some aspects of actual research topics. In particular, we notice that the wonderful world of nanostructures can be looked at from a classical viewpoint, even within the limits that classical dynamics imposes to the validity of the present treatment. In fact, in order to obtain more realistic results, noting that the characteristic scale of these systems calls for a quantum mechanical extension of the present concepts, we may still consider this classical analysis as a starting point for further studies. In the quantum case one however needs to consider much less simple expressions for the overall potential energy. Furthermore, the dynamics of the system is governed by the Schrödinger equation, rather than Newton' second law for a classical particle. Obviously, quantum mechanical extensions of the present analysis goes beyond the purpose of the present work. Finally, we may also consider that, by studying the characteristic features of these systems, physics teachers could connect the fascinating topic of nanoscale devices to elementary physics concepts.

Acknowledgments

One of the authors (RDL) would like to thank F. Romeo for helpful discussions on the subject.

Recebido em 27/10/2008

Revisado em 15/1/2009

Aceito em 5/2/2009

Publicado em 30/6/2009

The equilibrium conditions giving the n charges placed at the vertices of a regular polygon inscribed within the ring circumference are analytically solved for n = 3.

We assume that the angular position of the i-th charge is given by the angle θi, so that the electrostatic potential U may be written as follows

The minimum of U is obtained by setting

Therefore, by recalling Eq. (A1), and defining θj_i = θ_i - θj we have

where each equation contains N = addends and where

The set of equations (A3) can be solved rather easily for n = 3. In particular, by setting [θ_ji] = noticing that [θ_ji] = [θ_ij], for n = 3, we have

which immediately gives [θ₁₂] = [θ23] = [θ] and [θ12] = - [θ₁₃] = - [2θ]. From this last expression, we can define the angle θ, by writing

The above trigonometric equation can be recast in the following algebraic form

where x = cos . Therefore, we need to solve the following third degree equation

which allows only one real solution, namely, x = , giving . In this way, once again, the positions of the point charges on the thin ring coincide with the angular positions of the third roots of unity, if we place the first charge in the point (R, 0) of the x - y plane.

• [1] J.F. Federici, B. Schulkin, F. Huang, D. Gary, R. Barat, F. Oliveira and D. Zimdars, Semicond. Sci. Technol. 20, S266 (2005).
• [2] Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, Adv. Mater. 15, 353 (2003).
• [3] S. Earnshaw, Trans. Camb. Phil. Soc. 7, 97 (1842).
• [4] P. Mazzoldi, M. Nigro and C. Voci, Físíca (EdiSes, Napoli, 2002), v. II, p. 525.

Appendix

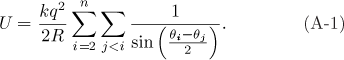
Publication Dates

• Publication in this collection
  08 Oct 2009
• Date of issue
  June 2009

History

• Accepted
  05 Feb 2009
• Reviewed
  15 Jan 2009
• Received
  27 Oct 2008