Grõbner bases and minimum distance of affine varieties codes

Grõbner bases and minimum distance of affine varieties codes

C. Carvalho

Faculdade de Matemática, Universidade Federal de Uberlândia. Av. J. N. Ávila 2121, 38.408-902 Uberlândia, MG, Brazil. [e-mail]

ABSTRACT

We present a method to estimate the minimum distance of affine varieties codes. Our technique uses properties of the footprint of an ideal obtained by enlarging the defining ideal of the variety, and may be applied also to codes which do not come from the so-called weight domains.

Keywords: Affine varieties codes, Grõbner bases, footprint of an ideal, minimum distance.

AMS Classification: 13P10, 13F20, 94B27

RESUMO

Nesse trabalho apresentamos um método para estimar a distância mínima de códigos de variedades afins. Nossa técnica usa propriedades da pegada de um ideal obtido através do aumento do ideal de definição da variedade em questão, e também pode ser aplicada a códigos de que não são produzidos utilizando-se domínios-pesos.

Palavras-chave: Códigos de variedade afim, bases de Grõbner, pegada de um ideal, distância mínima.

1. Introduction

Since the appearance of the geometric Goppa codes in the eighties, many papers have dealt with improvements on the lower bound for the minimum distance of a code. One of the most successful methods for this improvement was obtained by Feng and Rao (see [6] and [7]). Many related bounds appeared after their work, one of them being a bound derived by Andersen and Geil in [1]. In that paper the authors first derive a general approach to obtain a bound for the minimum distance (actually, for the generalized Hamming weights) of a linear code, and then show how to apply their method to codes defined from weight domains. A weight domain is an -algebra, where is a field, which admits a function to satisfying certain properties, which makes the domain suitable to be used for defining codes, defining codes, when is a finite field. They were introdued in [12] by T. Høholdt, J. H. van Lint and R. Pellikaan in order to present an alternative construction for geometric Goppa codes with simple tools from commutative algebra. In the present work we show how to apply Andersen and Geil's general approach to affine variety codes. Similarly to codes obtained from weight domains, these are evaluation codes obtained from the ring of regular functions of an affine variety but weight functions play no role in this theory. Since the algebras which appear in the weight function theory are the ring of regular functions of certain type of variety (see [11]) our result applies to a more comprehensive class of rings (see Example 3.2). Thus, distinctly from recent works (see e.g. [9] and [10]) we do not need concepts like "well-behaving basis" or "one-way well behaving basis". An important set of data to obtain a bound for the minimum distance is the set of indexes where there is a "dimension jump" in a sequence of nested vector spaces. While in fl] there are several results on such set for the case of codes from weight domains, and in particular, one-point geometric Goppa codes, here we show that this set may be read directly from the footprint of an ideal obtained by enlarging the defining ideal of the curve.

In the next section we recall Andersen and Geil's approach to obtain a bound for the minimum distance of a linear code, we introduce the affine variety codes and recall the definition and some properties of the footprint of an ideal, then we prove our main result. Following that, we present some examples to illustrate our method, including codes obtained from an algebra which does not admit a weight function.

2. Main result

Let

_q be a finite field with q elements, η a positive integer and for a := (α₁,..., a_n), b := (b₁, . . . , b_n) ∈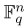 define a * b := (a₁b₁, . . . , a_nb_n). Let C be a vector subspace of 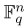. The idea of Andersen and Geil for finding a lower bound for the minimum distance of C stems from the fact that if c ∈ C and {b₁,..., b_n} =: B is a basis for 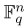then the subs pace c * B generated by {c * b₁;..., c* b_n} has dimension equal c.Thus we have the following result, which is not expleicitly stated in [1] but is used there.

Lemma 2.1.The minimum distance d(C) is equal to min{dim c * B ; c ∈ C\ {0}}.

We will use this result to estimate the minimum distance of the so-called affine variety codes, which were introduced by J. Fitzgerald and R. F. Lax in [8]. Let be an ideal, let be the associated variety of Consider the evaluation morphism and let L be an vector subspace of R.

Definition 2.1.The affine variety code C (L) is the image (L).

We observe that as an vector space R may not have finite dimension. A useful way of finding a basis for R is by means of the so-called footprint an ideal.

Definition 2.2.Assume that is endowed with a monomial order . The footprint of I (with respect to ), denoted by Δ(Ι), is the set of monomialswhi h are not leading monomials of any polynomial in I.

Let α = (α₁,..., a_m) ∈ (where is the set of nonnegative integers), we will denote by M_α the monomial · Then the map M_αα gives a bijection between the set of monomials of and . Denote by Λ the subset of corresponding to the monomials which are not leading monomials of any polynomial in I with respect to a monomial order . Then is ∆ (I) = {M_λ| _λ ∈ ∧} the footprint of I (with respect to ). One of the main properties of Δ(I) is that {Μλ + I | λ G Λ} is a basis for R as an vector space (see e.g. [5, Prop. 4, § 3, Ch. and we observe that it is a basis which already arries an order.

Thus, for each we consider the which is generated by all monomials in which are less or equal than . Clearly, if then . The next result shows for which values of λ we get .

Theorem 2.1. Lei then din if and only if .

Proof. Observe initially that since so that the claim makes sense. Denote by an algebraic closure of , clearly we have and denoting by the variety of Iq as an ideal of we also get (considering the natural inclusion ). From Seidenberg's Lemma 92 (see [16] or [2, Lemma 8.13]) we get that Iq is a radical ideal, so from [2, Thm. 8.32] we get that R/I_q is an vector space of finite dimension , and since the classes of the monomials in A(I_q) form a basis for R/I_q we get . We will prove now that if then dim . Assume that it is not the case, so there exists σ with . In particular, there exists a nonzero finite linear combination such that for all i = l,...,n. From Hilbert's Nullstellensatz (see e.g. [5, Thm. 2, §1, Ch. 4]) we get that the polynomial and a fortiori , a contradiction. This completes the proof of the "if assertion, for the "only if" part observe that the dimension of the spaces dim may jump from 1 to n at most n - l times, but n - l element of .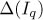

From the (proof of the) above theorem we get the following result.

Corollary 2.1.1. is a basis for .

For simplicity we will denote by Mi,..., Mn the elements of 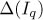and we assume that Mi < · · · < M„. We now show how to use the above results to find a lower bound for the minimum distance of an affine variety code . Let he a tosis for C, axià denote by B := {bi,..., bn} the (ordered) basis for where write c_t *b_i as linear combination of the elements in B. One way to do this is to write . Now observe that if R_tj is the remainder in the division of c_t * b_i by a Grõbner basis of I_q whith respect to ) then is a linear combination of the elements in 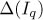and the evaluation of fM_i at the points of coincides with the evaluation of R_ti at these points, which produces the desired linear combination. denote the set of monomials M_i such that the coefficient of bj in that linear combination is not zero. Let M_tj be the greatest element in . We want to find a lower bound for the weight of words of the type . For this we define and then for all i = 2,..., n we add Mti to the set . We claim that the weight of c satisfies , then the v χ n matrix A whose lines are the coordinates of the vectors biv in the base Β has a v χ v invertible minor. To see this, let be the distinct elements of Dt, then for each , and from the construction of Dt we get that in the j-th line of A the entry is nonzero and all entries after it are equal to zero. This proves that , so the minimum distance of C is lower bounded by min{#(Dt) 11 = 1,..., dim(C)}.

The above method applies to any affine variety code in but to simplify the calculations in the following examples we use codes which are generated by some vectors of the base Β induced by 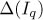. These examples also show that the method can yield sharp bounds, and may be applied to codes which do not come from evaluation order domains.

3. Examples

Example 3.1. For the first example we take the hermitian curve given by Y³ + Y - X⁴ = 0, defined over . Codes over this curve has been studied extensively, and the minimum distance of one point geometric Goppa codes has been determined by Stichtenoth ([17]) and Yang and Kumar ([18]). Building on the experience of those who have dealt with these codes we choose a weighted lexicographic order for [X, Y] by stating that ' if and only if , and if equality holds then . These weights come from the pole orders of the rational functions x = X/Z and y = Y/Z at the point at infinity := (0 : 1 : 0), which is their only pole. Using CoCoA ([4]) or Macaulay2 ([13]) we may calculate a Grobner basis for the ideal with respect to 4, which is and from that the footprint of Ig (w.r.t. 4 is The curve has 27 rational points (in the affine plane), which is the same number of elements in the footprint, as expected from the proof of theorem 2.1. When we order the monomials in toe get

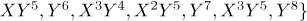so denoting by M_i the i-th monomial in 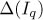we get that 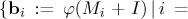1,..., 27} is a basis for 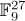. Let C be the code generated by the evaluation of (the class of) the first 5 elements of the basis, namely, 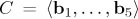. We start by finding a lower bound for the weight of codewords of the type 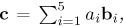aibi, where 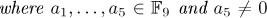Following the procedure (and the notation) described at the end of the last section, since 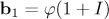we must set D5 = {XY} to start. Then, from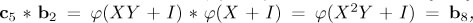

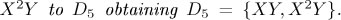, then we must add . actually, since for any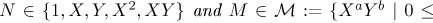 we have 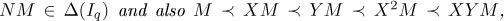them we must 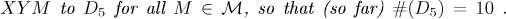We get ten other elements

to be added to D5 from the tables below which are , so that ηow #(DS) = 20. The product of the elements in the basis of C with will not yield any monomial to be added to D5; for example, the remainders in the division of by the Grõbner basis of I₉ are respectively and X, so we cannot add X to D5 (because, for instance,. Likewise, we compute #(D4), #(D3), #(D2) and #(Di) obtaining respectively 21, 22, 24 and 27. Thus our bound for the minimum distance is 20 but this is the actual value of the minimum distance, which we may check by observing that the code corresponds to the geometric Goppa code generated by a basis o/L(, see [17].

Example 3.2. In this example we deal with the affine curve defined over by the equation . Observe that the closure of the curve in has two nonsingular points, namely, P₁ := (0 : 1 : 0) and P₂ := (1 : 0 : 0) so is not a weight domain (see [14], see also [3] for results on codes defined by means of near weight domains, which include the ring R). The pole divisor of the functions χ mid y in the function field of the curve are respectively, (calculations done with Κ ASH/KANT - [15]) so we choose a weighted lexicographic order for [X, Y] by stating that , and if equality holds then . Using CbCoA ([4]) or Macaulay2 ([13]) we may calculate a Grõbner basis for obtaining {X⁴ - 1, Y⁴ - X⁶} so thai the footprint is , C code generated by evaluating the classes at the rational points in the affine plane (hence, from the above theorem we know that this code has dimension 6). Observe that this is the geometric Goppa code generated by a base of L(7P₁ + 7P₂), or in other words, the geometric Goppa code associated with the divisors G = 7P₁+ 7P₂ an d D, -where D is the sum of all rational points. Let let be greatest index for which . Denoting by B the (ordered) basis and proceeding as in the example above we see that has dimension at least 9 (respectively, 4, 12, 8, 12, j=6 4, and one may check that this is the actual bound. We also see that if we discard X3 {1 + I, X + I, X² + I, Y + I, XY + I} is now 8, and again one may check that this is the actual bound.

Acknowledment. The author would like to express his warm thanks to the referees for their careful reading and many suggestions which have improved very much the readability of this text.

[3] C. Carvalho, Ε. Silva, On algebras admitting a complete set of near weights, evaluation codes, and Goppa codes, Des. Codes Cryptography 53 (2) (2009), 99-110.

Recebido em 20 Julho 2012;

Aceito em 20 Novembro 2012.

The author was supported in part by CNPq grants 302280/2011-1 and 470416/2011-4, and also by FAPEMIG proc. CEX-PPM-00127-12.

• [1] H.E. Andersen, O. Geil, Evaluation codes from order domain theory, Finite Fields Appl, 14, (1) (2008), 92-123.
• [2] T. Becker, V. Weispfenning, "Grõbner Bases - A computational approach to commutative algebra", Springer Verlag, Berlin, 1993.
• [4] CoCoA Team - CoCbA: a system for doing Computations in Commutative Algebra. Available at http://cocoa.dima.unige.it.
• [5] D. Cox, J. Little, D. O'Shea, "Ideals, Varieties, and Algorithms", Third ed., Springer, New York, 2007.
• [6] G.-L. Feng, T.R.N. Rao, A simple approach for construction of algebraic-geometric codes from affine plane curves, IEEE Trans. Inform. Theory, 40 (1994), 1003-1012.
• [7] G.-L. Feng, T.R.N. Rao, Improved geometric Goppa codes, Part LBasic theory, IEEE Trans. Inform. Theory, 41), (1995), 1678-1693.
• [8] J. Fitzgerald, R.F. Lax, Decoding affine variety codes using Gõbner bases, Designs, Codes and Cryptography, 13, (2) (1998), 147-158.
• [9] O. Geil, "Algebraic geometry codes from order domains, in Grõbner Bases, Coding, and Cryptography, Springer", 2009, Eds.: Sala, Mora, Ferret, Sakata, Traverse-, 121-141
• [10] O. Geil, Evaluation Codes from an Affine Variety Code Perspective, in Advances in algebraic geometry codes, Ser. Coding Theory Cryptol., 5, World Sci. Publ., Hackensack, NJ, 2008, Eds.: E. Martinez-Moro, C. Munuera, D. Ruano, 153-180
• [11] O. Geil, R. Pellikaan, On the Structure of Order Domains, Finite Fields Appl., 8 (2002), 369-396.
• [12] T.HØholdt, J.H. van Lint, R. Pellikaan, Algebraic geometric codes, in: V. Pless, W. C. Huffman (Eds.), Handbook of Coding Theory, Elsevier, 1998, pp. 871961.
• [13] D. Grayson, M. Stillman, Macaulay2, a software system for research in algebraic geometry, available at http://www.math.uiuc.edu/Macaulay2/
• [14] R. Matsumoto, Miuras's generalization of one-point AG codes is equivalent to HØholdt, van Lint and Pellikaan's generalization, IEICE Trans. Fundamentals, E82-A (1999), 665-670.
• [15] M.E. Pohst, et al., The Computer Algebra System KASH/KANT, available at http://www.math.tu-berlin.de/~kant
• [16] A. Seidenberg, Constructions in algebra, Transactions of the American Mathematical Society, 197 (1974), 273-313.
• [17] H. Stichtenoth, A note on Hermitian codes over GF(q2), IEEE Trans. Inform. Theory, 34 (1988), 1345-1348.
• [18] K. Yang, P.V. Kumar, On the true minimum distance of Hermitian codes, Lectures Notes in Math.,1518 (1992), 99-107.

Publication Dates

• Publication in this collection
  21 Jan 2013
• Date of issue
  Dec 2012

History

• Received
  20 July 2012
• Accepted
  20 Nov 2012