Remarks on symmetry analysis of Lane-Emden systems of dimensions one and two

Remarks on symmetry analysis of Lane-Emden systems of dimensions one and two

Y. Bozhkov^I; I.L. Freire^II,*

^IInstituto de Matemática, Estatística e Computação Científica - IMECC, Universidade Estadual de Campinas - UNICAMP, Rua Sérgio Buarque de Holanda, 651, 13083-859Campinas, SP, Brazil. E-mail: [e-mail]

^IICentro de Matemática, Computação e Cognição, CMCC, UFABC - Universidade Federal do ABC, Rua Santa Adélia, 166, Bairro Bangu, 09210-170 Santo André, SP, Brazil. E-mails: [e-mail]; [e-mail]

ABSTRACT

Some recent results on Lie group analysis of the one and bi-dimensional Lane-Emden systems are revisited.

Keywords: Lane-Emden systems, Lie symmetries.

RESUMO

Alguns resultados recentes sobre simetrias de Lie de sistemas de Lane-Emden uni e bidimensionais são revisitados.

Palavras-chave: sistemas de Lane-Emden, simetrias de Lie.

1 INTRODUCTION

This work corresponds to the talk [4] given during the XXXIV CNMAC - XXXIV Congresso Nacional de Matemática Aplicadae Computacional - September, 17-212012, Águas de Lindóia SP, Brazil, where the second author had the opportunity to discuss some recent contributions from us [5, 6] concerning the Lie symmetry analysis of the two and one-dimensional Lane-Emden systems, respectively. In that event, it was first discussed the Lie group classification of the system

which was first introduced, at least up to our knowledge, in [5]. Our main result proved there was the following:

Theorem 1.1. Fo r arbitrary value of p and q, a basis to the Lie point symmetry generators of the Lane-Emden system is given by

and

For some special choices of p and q, the Lie point symmetry group can be enlarged. Below we list the special cases and the additional generators to (1.2).

1. For p arbitrary and q = 0, the generators are L_p,0and

whereψsatisfies the constraint Δψ = const.

2. For p arbitrary and q = 1, the generator is L _p,1.

3. For p arbitrary and q = -1, the generator is L _{p ,-1}.

4. Forp = 0 and q arbitrary, the generators are L_{0, q}and

where φ satisfies the constraint Δφ = const.

5. Forp = 1 and q arbitrary, the generator is L_1,q.

6. Forp =-1 and q arbitrary, the generator is L_-1,q

7. Forp = 1 and q = -1 the generator is L_{1, -1}.

8. Forp = -1 and q = 1 the generator is L_{-1, 1}.

9. Forp = -1 and q = 0 arbitrary, the generators are L_-1,0and (1.4).

10. For p = 0 and q = -1 arbitrary, the generators are L_0,-1and (1.5).

11. For p = q = -1 arbitrary, the generators are

V₁ = x + y + 2u , V₂ = x +y +2v.

12. For pq = 1, q(q -1) (q +1) ≠ 0, the generator is

13. For p = q, q(q -1)(q +1 )≠ 0, the generator is

Lp, p = x +y + u + v .

We recall that if x = (x¹ , ..., xⁿ) ∈ Ω ⊆ Rⁿand u = (u¹ , ..., u^m) ∈ ∧ ⊆ R^mare n and m independent and dependent variables, respectively, u(l), 1 < l <p, denotes the set of lth order derivatives of u with respect to the independent variables and

Fα =Fα(x, u₍₁₎, ..., u_(p)) =0, α =1, ..., k

are either k partial or ordinary differential equations, a Lie point symmetry is a set of local one-parameter group of transformations

acting on Ω × ∧ ⊆ Rⁿ× R^m≈ R^n+mwhich preservs the equation. Given a transformation (1.7), we can associate to it the linear operator

hereafter the summation over the repeated indices is presupposed. Such operator is called generator of the transformation (1.7) and it is said to be a Lie point symmetry generator if the following condition, called the invariance condition, holds

X^(p)Fα ≡ 0 (mod Fα =0),

where X^(p) is the p-th order prolongation of X.

We direct the interest reader to consult [1, 2, 8, 13] for further details on this subject.

The knowledge of symmetries allows us to construct solutions to the equations under consideration. If fact, from the symmetries, it is possible

• to construct special solutions, known as invariant solutions, or

• from an known solution, it is possible to construct another solution, by acting on the known solution with the symmetry group.

In this review paper we will have the opportunity to illustrate both facts.

It is easy to observe that the invariance under the translational symmetry in y of the system (1.1), corresponding to the generator L₂, leads us to the one-dimensional Lane-Emden system

The Lie point symmetries of the system (1.9) were studied in [6] and they can be summarized in the following

Theorem 1.2. Fo r arbitrary p and q, a basis to the Lie point symmetry generators of the Lane-Emden system (1.9) is given by the translation

and the dilation

If p = q = -3, in addition to (1.10) and (1.11) we have the generator

If p = q = -1 the Lie point symmetry group is generated by (1.10) and

We observe that the connections between Lie symmetries and the Lane-Emden systems have begun with the paper [3], where the Lie symmetries of the radial form of the Lane-Emden systems in Rⁿ

were studied.

After this result, some authors have been researching in this field, such as [9, 10, 11]. However, up to our knowledge, the first work dealing with Lie symmetries of non-radial forms of the Lane-Emden system was [5], where we considered the system (1.1). In this paper we revisit our main results regarding this field. We assume that the reader is familiar with the Lie symmetry theory. For further details, we recommend [1, 2, 8, 13].

The paper is organized as the follows. In the next section we investigate which of the Lie point symmetries of the systems (1.1) and (1.9) are Noether symmetries. Then the corresponding conserved quantities are found. Next we construct exact solutions to the one-dimensional Lane-Emden system (1.9). This allows us to construct exact solutions to the bi-dimensional Lane-Emden system (1.1) taking the rotational symmetry into account. In some parts the exposition follows that of our papers [5] and [6].

2 NOETHER CLASSIFICATION

First of all, it is easy to observe that the systems (1.1) and (1.9) are the Euler-Lagrange equations of the following Lagrangians

and

respectively, where

We recall that a Lie point symmetry generator (1.8) determines a Noether symmetry of the Lane-Emden (1.1) system if the equation

holds for some function A = (A¹ , A²) depending on x, u, v, ∇u, ∇v, where ∇ is the gradient operator. With respect to the system (1.9), equation (2.16) is rewritten as

X⁽¹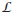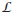⁾ +D_xξ = D_xA,

where the potential A now is a scalar function depending on x, u, v, u' , v'.

The vector field X is called variational symmetry if equation (2.16) holds with A = 0. A Noether symmetry which is not a variational symmetry is called divergence symmetry.

2.1 Noether symmetries of the bi-dimensional Lane-Emden system

It is a straightforward calculation to show that the invariance under translations in x and y and rotations in the xy plane provides a Noether symmetry.

Taking (1.3) into account, it is obtained

and

where 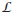is given by (2.14). Then the dilational symmetry L _p,q provides a Noether symmety, for any value of p and q, if and only if p + q +2 = 0.

Suppose p = -1 in (2.14). In this case, the Lane-Emden system is the Euler-Lagrange equations of the Lagrangian (2.14) with F(u) = ln u or G(v) = ln v. Then

and it follows that L_-1,q is not a Noether symmetry. The same argument proves that L _p,-1 cannot be a Noether symmetry and, in particular, this holds for the generator L _p,p.

2.2 Noether symmetries of the one-dimensional Lane-Emden system

The Noether classification to the system (1.9) was presented in [6]. To begin with, it is easy to see that translation in x is a variational symmetry.

Now, considering the case p ≠-1, q ≠ -1, a straightforward calculation shows that

Then

Hence X

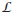+ (D_x ξ) 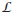= 0 if and only if 3 + 2(p + q) + pq = 0.

Finally, considering

and

22 we obtain that

3 CONSERVATION LAWS AND FIRST INTEGRALS

A conservation law for partial differential equations is a vector field whose divergence vanishes identically on the solution on considered system. Important physical quantities are given by conservation laws, such as conservation of energy or momentum. On the other hand, regarding to ordinary differential equations, the analogous to conservation laws is a first integral, which is an ordinary differential equation with a low order than the original equation.

Whenever an equation arises from the Euler-Lagrange equations, the celebrated Noether's theorem provides an elegant and efficient approach for finding conserved quantities. The main problem for finding conserved quantities employing the Noetherian method is to find the potential. However, from our previous results, we have at our hands all necessary ingredients for invoking this approach. Thus, firstly we establish the conservation laws for the bidimensional Lane-Emden systems and next, the first integrals are obtained.

3.1 Conservation laws for the bidimensional Lane-Emden systems

According to the Noether's theorem, given a Noether symmetry generator (1.8), associated with it, the conserved field is given by

Then, taking the Lagrangian (2.14) into account, the following conservation laws are straightforwardly obtained

• For the translational symmetry

L

₁

, the components of the conserved vector are

• For the translational symmetry

L

₂

, the components of the conserved vector are

• For the rotational symmetry

L

₃

, the components of the conserved vector are

•For the dilational symmetry

L_p,q

, with

p + q

+ 2 = 0 and

p

≠

q

, the components of the conserved vector are

3.2 First integrals of the one-dimensional Lane-Emden systems

For ordinary differential equations, the analogous to the formula (3.19) is

Thus, a straightforward procedure, and invoking equations (3.24) and (2.15), we construct the following first integrals to the one-dimensional Lane-Emden systems (1.9)

• For the translational symmetry

X

:

C = u' v' ^"+ F(u) + G(v).

• For the dilational symmetry

X p,q

, with

p

≠ -1,

q

≠ -1 satisfying (2.17):

C = (1 - pq)xu' v' -2 (1 +q)uv' -2(1 + p)u' v + (1 - pq)x .

• With regard to the divergence symmetry (1.12), the potential function is

A = u

v.Then we get:

C =- x²u' v' + xu' v + xuv' + (u^-2 + v^-2) - uv.

4 INVARIANT SOLUTIONS

Here we employ the Lie symmetry theory to find some exact solutions to the systems (1.9) and (1.1). We proceed in the following way:

• Firstly, we obtain solutions to (1.9) and

• in the following, using the invariance under rotational symmetry, we use the transformation (x, y) (x cos ε -y sin ε, x sin ε +y cos ε) to construct a solution to (1.1).

The first invariant solution can be obtained using the scaling symmetry generator (1.11) for the case p = q = -3. Then, from the invariance condition, we arrived at the following characteristic system

whose solution is

u = A√x, v = B√x.

Now, by substituting these functions into (1.9), it is obtained the solutions

to the one-dimensional Lane-Emden systems. Under the change

(x, y) (x cos ε - y sin ε, x sin ε + y cos ε),

it is constructed the following two one-parameter family of solutions

to the bidimensional Lane-Emden system

5 FINAL REMARKS

Although it is common to find papers dealing with Lane-Emden systems, with respect to their connections with Lie symmetries, the big part of the works deal with radial forms of these systems. Moreover, such papers also consider these systems in n-dimensional spaces, including papers focused in other approaches.

As it has been already mentioned, the first paper dealing with the bidimensional Lane-Emden systems, up to our knowledge, was the work [5]. Recently, a Noether symmetry classification of the system (1.1), with a more general nonlinear term was obtained in [12].

With respect to the one-dimensional Lane-Emden systems (1.9), we have found in the literature only the work [7]. However, from our previous results regarding the bidimensional Lane-Emden systems (and it still holds to the multidimensional case), such a particular system naturally arise as a special case of the bidimensional system with translational invariance with respect to the variable y.

Last, but not least, we present some solutions to the considered Lane-Emdens which are obtained using the Lie symmetry approach. This, up to our knowledge, has not been done before.

In conclusion, we point out that many interesting problems concerning the Lane-Emden system and its generalizations remain to be investigated thoroughly.

ACKNOWLEDGMENTS

Y. Bozhkov is grateful to FAPESP and CNPq, Brazil, for partial financial support. I.L. Freire thanks FAPESP, project nº2011/19089-6.

Received on September 30, 2012

Accepted on July 5, 2013

• [1] G.W. Bluman & S. Anco. "Symmetry and Integration Methods for Differential Equations'. Springer, New York, (2002).
• [2] G.W. Bluman & S. Kumei. "Symmetries and Differential Equations". Applied Mathematical Sciences 81, Springer, New York, (1989).
• [3] Y. Bozhkov & A.C.G. Martins. Lie point symmetries of the Lane-Emden systems. J. Math. Anal. Appl., 294(2004),334-344.
• [4] Y. Bozhkov & I.L. Freire. Symmetry analysis of the Lane-Emden systems in dimensions one and two. CNMAC, (2012).
• [5] Y. Bozhkov & I.L. Freire. Symmetry analysis of the bidimensional Lane-Emden systems. J. Math. Anal. Appl., 388(2012),1279-1284.
• [6] Y. Bozhkov & I.L. Freire. On the Lane-Emden system in dimension one. Appl. Math. Comp., 218(2012),10762-10766.
• [7] Q. Dai & C. Tisdell. Nondegeneracy of positive solutions to homogeneous second-order differential systems and its applications. Acta Math. Sci. Ser., 29(2009),435-446.
• [8] N.H. Ibragimov. "Transformation groups applied to mathematical physics". Translated from the Russian Mathematics and its Applications (Soviet Series), D. Reidel Publishing Co., Dordrecht, (1985).
• [9] B. Muatjetjeja & C.M. Khalique. Lagrangian approach to a generalized coupled Lane-Emden system: symmetries and first integrals. Commun. Nonlinear Sci. Numer. Simulat., 15(2010),1166-1171.
• [10] B. Muatjetjeja & C.M. Khalique. Noether, partial Noether operators and first integrals for the coupled Lane-Emden system. Mathematical and Computational Applications, 15(2010),325-333.
• [11] B. Muatjetjeja & C.M. Khalique. First integrals for a generalized coupled Lane-Emden system. Nonlinear Anal. - Real World Applications, 12(2011),1202-1212.
• [12] B. Muatjetjeja & C.M. Khalique. Conservation laws for a generalized coupled bidimensional Lane-Emden system. Commun. Nonlin. Sci. Num. Simil., DOI: 10.1016/j.cnsns.2012.09.006, (2012).
• [13] P.J. Olver. "Applications of Lie groups to differential equations". Springer, New York, (1986).

*

Corresponding author: Igor Leite Freire

Publication Dates

• Publication in this collection
  11 Oct 2013
• Date of issue
  Aug 2013

History

• Received
  30 Sept 2012
• Accepted
  05 July 2013