Equivalent absorbing boundary conditions for heterogeneous acoustic media

Equivalent absorbing boundary conditions for heterogeneous acoustic media

M.L. Castro^{I, *}; J. Diaz^II; V. Péron^II

^IUFRGS – Departamento de Matemática Pura e Aplicada, 91509-900, Porto Alegre, RS, Brasil. E-mail: [e-mail]

^IIMAGIQUE-3D, INRIA Bordeaux – Sud-Ouest, INRIA-CNRS – Université de Pau et des Pays de l'Adour, França. E-mails: [e-mail]; [e-mail]

ABSTRACT

In this work, we derive high order Equivalent Absorbing Boundary Conditions EABCs that model the propagation of waves in semi-infinite bilayered acoustic media. Our motivation is to restrict the computational domain in the simulation of seismic waves that are propagated from the earth and transmitted to the stratified heterogeneous media composed by ocean and atmosphere. These EABCs are adapted to Hagstrom-Warburton ABCs and appear as first and second order of approximation with respect to a small parameter involved in a multiscale expansion. Computational tests illustrate the accuracy of the first approximate model with respect to the small parameter.

Keywords: artificial boundaries, computational wave propagation, equivalent boundary conditions, heterogeneous media, acoustic waves.

RESUMO

Partindo de uma modelagem no domínio de frequências, utilizamos condições de contorno artificiais de Higdon e aproximações assintóticas para obter condições de contorno equivalentes que viabilizem a redução do domínio computacional para a simulação da propagação de ondas em meios acústicos heterogêneos. A motivação para este trabalho é a obtenção de condições de contorno artificiais e aproximadas para a simulação da propagação de ondas sísmicas, oriundas do interior da terra e transmitidas ao meio acústico heterogêneo composto pelos oceanos e pela atmosfera.

Palavras-chave: contornos artificiais, condições de contorno equivalentes, ondas acústicas, meio heterogêneo.

1 INTRODUCTION

The numerical simulation of geophysical phenomena is of utmost importance in our society. Considering the massive destruction seismic activities can generate, it is crucial to apply science towards a better understanding of the impact of earthquake waves.

Part of the job is to obtain effective models yielding the numerical simulation of seismic activity at an affordable computational cost – observe that running times are a very important factor when dealing with eminent tragedies. On the other hand, a complete description of the physical problem at hand is extremely intricated. In particular, it involves the coupling of elastic and acoustic waves in heterogeneous media, and the absence of viscosity produces waves that travel long distances without changing much their shape or amplitude. This aspect of the problem generates difficulties for the numerical simulation, since the physical domain, if one includes the atmosphere, is unbounded. Moreover, as waves propagate much slower in the atmosphere than in the sea or in the subsurface, one has to consider meshes composed of very thin cells in this region. Since the primary interest is to compute seismograms in the subsurface, it is necessary to consider techniques allowing to reduce at most as possible the computations inside the atmosphere. The imposition of artificial contours and appropriate boundary conditions (BCs) is an aspect to be considered. Among many possibilities, one could use a non-reflecting BC, defined through pseudo-differential operators [1, 2, 3, 4], or choose from a variety of approximate BCs, such as PMLs [5, 6, 7] or Absorbing Boundary Conditions (ABCs) [8, 9, 10, 11, 12, 13]. In this work the Hagstrom-Warburton ABC [10, 14] is chosen. The benefit of implementing non-reflecting BCs is discussed in [8] and it has been proven in [15] that the Hagstrom-Warburton ABC is equivalent to the popular Higdon ABC, with advantages with respect to implementation and computational cost.

However, even when using High-Order BCs, the artificial boundary should be placed at a distance є of the subsurface, in order to avoid spurious reflections. Hence, it is still necessary to mesh the small layer of the atmosphere with very thin cells. In this work, an alternative method is proposed, based on the use of asymptotic techniques in order to obtain Equivalent BCs that we could impose directly at the interface between the atmosphere and the subsurface.

The concept of equivalent boundary conditions (ECs) has become well-known in the mathematical modeling of wave propagation phenomena [16, 17, 18, 19, 20]. Such conditions are usually used to reduce and simplify the computational domain, replacing an exact model that must be applied in the periphery of the domain by an artificial contour and a BC that resembles the effects of the exact model on the part of the domain that was excluded. The main tool for the construction of ECs are two scale asymptotic expansions on the parameter defining the thickness of the layer to be eliminated.

A key hypothesis for the validation of this technique relies on the smallness of the ratio between the thickness of the layer to be eliminated and the remainder of the domain, typically with respect to the wavelength. It is worth to notice that the original physical problem inspiring this work does not satisfy such hypothesis. As a matter of fact in the original problem the atmosphere layer is an unbounded layer. What motivates this model is that, according to [14], it is possible to approximate the solution in the unbounded domain with any set precision tolerance if one applies an ABC of order high enough. At this stage, therefore, the focus is on the approximation of this problem with an absorbing boundary, rather than the physical problem with an unbounded layer.

The originality of this work is the derivation of ECs adapted to Hagstrom-Warburton ABCs, that will be called Equivalent Absorbing Boundary Conditions (EABCs). The EABCs appear as a first and second order approximations (Section 3.2) with respect to the small parameter and which are satisfied by the acoustic pressure. This paper presents a preliminary study that illustrates the feasibility of the approach. It focuses essentially on the formal derivation of EABCs and on the numerical accuracy of low order EABCs.

This article is organized as follows. In Section 2, we introduce the mathematical model. Section 3 is devoted for the equivalent boundary conditions obtained through asymptotical methods. We conclude presenting some numerical results obtained so far.

2 MATHEMATICAL MODELLING

In this work, a region of interest consisting of two media (ocean and atmosphere, for instance) is considered. Starting from a rectangularly shaped, double layered spatial model (see Fig. 1), where the boundaries Γ⁺ , Γ^– , Γ_Wand Γ_Eare artificial. The focus here is on the treatment of Γ⁺ defined as an absorbing boundary, whereas the countours Γ_Wand Γ_Eare modeled as periodical boundaries and a Dirichlet boundary condition (BC) is set on Γ^– (4). The Dirichlet data f set on Γ^– can be thought as a forcing term generated by waves that were transmitted to Ω^– from an elastic media underneath Γ^–. The goal is to obtain a reduced model for the acoustic pressure p^– in Ω^– of a wave with frequency ω that propagates with velocity c₁ in Ω^– and is transmitted to 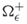(є is the thickness of the layer 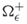) with velocity c₂. Denoting by one has

complemented with periodic BCs set on Γ_Wand Γ_E:

The time-harmonic wave field is characterized by using the Helmholtz equations (1)-(2) for the acoustic pressures p⁺ in 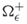and p^– in Ω^–. The transmission conditions (3) require that the pressures and the normal velocities match on the interface Γ; the first condition results from the equilibrium of forces on Γ. The boundary condition (5) is a Higdon BC [9] and coefficients a_j∈ (0, 1] are given parameters. Rewriting (5) according to the Hagstrom-Warburton formulation [10, 14, 15], adapted to the problem stated in the frequency domain, BC (5) becomes

Here the functions ϕ ^j ( j = 1, ..., P + 1) are auxiliary variables, defined on Γ⁺and in a vicinity V which is located above the domain 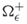, and we assume that (7)-(8)-(9) hold on Γ⁺∪ V . Then, following the procedure stated in [10], we have that (Δ + )ϕ ^j = 0 in V ; what leads to the elimination of the normal derivatives with respect to the boundary Γ⁺. This yields rewriting (7)-(9) as

where Φ = (ϕ¹, ..., ϕ^P)^T and L, M are tridiagonal matrices P × P whose entries l_ijand m_ijdepend on the parameters a_j. More specifically,

Unlike (7)-(8)-(9), the formulation (10)-(11) involves only the values of ϕ ^j on the boundary Γ⁺. This decreases considerably the computational cost of numerical simulations. Finally the problem of interest writes (1)-(4) with the BCs (6) and (10)-(11).

3 MAIN RESULTS – EQUIVALENT CONDITIONS

In the framework above, it is possible to replace the region 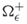by appropriate boundary conditions (BCs) set on є called equivalent absorbing boundary conditions (EABCs). Firstly, a two-step formal derivation of EABCs is presented. In Section 3.2, the first two EABCs are stated. Elements of derivation are presented in Section 3.3.

3.1 Formal derivation of equivalent conditions

First step: a multiscale expansion. The first step consists to derive a multiscale expansion for the solution p⁺ = , p^– = and Φ = Φ_є of the problem (1)-(4) complemented with the BCs (6)-(10)-(11): it possesses an asymptotic expansion in power series of the small parameter є

Here x = (x, y) ∈ ² are the cartesian coordinates. The "profiles" _jare defined on Γ × (0, 1) whereas the terms (resp. Φ_j) are defined in Ω^– (resp. on Γ).

Second step: construction of equivalent conditions. The second step consists to identify a simpler problem satisfied by the truncated expansions

up to a residual term in O(є^k+1). The simpler problems are stated in Section 3.2 when k ∈{0, 1}. There holds (at least) formal estimates

where solves the simpler problem, an equivalent model of order k.

3.2 Main results – Equivalent models

In the framework above, the equivalent models (EABCs) of order k ∈{0, 1} are stated.

Order 0 model. and solves the problem

complemented with periodic BCs on Γ_Wand Γ_E.

Order 1 model. and solves the problem

with periodic BCs set on Γ_Wand Γ_E.

3.3 Derivation of equivalent models

After applying a change of scale y

Y =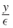 in 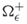, equations (1)-(4) complemented with the BCs (10)-(11) become

Here

⁺(x,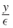 ) = p⁺(x, y) and Φ = (Φ¹, ..., Φ^P )^T .

Equations for the first asymptotics. Substituting the ansatz (12) for p⁺, p^– and Φ into previous equations and performing the identification of terms with the same power of є, a collection of equations for the coefficients (p_j^-, _j) and Φ_jis obtained. One finds that (, ₀) and Φ₀ = solve

with periodic BCs set on Γ_Wand Γ_E,and (, ₁, Φ₁) solves

with periodic BCs set on Γ_Wand Γ_E.

Construction of the first asymptotics and equivalent conditions. From (15), (18) and (20), must have the form

(x, Y ) = α₀(x).

Equation (17) provides α₀(x) = (x, 0). Also, from (22) one has

(x, Y) = β₀(x) + β₁(x)Y.

Additionally, (25) provides

whereas equation (27) rewrites as

Therefore one gets

Finally (21) and (x, Y) = α₀(x) = (x, 0) yield

where

providing the order 0 model (14). Further computations also provide the order 1 model, Section 3.2.

4 NUMERICAL RESULTS

For the model problem considered, our findings indicate that the use of an equivalent absorbing boundary condition can be a viable and effective alternative for numerical simulation; mainly for the gain in computational cost provided by such conditions.

The numerical solution was obtained using the Interior Penalty Discontinuous Galerkin Method [21] with P³ elements. The normal derivative of p₀ that arise after applying the classical IPDG discretization to the first equation of (14) is replaced using the second equation of (14).

Finally, the third equation of (14) is discretized by applying a 1D IPDG method on Γ. Hence, for P = 1, we have to solve a linear system that reads as

where P and Ψ are the vectors containing respectively the value of p₀ and at their degrees of freedom (recalling that is a 1D function defined only on Γ). M_2D and K_2D are the mass and stiffness matrices obtained by the 2D IPDG method, M_1D and K_1D are the mass and stiffness matrices obtained by the 1D IPDG method and B_2D1D and B_1D2D are the two matrices that ensures the coupling between the two equations.

In a test problem, we have compared the solution of (1)-(4) with the boundary conditions (10)-(11)-(6) for p ^– in Ω^– with the solution p₀ obtained using the order 0 model (14) here presented. The Dirichlet data

models the diffraction of an incident wave of frequency ω = 10 Hz and hitting the boundary Γ^– at an angle of θ = . Taking c₁/c₂ = 2, P = 1 (with a₀ = 1and a₁ = 1) and modelling f as an incident wave, we have reached relative errors below 0.2%, considering the ratio of 10^–2 for є/H ,where H is the thickness of the layer Ω^– (see Fig. 2). The results are summarized for various values of є/H in Table 1. The convergence rate coincides with the formal estimate (13) when k = 0. It is worth to notice that in order to satisfy periodicity, the parameters chosen must relate to the width L of the domain respecting L = , where q ∈ IN . Besides, there should be some extra care in the choice of ω: it should not be too big (else the condition є will not be satisfied) or too small (this would demand a very large domain, since L is inversely proportional to ω). In the test case presented, c₁ = 1500 m/s and L was set to approximately 1885 m. The triangular double layer meshes (necessary to compute p₀) used had around 10⁵ elements, with triangle sizes set around 0.08 in the thin layer and its vicinity.

5 CONCLUSION

We have derived high order Equivalent Absorbing Boundary Conditions EABCs that model the propagation of waves in semi-infinite bilayered acoustic media. The numerical results illustrate the fact that for P = 1and k = 0, the EABC models very accurately problem (1)-(4) with the conditions (10)-(11) and (6), as soon as є/H < 0.0005. Obviously, for such small values of є/H, this problem is not able to reproduce accuratly the case where the upper media is infinite. Hence, the next step will be to study the effect of P on the solution. This will provide a minimal value P₀ for which the EABC in (14) is efficient enough. Finally, the order 1 model is expected to allow for considering higher values of є/H and to provide a smaller value for P₀, which would reduce the number of auxiliary functions φ and the computational costs.

Received on November 30, 2013

Accepted on August 19, 2014

• [1] B. Alpert, L. Greengard & T. Hagstrom. "Rapid evaluation of nonreflecting boundary kernels for time-domain wave propagation". SIAM Journal on Numerical Analysis, 37(4) (2000), 11381164.
• [2] T. Hagstrom & S. Hariharan. "A formulation of asymptotic and exact boundary conditions using local operators". Appl. Numer. Math., 27 (1998), 403416.
• [3] B. Alpert, L. Greengard & T. Hagstrom. "Nonreflecting boundary conditions for the time-dependent wave equation". Journal of Computational Physics, 180(1) (2002), 270296.
• [4] M.J. Grote & J.B. Keller. "Exact nonreflecting boundary conditions for the time dependent wave equation". SIAM Journal on Applied Mathematics, 55(2) (1995), 280297.
• [5] J.P. Bérenger. "A perfectly matched layer for the absorption of electromagnetic waves". J. Comput. Phys., 114 (1994), 185200.
• [6] S. Abarbanel & D. Gottlieb. "A mathematical analysis of the pml method". Journal of Computational Physics, 134(2) (1997), 357363.
• [7] I. Navon, B. Neta & M. Hussaini. "A perfectly matched layer approach to the linearized shallow water equations models." Monthly Weather Review, 132(6) (2004).
• [8] D. Givoli & B. Neta. "High-order nonreflecting boundary scheme for timedependent waves". J. Comput. Phys., 186, 2446, March 2003.
• [9] R.L. Higdon. "Absorbing boundary conditions for difference approximations to the multidimensional wave equation". Mathematics of computation, 47(176) (1986), 437459.
• [10] T. Hagstrom & T. Warburton. "A new auxiliary variable formulation of high-order local radiation boundary conditions: corner compatibility conditions and extensions to first-order systems". Wave motion, 39, 327338, April 2004.
• [11] D. Givoli. "High-order local non-reflecting boundary conditions: a review". Wave Motion, 39(4) (2004), 319326.
• [12] V. van Joolen, B. Neta & D. Givoli. "A stratified dispersive wave model with high-order nonreflecting boundary conditions". Comput. Math. Appl., 48(7-8) (2004), 11671180.
• [13] J.M. Lindquist, F.X. Giraldo & B. Neta. "Klein-Gordon equation with advection on unbounded domains using spectral elements and high-order non-reflecting boundary conditions". Appl. Math. Comput., 217(6) (2010), 27102723.
• [14] T. Hagstrom, M.L. De Castro, D. Givoli & D. Tzemach. "Local highorder absorbing boundary conditions for time-dependent waves in guides". Journal of Computational Acoustics, 15(1) (2007), 122.
• [15] D. Givoli, T. Hagstrom & I. Patlashenko. "Finite element formulation with high-order absorbing boundary conditions for time-dependent waves". Computer Methods in Applied Mechanics and Engineering, 195(29) (2006), 36663690.
• [16] B. Engquist & J.-C. Nédélec. "Effective boundary conditions for acoustic and electromagnetic scattering in thin layers". Technical Report of CMAP 278,Centre de Mathématiques Appliquées, (1993).
• [17] A. Bendali & K. Lemrabet. "The effect of a thin coating on the scattering of a time-harmonic wave for the helmholtz equation". SIAM Journal on Applied Mathematics, 56(6) (1996), 16641693.
• [18] T. Abboud & H. Ammari. "Diffraction at a curved grating: TM and TE cases, homogenization". J. Math. Anal. Appl., 202(3) (1996), 9951026.
• [19] O.D. Lafitte. "Diffraction in the high frequency regime by a thin layer of dielectric material i: The equivalent impedance boundary condition". SIAM Journal on Applied Mathematics, 59(3) (1998), 10281052.
• [20] V. Péron. "Equivalent boundary conditions for an elasto-acoustic problem set in a domain with a thin layer". ESAIM: Mathematical Modelling and Numerical Analysis, EDP Sciences, 48(5) (2014), 14311449.
• [21] M.J. Grote, A. Schneebeli & D. Schötzau. "Interior penalty discontinuous Galerkin method for maxwell's equations: Energy norm error estimates". Journal of Computational and Applied Mathematics, 204(2) (2007), 375386. Special Issue: The Seventh International Conference on Mathematical and Numerical Aspects of Waves (WAVES'05).

*

Corresponding author: Manuela L. De Castro

Publication Dates

• Publication in this collection
  09 Feb 2015
• Date of issue
  Dec 2014

History

• Received
  30 Nov 2013
• Accepted
  19 Aug 2014