Alternatives for analysis of performance data and ranking of Charolais x Nellore crossbred bulls in performance tests

Alternativas para análise dos dados de desempenho e classificação de touros mestiços Charolês x Nelore em provas de ganho de peso

BREEDING, GENETIC AND REPRODUCTION

Alternatives for analysis of performance data and ranking of Charolais x Nellore crossbred bulls in performance tests¹

Alternativas para análise dos dados de desempenho e classificação de touros mestiços Charolês x Nelore em provas de ganho de peso

Fábio Luiz Buranelo ToralI,^*; Maurício Mello de Alencar^II

^IUniversidade Federal de Minas Gerais

^IIEmbrapa Pecuária Sudeste. Bolsista do CNPq

ABSTRACT

It was evaluated alternatives for analysis of performance records and ranking of Charolais x Zebu crossbred bulls. Data of weight at six ages and average daily weight gain in eight periods of 883 21/32 Charolais + 11/32 Nellore bulls in performance tests were used. The direct additive genetic values were predicted in single trait analysis using animal models with classificatory fixed effects of contemporary groups and age of dam at calving and age of animal at weighing as linear covariable, depending on the trait. As random effects, it was considered the direct additive genetic effect, the permanent maternal environmental and residual effects for all traits. Phenotypic values adjusted for fixed effects included in the model of each trait were also obtained. The Spearman correlation between predicted direct additive genetic values and adjusted phenotypic values ranged from 0.43 to 0.95, depending on the trait and year of birth of the animals. The accuracies of genetic values increased according to the number of animals with utilized data and they were always higher to those estimated for the adjusted phenotypic values. The magnitude of change in ranking the bulls depends on the considered trait. The estimates of correlations of predicted genetic values with the real genetic values of the analyzed traits of growth are higher than those among the adjusted phenotypic values and the real genetic values.

Key words: crossbred bulls, least square, mixed models, selection

RESUMO

Avaliaram-se alternativas para análise de dados de desempenho e classificação de tourinhos mestiços Charolês x Nelore. Foram utilizados os dados de peso em seis idades e de ganho médio diário em oito períodos de 883 tourinhos 21/32 Charolês + 11/32 Nelore em provas de ganho de peso. Os valores genéticos aditivos diretos foram preditos em análises unicaracterísticas considerando modelos animais com os efeitos fixos classificatórios de grupo de contemporâneos e idade da vaca ao parto e a idade do animal no momento da pesagem como covariável linear, dependendo da característica. Como aleatórios, foram considerados o efeito genético aditivo direto, o efeito de ambiente permanente materno e o resíduo, para todas as características. Foram obtidos também os valores fenotípicos ajustados para os efeitos fixos incluídos no modelo de cada característica. As correlações de Spearman entre os valores genéticos aditivos diretos preditos e os valores fenotípicos ajustados variaram entre 0,43 e 0,95, dependendo da característica e do ano de nascimento dos animais. As acurácias dos valores genéticos aumentaram de acordo com o número de animais com dados utilizados e foram sempre superiores àquelas estimadas para os valores fenotípicos ajustados. A magnitude das alterações na classificação dos tourinhos depende da característica considerada. As estimativas das correlações dos valores genéticos preditos com os valores genéticos verdadeiros das características de crescimento analisadas são maiores que aquelas entre os valores fenotípicos ajustados e os valores genéticos verdadeiros.

Palavras-chave: modelos mistos, quadrados mínimos, seleção, touros mestiços

Introduction

Selection based on phenotypic values of individuals adjusted for the known fixed effects have been used in beef breeding programs (Mello et al., 2002; Razook et al., 1993) aiming to improve productivity and profitability in beef cattle. The efficiency of this technique to provide genetic gain depends, among other factors, on the precision in which the adjustments are made and on the heritability of the selection criteria since the correlation between the adjusted phenotypic value and the true genetic value is the square root of heritability (Mrode, 2005). Selection based on adjusted phenotypic values could be more appropriate for moderate or high heritability traits or when technical or financial resources limit the adoption of more refined methods, such as the mixed model method by Henderson et al. (1959), which gives genetic values with best linear unbiased predictor properties (Henderson, 1963).

In the mixed model methodology, the prediction of genetic values and the estimation of fixed effects solutions included in the model are performed together; the genetic value of an animal is predicted from the its own data and from its relatives data included in the database because of the inclusion of the genetic relationship matrix among the individuals in the analysis. However, the application of the mixed model methodology to evaluate animal performance data requires computational resources and technical expertise and, consequently, higher costs. Lack of knowledge and/or difficulty in understanding and interpreting the results obtained by the use of mixed models, mainly by commercial producers, may also be considered barriers to the use of mixed model methodology in evaluating the animals participating in in performance tests.

These two alternatives for analyzing data of individual performance have advantages and disadvantages, and a comparative study can be instrumental in choosing the most adequate one, from a technical and practical perspective. This work was done with the objective of evaluating alternatives for analysis of performance records and ranking of 21/32 Charolais + 11/32 Nellore bulls in performance tests.

Material and Methods

The data used in this work were obtained from the MA genetic group, evaluated in ten performance tests (Agropecuária Ipameri, Jussara, GO, Brazil). According to the standards of the Associação Brasileira de Criadores de Canchim, the MA genetic group (21/32 Charolais + 11/32 Nellore, on average) can be formed by mating Charolais bulls with crossbred Canchim x Nellore dams, which themselves belong to the A genetic group (ABCCAN, 2008). The animals were born from 1995 to 2005, except for 1997, and the tests were concluded from 1997 to 2007, except for 1999.

The calves were weaned at 225 days of age, on average, and they remained on pastures of Brachiara and Panicum genus until the end of the test, always in one lot per year. The animals were given mineral salt during the entire evaluation period. During the dry season, the animals also received food supplements, which varied from protein mineral salt to a corn and soy mixture, depending on the year. The beginning of the supplementation period varied from June to August, and the end of it ranged from October to December, depending on the year. The supplementation period was 117, 106, 197, 71, 52, 84, 120, 116, 125 and 92 days for the animals born in 1995, 1996, 1998, 1999, 2000, 2001, 2002, 2003, 2004 and 2005, respectively.

The animals were weighed at birth, at weaning, at the beginning and end of the food supplementation, and at the end of the test. The final weighing was done in January, for the animals born in 1999; in February, for the animals born in 1995, 1998, 2000, and 2005; in March, for those born in 1996, 2001, 2002 and 2004; and in April, for those born in 2003. The average age of the animals at the end of the test varied over the years, as well as it depended on the time of birth (Table 1) because all the animals born in the same year were managed in the same group after weaning.

The evaluated traits were weight at birth, weaning, at 365, 450 and 550 days of age and at the end of the test. The weights at weaning (165 to 285 days of age) were adjusted to 225 days of age considering the average daily weight gain from birth to weaning. The weights at 365, 450 and 550 days of age and at the end of test were also obtained by linear adjustment, considering the weights taken from 305 to 425, from 390 to 510, from 490 to 610 and from 469 to 707 days of age, respectively, and the average daily weight gains from weaning to the target ages. Concerning the body weight measurement at the end of the test, the age considered to be the standard varied over the years and according to the season of birth (Table 1). In addition, the average daily weight gain from birth to weaning, from weaning to 365, to 450 and to 550 days of age, from weaning to the end of the test, from weaning to the beginning of the dry season, during the dry season, and between the beginning of the rainy season and the end of the test were also analyzed.

The variance components were estimated by the Restricted Maximum Likelihood method (REML), using the REMLF90 program (Misztal, 2002), in single trait analyses. This program uses the Expectation Maximization algorithm with acceleration to find the solution for the REML system of equations (Misztal, 2002). Animal models were used, which contemplated the random direct additive genetic, permanent maternal environmental and residual effects.

Generally, the model used is the following:

in which y_hijklm = the phenotypic value of trait h, of the animal i, calf of dam j, at which the age of dam at calving is equal to k, raised in the contemporary group l, with age m at weighing used to obtain the trait h; µ_h= constant specific to the trait h, present in all observations of this trait; a_hi = direct additive genetic effect of animal i for the trait h; p_hj= effect of the permanent environmental of the dam j for the trait h; AOD_hk= effect of the age of the dam at calving k for the trait h; CG_hl= effect of the contemporary group l for the trait h; b_ih(l) = linear regression coefficient of calf age on the day of weighing used to obtain the trait h, nested in the contemporary group l; and e_hijklm= random error associated with each observation.

The classificatory effect of age of dam at calving was considered only for weight at birth and at 225 days of age, and for average daily gain from birth to weaning. There were 13 annual classes formed by the dam age at calving that ranged from 2 to 14 or more years. The contemporary groups were formed by animals born in the same year and season (season 1: from January to March; season 2: from April to June; season 3: from July to September; and season 4: from October to December). The b_1h(l) coefficient was not included in the statistical model of birth weight and age_hm corresponded to the age of the animal at weaning (for weight at 225 days of age and weight gain from birth to weaning), age of the animal at weighing closest to 365days of age (for weight at 365 days of age and gain from weaning to 365 days of age), 450 (for weight at 450 days of age and gain from weaning to 450 days of age) and 550 (for weight at 550 days of age and gain from weaning to 550 days of age), at the end of the test (for weight at the end of test and weight gain from weaning to the end of the test), age at the beginning (for weight gain from weaning to the beginning of dry season) and at the end of the dry season (for weight gain during the dry season) and age at the end of the rainy season (for weight gain during the rainy season).

Under the matrix form, [1] can be represented by:

in which: = vector with phenotypic values of trait h; X_h = incidence matrix of the fixed effects considered in the statistic model of trait h; = vector of solutions for the fixed effects; Z_1h and Z_2h = incidence matrices of the direct additive genetic and of permanent maternal environment effects, respectively; and = vectors of solutions for the direct additive genetic and the permanent maternal environment effects, respectively; and = vector with the residuals. The presumptions taken for the random effects were:

in which: G_h = Aσ direct additive genetic covariance matrix; A = numerator relationship matrix; σ = direct additive genetic variance of trait h; P_h = IJ_hσ = permanent maternal environment variance matrix; IJ_h= identity matrix of order equal to the number of dams with calves evaluated for the trait h; σ = permanent maternal environment variance;R_h = IN_hσ = residual variance matrix; IN_h = identity matrix of order equal to the number of observations of trait h (N_h); and σ = residual variance.

For the composition of the numerator relationship matrix, a recursive algorithm was used to maintain the pedigree dataset comprised by individuals with data and their ancestors. In addition to this, the individuals who did not have data, were not dams of animals with data, which did not have at least one known ancestor and were connected to only one animal in the database were also excluded from the pedigree file and from the pedigree of its descendents. These procedures were repeated until there were no more animals of this type. Thus, a relationship numerator matrix was composed only of genealogical data of animals considered informative, that is, 1,489 animals. Out of these animals, 883 from MA genetic group were included (all of the known dams and 880 with known sires), 555 dams from A genetic group (all of unknown origin, but with birth records), 50 Charolais bulls (30 with completely disregarded or unknown parents) and one Charolais dam (of unknown lineage, but that had two Charolais calves as sires of MA animals).

The estimated variance components were utilized to obtain the solutions with BLUP properties for the direct additive genetic values (), using the mixed model methodology. Considering the system of equations:

the values of were obtained through Cholesky's decomposition, implemented in the MTDFREML program (Boldman et al., 1995). Cholesky's decomposition was also utilized to obtain the prediction error variance of .

The first step was to obtain , in which C_h is the coefficient matrix of the mixed model equations (left side of [3]), with necessary restrictions to be a full rank. The prediction error variance of the given element of (â_ih) can be obtained by k'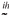C

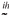k, in which k 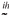= contrast vector with an element 1 in the position of animal i and zeros in the other positions. To avoid the direct calculation of C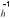, Cholesky's factorization and the property of inversed matrices are used, whereby the inverse of the matrices product is the inverse product in reversed order, as long as those matrices possess inverses (Searle, 1982), that is: C_h = L_hL'_h and C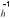= (L'_h)^-1L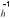. In this way, Var(â_ih)=k'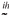(L'_h)^-1L

k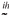. Thus, the predicted accuracy of the genetic value of animal i (acc_ih) was obtained through the equation:

The accuracies of the breeding values were obtained using the MTDFREML program (Boldman et al., 1995).

The animals were classified in two ways: a) using the BLUP of the breeding value, as previously shown; and b) using the adjusted phenotypic data for the fixed effects included in [1], that is:

in which:

_ijklm= phenotypic value of animal i for trait h adjusted for the corresponding fixed effects; and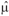 _h, 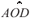_hk, C

_hl , and 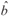_1h(l)= the estimates of µ_h, AOD_hk, CG_hl, and b_1h(l), respectively, obtained by the method of least squares. The second alternative used for classification of the animals is similar to that used for classification of participating animals in in performance tests using only one trait as selection criterion. In this case, the accuracy of the selection criteria (phenotypic value adjusted for the fixed effects) is the square root of trait heritability (Mrode, 2005). The phenotypic values were not adjusted for the permanent maternal environmental effect used in [1]. The adjusted phenotypic value of animal i contains its additive genetic value, the permanent maternal environmental effect of dam j and a random residual.

To obtain the BLUP of the additive genetic values [3], its respective accuracies [4] and its adjusted phenotypic values [5], files were generated containing only the records of animals born in the year of interest and in the previous years. Therefore, for the acquisition of the BLUP, the accuracies and the adjusted phenotypic values of animals born in 1995, it was only considered records of animals born in 1995; for estimation/prediction of these parameters for the animals born in 1996, data from animals born in 1995 and 1996 were used; and so on, until the acquisition of the BLUP, accuracies and adjusted phenotypic values of the animals born in 2005, when all of the available records were used. These procedures were designed to simulate what would happen in actual evaluations of performance tests if the data previously obtained were used for evaluating animals of a given year.

The Spearman correlations between the BLUP and the adjusted phenotypic values of each trait were calculated with data of animals born in each year, using the solutions obtained in the analysis with the data from the year of interest and from previous years. This correlation was obtained using the PROC CORR of SAS (SAS, 2003).

The average BLUP accuracies were calculated with the accuracies obtained for the BLUP of each trait of the animals born in a given year, using the accuracies obtained in the analysis with the data from the year of interest and from previous years.

Results and Discussion

The heritability estimates were low or medium, depending on the trait (Table 2). In general, the direct heritability estimates for the weight traits obtained in this work were lower than those related in literature for similar traits (Eler et al. 1995; Gianlorenço et al., 2003; Meyer, 1992; Oliveira et al., 2001; Toral et al., 2008 and 2009), but with data from Zebu, European or crossbred European x Zebu. Similar tendencies were observed for the heritability estimates of average daily weight gain from birth to weaning and from weaning to 365 days (Alencar et al., 2005; Castor-Pereira et al., 2007). The heritability estimates for average daily weight gain from weaning to yearling (from weaning to 450 days, from weaning to 550 days and from weaning to the end of the test) are within the range observed in literature for this parameter, which was from 0.06 (Simonelli et al., 2004) to 0.44 (Boligon et al., 2006). The heritability estimates for average daily weight gain during the dry season (0.10) and weight gain during the rainy season (0.16) were close to the lowest limit observed for the average daily weight gain from weaning to yearling. The heritability estimate of average daily gain from weaning to the beginning of the dry season was low (0.01), probably due to the high variability in the duration of this period and to the behavior of the animals because of changes in the environment where the animals were raised.

For the proportion of phenotypic variance attributed to the permanent maternal environmental effect, the averages obtained for the weight traits and average daily gain were higher than the values estimated by Eler et al. (1995), Guterres et al. (2006), Mello et al. (2002) and Meyer (1992).

According to Visscher et al. (2008), the heritability of a trait is specific to a population, but in practice it is possible to observe similarities among heritabilities for the same trait in different populations. Overall, the heritabilities obtained in this study were lower than the values found in literature. Part of the differences obtained in the heritability estimates can be explained by the following factors: utilization of different methods for estimation of variance components (Toral et al. 2007); utilization of the data only from males (Garrick et al. 1989); and differences in the statistic models, especially in the partition of the direct and maternal effect (Meyer, 1992).

The Spearman correlations between the direct additive genetic values and the adjusted phenotypic values varied from 0.43 to 0.95, depending on the trait and on the year of birth of the animals (Table 3).

Generally, the highest Spearman correlations were obtained among the predicted genetic values and the adjusted phenotypic values for weight at 450 days, at 550 days and at the end of the test, and the lowest correlations were obtained for weight at 225 days. Considering the predicted genetic values and the adjusted phenotypic values for the traits of average daily gain, the highest Spearman correlations were found for weight gain from weaning to 450 days and weight gain from weaning to the end of the test, and the lowest correlations were estimated for weight gain from birth to weaning.

The highest Spearman correlations between the predicted genetic values and the adjusted phenotypic values were found for the traits of the greatest heritability and the lowest, for traits of low heritability. These results are consistent and in agreement with what was expected. The correlation between the adjusted phenotypic value of the animal and its real genetic value depends on the heritability of the trait, that is, the higher the heritability, the higher the correlation between the adjusted phenotypic value and the true genetic value (Mrode, 2005). Consequently, the traits with higher heritability are recommended for use in animal breeding programs based on selection according to the adjusted phenotypic value.

When the heritability is low, unknown environmental factors and non-additive genetic factors can cause phenotypic differences among the animals. In this case, the permanent maternal environmental effects which were included in the prediction of the additive genetic values and not for the adjustment of the phenotypic values, also contributed to the reduction of the Spearman correlations between the predicted additive genetic values and the adjusted phenotypic values, especially for the weight at 225 days and average daily weight gain from birth to weaning, which are the most influenced by the maternal effects (Table 2).

The mean correlations between the predicted breeding values and the adjusted phenotypic values according to the year of birth of the animals, considering all of the traits, were 0.81 (1995); 0.78 (1996); 0.81 (1998); 0.78 (1999); 0.80 (2000); 0.79 (2001); 0.84 (2002); 0.77 (2003); 0.76 (2004); and 0.75 (2005). Low Spearman correlations, generally under 0.8, indicate alteration in the classification of the animals, which implies selection of different animals and alteration to the response to selection, depending on whether the selection is based on predicted breeding values or on adjusted phenotypic values. Furthermore, a tendency in a reduction of the mean correlations between the predicted breeding values and the adjusted phenotypic values over the years could be indicative that the differences among techniques increased according to the amount of records for analysis.

The most appropriate manner to choose the best alternative for classification of the animals can only be indicated with certainty if the real genetic values of the animals are available, which only happens with a simulation of the data. With real data, the use of accuracy and of some theoretic properties of the involved alternatives could be considered a viable option toward this goal.

Using the adjusted individual performance data, the correlation between the real genetic value and the adjusted phenotypic value is the square root of heritability (Mrode, 2005). This correlation was 0.37; 0.25; 0.25; 0.37; 0.46; 0.39; 0.22; 0.14; 0.50; 0.28; 0.42; 0.10; 0.32 and 0.40 for the weight at birth, at 225, at 365, at 450 and at 550 days of age, weight at the end of the test, average daily weight gain from birth to weaning, from weaning to 365, to 450, to 550, to the end of test, from weaning to the beginning of the dry season, during the dry season and during the rainy season, respectively. These values were lower than the correlations between the predicted direct additive genetic values and the real values (the accuracies of predicted breeding values) for all of the analyzed traits (Figure 1).

Even if only the data from a single year were considered (1995), the correlation between the predicted breeding values and the real breeding values are higher than that involving the adjusted phenotypic values and the real breeding values, which can be explained by the existence of paternal half-sibs in the database, so that the additive genetic value of an animal is not predicted only by its own records. Thus, it is expected that the use of predicted breeding values provides a greater response to selection in comparison to using the adjusted phenotypic values.

The accuracy means increased as the number of animals in the database also increased (Figure 1), a fact related to the enhanced number of observations used to predict the genetic value of each animal (increase in number of half-sibs in the database, mainly). Therefore, it is possible that the differences among the responses to selection, when based on predicted breeding values or on adjusted phenotypic values, increases with time.

If the only available option for evaluating the candidates for selection was the adjusted phenotypic values, the use of the previously obtained data could reduce the standard error associated with the solutions for some fixed effects, and thereby, improve the precision of the adjustments.

Conclusions

The classification of 21/32 Charolais + 11/32 Nellore bulls submitted to performance tests based on predicted breeding values is different than the one based on adjusted phenotypic values, and the magnitude of this difference depends on the used trait. The classification of 21/32 Charolais + 11/32 Nellore bulls based on predicted breeding values for the growth trait is better than the classification based on adjusted phenotypic values.

Received May 26, 2009 and accepted September 11, 2009.

* Corresponding author: [e-mail]

• ALENCAR, M.M.; MASCIOLI, A.S.; FREITAS, A.R. Evidências de interação genótipo x ambiente sobre características de crescimento em bovinos de corte. Revista Brasileira de Zootecnia, v.34, n.2, p.489-495, 2005.
• ASSOCIAÇÃO BRASILEIRA DE CRIADORES DE CANCHIM - ABCCAN [2008]. Novos esquemas de acasalamento para obtenção do Canchim Disponível em: <http://www. canchim.com.br/raca.asp#esquemas> Acesso em: 18/6/2008.
• BOLDMAN, K.G.; KRIESE, L.A.; VAN VLECK, L.D. A manual for use of MTDFREML. A set of programs to obtain estimates of variance and covariance (DRAFT) Lincon: Department of Agriculture, Agricultural Research Service, 1995. 120p.
• BOLIGON, A.A.; RORATO, P.R.N.; WEBER, T. et al. Herdabilidades para ganho de peso da desmama ao sobreano e perímetro escrotal ao sobreano e tendências genética e fenotípica para ganho de peso da desmama ao sobreano em bovinos Nelore-Angus. Revista Brasileira de Zootecnia, v.35, n.4, p.1323-1328, 2006.
• CASTRO-PEREIRA, V.M.; ALENCAR, M.M.; BARBOSA, P.F. Estimativas de parâmetros genéticos e de ganhos direto e indireto à seleção para características de crescimento de machos e fêmeas da raça Canchim. Revista Brasileira de Zootecnia, v.36, n.4, p.1037-1044, 2007 (supl.
• ELER, J.P.; VAN VLECK, L.D.; FERRAZ, J.B.S. et al. Estimation of variances due to direct and maternal effects for growth traits of Nelore cattle. Journal of Animal Science, v.73, n.11, p.3253-3258, 1995.
• GARRICK, D.J.; POLLAK, E.J.; QUAAS, R.L. et al. Variance heterogeneity in direct and maternal weight traits by sex and percent purebred for Simmental-sired calves. Journal of Animal Science, v.67, n.10, p.2515-2528, 1989.
• GIANLORENÇO, V.K.; ALENCAR, M.M.; TORAL, F.L.B. et al. Herdabilidades e correlações genéticas de características de machos e fêmeas, em um rebanho bovino da raça Canchim. Revista Brasileira de Zootecnia, v.32, n.6 (supl.1), p.1587-1593, 2003.
• GUTERRES, L.F.W.; RORATO, P.R.N.; BOLIGON, A.A. et al. Inclusão da covariância genética direta-materna no modelo para estimar parâmetros e predizer valores genéticos para ganho de peso em bovinos da raça Angus. Revista Brasileira de Zootecnia, v.35, n.6, p.2268-2274, 2006.
• HENDERSON, C.R. Selection index and expected genetic advance. In: HANSON, W.D.; ROBINSON, H.F. (Eds.) Statistical genetics and plant breeding Washington, D.C.: National Academy of Sciences, National Research Council, 1963. p.141-163.
• HENDERSON, C.R. KEMPTHORNE, O.; SEARE, S.R. et al. The estimation of environmental and genetic trends from records subject to culling. Biometrics, v.15, n.2, p.192-218, 1959.
• MELLO, S.P.; ALENCAR, M.M.; SILVA, L.O.C. et al. Estimativas de (co)variâncias e tendências genéticas para pesos em um rebanho Canchim. Revista Brasileira de Zootecnia, v.31, n.4, p.1707-1714, 2002.
• MEYER, K. Variance components due to direct and maternal effects for growth traits of Australian beef cattle. Livestock Production Science, v.31, n.3-4, p.179-192, 1992.
• MISZTAL, I. REMLF90 manual Athens: University of Georgia, 2002. 5p.
• MRODE, R.A. Linear models for the prediction of animal breeding values 2.ed. Wallingford: CABI Publishing, 2005. 344p.
• OLIVEIRA, C.A.L.; MARTINS, E.N.; FREITAS, A.R. et al. Heterogeneidade de variâncias nos grupos genéticos formadores da raça Canchim. Revista Brasileira de Zootecnia, v.30, n.4, p.1212-1219, 2001.
• RAZOOK, A.G.; FIGUEIREDO, L.A.; BONILHA NETO, L.M. et al. Intensidades de seleção e respostas direta e correlacionadas em 10 anos de progênies de bovinos das raças Nelore e Guzerá selecionadas para peso pós-desmama. Boletim da Indústria Animal, v.50, n.2, p.147-163, 1993.
• SEARLE, S.R. Matrix algebra useful for statistics New York: John Wiley & Sons, 1982. 438p.
• SIMONELLI, S.M.; SILVA, M.A.; SILVA, L.O.C. et al. Critérios de seleção para características de crescimento em bovinos da raça Nelore. Arquivos Brasileiros de Medicina Veterinária e Zootecnia, v.56, n.3, p.374-384, 2004.
• STATISTICAL ANALYSES SYSTEM - SAS. User's guide Version 9.1. Cary: SAS Institute, 2003. (CD-ROM).
• TORAL, F.L.B.; ALENCAR, M.M.; FREITAS, A.R. Abordagens freqüentista e bayesiana para avaliação genética de bovinos da raça Canchim para características de crescimento. Revista Brasileira de Zootecnia, v.36, n.1, p.43-53, 2007.
• TORAL, F.L.B.; TORRES JR., R.A.A.; LOPES, P.S. et al. Variâncias e herdabilidades heterogêneas para o peso à desmama de bovinos Charolês-Zebu. In: REUNIÃO ANUAL DA SOCIEDADE BRASILEIRA DE ZOOTECNIA, 45., 2008, Lavras. Anais Lavras: Sociedade Brasileira de Zootecnia/Aptor, [2008] (CD-ROM).
• TORAL, F.L.B.; ALENCAR, M.M.; FREITAS, A.R. Estruturas de variância residual para estimação de funções de covariância para o peso de bovinos da raça Canchim. Revista Brasileira de Zootecnia, v.38, n.11, p.2152-2160, 2009.
• VISSCHER, P.M.; HILL, W.G.; WRAAY, N.R. Heritability in the genomics era - concepts and misconceptions. Nature Reviews, v.9, n.4, p.255-266, 2008.

¹

Apoio financeiro do CNPq (Processo 502401/2009-5)

Publication Dates

• Publication in this collection
  31 Aug 2010
• Date of issue
  July 2010

History

• Received
  26 May 2009
• Accepted
  11 Sept 2009