Abstracts
This paper addresses the issue of measuring the degree of inertia in inflation in the presence of potential 'inliers'. It shows that by using robust unit root tests one reaches the same inference on the order of integration of the series as what is revealed by the modified procedure proposed by Cati et al. (1999). The results also suggest that, contrary to previous findings, the degree of inertia in inflation is rather small. Finally, the paper presents simulation results on the finite-sample behavior of unit root tests and of a persistence measure when the data contain inliers.
inflation inertia; inliers; persistence; unit roots
Este artigo analisa a mensuração do grau de inércia na inflação na presença de potenciais inliers. O artigo mostra que testes robustos de raízes unitárias conduzem à mesma inferência sobre a ordem de integração da série do que o procedimento modificado proposto por Cati et al. (1999). Os resultados sugerem que o grau de inércia na inflação brasileira é pequeno. Por fim, o artigo apresenta resultados de simulação de Monte Carlo sobre o desempenho em amostras finitas de testes de raízes unitárias e de uma medida de persistência quando os dados contêm inliers.
Inflation inertia and inliers: the case of Brazil* * We gratefully acknowledge financial support from CAPES and CNPq. We thank Roger Koenker, and seminar participants at the XVII Latin American Meeting of the Econometric Society (Cancun), 1998 Illinois Economic Association Meeting (Chicago), Getulio Vargas Foundation, University of Brasilia, Federal University of Minas Gerais, Federal University of Pernambuco, Federal University of Rio de Janeiro, and Brazilian Meeting on Probability and Statistics for comments and suggestions. We also thank two anonymous referees.
Ana Katarina CampêloI; Francisco Cribari-NetoII
IDepartment of Economics, Federal University of Pernambuco. E-mail: campelo@ufpe.br
IIDepartment of Statistics, Federal University of Pernambuco. E-mail: cribari@ufpe.br
ABSTRACT
Summary: 1. The issue; 2. The data; 3. Unit root tests; 4. Measuring inflation inertia; 5. Some simulation results; 6. Concluding remarks and discussion.
This paper addresses the issue of measuring the degree of inertia in inflation in the presence of potential 'inliers'. It shows that by using robust unit root tests one reaches the same inference on the order of integration of the series as what is revealed by the modified procedure proposed by Cati et al. (1999). The results also suggest that, contrary to previous findings, the degree of inertia in inflation is rather small. Finally, the paper presents simulation results on the finite-sample behavior of unit root tests and of a persistence measure when the data contain inliers.
Keywords: inflation inertia; inliers; persistence; unit roots.
JEL codes: C22; C12; C15.
RESUMO
Este artigo analisa a mensuração do grau de inércia na inflação na presença de potenciais inliers. O artigo mostra que testes robustos de raízes unitárias conduzem à mesma inferência sobre a ordem de integração da série do que o procedimento modificado proposto por Cati et al. (1999). Os resultados sugerem que o grau de inércia na inflação brasileira é pequeno. Por fim, o artigo apresenta resultados de simulação de Monte Carlo sobre o desempenho em amostras finitas de testes de raízes unitárias e de uma medida de persistência quando os dados contêm inliers.
1 The Issue
It has been argued that some inflationary processes contain an 'inertial component' thus implying that, in the absence of economic shocks, inflation displays a tendency to reproduce itself from one period to the next.1
1
See, for instance, Simonsen (1988), Novaes (1993) and Durevall (1998, 1999)
concerning the Brazilian experience.
The fully inertial case corresponds to a random walk in inflation, that is, yt = yt1 + ut, where yt denotes the inflation rate at time t and ut is a white noise disturbance with mean 0 and variance s2. A 1% shock to inflation then becomes fully persistent in the sense that it changes one's long-run forecast of the inflation rate by exactly 1%. This can be easily seen when the process is rewritten, under the assumption that the process starts at zero (i.e., y0 = 0), as yt =  uj. That is, the inflation rate at time t is nothing more than the accumulation of past innovations. When ut is not a white noise disturbance but has some stationary and invertible ARMA(p, q) representation, the degree of long-run persistence is not necessarily equal to 1, and can take any value in the interval (0, ¥). Here, inflation displays some inertia which can be quite small (say, close to zero) or large (say, greater than 1). When yt is integrated of order zero instead, shocks to inflation have no long-run effects and there is no inertia in inflation.
uj. That is, the inflation rate at time t is nothing more than the accumulation of past innovations. When ut is not a white noise disturbance but has some stationary and invertible ARMA(p, q) representation, the degree of long-run persistence is not necessarily equal to 1, and can take any value in the interval (0, ¥). Here, inflation displays some inertia which can be quite small (say, close to zero) or large (say, greater than 1). When yt is integrated of order zero instead, shocks to inflation have no long-run effects and there is no inertia in inflation.
Brazil has often been cited as the prime example of a country with a large inertial component in inflation. Simonsen (1988:260), for instance, analyzing the Brazilian experience writes that ''anti-inflationary policies in the 1980s were painful enough to suggest that inflation rates might be held back by a force ignored in rational expectations models, namely, inertia caused by strategic interdependence among private economic agents''. ''The inertia was considered so large that negative shocks to inflation, such as the oil-price hikes in the 1970s, were believed to shift inflation to a new level, where it would stay until a new shock occurred. Empirical studies of the Phillips curve and the finding of a random-walk component in the inflation rate supported the hypothesis of inertial inflation'' (Durevall, 1998:424).
Novaes (1993) measured the degree of inertia in the Brazilian inflation using cumulative impulse response functions from fitted ARIMA models, and found it to be roughly 1/3, thus implying that one third of the inflationary dynamics is due to inertia. Durevall (1998), using an error correction formulation, found the level of inflation inertia in Brazil to be 0.41. Cati et al. (1999) have argued that nearly all of the so-called shock plans which were designed to curb inflation and were implemented in Brazil since the mid-1980s brought inflation down for a few months and then failed.The observations corresponding to these months when inflation was artificially low have been termed 'inliers', and the authors have claimed that they tend to bias traditional unit root tests. This motivated them to design corrected tests by adding dummy variables to the usual augmented Dickey-Fuller (ADF) test. The initial puzzle they addressed was the following: the ADF test rejected the unit root null (thus suggesting no inertia), and yet an estimate of the degree of long-run persistence (i.e., inertia) indicated that such persistence was 0.97, i.e., nearly what is expected for a pure random walk process (i.e., full inertia). The modified tests they proposed, unlike the ADF test, did not reject the unit root null at the usual significance levels, thus being consistent with the high inertia levels they found. The main idea behind their approach was to move the shock plans from the noise to the trend function, thus isolating their effects. Overall, they identify five shock plans that took place between 1986 and 1991 and covered a total of 22 months. Durevall (1999) finds that inflation inertia is low in Brazil. However, the data he used does not include the most recent period of the Brazilian economic history, and hence he does not have to deal with the issue of handling potential inliers.
In this paper we show that robust unit root tests achieve the same conclusion as ADF-type tests that have been properly modified to account for inliers and shock plans through the specification and placement of dummy variables. The robust tests require no such variables. The tests suggest that there is some inertia in the Brazilian inflationary dynamics. We then measure how much inertia has been driving Brazilian inflation, and find that inflation inertia is, conversely to what has been previously found, small and of second order. In effect, we find that prior to 1986 the Brazilian inflationary dynamics displayed no inflation inertia. As a consequence, the series of shock plans put into effect after February 1986 may have been based on an incorrect diagnosis of the inflationary driving forces.
2 The Data
We use two different monthly time series for the Brazilian inflation. The first one is the series used by Cati et al. (1999), which ranges from January 1974 to June 1993 (234 observations). It consists of the so-called 'official inflation index' and is a splice of several indices that were used by the Brazilian government as the official index to all mandatory indexation schemes. The series has been modified by the authors, who have replaced each observation by the geometric mean of every two consecutive observations. The second series used in this paper is considerably longer. It ranges from February 1944 through February 2000 (673 observations) and consists of the IGP-DI (índice geral de preços-disponibilidade interna) computed by the Getulio Vargas Foundation. The series is presented in figure 1. The source of the data are several issues of Conjuntura Econômica and Instituto Brasileiro de Geografia e Estatística (1990).
3 Unit Root Tests
Although augmented Dickey-Fuller tests are useful for testing the null hypothesis of nonstationarity, they may not be robust when the data generating process follows a fat-tailed distribution. In such cases, the ADF test may suffer from low power. An alternative test based on regression rank scores was recently proposed by Hasan and Koenker (1997). Their test is based on the following model:
yt = ryt1 + ut,
ut = a1ut1 + + aputp+ Ît
where the Ît's are a sequence of i.i.d. variates with mean zero and constant variance s2, and the roots of 1a1z apzp = 0 lie outside the unit circle. The model can be written using an ADF-like specification as
or, more concisely, as
with Xt = yt1, Zt = 1, Dyt1, , Dytp. The null hypothesis of a unit autoregressive root is  0: g = 0, which is equivalent to r = 1 in the original formulation. In order to perform the test, we estimate the restricted model (i.e., omitting the yt1 term), obtain the regression rank score process âT(t) and the associated 'ranks'
0: g = 0, which is equivalent to r = 1 in the original formulation. In order to perform the test, we estimate the restricted model (i.e., omitting the yt1 term), obtain the regression rank score process âT(t) and the associated 'ranks'
where y(·) is the score function, and then compute the statistic
where
t1 denotes the projection of yt1 on the matrix Zt = 1, Dyt1, , Dytp. When the model includes a time trend, we use Zt = 1, t, Dyt1, , Dytp. The statistic above has a complicated non-normal asymptotic null distribution, but it can be shown that a modified version of it has a limiting standard normal null distribution. Hence, critical values for the test can be easily obtained from a normal table. The modified 'statistic' can be written as
with
where
with (ut, vt) being a bivariate process where vt = y(F(Ît)).
The modified test statistic is then defined by replacing the unknown parameters by consistent estimators. The resulting statistic has a limiting standard normal distribution. Such a modified test statistic requires one to select a value for another lag truncation parameter,  .This parameter is needed for the estimation of S, which is performed using a Newey-West type covariance matrix estimator (Newey and West, 1987).2
2
See Hasan (1993), Hasan and Koenker (1997), and Koenker (1997) for further details.
Thompson (2001) argues that this modification seriously affects the power of the test, especially when the innovation distribution is similar to the normal distribution, e.g., a t distribution with a large number of degrees of freedom. The simulation results in this paper are in agreement with Thompson's claim. This led us to also consider unmodified versions of robust M-tests (type e and type t tests) proposed by Thompson (2001). Thompson's type t test is analogous to the test suggested by Gutenbrunner et al. (1993). Indeed, the unmodified type t test has proven to work quite well in the presence of inliers in the simulations in this paper, while the Hasan and Koenker (1997) test, a modified version of the t test, does not work well in this case. The test statistics (two versions, an e and a t test) suggested by Thompson (2001) are given by
.This parameter is needed for the estimation of S, which is performed using a Newey-West type covariance matrix estimator (Newey and West, 1987).2
2
See Hasan (1993), Hasan and Koenker (1997), and Koenker (1997) for further details.
Thompson (2001) argues that this modification seriously affects the power of the test, especially when the innovation distribution is similar to the normal distribution, e.g., a t distribution with a large number of degrees of freedom. The simulation results in this paper are in agreement with Thompson's claim. This led us to also consider unmodified versions of robust M-tests (type e and type t tests) proposed by Thompson (2001). Thompson's type t test is analogous to the test suggested by Gutenbrunner et al. (1993). Indeed, the unmodified type t test has proven to work quite well in the presence of inliers in the simulations in this paper, while the Hasan and Koenker (1997) test, a modified version of the t test, does not work well in this case. The test statistics (two versions, an e and a t test) suggested by Thompson (2001) are given by
with
where the  = Dyt
= Dyt  are the residuals from estimating the model under the null,
are the residuals from estimating the model under the null,  is their average,
is their average,  R,i is the ith element of
R,i is the ith element of  R, and M = I (Z¢Z)1Z¢ is the projection matrix.3
3
Denote the cumulative distribution function of the errors Î
t by
F(·). For the rank test based on Wilcoxon scores, y(
x) behaves asymptotically as
F(
x) 0.5. For normal scores, y(
x) is asymptotically F
1(
F(
x)), where F(·) is the standard normal cumulative distribution function. For sign scores, y(
x) behaves asymptotically as 0.5 × sign(
F(
x) 0.5). The
parameter does not depend on the error density. For tests based on normal, Wilcoxon and sign ranks, it can be shown to be equal to 1, 1/12 and 1/4, respectively.
Here we consider the model which includes a time trend. Thompson (2001) approximates the critical values of the test using a Cornish-Fisher expansion. The approximations to the 5% quantiles of the asymptotic null distributions are given by expansions in the correlation parameter (
R, and M = I (Z¢Z)1Z¢ is the projection matrix.3
3
Denote the cumulative distribution function of the errors Î
t by
F(·). For the rank test based on Wilcoxon scores, y(
x) behaves asymptotically as
F(
x) 0.5. For normal scores, y(
x) is asymptotically F
1(
F(
x)), where F(·) is the standard normal cumulative distribution function. For sign scores, y(
x) behaves asymptotically as 0.5 × sign(
F(
x) 0.5). The
parameter does not depend on the error density. For tests based on normal, Wilcoxon and sign ranks, it can be shown to be equal to 1, 1/12 and 1/4, respectively.
Here we consider the model which includes a time trend. Thompson (2001) approximates the critical values of the test using a Cornish-Fisher expansion. The approximations to the 5% quantiles of the asymptotic null distributions are given by expansions in the correlation parameter (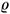 ),4
4
Thompson (2001) computed
by numerical integration for the three score functions (Wilcoxon, normal and sign-median) and several densities including normal, Student
t
3 and double exponential.
),4
4
Thompson (2001) computed
by numerical integration for the three score functions (Wilcoxon, normal and sign-median) and several densities including normal, Student
t
3 and double exponential.
One can estimate 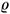 as
as
The main motivation for working with robust unit root tests is that they enjoy robustness properties that the traditional least squares-based tests do not enjoy. In particular, their performance is not as sensitive to extreme observations as that of the ADF test.5 5 One could argue that any identified outliers (or inliers) should be removed from the series prior to unit root testing. However, this approach can have an adverse effect on the power of the test since extreme observations usually convey important information as to whether or not there is mean reversion. Removing observations one believes to be outliers thus has important power implications. This point is made by Maddala and Kim (1998:449), who also discuss the HK test.
At the outset, we have run the ADF test for the two series, i.e., the CGP and the IGP-DI series. The former is the series used by Cati et al. (1999) and the latter is the longer series that ranges from February 1944 through February 2000. Since the presence of inliers in the data can potentially bias the inference, we have also used truncated versions of these two datasets. Their truncated versions (CGP(T) and IGP-DI(T)) stop in December 1985. Since the first shock plan was introduced in early 1986, these two truncated series are known to not contain inliers. Finally, the truncation lag parameter in the ADF especification (p) was chosen using four different approaches, namely: minimization of the Bayesian information criterion (BIC); minimization of the Akaike information criterion (AIC); general-to-specific sequential testing at the 10% level (SQ10); general-to-specific sequential testing at the 5% level (SQ5). In all cases the ADF regression was run using p = 20, 19, ,1, 0, where p denotes the lag truncation parameter. The results are summarized in table 1.
Next, we apply the Hasan and Koenker's and Thompson's rank tests to the two inflation time series (CGP and IGP-DI). These will be denoted as HK test and ST tests throughout the paper, respectively. We report results for the lag truncation parameter of the ADF specification (p) ranging from 1 to 20 and for three different score functions (Wilcoxon, sign-median, and normal). For the HK test, the values of the lag truncation parameter of the Newey-West covariance matrix estimator were  = 2, 4, 6, 8. The results of the ST type t test (with the respective estimated critical values) for the CGP series and the longer IGP-DI series are given in table 2.
= 2, 4, 6, 8. The results of the ST type t test (with the respective estimated critical values) for the CGP series and the longer IGP-DI series are given in table 2.
The results in table 2 show that the ST type t test does not reject the unit root null against a stationary alternative for both series in any of the cases considered at the 5% significance level. The same conclusion holds for the ST type e test and the HK test.6 6 The tables are available from the authors upon request. That is, for both series, the HK and ST tests lead one to not reject a unit root in the Brazilian inflationary dynamics regardless of the score function used and regardless of the values of the truncation parameters. Given the good power properties of the ST t test under a wide range of distributional forms for the error term, even when the data contain atypical observations (see the simulation results in section 5), we view such strong acceptance of the unit root null as evidence of some inflation inertia.
It is noteworthy that Cati et al. (1999) developed modified ADF tests that use dummy variables to account for the shock plans. Their modified tests did not reject the unit root null when applied to the Brazilian inflation. In order to construct the dummies used in the test, one needs to know the starting and ending dates of all 'shock plans', and yet it is not easy to determine when a plan was no longer in effect.7 7 The authors recognize the difficulty involved in choosing the ending dates of the several stabilization plans, and opt for choosing such dates in a way that minimizes the number of possible outliers in the residuals from an error correction model that includes inflation and nominal interest rates.
The HK, ST, and modified ADF tests therefore do not reject the unit root null for the full sample, as one would expect. The two complete samples include periods of uncontrolled growth in inflation, some failed attempts at stabilizing its level and even brief periods of hyperinflation, thus yielding evidence that the series has a stochastic trend (i.e., a unit root). All tests appear to deliver the correct inference, but the HK and ST tests do so without requiring the specification and placement of dummy variables.
We also applied the HK and ST tests to the two truncated series, i.e., the CGP(T) and IGP-DI(T) series. For brevity, we concentrate on the results based on the Wilcoxon score function, which is the most commonly used score function.8 8 The Wilcoxon score function enjoys the property that its asymptotic relative efficiency is bounded below by 0.86 for all symmetric distributions. Overall, the simulation results in Hasan (1993) favor this score function; see the discussion on pages 86-87. The results are given in tables 3 and 4, respectively.
We conclude from table 3 that the HK test yields rejection of the unit root null hypothesis at the 5% level in all but one case (CGP(T) series, p = 7,  = 2). In nearly all cases we reject the unit root null at the 1% siginificance level. Indeed, rejection of the null occurs at very low significance levels for the longer IGP-DI(T) series. Moving to table 4, rejection of the unit root null by the ST tests occurs for low values of the lag truncation parameter p. That is, the figures in table 4 and, particularly, in table 3, indicate that the Brazilian inflation rate followed a stationary inflationary dynamics up until the introduction of the first shock plan in early 1986. Such dynamics had no inertial component. This is in agreement with the persistence values (close to zero) for these truncated series given in section 4. Therefore, the first shock plan (the so-called Cruzado Plan) may have been based on a mistaken diagnosis of the Brazilian inflation.
= 2). In nearly all cases we reject the unit root null at the 1% siginificance level. Indeed, rejection of the null occurs at very low significance levels for the longer IGP-DI(T) series. Moving to table 4, rejection of the unit root null by the ST tests occurs for low values of the lag truncation parameter p. That is, the figures in table 4 and, particularly, in table 3, indicate that the Brazilian inflation rate followed a stationary inflationary dynamics up until the introduction of the first shock plan in early 1986. Such dynamics had no inertial component. This is in agreement with the persistence values (close to zero) for these truncated series given in section 4. Therefore, the first shock plan (the so-called Cruzado Plan) may have been based on a mistaken diagnosis of the Brazilian inflation.
4 Measuring Inflation Inertia
A unit root in inflation indicates the existence of some inertia, that is, some long-run persistence. It remains to be determined how much inertia there is in the inflationary process. In this section, we use a nonparametric measure of long-run persistence known as the 'variance ratio' to measure the degree of inertia in the Brazilian inflationary process. The persistence measure can be written either as a ratio of variances or as a function of autocorrelations:
where rj is the jth autocorrelation of Dyt. One can estimate the persistence measure Vk by replacing the population autocorrelations with the sample autocorrelations.9
9
It is customary to multiply the estimated variance ratio by
T/(
T k) to correct for a downward finite-sample bias.
If yt follows a random walk, the above ratio equals 1. On the other hand, if the series is stationary, the ratio approaches zero as k increases. Finally, it is noteworthy that an asymptotic standard error for the estimated variance ratio can be obtained using Bartlett's formula: s.e.  . We have computed the variance ratios up to k = 84, but, for brevity, we only report results for some selected values of the parameter k in table 5.
. We have computed the variance ratios up to k = 84, but, for brevity, we only report results for some selected values of the parameter k in table 5.
The results in table 5 suggest that the degree of inertia in the Brazilian inflationary dynamics is rather small, ranging from 0.12 (CGP series) to 0.16 (IGP-DI series). It is noteworthy that these numbers are smaller than the degree of inertia found by Novaes (1993) who used a parametric measure from fitted ARIMA models and a shorter series. As a check of the results presented above, we consider the yearly inflation rate from 1862 through 1999 (138 observations), this series having been constructed using estimates from Contador and Haddad (1975) and data on the yearly IGP-DI obtained from Conjuntura Econômica. It is noteworthy that the effects of possible outliers/inliers are downplayed when we work with a longer yearly series since the impact of a couple of atypical monthly observations on the yearly inflation figure is partially offset by the remaining monthly inflation rates and, as a consequence, the yearly figure does not end up being as atypical. We have computed the variance ratio for this series up to k = 30 and found that  30 = 0.11, which is in agreement with the previous results.
30 = 0.11, which is in agreement with the previous results.
One could argue that when using the variance ratio as a measure of long-run persistence, the choice of k is arbitrary and that the variance ratio is biased towards zero when k is large. The key is to note that k must be large so that the variance ratio is able to capture the long-run dynamics of the series, and yet k must not be large in relation to the sample size, in which case bias towards zero would occur. The conclusion drawn from table 5 is based on k = 84 (i.e., 84 months or seven years after the initial shock) and 672 observations (IGP-DI series, after differencing), thus yielding k/T = 0.125 (less than 13%).
A different persistence measure oftentimes used is based on an autoregressive spectral estimation:
where
with
and  . Here, T is the number of observations, and
. Here, T is the number of observations, and  and êtp are obtained from a pth order autoregression (Perron and Ng, 1998):
and êtp are obtained from a pth order autoregression (Perron and Ng, 1998):
The truncation parameter p must be large enough to filter any serial correlation so that etp is white noise. Cati et al. (1999) used this measure. They selected the value of p (p = 2) that minimized the BIC and found the long-run persistence of Brazilian inflation to be 0.97.
A potential problem with the approach used by Cati et al. (1999) is that the order of autoregression selected by the BIC may not be large enough to approximate well the true data generating process, and the persistence measure is heavily dependent on the order of autoregression selected.Clearly, k must be large enough to filter out any serial correlation present in the data, and a value of k which is too small will induce residual serial correlation that will likely be translated into larger persistence levels. In order to investigate that, we have computed the persistence measure above for both series and for p = 0, ...,25. We have also computed the AIC for each of the estimated models. Unlike the AIC, the BIC is consistent under quite general conditions. However, for autoregressive models the AIC is, unlike the BIC, asymptotically efficient (Brockwell and Davis, 1991). The AIC has a tendency to overparameterize the selected model. If we think of p as a parameter to be estimated, then it is well known that the BIC yields a consistent estimate of p. However, if we do not think of the autoregressive specification as the correct one, but as an approximation to an unknown data generating mechanism, then it may be sensible to use the AIC and choose a more elaborate model in the hope that this may provide a better approximation (Newbold and Bos, 1994:263).
The estimated persistence levels for the CGP and IGP-DI series corresponding to the values of p which minimize the AIC (18 both series) are 0.10 and 0.17, respectively. For the CGP series, p = 15 and p = 19 also deliver small AIC values, and their respective persistence levels are 0.13 and 0.12. These numbers are in agreement with the results obtained using the nonparametric variance ratio in table 5, and are considerably smaller than Cati et al.'s (1999) persistence estimate (which corresponds to p = 2). The estimated persistence levels are quite sensitive to the order of autoregression selected, and the high persistence level obtained by these authors is due to the small value of p they have used. Figure 2 shows the estimated autocorrelation functions of the two residual series (p = 2 and p = 18, CGP series). Some of the residual autocorrelations for the residual series obtained using p = 2 (i.e., lag truncation selection based on the BIC) lie outside the 95% confidence bands, thus suggesting that the autoregression was not long enough to filter out all serial correlation. The same does not happen for the residuals obtained using p = 18 (i.e., lag truncation selection using the AIC). Cati et al. (1999) show that, when the data contain inliers, the autoregressive spectral persistence measure is biased towards 1 when p is less than the duration of the plans (n). When p is chosen at least as large as n, the result depends on the specific values of p and n. When int(n/p) = 1, the persistence measure converges in probability to 1/3. They correct the persistence measure in much the same way they correct the ADF test, and find the corrected persistence figure to be even higher, namely 1.67. Again, p = 2 was selected using the BIC. It is noteworthy that using the AIC to select p for the corrected persistence meausure delivers substantially smaller persistence values. We computed Cati et al. (1999) corrected persistence measure for p ranging from 1 to 25, and the estimated persistence levels for the CGP and IGP-DI series corresponding to the values of p which minimize the AIC are 0.01 (p = 22) and 0.15 (p = 15), respectively.
In order to investigate whether the low persistence estimates we obtain are due to inliers-induced biases, we have computed the variance ratio for up to k = 84 for the IGP-DI(T) series. That is, we restrict the data to the period from February 1944 through December 1985. This subperiod does not include any so-called shock plans, and hence has no potential inliers. Figure 3 displays the variance ratios (solid lines) for both the entire period and the subsample of interest. The dotted lines represent the variance ratio estimates plus and minus their corresponding standard errors. The 'inner' solid line displays the variance ratio for the no-inliers subsample and the 'outer' solid line plots the variance ratio for the entire sample. Figure 3 shows that inflation long-run persistence is even lower when there are no inliers in the sample. Indeed, the variance ratio estimate for the chosen subsample corresponding to k = 84 is 0.08, i.e., half of that found for the entire sample (see table 5). The autoregressive spectral persistence estimate (with p selected by the AIC: p = 16) for the IGP-DI(T) series equals 0.04. Accordingly, this figure is even smaller than the one obtained for the entire sample (0.17). For the persistence measures to be inliers-biased, one would expect the estimated persistences for the truncated sample periods (which do not contain inliers) to be larger than the ones for the complete sample periods (which may include inliers). This does not happen. Indeed, the opposite happens. This therefore suggests that the low degree of inflation inertia obtained is not inliers-based biased.
We also note that the measured degree of inflation inertia in the truncated IGP-DI series is nearly zero regardless of the measure used, which is in agreement with the inference (rejection of the unit root null) based on the HK test (table 3). The HK test rejected the unit root null for this series, thus indicating no inflation inertia prior to 1986. Since the truncated series has no inliers, one cannot claim that the results of the HK test and the persistence estimates are biased towards mean reversion due to inliers.
5 Some Simulation Results
In this section we report the results of Monte Carlo experiments designed to evaluate the finite sample performance of the ADF and rank tests (HK and ST tests) in the presence of inliers. For means of comparison we also present simulation results for the case where the data generating process (DGP) is inliers-free.10 10 We used the same starting seed for each entry to enable one to compare the simulation results across tables. We consider the first order autoregressive model
yt = y0 + mt + ut, Dut = gut1 + vt, vt = 0.5 vt1 + xt, t = 1, ,T
xt being a white noise disturbance. When the data contain shock plans, the above DGP is interrupted by occasional 'inliers',
yt = a for t Î ti,j (j = 1, m; i = 1, , nj)
Here, ti,j refers to the time index of the ith observation of plan j. There are m shock plans and each contains nj observations. We consider two error distributions: standard normal and Student t3. We used the following specific values for the parameters. First, a = 4, which can be viewed as an initial level of 4% for the inflation rate. There are m = 3 plans irrespective of the sample size and each plan contains nj = 6 (j = 1, 2, 3) observations corresponding to plans that last six months. To complete the specifications, the initial condition is y0 = a and m = 0.1. We consider three different sample sizes: T = 250,500,750; the first and the latter are roughly the sample sizes of the CGP and IGP-DI series, respectively. The starting dates of the inliers are T = 50, 100, 150. All results are based on 1,000 replications. The critical value for the ADF test is taken from Fuller (1976) (-3.41, 5% level), the critical values for the HK tests are taken from a normal table, and the critical values for the ST tests are based on the Cornish-Fisher approximations given in section 3 with the values of 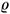 taken from table 1 of Thompson (2001).
taken from table 1 of Thompson (2001).
Starting with the ADF simulation results, the figures in table 6 show that the ADF test is severely oversized in the presence of inliers. Next, the figures in table 7 reveal that the HK test is undersized under normal errors. This problem is more severe in the presence of inliers under both the normal and Student t3 densities (tables 7 and 8), regardless of the score function used. The figures in tables 7 and 8 show that Thompson's type e test is also biased in the presence of inliers, with the bias occuring in the same direction as that of the ADF test. The bias is of minor significance only for the sign score, particularly under normal errors. The results in tables 7 and 8 also suggest that the size of the type t version of Thompson's test is close to the nominal 5% level in the presence of inliers, for both the normal and Student t3 densities, except for the sign score under normal errors.
Moving to the power results, the figures in table 9 reveal that the power of the HK rank tests for the inliers-free DGP is significantly lower than the power of the ADF and of Thompson's tests under normal errors. For this specification, Thompson's tests (both versions e and t) have power similar to that of the ADF test under the normal distribution (particularly for Wilcoxon and normal scores) and have power at least as good as the ADF test for T = 500,750 and higher power for T = 250 under the Student t3 distribution. The results in table 9 also reveal that Thompson's tests still have good power in the presence of inliers under the normal distribution, the best performance being the rank test based on normal scores, as expected, followed by the Wilcoxon scores. The tests based on the sign score are the least powerful. The power performance of the ST tests in the presence of inliers is even better under the Student t3 density (see table 10), being close to 1 for the rank tests based on the scores Wilcoxon and normal for all sample sizes considered and (1 + g) = 0.9.11 11 The sample kurtosis of the first differences of CGP and IGP-DI series are much greater than the kurtosis of a normal variate (39.9 and 161.5, respectively; the kurtosis of a normal random variable is 3). The sample kurtosis of D yt for the (complete) IGP-DI series is therefore over 50 times greater than that of the first difference of a Gaussian random walk. This can be viewed as an indication of fat tails or generation of atypical observations by the data generating process. Again, the sign scores have the least accurate performance. We, therefore, conclude that the ST t test based on normal and Wilcoxon scores (which also have size close to the nominal level) seems to have an adequate performance in the presence of inliers.
As suggested by a referee, we have also carried out simulations with smaller sample sizes. For instance, consider the situation where T = 150 and there are two shock plans of six months each; the first shock plan starts at observation 50 and the second at observation 100, as before. Here, we only report results for Thompson's t test (STt) with Wilcoxon scores, since this test outperformed the other ones in the previous simulations. The error distribution was Student-t with three degrees of freedom, and the remaining simulation settings are as before. The null rejection rate of the test at the 5% significance level was 5.6%. As for the power of the test, the estimated powers for 1 + g = 0.8, 0.9 were 86.6% and 54.8%, respectively. The results for normal scores were similar; the use of sign scores resulted in a test with poorer performance, as in the previous simulations.
Next, we address the following question: Does the same hold for measures of long-run shock persistence? Here we shall focus on the variance ratio, since it is nonparametric and does not require model selection or the choice of truncation parameters. We note that second moments are assumed finite for the variance ratio to be defined, which rules out infinite variance processes, although many other forms of leptokurtosis, such as ARCH, are allowed (Cambpell, Lo and MacKinlay, 1997:54). We again consider DGPs with and without inliers.
Our Monte Carlo simulation is based on a random walk process (yt = yt1 + ut), for which the variance ratio is expected to equal 1 for all lags, where the error term (ut) is generated from the following distributions: normal; t5; t3. Note, in particular, that the third case allows for very fat tails. The sample size consists of 101 observations (so that Dyt has 100 observations), and all results are based on 10,000 Monte Carlo replications. The mean variance ratios for k = 1, 2, , 25 are given in table 11. Note that the sample size is considerably smaller than either of the series we use in section 4.
The figures in table 11 show that the variance ratios are all close to 1 (their true value), regardless the lag (k) considered or the underlying distribution of the process, even when obtained from a sample considerably smaller than the ones used in this paper. That is, the variance ratio appears to be robust against fat-tailed processes. Therefore, the low measures of inflation inertia obtained in this study are not likely to be biased as a result of a long-tailed data generating process.12 12 We have also performed Monte Carlo simulations as described above, but using a stationary data generating process. In all three cases, the variance ratio approaches zero, as expected.
Tables 12, 13 and 14 report simulation results for the variance ratio in the presence of inliers under normally distributed errors and sample sizes T = {250, 750, 5000}. The DGP is the same as that which generated the results in table 11 but is now interrupted by inliers or shock plans.13 13 Here we also set y 0 = a so that the shock plans bring inflation to its initial level. The figures in tables 12, 13 and 14 show that the variance ratio is biased in the presence of inliers. However, its bias tends to vanish as the sample size increases. For samples sizes of T = 250,750 the bias is roughly half the true value and for T = 5000 the bias is of second order.
6 Concluding Remarks and Discussion
Many time series contain groups of observations which are not typical but due to abrupt governmental interventions. One example is the time series on the Brazilian inflation rate, which contain several groups of observations that were artificially lowered below their 'natural level' by soon-to-fail stabilization plans. Such observations have been termed 'inliers' and can potentially bias traditional unit root tests. Cati et al. (1999) have focused on this time series and proposed modified Dickey-Fuller tests that are not size-distorted in the presence of such inliers. They show that the ADF test rejects the unit root null in favor of a stationary alternative and that their modified test does not reject the unit root null. We show that the same conclusion can be reached when one uses robust rank regression-based unit root tests whose size and power robustness properties also hold against fat-tailed innovational processes. The simulation results in this study also suggest that Thompson's (2001) t test performs well in the presence of inliers in terms of both size and power when the rank tests are based on the Wilcoxon and normal scores. In addition, the results of the rank tests together with a persistence measure value close to zero for the two truncated series (CGP(T) and IGP-DI(T)) suggest that the Brazilian inflation may have followed a stationary dynamics (with no inflation inertia) up until the introduction of the first shock plan by the Brazilian government in early 1986.
Our second main result relates to the degree of inertia in the Brazilian inflationary process. Cati et al. (1999) obtained an estimate for such an inertial level close to what is expected for a random walk process, which would correspond to a fully inertial inflationary dynamics. At the closing of their paper, they write: ''The macroeconomic interpretation of our results is a support of the inflation inertia hypothesis which essentially states that shocks to inflation are highly persistent''. Our results, however, reveal a different picture, that is, a low degree of inflation inertia regardless of the persistence measure or the dataset used. In particular, our results suggest that the size of the inertial component in the Brazilian inflationary dynamics is somewhere between 0.1 and 0.2, thus implying that it is a minor component relative to other inflationary forces. Durevall (1998:430) found that the degree of inflation inertia in Brazil is 0.41, and noted that ''this is much less than obtained from other studies and much less than what is assumed by many theoretical models''. Our results point to inflation inertia levels even lower. That is, we find that inflation inertia is a minor driving force in the inflationary dynamics in Brazil, and that its importance has been overstated since the mid 1980s. A clear example of that was the sudden and large devaluation of the Brazilian currency in early 1999. The inflation rate suddenly rose from 1.2% in January 1999 to 4.4% in the following month. By April 1999 the inflation rate was nearly zero. Such dynamics is consistent with our results. Although the estimated persistence values for the complete series may be biased downward due to the presence of governmental interventions, it is also low for the corrected persistence measure (using the AIC to select the lag truncation parameter), which takes into account the shock plans, and for the truncated series, which do not contain inliers. Thus, our results suggest that the inertial component is of second order in the Brazilian inflationary dynamics.
Paper received in Aug. 2001 and approved in Sep. 2002.
- Agiakloglou, C. & Newbold, P. (1996). The balance between size and power in dickey-fuller tests with data-dependent rules for the choice of the truncation lag. Economics Letters, 52:229234.
- Brockwell, P. J. & Davis, R. A. (1991). Time Series: Theory and Methods Springer-Verlag, New York, 2nd edition.
- Campbell, J. Y., Lo, A. W., & MacKinlay, A. C. (1997). The Econometrics of Financial Markets Princeton University Press, Princeton.
- Cati, R. C., Garcia, M. G. P., & Perron, P. (1999). Unit roots in the presence of abrupt governmental interventions with an application to Brazilian data. Journal of Applied Econometrics, 14:2756.
- Cochrane, J. (1988). How big is the random walk in GNP? Journal of Political Economy, 96:893920.
- Contador, C. R. & Haddad, C. L. (1975). Produto real, moeda e preços: A experiência brasileira no período 19861-1970. Revista Brasileira de Estatística, 36:407440.
- Durevall, D. (1998). The dynamics of chronic inflation in Brazil, 1968-1985. Journal of Business and Economic Statistics, 16:423432.
- Durevall, D. (1999). Inertial inflation, indexation and price stickness: Evidence from Brazil. Journal of Development Economics, 60:407421.
- Fuller, W. A. (1976). Introduction to Statistical Time Series Wiley, New York.
- Gutenbrunner, C., Jurecková, J., Koenker, R., & Portnoy, S. (1993). Tests of linear hypotheses based on regression rank scores. Journal of Nonparametric Statistics, 2:307331.
- Hasan, M. N. (1993). Robust testing for unit roots based on regression rank scores. Dissertation Ph.D. Department of Economics, University of Illinois at UrbanaChampaign.
- Hasan, M. N. & Koenker, R. W. (1997). Robust rank tests of the unit root hypothesis. Econometrica, 65:133161.
- Instituto Brasileiro de Geografia e Estatística (1990). Estatísticas históricas do Brasil: Séries econômicas, demográficas e sociais. v. 3, 2 ed. Rio de Janeiro, IBGE.
- Koenker, R. (1997). Rank tests for linear models. In Maddala, G.S. & Rao, C. E., editor, Handbook of Statistics Elsevier Science, New York.
- Maddala, G. S. & Kim, I.-M. (1998). Unit Roots, Cointegration, and Structural Change Cambridge University Press, New York.
- Newbold, P. & Bos, T. (1990). Introductory Business and Economic Forecasting South-Western Publishing, Cincinnati, 2nd edition.
- Newey, W. K. &West, K. D. (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica, 55:819847.
- Novaes, A. D. (1993). Revisiting the inertial inflation hypothesis for Brazil. Journal of Development Economics, 42:89110.
- Perron, P. & Ng, S. (1998). An autoregressive spectral density estimator at frequency zero for nonstationarity tests. Econometric Theory, 14:560603.
- Simonsen, M. H. (1988). Price stabilization and income policies: Theory and the Brazilian case study. In Bruno, M., Di Tella, G., & Dornbusch, R. & Fischer, S. E., editors, Inflation Stabilization: The Experiences of Israel, Argentina, Brazil, Bolivia, and Mexico MIT Press., Cambridge.
- Thompson, S. (2001). Robust unit root testing with correct size and good power. Department of Economics, Harvard University.
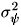 parameter does not depend on the error density. For tests based on normal, Wilcoxon and sign ranks, it can be shown to be equal to 1, 1/12 and 1/4, respectively.
parameter does not depend on the error density. For tests based on normal, Wilcoxon and sign ranks, it can be shown to be equal to 1, 1/12 and 1/4, respectively. 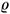 by numerical integration for the three score functions (Wilcoxon, normal and sign-median) and several densities including normal, Student
by numerical integration for the three score functions (Wilcoxon, normal and sign-median) and several densities including normal, Student Publication Dates
-
Publication in this collection
14 June 2004 -
Date of issue
Dec 2003
History
-
Received
Aug 2001 -
Accepted
Sept 2002



































