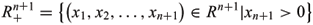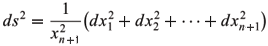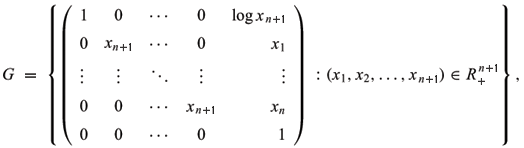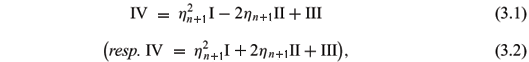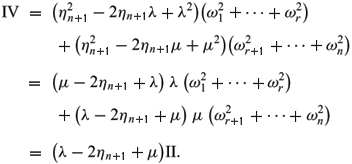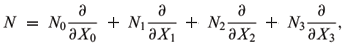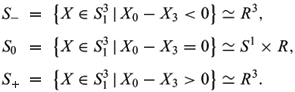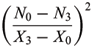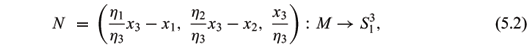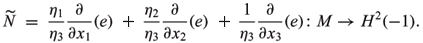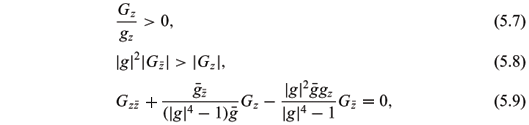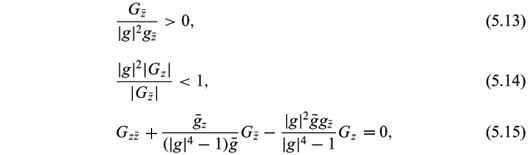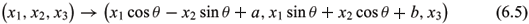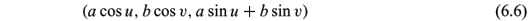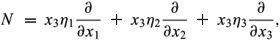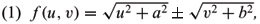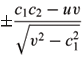Abstracts
In this paper, we introduce the fourth fundamental forms for hypersurfaces in Hn+1 and space-like hypersurfaces in S1n+1, and discuss the conformality of the normal Gauss map of the hypersurfaces in Hn+1 and S1n+1. Particularly, we discuss the surfaces with conformal normal Gauss map in H³ and S³1, and prove a duality property. We give a Weierstrass representation formula for space-like surfaces in S³1 with conformal normal Gauss map. We also state the similar results for time-like surfaces in S³1. Some examples of surfaces in S³1 with conformal normal Gauss map are given and a fully nonlinear equation of Monge-Ampère type for the graphs in S³1 with conformal normal Gauss map is derived.
fourth fundamental form; conformal normal Gauss map; generalized Gauss map; duality property; de Sitter Gauss map; Monge-Ampère equation
Neste artigo, introduzimos a quarta forma fundamental de uma hipersuperfície em Hn+1 de uma hipersuperfície tipo-espaço em S1n+1, e discutimos a conformalidade da aplicação normal de Gauss de tais hipersuperfícies. Em particular, investigamos o caso de superfícies com aplicação normal de Gauss conforme em H³ e S³1, e provamos um teorema de dualidade. Apresentamos uma representação de Weierstrass para superfícies tipo-espaço em S³1 com aplicação de Gauss conforme. Enunciamos também resultados semelhantes para superfícies tipo-tempo em S³1. São dados alguns exemplos de superfícies em S³1 com aplicações de Gauss conformes, e é deduzida uma equação totalmente não-linear do tipo Monge-Ampère para gráficos em S³1 com aplicações de Gauss conformes.
quarta forma fundamental; aplicação normal de Gauss conforme; aplicação de Gauss generalizada; propriedade de dualidade; aplicação de Gauss de Sitter; equação de Monge-Ampère
MATHEMATICAL SCIENCES
The hypersurfaces with conformal normal Gauss map in Hn+1 and S1n+1
Shuguo Shi
School of Mathematics and System Sciences, Shandong University, Jinan 250100, P.R. China
ABSTRACT
In this paper, we introduce the fourth fundamental forms for hypersurfaces in Hn+1 and space-like hypersurfaces in S1n+1, and discuss the conformality of the normal Gauss map of the hypersurfaces in Hn+1 and S1n+1. Particularly, we discuss the surfaces with conformal normal Gauss map in H3 and S31, and prove a duality property. We give a Weierstrass representation formula for space-like surfaces in S31 with conformal normal Gauss map. We also state the similar results for time-like surfaces in S31. Some examples of surfaces in S31 with conformal normal Gauss map are given and a fully nonlinear equation of Monge-Ampère type for the graphs in S31 with conformal normal Gauss map is derived.
Key words: fourth fundamental form, conformal normal Gauss map, generalized Gauss map, duality property, de Sitter Gauss map, Monge-Ampère equation.
RESUMO
Neste artigo, introduzimos a quarta forma fundamental de uma hipersuperfície em Hn+1 de uma hipersuperfície tipo-espaço em S1n+1, e discutimos a conformalidade da aplicação normal de Gauss de tais hipersuperfícies. Em particular, investigamos o caso de superfícies com aplicação normal de Gauss conforme em H3 e S31, e provamos um teorema de dualidade. Apresentamos uma representação de Weierstrass para superfícies tipo-espaço em S31 com aplicação de Gauss conforme. Enunciamos também resultados semelhantes para superfícies tipo-tempo em S31. São dados alguns exemplos de superfícies em S31 com aplicações de Gauss conformes, e é deduzida uma equação totalmente não-linear do tipo Monge-Ampère para gráficos em S31 com aplicações de Gauss conformes.
Palavras-chave: quarta forma fundamental, aplicação normal de Gauss conforme, aplicação de Gauss generalizada, propriedade de dualidade, aplicação de Gauss de Sitter, equação de Monge-Ampère.
1 INTRODUCTION
It is well known that the classical Gauss map has played an important role in the study of the surface theory in R3 and has been generalized to the submanifold of arbitrary dimension and codimension immersed into the space forms with constant sectional curvature (see Osserman 1980).
Particularly, for the n-dimensional submanifold x: M ® V in space V with constant sectional curvature, Obata (Obata 1968) introduced the generalized Gauss map which assigns each point p of M to the totally geodesic n-subspace of V tangent to x(M) at x(p). He defined the third fundamental form of the submanifold in constant curvature space as the pullback of the metric of the set of all totally geodesic n-subspaces in V under the generalized Gauss map. He derived a relationship among the Ricci tensor of the immersed submanifold and the first, the second and the third fundamental forms of the immersion. Meanwhile, Lawson (Lawson 1970) discussed the generalized Gauss map of the immersed surfaces in S3, and prove a duality property between the minimal surfaces in S3 and their generalized Gauss map images.
Epstein (Epstein 1986) and Bryant (Bryant 1987) defined the hyperbolic Gauss map for surfaces in H3, and Bryant (Bryant 1987) obtained a Weierstrass representation formula for constant mean curvature one surfaces with conformal hyperbolic Gauss map. Using the Weierstrass representation formula, Bryant also studied the properties of constant mean curvature one surfaces. Using the hyperbolic Gauss map, Gálvez and Martínez and Milán (Gálvez et al. 2000) studied the flat surfaces in H3 with conformal hyperbolic Gauss map with respect to the second conformal structure on surfaces (see (Klotz 1963) for the definition), and obtained a Weierstrass representation formula for such surfaces.
Kokubu (Kokubu 1997) considered the n-dimensional hyperbolic space Hn as a Lie group G with a left-invariant metric, and defined the normal Gauss map of the surfaces which assigns each point of the surface to the tangent plane left translated to the Lie algebra of G. He also gave a Weierstrass representation formula for minimal surfaces in Hn. On the other hand, Gálvez and Martínez (Gálvez and Martínez 2000) studied the properties of the Gauss map of a surface S immersed into the Euclidean 3-space R3 by using the second conformal structure on surface, and obtained a Weierstrass representation formula for surfaces with prescribed Gauss map. Motivated by their work, the author (Shi 2004) gave a Weierstrass representation formula for surfaces with prescribed normal Gauss map and Gauss curvature in H3 by using the second conformal structure on surfaces. From this, the surfaces whose normal Gauss maps are conformal have been found, and the translational surfaces with conformal normal Gauss map locally are given. In (Shi 2006), the author classified locally the ruled surfaces with conformal normal Gauss map within the Euclidean ruled surfaces, and studied some global properties of the ruled surfaces and translational surfaces with conformal normal Gauss map.
Aiyama and Akutagawa (Aiyama and Akutagawa 2000) defined the normal Gauss map for space-like surfaces in the de Sitter 3-space  , and gave a Weierstrass representation formula for space-like surfaces in
, and gave a Weierstrass representation formula for space-like surfaces in  with prescribed mean curvature and normal Gauss map.
with prescribed mean curvature and normal Gauss map.
The purpose of this paper is to study the conformality of the normal Gauss map for hypersurfaces in Hn+1 and space-like hypersurfaces in  , and to prove a duality property between the surfaces in H3 and the space-like surfaces in
, and to prove a duality property between the surfaces in H3 and the space-like surfaces in  with conformal normal Gauss map. The rest of this paper is organized as follows. In the second section, we describe the generalized definition of the normal Gauss map for hypersurfaces in Hn+1 and space-like hypersurfaces in
with conformal normal Gauss map. The rest of this paper is organized as follows. In the second section, we describe the generalized definition of the normal Gauss map for hypersurfaces in Hn+1 and space-like hypersurfaces in  (cf. Kokubu 1997, Aiyama and Akutagawa 2000). The third section introduces the fourth fundamental forms for hypersurfaces in Hn+1 and
(cf. Kokubu 1997, Aiyama and Akutagawa 2000). The third section introduces the fourth fundamental forms for hypersurfaces in Hn+1 and  , and obtains a relation among the first, the second, the third and the fourth fundamental forms of the hypersurfaces. As an application, we discuss the conformality of the normal Gauss map for hypersurfaces in Hn+1 and space-like hypersurfaces in
, and obtains a relation among the first, the second, the third and the fourth fundamental forms of the hypersurfaces. As an application, we discuss the conformality of the normal Gauss map for hypersurfaces in Hn+1 and space-like hypersurfaces in  . By means of the generalized Gauss map of the surfaces in H3 and
. By means of the generalized Gauss map of the surfaces in H3 and  , the fourth one proves a duality property between the surfaces in H3 and the space-like surfaces in
, the fourth one proves a duality property between the surfaces in H3 and the space-like surfaces in  with conformal normal Gauss map. The fifth one gives a Weierstrass representation formula for space-like surfaces in
with conformal normal Gauss map. The fifth one gives a Weierstrass representation formula for space-like surfaces in  with conformal normal Gauss map, and the sixth one derives the fully nonlinear equation of Monge-Ampère type for space-like graphs in
with conformal normal Gauss map, and the sixth one derives the fully nonlinear equation of Monge-Ampère type for space-like graphs in  with conformal normal Gauss map and classifies locally the translational surfaces and the Euclidean ruled surfaces in
with conformal normal Gauss map and classifies locally the translational surfaces and the Euclidean ruled surfaces in  with conformal normal Gauss map. In the last section, we state the similar results for time-like surfaces in
with conformal normal Gauss map. In the last section, we state the similar results for time-like surfaces in  with conformal normal Gauss map.
with conformal normal Gauss map.
2 PRELIMINARIES
Take upper half-space models of hyperbolic space Hn+1(-1) and de Sitter space  (1)
(1)
with respectively Riemannian metric
and Lorentz metric
(see Aiyama and Akutagawa 2000 or section 4).
Let M be a n-dimensional Riemannian manifold and x: Mn ® Hn+1 (resp. x: Mn ®  ) be an immersed hypersurface (resp. space-like hypersurface) with local coordinates u1,u2,...,un. In this paper,we agree with the following ranges of indices: 1 < i,j,k,... < n and 1 < A,B,C,... < n + 1. The first and the second fundamental forms are given, respectively, by I = gijduiduj and II = hijduiduj. The unit normal vector ( resp. time-like unit normal vector) of x(M) is
) be an immersed hypersurface (resp. space-like hypersurface) with local coordinates u1,u2,...,un. In this paper,we agree with the following ranges of indices: 1 < i,j,k,... < n and 1 < A,B,C,... < n + 1. The first and the second fundamental forms are given, respectively, by I = gijduiduj and II = hijduiduj. The unit normal vector ( resp. time-like unit normal vector) of x(M) is
where  = 1 (resp.
= 1 (resp.  = -1).
= -1).
We have the Weingarten formula
Identitying Hn+1 and  with Lie group (Kokubu 1997)
with Lie group (Kokubu 1997)
the multiplication is defined as matrix multiplication and the identity is e = (0,0,¼,0,1). The Riemannian metric of Hn+1 and the Lorentz metric of  are left-invariant, and
are left-invariant, and
are the left-invariant unit orthonormal vector fields. Now, the unit normal vector (resp. time-like unit normal vector) field of x(M) can be written as N = h1  1 + h2
1 + h2  2 + ... + hn+1
2 + ... + hn+1  n+1. Left translating N to Te(
n+1. Left translating N to Te( ), we obtain
), we obtain
Call  the normal Gauss map of the immersed hypersurface x: M ® Hn+1 (resp. space-like hypersurface x: M ®
the normal Gauss map of the immersed hypersurface x: M ® Hn+1 (resp. space-like hypersurface x: M ®  ) (Kokubu 1997, Aiyama and Akutagawa 2000).
) (Kokubu 1997, Aiyama and Akutagawa 2000).
3 THE FOURTH FUNDAMENTAL FORM
DEFINITION. Let M be a n-dimensional Riemannian manifold. Call IV = ád , d
, d ñ the fourth fundamental form of the immersed hypersurface x: M ®
ñ the fourth fundamental form of the immersed hypersurface x: M ®  (resp. space-like hypersurface x: M ®
(resp. space-like hypersurface x: M ®  ), where the scalar product á·,·ñ is induced by the Euclidean metric of Rn+1 (resp. the Lorentz-Minkowski metric of Ln+1).
), where the scalar product á·,·ñ is induced by the Euclidean metric of Rn+1 (resp. the Lorentz-Minkowski metric of Ln+1).
THEOREM 3.1. Let M be a n-dimensional Riemannian manifold with Ricci tensor Ric. Let x: M ® Hn+1 (resp. x: M ®  ) be an immersed hypersurface (resp. space-like hypersurface) with mean curvature H =
) be an immersed hypersurface (resp. space-like hypersurface) with mean curvature H =
where III = nHII - (n - 1)I - Ric (resp. III = nHII - (n - 1)I + Ric) is Obata's third fundamental form of x(M) (see Obata 1968).
PROOF. At first we prove the Theorem for Hn+1. Choose the normal coordinates u1,u2,...,un near p Î M. By the Weingarten formula, we get
III = hikhjkduiduj is the third fundamental form (Obata 1968) and by the Gauss equation, III = nHII - (n - 1)I - Ric. (3.1) is proved.
Next, similar to the above proof, for  , we have
, we have
Similar to the proof of (3.1), we can prove (3.2).
Next, we consider the applications of these formulas (3.1)-(3.4). In the following of this paper, that the normal Gauss map is conformal means that the fourth fundamental form is proportional to the second fundamental form, i.e. IV = rII for some smooth function r on M (Shi 2004, 2006).
THEOREM 3.2. Let M be a n-dimensional Riemannian manifold and x: M ® Hn+1 (resp. x: M ®  ) be an immersed hypersurface ( resp. space-like hypersurface) without umbilics. Then the normal Gauss map of x(M) is conformal if and only if at each point of M, there exists exactly two distinct principal curvatures and the sectional curvature R(X Ù Y) = -1 +
) be an immersed hypersurface ( resp. space-like hypersurface) without umbilics. Then the normal Gauss map of x(M) is conformal if and only if at each point of M, there exists exactly two distinct principal curvatures and the sectional curvature R(X Ù Y) = -1 +
PROOF. The case of Hn+1. For any point p Î M, let {e1,e2,...,en} be a local frame field so that (hij) is diagonalized at this point, i.e. hij(p) = lidij. By IV = rII and (3.3), we get, for i = 1,2,...,n, that
i.e.
Because x(M) has no umbilics, the equation (3.6) with respect to li has exactly two distinct solutions l and µ and lm = 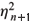 . By the Gauss equation, one may prove R(X Ù Y) = -1 + lm = -1 +
. By the Gauss equation, one may prove R(X Ù Y) = -1 + lm = -1 + 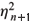 .
.
Conversely, choose the local tangent frame {e1,e2,..., en} and the dual frame {w1,w2, ...,wn} near p, such that hij = 0, i ¹ j and h11 = h22 = ... = hrr = l ¹ m = hr+1r+1 = ... = hnn at p.Then 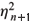 = lm. By (3.3),
= lm. By (3.3),
The sufficiency has been proved for Hn+1. Similarly, we can prove Theorem 3.2 for  .
.
REMARK. By (3.5), we know that the normal Gauss map of all totally umbilical hypersurfaces except totally geodesic hyperspheres in Hn+1 are conformal. Similarly, for space-like hypersurfaces in  , since hn+1¹ 0, the normal Gauss maps of all totally umbilical space-like hypersurfaces except totally geodesic space-like hypersurfaces are conformal.
, since hn+1¹ 0, the normal Gauss maps of all totally umbilical space-like hypersurfaces except totally geodesic space-like hypersurfaces are conformal.
For H3 and  , by Theorem 3.2, we immediately get
, by Theorem 3.2, we immediately get
THEOREM 3.3. Let M be a 2-dimensional Riemannian manifold and x: M ® H3 (resp. x: M ®  ) be an immersed surface (resp. space-like surface) without umbilics. Then the normal Gauss map of x(M) is conformal if and only if the Gauss curvature K = -1 +
) be an immersed surface (resp. space-like surface) without umbilics. Then the normal Gauss map of x(M) is conformal if and only if the Gauss curvature K = -1 +
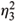 ).
).
REMARK. In (Shi 2004, 2006), we assume that the second fundamental form is positive definite and induces the conformal structure on the surfaces in H3. Here, the assumption with respect to the positive definite second fundamental form is dropped.
THEOREM 3.4. Let M be a n-dimensional Einstein manifold and x: M ® Hn+1 (resp. x: M ®  ) be an immersed hypersurface (resp. space-like hypersurface) with non-degenerate second fundamental form and without umbilics. If the normal Gauss map of x(M) is conformal map, i.e. IV = rII, then n = 2 and r = 2(H - h3) (resp. r = 2(H + h3)).
) be an immersed hypersurface (resp. space-like hypersurface) with non-degenerate second fundamental form and without umbilics. If the normal Gauss map of x(M) is conformal map, i.e. IV = rII, then n = 2 and r = 2(H - h3) (resp. r = 2(H + h3)).
PROOF. We only prove the Theorem for Hn+1. M is an Einstein manifold, so Ric =  I, where S is the scalar curvature of M. (3.1) becomes
I, where S is the scalar curvature of M. (3.1) becomes
Because x(M) has no umbilics, we have
nH = 2hn+1 + r.
By Theorem 3.2 and its proof, we assume that l1 = ... = lr = l ¹ m = lr+1 = ... = ln, then
rl + (n - r)µ = 2hn+1 + r.
By (3.6),
l + µ = 2hn+1 + r.
So (r - 1)l + (n - r - 1)µ = 0. By Theorem 3.2, l and µ have same signature. So r = 1 and n = 2. Hence r = 2H - 2h3.
4 A DUALITY FOR THE SURFACES IN H3 AND  WITH CONFORMAL NORMAL GAUSS MAPS
WITH CONFORMAL NORMAL GAUSS MAPS
Let L4 be the Minkowski 4-space with canonical coordinates X0,X1, X2,X3 and Lorentz-Minkowski scalar product  . The Minkowski model of H3 is given by
. The Minkowski model of H3 is given by
H3 = {(X0, X1, X2, X3) |  = -1, X0 > 0}
= -1, X0 > 0}
and is identified with the upper half-space model  of H3 by
of H3 by
Accordingly, the space-like normal vector of the surface in the Minkowski model of H3 is
where
We get
The Minkowski model of the de Sitter 3-space is defined as
and can be divided into three components as follows (cf. Aiyama and Akutagawa 2000),
Identify S- and S+ with upper half-space model  of the de Sitter 3-space by (cf. Aiyama and Akutagawa 2000)
of the de Sitter 3-space by (cf. Aiyama and Akutagawa 2000)
For space-like surface X: M ®  , let U- = X-1(S-) and U+ = X-1(S+), then U-È U+ is the open dense subset of M. On U-È U+, the time-like unit normal vector is
, let U- = X-1(S-) and U+ = X-1(S+), then U-È U+ is the open dense subset of M. On U-È U+, the time-like unit normal vector is
where
We get
REMARK. In (Aiyama and Akutagawa 2000), the normal Gauss map of the space-like surface X: M ®  is defined globally on M. Because of the density of U- and U+ in M, in this paper, we may consider that the normal Gauss map of the space-like surface X: M ®
is defined globally on M. Because of the density of U- and U+ in M, in this paper, we may consider that the normal Gauss map of the space-like surface X: M ®  is defined on U- and U+.
is defined on U- and U+.
Let X: M ® H3 (resp. X: M ®  ) be an immersed surface (resp. space-like surface). Parallel translating the space-like ( resp. time-like) unit normal vector N to the origin of L4, one gets the map N: M ®
) be an immersed surface (resp. space-like surface). Parallel translating the space-like ( resp. time-like) unit normal vector N to the origin of L4, one gets the map N: M ®  ( resp. N: M ® H3) which is usually called generalized Gauss map of X: M ® H3 (resp. X: M ®
( resp. N: M ® H3) which is usually called generalized Gauss map of X: M ® H3 (resp. X: M ®  ). The generalized Gauss map image can be considered as the surface in
). The generalized Gauss map image can be considered as the surface in  (resp. H3).
(resp. H3).
THEOREM 4.1. (Kokubu 2005, Prop. 3.5). (1) Let X: M ® H3be a 2-dimensional immersed surface. Then its generalized Gauss map N: M ®  is a branched space-like immersion into
is a branched space-like immersion into  with branch points where K = -1. And, when K ¹ -1, the curvature of N: M ®
with branch points where K = -1. And, when K ¹ -1, the curvature of N: M ®  is K* =
is K* =  and the volume element is dVN = |K + 1|dVX.
and the volume element is dVN = |K + 1|dVX.
(2) Let X: M ®  be a 2-dimensional space-like immersed surface. Then its generalized Gauss map N: M ® H3is a branched immersion into H3with branch points where K = 1. And, when K ¹ 1, the curvature of N: M ® H3is K* =
be a 2-dimensional space-like immersed surface. Then its generalized Gauss map N: M ® H3is a branched immersion into H3with branch points where K = 1. And, when K ¹ 1, the curvature of N: M ® H3is K* =  and the volume element is dVN = |1 - K|dVX.
and the volume element is dVN = |1 - K|dVX.
PROOF. In the context of this paper, we prove (2). For any p Î M, let {e0,e1,e2,e3} be the orthonormal frame near p, such that e3 = X, e0 = N. Let {w0,w1,w2,w3} be the dual frame. The connection 1-forms is  , a,b = 0,1,2,3. The coefficients of the second fundamental form of X: M ®
, a,b = 0,1,2,3. The coefficients of the second fundamental form of X: M ®  is given by
is given by  = hijwj, hij = hji, i,j = 1,2. The induced metric of N : M ® H3 is
= hijwj, hij = hji, i,j = 1,2. The induced metric of N : M ® H3 is  = ádN, dNñ = hikhjkwiwj. Choose the local tangent frame {e1,e2} near p, such that hij = lidij. Then
= ádN, dNñ = hikhjkwiwj. Choose the local tangent frame {e1,e2} near p, such that hij = lidij. Then  =
=  . So, when l1l2¹ = 0, i.e. K ¹ 1, N(M) is an immersed surface into H3. Its space-like unit normal vector is X and the second fundamental form is II = -ádX, dNñ = -l1(w1)2 -l2(w2)2. By the Gauss equation, K* = -1 +
. So, when l1l2¹ = 0, i.e. K ¹ 1, N(M) is an immersed surface into H3. Its space-like unit normal vector is X and the second fundamental form is II = -ádX, dNñ = -l1(w1)2 -l2(w2)2. By the Gauss equation, K* = -1 +  =
=  .
.
By Theorem 3.3, (4.1), (4.2) and Theorem 4.1, we get the following duality.
THEOREM 4.2. Let M be a connected 2-dimensional manifold. Let X: M ® H3 be an immersed surface with K ¹ -1 and without umbilics and let N: M ®  be a space-like surface with K ¹ 1 and without umbilics. Suppose that N: M ®
be a space-like surface with K ¹ 1 and without umbilics. Suppose that N: M ®  is the generalized Gauss map of X: M ® H3 and vice versa. Then, the normal Gauss map of X: M ® H3 is conformal if and only if one of N: M ®
is the generalized Gauss map of X: M ® H3 and vice versa. Then, the normal Gauss map of X: M ® H3 is conformal if and only if one of N: M ®  is conformal. And, at this time, dVN =
is conformal. And, at this time, dVN =
REMARK. Like (Lawson 1970) for minimal surfaces in S3, we call the generalized Gauss map N: M ®  the polar variety of the immersed surface X: M ® H3 with conformal normal Gauss map and vice versa.
the polar variety of the immersed surface X: M ® H3 with conformal normal Gauss map and vice versa.
5 WEIERSTRASS REPRESENTATION FORMULA
In this section, we give a Weierstrass representation formula for space-like surfaces in  with conformal normal Gauss map. At first, we describe the normal Gauss map and the de Sitter Gauss map of the space-like surfaces in
with conformal normal Gauss map. At first, we describe the normal Gauss map and the de Sitter Gauss map of the space-like surfaces in  . Take upper half-space model
. Take upper half-space model  of
of  .
.
The normal Gauss map of the space-like surface x: M ®  is given by
is given by
By means of the stereographic projection from the north pole (0,0,1) of H2(-1) to the (x1, x2)-plane identified with C, we get
which is also called the normal Gauss map of the space-like surface x: M ®  ·
·  can be written as
can be written as
Next, we describe the definition of the de Sitter Gauss map for space-like surfaces in  (in (Lee 2005), it is still called hyperbolic Gauss map), which is the analogue of Epstein and Bryant's hyperbolic Gauss map for surfaces in H3 (Epstein 1986, Bryant 1987, Shi 2004). The time-like geodesic is either the Euclidean equilateral half-hyperbola consisting of two branches which is orthonormal to the coordinate plane {(x1, x2,0)|(x1,x2) Î R2} or the Euclidean straight line which is orthonormal to the above coordinate plane. For the space-like surface x = (x1,x2,x3)\colon M ®
(in (Lee 2005), it is still called hyperbolic Gauss map), which is the analogue of Epstein and Bryant's hyperbolic Gauss map for surfaces in H3 (Epstein 1986, Bryant 1987, Shi 2004). The time-like geodesic is either the Euclidean equilateral half-hyperbola consisting of two branches which is orthonormal to the coordinate plane {(x1, x2,0)|(x1,x2) Î R2} or the Euclidean straight line which is orthonormal to the above coordinate plane. For the space-like surface x = (x1,x2,x3)\colon M ®  , at each point x Î M, the oriented time-like geodesic in
, at each point x Î M, the oriented time-like geodesic in  passing through x with time-like tangent vector N meets {(x1,x2,0)|(x1,x2) Î R2}È{¥} at two points. Since the geodesic is oriented, we may speak of one of the two points as the initial point and the other one as the final point. Call the final point the image of the de Sitter Gauss map for x(M) at the point x. Denote the de Sitter Gauss map by GS. On the coordinate plane {(x1,x2,0)|(x1,x2) Î R2}, we introduce the natural complex coordinate z = x1 + 2. Using the Euclidean geometry, as similar as done in the Theorem 5.1 of (Shi 2004), we get
passing through x with time-like tangent vector N meets {(x1,x2,0)|(x1,x2) Î R2}È{¥} at two points. Since the geodesic is oriented, we may speak of one of the two points as the initial point and the other one as the final point. Call the final point the image of the de Sitter Gauss map for x(M) at the point x. Denote the de Sitter Gauss map by GS. On the coordinate plane {(x1,x2,0)|(x1,x2) Î R2}, we introduce the natural complex coordinate z = x1 + 2. Using the Euclidean geometry, as similar as done in the Theorem 5.1 of (Shi 2004), we get
Let x = (x1,x2,x3) : M ® H3 be an immersed surface with unit normal vector
By the duality given in section 4, the generalized Gauss map of x: M ® H3 is given, when h3 > 0, by
and when h3 < 0, by
and in the Minkowski model of the de Sitter 3-space, their time-like unit normal vector is X: M ® H3. Again by the duality given in section 4, a straightforward computation shows us that the normal Gauss map of N: M ®  is given by
is given by
So,
where gH: M ® C È{¥} is exactly the normal Gauss map of x: M ® H3 (Kokubu 1997, Shi 2004, 2006). From this, we also prove the Theorem 4.2.
By (5.1)-(5.4) and the Theorem 5.1 of (Shi 2004), we get that when h3 > 0, i.e. |gS| > 1,
and when h3 < 0, i.e. |gS| < 1,
where GH is exactly the hyperbolic Gauss map of x: M ® H3 (Epstein 1986, Bryant 1987, Shi 2004).
In the following, we write respectively gS and GS as g and G.
By (5.2)-(5.6) and the Weierstrass representation for surfaces in H3 with conformal normal Gauss map (Shi 2004), we get the Weierstrass representation formula for space-like surfaces in  with conformal normal Gauss map.
with conformal normal Gauss map.
THEOREM 5.1. Let M be a simply connected Riemann surface. Given the map G: M ® C È{¥} and the nonconstant conformal map g: M ® C È{¥}\{|z| = 1}.
(1) When the holomorphic map g: M ® CÈ{¥}\{|z| = 1} satisfies |g| > 1 and
put
Then x = (x1,x2,x3): M ®  is a space-like surface with de Sitter Gauss map G and holomorphic normal Gauss map g and Gauss curvature K satisfying
is a space-like surface with de Sitter Gauss map G and holomorphic normal Gauss map g and Gauss curvature K satisfying
 with
with 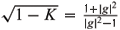 ( = h3) can be given by (5.10), (5.11), (5.12), and the de Sitter Gauss map G and the normal Gauss map g must satisfy (5.7), (5.8), (5.9), where the conformal structure on M is induced by the negative definite second fundamental form.
( = h3) can be given by (5.10), (5.11), (5.12), and the de Sitter Gauss map G and the normal Gauss map g must satisfy (5.7), (5.8), (5.9), where the conformal structure on M is induced by the negative definite second fundamental form.
(2) When the antiholomorphic map g: M ® C È{¥}\{|z| = 1} without holomorphic points satisfies |g| < 1 and
put
Then x = (x1,x2,x3): M ®  is a space-like surface with de Sitter Gauss map G and antiholomorphic normal Gauss map g and Gauss curvature K satisfying
is a space-like surface with de Sitter Gauss map G and antiholomorphic normal Gauss map g and Gauss curvature K satisfying
 with
with 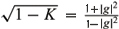 ( = -h3) can be given by (5.16), (5.17), (5.18), and the de Sitter Gauss map G and the normal Gauss map g must satisfy (5.13), (5.14), (5.15), where the conformal structure on M is induced by the negative definite second fundamental form.
( = -h3) can be given by (5.16), (5.17), (5.18), and the de Sitter Gauss map G and the normal Gauss map g must satisfy (5.13), (5.14), (5.15), where the conformal structure on M is induced by the negative definite second fundamental form.
6 GRAPHS AND EXAMPLES
In this section,we give the examples of surfaces in  with conformal normal Gauss map within the translational surfaces and the Euclidean ruled surfaces.
with conformal normal Gauss map within the translational surfaces and the Euclidean ruled surfaces.
In H3, the graph (u,v,f(u,v)) with conformal normal Gauss map satisfies the following fully nonlinear equation of Monge-Ampère type (Shi 2004, 2006)
Take upper half-space model of  . Consider the space-like graph (u,v,f(u,v)) in
. Consider the space-like graph (u,v,f(u,v)) in  with
with  < 1. Its Gauss curvature is given by
< 1. Its Gauss curvature is given by
So K = 1 - 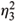 is equivalent to
is equivalent to
where  < 1. This is the fully nonlinear equation of Monge-Ampère type which the space-like graph in
< 1. This is the fully nonlinear equation of Monge-Ampère type which the space-like graph in  with K = 1 -
with K = 1 - 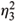 must satisfy.
must satisfy.
REMARK. There exists a nice duality between the solutions of minimal surface equation
in R3 and the ones of maximal surface equation
in Lorentz-Minkowski 3-space L3 (Alías and Palmer 2001). Here, by the duality given by (5.2) (or (5.3)), we know that if f(u,v) is a solution of (6.1), then the local graph of the space-like surface (-ffu -u, -ffv -v,f ) (or (ffu + u, ffv + v,f
) (or (ffu + u, ffv + v,f )) in
)) in  satisfies (6.2). Conversely, if f(u,v) is a solution of (6.2) with
satisfies (6.2). Conversely, if f(u,v) is a solution of (6.2) with  < 1, then the local graph of the surface (ffu -u,ffv -v,f
< 1, then the local graph of the surface (ffu -u,ffv -v,f ) (or (u -ffu, v -ffv, f
) (or (u -ffu, v -ffv, f )) in H3 satisfies (6.1).
)) in H3 satisfies (6.1).
Next, as similar as done in section 6 of (Shi 2004), we get the following Theorem.
THEOREM 6.1. The nontrivial translational space-like surfaces with form f(u,v) = f(u) + y(v) in
with conformal normal Gauss map are given, up to a linear translation of variables, by
with
< 1, where a and b are nonzero constants. The parameter form of these translational surfaces are locally given by
REMARK. We may check that the isometric transformation
preserves the concept of the ruled surfaces and the conformality of the normal Gauss map of the space-like surface in  .
.
Considered as surfaces in 3-dimensional Minkowski space L3, the space-like ruled surfaces in  can be represented as x(u,v) = a(v) + ub(v): D ®
can be represented as x(u,v) = a(v) + ub(v): D ®  , where D(Ì R2) is a parameter domain and a(v) and b(v) are two vector valued functions into L3 corresponding to two curves in L3. When b is locally nonconstant, without loss of generality we can assume that either áb,bñ = 1, áb',b'ñ = ±1, and áa',b'ñ = 0 or áb,bñ = 1, áb',b'ñ = 0, and áa',bñ = 0, where á·,·ñ is the scalar product in L3. As similar as done in Theorem 2 of (Shi 2006), we have
, where D(Ì R2) is a parameter domain and a(v) and b(v) are two vector valued functions into L3 corresponding to two curves in L3. When b is locally nonconstant, without loss of generality we can assume that either áb,bñ = 1, áb',b'ñ = ±1, and áa',b'ñ = 0 or áb,bñ = 1, áb',b'ñ = 0, and áa',bñ = 0, where á·,·ñ is the scalar product in L3. As similar as done in Theorem 2 of (Shi 2006), we have
THEOREM 6.2. Up to an isometric transformation (6.5) in
, every space-like ruled surface in with conformal normal Gauss map is locally a part of one of the following,(1) ordinary Euclidean space-like planes in
,(2) (u cosh v, c · sinh v, u sinh v), for a constant c ¹ 0,
(3) (c2 sinh v + u cosh v, c1 sinh v, c2 cosh v + u sinh v), for constants c1¹ 0 and c2¹ 0.
We should note that in the proof of Theorem 6.2, only when áb',b'ñ = -1, we may get the nontrivial cases (2) and (3).
Locally, the ruled surfaces (2) and (3) in Theorem 6.2 can be represented as the graph (u,v,f(u,v)) as follows,
COROLLARY. f(u,v) =
is a solution of equation (6.2), where c1¹ 0 and c2 are constants.REMARK. In H3, the translational surfaces
and the ruled surfaces
and
with conformal normal Gauss map have been obtained (Shi 2004, 2006), where a,b,c,c1 and c2 are nonzero constants. Using (5.2) (or (5.3)) and Theorem 4.2, we may check that up to a isometric transformation (6.5) in  (q = ±
(q = ± ), (6.4) in Theorem 6.1 and (2) and (3) in Theorem 6.2 are, respectively, the polar varieties of (6.6), (6.7) and (6.8) and vice versa.
), (6.4) in Theorem 6.1 and (2) and (3) in Theorem 6.2 are, respectively, the polar varieties of (6.6), (6.7) and (6.8) and vice versa.
REMARK. Every geodesic of H3, corresponding respectively to u = 0, u = p, v = 0 and v = p on surfaces (6.6) and to v =  on surfaces (6.7) and to v = ±
on surfaces (6.7) and to v = ± on surfaces (6.8) follow which K = -1 is mapped to a single point in S0 by the generalized Gauss map.
on surfaces (6.8) follow which K = -1 is mapped to a single point in S0 by the generalized Gauss map.
7 TIME-LIKE SURFACES IN  WITH CONFORMAL NORMAL GAUSS MAP
WITH CONFORMAL NORMAL GAUSS MAP
In this section, we state the similar results as above for time-like surfaces in  without proofs.
without proofs.
Take upper-half space model of  . Let M be a 2-dimensional Lorentz surface and x: M ®
. Let M be a 2-dimensional Lorentz surface and x: M ®  be the time-like immersion with local coordinates u1,u2. The first and the second fundamental forms are given, respectively, by I = gijduiduj and II = hijduiduj. The space-like unit normal vector is
be the time-like immersion with local coordinates u1,u2. The first and the second fundamental forms are given, respectively, by I = gijduiduj and II = hijduiduj. The space-like unit normal vector is
where  = 1. We have the Weingarten formula
= 1. We have the Weingarten formula
Left-translating N to Te( ), we obtain
), we obtain
which is called the normal Gauss map of time-like surface x: M ®  (Aiyama and Akutagawa 2000). Call IV = ád
(Aiyama and Akutagawa 2000). Call IV = ád ,d
,d ñ the fourth fundamental form of the time-like surface x: M ®
ñ the fourth fundamental form of the time-like surface x: M ®  . We have
. We have
IV =
gij - 2h3hij + gkl hikhjl) duiduj.Of course, we may also define the high-dimensional version of the fourth fundamental form for time-like hypersurfaces in  (1).
(1).
THEOREM 7.1. Let M be a 2-dimensional Lorentz surface and x: M ®  be a time-like immersed surface without umbilics. Then the normal Gauss map of x(M) is conformal if and only if the Gauss curvature K = 1 +
be a time-like immersed surface without umbilics. Then the normal Gauss map of x(M) is conformal if and only if the Gauss curvature K = 1 +
In the Minkowski model of the de Sitter 3-space  , the generalized Gauss map N: M ®
, the generalized Gauss map N: M ®  of the time-like surface X: M ®
of the time-like surface X: M ®  is a branched time-like immersion with branch points where K = 1.
is a branched time-like immersion with branch points where K = 1.
THEOREM 7.2. Let M be a connected 2-dimensional Lorentz surface. Let X: M ®  be a time-like surface with K ¹ 1 and without umbilics. If the normal Gauss map of X: M ®
be a time-like surface with K ¹ 1 and without umbilics. If the normal Gauss map of X: M ®  is conformal, then the normal Gauss map of its generalized Gauss map N: M ®
is conformal, then the normal Gauss map of its generalized Gauss map N: M ®  is also conformal and vice versa.
is also conformal and vice versa.
The time-like graph (u,v,f(u,v)) in  with conformal normal Gauss map also satisfies the fully nonlinear equation of Monge-Ampère type (6.2) with
with conformal normal Gauss map also satisfies the fully nonlinear equation of Monge-Ampère type (6.2) with  > 1.
> 1.
THEOREM 7.3. The nontrivial translational time-like surfaces with form f(u,v) = f(u) + y(v) in
with conformal normal Gauss map are given, up to a linear translation of variables, by
Flaherty's time-like surfaces in  (Milnor 1987) f(u,v) = ±u + y(v) and f(u,v) = ±v + j(u), where a and b are nonzero constants and y'(v) ¹ 0 and j'(u) ¹ 0.
(Milnor 1987) f(u,v) = ±u + y(v) and f(u,v) = ±v + j(u), where a and b are nonzero constants and y'(v) ¹ 0 and j'(u) ¹ 0.
REMARK. We may check that the isometric transformation (6.5) preserves the concept of the ruled surfaces and the conformality of the normal Gauss map of the time-like surfaces in  .
.
We may prove that the normal Gauss map of the time-like surfaces (2) and (3) in Theorem 6.2 are also conformal. In addition, for the time-like ruled surface x(u,v) = a(v) + ub(v) in  , we may also assume the remained four cases:
, we may also assume the remained four cases:
(i) áb, bñ = -1, áb¢, b¢ñ = 1, and áa¢, b¢ñ = 0,
(ii) b is constant null vector,
(iii) b is constant and áb, bñ = -1, áa¢, bñ = 0,
(iv) áb, bñ = 0, áb¢, b¢ñ = 1, and áa¢, b¢ñ = 0, where á·,·ñ is the scalar product in L3. Hence, we have
THEOREM 7.4. Up to an isometric transformation (6.5) in
, every time-like ruled surface in with conformal normal Gauss map is locally a part of one of the following,(1) ordinary Euclidean time-like planes in
,(2) ordinary Euclidean generalized cylinder x(u,v) = a(v) + ub, where b = (0,0,1) and a(v) is arbitrary curve in L3 with áa¢,a¢ñ > 0 and áa¢,bñ = 0,
(3) (u cosh v, c · sinh v, u sinh v), for a constant c ¹ 0,
(4) (c2 sinh v + u cosh v, c1 sinh v, c2 cosh v + u sinh v), for constants c1¹ 0 and c2¹ 0,
(5) (u sinh v, c · cosh v, u cosh v), for a constant c ¹ 0,
(6) (c2 cosh v + u sinh v, c1 cosh v, c2 sinh v + u cosh v), for constants c1¹ 0 and c2¹ 0,
(7) Flaherty's time-like surfaces in  (Milnor 1987), x(u,v) = a(v) + ub, where b = (1,0,1) and a(v) is arbitrary curve in L3with áa¢, bñ ¹ 0.
(Milnor 1987), x(u,v) = a(v) + ub, where b = (1,0,1) and a(v) is arbitrary curve in L3with áa¢, bñ ¹ 0.
We should note that in the proof of Theorem 7.4, only for case (i) and (ii), we may get the surfaces (5), (6), (7) in Theorem 7.4. For case (iv), we may assume b(v) = (r(v) cos q(v), r(v) sin q(v), r(v)) with r2(q¢)2 = 1. Next, we get a contradictory system of equations.
Locally, the ruled surfaces (5) and (6) in Theorem 7.4 can be represented as the graph (u,v,f(u,v)) as follows,
COROLLARY. f(u,v) =
is a solution of equation (6.2), where c1¹ 0 and c2 are constants. REMARK. The totally umbilical time-like surfaces in  given by (x1 - a)2 + (x2 - b)2 - (x3 - c)2 = R2, where constants c ¹ 0 and R > 0, are Euclidean ruled surfaces but K ¹ 1 +
given by (x1 - a)2 + (x2 - b)2 - (x3 - c)2 = R2, where constants c ¹ 0 and R > 0, are Euclidean ruled surfaces but K ¹ 1 + 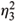 . Their normal Gauss maps are also conformal.
. Their normal Gauss maps are also conformal.
REMARK. Up to a isometric transformation (6.5) in  (q = ±
(q = ± ), the time-like surfaces (3) and (4) in Theorem 7.4 are, respectively, the polar varieties of the time-like surfaces (5) and (6) in Theorem 7.4 and vice versa. The similar result also holds for the time-like surfaces in Theorem 7.3. Generally, if f(u,v) is a solution of (6.2) with
), the time-like surfaces (3) and (4) in Theorem 7.4 are, respectively, the polar varieties of the time-like surfaces (5) and (6) in Theorem 7.4 and vice versa. The similar result also holds for the time-like surfaces in Theorem 7.3. Generally, if f(u,v) is a solution of (6.2) with  > 1, then the local graph of the time-like surface (ffu -u,ffv -v,f
> 1, then the local graph of the time-like surface (ffu -u,ffv -v,f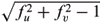 ) (or (u - ffu, v -ffv, f
) (or (u - ffu, v -ffv, f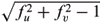 )) in
)) in  also satisfies (6.2).
also satisfies (6.2).
REMARK. When we do not assume that f > 0, (6.3) and
f(u, v) = ±  and f(u, v) = ±u + y(v) and f(u, v) = ±v + j(u)
and f(u, v) = ±u + y(v) and f(u, v) = ±v + j(u)
with y¢(v) ¹ 0 and j¢(u) ¹ 0 are all nontrivial entire solutions of the equation (6.2) defined on R2. In addition, the cone f(u,v) =  is also the special solution of the equation (6.2), but its graph is the light-like surface. By Omori-Yau's Maximum Principle (Omori 1967, Yau 1975), there exist no entire solution f(u,v) of (6.2) satisfying
is also the special solution of the equation (6.2), but its graph is the light-like surface. By Omori-Yau's Maximum Principle (Omori 1967, Yau 1975), there exist no entire solution f(u,v) of (6.2) satisfying  > 1 and f > 0 on R2. Does there exist nontrivial entire solutions of equation (6.2) defined on R2 satisfying
> 1 and f > 0 on R2. Does there exist nontrivial entire solutions of equation (6.2) defined on R2 satisfying  < 1 and f > 0?
< 1 and f > 0?
ACKNOWLEDGMENTS
The author would like to express his sincere gratitude to Professor Detang Zhou for his enthusiastic concern, encouragement, support and valuable help, as well as for his significant suggestions and heuristic discussions with the author, and for his providing the author with Omori and Yau's papers (Omori 1967, Yau 1975). The author would like to express his sincere gratitude to the referees for their interest, careful examination and valuable suggestions.
This work is supported by the starting foundation of science research of Shandong University.
Manuscript received on April 4, 2007; accepted for publication on October 1, 2007; presented by MANFREDO DO CARMO
AMS Classification: 53C42, 53A10.
E-mail: shishuguo@hotmail.com
- AIYAMA R AND AKUTAGAWA K. 2000. Kenmotsu type representation formula for space-like surfaces in the de Sitter 3-space. Tsukuba J Math 24: 189196.
- ALÍAS LJ AND PALMER B. 2001. A duality result between the minimal surface equation and the maximal surface quation. An Acad Bras Cienc 73: 161164.
- BRYANT RL. 1987. Surfaces of mean curvature one in hyperbolic space. Astérisque 154155: 321347.
- EPSTEIN CL. 1986. The hyperbolic Gauss map and quasiconformal reflections. J Reine Angew Math 372: 96135.
- GÁLVEZ JA AND MARTÍNEZ A. 2000. The Gauss map and second fundamental form of surfaces in R3 Geom Dedicata 81: 181192.
- GÁLVEZ JA, MARTÍNEZ A AND MILÁN F. 2000. Flat surfaces in the hyperbolic 3-space. Math Ann 316: 419435.
- KLOTZ T. 1963. Some uses of the second conformal structure on strictly convex surfaces. Proc Amer Math Soc 14: 793799.
- KOKUBU M. 1997. Weierstrass representation for minimal surfaces in hyperbolic space. Tôhoku Math J 49: 367377.
- KOKUBU M. 2005. Surfaces and fronts with harmonic-mean curvature one in hyperbolic three-space. arXiv: math. DG/0504124.
- LAWSON JR HB. 1970. Complete minimal surfaces in S3 Ann Math 92: 335374.
- LEE S. 2005. Spacelike CMC 1 surfaces in de Sitter 3-space S31(1): their construction and some examples. Differential Geometry-Dynamical Systems 7: 4973.
- MILNOR TK. 1987. A conformal analog of Bernsteins Theorem for timelike surfaces in Minkowski 3-space. Contemp Math 64: 123132.
- OBATA M. 1968. The Gauss map of immersions of Riemannian manifolds in spaces of constant curvature. J Differential Geom 2: 217223.
- OMORI H. 1967. Isometric immersions of Riemannian manifolds. J Math Soc Japan 19: 205214.
- OSSERMAN R. 1980. Minimal surfaces, Gauss maps, total curvature, eigenvalue estimates, and stability. The Chern Symposium 1979. Springer, Berlin Heidelberg, New York, p. 199227.
- SHI SG. 2004. Weierstrass representation for surfaces with prescribed normal Gauss map and Gauss curvature in H3 Chin Ann Math B 25: 567586.
- SHI SG. 2006. New examples of surfaces in H3 with conformal normal Gauss map. An Acad Bras Cienc 78: 716.
- YAU ST. 1975. Harmonic functions on complete Riemannian manifolds. Comm Pure Appl Math 28: 201228.
Publication Dates
-
Publication in this collection
10 Mar 2008 -
Date of issue
Mar 2008
History
-
Accepted
01 Oct 2007 -
Received
04 Apr 2007