Resumos
A luz se propaga uniformemente a partir de um ponto luminoso na mesma velocidade em todas as direções. Sua posição em cada determinado momento é uma esfera formada juntando-se todos os pontos em uma mesma fase e tendo como centro a sua própria fonte. Tais superfícies esféricas imaginárias chamam-se frentes de luz ou frentes de ondas. Há três fatores limitadores de detalhes mais finos para o olho humano: óptico (por causa da dispersão, difração, aberração cromática e aberração monocromática), retínico e neural (limitação máxima de acuidade visual de aproximadamente 2,0 ou 20/10).Um sistema de equações matemáticas, polinômios de Zernike, pode definir superfícies geométricas para descrever aberrações ópticas monocromáticas, tanto as de baixa ordem ('prisma', 'esfera' e 'astigmatismo'), quanto às de alta ordem ('coma', 'aberração esférica' e outros). Medida das aberrações ópticas nos dá informação sobre o desempenho total de todos os elementos ópticos do olho em conjunto. Dois sistemas descritos aqui, o aberrômetro baseado no princípio de Tscherning e o originado do sensor Hartmann-Shack, têm a mesma lógica: comparar a posição atual das frentes de onda com a ideal, calcular matematicamente qual é a superfície geométrica que descreve essa discrepância e representá-la em termos de polinômios de Zernike. A topografia corneana computadorizada também pode, com "software" adequado, descrever as frentes de ondas definidas por irregularidades corneanas com polinômios de Zernike, porém tal caracterização representa somente a superfície anterior da córnea. Em conclusão, a tecnologia de frentes de ondas oferece nova maneira de quantificar e classificar os erros de imagem óptica do olho humano. O próximo artigo abordará as peculiaridades da análise de frentes de ondas, bem como algumas aplicações clínicas e cirúrgicas no dia-a-dia da prática oftalmológica.
Luz; Córnea; Topografia da córnea; Erros de refração; Acuidade visual; Refração ocular
Light spreads out uniformly at the same speed in all directions. Its position at any given moment is a sphere that connects all the corresponding phase points, having the source at its center. Such imaginary spherical surfaces are called light fronts or wavefronts. There are three principal factors that limit the finest details an eye can see: optical (due to scattering, diffraction, chromatic and monochromatic aberration), retinal and neural factors (limiting visual acuity to an approximate maximum of 20/10 or 2.0). A mathematical system, the Zernike polynomials, can define geometrical surfaces in order to describe the monochromatic aberrations, both for the lower order aberrations ('prism', 'sphere' and 'astigmatism') and the higher order ones ('coma', 'spherical aberration' and others). The wavefront measures the performance of the whole optical system of the eye. Both systems described herein, the aberrometer based on the Tscherning principle and the one originated from the Hartmann-Shack sensor, start from the same logic: to compare the actual position of the wavefronts with the ideal one, calculate mathematically the geometrical surface that describes that discrepancy and represent it in the terms of the Zernike polynomials. Corneal topography measurement, with adequate software, can also express the wavefront, caused by the corneal irregularities, with the Zernike polynomials, but it still represents the anterior corneal surface only. Wavefront technology offers a new way to quantify and classify optical imaging errors of the human eye. The next article will deal with the peculiarities of the wavefront analysis, as well as with some of the clinical and surgical applications to the day-to-day ophthalmic practice.
Light; Cornea; Corneal topography; Refractive errors; Visual acuity; Ocular refraction
ATUALIZAÇÃO CONTINUADA
Frentes de ondas (wavefronts) e limites da visão humana
Parte 1 - Fundamentos
Wavefronts and the limits of human vision
Part 1 - Fundamentals
Mirko Jankov1 1 Augenklinik, UniversitätsSpital Zürich, Suiça e Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 2 Augenklinik, UniversitätsSpital Zürich, Suíça e ETH (Instituto de Física Aplicada), Zürich, Suiça. 3 Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 4 Augenklinik, UniversitätsSpital Zürich, Suiça.
Michael Mrochen2 1 Augenklinik, UniversitätsSpital Zürich, Suiça e Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 2 Augenklinik, UniversitätsSpital Zürich, Suíça e ETH (Instituto de Física Aplicada), Zürich, Suiça. 3 Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 4 Augenklinik, UniversitätsSpital Zürich, Suiça.
Paulo Schor3 1 Augenklinik, UniversitätsSpital Zürich, Suiça e Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 2 Augenklinik, UniversitätsSpital Zürich, Suíça e ETH (Instituto de Física Aplicada), Zürich, Suiça. 3 Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 4 Augenklinik, UniversitätsSpital Zürich, Suiça.
Wallace Chamon3 1 Augenklinik, UniversitätsSpital Zürich, Suiça e Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 2 Augenklinik, UniversitätsSpital Zürich, Suíça e ETH (Instituto de Física Aplicada), Zürich, Suiça. 3 Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 4 Augenklinik, UniversitätsSpital Zürich, Suiça.
Theo Seiler4 1 Augenklinik, UniversitätsSpital Zürich, Suiça e Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 2 Augenklinik, UniversitätsSpital Zürich, Suíça e ETH (Instituto de Física Aplicada), Zürich, Suiça. 3 Setor de Bioengenharia, Departamento de Oftalmologia, Universidade Federal de São Paulo - UNIFESP, Brasil. 4 Augenklinik, UniversitätsSpital Zürich, Suiça.
RESUMO
A luz se propaga uniformemente a partir de um ponto luminoso na mesma velocidade em todas as direções. Sua posição em cada determinado momento é uma esfera formada juntando-se todos os pontos em uma mesma fase e tendo como centro a sua própria fonte. Tais superfícies esféricas imaginárias chamam-se frentes de luz ou frentes de ondas. Há três fatores limitadores de detalhes mais finos para o olho humano: óptico (por causa da dispersão, difração, aberração cromática e aberração monocromática), retínico e neural (limitação máxima de acuidade visual de aproximadamente 2,0 ou 20/10).Um sistema de equações matemáticas, polinômios de Zernike, pode definir superfícies geométricas para descrever aberrações ópticas monocromáticas, tanto as de baixa ordem ('prisma', 'esfera' e 'astigmatismo'), quanto às de alta ordem ('coma', 'aberração esférica' e outros). Medida das aberrações ópticas nos dá informação sobre o desempenho total de todos os elementos ópticos do olho em conjunto. Dois sistemas descritos aqui, o aberrômetro baseado no princípio de Tscherning e o originado do sensor Hartmann-Shack, têm a mesma lógica: comparar a posição atual das frentes de onda com a ideal, calcular matematicamente qual é a superfície geométrica que descreve essa discrepância e representá-la em termos de polinômios de Zernike. A topografia corneana computadorizada também pode, com "software" adequado, descrever as frentes de ondas definidas por irregularidades corneanas com polinômios de Zernike, porém tal caracterização representa somente a superfície anterior da córnea. Em conclusão, a tecnologia de frentes de ondas oferece nova maneira de quantificar e classificar os erros de imagem óptica do olho humano. O próximo artigo abordará as peculiaridades da análise de frentes de ondas, bem como algumas aplicações clínicas e cirúrgicas no dia-a-dia da prática oftalmológica.
Descritores: Luz; Córnea; Topografia da córnea; Erros de refração; Acuidade visual; Refração ocular/fisiologia
O QUE SÃO FRENTES DE ONDAS?
Luz é uma forma de energia radiante, similar às ondas de rádio, calor, raios ultra-violetas e raios X, e é transmitida através do meio óptico a partir das fontes luminosas. Num meio óptico homogêneo, a luz se propaga uniformemente a partir de um ponto luminoso e na mesma velocidade em todas as direções, assemelhando-se às ondas na superfície da água originadas a partir de uma pedra nela lançada. Sua posição em cada determinado momento é uma esfera formada juntando-se todos os pontos em uma mesma fase e tendo como centro a sua própria fonte. Tais superfícies esféricas imaginárias chamam-se frentes de luz ou frentes de ondas. Portanto, nas frentes de ondas, todos os feixes de luz possuem a mesma fase e o mesmo comprimento de caminho óptico (o comprimento de caminho óptico refere-se ao produto entre o comprimento do caminho geométrico e o índice refracional do meio óptico).
QUAIS SÃO OS LIMITES DE VISÃO HUMANA?
Há três fatores limitadores de detalhes mais finos para o olho humano: óptico, retínico e neural(1). Os fatores retínico e neural não serão discutidos aqui devido à complexidade do assunto, valendo lembrar que a limitação máxima de acuidade visual imposta por esses dois fatores é de aproximadamente meio minuto de arco, ou aproximadamente 2,0 (20/10) pela tabela de Snellen tradicional.
Em relação ao limite óptico há quatro fontes de embaçamento de imagem: dispersão, difração, aberração cromática e aberração monocromática. Dispersão será desprezada nesta ocasião tendo-se em vista que ela é pouco relevante em olhos sãos de indivíduos jovens. A difração depende do diâmetro da pupila e deve ser considerada quando temos pupilas menores que 1 mm, praticamente impossível na prática clínica. Portanto, as principais causas de embaçamento visual em pupilas naturais dos olhos sadios e jovens são as aberrações cromáticas e monocromáticas.
A luz de cada comprimento de onda (determinando cores diferentes) possui índice refracional levemente distinto e por isso uma cor é refratada diferentemente quando comparada com outra; esse fenômeno chama-se aberração cromática. A luz com comprimento de onda mais curto (por exemplo, verde) terá seu foco mais perto de córnea e cristalino comparada com a luz com comprimento de onda mais longo (por exemplo, vermelho), mas somente uma imagem poderá ser focalizada nitidamente na retina num determinado momento. A diferença cromática total no espectro visual inteiro é de quase 2 dioptrias, e sendo assim, tem efeitos importantes na degradação da qualidade de imagem retínica e conseqüentemente na acuidade visual. Por tal motivo os óculos amarelos melhoram o contraste da imagem pois eliminam o azul, o qual tem relação muito distante das outras cores e apresenta-se abundantemente na natureza (céu, água etc.). Dessa forma, a eliminação da cor azul do espectro permite a localização mais próxima do espectro restante (verde-vermelho), aprimorando os focos e diminuindo o círculo de menor confusão.
Imagine-se um grupo de raios de luz paralelos incidindo numa lente ideal, em que todos os pontos na mesma fase são perpendiculares à propagação dos raios e formam um plano perfeito de frente de ondas. Essa lente ideal transformará a frente de ondas plana em frente esférica; conseqüentemente, todas as frentes de ondas serão esferas concêntricas cujo centro estará no ponto focal da lente. As lentes reais (não-ideais) modificarão essas frentes de ondas ideais de maneira que raios paracentrais sejam alterados do modo diferente em comparação com os periféricos, causando a não coincidência num ponto focal único. Esse fenômeno denomina-se aberração monocromática.
A natureza permite ao olho humano compensar parcialmente tais aberrações dando à córnea uma forma menos curva na periferia do que no centro. Desta maneira, a forma asférica da córnea, em conjunto com a asfericidade do próprio cristalino, contribui à atenuação das aberrações ópticas.
COEFICIENTES DE ZERNIKE
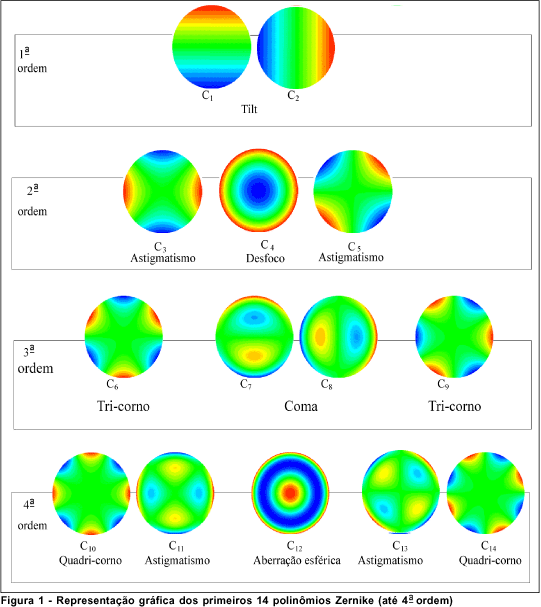
Frits Zernike (1888-1966), matemático holandês e ganhador do Prêmio Nobel em 1953, desenvolveu um sistema de equações matemáticas que definem superfícies geométricas para descrever aberrações ópticas ¾ polinômios de Zernike, em que cada polinômio representa uma determinada forma geométrica. Esses polinômios, bastante complexos, hoje em dia já bem estabelecidos na óptica técnica e fisiológica, são um modo eficiente de representar as alterações de forma, ou aberrações de frentes de ondas no olho humano também. Cada polinômio representando uma aberração isolada típica, permite definir Desfoco (C4) ou 'esfera' e Astigmatismo (C3 e C5) ou 'cilindro', bem como outras aberrações de ordem mais alta (Figura 1).
As aberrações ópticas tornam-se mais complexas com o aumento de ordem (nível) do polinômio e são dependentes do diâmetro da pupila.Para descrever uma forma simples de Aberração Esférica (C12), é preciso um complexo polinômio de 4a ordem (função dependente da quarta potência do raio da pupila - r4). Tendo-se em vista a correlação forte entre as aberrações ópticas e tamanho da pupila, as medidas de aberrações têm sentido somente nas pupilas maiores que 5 mm, pois nas pupilas pequenas os raios centrais são pouco afetados.
Qual é o significado prático de polinômios de Zernike? Para explicar isso usaremos um exemplo de uma outra área da física. Lembremos dos tempos dos primeiros sintetizadores de som (órgãos), com teclados capazes de 'imitar' vários instrumentos musicais. Eles produziam eletronicamente os sons 'puros' com freqüência de base e acrescentavam alguns harmônicos com outras freqüências para maquiá-los e construir o 'timbre' que os faziam soar mais 'naturais'. Mesmo quando no teclado escolhíamos piano ou violino, por exemplo, era bastante óbvio o quanto o som ainda era artificial, porém havia alguma semelhança grosseira com os sons dos instrumentos verdadeiros. As gerações mais novas dos órgãos já produziam sons bem mais 'naturais' enriquecendo-os com vários harmônicos de intensidades e entonações diferentes. Se isso já era suficiente, hoje em dia a tecnologia de som artificial facilmente 'engana' o ouvido humano que não consegue distinguir sons produzidos por sintetizadores de sons no órgão ou no reprodutor de CD, do som 'real'. Isso significa que qualquer som natural pode ser decomposto em componentes de som (som de base e seus harmônicos) e também pode, dependendo do seu número e precisão, representar matematicamente o som natural por si.
Voltando para a aberração do olho humano, uma representação matemática semelhante pode ser feita usando-se polinômios de Zernike; as aberrações podem ser representadas pelas suas subcomponentes (aberrações de diferentes ordens de Zernike, correspondendo aos diversos harmônicos no exemplo anterior) e sua fidelidade depende unicamente do número e precisão de seus componentes. A aberração total (correspondendo ao som 'real') é representada pela soma de todos os seus componentes.
Na Figura 1 encontram-se as simulações computadorizadas das aberrações de até 4a ordem de Zernike. Dentre as aberrações de baixa ordem de Zernike (até 2a ordem) as mais bem conhecidas e amplamente utilizadas para prescrição de lentes corretivas são C4 (Desfoco) e combinação de C3 e C5 (Astigmatismo) em forma de Esfera / Cilindro x Eixo para o diâmetro de pupila R, conforme as fórmulas em seguida:
Caso C5³ 0, o Eixo precisa ser alterado em Eixo = 90 ¾ Eixo. Esses três coeficientes da 2a ordem representam a quase a totalidade de aberrações num olho com erro refracional existente(2), e essa é a razão pela qual a correção com as lentes clássicas esfero-cilíndricas é tão efetiva, mesmo não sendo perfeita.
As aberrações de alta ordem representam aproximadamente 20% das aberrações num olho com baixo erro refracional e são significativamente maiores após os tratamentos cirúrgicos refracionais tradicionais(3). Coma de 3a ordem, ou aberração em forma de cometa, e Aberração Esférica de 4a ordem, na qual os raios periféricos são refratados mais que os para-centrais, são as aberrações de alta ordem mais freqüentes.
MEDIDA DAS ABERRAÇÕES ÓPTICAS
As aberrações ópticas de alta ordem foram consideradas parte das propriedades ópticas do olho humano ainda no século XIX, e a partir de então o olho foi considerado um sistema óptico de razoável qualidade.Tscherning estabeleceu no final de século XIX um método para se medir aberrações do olho humano e construiu um aberrômetro simples para tal finalidade(4). Somente na segunda parte do século XX o mesmo tópico foi novamente abordado e resolvido por um outro método envolvendo o cilindro cruzado, por Howland, Howland(5). No início dos anos 90 Liang et al.(6) otimizaram para análise de frentes de ondas do olho humano um outro tipo de sensor, denominado Hartmann-Shack, usado em astronomia até então, enquanto na mesma época Mierdel et al.(7) atualizaram e modernizaram o aberrômetro original de Tscherning.
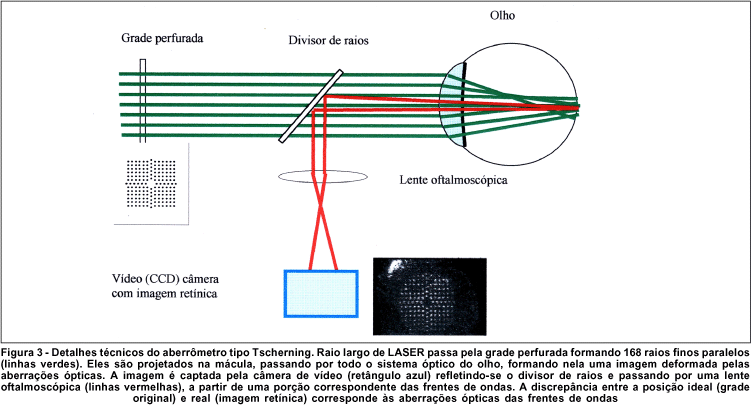
Os dois sistemas são chamados "double pass", o que significa que a luz passa duas vezes pelo aparelho óptico do olho entre a fonte de luz e câmara-sensor. A diferença entre ambos repousa na forma pela qual a luz entra no olho e o deixa (Figuras 2 e 3). No princípio usado por Tscherning, a luz de LASER é projetada na córnea através de uma grade regular e simétrica (diâmetro de 10 mm na córnea). Uma imagem de tamanho de 1 mm real e invertida é formada na mácula e captada por uma vídeo-câmera através do centro da pupila, para ser então analisada pelo programa específico no microcomputador. Entretanto, no aberrômetro Hartmann-Shack, um raio fino de 0,1 mm é projetado na fovéola e a imagem refletida pelas estruturas profundas da retina ou da própria coróide é capturada através de todo o diâmetro da pupila por micro-lentes dispostas uniformemente em uma grade externa. Tal arranjo compõe uma imagem real e direta e é analisado pelo programa específico no microcomputador. A lógica dos dois sistemas é a mesma: comparar a posição atual dos pontos com a ideal, calcular matematicamente qual é a superfície geométrica que descreve essa discrepância e representá-la em termos de polinômios de Zernike. A lista dos aberrômetros comercialmente disponíveis no mercado encontra-se na Tabela 1.
A topografia corneana computadorizada também pode, com "software" adequado, descrever as frentes de ondas definidas por irregularidades fisiológicas e não-fisiológicas, porém tal caracterização representa somente a superfície anterior da córnea. O aberrômetro, por sua vez, nos dá informação sobre o desempenho total de todos os elementos ópticos do olho em conjunto: córnea, câmara anterior, cristalino e corpo vítreo (Figura 4).
Em conclusão, a tecnologia de frentes de ondas oferece uma nova maneira de quantificar e classificar os erros de imagem óptica do olho humano. Muitos ensaios clínicos com esta técnica estão sendo efetuados em vários centros de pesquisa nacionais e internacionais e em breve nos darão a relevância clínica e terapêutica de modificação cirúrgica de erros de frentes de ondas. O próximo artigo abordará esses aspectos, ressaltando as peculiaridades da análise de frentes de ondas bem como algumas aplicações clínicas e cirúrgicas no dia-a-dia da prática oftalmológica.
ABSTRACT
Light spreads out uniformly at the same speed in all directions. Its position at any given moment is a sphere that connects all the corresponding phase points, having the source at its center. Such imaginary spherical surfaces are called light fronts or wavefronts. There are three principal factors that limit the finest details an eye can see: optical (due to scattering, diffraction, chromatic and monochromatic aberration), retinal and neural factors (limiting visual acuity to an approximate maximum of 20/10 or 2.0). A mathematical system, the Zernike polynomials, can define geometrical surfaces in order to describe the monochromatic aberrations, both for the lower order aberrations ('prism', 'sphere' and 'astigmatism') and the higher order ones ('coma', 'spherical aberration' and others). The wavefront measures the performance of the whole optical system of the eye. Both systems described herein, the aberrometer based on the Tscherning principle and the one originated from the Hartmann-Shack sensor, start from the same logic: to compare the actual position of the wavefronts with the ideal one, calculate mathematically the geometrical surface that describes that discrepancy and represent it in the terms of the Zernike polynomials. Corneal topography measurement, with adequate software, can also express the wavefront, caused by the corneal irregularities, with the Zernike polynomials, but it still represents the anterior corneal surface only. Wavefront technology offers a new way to quantify and classify optical imaging errors of the human eye. The next article will deal with the peculiarities of the wavefront analysis, as well as with some of the clinical and surgical applications to the day-to-day ophthalmic practice.
Keywords: Light; Cornea; Corneal topography; Refractive errors; Visual acuity; Ocular refraction/physiology
Endereço para correspondência: R. Mal. José B. Bormann 586 ¾ Curitiba (PR) CEP 80730-350.
Email: mirkojankov@hotmail.com
- 1. Applegate RA. Limits to vision: can we do better than nature? J Refract Surg 2000;16:S547-51.
- 2. Hong X, Thibos L, Bradley A, Miller D, Cheng X, Himebaugh N. Statistics of aberrations among healthy young eyes. OSA TOPS 2001;54:90-3.
- 3. Mrochen M, Kaemmerer M, Mierdel P, Seiler T. Increased higher-order optical aberrations after laser refractive surgery: a problem of subclinical decentration. J Cataract Refract Surg 2001;27:362-9.
- 4.Tscherning M. Die monocrhomatischen aberrationene des menschlichen Auges Z Psychol Sinne 1894;6:456-71.
- 5. Howland HC, Howland B. A subjective method for the measurement of monochromatic aberrations of the human eye. J Opt Soc Am 1977;67:1508-18.
- 6. Liang J, Grimm B. Goelz S, Bille JF. Objective measurement of wave aberrations of the human eye with the use of a Hartmann-Shack wave-front sensor. J Opt Soc Am A 1994;11:1949-57.
- 7. Mierdel P, Kaemmerer M. Mrochen M, Krinke HE, Seiler T. Automated ocular wavefront analyzer for clinical use. In: 10º Conference on Ophthalmic Technologies; 2002 June 29-July 4; San Jose, EUA. Proceedings. San Jose: SPIE; 2000. p.86-92.
Datas de Publicação
-
Publicação nesta coleção
04 Fev 2003 -
Data do Fascículo
Dez 2002