Abstracts
This paper estimates the Brazilian NAIRU (Nonaccelerating Inflation Rate of Unemployment) and investigates several empirical questions: the stability of coefficients of the Brazilian price Phillips curve, the behavior of the NAIRU along time, and error bands for the NAIRU. This article innovates, with respect to previous research work done for Brazil, because it estimates error bands for the NAIRU and adopts econometric models that, in our judgment, deal more adequately with the still recent instability of the Brazilian economy. We estimate two different state-space models: one with a time-varying NAIRU and another in which the NAIRU is changing over time according to a hidden Markov chain specification. The study presents some new evidence on several questions. It shows that while the slope of the Brazilian price Phillips curve is stable the NAIRU has not been stable. It concludes that there is a statistically significant relationship, with correct sign, between deviations of unemployment from the NAIRU and inflation. It also shows that, after the second semester of 1995, there is no significant evidence that the NAIRU has been different from the observed unemployment rate.
time-varying NAIRU; Markov switching; Phillips curve; Kim filter; unobserved-components model
Neste artigo estima-se a NAIRU (a taxa de desemprego que mantém estável a taxa de inflação) do Brasil e investiga-se diversas questões empíricas: a estabilidade dos coeficientes da Curva de Phillips (para preços) brasileira , o comportamento da NAIRU ao longo do tempo, e os intervalos de confiança para a NAIRU. O presente trabalho inova, em relação aos anteriores, ao adotar modelos econométricos que, acredita-se, são mais adequados para lidar com as instabilidades defrontadas pela economia brasileira em período recente. Estimam-se dois modelos diferentes em espaço-de-estados: um com uma NAIRU que muda ao longo do tempo e outro no qual a NAIRU muda, ao longo do tempo, de acordo com a especificação de uma cadeia de Markov oculta. Obtém-se novas evidências sobre diversas questões empíricas. Mostra-se que a inclinação da Curva de Phillips do Brasil é estável mas que a NAIRU brasileira vem se alterando ao longo do tempo. Conclui-se que existe uma relação estatisticamente significante, e com o sinal correto, entre os desvios da taxa de desemprego em relação à NAIRU e a taxa de inflação. No entanto, devido à imprecisão das suas estimativas, não há evidência significativa de que a NAIRU, depois do segundo trimestre de 1995, tenha sido diferente da taxa de desemprego observada.
The NAIRU, unemployment and the rate of inflation in Brazil* * The author thanks Christopher C. Sims, whose lectures at Yale have inspired this paper, Eustáquio J. Reis, Paulo M. Levy and three anonymous referees for their comments on an initial version of this article, and the CNPq for the financial support given to this research during the postdoctoral program at Yale University , in the United States.
Elcyon Caiado Rocha Lima
Directorate of Macroeconomic Studies - IPEA and UERJ. E-mail: elcyon@ipea.gov.br
ABSTRACT
Summary: 1. Introduction; 2. The NAIRU and the natural rate of unemployment; 3. The data and the estimated models; 4. The estimation procedures; 5. The model's estimation results; 6. The estimated NAIRU and the response of Dp to cyclical unemployment; 7. Conclusions.
This paper estimates the Brazilian NAIRU (Nonaccelerating Inflation Rate of Unemployment) and investigates several empirical questions: the stability of coefficients of the Brazilian price Phillips curve, the behavior of the NAIRU along time, and error bands for the NAIRU. This article innovates, with respect to previous research work done for Brazil, because it estimates error bands for the NAIRU and adopts econometric models that, in our judgment, deal more adequately with the still recent instability of the Brazilian economy. We estimate two different state-space models: one with a time-varying NAIRU and another in which the NAIRU is changing over time according to a hidden Markov chain specification.
The study presents some new evidence on several questions. It shows that while the slope of the Brazilian price Phillips curve is stable the NAIRU has not been stable. It concludes that there is a statistically significant relationship, with correct sign, between deviations of unemployment from the NAIRU and inflation. It also shows that, after the second semester of 1995, there is no significant evidence that the NAIRU has been different from the observed unemployment rate.
Keywords: time-varying NAIRU, Markov switching, Phillips curve, Kim filter, unobserved-components model.
JEL codes: C22; E32.
RESUMO
Neste artigo estima-se a NAIRU (a taxa de desemprego que mantém estável a taxa de inflação) do Brasil e investiga-se diversas questões empíricas: a estabilidade dos coeficientes da Curva de Phillips (para preços) brasileira , o comportamento da NAIRU ao longo do tempo, e os intervalos de confiança para a NAIRU.
O presente trabalho inova, em relação aos anteriores, ao adotar modelos econométricos que, acredita-se, são mais adequados para lidar com as instabilidades defrontadas pela economia brasileira em período recente. Estimam-se dois modelos diferentes em espaço-de-estados: um com uma NAIRU que muda ao longo do tempo e outro no qual a NAIRU muda, ao longo do tempo, de acordo com a especificação de uma cadeia de Markov oculta.
Obtém-se novas evidências sobre diversas questões empíricas. Mostra-se que a inclinação da Curva de Phillips do Brasil é estável mas que a NAIRU brasileira vem se alterando ao longo do tempo. Conclui-se que existe uma relação estatisticamente significante, e com o sinal correto, entre os desvios da taxa de desemprego em relação à NAIRU e a taxa de inflação. No entanto, devido à imprecisão das suas estimativas, não há evidência significativa de que a NAIRU, depois do segundo trimestre de 1995, tenha sido diferente da taxa de desemprego observada.
1 Introduction
In this article we estimate the Brazilian Phillips curve aiming to obtain the Nonaccelerating Inflation Rate of Unemployment (NAIRU) for Brazil. We investigate the stability of coefficients of the Brazilian Phillips curve and the relationship between the rate of inflation and the deviation of the observed rate of unemployment from the NAIRU. We also estimate error bands for the NAIRU in order to determine whether there is any significant difference between the NAIRU and the observed unemployment rate.
Estimating the relationship between nominal and real variables in Brazil is a very hard task due to the instability experienced by the Brazilian economy in its recent past. The macroeconomic models are estimated using information provided by time series data, and the number of required observations outnumbers what is available for the most recent period of stability after the Real Plan. This is a challenge for anyone who works with Brazilian macroeconomic data. The great instability of the Brazilian economy, especially when the nominal side is modeled, makes it crucial to deal with structural breaks. The strong nominal shocks faced by the economy at different periods and at the beginning of the many stabilization plans point in the direction of using models that allow for large breaks and frequent alternations of the states of the economy.
Portugal et al. (1999) estimate two different models for the Brazilian NAIRU. The first model is a traditional Phillips curve with constant intercept, autoregressive residuals and dummies to allow for structural breaks. The second model is a univariate structural model with trend and cycle, Harvey (1989), in which the NAIRU is defined as the trend component. The definition of the NAIRU, used in the second model, is questionable and in the literature (Staiger et al., 2001, Cogley and Sargent, 2001, Hall, 1999)there is a distinction between the natural rate of unemployment, usually defined as the unemployment trend, and the NAIRU.
In Corseuil et al. (1996) there are no calculations for the NAIRU but there is a careful analysis of the components of unemployment (trend and cycle), for the main metropolitan regions of Brazil. They test the relative importance of aggregate and regional shocks in the determination of unemployment and conclude that there is evidence in favor of a strong influence of aggregate factors.
We believe that the structural breaks in the models for the Brazilian NAIRU cannot be dealt with by models with dummies and autoregressive residuals (Portugal et al., 1999), thresholds [TAR model, (Tong, 1990)] or with time-varying smooth transitions between states [STAR model, TerÄasvirta (1994) or TV-STAR model, Lundbergh et al. (2002)]. Fortunately, since the beginning of the '90s there has been a variety of theoretical developments in time series analysis that enable us to extract information from data even when instabilities, like the ones observed for Brazilian data, are present [Hamilton (1989); Kim (1994); Kim and Nelson (1999); Sims (1999); Sims and Zha (2002)]. These developments allow us to deal with a larger set of data.
Our research innovates, when compared to other research work done for Brazil, because it adopts some of these developments which, in our view, deal more adequately with abrupt structural breaks in the model's equation and frequent alternations of the states of the economy. We estimate two different models to calculate the natural rate of unemployment and its confidence interval: one model with a time-varying NAIRU and another model in which the NAIRU is changing over time according to a hidden Markov chain specification. The first model allows for the presence of ARCH residuals; the second model allows for persistent heteroscedasticity1 1 Sims (1999), using monthly data on a short term interest rate and a commodity price index for a considerably more stable country like the USA, has found evidence of the presence of persistent heteroscedasticity in the model. Kim and Nelson (1999), using quarterly data for the 1962.I - 1985.IV period, found very strong ARCH effects in estimates of a fixed coefficient version of the U.S. monetary growth function. as well as a richer pattern of time variation for the NAIRU. We could not reject the absence of ARCH residuals in the first model under the maintained hypothesis of a time-varying NAIRU. Under the specification for the second model, we could not reject the presence of both Markov-switching heteroscedasticity and a time-varying NAIRU. A detailed description of both models and of the estimation methods can be found in Kim and Nelson (1999). The models were estimated using quarterly data for the average rate of open unemployment in six Metropolitan Regions and for the rate of inflation measured by the national consumer price index (INPC) in eleven Metropolitan Regions (including the six regions where unemployment is measured), both collected by IBGE for the period 1982:1 - 2001:4.
Following Staiger et al. (2001), the recent theories that have been proposed to explain the relationship between inflation and unemployment can be classified into two groups: theories in which ''the Phillips curve is alive and well but...'' and those that proclaim the ''the Phillips curve is dead''. The theories in the first group ((Staiger et al., 1997, 2001); Gordon (1982, 1997, 1998);King and Watson (1994); Blanchard and Katz (1997)) conclude that the Phillips curve continues to have the same negative slope but it has been shifting. A good survey of these theories can be found in Katz and Krueger (1999). The theories in the second group interpret the recent events as a change in the slope of the Phillips curve (Akerlof et al. (1996, 2000) ; Taylor (2000)). For Brazil, the most recent study (Portugal et al., 1999) can be classified in the first group. This study did not find evidence that the slope of the Brazilian Phillips curve has changed, but it could not reject that the curve has been shifting.
The article is organized as follows: In section 2, we describe the data used, how the monthly data were transformed into quarterly data and the estimated models; in section 3, we present the estimation procedures adopted, and in the appendix, we describe the Kim filter and its use in the estimation of one of the models; in section 4, we show the estimation results and discuss some statistical tests; in section 5, we conclude.
2 The NAIRU and the Natural Rate of Unemployment
For many researchers, the NAIRU is a synonym for the natural rate of unemployment. However, we find it convenient to separate these two concepts, just as do many others (Staiger et al. (2001), Cogley and Sargent (2001), Hall (1999)).
The idea of a natural rate of employment was first proposed in Friedman's (1968) presidential address to the American Economic Association: ''The natural rate of unemployment is the level which would be ground out by the Walrasian system of general equilibrium equations, provided that there is embedded in them the actual structural characteristics of the labor and commodity markets, including market imperfections, stochastic variability in demands and supplies, the cost of gathering information about job vacancies and labor availabilities, the costs of mobility, and so on''. The main point of Friedman's address was to argue that there was no permanent (long-run) tradeoff between inflation and unemployment. His definition does not require the existence of a short-run inflation-unemployment tradeoff. Therefore, there is a natural rate of unemployment, even in the absence of any short-run unemployment-inflation tradeoff. Besides, as pointed out by Rogerson (1997), his definition is not inconsistent with the natural rate of unemployment being equal to the low frequency (trend) movements in unemployment.
The NAIRU concept, on the other hand, needs the view (a view which is very prominent among central bankers and monetary economists) that there is a short-run inflation-unemployment tradeoff. Even though, for many economists, the existence of this short-run tradeoff is purely speculative, its existence is one of the most enduring ideas in macroeconomics: shocks in monetary policy push inflation and unemployment in opposite directions in the short run. If this tradeoff is admitted, there must be some level of unemployment (NAIRU) consistent with constant inflation. Therefore, if a contractionary shock in monetary policy increases unemployment above the NAIRU, the inflation rate will decrease, and if an expansionary monetary shock decreases the unemployment rate below the NAIRU, the inflation rate will increase.
One simple model for the relationship between unemployment (u), inflation change (Dp) and the NAIRU (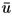 ) is given by Dpt = b(ut
) is given by Dpt = b(ut 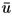 )+Ît = b
)+Ît = b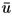 + but + Ît = a + but + Ît, where a = b
+ but + Ît = a + but + Ît, where a = b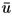 and Ît is the error term. In this model the NAIRU (
and Ît is the error term. In this model the NAIRU (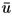 ) is a/b. This relationship for Brazil, from 1982:I-2001:IV, is illustrated by the scatterplot in figure 1. The horizontal axis shows the average rate of open unemployment in quarter t and the vertical axis shows the difference between the monthly inflation rate in quarter t and the monthly inflation rate in quarter t-1. Figure 1 also plots the OLS, ordinary least squares, regression line - the simple model - estimated over the full sample. The regression line shows a negative relationship between unemployment and inflation change, and its intersection with the unemployment axis is the ordinary least squares estimate of the NAIRU.
) is a/b. This relationship for Brazil, from 1982:I-2001:IV, is illustrated by the scatterplot in figure 1. The horizontal axis shows the average rate of open unemployment in quarter t and the vertical axis shows the difference between the monthly inflation rate in quarter t and the monthly inflation rate in quarter t-1. Figure 1 also plots the OLS, ordinary least squares, regression line - the simple model - estimated over the full sample. The regression line shows a negative relationship between unemployment and inflation change, and its intersection with the unemployment axis is the ordinary least squares estimate of the NAIRU.
The problem with this estimate of the NAIRU is that it does not control for other factors that may affect the relationship between inflation and unemployment, such as inflation stabilization plans, seasonal effects and lagged effects of unemployment and inflation. This lack of control for other factors may explain why both coefficient of the regression line are not significantly different from zero.
Figure 2 is identical to figure 1 but shows data from 1995:1-2001:IV, which is the period after the Real Plan with much lower inflation. Figure 2 shows no evident relationship between inflation change and unemployment. One possible explanation is the absence of the short-run tradeoff between inflation and unemployment under low inflation. However, we will show that this relationship can still be recovered from the most recent data if a more complicated model, one with time-varying parameters, is adopted.
It should be emphasized that the models used to estimate the NAIRU need more than the existence of the short-run tradeoff. They need the notion that monetary policy affects the price level by first affecting unemployment, which, then, via a Phillips Curve, affects inflation. In the next section we describe the specification adopted to identify the Brazilian NAIRU.
3 The Data and the Estimated Models
The basic data comprise the national consumer price index (INPC) of IBGE from 1981:12 to 2002:01 and the average rate of open unemployment of IBGE from 1982:1 to 2001:12. These monthly data were averaged into quarterly data resulting in a sample size of 80 observations. The model was estimated using only quarterly data, from the first quarter of 1982 to the last quarter of 2001. The monthly data was transformed into quarterly data as follows:
pt = (1/3).log(Pt, f / Pt1, f) = monthly geometric average of the quarterly rate of inflation;
Pt, f = centered INPC ( national consumer price index) of IBGE for the last month of quarter t;
Ut = quarterly average of the monthly average rate of open unemployment of IBGE.
3.1 The basic model
Our basic model for the relationship between the change of the rate of inflation and the rate of unemployment can be represented by the following equations:2 2 This is the standard specification used for the Phillips curve (Staiger et al. (1997, 2001), Gordon (1997), etc.). Vector and matrixes are bold faces.
and
where
Dit = seasonal dummy of quarter i;
t1 = NAIRU at t 1;Zt = is a row vector of control variables with the two first lags of Dpt;4 4 We use two lags of Dp because the basic model is one of the equations of a three lags VAR on inflation and unemployment in which the sum of coefficients of lagged inflation is equal to 1. Sargent (1971) has pointed out that, under rational expectations, this restriction is only valid if inflation has a unit root. We tested and did not reject that inflation in Brazil is I(1). This restriction is necessary for the existence of the NAIRU and implies the absence of any long-run trade off between inflation and unemployment.
Ît ~ N (0, s2)
Equation (1) can also be represented in the following form:
where x1t = b1t b2t, x2t = b3t, x0t = b1t + b2t + b3t and D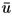 ts =
ts = 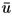 ts
ts 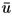 ts1.
ts1.
If the NAIRU slowly changes over time then  xs D
xs D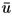 ts@ 05
5
We are using here the same restriction adopted by Staiger et al. (2001). Alternatively, this restriction can be justified, if the initial model is similar to the one in King et al. (1995) and is given by Dp
t = m
t +
b
st (
ut
s
t
1) +
Z
t
gt +
Ît.
Furthermore,
ts@ 05
5
We are using here the same restriction adopted by Staiger et al. (2001). Alternatively, this restriction can be justified, if the initial model is similar to the one in King et al. (1995) and is given by Dp
t = m
t +
b
st (
ut
s
t
1) +
Z
t
gt +
Ît.
Furthermore,  mt+s = 0 implies that a0t = a1t /4 a2t /4 a3t /4. Therefore,
mt+s = 0 implies that a0t = a1t /4 a2t /4 a3t /4. Therefore,
where b0tº x0t
t1º (b1t + b2t + b3t)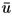 t1.
t1.
If (b1t + b2t + b3t) < 0 and b0t > 0, for all t, then we can obtain 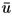 t1 estimating the model and using the last equation:
t1 estimating the model and using the last equation:
The inflation stabilization plans adopted by Brazil (Cruzado (1986:1 and 1986:2), Bresser (1987:3), Verão (1989:1), Collor I (1990:2), Collor II (1991:2) and Real (1994:3)) have produced, in the quarters of their implementation, an abrupt reduction of the rate of inflation. To deal with these shocks, interventions were made in the model at each quarter of implementation of each stabilization plan. The basic model with interventions at each stabilization plan is described by the following equation:
qt t = 0, if there was no stabilization plan at quarter t;
qt t = qt = nonlinear intercept intervention parameters when stabilization plan ''t'' happens at period t[t = 1 (Cruzado and Collor II Plans), t = 2 (Bresser and Verão Plans), t = 3 (Collor I and Real Plans)]
To simplify the description of the model we summarize the representation of the model as follows:
Let
therefore the model can be represented, in a compact form, by
In its recent past, the Brazilian economy has experienced a period of great economic instability and the above equation may show structural breaks in its parameters. To deal with possible structural breaks we estimate two different versions of the above model: the TVP model (which allows for parameter change over time and ARCH residuals); the MSR model (which allows for parameter change over time and Markov-switching regimes).
3.2 The TVP and the MSR models
The TVP Model
The TVP model is a state-space model with ARCH residuals and is a simplified version of the model proposed by Harvey et al. (1992):
where
1 = [yt1 , yt2, ...., y1] , information available up to time t 1; L,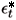 and s are scalars and Q is, by hypothesis, diagonal and 9 x 9.
and s are scalars and Q is, by hypothesis, diagonal and 9 x 9.
The ARCH effect is introduced through the scalar residual 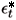 . The variance of
. The variance of 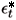 is given by
is given by
The MSR Model
The MSR model is a state-space model with a Markov-switching regime. It is a simplified version of the model suggested by Kim and Nelson (1999):
The subscript St denotes that s2 and the parameters at the diagonal of matrix Q take values that depend on a discrete, nonobserved variable, that follows a Markov-switching process with 2 different states (regimes). The transition probabilities are given by
where, piJ = probability of state J, at period t, given state i at period t 1 and
4 The Estimation Procedures
4.1 The TVP model estimation procedure
Harvey et al. (1992) substitute the  variable in equation (10) , which is nonobserved, by its conditional expectation, h1t = 1 + gE [
variable in equation (10) , which is nonobserved, by its conditional expectation, h1t = 1 + gE [ /
/ 1]. Therefore, the algorithm is an approximation. To get E[
1]. Therefore, the algorithm is an approximation. To get E[ /
/ 1] , Harvey, Ruiz and Sentana augmented the original state vector in the transition equation (9) in the following way:
1] , Harvey, Ruiz and Sentana augmented the original state vector in the transition equation (9) in the following way:
where I9 is the identity matrix with 9x9 dimension. Therefore, the measurement equation (8) is replaced by
It is not hard to show that
The two expectations at the right-hand side of the last equation can be computed, recursively, using the Kalman filter. The first expectation is equal to the recursive estimation of the second element of the state vector (
1) squared and the second expectation is equal to its recursively estimated covariance matrix. Given the intercept intervention parameters qt[t = 1, 2 and 3], s, L, g0 and Q, it is possible to obtain the model's likelihood value and 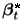 through the Kalman Filter recursions. That is, we can concentrate the likelihood with respect to
through the Kalman Filter recursions. That is, we can concentrate the likelihood with respect to 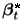 , using the Kalman filter and, with the help of a numerical optimization routine, estimate the value of the other parameters
, using the Kalman filter and, with the help of a numerical optimization routine, estimate the value of the other parameters  qt(t = 1, 2 and 3), s, L, g0 and the elements at the diagonal of matrix Q
qt(t = 1, 2 and 3), s, L, g0 and the elements at the diagonal of matrix Q that maximizes the likelihood.
that maximizes the likelihood.
To arrive at a more parsimonious model the following restrictions were imposed a priori:
Q(2,2) = Q(3,3) = Q(4,4), equality between parameters, at the diagonal of matrix Q, which controls for the time change of seasonal dummies coefficients;
Q(5,5) = Q(6,6) = Q(7,7), equality between parameters, at the diagonal of matrix Q, which controls for the time change of lag unemployment coefficients;
Q(8,8) = Q(9,9), equality between parameters, at the diagonal of matrix Q, which controls for the time change of lag Dpt coefficients.
With these restrictions matrix Q has only 4 unknown parameters. Therefore, the TVP model has, if we exclude the parameters of 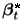 from the counting, a total of 10 parameters to be estimated. In section 5.1 we describe how, departing from this more general model and using a few statistical tests, we are able to reduce, from 10 to 5, the number of parameters to be estimated.
from the counting, a total of 10 parameters to be estimated. In section 5.1 we describe how, departing from this more general model and using a few statistical tests, we are able to reduce, from 10 to 5, the number of parameters to be estimated.
4.2 The MSR model estimation procedure
In order to estimate the MSR model, it is necessary to make inferences about both the unobserved states and the latent Markov state. The regime shifts of the MSR model imposes a nonlinearity that precluded the estimation of this type of model until the estimation methods by Albert and Chib (1993), Shephard (1994) and Kim (1994) were developed. I use the Kim's method to estimate the MSR model. The Kim filter is an optimal estimator in the sense that no other estimator, based on a linear function of the information set, yields a smaller mean squared error (Smith and Makov, 1980). In the appendix we describe the Kim filter and its use in the MSR model estimation.
We adopt the same restrictions for the MSR model - on the parameters of the diagonal of matrix Qi (state i = 1, 2) - which were imposed on the TVP model in section 3.1. Furthermore, equation (15) shows that we can estimate only p11 and p21 in order to obtain the entire matrix P. Therefore, given p11 , p22, qt(t = 1, 2, 3 ), si (the measurement equation residual's standard deviation at state i, i = 1, 2), and the 4 parameter in the diagonal of matrix Qi, at each state, we can use Kim's filter and smoothing algorithm (Kim and Nelson, 1999) to estimate 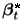 and calculate the value of the likelihood of the MSR model. The Kim's filter obtains the nonlinear mapping from the hyperparameters (si and Qi; i = 1,2), the parameters in P, and the intervention parameters qt(t = 1, 2, 3) to the likelihood value. We use this mapping to estimate the likelihood maximizing values of these hyperparameters and parameters using a numerical optimization routine. That is, the likelihood can be concentrated with respect to
and calculate the value of the likelihood of the MSR model. The Kim's filter obtains the nonlinear mapping from the hyperparameters (si and Qi; i = 1,2), the parameters in P, and the intervention parameters qt(t = 1, 2, 3) to the likelihood value. We use this mapping to estimate the likelihood maximizing values of these hyperparameters and parameters using a numerical optimization routine. That is, the likelihood can be concentrated with respect to 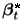 making it easier to estimate p11 , p22 , qt(t = 1, 2, 3 ) , s1 , s2 and the parameters at the diagonal of matrix Q, at each state, with the help of a numerical optimization routine. The results of this estimation are presented in section 5.2.
making it easier to estimate p11 , p22 , qt(t = 1, 2, 3 ) , s1 , s2 and the parameters at the diagonal of matrix Q, at each state, with the help of a numerical optimization routine. The results of this estimation are presented in section 5.2.
The MSR model has 15 parameters to be estimated through the numerical optimization routine6 6 The parameter of do not enter explicitly in the numerical optimization routine. They are concentrated out by the Kim filter. . Therefore, there is an excessive number of parameters. We show, in the next section, how departing from this more general model and using a few statistical tests, we impose some restrictions and end up with a model with only 8 parameters to be estimated through the numerical optimization routine.
5 The Model's Estimation Results
The two models were estimated using computer programs developed with the help of the ''Matlab'' software. The log likelihood for the two models, and for a variety of alternative hypothesis, is presented in table 1.
5.1 The TVP model results and the stability of coefficients of the brazilian price Phillips curve
The TVP model was initially estimated with 10 parameters if we exclude from the counting the parameters that belong to 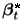 and which were concentrated out of the likelihood using the Kalman filter. We could not reject - at a significance level higher than 10% and using the likelihood ratio test - that L, g0 and the parameters of the diagonal of matrix Q, which controls for the time variation of coefficients of the dummy variables, of the rate of unemployment and of the lags of the rate of inflation, are all equal to zero. The log likelihood values with and without the restrictions are presented in table 1. Therefore, we could not reject the stability of the Brazilian price Phillips Curve. The TVP model, without ARCH residual in the measurement equation, with a time-varying intercept (time-varying NAIRU) and with intercept intervention at the stabilization Plans, has only 5 parameters to be estimated through the numerical optimization routine. This simplified version of the TVP model fits the data as well as the initial less parsimonious model with 10 parameters. Table 1 shows that the model with 10 parameters has a log likelihood value of 112.07 and the simplified model with 5 parameters has a likelihood value of 111.43. We can also reject the hypothesis of a stable NAIRU. If we add this hypothesis to the already simplified 5 parameters TVP model, the number of parameters drops from 5 to 4, but the log likelihood drops from 111.43 to 107.87. The estimated values of the 5 parameters of the selected TVP model and those of the one-step ahead Theil-U7
7
The one-step ahead Theil-U statistic is equal to
, where
et is the one-step ahead forecast error,
k is the number of parameters of the model and T is the sample size. The one-step ahead forecast is obtained using the full sample to estimate the parameters that enter the numerical optimization routine (5 parameters for the TVP model and 8 parameters for the MSR model). Fixing the parameters, that enters the optimization routine, at their maximizing levels, the other 9 parameters used in the one-step ahead forecast for period t use, in their estimation, only observations up to
t 1.
can be found in table 2. The one-step ahead forecast and fitted values of the TVP model are presented in figure 3. The estimated NAIRU and its confidence interval are presented in section 6.
and which were concentrated out of the likelihood using the Kalman filter. We could not reject - at a significance level higher than 10% and using the likelihood ratio test - that L, g0 and the parameters of the diagonal of matrix Q, which controls for the time variation of coefficients of the dummy variables, of the rate of unemployment and of the lags of the rate of inflation, are all equal to zero. The log likelihood values with and without the restrictions are presented in table 1. Therefore, we could not reject the stability of the Brazilian price Phillips Curve. The TVP model, without ARCH residual in the measurement equation, with a time-varying intercept (time-varying NAIRU) and with intercept intervention at the stabilization Plans, has only 5 parameters to be estimated through the numerical optimization routine. This simplified version of the TVP model fits the data as well as the initial less parsimonious model with 10 parameters. Table 1 shows that the model with 10 parameters has a log likelihood value of 112.07 and the simplified model with 5 parameters has a likelihood value of 111.43. We can also reject the hypothesis of a stable NAIRU. If we add this hypothesis to the already simplified 5 parameters TVP model, the number of parameters drops from 5 to 4, but the log likelihood drops from 111.43 to 107.87. The estimated values of the 5 parameters of the selected TVP model and those of the one-step ahead Theil-U7
7
The one-step ahead Theil-U statistic is equal to
, where
et is the one-step ahead forecast error,
k is the number of parameters of the model and T is the sample size. The one-step ahead forecast is obtained using the full sample to estimate the parameters that enter the numerical optimization routine (5 parameters for the TVP model and 8 parameters for the MSR model). Fixing the parameters, that enters the optimization routine, at their maximizing levels, the other 9 parameters used in the one-step ahead forecast for period t use, in their estimation, only observations up to
t 1.
can be found in table 2. The one-step ahead forecast and fitted values of the TVP model are presented in figure 3. The estimated NAIRU and its confidence interval are presented in section 6.
5.2 The MSR model results and the stability of coefficients of the price Phillips curve
The MSR model was initially estimated, in its more general version, with 15 parameters, if we exclude from the counting the parameters belonging to 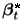 . It could not be rejected - at a significance level higher than 10% and using the likelihood ratio test - that all the parameters at the diagonal of matrix Q are equal to zero at state 2 and that these parameters (with the exception of the parameter that controls for the time variability of the intercept) are also equal to zero at state 1. With these restrictions, the MSR model has 8 parameters to be estimated through the numerical optimization routine.
. It could not be rejected - at a significance level higher than 10% and using the likelihood ratio test - that all the parameters at the diagonal of matrix Q are equal to zero at state 2 and that these parameters (with the exception of the parameter that controls for the time variability of the intercept) are also equal to zero at state 1. With these restrictions, the MSR model has 8 parameters to be estimated through the numerical optimization routine.
Table 1 presents the log likelihood for the simplified selected MSR model (with the above restrictions)as 121.09 and for the initial MSR model (without these restrictions)as 121.26. Furthermore, as table 1 shows, if we impose the additional restriction of no time-varying intercept in state 1 (stable NAIRU), the number of parameters drops from 8 to 7 but the log likelihood drops from 121.09 to 113.14. Therefore, we cannot reject the stability of coefficients of the Brazilian price Phillips curve but, given this stability, we can reject a constant NAIRU.
In table 3 we present the estimated values of these 8 parameters. The estimated transition probability matrix (P) can be found in table 4. The one-step ahead forecast and fitted values of the MSR model are presented in figure 3. The state 1 probability, at each period, can be viewed in figure 4. The estimated NAIRU and its confidence interval are presented in section 6.
5.3 The comparison between the TVP and MSR models and some additional statistical tests
Table 1 shows that the maximizing value of log likelihood for the selected MSR model is 121.09 and the same value for the selected TVP model is 111.43. The TVP model is more parsimonious than the MSR model, since it has 3 parameters less. It is also true that the TVP model (without ARCH residuals) is nested in the MSR model. Nevertheless, as it has been pointed out by Engel and Hamilton (1990), if the information matrix is singular in the region of the parameter space where the MSR model becomes the TVP model, then the standard regularity conditions needed to establish asymptotically valid hypothesis tests are not satisfied. Therefore, we cannot test, using the usual tests, which of the models better fits the data and the results, for both models are going to be presented.
The MSR model, as can be seen in table 5, satisfactorily passes two tests: one test, suggested by Engel and Hamilton (1990), designed to test if the measurement equation residuals are homoscedastic without regime switching (p11 = 1 p22) but with a time-varying intercept in the measurement equation at state 1; another to test if there is no time-varying intercept at state 1 (Q1(1, 1) = 0) when the hypothesis of Markov-switching, for the standard deviation of the residual of the measurement equation, is in place. When the hypothesis p11 = 1 p22 is imposed to the MSR model, there is no longer a Markov-switching process and the rate of inflation is an i.i.d. sequence with individual densities given by a mixture of two normals. We are able to reject both hypotheses, at a significance level smaller than 1%, using the likelihood ratio and Wald tests.
We did not detect significant serial correlation, in the MSR model, for either the standardized one-step ahead forecast error or the squares of the standardized one-step ahead forecast errors. Nevertheless, the same is not true for the TVP model. Tables 6 and 7 present these tests.
6 The Estimated NAIRU and the Response of Dp to Cyclical Unemployment
Figure 5 shows the smoothed estimates of the NAIRU for the TVP and MSR models, as defined in section 2, and its confidence intervals computed from the smoothed estimates of b* and of Var(b*), at each period t. The confidence intervals for the NAIRU were computed from 1,000 extractions of the distribution of the estimator of b* and, in each extraction, the NAIRU was computed as explained in section 2.
After the Real Plan, there is growing evidence of the presence of seasonality in the unemployment data. Therefore, we also have estimated both previously selected models, with seasonally adjusted unemployment data8 8 The unemployment rate was seasonally adjusted using the x12-arima software. The presence of seasonality in Dp is dealt with, in our model, by the seasonal dummies. Nevertheless, if we exclude these dummies from the model, the results do not change in any significant way. 9 A detailed discussion of the Kim's filter can be found in Kim (1994) and Kim and Nelson (1999). . The estimated NAIRU and its confidence intervals for both models, with seasonally adjusted unemployment data, are presented in figure 6.
The cyclical unemployment is defined as the difference, at each date t, between the observed rate of unemployment and the estimated NAIRU. If we consider as given the cyclical unemployment then, from equation (1), we get:
where Ct = ut 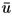 t = cyclical unemployment.
t = cyclical unemployment.
The response of Dpt (the first difference of inflation) to a permanent +0.5% cyclical unemployment, which has started at period t-h, can be computed through the following recursions:
and
R(h) is the annualized percent response of Dp to a 0.5% cyclical unemployment that has been persistent for the last h quarters. Given the distributions of the parameters of equation (1¢¢), we can construct error bands for R(h) through Monte Carlo simulations. Figure 7 presents the cyclical unemployment, R(h) and its error bands for the TVP and MSR models with nonseasonally adjusted unemployment. Figure 8 presents the same results for the TVP and MSR models when both are estimated using seasonally adjusted unemployment.
The main conclusions are as follows: There is a statistically significant relationship between cyclical unemployment and the change in inflation rate; if the TVP model is considered, a permanent 0.5% cyclical unemployment, after 3 quarters, reduces by 7.5% the annualized monthly inflation rate; if the MSR model is considered a permanent 0.5% cyclical unemployment, after 1 quarter, reduces by 5% the annualized monthly inflation rate.
7 Conclusions
In our analysis of the results we emphasize two main aspects: Is there a statistically significant relationship between an upward (downward) deviation of the rate of unemployment from our estimated value of the NAIRU and a reduction (increase) in the rate of inflation? To what degree our measure of the NAIRU is significantly different from the observed rate of unemployment across time?
The first question can be easily answered by observing the response of inflation to cyclical unemployment, presented in section 5. There is a significant and negative response of inflation to an increase in cyclical unemployment. Nevertheless the effect is not measured with high precision if we consider model uncertainty. The response of annual inflation to 0.5% cyclical unemployment that is persistent for 3 quarters belongs, with a 95% degree of confidence, to the (-11%, -7.5%) interval for the TVP model and to the (-6%,-4%) interval for the MSR model. The two models do not allow for time-varying coefficients for lag unemployment and lag inflation. Therefore, it cannot be rejected that the deviations of the rate of unemployment from the NAIRU can have a significant effect, with correct sign, on the rate of inflation. Nevertheless, it is also true that the above estimates of the effect are not very precise. If we consider the uncertainty with respect to what the right model is, then any value between -11% and -4% cannot be rejected.
The answer to the second question depends on the degree of precision with which the NAIRU is estimated. Observing figures 5 and 6 we can conclude that the estimates of the NAIRU, considering both models, are very imprecise and that from the second quarter of 1995 the estimated value of the NAIRU is contained within its error bands and therefore it cannot be rejected that the observed rate of unemployment was equal to the NAIRU.
Despite what we have said, one cannot conclude that our estimates of the NAIRU are useless. It should be pointed out that, during a good part of the period of high inflation faced by Brazil, the rate of unemployment was systematically below the error bands estimated for the NAIRU. Therefore, there was a continuous uptrend in the rate of inflation, whose upward trajectory was only broken by the stabilization plans. This is true for the MSR model from the beginning of 1985 until the second semester of 1995. For the TVP model, this is true from the beginning of 1986 to the beginning of 1991. It is also interesting to note that the two models indicate that there was a decrease in the NAIRU from 1994 until the middle of 1995, when it started increasing again until it reached values next to its previous 1994 level by 1999. The NAIRU has been decreasing since the year 2000.
Unfortunately, there is not a large number of articles with different models and with estimates of the NAIRU for Brazil. The degree of confidence in the results depends critically on the increase of research in this area.
This paper was received in Apr. 2002 and approved in Dec. 2002.
Appendix
Let,
1 = [yt1, yt2, ...., y1] , information available up to time t-1; = E(
= E(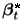
 = E[(
= E[(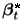
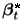 /t1)(
/t1)(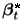
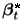 /t1)¢/
/t1)¢/ 1, St = j, St1 = i];
1, St = j, St1 = i];
 = E(
= E(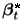 1/
1/ 1, St1 = i);
1, St1 = i);
 = E[(
= E[(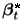 1
1 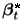 1/t1)(
1/t1)(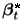 1
1 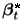 1/t1)¢/
1/t1)¢/ 1, St1 = i];
1, St1 = i];
Pr[St = j, St1 = i] = pi J;
P = [pij] = matrix of transition probabilities;
Pr[St = i| ] = probability of state i, at period t, given information up to time t.
] = probability of state i, at period t, given information up to time t.
The objective of Kim's nonlinear filter is to obtain estimates of the unobserved state vector (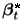 ) and its associated mean squared error matrix (St), and of the marginal probability of the latent Markov state variable St, at each date t. The estimates are based on information available up to time t. That is, at each date t, given
) and its associated mean squared error matrix (St), and of the marginal probability of the latent Markov state variable St, at each date t. The estimates are based on information available up to time t. That is, at each date t, given  ,
,  , Pr[St1 = i|
, Pr[St1 = i| 1], yt, Qj, sj, (for i = 1, 2 and j = 1, 2), qt(t = 1, 2 and 3) and the matrix of transition probabilities (P) the Kim's filter allows us to obtain approximate estimations of
1], yt, Qj, sj, (for i = 1, 2 and j = 1, 2), qt(t = 1, 2 and 3) and the matrix of transition probabilities (P) the Kim's filter allows us to obtain approximate estimations of  ,
,  , and Pr[St = j|
, and Pr[St = j| ](j = 1, 2). To start the filter we need the initial values of
](j = 1, 2). To start the filter we need the initial values of  ,
,  and Pr[S0 = i/
and Pr[S0 = i/ 0](i = 1, 2). We set
0](i = 1, 2). We set  = 0 ,
= 0 ,  = Ix100.000 and Pr[S0 = i/
= Ix100.000 and Pr[S0 = i/ 0](i = 1, 2) equal to the ergodic distribution of the Markov chain (the steady-state marginal distribution of the states). What we have called Kim filter is actually a combination of the Kalman filter, Hamilton filter and a collapsing procedure. We describe the
0](i = 1, 2) equal to the ergodic distribution of the Markov chain (the steady-state marginal distribution of the states). What we have called Kim filter is actually a combination of the Kalman filter, Hamilton filter and a collapsing procedure. We describe the
Part I of Kim Filter - The Kalman Filter
Given  ,
,  , yt, Qi , si, ( for i = 1, 2) and qt(t = 1, 2, 3), the Kalman Filter gives
, yt, Qi , si, ( for i = 1, 2) and qt(t = 1, 2, 3), the Kalman Filter gives  ,
,  , the conditional one-step prediction error (
, the conditional one-step prediction error ( ), and the conditional variance of the one-step prediction error,
), and the conditional variance of the one-step prediction error,  ( for i = 1, 2 and j = 1, 2). The algorithm estimates 2 (number of different possible regimes) state vectors for each possible value of St1. Therefore, at each date t, the algorithm estimates 4 state vectors. The Kalman filter recursions are presented below:
( for i = 1, 2 and j = 1, 2). The algorithm estimates 2 (number of different possible regimes) state vectors for each possible value of St1. Therefore, at each date t, the algorithm estimates 4 state vectors. The Kalman filter recursions are presented below:
Part II of Kim Filter - The Hamilton Filter
Given Pr[St1 = i| 1],P,
1],P,  ,
,  , the Hamilton Filter obtains Pr[St1 = i, St = j|
, the Hamilton Filter obtains Pr[St1 = i, St = j| ] and Pr[St = i|Ît]. The Hamilton Filter is presented below:
] and Pr[St = i|Ît]. The Hamilton Filter is presented below:
Where,
and
Part III of Kim Filter - The Collapsing
Given  ,
,  (both estimated by the Kalman filter) , Pr[St1 = i, St = j|
(both estimated by the Kalman filter) , Pr[St1 = i, St = j| ], Pr[St = i|
], Pr[St = i| ] (both estimated by the Hamilton filter) and P, the filter collapses
] (both estimated by the Hamilton filter) and P, the filter collapses  into
into  and
and  into
into  . The collapsing is of crucial importance because without it the number of filter evaluations is multiplied by 2, at each date t, and it is computationally unfeasible to estimate the model. The collapsing is an approximation based on the work of Harrison and Stevens (1976). The approximation consists of a weighted average of the updating procedures by the probabilities of the Markov state, in which the mixture of 4 Gaussian densities is collapsed, after each observation, into a mixture of 2 densities. It is done as follows:
. The collapsing is of crucial importance because without it the number of filter evaluations is multiplied by 2, at each date t, and it is computationally unfeasible to estimate the model. The collapsing is an approximation based on the work of Harrison and Stevens (1976). The approximation consists of a weighted average of the updating procedures by the probabilities of the Markov state, in which the mixture of 4 Gaussian densities is collapsed, after each observation, into a mixture of 2 densities. It is done as follows:
Collapsing equations:
The Likelihood
The likelihood is given by : L =  f(yt/
f(yt/ 1)
1)
The Recursive Estimate
Therefore, given p11, p22, qt(t = 1, 2, 3) , si (the measurement equation residual's standard deviation at state i, i = 1, 2), and the 4 parameter at the diagonal o matrix Qi at each state, we can use the Kim's filter to estimate  , St|t, Pr[St = j|
, St|t, Pr[St = j| ] and calculate the value of the likelihood of the MSR model. The Kim filter obtains the nonlinear mapping from the hyperparameters (si and Qi; i = 1, 2), the parameters in P, and the intervention parameters qt(t = 1, 2, 3) to the likelihood value. We use this mapping to estimate the likelihood maximizing values of these hyperparameters and parameters using a numerical optimization routine. Given the output of the Kim filter we can use Kim's smoothing algorithm (Kim and Nelson, 1999) to estimate - using all the sample information -
] and calculate the value of the likelihood of the MSR model. The Kim filter obtains the nonlinear mapping from the hyperparameters (si and Qi; i = 1, 2), the parameters in P, and the intervention parameters qt(t = 1, 2, 3) to the likelihood value. We use this mapping to estimate the likelihood maximizing values of these hyperparameters and parameters using a numerical optimization routine. Given the output of the Kim filter we can use Kim's smoothing algorithm (Kim and Nelson, 1999) to estimate - using all the sample information - 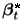 and its covariance matrix.
and its covariance matrix.
- Akerlof, G. A., Dickens, W. T., & Perry, G. L. (1996). The macroeconomics of low inflation. Brookings Papers on Economic Activity, (1):176.
- Akerlof, G. A., Dickens, W. T., & Perry, G. L. (2000). Near-rational wage and price setting and the optimal rates of inflation and unemployment. Brookings Papers on Economic Activity, (1).
- Albert, J. & Chib, S. (1993). Bayes inference via gibbs sampling of autoregressive time series subject to markov mean and variance shifts. Journal of Business and Economic Statistics, 11.
- Blanchard, O. & Katz, L. F. (1997). What we know and do not know about the natural rate of unemployment. The Journal of Economic Perspectives, 11(1).
- Cogley, T. & Sargent, T. J. (2001). Evolving post-world war II U. S. inflation dynamics.
- Corseuil, C. H., Gonzaga, G., & Issler, J. V. (1996). Desemprego regional no Brasil: Uma abordagem empírica. Série seminários da Diretoria de Pesquisa do Ipea, nº 09/96.
- Engel, C. & Hamilton, J. D. (1990). Long swings in the dollar: Are they in the data and do markets know it? The American Economic Review, 80:689713.
- Friedman, M. (1968). The role of monetary policy. American Economic Review, 68(1):117.
- Gordon, R. J. (1982). Inflation, flexible exchange rates, and the natural rate of unemployment. In Baily, M. N., editor, Workers, Jobs and Inflation Brookings.
- Gordon, R. J. (1997). The time-varying NAIRU and its implications for economic policy. Journal of Economic Perspective, 11(1):1132.
- Gordon, R. J. (1998). Foundations of the goldilocks economy: Supply shocks and the Time-Varying NAIRU. Brooking Papers on Economic Activity, 2:297333.
- Hall, R. (1999). Comment on rethinking the role of the NAIRU in monetary policy: Implications of model formulation and uncertainty. In Taylor, J. B., editor, Monetary Policy Rules University of Chicago Press, Chicago-IL.
- Hamilton, J. D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica, 57(2):357384.
- Harrison, P. J. & Stevens, C. F. (1976). Bayesian forecasting. Journal of the Royal Statistic Society, 38:205247.
- Harvey, A. C. (1989). Forecasting Structural Time Series Models and the Kalman Filter Cambridge University Press, Cambridge.
- Harvey, A. C., Ruiz, E., & Sentana, E. (1992). Unobserved component time series models with ARCH disturbances. Journal of Econometrics, 52:129157.
- Katz, L. F. & Krueger, A. B. (1999). The high-pressure U.S. labor market of the 1990's. Brookings Papers on Economic Activity, 1:187.
- Kim, C. & Nelson, R. C. (1998). The time-varying-parameter model for modeling changing conditional variance: The case of the lucas hypothesis. Journal of Business and Economic Statistics, 7(4):433440.
- Kim, C. & Nelson, R. C. (1999). State Space Models with Regime Switching The MIT Press, London, England.
- Kim, C.-J. (1994). Dynamic linear models with Markov-switching. Journal of Econometrics, 60:122.
- King, R. G., Stock, J. H., & Watson, M. (1995). Temporal instability of the unemployment inflation relationship. Economic Perspectives, pages 2-12. Federal Reserve Bank of Chicago.
- King, R. G. & Watson, M. W. (1994). The post-war U.S. Phillips curve: A revisionist econometric history. Carnegie-Rochester Conference Series on Public Policy, 41:157219.
- Lundbergh, S., Teräsvirta, T., & Van Dijk, D. (2002). Time-varying smooth transition autoregressive models. Journal of Business and Economic Statistics
- Portugal, M. S., Madalozzo, R. C., & Hilllbrecht, R. O. (1999). Inflation, unemployment and monetary policy in Brazil.
- Rogerson, R. (1997). Theory ahead of language in the economics of unemployment. Journal of Economics Perspective, 11(1):7392.
- Sargent, T. J. (1971). A note on the accelerationist controversy. Journal of Money Credit and Banking, 8(3):721725.
- Shephard, N. (1994). Partial non-gaussian state space. Biometrika, 81:115131.
- Sims, C. A. (1999). Drift and breakes in monetary policy. Discussion paper, Princeton University, http://www.princeton.edu/ Sims/
- Sims, C. A. & Zha, T. (2002). Macroeconomic switching. Discussion paper, Princeton University, http://www.princeton.edu/ Sims/
- Smith, A. F. M. & Makov, U. E. (1980). Bayesian detection and estimation of jumps in linear systems. In Jacobs, O. L. R., Davis, M. H. A., Dempster, M. A., & Harris, C. J. & Parks, P. C., editors, Analysis and Optimization of Stochastic Systems, pages 333345. Academic Press, New York.
- Staiger, D., Stock, J. H., & Watson, M. W. (1997). The NAIRU, unemployment and monetary policy. The Journal of Economic Perspectives, 11(1).
- Staiger, D., Stock, J. H., & Watson, M. W. (2001). Prices,wages and the U.S. NAIRU in the 1990's.
- Taylor, J. B. (2000). Low inflation, pass-through, and the pricing power of firms. European Economic Review, 44:13891408.
- Teräsvirta, T. (1994). Specification, estimation, and evaluation of smooth transition autoregressive models. Journal of the American Statistical Association, 89:208218.
- Tong, H. (1990). Nonlinear Time Series: A Dynamic Systems Approach Oxford University Press, Oxford, U.K.
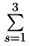 b
b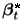 do not enter explicitly in the numerical optimization routine. They are concentrated out by the Kim filter.
do not enter explicitly in the numerical optimization routine. They are concentrated out by the Kim filter. 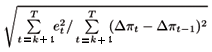 , where
, where Publication Dates
-
Publication in this collection
14 June 2004 -
Date of issue
Dec 2003
History
-
Received
Apr 2002 -
Accepted
Dec 2002











































