Abstracts
This paper investigates the presence of nonlinear mechanisms of pass-through from the exchange rate to inflation in Brazil. In particular, it estimates a Phillips curve with a threshold for the pass-through. The paper examines whether the short-run magnitude of the pass-through is affected by the business cycle, direction and magnitude of exchange rate changes, and exchange rate volatility. The results indicate that the short-run pass-through is higher when the economy is growing faster, when the exchange rate depreciates above some threshold and when exchange rate volatility is lower.
Exchange Rate Pass-Through; Threshold; Inflation; Nonlinearity; Brazil
Este trabalho investiga a presença de mecanismos não-lineares de repasse cambial para a inflação no Brasil. Em particular, estima-se uma curva de Phillips com limiar (threshold) para o repasse cambial. O artigo examina se a magnitude de curto prazo do repasse é afetada pelo ciclo econômico, pela direção e magnitude da variação cambial e pela volatilidade da taxa de câmbio. Os resultados indicam que o repasse de curto prazo é maior quando a economia está em expansão, quando a taxa de câmbio se deprecia acima de certo valor e quando a volatilidade da taxa de câmbio é menor.
Nonlinear mechanisms of the exchange rate pass-through: a Phillips curve model with threshold for Brazil* * We are thankful to Fabio Araújo and Tomiê Sugahara for their participation in initial estimations, Carlos Hamilton Araújo, Afonso Bevilaqua, Ana Beatriz Galvão and Marcelo K. Muinhos for suggestions, Érica Oliveira and Ibitisan Santos for assistance with data, and others colleagues at the Research Department of the Central Bank of Brazil for their contributions and comments. The views herein are those of the authors and do not necessarily reflect those of the Central Bank of Brazil.
Arnildo da Silva CorreaI; André MinellaII
IResearch Department, Central Bank of Brazil and Department of Economics, Pontifical Catholic University of Rio de Janeiro (PUC-Rio). E-mail: arnildo.correa@bcb.gov.br
IIResearch Department, Central Bank of Brazil. E-mail: andre.minella@bcb.gov.br
ABSTRACT
This paper investigates the presence of nonlinear mechanisms of pass-through from the exchange rate to inflation in Brazil. In particular, it estimates a Phillips curve with a threshold for the pass-through. The paper examines whether the short-run magnitude of the pass-through is affected by the business cycle, direction and magnitude of exchange rate changes, and exchange rate volatility. The results indicate that the short-run pass-through is higher when the economy is growing faster, when the exchange rate depreciates above some threshold and when exchange rate volatility is lower.
Keywords: Exchange Rate Pass-Through, Threshold, Inflation, Nonlinearity, Brazil.
JEL Code: E31, E50, E58.
RESUMO
Este trabalho investiga a presença de mecanismos não-lineares de repasse cambial para a inflação no Brasil. Em particular, estima-se uma curva de Phillips com limiar (threshold) para o repasse cambial. O artigo examina se a magnitude de curto prazo do repasse é afetada pelo ciclo econômico, pela direção e magnitude da variação cambial e pela volatilidade da taxa de câmbio. Os resultados indicam que o repasse de curto prazo é maior quando a economia está em expansão, quando a taxa de câmbio se deprecia acima de certo valor e quando a volatilidade da taxa de câmbio é menor.
1. INTRODUCTION
The presence of nonlinearities in the Phillips curve has relevant implications for monetary policy. The slope of the Phillips curve - measuring the response of inflation to output gap - affects directly the cost of disinflation. Schaling (2004) shows that, when the Phillips curve is convex, that is, the sensitivity of inflation to economic activity increases with the level of output, the optimal monetary policy reaction function is asymmetric. Nonlinearity may also be present in the pass-through from exchange rate changes to prices. If the pass-through, for instance, is greater when the economy is booming, we may consider that the central bank's reaction to a depreciation of the domestic currency will be stronger in this context.
In fact, the investigation of the presence of nonlinear mechanisms in the Phillips curve has been an important topic in the recent literature1 1 See, for instance, Chadha et al. (1992), Laxton et al. (1995), Dupasquier and Ricketts (1998), Nobay and Peel (2000), Aguiar and Martins (2002), Tambakis (1999), and Clements and Sensier (2003). . Most studies on nonlinear Phillips curves for developed economies have focused on the slope of the Phillips curve and the exchange rate pass-through.In the first case, Laxton et al. (1999) and Bean (2000) find evidence that the Phillips curve is convex, while Stiglitz (1997) and Eisner (1997) claim that the Phillips curve is concave.2 2 Filardo (1998), in turn, considers that the Phillips curve is neither entirely convex nor concave, but a combination of both (a concave-convex curve). The literature on exchange rate pass-through, in turn, reports several sources of nonlinearity, indicating that the degree of pass-through can be related to some macroeconomic variable, including the exchange rate. Mann (1986), Goldberg (1995), Gil-Pareja (2000), Mahdavi (2002) and Olivei (2002) have found asymmetric pass-through related to the direction of exchange rate changes, while Ohno (1989) and Pollard and Coughlin (2004) have indicated the presence of asymmetry associated with the magnitude of exchange rate changes.
The business cycle is also pointed out as an important source of nonlinearity for the pass-through. The transmission of exchange rate depreciations to domestic prices would be lower during an economic slowdown. Goldfajn and Werlang (2000), estimating a panel data model for 71 countries, have found that depreciations have a higher pass-through to prices when the economy is booming. In the case of Brazil, Carneiro et al. (2002) have found similar results estimating a backward-looking Phillips curve with the pass-through coefficient as a function of unemployment rate and real exchange rate level3 3 Muinhos (2001) has found mixed results, and Bogdansky et al. (2000) have worked with a model for Brazil with a nonlinear pass-through as well. . In these papers, the magnitude of the pass-through coefficient is a function of some variables.
This paper investigates the possibility of a nonlinear pass-through in Brazil using threshold models. These models are part of a class of models that consider different states of nature or regimes and allow different dynamic behavior for the variables, conditional on the regime prevailing in each moment (Franses and van Dijk, 2000). In the case of threshold models, the sample is divided into classes based on whether the value of an observed variable surpasses or not some threshold. This kind of model - Threshold Autoregressive (TAR) Model - was initially proposed by Tong (1978) and Tong and Lim (1980) and has spread in the recent applied economic literature.
We focus on the pass-through because exchange rate movements have played a key role in the inflation dynamics in Brazil, especially in the early years of the inflation targeting regime with recurrent bouts of exchange rate depreciation in response to shocks, in the context of balance of payments vulnerabilities. We estimate three specifications for the Phillips curve, which differ basically by the variable used as the threshold for the pass-through:
i) output gap;
ii) nominal exchange rate change; and
iii) exchange rate volatility.
Thus, we can deal with different possible sources of nonlinearity. The first question is whether economic activity affects the magnitude of the pass-through. The second one is whether the pass-through is symmetric with respect to the direction of the exchange rate change - whether appreciations or depreciations have symmetric effects on prices - and to the magnitude of the exchange rate change.
The estimations indicate that the short-run pass-through is higher when the economy is growing faster, when the exchange rate depreciates above a threshold value and when exchange rate volatility is lower. These results have implications for monetary policy and are possibly related to pricing-to-market behavior, costs of changing prices, and uncertainty regarding the degree of persistence of exchange rate changes.
The article is organized as follows. Section 2 sets forth the methodology of threshold models with the presence of endogenous variables. Section 3 presents the specifications of the Phillips curve with threshold and the estimation results. The last section concludes the text.
2. THRESHOLD MODELS WITH ENDOGENOUS VARIABLES
In threshold models, the sample is divided into classes based on the value of an observed variable - whether it surpasses or not some threshold. As usual in practice, the threshold is not known and needs to be estimated. The simplest model is the SETAR (Self-Exciting Threshold Autoregressive Model), where the threshold is given by a lagged term of the dependent variable - yt-d , where d > 0. An AR(1) model of two regimes and d = 1 can be written as:
where τ is the threshold value, are the parameters i of the regime j, and {εt} are independent, identically distributed (i.i.d.) random variables conditional on the history of the series, denoted by Ωt-1 = {yt-1,...,yt-p-1,yt-p}, with zero mean and variance σ2. Alternatively, this model can be expressed as:
are the parameters i of the regime j, and {εt} are independent, identically distributed (i.i.d.) random variables conditional on the history of the series, denoted by Ωt-1 = {yt-1,...,yt-p-1,yt-p}, with zero mean and variance σ2. Alternatively, this model can be expressed as:
where I(.) is an indicator function that takes a value equal to either one or zero, depending on the regime at time t. If yt-1> τ, I(.) = 1, otherwise I(.) = 0.
For these models with exogenous regressors, there is a well-developed theory of inference and estimation4 4 See, for example, Chan (1993), Hansen (1996, 1999, 2000) and Caner (2002). . In the case of models with endogenous variables, in turn, the theory is still working in progress. Caner and Hansen (2004) develop an estimator and an inference theory for this kind of model, with the restriction that the threshold variable must be exogenous. We are interested in models with endogenous variables because we want to estimate a Phillips curve for inflation in Brazil with an expectations term. Expectations have become a key feature of inflation modeling in the literature. However, the presence of an expectations term leads to endogeneity in the regression, warranting the use of instruments.
A model with endogenous regressors can be described as follows. Let  be the information set, where yt is unidimensional, zt is an m-dimension vector (regressors), and xt is a k-dimension vector (instruments), with k > m. The threshold variable qt= q(xt) can be an element or a function of the vector xt. In a general way, the structural equation can be written as:
be the information set, where yt is unidimensional, zt is an m-dimension vector (regressors), and xt is a k-dimension vector (instruments), with k > m. The threshold variable qt= q(xt) can be an element or a function of the vector xt. In a general way, the structural equation can be written as:
or in a more compact way,
where θj are parameter vectors, τ ∈ T, and T is the set of the possible threshold values. I(.) = 1 when qt > τ, and I(.) = 0, otherwise.
Since the error term ζt is correlated with zt- at least one variable in vector zt is endogenous - equation (4) cannot be estimated by ordinary least squares (OLS) because parameters would be biased and inconsistent.
Following the method proposed by Caner and Hansen (2004), in the first step of the estimation process, we estimate the endogenous variables as a function of instrumental variables, that is, we model the conditional mean of the endogenous variables as a function of exogenous variables. The fitted values for the endogenous variables are then plugged into the structural equation (4), and the threshold value is estimated by minimizing the sum of the squared residuals. The final parameters of the structural equation are estimated in a third step, when the sample is divided according to the estimated threshold. The estimation is conducted using the two-stage least square method (2SLS) or the generalized method of moments (GMM).
Therefore, the first stage (conditional expectations model of zt) is given by:
where β is a vector with parameters, ut is the error term, and f(.,.) is a function. In particular, this function can also be conditioned on the threshold value (which can be equal or different from that in the structural equation):5 5 In this paper, we do not condition on the threshold value in this first stage.
The parameter vector β in equation (5) can be obtained by OLS, for each τ ∈ T, as:
Using parameters  , we can obtain the values
, we can obtain the values  t that will replace zt in the structural equation. Doing it recursively for every τ ∈ T, the threshold value in the structural equation can be chosen by the minimization of the sum of the squared residuals, using a grid search. For every τ, let Y, ZL and ZG denote the vector yt and the matrices zt[I(qt < τ)] and zt[I(qt > τ)], respectively. Thus, the threshold estimator is obtained from:
t that will replace zt in the structural equation. Doing it recursively for every τ ∈ T, the threshold value in the structural equation can be chosen by the minimization of the sum of the squared residuals, using a grid search. For every τ, let Y, ZL and ZG denote the vector yt and the matrices zt[I(qt < τ)] and zt[I(qt > τ)], respectively. Thus, the threshold estimator is obtained from:
where Sn(τ) is the sum of the squared residuals in the regression of Y on 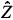 L and
L and 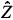 G . The set of threshold values in (10) should be such that each regime has sufficient observations to generate reliable parameter estimation. According to Franses and van Dijk (2000), a safe choice is at least 15% of the sample.
G . The set of threshold values in (10) should be such that each regime has sufficient observations to generate reliable parameter estimation. According to Franses and van Dijk (2000), a safe choice is at least 15% of the sample.
Given the estimated threshold value 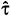 , the sample is divided into subsamples, and parameters of equation (10) can be estimated by 2SLS as:
, the sample is divided into subsamples, and parameters of equation (10) can be estimated by 2SLS as:
where
L,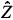 G,
G, 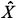 L and
L and 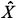 G stand for the matrices with observations zt[I(qt <
G stand for the matrices with observations zt[I(qt < 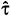 )], zt[I(qt >
)], zt[I(qt > 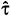 )], xt[I(qt <
)], xt[I(qt < 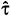 )] and xt[I(qt >
)] and xt[I(qt > 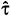 )], respectively.
)], respectively.
Caner and Hansen (2004) show that those estimators are consistent, although not necessarily efficient. Their applicability is conditioned on the exogeneity of the threshold variable.
3. PHILLIPS CURVE MODEL FOR BRAZIL
Aiming to test the possibility of the presence of a nonlinear pass-through from the exchange rate to inflation, we estimate some Phillips curve models for Brazil combined with the methodology of regime switching described in the previous section.
The estimated Phillips curve relates inflation to a measure of real disequilibrium (output gap), inflation expectations, past inflation, exchange rate changes and external inflation, with a threshold variable:
where  is the parameter of a specific regressor i when the economy is in regime j,
is the parameter of a specific regressor i when the economy is in regime j,  is free IPCA inflation (headline inflation measured by the Broad National Consumer Price Index, but excluding administered prices), πt is headline IPCA inflation,
is free IPCA inflation (headline inflation measured by the Broad National Consumer Price Index, but excluding administered prices), πt is headline IPCA inflation,  is a measure of external inflation (PPI in the U.S.), yt is the output gap (actual minus potential output),6
6
The output gap used in the estimation was generated using a production function model. See, for example, the box "Methodologies for estimating the potential output" in BACEN (2003) and Muinhos and Alves (2003) for a description of the methodology.
et is the natural logarithm of the average nominal exchange rate (domestic currency units per dollar), Et(.) is the expectations operator conditional on the information available at t, Δ is the difference operator (Δet-1 = et-1- et-2), εt is a residual, qt is the threshold variable, and τ ∈ T, where T is the set of possible values for qt .
is a measure of external inflation (PPI in the U.S.), yt is the output gap (actual minus potential output),6
6
The output gap used in the estimation was generated using a production function model. See, for example, the box "Methodologies for estimating the potential output" in BACEN (2003) and Muinhos and Alves (2003) for a description of the methodology.
et is the natural logarithm of the average nominal exchange rate (domestic currency units per dollar), Et(.) is the expectations operator conditional on the information available at t, Δ is the difference operator (Δet-1 = et-1- et-2), εt is a residual, qt is the threshold variable, and τ ∈ T, where T is the set of possible values for qt .
The dependent variable is the free price component of headline inflation because administered prices have a different dynamics, partially obeying contract rules. Note that the estimated pass-through refers to the transmission from exchange rate change in the previous quarter to the current inflation, that is, it captures only the short-run effect of exchange rate movements.
To enable the joint estimation, the previous equations become:
Based on theoretical indications for a nonlinear exchange rate pass-through, we evaluate three threshold variables:
i) business cycle, measured by the output gap;
ii) magnitude of nominal exchange rate changes; and
iii) a measure of exchange rate volatility.
We use quarterly data from 1995:1 through 2005:4 and estimate using 2SLS, with instrumental variables for the inflation expectations term.
The first estimated specification has the output gap as the threshold variable. In this model, all parameters, except for that of the output gap, are subject to regime switching.7 7 We do not allow the coefficient on the output gap to change because we want to capture nonlinearities in the pass-through. The estimation results are the following (p-values in parentheses):
According to the estimation results, there is a nonlinearity in the pass-through term related to the business cycle: the exchange rate pass-through is not statistically different from zero in the regime when the economy is below the threshold, whereas it is around 9% when economic activity is higher. According to the Wald test, we reject the null that the two pass-through coefficients are equal. The exchange rate pass-through is significantly greater when output is above some threshold,8 8 This result is in line with those in Goldfajn and Werlang (2000), and Carneiro et al. (2002). estimated at 1.89% below the potential output. This means that, during an economic slowdown, an exchange rate variation will have a smaller impact on domestic prices. This is usually pointed as one of the factors that limited the pass-through in Brazil during the 1999 exchange rate crisis. One limitation of this result is its implication that exchange rate appreciations have a higher pass-through when the economy is booming than when the output gap is below the threshold.
The other parameter estimates are in line with those found in the literature using models without a threshold variable. Except for the backward-looking term, all coefficients are statistically significant at 5%. In addition, the estimated value for the threshold splits the sample into two approximately equal parts (19 observations when yt-1 < -1.89%, and 25 when yt-1> -1.89%). This means that, although the sample size is not large, none of the regimes was estimated with an extremely low number of observations.9 9 Including the period previous to the launch of the Real Plan is not recommendable because the inflation dynamics in a high inflation regime is substantially different, distorting the estimation. Actually, we have tried several specifications, using different instruments for the expectations term, and the results were robust.
The second estimated model considers nominal exchange rate changes as the threshold variable. Similarly to the previous model, all parameters are allowed to vary with the regime change, except for the output gap parameter, kept constant in both regimes. The estimation results are the following:10 10 In that specification, we have used for the backward-looking inflation and output gap terms the average of their values at t-1 and t-2, that is, π t-1 = ( + )/2 and y t-1 = ( + )/2, where the superscript A means actual values. That specification generates better fitting.
Those results indicate that the short-run effect of exchange rate changes on inflation is asymmetric. In the case of large exchange rate depreciations, the estimated pass-through for the following quarter is around 11%, whereas appreciations or small depreciations do not have a statistically significant effect. The Wald test rejects the null hypothesis that both coefficients are equal (at the 10% significance level). Therefore, the pass-through is greater when quarter-on-quarter depreciations are equal to or larger than 2.1%. Although the results on the effect of an appreciation in the previous quarter on current inflation were not statistically significant, we should not infer that appreciations are not transmitted to prices. This transmission can take place with more lags than in the case of depreciation.
As before, the estimated parameters are robust with respect to the instruments used and are statistically significant at 5% (except the coefficient on lagged inflation when Δet-1> 2.10% ). Moreover, the number of observations in each regime was reasonably balanced (15 observations in the large depreciation regime, and 29 in the other) and the estimated values for the coefficients are close to those reported in the literature. Note that in both estimations the forward-looking inflation coefficient is greater than the backward-looking component.
Since the estimated threshold is not zero, its slightly positive value (close to 2%) suggests the presence of price adjustment costs, where small exchange rate changes are not promptly transmitted to prices. If price changes are costly, a small change in the currency value can be accommodated within the markup margin. In this case, firms tend to postpone their decisions, adjusting their markup in the short run. However, if exchange rate changes surpass some limit, the costs of not adjusting prices are higher, leading firms to change prices more rapidly. Consequently, the presence of price adjustment costs increases the possibility that firms will adjust price mainly if exchange rate changes surpass some threshold, resulting in an asymmetric pass-through related to small and large exchange rate changes.
Furthermore, pricing-to-market theory also delivers an explanation for a partial pass-through and for an asymmetry related to appreciations and depreciations in the exchange rate. Consider the domestic sector formed by subsidiaries of foreign firms that produce abroad and sell their products internally. In the case of an exchange rate depreciation, those firms have three options:
i) to reduce their markup to keep stable the price in local currency (absence of pass-through);
ii) to keep their markup, increasing the price charged in local currency to reflect completely the exchange rate change (complete pass-through), which may imply a market share reduction; or
iii) a combination of the previous two possibilities (partial pass-through).
When subsidiary firms are trying to build up or keep their market shares, a local currency depreciation results in a lower pass-through than that when there is an appreciation. Nevertheless, if the depreciation of the domestic currency is high, there is less room for markup adjustments, and at least partially the depreciation is transmitted to domestic prices to avoid losses. In the case of appreciation, firms' profits increase if they keep constant domestic prices, which could result in a longer period to adjust prices downwards. The extension of these effects on the price level in the economy depends on the price-elasticity of demand for these firms' goods and on the degree of openness of the economy. In addition, if the firms that produce abroad face a restriction on their production capacity, an exchange rate appreciation can result in a lower pass-through than in the case of a depreciation. The restriction capacity limits the fall in domestic price that the appreciation could generate.
The previous estimated models do not make any distinction between the pre-1999 period, when the exchange rate was managed - following in practice a crawling peg system - and the following period of a floating rate. In fact, when we include a step dummy into the exchange rate term, the results deteriorate substantially in terms of signs and statistical significance of the parameters. This result may be related to the increase in the number of parameters to be estimated when we include a dummy variable, reducing the degree of freedom of the estimation.
Because of those limitations, we have estimated a third model, using exchange rate volatility as the threshold variable. This estimation would tend to resolve, at least partially, the problem of the separation of the exchange rate regimes (before and after January 1999) because the threshold estimation tends to classify the observations of the managed system period into the low volatility regime. In principle, the low volatility estimated regime could also contain observations from when the exchange rate was relatively stable during the float period.
In addition, that estimation aims to capture the inflationary effects in two different situations:
i) when agents perceive exchange rate changes as transitory; and
ii) when they perceive them as permanent.
When agents consider exchange rate variations as more permanent, more promptly they will be transmitted to prices. Our assumption is that the probability that agents consider changes as permanent is higher in periods of low exchange rate volatility and smaller in periods of greater volatility.11 11 Albuquerque and Portugal (2006), for example, explore the relationship between exchange rate volatility and inflation in Brazil, using a bivariate GARCH model. Thus, we would expect a lower pass-through in periods of higher exchange rate instability.
We have used the standard deviation of daily changes in the exchange rate within each quarter as the measure of volatility. The estimation results were the following:12 12 In that specification, we have used for the backward-looking inflation term the average of their values at t-1, t-2 and t-3, that is, π t-1 = ( + + )/3, and for the output gap term, the average at t-1 and t-2, that is, yt -1 = ( + )/2, where the superscript A means actual values. That specification has generated better fitting.
In terms of magnitude, the point estimates indicate a greater pass-through in low volatility periods than in high volatility moments (80% and 7%, respectively). However, the estimated pass-through is not statistically significant in the low volatility regime, although it is significant in the other regime and the parameter values are close to those reported in the literature for the periods of managed and floating exchange rates.13 13 Muinhos and Alves (2003), por instance, have found a coefficient reduction from 51% to 6% after the change in the exchange rate regime, and Albuquerque and Portugal (2005), using a Kalman filter model, have estimated parameters values around 42% and 4%, respectively. The resulting sample division assigned most of the observations of the managed system to the low volatility regime. The observations corresponding to values below the threshold comprise the 1995:4-1998:2 period. Nevertheless, according to the Wald test, we cannot reject the null that both coefficients are equal, and the results of this Phillips curve specification are less robust than those of the two previous models. Therefore, these results should be considered with more caution.
Figure 1 illustrates the results concerning the first estimated model. It presents the quarterly free price inflation, the exchange rate change (lagged one period), and a line that indicates the threshold value (-1.89%) of the output gap. This line separates the periods when the output gap is above and below the threshold. We point out some periods, described in Table 1, in which the estimated model can explain, at least partially, the relation between exchange rate changes and free price inflation. The table records the corresponding values, besides including headline inflation (measured by the IPCA).
In the second quarter of 1999 (immediately after the float), for instance, in spite of the 39% exchange rate depreciation in the previous quarter, free price inflation was only 0.49% and the headline inflation stood at 1.05%, both below the previous quarter values. In that period, the output gap was below the estimated threshold (economic slowdown), which implies, according to the model, a low pass-through to inflation. The depreciations in the third quarter of 2000 and during 2001, in turn, were followed by higher increases in the inflation rate. In that period, the output gap was higher than the estimated threshold.
In mid-2002, when the economy was growing faster, a strong depreciation was accompanied by a great inflation rise. In the last quarter, for instance, when the depreciation in the previous quarter reached 22%, free price inflation went from 2.56% to 6.34%, and headline inflation rose from 2.58% to 6.56%.
On the other hand, although inflation fell along 2005, it did not follow so promptly the exchange rate appreciation started in the last quarter of 2004. One possible explanation lies on the asymmetry of the short-run pass-through with respect to appreciation and depreciation, put in evidence by the model with the threshold given by exchange rate changes. Furthermore, initial movements of appreciation were possibly not perceived immediately as having longer duration, postponing the effect on prices. In fact, the model estimates the short-run pass-through, that is, the effect on current inflation of the change in the exchange rate in the previous quarter. The appreciation contributed to the reduction in inflation, but probably with lags greater than one quarter.
4. CONCLUSIONS
This paper explores the possibility of the presence of a nonlinear pass-through from the exchange rate to inflation in Brazil. We have estimated models for the Phillips curve combined with the methodology of threshold models. In these models, the parameter values depend on which regime the economy is, which are determined endogenously by means of an observed variable.
The choice of variables used was based on the possible sources of nonlinearity of the pass-through reported in the literature. In particular, we have examined three sources:
i) business cycle;
ii) exchange rate changes; and
iii) exchange rate volatility.
The estimations indicate the presence of nonlinear mechanisms in the short-run pass-through in Brazil. The short-run pass-through is higher when the economy is booming, when the exchange rate depreciates above some threshold, and when exchange rate volatility is lower. These results have important implications for monetary policy and are possibly related to a pricing-to-market behavior, the presence of price adjustment costs, and uncertainty about the degree of persistence of exchange rate changes.
BIBLIOGRAPHY
- Aguiar, A. & Martins, M. F. (2002). Trend, Cycle and Nonlinear Trade-Off in the Euro-Area 1970-2001 CEMPRE.
- Albuquerque, C. R. & Portugal, M. S. (2005). Pass-through from exchange rate to prices in Brazil: An analysis using time-varying parameters for the 1980-2002 period. Revista de Economía, 12(1):1773. Montevideo.
- Albuquerque, C. R. & Portugal, M. S. (2006). Testing nonlinearities between Brazilian exchange rate and inflation volatilities. Banco Central do Brasil. Working Paper Series 106.
- BACEN (2003). Inflation report. Banco Central do Brasil, p. 11618, Dec.
- Bean, C. (2000). The convex Phillips curve and macroeconomic policymaking under uncertainty. Mimeo, London School of Economics.
- Bogdansky, J., Tombini, A., & Werlang, S. (2000). Implementing inflation targeting in Brazil. Banco Central do Brasil. Working Paper Series 1.
- Caner, M. (2002). A note on least absolute deviation estimation of a threshold model. Econometric Theory, 18(3):80014.
- Caner, M. & Hansen, B. (2004). Instrumental variable estimation of a threshold model. Econometric Theory, 20(5):81343.
- Carneiro, D., Monteiro, A. M., & Wu, T. (2002). Mecanismos não-lineares de repasse cambial para o IPCA. Departamento de Economia PUC-Rio, Texto para Discussão 462.
- Chadha, B., Masson, P., & Meredith, G. (1992). Models of inflation and the costs of disinflation. IMF Staff Papers, 39(2):395431.
- Chan, K. S. (1993). Consistency and limiting distribution of the least squares estimator of a threshold autoregressive mocel. The Annals of Statistics, 21(1):520533.
- Clements, M. & Sensier, M. (2003). Asymmetric output gap effects in Phillips curve and mark-up pricing models: Evidence for the US and the UK. Scottish Journal of Political Economy, 50(4):35974.
- Dupasquier, C. & Ricketts, N. (1998). Nonlinearities in the output-inflation relationship: Some empirical results for Canada. Bank of Canada Working Paper 9814.
- Eisner, R. (1997). New view of the NAIRU. In Davidson, P. & Kregel, J., editors, Improving the Global Economy: Keynesian and the Growth in Output and Employment Edward Elgar Publishing, Cheltenham, UK and Lyme, US.
- Filardo, A., J. (1998). New evidence on the output cost of fighting inflation. Economic Review, 83(3):3361.
- Franses, P. H. & van Dijk, D. (2000). Nonlinear Time Series Models in Empirical Finance Cambridge University Press.
- Gil-Pareja, S. (2000). Exchange rates and European countries' export prices: An empirical test for asymmetries in pricing to market behavior. Weltwirtschaftliches Archiv, 136(1):123.
- Goldberg, P. K. (1995). Product differentiation and oligopoly in international markets: The case of the US automobile industry. Econometrica, 63(4):891951.
- Goldfajn, I. & Werlang, S. (2000). The pass-through from depreciation to inflation: A panel study. Banco Central do Brasil. Working Paper Series 5.
- Hansen, B. E. (1996). Inference when a nuisance parameter is not identified under the null hypothesis. Econometrica, 64(2):41330.
- Hansen, B. E. (1999). Threshold effects in non-dynamic panels: Estimation, testing and inference. Journal of Econometrics, 93(2):34568.
- Hansen, B. E. (2000). Sample splitting and threshold estimation. Econometrica, 68(3):575603.
- Laxton, D., Meredith, G., & Rose, D. (1995). Asymmetric effects of economic activity on inflation: Evidence and policy implications. IMF Staff Papers, 42(2):34474.
- Laxton, D., Rose, D., & Tambakis, D. (1999). The US Phillips curve: The case for asymmetry. Journal of Economic Dynamics and Control, 23(910):145985.
- Mahdavi, S. (2002). The response of the US export prices to changes in the dollar's effective exchange rate: Further evidence from industrial level data. Applied Economics, 34(17):211525.
- Mann, C. L. (1986). Prices, profit margins and exchange rates. Federal Reserve Bulletin, 72(6):36679.
- Muinhos, M. K. (2001). Inflation targeting in an open financially integrated emerging economy: The case of Brazil. Banco Central do Brasil. Working Paper Series 26.
- Muinhos, M. K. & Alves, S. A. L. (2003). Medium-size macroeconomic model for the Brazilian economy. Banco Central do Brasil. Working Paper Series 64.
- Nobay, A. R. & Peel, D. A. (2000). Optimal monetary policy with a nonlinear Phillips curve. Economics Letters, 67(2):15964.
- Ohno, K. (1989). Export pricing behavior of manufacturing: A US-Japan comparison. IMF Staff Papers, 36(3):55079.
- Olivei, G. P. (2002). Exchange rates and the prices of manufacturing products imported into the United States. New England Economic Review, 1st Quarter:318.
- Pollard, P. S. & Coughlin, C. C. (2004). Size matters: Asymmetric exchange rate pass-through at the industrial level. University of Nottingham. Research Paper Series 2004/13.
- Schaling, E. (2004). The nonlinear Phillips curve and inflation forecast targeting: Symmetric versus asymmetric monetary policy rules. Journal of Money, Credit and Banking, 36(3):36186.
- Stiglitz, J. (1997). Reflections on the natural rate hypothesis. Journal of Economic Perspectives, 11(1):310.
- Tambakis, D. N. (1999). Monetary policy with a nonlinear Phillips curve and asymmetric loss. Studies in Nonlinear Dynamics and Econometrics, 3(4):22337.
- Tong, H. (1978). On a threshold model. In Chen, C. H., editor, Pattern Recognition and Signal Processing, pages 10141. Sijthoff & Noordgoff, Amsterdam.
- Tong, H. & Lim, K. S. (1980). Threshold autoregressions, limit cycles and data. Journal of the Royal Statistical Society, 42(3):24592.
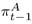 +
+ 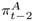 )/2 and
)/2 and 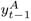 +
+ 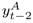 )/2, where the superscript
)/2, where the superscript 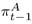 +
+ 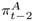 +
+ 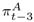 )/3, and for the output gap term, the average at
)/3, and for the output gap term, the average at 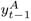 +
+ 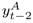 )/2, where the superscript
)/2, where the superscript Publication Dates
-
Publication in this collection
10 Nov 2010 -
Date of issue
Sept 2010

















