Resumos
O projeto do processo de desterpenação do óleo da casca de laranja com CO2 supercrítico exige o bom conhecimento do comportamento de fases da mistura envolvida. Neste trabalho, faz-se uma análise termodinâmica preliminar desse processo, calculando-se a seletividade a partir da modelagem do equilíbrio líquido-vapor (ELV) para o sistema CO2-limoneno-linalol, com base em dados ternários medidos recentemente. Utilizou-se uma modificação da equação de Peng-Robinson e, com dados binários de ELV, avaliou-se a sua capacidade preditiva considerando-se 2 aspectos: a predição do equilíbrio a uma certa temperatura usando-se os parâmetros estimados em outra temperatura e a predição do comportamento de fases do sistema ternário com os parâmetros estimados dos sistemas binários. Foram determinados também os parâmetros de interação entre limoneno e linalol a partir dos dados experimentais do ternário.
CO2+limoneno+linalol; equilíbrio líquido-vapor; equação de Peng-Robinson; desterpenação; seletividade
Process design for supercritical CO2 deterpenation of orange peel oil requires accurate knowledge of phase behavior. This work is focused on modeling high-pressure vapor-liquid equilibrium for the ternary system CO2-limonene-linalool, owing to do a preliminary thermodynamics analysis of this process based on calculated selectivity values. A modification of Peng-Robinson equation of state was adopted to regress binary interaction parameters from experimental VLE data and its capacity for temperature extrapolating calculations was investigated. A comparison of ternary VLE obtained from the respective binary systems and that calculated using additionally ternary informations was done.
CO2+limonene+linalool; vapor-liquid equilibrium; Peng-Robinson EOS; deterpenation; selectivity
ANÁLISE TERMODINÂMICA DA DESTERPENAÇÃO DO ÓLEO DA CASCA DE LARANJA COM CO2 SUPERCRÍTICO A PARTIR DE UMA MISTURA SINTÉTICA11 Recebido para publicação em 05/08/97. Aceito para publicação em 23/11/97.2 PEQ-COPPE-UFRJ, Centro de Tecnologia, bloco G, sala 115, Cidade Universitária, Ilha do Fundão, CEP 21945-970, Rio de Janeiro/RJ. E-mail:
Silvio A.B. VIEIRA DE MELO21 Recebido para publicação em 05/08/97. Aceito para publicação em 23/11/97.2 PEQ-COPPE-UFRJ, Centro de Tecnologia, bloco G, sala 115, Cidade Universitária, Ilha do Fundão, CEP 21945-970, Rio de Janeiro/RJ. E-mail: , Angela M.C. ULLER21 Recebido para publicação em 05/08/97. Aceito para publicação em 23/11/97.2 PEQ-COPPE-UFRJ, Centro de Tecnologia, bloco G, sala 115, Cidade Universitária, Ilha do Fundão, CEP 21945-970, Rio de Janeiro/RJ. E-mail: , Fernando L.P. PESSOA31 Recebido para publicação em 05/08/97. Aceito para publicação em 23/11/97.2 PEQ-COPPE-UFRJ, Centro de Tecnologia, bloco G, sala 115, Cidade Universitária, Ilha do Fundão, CEP 21945-970, Rio de Janeiro/RJ. E-mail: , *1 Recebido para publicação em 05/08/97. Aceito para publicação em 23/11/97.2 PEQ-COPPE-UFRJ, Centro de Tecnologia, bloco G, sala 115, Cidade Universitária, Ilha do Fundão, CEP 21945-970, Rio de Janeiro/RJ. E-mail:
RESUMO
O projeto do processo de desterpenação do óleo da casca de laranja com CO2 supercrítico exige o bom conhecimento do comportamento de fases da mistura envolvida. Neste trabalho, faz-se uma análise termodinâmica preliminar desse processo, calculando-se a seletividade a partir da modelagem do equilíbrio líquido-vapor (ELV) para o sistema CO2-limoneno-linalol, com base em dados ternários medidos recentemente. Utilizou-se uma modificação da equação de Peng-Robinson e, com dados binários de ELV, avaliou-se a sua capacidade preditiva considerando-se 2 aspectos: a predição do equilíbrio a uma certa temperatura usando-se os parâmetros estimados em outra temperatura e a predição do comportamento de fases do sistema ternário com os parâmetros estimados dos sistemas binários. Foram determinados também os parâmetros de interação entre limoneno e linalol a partir dos dados experimentais do ternário.
Palavras-chave: CO2+limoneno+linalol, equilíbrio líquido-vapor, equação de Peng-Robinson, desterpenação, seletividade
SUMMARY
THERMODYNAMIC ANALYSE OF DETERPENATION OF ORANGE PEEL OIL. Process design for supercritical CO2 deterpenation of orange peel oil requires accurate knowledge of phase behavior. This work is focused on modeling high-pressure vapor-liquid equilibrium for the ternary system CO2-limonene-linalool, owing to do a preliminary thermodynamics analysis of this process based on calculated selectivity values. A modification of Peng-Robinson equation of state was adopted to regress binary interaction parameters from experimental VLE data and its capacity for temperature extrapolating calculations was investigated. A comparison of ternary VLE obtained from the respective binary systems and that calculated using additionally ternary informations was done.
Keywords: CO2+limonene+linalool, vapor-liquid equilibrium, Peng-Robinson EOS, deterpenation, selectivity
1 INTRODUÇÃO
O óleo da casca de laranja constitui-se numa matéria-prima importante para as indústrias de alimentos, bebidas, cosméticos e perfumes. O seu aproveitamento in natura, porém, é tecnicamente inviável, pois o alto teor de monoterpenos presentes implica num produto instável, muito sensível a luz e calor. As técnicas tradicionalmente utilizadas para a remoção parcial de terpenos (desterpenação) levam a resultados pouco satisfatórios, seja por provocarem degradação térmica dos compostos, seja pela presença de quantidades residuais de solventes no produto final ou pelos baixos rendimentos obtidos. Nesse contexto é que a extração com fluido supercrítico surgiu como tecnologia alternativa.
Embora seja uma mistura complexa de mais de 200 componentes, o óleo da casca de laranja pode ser estudado como uma mistura sintética dos seus 2 componentes-chave: o limoneno, representante da fração terpênica, e o linalol, representante da fração oxigenada.
A aplicação do CO2 supercrítico à desterpenação do óleo essencial de laranja vem sendo considerada em vários trabalhos publicados na literatura (2, 5, 11, 12, 13). Porém, a escassez de dados experimentais de equilíbrio líquido-vapor (ELV) sempre impôs dificuldades à análise termodinâmica do processo de modo rigoroso. A publicação recente de dados experimentais de ELV para os sistemas binários CO2+limoneno e CO2+linalol e para o ternário CO2+limoneno+linalol permite hoje que tal análise seja feita (3, 4, 16, 17, 19).
No presente trabalho, uma modificação da equação de Peng-Robinson é usada para correlacionar os dados de ELV acima citados. Além disso, é investigada a capacidade preditiva do modelo proposto quanto à extrapolação para outras temperaturas e quanto à predição do comportamento de fases do sistema ternário com os parâmetros estimados a partir dos correspondentes sistemas binários. É dada ênfase ao problema da seletividade entre limoneno e linalol, através do cálculo do equilíbrio líquido-vapor para o sistema CO2 + limoneno + linalol, sendo os parâmetros de interação binária limoneno/linalol determinados a partir dos dados experimentais de ELV deste sistema.
2 MODELAGEM DO EQUILÍBRIO LÍQUIDO-VAPOR
O bom conhecimento do equilíbrio de fases a alta pressão passa necessariamente pela determinação experimental da pressão, temperatura e composição das fases em equilíbrio. A conseqüência natural desta etapa é correlacionar acuradamente os dados experimentais através de modelos termodinâmicos, permitindo a interpolação de dados para outras condições.
As dificuldades envolvidas em um estudo experimental conduzido a alta pressão, aliadas ao custo operacional e ao tempo empregado, fazem com que a quantidade de pontos experimentais determinados seja a menor possível. Disso decorre a importância de avaliação da capacidade preditiva do modelo, ou seja, da possibilidade de seu uso na extrapolação, a partir dos dados experimentais disponíveis, para condições além daquelas medidas.
Assim, a escolha de um modelo termodinâmico, para ser usado na descrição do equilíbrio de fases como parte importante da simulação de um processo de separação, é condicionada preponderantemente pela sua capacidade correlativa e preditiva.
Os sistemas presentes na extração com fluido supercrítico (EFSC) caracterizam-se geralmente pela grande diferença de tamanho entre as moléculas do solvente e dos solutos, o que explica valores bastante distintos para propriedades como pressão de vapor, volatilidade, temperatura e pressão críticas destes compostos, entre outras. Consequentemente, as misturas apresentam forte assimetria. Em decorrência, deve-se considerar a diferença de intensidade das forças de atração intermoleculares, ou seja, as polaridades das substâncias envolvidas.
O cálculo do equilíbrio líquido-vapor (ELV) a alta pressão é preferencialmente realizado seguindo-se a abordagem f-f , ou seja, ambas as fases são modeladas através de uma equação de estado e caracterizadas por seus respectivos coeficientes de fugacidade. A principal vantagem desta abordagem é poder ser aplicada para toda a faixa de temperatura e pressão, além do estado de referência para a fugacidade (o gás ideal) ser o mesmo para as duas fases, garantindo a continuidade.
Com base em experiência anterior e em estudos recentes, escolheu-se uma modificação da equação de Peng-Robinson para descrever o equilíbrio líquido-vapor dos sistemas binários e ternários envolvendo CO2, limoneno e linalol (14, 18).
2.1 A equação de Peng-Robinson
Escolheu-se a equação de estado cúbica de Peng-Robinson para o cálculo do equilíbrio líquido-vapor (8). A forma explícita na pressão é dada por
 (1)
(1)
Para os componentes puros, tem-se que
 (2)
(2)
 (3)
(3)
A modificação da equação de Peng-Robinson consistiu na substituição da expressão f(Tr) original pela expressão de Aznar-Telles, anteriormente utilizada com sucesso para descrever sistemas contendo produtos naturais e fluido supercrítico (1, 7).
A expressão de Aznar-Telles é dada por:
 (4)
(4)
sn(x) = 1 se x>0
sn(x) = -1 se x<0.
onde:
m,n e G são os parâmetros estimados a partir de dados de pressão de vapor.
A extensão da equação de Peng-Robinson para misturas implica na substituição das expressões (2) e (3) pelas seguintes regras de mistura, selecionadas com base num estudo comparativo realizado recentemente pelos autores (18):
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
onde:
kij e lij são os parâmetros de interação binária ajustáveis.
2.2 Cálculos e Resultados para os Sistemas Binários
O cálculo do ELV para os sistemas CO2-limoneno e CO2-linalol foi realizado através de um algoritmo de ponto de bolha. A estimação dos parâmetros de interação binária foi feita utilizando-se o método da máxima verossimilhança de forma simplificada, equivalente ao método dos mínimos quadrados ponderados, onde os pesos foram os desvios padrão dos valores experimentais das variáveis calculadas, neste caso a pressão e a fração molar da fase vapor (9).
O desvio relativo percentual na pressão e o desvio absoluto percentual na fração molar da fase vapor foram obtidos, respectivamente, pelas seguintes fórmulas:
 (9)
(9)
 (10)
(10)
onde:
NPE é o número de pontos experimentais.
Os valores de todas as propriedades dos componentes puros necessárias ao cálculo do ELV com a equação cúbica apresentada estão dispostos na Tabela 1. Os valores de Tc e Pc para o limoneno e o linalol foram calculados por contribuição de grupos, seguindo-se uma metodologia proposta anteriormente (15). Para o CO2, foram usados os valores experimentais reportados em (10). Os parâmetros da expressão de Aznar-Telles foram obtidos segundo o modo descrito em (7).
Propriedades críticas e parâmetros da expressão de Aznar-Telles para o dióxido de carbono, limoneno e linalol.
A Tabela 2 mostra os valores dos parâmetros estimados e dos desvios de pressão e composição da fase vapor para os sistemas CO2-limoneno e CO2-linalol. Para ambos os sistemas, os desvios na pressão não ultrapassaram 3 % e para a maioria dos casos o desvio na fração molar da fase vapor foi inferior a 0.01. O valor deste desvio de 0.0173 para o CO2-limoneno a 50 oC foi sobretudo devido às incertezas relativamente altas dos pontos experimentais publicados em (6).
Parâmetros de interação binária estimados e desvios de pressão e composição calculados para os sistemas CO2-limoneno e CO2-linalol.
NPE é o número de pontos experimentais.
Nas Tabelas 3 e 4 apresentam-se os resultados da extrapolação dos cálculos para outras temperaturas, diferentes daquela onde foram estimados os parâmetros, para os sistemas CO2-limoneno e CO2-linalol, respectivamente. Os resultados para o primeiro sistema indicaram a boa performance do modelo, sobretudo quando os parâmetros estimados a 50 oC são utilizados para predizer as outras isotermas. Mesmo no pior dos casos, com os parâmetros estimados a 40 oC empregados para o cálculo a 70 oC, o desvio na pressão foi inferior a 9 %. Para o CO2-linalol, os resultados foram ainda melhores, o que pode ser justificado pelo fato dos dados experimentais estarem disponíveis apenas para 3 isotermas, ou seja, uma a menos que o outro sistema.
Predição de P e y1 (desvios calculados) a partir dos parâmetros estimados em outras condições de T para o sistema CO2(1)-limoneno(2).
NPC é o número de pontos calculados
Te é a temperatura em que foram estimados os parâmetros
Tp é a temperatura em que foi feita a predição do ELV
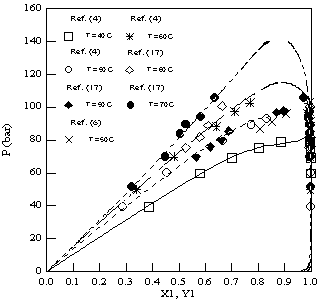
As Figuras 1 e 2 ilustram as curvas de ELV para o sistema CO2-limoneno, calculadas pela equação de Peng-Robinson e comparadas com os dados experimentais disponíveis. Observa-se a boa concordância entre os valores experimentais e calculados para as quatro isotermas, porém a 70 oC o ponto crítico da mistura é supostamente superpredito pelo modelo utilizado.
Nas Figuras 3 e 4 são traçadas as curvas de ELV, experimentais e calculadas, para o sistema CO2-linalol. Neste caso, além da boa representação dos dados experimentais pela equação de Peng-Robinson, tem-se uma descrição satisfatória do ponto crítico da mistura para as 3 isotermas existentes.
Equilíbrio líquido-vapor para o sistema CO2(1)-limoneno(2) a 40, 50, 60 e 70 oC calculado pela equação de Peng-Robinson modificada.
Equilíbrio líquido-vapor para o sistema CO2(1)-linalol(2) a 40, 50 e 60 oC calculado pela equação de Peng-Robinson modificada.
Predição de P e y1 (desvios calculados) a partir dos parâmetros estimados em outras condições de T para o sistema CO2-linalol.
NPC é o número de pontos calculados
Te é a temperatura em que foram estimados os parâmetros
Tp é a temperatura em que foi feita a predição do ELV
2.3 Cálculos e Resultados para o Sistema Ternário
O cálculo do ELV para o sistema ternário CO2-limoneno-linalol foi feito de modo análogo ao usado para os sistemas binários, ou seja, por meio de um algoritmo de ponto de bolha. Duas estratégias foram utilizadas. A primeira consistiu em tentar predizer o ELV do sistema ternário a partir dos sistemas binários CO2-limoneno e CO2-linalol, ou seja, usando-se os valores dos respectivos parâmetros de interação binária ajustados e o parâmetro de interação entre limoneno e linalol considerado nulo.
A segunda estratégia de cálculo efetuou a estimação dos parâmetros de interação binária entre limoneno e linalol a partir dos dados de ELV do sistema ternário. Os valores dos parâmetros de interação entre os pares CO2-limoneno e CO2-linalol foram considerados aqueles estimados com os pontos experimentais dos respectivos sistemas binários.
O desvio relativo percentual na pressão é dado pela expressão (9) e os desvios absolutos percentuais nas frações molares dos componentes 1 e 2 na fase vapor são obtidos de forma análoga à da expressão (10).
A Tabela 5 reporta a seguir os valores de todos os parâmetros de interação binária do sistema CO2-limoneno-linalol e os respectivos desvios são apresentados na tabela 6.
Desvios de pressão e composição da fase vapor calculados a 50 oC para o sistema CO2-limoneno-linalol.
Os resultados apresentados na Tabela 6 indicam que o desvio relativo percentual médio na pressão se reduz à metade quando os parâmetros de interação entre o limoneno e o linalol são estimados a partir dos dados do sistema ternário. Para a fração molar do CO2 na fase vapor, os desvios são bastante próximos e razoáveis. Porém, os desvios obtidos para a fração molar do limoneno foram da mesma ordem de grandeza do valor desta. Isto pode levar a uma grande incerteza no valor da seletividade, já que esta é a razão entre os coeficientes de partição (K=y/x) de limoneno e linalol.
A existência de poucos dados experimentais para o sistema ternário CO2-limoneno-linalol constitui, sem dúvida, um fator limitante para a modelagem completa do comportamento de fases do mesmo. Porém, apesar de poucos, os pontos experimentais são indicativos de que a interação entre as moléculas de limoneno e linalol não pode ser desprezada, ou seja, os parâmetros k23 e l23 não devem ser considerados nulos.
A seguir faz-se a análise da seletividade com base nos parâmetros do modelo estimados a partir deste sistema ternário.
3 ANÁLISE DA SELETIVIDADE
A seletividade é um indicador da afinidade que um solvente tem em dissolver preferencialmente um determinado soluto em relação a outro. Logo, sob o ponto de vista da extração, o melhor solvente será o que dissolver o máximo e o mínimo dos componentes a serem separados. Quando a extração supercrítica envolve o equilíbrio líquido-gás, a seletividade, ou volatilidade relativa, pode ser definida como
 (11)
(11)
isto é, a seletividade b do componente 2 em relação ao componente 3, no mesmo solvente, é a razão entre os coeficientes de partição dos componentes 2 e 3, nas duas fases em equilíbrio. Geralmente, o componente 2 é o mais volátil, o que implica que o valor de b seja sempre maior do que 1. Quanto maior este valor, melhor, pois mais fácil (mais seletiva) será a separação.
Pela definição anterior, a seletividade pressupõe a existência de pelo menos 3 componentes no mesmo sistema. Porém, dados de ELV de sistemas ternários nem sempre estão disponíveis, principalmente a alta pressão. Uma forma aproximada de avaliar a seletividade de um solvente supercrítico por dois solutos líquidos é a partir da razão entre as constantes de equilíbrio destes, obtidas cada uma independentemente dos dados de ELV dos respectivos sistemas binários solvente-soluto. Esta forma será referida aqui como pseudo-seletividade, sendo definida pela expressão:
 (12)
(12)
onde:
As frações molares dos componentes são obtidas de sistemas binários.
Comparação entre os valores experimentais e calculados da seletividade a 50 oC para o sistema CO2(1)-limoneno(2)-linalol(3).
Nota: bexp e P são a seletividade e a pressão experimentais; bcal1 e Pcal1 são a seletividade e a pressão calculadas com k23 = 0 e l23 = 0, respectivamente; bcal2 e Pcal2 são a seletividade e a pressão calculadas com k23 = 0.204423 e l23 = 0.244101.
O valor experimental da seletividade para o sistema CO2-limoneno-linalol a 50 oC é conhecido (16). Para os sistemas CO2-limoneno e CO2-linalol a pseudo-seletividade "experimental" foi determinada apenas para os pontos onde os valores experimentais das constantes de equilíbrio do limoneno e do linalol estão na mesma pressão, o que nem sempre acontece. Os valores das seletividades calculadas preditivamente, a partir dos sistemas binários com os parâmetros entre o limoneno e o linalol iguais a zero, e calculadas a partir do sistema ternário, com k23 e l23 diferentes de zero, são comparados com os valores experimentais na tabela 7. Nota-se claramente a melhoria dos resultados quando os cálculos são feitos incluindo-se as informações do sistema ternário. O terceiro ponto mostra um aumento do valor da seletividade, calculado pelos 2 modos descritos, em discordância com a tendência experimental. A princípio, poder-se-ia atribuir esta discrepância a possíveis erros experimentais do sistema ternário, já que poucos dados foram determinados. Porém, a figura 6, discutida adiante, sugere que este tipo de comportamento é inerente ao modelo utilizado, já que o cálculo da pseudo-seletividade a partir dos sistemas binários revelou curvas com comportamentos qualitativamente semelhantes.
A Figura 5 mostra a seguir os valores experimentais de h23 para 3 isotermas, ajustados por curvas "splines". Pode-se dizer que, para as isotermas de 50 e 60oC, a pseudo-seletividade diminui com o aumento da pressão à temperatura constante. À pressão constante, a pseudo-seletividade diminui com o aumento de temperatura até 80 bar, invertendo esta tendência após este ponto, isto é, a seletividade passa a aumentar com o aumento da temperatura. Este comportamento acontece provavelmente como conseqüência dos cruzamentos das curvas de bolha a 50 e 60oC, fenômeno bastante conhecido e denominado de "crossing-over". A isoterma a 40oC mostra um comportamento diferente, onde aparece uma pequena região, aproximadamente entre 70 e 75 bar, em que a pseudo-seletividade aumenta com o aumento da pressão. Uma possível explicação para este fato é o efeito concorrente entre a pressão de vapor dos solutos e a densidade do solvente, que é mais expressiva nesta temperatura. Vale lembrar que esta região está bastante próxima do ponto crítico do dióxido de carbono, cujas coordenadas reduzidas nestas condições são Tr = 1.03 e 0.96<Pr<1.03, e consequentemente as influências da pressão e temperatura são mais pronunciadas.
Influência da pressão na pseudo-seletividade entre o limoneno e o linalool em CO2: valores experimentais a 40 (¨), 50 (¡) e 60oC (X) ajustados por curvas "spline".
Na Figura 6, as pseudo-seletividades calculadas são traçadas para as mesmas temperaturas e faixa de pressão da figura 5. Comparando-se estas 2 figuras, verifica-se que as curvas calculadas são qualitativamente similares, porém apresentam-se todas deslocadas em relação aos pontos experimentais, sendo os valores das pseudo-seletividades calculados, em média, o dobro dos valores experimentais. Além disso, observa-se também a predição discordante quanto ao efeito da temperatura e pressão, já que nesse caso a pseudo-seletividade aumenta com o aumento da temperatura à pressão constante.
Variação com a pressão da pseudo-seletividade entre o limoneno e o linalol em CO2, calculada com o modelo M1, a 40, 50 e 60oC.
Na Figura 7 ilustram-se as curvas de pseudo-seletividade e seletividade, valores experimentais e calculados, a 50 oC. Nota-se que os valores experimentais da pseudo-seletividade e da seletividade são bastante próximos entre 75 e 90 bar. Porém, os valores calculados revelam que a tentativa de predizer a seletividade a partir dos binários leva a erros de até 200%. Em compensação, verifica-se a grande melhoria nos resultados quando os cálculos da seletividade são feitos usando-se os parâmetros estimados a partir dos dados experimentais do sistema ternário. Isto reforça a premissa de que os dados experimentais do sistema ternário são fundamentais para a avaliação correta do comportamento de fases do sistema CO2-limoneno-linalol.
Influência da pressão na seletividade entre o limoneno e o linalol em CO2 a T = 50 oC: (¨) experimental; (¡) "experimental" obtida dos binários (pseudo-seletividade) ; (x) calculada dos binários (pseudo-seletividade); (¨) calculada do ternário, com k23 = 0.204423 e l23 = 0.244101.
A Figura 8 foi construída visando-se responder à seguinte pergunta: na ausência de dados experimentais do sistema ternário, é melhor calcular a pseudo-seletividade a partir dos binários ou obter a seletividade a partir do cálculo preditivo do ternário? As curvas calculadas indicam que é preferível tentar predizer o sistema ternário, mesmo com os parâmetros k23 e l23 iguais a zero.
Influência da pressão na seletividade entre o limoneno e o linalol em CO2 a T = 50 oC: (¨) experimental; (¡) calculada com k23 = 0 e l23 = 0; ( ) calculada com k23 = 0.204423 e l23 = 0.244101.
A figura 9 mostra a superioridade dos resultados da seletividade obtidos com os parâmetros k23 e l23 estimados diretamente do ternário frente àqueles alcançados com estes parâmetros iguais a zero. Os resultados indicam que a melhor concordância entre o modelo e os pontos experimentais ocorre a 80 bar, que corresponde também à região onde os valores de seletividade são relativamente mais interessantes do ponto de vista da separação limoneno-linalol.
Influência da pressão na seletividade entre o limoneno e o linalol em CO2 a T = 50 oC: (¨) calculada dos binários (pseudo-seletividade); (¡) calculada do ternário com k23 = 0 e l23 = 0.
4 CONCLUSÕES
A modelagem termodinâmica do equilíbrio líquido-vapor para os sistemas CO2-limoneno, CO2-linalol e CO2-limoneno-linalol foi realizada pela equação de Peng-Robinson modificada, com as regras de mistura quadráticas para os parâmetros a e b, conforme sugerido em trabalho recentemente publicado (8). Levando-se em conta a complexidade existente em uma mistura soluto-fluido supercrítico, onde o alto grau de não-idealidade é decorrência da forte assimetria entre as moléculas e das suas interações num fluido denso, pode-se afirmar que os resultados foram bastante satisfatórios. A razão mais provável para este fato é o uso da regra quadrática, com um parâmetro de interação binária, também para o parâmetro b, que está diretamente relacionado ao tamanho das moléculas. Além disso, cabe destacar a boa capacidade preditiva do modelo na extrapolação para outras temperaturas.
Ficou demonstrada a importância da modelagem do ELV incluindo-se também o sistema ternário e a comparação dos valores de seletividade experimentais e calculados são indicativos da viabilidade técnica da separação entre limoneno e linalol em presença de CO2 supercrítico.
A partir do exposto, sugere-se que esta separação seja simulada a 50 oC e pressões variando de 80 a 90 bar, onde a seletividade apresenta valores razoáveis. Contribuíram também para esta decisão o fato desta ser a temperatura em que mais pontos experimentais estão disponíveis para os sistemas binários e a única temperatura em que dados experimentais para o sistema ternário foram determinados, isto é, uma condição de maior confiabilidade.
5 REFERÊNCIAS BIBLIOGRÁFICAS
[1] ALMEIDA,G.S., AZNAR,M. & TELLES,A.S., 1991, RBE, Caderno de Eng. Química, vol.8 (2), 95-123.
[2] BÜDICH,M. et al., 1996, In: Proc. of the 3ème Colloque sur le Fluides Supercritiques, 197-204, Grasse.
[3] IWAI,Y. et al., 1994, J. Chem. Eng. Data, 39, 900-902.
[4] IWAI,Y. et al., 1996, J. Chem. Eng. Data, 41, 951-952.
[5] JAUBERT,J.-N., GONÇALVES,M.M. & BARTH,D., 1997, In: Proc. of the 4th Int. Symp. on Supercrit. Fluids, 195-198, Sendai.
[6] MATOS,H.A. et al., 1989, Fluid Phase Equilibria, 52, 357-364.
[7] MELO,S.A.B.V. de, 1994. Cálculo de Propriedades Termodinâmicas em Sistemas Contendo Produtos Naturais e Fluido Supercrítico, Tese de M.Sc., COPPE/UFRJ, Rio de Janeiro, RJ, Brasil.
[8] PENG,D.Y. & ROBINSON,D.B., 1976, Ind. Eng. Chem. Fundam., vol.15, 58-64.
[9] PINTO,J.C. et al., 1987, "ESTIMA: Um Pacote Computacional para Estimação de Parâmetros e Projeto de Experimentos", PEQ/COPPE/UFRJ.
[10] REID,R.C., PRAUSNITZ,J.M. & POLING,B.E.. The Properties of Gases & Liquids, 4ed. Singapore, McGraw-Hill, 1989.
[11] REVERCHON,E., PERRE,C. & PERRUT,M., 1996, In: Proc. 3ème Colloque sur les Fluides Supercritiques, 35-44, Grasse.
[12] SATO,M., GOTO,M. & HIROSE,T., 1995, "Fractional Extraction with Supercritical Carbon Dioxide for the Removal of Terpenes from Citrus Oil", Ind. Eng. Chem. Res., 34, 3941-3946.
[13] TEMELLI,F. et al., 1988, "Supercritical Carbon Dioxide Extraction of Terpenes from Orange Essential Oil". In: Supercritical Fluid Extraction and Chromatography, Ed. Charpentier,B.A. and Sevenants,M.R., ACS Symp. Series 366, 109-126.
(14) VIEIRA DE MELO,S.A.B. & PESSOA,F.L.P., 1994, Ciência e Tecnologia de Alimentos, 14, 145-157.
[15] VIEIRA DE MELO,S.A.B., MENDES,M.F. & PESSOA,F.L.P., 1996, Brazilian Journal of Chemical Engineering, 13 (4), 192-199.
[16] VIEIRA DE MELO,S.A.B. et al., 1996, In: Proc. of the 3rd Int. Symp. on High Pressure Chemical Engineering, Zürich.
[17] VIEIRA DE MELO,S.A.B. et al., "Ternary Phase Equilibria of CO2 + Limonene + Linalol at 50 oC and Pressures to 9 MPa", submetido ao Journal of Supercritical Fluids, 1997.
[18] VIEIRA DE MELO,S.A.B. et al., "Vapor-Liquid Equilibrium of Orange Peel Oil Components+SC-CO2 System Using Cubic Equation of State - Excess Gibbs Free Energy Models", aprovado para ser apresentado na Fourth Italian Conference on Supercritical Fluids and their Applications, Capri, Itália, setembro de 1997.
[19] BERTUCCO,A. et al., "Binary and Ternary Vapor-Liquid Equilibrium Data for the System CO2-Limonene-Linalol", aprovado para ser apresentado na Fourth Italian Conference on Supercritical Fluids and their Applications, Capri, Itália, setembro de 1997.
6 AGRADECIMENTOS
S.A.B.V.M. e F.L.P.P. agradecem ao CNPq pelas bolsas de pesquisa concedidas.
3
DEQ-EQ-UFRJ, Centro de Tecnologia, bloco E, sala 209, C.P. 68502, Cidade Universitária, Ilha do Fundão, CEP 21949-900, Rio de Janeiro/RJ.
* A quem a correspondência deve ser endereçada.
- (14) VIEIRA DE MELO,S.A.B. & PESSOA,F.L.P., 1994, Cięncia e Tecnologia de Alimentos, 14, 145-157.
Datas de Publicação
-
Publicação nesta coleção
17 Dez 1998 -
Data do Fascículo
Dez 1997
Histórico
-
Aceito
23 Nov 1997 -
Recebido
05 Ago 1997