Resúmenes
La cobertura espacial de las redes de medición en tierra no puede satisfacer todas las necesidades de los usuarios debido a su baja densidad esto es más notable en el caso de la radiación solar. La escasez de datos de irradiación global es la razón para utilizar la heliofanía para su estimación mediante el empleo de diferentes correlaciones que han probado tener un buen ajuste con las mediciones. Para trazar cartas de heliofanía (y a partir de ellas, de irradiación solar global) en un territorio tan extenso como América del Sur es necesario estudiar la relación error-distancia entre estaciones en zonas homogéneas. Para ello, lo habitual es analizar el comportamiento espacial de algunos estadísticos de campos aleatorios, como por ejemplo, la función estructura. En este trabajo, se han utilizado datos medios mensuales de heliofanía de Uruguay y se analizó su variación con la distancia entre estaciones. Se presentan gráficos obtenidos para diferentes épocas del año, analizándose las condiciones de extrapolación espacial de la información. Además, se muestran los resultados del análisis estadístico de series temporales de valores medios anuales de la heliofanía diaria mediante la aplicación del test de Mann-Kendall. Finalmente, se presentan 12 cartas con la distribución espacial de la media mensual de la heliofanía diaria.
Heliofanía; comportamiento temporal y espacial; Uruguay
The spatial coverage of land measurement networks cannot fulfill all the user's needs because their density is low; and this fact becomes more important in the case of solar radiation. The scarcity of global irradiation data is the reason for using sunshine hours in order to estimate them through different correlations which have shown a good fit with the measurements data. In order to draw charts with the spatial distribution of the sunshine-hours monthly averages (and from them, global solar radiation charts also) on such a vast territory as South America, it is necessary to study the error-distance relationship between stations in homogeneous zones. For that purpose, it is usual to analyze the spatial behavior of certain statistics of a random data such as, for example, the structure function. In this paper, sunshine-hours monthly data from Uruguay were used and their variation according to the distance between stations was analyzed. Several graphs, corresponding to different periods within the year are presented, analyzing the spatial extrapolation conditions of the information. Also, the results of the statistical analysis of the annual mean values of the time series of sunshine-hours, using the Mann-Kendall rank test were presented. Finally, 12 charts with the space distribution of sunshine-hours monthly averages were presented.
Sunshine hours; temporal and spatial behavior; Uruguay
ARTIGOS
Algunos aspectos de la climatología solar del Uruguay
Some aspects of the solar climatology of Uruguay
Hugo Grossi Gallegos; Carlos Raichijk; Raúl Righini
GERSolar, Instituto de Ecología y Desarrollo Sustentable (INEDES), Departamento de Ciencias Básicas, Universidad Nacional de Lujan, Lujan, Buenos Aires, Argentina. gersolar@mail.unlu.edu.ar
RESUMEN
La cobertura espacial de las redes de medición en tierra no puede satisfacer todas las necesidades de los usuarios debido a su baja densidad esto es más notable en el caso de la radiación solar. La escasez de datos de irradiación global es la razón para utilizar la heliofanía para su estimación mediante el empleo de diferentes correlaciones que han probado tener un buen ajuste con las mediciones. Para trazar cartas de heliofanía (y a partir de ellas, de irradiación solar global) en un territorio tan extenso como América del Sur es necesario estudiar la relación error-distancia entre estaciones en zonas homogéneas. Para ello, lo habitual es analizar el comportamiento espacial de algunos estadísticos de campos aleatorios, como por ejemplo, la función estructura. En este trabajo, se han utilizado datos medios mensuales de heliofanía de Uruguay y se analizó su variación con la distancia entre estaciones. Se presentan gráficos obtenidos para diferentes épocas del año, analizándose las condiciones de extrapolación espacial de la información. Además, se muestran los resultados del análisis estadístico de series temporales de valores medios anuales de la heliofanía diaria mediante la aplicación del test de Mann-Kendall. Finalmente, se presentan 12 cartas con la distribución espacial de la media mensual de la heliofanía diaria.
Palabras claves: Heliofanía, comportamiento temporal y espacial, Uruguay.
ABSTRACT
The spatial coverage of land measurement networks cannot fulfill all the user's needs because their density is low; and this fact becomes more important in the case of solar radiation. The scarcity of global irradiation data is the reason for using sunshine hours in order to estimate them through different correlations which have shown a good fit with the measurements data. In order to draw charts with the spatial distribution of the sunshine-hours monthly averages (and from them, global solar radiation charts also) on such a vast territory as South America, it is necessary to study the error-distance relationship between stations in homogeneous zones. For that purpose, it is usual to analyze the spatial behavior of certain statistics of a random data such as, for example, the structure function. In this paper, sunshine-hours monthly data from Uruguay were used and their variation according to the distance between stations was analyzed. Several graphs, corresponding to different periods within the year are presented, analyzing the spatial extrapolation conditions of the information. Also, the results of the statistical analysis of the annual mean values of the time series of sunshine-hours, using the Mann-Kendall rank test were presented. Finally, 12 charts with the space distribution of sunshine-hours monthly averages were presented.
Keywords: Sunshine hours, temporal and spatial behavior, Uruguay.
1. INTRODUCCIÓN
La heliofanía (también denominada horas de brillo solar o insolación) es un parámetro meteorológico de importancia. Datos de heliofanía pueden ser empleados para estimar promedios mensuales de irradiación solar global. El rescate de los registros existentes, de gran extensión temporal y amplia cobertura espacial, brinda la posibilidad de completar series históricas de radiación solar interrumpidas por circunstancias diversas; o incluso estimarlas por completo, en aquellos lugares donde no se cuenta aún con datos de irradiación solar.
Además, otras variables de interés agronómico, tales como la evapotranspiración potencial o el rendimiento de cultivos (Grossi Gallegos y Magrin, 1993), están directamente relacionadas con la radiación solar. Contar con series temporales extensas de radiación, permitiría evaluar eventuales cambios en el régimen solar y sus posibles consecuencias sobre los sistemas agrícolas (Magrin et al., 1997).
El análisis del comportamiento espacial y temporal de las horas de sol será determinante al querer efectuar interpolaciones y extrapolaciones de este parámetro en áreas extensas. Un antecedente lo constituyen los trabajos de Grossi Gallegos y Atienza (1992) y de Grossi Gallegos y Spreafichi (2004, 2006), quienes estudiaron el comportamiento espacial de la heliofanía en la región de la Pampa Húmeda argentina como así también sus series temporales a nivel nacional.
Este artículo continúa el estudio de la heliofanía en Uruguay iniciado en un trabajo anterior (Raichijk et al., 2006a), sumando al análisis de la variabilidad espacial y temporal de los datos, el trazado de las cartas mensuales de horas de sol sobre toda la República Oriental del Uruguay.
2. MATERIALES Y MÉTODO
Fueron procesados los datos de insolación total mensual facilitados por la División Climatología Aplicada de la Dirección Nacional de Meteorología de la República Oriental del Uruguay, adquiridos entre 1986 y 2005 en 11 de sus estaciones (Figura 1 y Tabla 1), calculándose los promedios tanto mensuales como anuales de la heliofanía efectiva diaria.
El instrumento recomendado para la medición de la duración de la insolación consiste en una esfera sólida de vidrio pulido que se comporta como una lente convergente montada de tal manera que en su foco se aloja la faja de registro diario. Se denomina heliógrafo del tipo Campbell-Stokes y utiliza fajas de papel especificadas por el Servicio Meteorológico de Francia, las que fueron diseñadas de conformidad con la Organización Meteorológica Mundial (OMM, 1982); las mismas tienen impresa una escala con un paso de media hora, siendo posible apreciar por un observador experimentado hasta décimos de hora.
Los heliógrafos (también conocidos como heliofanógrafos) tienen por objeto medir la duración de la insolación (heliofanía efectiva). La OMM se encargó de estudiar el principio de funcionamiento de este equipo, esencialmente la convergencia de los rayos solares sobre una faja de papel que provoca que ésta se queme. Se encontró que esto ocurre cuando los valores de la radiación solar directa superan un umbral que presenta cierta variabilidad, dependiendo de la ubicación geográfica del instrumento, del clima y del tipo de faja utilizada. En promedio, ese valor se encontró que variaba de 100 a 200 W/m² (WMO, 1981), conviniéndose posteriormente en que el mismo fuera de 120 W/m² cuando se usan las fajas fabricadas a tal efecto (OMM, 1982); sin embargo, se han encontrado valores que van de 16 a 400 W/m² (Gueymard, 1993).
La forma habitual de analizar las condiciones de extrapolación de variables meteorológicas es la propuesta por Gandin (1970) a través de la función estructura, metodología ya aplicada para analizar, por ejemplo, datos de radiación solar en Canadá (Suckling y Hay, 1976), en los Estados Unidos de Norteamérica (Suckling, 1985) y en Argentina (Grossi Gallegos y Lopardo, 1988) y de heliofanía relativa (Grossi Gallegos y Atienza, 1992) en la Pampa Húmeda de Argentina, suponiendo que la misma es una región homogénea y que ambos parámetros varían de manera isotrópica.
Para este caso, si denominamos con n(x,y) a las horas de insolación o heliofanía efectiva medidas en una localidad e indicamos su valor medio con una barra sobre el símbolo, podemos notar la desviación con respecto al valor medio (anomalía) de la siguiente manera:
En base a este formalismo se define la función estructura como:
Dado que todas las estaciones de medición analizadas se encuentran dentro de una misma región climática de tipo templado húmedo (Cfa según la clasificación de Koeppen-Geiger, con precipitación suficiente en todos los meses y temperatura media del mes más caluroso superior a 22°C) y prácticamente a una misma altura (con una diferencia máxima de 225 m, en una zona plana sin accidentes orográficos importantes (ver Tabla 1)) se intentará definir la función estructura en dependencia únicamente de la distancia entre estaciones, lo que permitirá luego realizar extrapolaciones e interpolaciones en toda la región considerada.
Se deberá tener en cuenta que la incerteza en la medición en cada una de las estaciones introduce un error sistemático en el valor de esta función. Suponiendo que dichos errores en diferentes lugares no están correlacionados entre sí o con los valores medidos, ni que dependen de las coordenadas, como mostró Gandin (1970), se podrá estimar la incerteza introducida en la medición si se extrapola la función estructura a distancia cero a partir de la expresión:
donde σn es el error de medición.
Se define, utilizando la expresión introducida por Hay y Suckling (1979), el coeficiente de variabilidad de la siguiente manera:
donde los valores en el denominador indican los promedios de la heliofanía en las localidades para las cuales se calcula la función estructura. Se analizó entonces la variación de este coeficiente con la distancia entre estaciones (Tabla 2), agrupando primero los datos estacionalmente (equinoccios y solsticios) y luego para todo el año.
3. RESULTADOS Y DISCUSIÓN
3. 1 Variabilidad Espacial
Tomando como referencia los valores promedios estacionales (verano: noviembre, diciembre, enero y febrero; equinoccios: marzo, abril, septiembre y octubre; invierno: mayo, junio, julio y agosto) se calculó, para cada par de estaciones del conjunto, el coeficiente de variabilidad en función de la distancia entre ellas para todo el año (Figura 2) y para cada uno de los períodos (Figura 3). Dado que no existen estaciones que disten a menos de 96 km no fue posible detectar la posible convergencia para pequeñas distancias, como se observa en algunos de los trabajos ya citados. De cualquier forma, aproximaciones lineales mostraron un nivel de correlación razonable, con un coeficiente de determinación R2 = 0,69 al considerar por ejemplo todos los casos del año.
De manera similar a lo obtenido con los valores de irradiación solar global en los trabajos ya mencionados, el coeficiente de variabilidad para la heliofanía resultó mayor en invierno que en verano. La proximidad y similitud de las distribuciones estacionales no justifica su diferenciación (Raichijk et al., 2006a), razón por la cual se analiza en detalle la que describe el comportamiento anual (prácticamente coincidente con la de primavera + otoño). En este caso, la expresión resultante es:
donde D es la distancia entre estaciones, medida en kilómetros.
La raíz cuadrada de la función estructura juega el rol de un desvío estándar; su uso en el algoritmo (4) implica que el coeficiente de variabilidad Cv sea representativo de un nivel de confidencia de sólo el 67%. Niveles más altos de confidencia pueden alcanzarse multiplicando los coeficientes obtenidos por el valor de Z apropiado, tal como 1,644 para el 90% (Z es denominada variable Normal tipificada, según García, 2004). Suckling (1983) observó que, aunque los valores de las anomalías no estén normalmente distribuidos, la aproximación utilizada en la definición del coeficiente de variabilidad se comporta como tal cuando se la convierte al nivel de confidencia del 90%. Si se procede de la manera indicada, la expresión lineal hallada se convierte en:
Vale la pena resaltar la importancia de obtener, directamente a partir de su comportamiento espacial, la incerteza cometida en la determinación de los promedios mensuales de heliofanía ya que, generalmente (Hay y Suckling, 1979) se trabaja con valores diarios y luego, suponiendo la validez del Teorema Central del Límite, se afectan los resultados del coeficiente de variabilidad multiplicándolos por 0,183 (esto es, 1/300.5). El conocimiento de esta incerteza es de mucha utilidad para el análisis de la estabilidad de las series temporales. De acuerdo con las Ecuaciones 3 y 6 se ve que los promedios mensuales de heliofanía obtenidos en las estaciones uruguayas son estimados con un error de 5,85%.
3.2 Variabilidad Temporal
Para analizar el comportamiento temporal de esta variable meteorológica en la República Oriental del Uruguay, a fin de detectar la existencia de posibles tendencias, Grossi Gallegos y Spreafichi (2006) utilizaron los métodos recomendados por el Grupo de Trabajo en Fluctuaciones Climáticas (Dzerdzeevskii et al., 1965), en particular, el planteado originalmente por Mann (1945) y que fuera reformulado por Kendall en 1948 (Kendall and Stuart, 1979).
Como los valores considerados se obtienen a partir de mediciones de las horas quemadas por el Sol en la faja de papel de los heliógrafos (a las que se identificará con la letra n), están afectados por el error de medición del sistema que podría llegar a enmascarar los resultados del test. Por esta razón, debe tenerse en cuenta la incerteza introducida en la medición de la heliofanía efectiva realizada en las estaciones uruguayas, suponiendo que el umbral de respuesta de las fajas utilizadas no cambió a través del tiempo.
Se calcularon en primer lugar los promedios anuales para los años que tenían completos los registros mensuales, con lo cual la muestra se redujo, y se analizaron las series históricas restantes. Se eliminaron además todos aquellos promedios que se apartaban del promedio general en más de ± 1,96σ, compatible con el nivel de significancia del test a emplear (límites que se ampliaron teniendo en cuenta el error de determinación de la heliofanía).
En la Tabla 3 se listan, para las estaciones consideradas, las pendientes y ordenadas halladas en las series, presentándose algunos resultados estadísticos (nivel de probabilidad del test de pendiente nula, valor medio de los valores anuales, desvío estándar y coeficiente de variabilidad de Pearson, CV).
De acuerdo con los resultados del nivel de probabilidad obtenidos con el test, la hipótesis de pendiente nula puede ser rechazada si el valor hallado es menor (o igual) que el nivel de significancia (en este caso, p=0,05); por los resultados obtenidos, ninguna de las estaciones uruguayas de medición de heliofanía muestra en sus series históricas de promedios anuales tendencias significativas al 5%.
Por otra parte, vale la pena recordar que, para que la media muestral sea estadísticamente representativa de la población (esto es, que difiera del promedio poblacional en menos del error de medición estimado a partir de la Ecuación 6), debería considerarse un número de años η tal que se cumpla con la condición (Roberti et al., 2005):
donde el coeficiente α está dado por el cociente entre Z (que depende del nivel de significancia) y el error relativo.
Aplicada al mayor valor del coeficiente de variabilidad hallado entre los promedios mensuales (CV = 0,28, mes de junio en la estación Salto), esta condición requiere que la extensión de la serie no sea inferior a 35 años para mantener tal afirmación con un nivel de confidencia del 90%; con la extensión considerada en este trabajo, se podría afirmar que esta media muestral es estadísticamente representativa con un nivel de confidencia del 78%. Pero, salvo en los meses de invierno (junio, julio y agosto), las cartas con la distribución espacial de las medias mensuales elaboradas con los 20 años analizados son estadísticamente representativas con un nivel de confidencia mayor o igual al 90%.
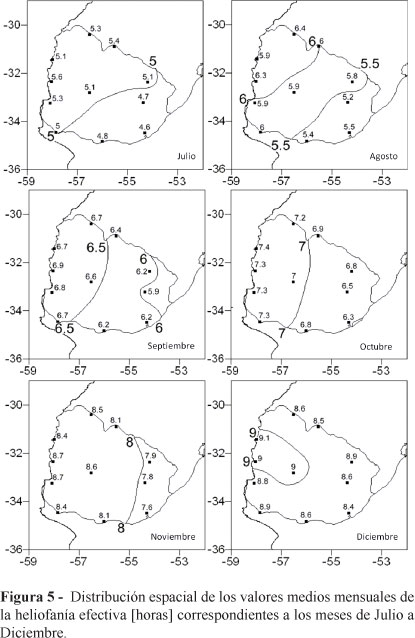
3.3 Cartografía de la Heliofanía Efectiva Mensual
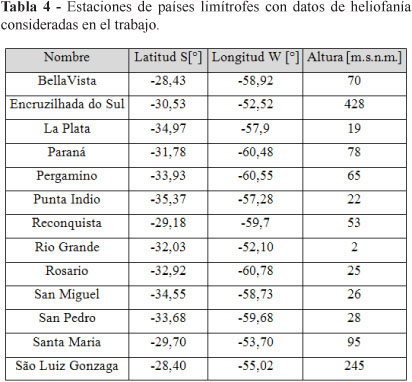
A fin de dar continuidad espacial a las isolíneas a trazar se tuvieron en cuenta estaciones de Brasil y de Argentina como condición de borde (Tabla 4). Como el Servicio Meteorológico Nacional de este último país utiliza en su heliógrafos fajas diferentes a las de Brasil y Uruguay, se analizó cómo variaban las condiciones de homogeneidad en la región completa.
Fue así que, en un trabajo anterior (Raichijk et al., 2006b), utilizando la misma metodología antes expuesta, determinaron al extrapolar la función estructura que la incerteza del sistema se incrementaba a 7,7 %, lo que motivó que la separación entre las isolíneas de los promedios mensuales de la heliofanía efectiva diaria no fuera inferior a 1 hora para los meses de verano (enero, febrero, noviembre y diciembre) y de media hora para los restantes meses.
Los promedios mensuales fueron divididos por la duración astronómica media del día, convirtiéndolos en heliofanía relativa; de esta manera, se removieron las tendencias asociadas a la variación de la duración del día con la latitud. Estos valores fueron luego tratados con un programa de interpolación estadística (kriging) y, luego de recuperar los valores medios de heliofanía efectiva, se trazaron las curvas con un programa de graficación. Al comparar los resultados obtenidos en este trabajo con cartas de heliofanía efectiva publicadas para Brasil (Tiba, 2000) y Argentina (Righini y Grossi Gallegos, 2005) se observa, para todos los meses, una aceptable correspondencia entre isolíneas. Eventuales diferencias son explicables si se tiene en cuenta que en los trabajos mencionados se empleó una metodología diferente en el trazado de las cartas y no se consideró información proveniente de estaciones uruguayas.
En las Figuras 4 y 5 se muestran las cartas mensuales resultantes para los promedios de la heliofanía efectiva diaria, recuperadas a partir de la distribución espacial de la heliofanía relativa.
Con el objeto de evaluar el error asociado al método de interpolación espacial empleado, se comparó en cada estación el valor observado con el valor estimado por medio de una validación cruzada, es decir estimándolo sin considerar el valor de dicha estación (one-leave-out cross validation). Se determinó para cada mes del año el error cuadrático medio relativo porcentual, RMSE%, y el sesgo medio relativo porcentual, MBE%, siendo:
donde  y
y  son los valores medios mensuales de heliofanía efectiva observados y estimados por validación cruzada respectivamente y k es el número de estaciones consideradas. En la Tabla 5 se consignan los valores de RMSE% y MBE% obtenidos para los distintos meses del año.
son los valores medios mensuales de heliofanía efectiva observados y estimados por validación cruzada respectivamente y k es el número de estaciones consideradas. En la Tabla 5 se consignan los valores de RMSE% y MBE% obtenidos para los distintos meses del año.
4. CONCLUSIONES
Al poder definir con un buen nivel de correlación el coeficiente de variabilidad en función de la distancia entre estaciones se garantiza, en primera instancia, la condición de homogeneidad e isotropía, necesaria para extrapolar en toda la región estudiada los valores obtenidos en un conjunto reducido de estaciones. A su vez, y a partir de la Ecuación 6 hallada para dicha correlación, se puede afirmar que, con un nivel de confidencia del 90%, es posible extrapolar radialmente valores de heliofanía efectiva en Uruguay hasta distancias de 285 km sin exceder un error del 15%. Esto está indicando que, tanto en número como en distribución espacial, su red de estaciones brinda una cobertura adecuada a todo el territorio. El estudio de validación cruzada muestra que, para los distintos meses del año, los desvíos medios asociados al método de interpolación espacial utilizado (kriging) son similares o menores al error de medición hallado de 5,85%.
Al analizar a nivel mensual el valor de los coeficientes de variabilidad de Pearson, CV, pudo verse que alcanzan máximos en invierno (junio o julio, del orden de 0,20, con un mínimo de 0,19 en Treinta y Tres) y mínimos en verano (diciembre o enero, del orden de 0,10, con mínimos absolutos de 0,06 en Mercedes y Colonia), lo cual es razonable si se observa que los desvíos estándares son siempre del mismo orden y que los valores medios alcanzan sus máximos en verano y sus mínimos en invierno. La única excepción es la estación Melo que, si bien alcanza también su máximo en invierno y su mínimo en verano, sus valores son respectivamente 0,28 y 0,13 debido a que sus desvíos estándares presentan valores mayores que los del resto de las estaciones.
Por otra parte, el análisis practicado a las series temporales de los promedios anuales, muestra que en ninguna de las estaciones estudiadas se observa tendencias significativas al 5%, como así también la consideración de la longitud de los registros en relación al error de medición del sistema, permite asegurar la validez de los promedios consignados con un nivel de confidencia del 78%.
5. AGRADECIMIENTOS
Los autores desean formular su agradecimiento a las autoridades del Servicio Meteorológico Nacional de Argentina, por haber tramitado y facilitado, una vez obtenida, la información utilizada, y a las de la Dirección Nacional de Meteorología de la República Oriental del Uruguay, sin cuyo aporte no hubiera sido posible la realización de este trabajo.
6. REFERENCIAS
Recibido Febrero 2008
Aceptado Marzo 2010
- DZERDZEEVSKII, B.; FLOHN, H.; HOFMEYR, W. L.; LAMB, H. H.; MITCHELL, J. M.; RAO, K. N.; WALLEN, C.C.. Report of Working Group on Climatic Fluctuations. Submitted to the Commission for Climatology, World Meteorological Organization, for the 4th Session. 135 p., 1965.
- GANDIN, L. S. The planning of meteorological station networks Geneva: World Meteorological Organization (Tech. Note, 111. WMO-No. 265.TP.149), 135 p., 1970.
- GARCÍA R. M. Inferencia estadística y diseño de experimentos Buenos Aires: EUDEBA, 736 p., 2004.
- GROSSI GALLEGOS, H.; ATIENZA, G. Análisis del comportamiento espacial de los datos de radiación solar en la Pampa Húmeda. In: ENCUENTRO METEO 92, I CONGRESO IBEROAMERICANO, V CONGRESO INTERAMERICANO DE METEOROLOGÍA, Madrid, 1, p. 216-220, 1992.
- GROSSI GALLEGOS, H.; MAGRIN, G. Evaluación de la influencia de la calidad de los datos de radiación solar global en los pronósticos de cosecha. In: VII CONGRESO LATINOAMERICANO DE ENERGÍA SOLAR, XVI REUNIÓN DE TRABAJO DE LA ASOCIACIÓN ARGENTINA DE ENERGÍAS RENOVABLES Y AMBIENTE, Salta, tomo I, p. 243-250, 1993.
- GROSSI GALLEGOS, H.; LOPARDO R. Spatial variability of the global solar radiation obtained by the Solarimetric Network in the argentine Pampa Húmeda. Solar Energy, v. 40, n. 5, p. 397-404, 1988.
- GROSSI GALLEGOS, H.; SPREAFICHI, M. I. Análisis de los datos de heliofanía en el sur de Argentina. Avances en Energías Renovables y Medio Ambiente, v. 8, n. 2, p. 11.19-11.24, CD-ROM, 2004.
- GROSSI GALLEGOS, H.; SPREAFICHI, M. I. Análisis de las series de datos de heliofanía en estaciones de Argentina ubicadas al norte de los 38°S. Avances en Energías Renovables y Medio Ambiente, v. 10, p. 11.21-11.26, CD-ROM, 2006.
- GUEYMARD, C. Analysis of monthly average solar radiation and bright sunshine hours for different thresholds al Cape Canaveral. Solar Energy, v. 51, n. 2, p. 139-145, 1993.
- HAY, J. E.; SUCKLING, PH. An assessment of the networks for measuring and modeling solar radiation in British Columbia and adjacent areas of Western Canada. Canad. Geographer v. XXIII, n. 3, p. 223-237, 1979.
- KENDALL, M.G.; STUART, A. The advanced theory of statistics, vol. 2, Inference and Relationship, London: C. Griffin and Co. Ltd., 748 p., 1979.
- MAGRIN, G.O.; TRAVASSO, M.I.; DIAZ, R.; RODRIGUEZ, R. Vulnerability of the agricultural systems of Argentina to climate change. Climate Research, v. 9, p. 31-36, 1997.
- MANN, H.B. Non-parametric test against trend. Econometrika, v. 13, p. 245-259, 1945.
- ORGANIZACIÓN METEOROLÓGICA MUNDIAL (OMM). Informe final abreviado de la Octava Reunión, Comisión de Instrumentos y Métodos de Observación, 19-30 de octubre de 1981, México. OMM - N° 590 Ginebra, Suiza, 1982.
- RAICHIJK, C.; GROSSI GALLEGOS, H.; RIGHINI R. Análisis de los datos de heliofanía en la República Oriental del Uruguay. Avances en Energías Renovables y Medio Ambiente, v. 8, n. 2, p. 11.101-11.105, CD-ROM, 2006a.
- RAICHIJK, C.; GROSSI GALLEGOS, H.; RIGHINI, R. Variabilidad espacial de la heliofanía (duración de la insolación) en la Pampa Húmeda argentina, Uruguay y sur del Brasil. Energías Renovables y Medio Ambiente, v. 19, p. 33-37, 2006b.
- RIGHINI, R.; GROSSI GALLEGOS, H. Distribución de la heliofanía en Argentina. Revista de la Asociación Argentina de Agrometeorología (RADA), v. 3-4, p. 1-7, 2005.
- ROBERTI, A.; GROSSI GALLEGOS, H.; SIERRA, V. Análisis de la representatividad temporal de los datos de horas de brillo solar (heliofanía) en Argentina. In: IX CONGRESO ARGENTINO DE METEOROLOGÍA, Buenos Aires, CD-ROM, 2005.
- SUCKLING, PH. W. Extrapolation of Solar Radiation Measurements: Mesoescale Analyses from Arizona and Tennessee Valley Authority Regions. J.Clim. and Appl. Meteor., v. 22, p. 488-494, 1983.
- SUCKLING, PH. W. Estimating daily solar radiation values in selected mid-latitude regions by extrapolating measurements from nearby stations. Solar Energy, v. 35, n. 6, p. 491-495, 1985.
- SUKLING, PH.; HAY, J. E. The spatial variability of daily values of solar radiation for British Columbia and Alberta, Canada. Climatological Bulletin, McGill University, n. 20, p. 1-7, 1976.
- TIBA, Ch. (Coordinador) Atlas Solarimétrico do Brasil: Banco de Dados Terrestres. Recife: Editorial Universitária da Universidade Federal de Pernambuco (UFPE), 111 p., 2000.
- WORLD METEOROLOGICAL ORGANIZATION (WMO). Meteorological aspects of the utilization of solar radiation as an energy source. Technical Note No. 172, WMO - No. 557 Geneva, Switzerland. 298 p., 1981.
Fechas de Publicación
-
Publicación en esta colección
15 Mar 2011 -
Fecha del número
Dic 2010
Histórico
-
Recibido
Feb 2008 -
Acepto
Mar 2010