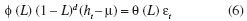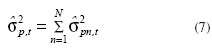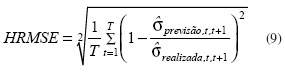Resumos
Neste trabalho foram avaliados os ajustes de cinco modelos para previsão da variância, utilizando-se uma série de preços de soja, uma commodity negociada na bolsa de mercadorias de Chicago (CBOT), com dados de alta frequência. Os modelos utilizados foram do tipo GARCH, FIGARCH e ARFIMA. Foi possível observar características desta série de preços de uma commodity negociada globalmente que se apresentaram inteiramente diferentes daquelas de ativos financeiros anteriormente estudados, possivelmente em virtude da característica contínua dos preços observados, induzida pela sua negociação global independente de pregões com início e fim. Foi possível concluir que a série de dados de alta frequência encerra informações adicionais às séries de dados diários, também no caso estudado de preços da soja, e que o tradicional modelo GARCH(1,1) tem um bom desempenho também no caso dos dados de alta frequência, assim como aqueles da família ARFIMA. Recomenda-se mais investigação para o caso dos modelos FIGARCH, procurando um melhor ajuste.
Volatilidade; Alta frequência; Volatilidade realizada; Soja; GARCH; ARFIMA
In the present study, five volatility prediction models were evaluated using a series of soybeans prices, a commodity traded in the Chicago Board of Trade (CBOT), using high-frequency data. The models used belonged to the GARCH, FIGARCH and ARFIMA families. It was possible to observe entirely different characteristics of this commodity price series, which is negotiated on a global scale, from those of the financial assets previously studied, possibly due to the continuity of the price series studied allowed by the global negotiation nature of this trade, fully independent of daily exchange markets subject to opening and closing times. It was possible to conclude that the high-frequency price data do provide additional information to the traditional daily time series, also in the case of soybeans, and that the traditional GARCH(1,1) model also has good performance on the high-frequency price data just like those of the ARFIMA family. Further investigation should be carried out on the FIGARCH models to get a better parameter fit.
Volatility; High-frequency; Realized volatility; Soybeans; GARCH; ARFIMA
Uma avaliação da volatilidade dos preços da soja no mercado internacional com dados de alta frequência
An evaluation of the volatility of soybeans prices in the international market using high frequency data
Mario Domingues Simões; Marcelo Cabus Klotzle; Antonio Carlos Figueiredo Pinto; Gabriel Levrini
Escola de Negócios da PUC-Rio IAG, Pontifícia Universidade Católica do Rio de Janeiro PUC-Rio, Rua Marquês de São Vicente, 225, Gávea, CEP22451-900, Rio de Janeiro, RJ, Brasil, e-mails: msimoes@alum.mit.edu; klotzle@iag.puc-rio.br; figueiredo@iag.puc-rio.br; gabriel.levrini@iag.puc-rio.br
RESUMO
Neste trabalho foram avaliados os ajustes de cinco modelos para previsão da variância, utilizando-se uma série de preços de soja, uma commodity negociada na bolsa de mercadorias de Chicago (CBOT), com dados de alta frequência. Os modelos utilizados foram do tipo GARCH, FIGARCH e ARFIMA. Foi possível observar características desta série de preços de uma commodity negociada globalmente que se apresentaram inteiramente diferentes daquelas de ativos financeiros anteriormente estudados, possivelmente em virtude da característica contínua dos preços observados, induzida pela sua negociação global independente de pregões com início e fim. Foi possível concluir que a série de dados de alta frequência encerra informações adicionais às séries de dados diários, também no caso estudado de preços da soja, e que o tradicional modelo GARCH(1,1) tem um bom desempenho também no caso dos dados de alta frequência, assim como aqueles da família ARFIMA. Recomenda-se mais investigação para o caso dos modelos FIGARCH, procurando um melhor ajuste.
Palavras-chave: Volatilidade. Alta frequência. Volatilidade realizada. Soja. GARCH. ARFIMA.
ABSTRACT
In the present study, five volatility prediction models were evaluated using a series of soybeans prices, a commodity traded in the Chicago Board of Trade (CBOT), using high-frequency data. The models used belonged to the GARCH, FIGARCH and ARFIMA families. It was possible to observe entirely different characteristics of this commodity price series, which is negotiated on a global scale, from those of the financial assets previously studied, possibly due to the continuity of the price series studied allowed by the global negotiation nature of this trade, fully independent of daily exchange markets subject to opening and closing times. It was possible to conclude that the high-frequency price data do provide additional information to the traditional daily time series, also in the case of soybeans, and that the traditional GARCH(1,1) model also has good performance on the high-frequency price data just like those of the ARFIMA family. Further investigation should be carried out on the FIGARCH models to get a better parameter fit.
Keywords: Volatility. High-frequency. Realized volatility. Soybeans. GARCH. ARFIMA.
1 Introdução
A previsão da volatilidade de preços de ativos, em geral, tem sido um assunto bastante explorado pelos pesquisadores desta área. Sua relevância em relação aos mecanismos de formação de preços, análise de alternativas de investimentos, precificação de derivativos e gerenciamento de riscos, principalmente por meio de estratégias de hedge, é bastante alta e reconhecida na literatura.
Ao mesmo tempo, o estudo da volatilidade baseado em dados de alta frequência é um tipo de trabalho relativamente recente, mas tem crescido em função da maior disponibilidade deste tipo de dado. Os chamados dados de alta frequência são aqueles que incluem informações de preço em períodos intradiários, cuja produção exige sistemas eletrônicos de coleta e armazenamento de informação. Estes apenas recentemente tornaram-se disponíveis, com o advento dos sistemas computadorizados e, no caso das commodities, após a adoção disseminada de práticas de negociação global.
Dentre os ativos considerados commodities com relevância para o mercado brasileiro, inclusive em relação a novos investimentos e suas opções, talvez a soja seja um dos poucos para os quais este tipo de informação de preços intradiários, em alta frequência, esteja disponível. No caso da soja, estes o são em função de sua negociação global ininterrupta na bolsa de mercadorias de Chicago.
Isso torna a soja um ativo cuja formação de preço é dada em um mercado altamente competitivo, fazendo com que os produtores comportem-se como tomadores de preços, sem capacidade de influenciá-los. Da mesma forma, a proteção contra flutuações dos preços via operações de hedge, torna fundamental o conhecimento da volatilidade desses ativos.
Assim, neste estudo foram usadas cotações de preços dos contratos futuros de soja de maior liquidez, negociados na CBOT (Chicago Board of Trade). Estes dados são referentes ao período iniciado em 22 de agosto de 2001 e finalizado em 2 de outubro de 2009, totalizando 97782 observações, com periodicidade de 15 minutos.
Estes dados são coletados durante todo o horário de negociação, que é global e não está limitado a horários diários de abertura e fechamento de pregão, desta forma, sendo apresentados por todo o período de uma semana iniciando-se no domingo às 18h 45 até a sexta-feira seguinte às 13h 15, apenas não havendo negociações no breve espaço de tempo entre esses horários nas sextas e domingos.
Desta forma, a conjugação dos dois tipos de estudos descritos acima, ou seja, o estudo da volatilidade de ativos reais, como preços de commodities, e a utilização de dados de alta frequência para estimação da volatilidade é, no mínimo, bastante rara e constitui a principal contribuição do presente trabalho.
Neste estudo, procura-se avaliar a capacidade de previsão de alguns tipos de modelagem da volatilidade, bem como testar a relevância das informações potencialmente contidas nos dados de alta frequência utilizados para uma série de preços de soja, negociada globalmente na CBOT (Chicago Board of Trade).
Para isso foram comparados modelos GARCH e FIGARCH ajustados às séries de retornos da soja, além de modelos autorregressivos de média móvel integrados fracionariamente (ARFIMA), ajustados a séries da volatilidade realizada extraída dos dados intradiários disponíveis, conforme o método introduzido por (ANDERSEN; BOLLERSLEV, 1998).
O restante deste trabalho está organizado da seguinte forma: na seção 2, está o referencial teórico deste trabalho, seguido de uma seção sobre a Metodologia empregada, que inclui aspectos da série de dados, dos modelos utilizados e das formas de Previsão empregadas. Depois disso, encontra-se a seção sobre os Resultados e Discussão destes, seguida da Conclusão e da lista de Referências Bibliográficas.
2 Referencial teórico
A literatura sobre volatilidade, principalmente quando relacionada à volatilidade de ativos a partir da análise e observação de dados de alta frequência, pode ser dividida em quatro subgrupos: estudos relacionados à volatilidade realizada, comparação e validação de modelos usando, alternativamente dados de alta frequência e dados diários, validação de modelos para volatilidade convencional usando dados de alta frequência e, por fim, propriedades ligadas à alta frequência em mercados específicos (ANDERSEN; BOLLERSLEV, 1998).
Dentre a literatura pesquisada neste artigo, inexistiam trabalhos usando dados de alta frequência para o mercado internacional de soja, embora existam estudos usando este tipo de modelagem com ativos financeiros (CAPPA; VALLS, 2010).
A noção da volatilidade realizada foi primeiramente introduzida em 1998 como uma forma de se extrair informações sobre a volatilidade a partir de séries de preços com muitos dados (ANDERSEN; BOLLERSLEV, 1998). Esta noção de volatilidade permite que uma abordagem a uma série de preços seja feita independente de qualquer modelo, com valores da volatilidade sendo extraídos dos dados observados e podendo ser usados para o ajuste e acerto de modelos teóricos, minimizando vieses (ANDERSEN et al., 2001a; ANDERSEN et al., 2001b; BARNDORFF-NIELSEN, 2002; ANDERSEN et al., 2003; HERWARTZ, 2006).
No segundo subgrupo, o objetivo é a validação de vantagens do uso de dados de alta frequência sobre bases de dados com menor número de observações, de manuseio intrinsecamente mais fácil. Neste grupo há vários trabalhos feitos, entretanto as bases utilizadas sempre versam sobre ativos financeiros, conforme já foi mencionado anteriormente, notadamente taxas de câmbio (HOL; KOOPMAN, 2002; MARTENS; ZEIN, 2004; CHORTAREAS; NANKERVIS; JIANG, 2007; CAPPA; VALLS, 2010).
Estes estudos indicam que há informações adicionais, de valor, contidas nos dados de alta frequência, inclusive em relação às previsões baseadas na volatilidade implícita nas opções, quando estas estão disponíveis. Por outro lado, o uso da volatilidade realizada também permite a obtenção de previsões superiores aos modelos de séries temporais convencionais.
Aplicando-se ao estudo em questão, procurar-se-á conhecer e detectar particularidades das séries de preços da soja negociada globalmente, como eventuais efeitos de sazonalidade de preços ou outros aspectos ligados à forma de comercialização deste ativo, e torna-se importante saber se a validade dos modelos convencionais, quando utilizados para modelar dados de alta frequência ainda persiste.
O terceiro subgrupo de trabalhos apresenta aqueles que buscam a validação de modelos convencionais usando dados de alta frequência, mas o predomínio dos dados básicos também é de preços e cotações relativas a ativos de mercados financeiros, sempre com a predominância de cotações de câmbio (TAYLOR; XU, 1997; LI; LEE; LEE, 2009). Aparentemente os modelos GARCH(1,1) podem ser utilizados com êxito, mas também há evidências contra esta posição (JONES, 2003).
De qualquer forma, os trabalhos utilizam ativos financeiros para suas simulações e avaliações, uma vez que esse tipo de dados é sempre mais facilmente disponível do que ativos reais.
Finalmente o último grupo de trabalhos busca informações sobre os dados de alta frequência em mercados específicos. Embora algumas propriedades como distribuições de retornos não normais e sazonalidade tenham surgidos em vários desses estudos, todas estas características estão levantadas para taxas de câmbio, cotações de ações e outros preços do mesmo tipo, e nada (foi levantado) sobre ativos reais como os preços da soja estudados no presente trabalho.
3 Metodologia
3.1 Série de dados
A base de dados para o presente trabalho é uma série de preços futuros de soja, negociada na CBOT (Chicago Board of Trade hoje parte do CME Group) e incluindo valores coletados de 22 de agosto 2001 a 2 de outubro de 2009 em intervalos de 15 minutos, apresentando um total de 97781 observações. Está série, cujos valores estão no formato usado pelos operadores deste tipo de mercadoria naquela bolsa (em que cada ponto de variação equivale a um valor de US$ 50.00), tem uma periodicidade de 15 minutos e a sua negociação é feita durante as 24 horas do dia durante toda a semana, apenas fechando às 13h 15 (UTC-6) de sexta-feira para reabrir às 18h 45 (UTC-6 ou Tempo Universal Coordenado menos seis horas) do domingo subsequente. Conforme indicado, estes horários referem-se ao fuso horário padrão de Chicago, USA, e significam 6 horas em relação ao horário de Greenwich, GBR.
Sua negociação é feita de acordo com as normas publicadas da Chicago Board of Trade que podem ser vistas na Tabela 1 (CME, 2009).
A soja é uma commodity que desponta como das mais negociadas, seus contratos apresentando liquidez considerável o suficiente para atrair o interesse dos negociadores. Uma outra commodity em situação semelhante é o trigo, mas a preferência pela primeira decorre da grande expressão do Brasil como produtor mundial.
O uso das chamadas séries de alta frequência é altamente debatido no meio acadêmico, com a racionalidade por trás das diversas opiniões, sendo que um maior número de dados permitiria um melhor conhecimento do fenômeno (variação de preços) e uma maior precisão na sua previsão.
Entretanto também é argumentado que uma frequência muito elevada de dados em presença de fenômenos de microestrutura do mercado pode não necessariamente levar ao melhor resultado (ANDERSEN et al., 1999). Embora não haja um consenso estabelecido a respeito da frequência a ser utilizada, um intervalo geralmente utilizado como uma boa solução intermediária é a de intervalos de 15 minutos, que adotaremos no presente trabalho.
A série analisada é a série de retornos obtidos que é construída a partir da série básica de preços de fechamento por meio da seguinte transformação
em que rt é o retorno; ft é o preço de fechamento no instante t; ft1 é o preço de fechamento no instante t 1.
A Figura 1 apresenta gráficos da série inicial de preços bem como da série de retornos calculada de acordo com a Equação 1 e que é objeto do trabalho. A Tabela 2, apresentada em sequência, apresenta as estatísticas descritivas para a série de retornos relativa aos preços apresentados, isto, da série de retornos apresentada na própria figura anterior.
Uma preocupação sempre presente em trabalhos deste tipo, que manuseiam séries de dados de alta frequência (ora em diante chamaremos séries de dados intradiários) é a sazonalidade intradiária por eles apresentada. A Tabela 2 apresenta as estatísticas descritivas e a Figura 2, histograma para a série de retornos em pauta, bem como gráfico de autocorrelação até 300 defasagens (um período diário tem 96 intervalos de 15 minutos).
Como pode ser inferido das estatísticas acima, na mesma forma de outros trabalhos semelhantes (ANDERSEN; BOLLERSLEV, 1997; TAYLOR; XU, 1997; CHORTAREAS; NANKERVIS; JIANG, 2007; CAPPA; VALLS, 2010), a distribuição de retornos apresenta um grande desvio da normalidade, com uma curtose alta (leptocurtose) e suas caudas pesada e alongadas.
Diferentemente dos trabalhos citados, a série em questão não apresenta qualquer significativa autocorrelação, mesmo observando-se a 300 defasagens, o que indica ausência de sazonalidade intradiária. Esta observação nos leva a crer que esta série seja intrinsicamente diferente das outras, aliás, todas de retornos de ativos financeiros (em sua maioria taxas de câmbio).
Imagina-se que essa diferente característica esteja ligada à negociação universal da soja, o que evita uma sazonalidade diária, visto que não há uma fronteira clara entre dia e noite e início e fim de negociação, pois tudo acontece em uma escala global.
Assim, o tratamento de dessazonalização normalmente adotado não foi usado para o manuseio desta série. Na realidade, uma dessazonalização, como descrita alhures (CHORTAREAS; NANKERVIS; JIANG, 2007), não demonstrou qualquer perceptível melhoria na série como pode ser visto nos gráficos da Figura 3, que mostram a função de autocorrelação com 300 defasagens para a série normal e para a série dessazonalizada.
3.2 Modelos
Os modelos que serão ajustados a fim de modelar a volatilidade serão 5: tentaremos ajustar dois modelos à série completa, isto é, com valores intradiários (alta frequência), quais sejam um tradicional GARCH e um FIGARCH, além de um modelo GARCH convencional a ser ajustado a uma série diária, extraída a partir da série completa com valores intradiários, como será explicado adiante; por fim, dois modelos aplicados diretamente à volatilidade extraída da série de alta frequência, modelos derivados da família ARFIMA.
Dentre os escolhidos, tentaremos verificar se podem ser auferidas vantagens substanciais por meio do uso de modelos de memória longa que pretendem capturar dados presentes nas séries de alta frequência, assim como comparar sua potencial vantagem em relação aos modelos mais tradicionais.
Assim, na estimação dos modelos, GARCH e FIGARCH serão aplicados às séries de alta frequência originais, sendo que o modelo GARCH(1,1) escolhido será aplicado também à série de retornos diários produzida a partir dos valores originais.
O modelo GARCH(1,1) é escolhido em função de sua parcimônia mas, principalmente, por ter sido usado em trabalhos com o mesmo objetivo do presente, mas com ativos de financeiros, mormente taxas de câmbio (ANDERSEN; BOLLERSLEV, 1998; ANDERSEN; BOLLERSLEV; LANGE, 1999; CHORTAREAS; NANKERVIS; JIANG, 2007; CAPPA; VALLS, 2010).
O modelo GARCH(1,1) pode ser representado pela Equação 2:
A série de retornos diários que são utilizados para a estimação da volatilidade por meio do modelo GARCH(1,1) acima é produzida a partir da série completa usando-se a soma dos retornos auferidos dentro de uma mesmo dia como o retorno daquele período.
No caso da aplicação do modelo GARCH(1,1) à série de alta frequência, foi feito um alisamento dos retornos por meio do ajuste de um processo MA(1) à equação dos retornos (média) de forma a filtrar a correlação serial causada pelos efeitos de microestrutura presentes nesta série de retornos intradiários. Assim a equação do modelo proposto MA(1)-GARCH(1,1) pode ser expressa na forma da Equação 3:
No caso do modelo FIGARCH a ser ajustado à série de retornos intradiários, este procura estender a sua estimação além da simples feita pelo GARCH com a inclusão de diferenças fracionárias da volatilidade condicional (BAILLIE; BOLLERSLEV; MIKKELSEN, 1996), desta forma tentando capturar as propriedades de memória longa contidas nesta. Assim, este modelo escolhido e especificado como MA(1)-FIGARCH(1,d,1) pode ser traduzido pela Equação 4:
em que d é a ordem de integração fracionária; L é o operador de lag.
Todos os modelos acima foram estimados pela otimização da Quase Máxima Verossimilhança e com uma distribuição de resíduos na forma de uma GED (Generalized Error Distribution), utilizando-se o pacote G@RCH da linguagem Ox. Todos estes modelos foram calculados usando-se a Distribuição de Erros Generalizada (GED) como a distribuição para os resíduos das séries calculadas.
Finalmente, o modelo ARFIMA(5,d,2) foi diretamente ajustado a uma série de volatilidades diárias, extraídas da série de alta frequência, conforme a Equação 5:
em que N é o número de períodos intradiários; t é o dia específico.
A variância realizada pode ser bem traduzida pelo somatório dos quadrados dos retornos diários (ANDERSEN; BOLLERSLEV, 1998;CHORTAREAS; NANKERVIS; JIANG, 2007) e a série de variâncias diárias foi assim construída por meio do somatório dos quadrados de todos os retornos de cada determinado dia, de forma consistente com o critério usado para construir a série de retornos diários, acima.
O modelo ARFIMA(5,d,2), ajustado com otimização da Máxima Verossimilhança e com ajuste automático do parâmetro d pelo pacote ARFIMA, escrito em linguagem Ox, pode ser traduzido pela Equação 6. A escolha entre modelos de uma mesma forma, isto
em que d é a ordem de integração fracionária; L é o operador de lag; µ é a média de ht.
é ARFIMA(4,d,0), ARFIMA(5,d,2) ou ARFIMA(3,d,1) é feita pela comparação do valor do logaritmo da máxima verossimilhança (LL) obtida no ajuste de cada um deles, escolhendo-se o maior valor. Como um critério adicional, também entre modelos da mesma classe, foi feita a comparação do valor do AIC, Critério de Informação de Akaike (AKAIKE, 1974).
Os componentes polinomiais AR e MA são descritos pelas Equações 6a,b, abaixo, consistentemente com a Equação 5:
em que p e q sobrescritos são ordens de integração fracionária; p e q subscritos são graus dos polinômios.
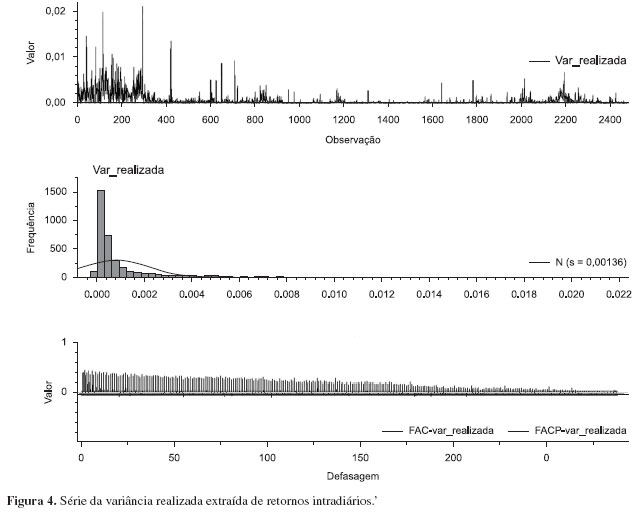
A série da variância realizada criada na forma descrita acima tem o aspecto mostrado na Figura 4.
Testes de raiz unitária ADF (Augmented Dickey Fuller) efetuados nestes dados confirmam a impressão de estacionaridade para a série acima e justificam a aplicação do modelo ARFIMA. Estes podem ser vistos na Tabela 3.
Por outro lado, o gráfico de FAC (função de autocorrelação) e FACP (função de autocorrelação parcial) mostrado na Figura 4 parece indicar que um modelo que junte um componente AR e outro MA parece ser justificado, ao mesmo tempo em que parece sugerir um processo com baixa taxa de decadência no caso de realmente ter estacionaridade.
Este modelo foi estimado pela maximização da função de Quase Máxima Verossimilhança utilizando-se o pacote ARFIMA, escrito em linguagem Ox.
3.3 Previsão
Conforme trabalhos anteriores (ANDERSEN; BOLLERSLEV, 1998; HOL; KOOPMAN, 2002; ANDERSEN et al., 2003; MARTENS; ZEIN, 2004; CHORTAREAS; NANKERVIS; JIANG, 2007), as previsões seguem o conhecido padrão in-sample e out-of-sample, com 100 dias (calendário e com presença na série de dados básica), sendo escolhidos para a avaliação das previsões.
Nas séries de alta frequência, em que os dados são relativos a períodos de 15 minutos de frequência, teoricamente haveria 96 tais períodos por dia, com um total de 9600 períodos correspondendo ao tamanho de 100 dias escolhidos para a previsão. Entretanto, como a série muitas vezes admite dados faltantes para alguns destes
em que N é o número de períodos intradiários; p,t refere-se à previsão do dia t; pn,t refere-se à previsão do período n do dia t.
períodos, o critério foi definido como observações em 100 dias, na prática indo de 24 de junho de 2009 a 2 de outubro de 2009, completando 4740 observações.
Ainda no caso dos modelos com estimações intradiárias (MA(1)-GARCH(1,1) e MA(1)-FIGARCH(1,d,0), as variâncias dos períodos intradiários previstas foram submetidas à extração da variância realizada diária, conforme descrito pela Equação 6, acima, e neste caso mostrado pela Equação 7.
A estratégia de produzir volatilidades diárias, inclusive com extração de uma volatilidade "realizada prevista" conforme acima, a partir de todos os modelos ajustados, vai permitir que as medidas de avaliação de qualidade de ajuste e desempenho de cada modelo possam ser comparadas todas entre si.
As previsões foram feitas com o mesmo software utilizado na estimação dos modelos, conforme informado anteriormente, quais sejam os pacotes G@RCH e ARFIMA escritos na linguagem Ox.
3.4 Alternativas de avaliação das previsões
A maior dificuldade em se fazer qualquer comparação a respeito da volatilidade de um ativo é o fato de que esta não pode ser observada diretamente, sendo sempre necessário algum preposto que a possa representar.
Ora, a volatilidade realizada é uma boa substituta para a volatilidade, sendo que Andersen e Bollerslev (1998) mostram não haver qualquer contradição entre boa previsão de volatilidade e reduzido de previsão para quadrados de retornos diários.
Assim, reproduzindo o raciocínio destes autores e considerando que uma inovação em um retorno seja representada pela equação rt = σt × zt, lembrando que zt ~N(0,h), temos que Et1(r2t) = Et1(s2t × z2t) = s2t o que justifica o retorno ao quadrado como uma estimativa não enviesada da volatilidade latente, embora os próprios valores possam embutir um grande ruído devido ao comportamento do termo de erro z2t.
Uma vez definida qual será a base de comparação para as previsões efetuadas por cada modelo, vamos falar sobre alguns testes de poder de previsão.
3.4.1 Teste do poder preditivo via teste de regressão linear
A ideia por trás deste teste é de que o valor previsto seria o estimador do meu valor latente. Assim, o valor da volatilidade real (traduzida pela volatilidade extraída conforme acima) sofreria uma regressão linear contra a volatilidade prevista na forma abaixo:
O indicador de ajuste R2 obtido por essa regressão é um indicador de quanto a volatilidade prevista pelo modelo utilizado pode ser usada para previsão da real volatilidade. Este tipo de procedimento foi introduzido por (ZARNOWITZ; MINCER, 1969) e posteriormente bastante empregado.
3.4.2 Teste da raiz quadrada da média dos Erros quadrados ajustada para Heterocedasticidade (HRMSE)
Vários tipos de erro são normalmente informados pelos diversos pacotes estatísticos, destacando-se o Erro Médio (ME), Média dos Erros Quadrados (MSE), Média dos Erros Absolutos (MAE), Raiz da Média dos Erros Quadrados (RMSE), Média dos Erros absolutos Percentuais (MAPE) e, entre eles, pode-se destacar o HRMSE - Raiz da Média dos Erros Quadrados ajustada para Heterocedasticidade.
em que T é o número total de dias; s^ é a volatilidade.
Conforme usado em trabalhos anteriores (ANDERSEN et al., 1999; HOL; KOOPMAN, 2002; MARTENS; ZEIN, 2004), o HRMSE, que será a expressão de erro adotada no presente trabalho, é calculado de acordo com a equação 9 e um número menor corresponde a uma melhor previsão pelo determinado modelo.
4 Resultados e discussão
Inicialmente, todos os modelos foram estimados com todos os dados disponíveis nas séries de retornos intradiários, diários e da volatilidade realizada de forma a comparar-se o ajuste destes e buscar alternativas que pudessem produzir melhores valores de LL bem como do critério de informação AIC. Para cada modelo, estas variações foram feitas a partir dos valores reportados na literatura (CHORTAREAS; NANKERVIS; JIANG, 2007), utilizados como base, e algumas variações foram experimentadas uma vez que as evidências apontavam na direção de uma grande diferença entre a série de retornos da commodity empregada e aquelas das taxas de câmbio do referido trabalho. Os resultados destas estimações estão apresentados na Tabela 4.
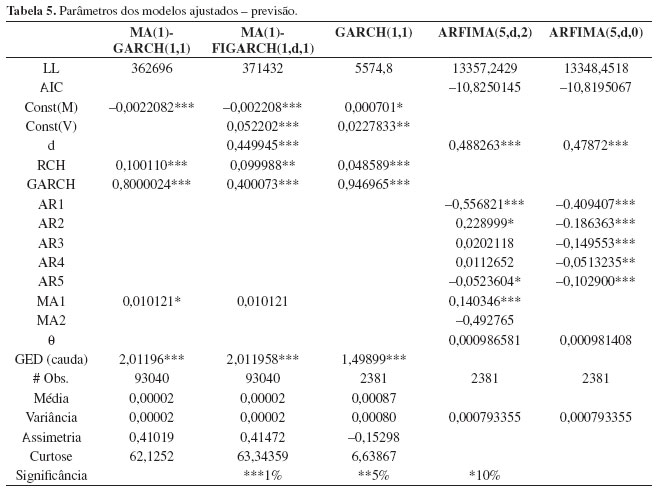
Os dados para os modelos ajustados podem ser vistos na Tabela 5. É importante notar que as tabelas apresentam os dados dos parâmetros exatamente na forma como são reportados pelos pacotes estatísticos usados na estimação dos modelos, não havendo qualquer estudo sobre a precisão do número de algarismos significativos.
4.1 Estimação
Como pode ser visto na Tabela 4, para ambos os processos MA(1)-GARCH(1,1) e GARCH(1,1), intradiário e diário, respectivamente, todos os parâmetros ARCH e GARCH são significativos e sua soma (ARCH + GARCH) < 1. Isto evidencia a qualidade do ajuste deste tipo de modelo aos dados em pauta, além do fato de que o processo é estacionário. Além disso, sua soma sendo próxima a 1 aponta para o fato da persistência da volatilidade, como indicava a Figura 1.
O fato do parâmetro d no processo MA(1)-FIGARCH(1,1) ser significante e diferente de zero também evidência que este tipo de especificação realmente captura a propriedade de memória longa presente nos dados de alta frequência.
Por outro lado, em ambos os modelos, o parâmetro MA1 mostrou-se não significativo ou com baixa significância, o que parece indicar que este processo de média móvel ajustado à média não parece ser apropriado. Some-se a esse fato a evidência de que a correlação de primeira ordem da série é negativa, embora bastante baixa, fica a indicação de que este tipo de especificação não deve ser apropriado.
Os modelos ARFIMA(5,d,x) utilizados foram ajustados à própria série da volatilidade extraída sem qualquer transformação desta, uma vez que tratava-se de uma série visivelmente diferente das séries de taxa de câmbio estudadas anteriormente (ANDERSEN et al., 2003; CHORTAREAS; NANKERVIS; JIANG, 2007). Os dois modelos ajustado (5,d,2) e (5,d,0) apresentam resultados interessantes, uma vez que para o primeiro caso os parâmetros AR não apresentam significância ou esta é baixa (10%), enquanto o parâmetro MA2 também não é significativo.
Por sua vez, o segundo modelo (ARFIMA(5,d,0)) apresenta todos os parâmetros significativos. Dado que o primeiro exige a estimação de 10 parâmetros e o segundo apenas 8, e que os valores de LL e AIC são bastante próximos para ambos, apenas uma grande diferença em poder de previsão poderá fazer a escolha recair sobre o modelo menos parcimonioso.
4.2 Previsão
A seguir foi feita a previsão dos valores da variância utilizando-se a técnica de divisão dos dados em duas amostras, uma considerada in-sample, na qual é feita a estimação dos modelos escolhidos, e a outra out-of-sample, na qual é feita a previsão.
Para podermos comparar as previsões feitas, foi usada uma mesma base de dados para o ajuste dos modelos de previsão, na qual foram separados 4740 dados para os modelos ajustados às informações intradiárias e 85 para os modelos com ajuste às informações diárias. Desta forma, em ambos os casos, as previsões iniciam-se no dia 24 de junho de 2009, sujeitas às mesmas variações de preços de mercado.
O resultado dos testes de poder de previsão pode ser visto nas Tabelas 6 e 7, bem como um gráfico das previsões das variâncias feitas pelos diversos modelos pode ser visto na Figura 5.
Em relação ao teste da regressão linear, os modelos podem ser ordenados na forma mostrada na Tabela 6, com uma clara divisão sendo feita em dois grupos: os modelos diários, melhores, e os modelos intradiários, muito inferiores.
Todos os valores de R2 para as regressões feitas são extremamente baixos, mas isto não causa muita estranheza, estando em linha com outros resultados obtidos, em se tratando de volatilidade (ANDERSEN et al., 2003; MARTENS; ZEIN, 2004; CHORTAREAS; NANKERVIS; JIANG, 2007).
Entretanto, uma rápida observação da Figura 5, na qual são plotadas as variâncias a partir das previsões feitas pelos diversos modelos, bem como a série de variâncias realizadas extraídas, pode explicar o aparente descompasso entre os modelos ajustados aos valores intradiários, que se esperava melhores, e os demais: dado que a volatilidade realizada oscila em torno das previsões dos modelos de memória curta, seu ajuste por regressão linear deve ser melhor do que qualquer previsão que tenda a posicionar seus resultados de um ou do outro lado desta oscilação.
Por outro lado, no caso das previsões ficarem como falado anteriormente, o teste do HRMSE deve retratar de forma melhor a qualidade das previsões feitas, uma vez que ele ajusta diferenças com correção de heterocedasticidade.
A Tabela 7 mostra uma ordenação bastante diferente da anterior, ressaltando a evidência de que o modelo GARCH ajustado aos resultados intradiários é superior, muito embora o modelo MA(1)-FIGARCH(1,1) tenha um desempenho desapontador.
No que diz respeito aos modelos ARFIMA, as duas tabelas mostram resultados inversos quanto ao poder de previsão dos dois modelos. Assim, levando-se em conta o argumento ao final da seção 4.1, acima, sugere-se uma opção pelo modelo mais simples, ARFIMA(5,d,0) (ANDERSEN et al., 2003; CHORTAREAS; NANKERVIS; JIANG, 2007).
Novamente, uma observação da Figura 5 mostra as previsões feitas pelo FIGARCH, estabilizando-se em um nível cerca de uma ordem de magnitude superior aos demais. Considerando-se que o modelo não parece bem ajustado, justamente pela imposição de um processo de média móvel à série de retornos subjacente à volatilidade, conforme trabalhos anteriores com taxas de câmbio (ANDERSEN et al., 2003; MARTENS; ZEIN, 2004; CHORTAREAS; NANKERVIS; JIANG, 2007; CAPPA; VALLS, 2010), e também que existem diferenças marcantes entre estas séries e as séries de retornos da commodity em estudo, sugere-se que outras tentativas sejam feitas para se obter um melhor ajuste com esse modelo aos dados de alta frequência.
5 Conclusão
Os chamados dados de alta frequência, isto é, aqueles dados que incluem observações feitas em períodos intradiários, apresentam informações adicionais também para a série de retornos de preços de soja estudada.
Modelos do tipo ARFIMA ajustados à série de volatilidades diárias realizadas extraídas da série de dados de alta frequência também deixam claro que há informação relevante embutida numa série de alta frequência.
Adicionalmente, o tradicional modelo de volatilidade GARCH(1,1), quando ajustado a dados intradiários, demonstra um surpreendente poder de previsão, embora o mesmo modelo, quando ajustado à série de valores apenas diários, não consiga um poder de previsão satisfatório. Isso é mais uma evidência da informação encerrada nos dados de alta frequência.
Esta característica não chega a ser surpreendente, uma vez que bons resultados desse tipo de modelo já estão reportados em outros trabalhos, além de ser o preferido nos trabalhos com volatilidade (BROOKS; BURKE, 1998; ANDERSEN; BOLLERSLEV; LANGE, 1999; ANDERSEN et al., 2003; CHORTAREAS; NANKERVIS; JIANG, 2007; LI; LEE; LEE, 2009).
Um aspecto interessante levantado no presente trabalho diz respeito às características da série de retornos dos preços da soja apresentarem grandes diferenças em relação àquelas dos ativos financeiros estudados na literatura.
Sugere-se que a negociação ininterrupta durante todo o período de uma semana seja responsável pela eliminação de aspectos sazonais diários encontrados nos retornos de taxas de câmbio e ausentes nos retornos da commodity estudada.
Possivelmente, trabalhos analisando negociações globais e mais recentes de moedas venham a descobrir evidências sobre a influência da negociação em pregão diário, em contraponto à negociação ininterrupta global. Naturalmente, há que observar a disponibilidade de dados de negociação do ativo, isto é, sua liquidez.
No caso do modelo FIGARCH, com sua característica teórica de integração fracionada e intrinsicamente mais bem adaptado ao manuseio de dados de alta frequência, nos quais sua memória longa é vantajosa, certamente o resultado conseguido deixou a desejar. Sugere-se que outros acertos de parâmetros sejam tentados para melhor otimizar seu funcionamento às particulares características da série de preços estudada.
Modelos baseados em volatilidade estocástica não foram utilizados neste estudo e são uma via de extensão desta abordagem. Da mesma forma, o uso de diferentes tipos de medida de poder de previsão, para os diversos modelos, deve ser investigado, além daquelas utilizadas neste trabalho.
Recebido em 27/1/2010
Aceito em 12/10/2011
Suporte financeiro: Nenhum.
- AKAIKE, H. A new look at the statistical model identification. Automatic Control, IEEE Transactions on, v. 19, n. 6, p. 716-723, 1974.
- ANDERSEN, T. G.; BOLLERSLEV, T. Intraday periodicity and volatility persistence in financial markets. Journal of Empirical Finance, v. 4, n. 2-3, p. 115-158, 1997. http://dx.doi.org/10.1016/S0927-5398(97)00004-2
- ANDERSEN, T. G.; BOLLERSLEV, T. Answering the Skeptics: Yes, Standard Volatility Models do Provide Accurate Forecasts. International Economic Review, v. 39, n. 4, p. 885-905, 1998. http://dx.doi.org/10.2307/2527343
- ANDERSEN, T. G. et al. Modeling and Forecasting Realized Volatility. Econometrica, v. 71, n. 2, p. 579-625, 2003. http://dx.doi.org/10.1111/1468-0262.00418
- ANDERSEN, T. G. et al. The distribution of realized stock return volatility. Journal of Financial Economics, v. 61, n. 1, p. 43-76, 2001a. http://dx.doi.org/10.1016/S0304-405X(01)00055-1
- ANDERSEN, T. G. et al. (Understanding, Optimizing, Using and Forecasting) Realized Volatility and Correlation New York University, 1999. (Working Paper Series).
- ANDERSEN, T. G. et al. The Distribution of Realized Exchange Rate Volatility. Journal of the American Statistical Association, v. 96, n. 453, p. 42-55, 2001b. http://dx.doi.org/10.1198/016214501750332965
- ANDERSEN, T. G.; BOLLERSLEV, T.; LANGE, S. Forecasting Financial Market vis-à-vis Forecast Horizon. Journal of Empirical Finance, v. 6, p. 457-477, 1999. http://dx.doi.org/10.1016/S0927-5398(99)00013-4
- BAILLIE, R. T.; BOLLERSLEV, T.; MIKKELSEN, H. O. Fractionally integrated generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, v. 74, n. 1, p. 3-30, 1996. http://dx.doi.org/10.1016/S0304-4076(95)01749-6
- BARNDORFF-NIELSEN, O. E. Econometric analysis of realized volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society: Series B (Statistical Methodology), v. 64, n. 2, p. 253-280, 2002. http://dx.doi.org/10.1111/1467-9868.00336
- BROOKS, C.; BURKE, S. P. Forecasting exchange rate volatility using conditional variance models selected by information criteria. Economics Letters, v. 61, n. 3, p. 273-278, 1998. http://dx.doi.org/10.1016/S0165-1765(98)00178-5
- CAPPA, L.; VALLS, P. L. Modelando a volatilidade dos retornos da Petrobras usando dados de alta freqüência Escola de Economia de São Paulo, Getulio Vargas Foundation, 2010. Textos para discussão 258.
- CHORTAREAS, G.; NANKERVIS, J.; JIANG, Y. Forecasting Exchange Rate Volatility at High Frequency Data: Is the Euro Different? SSRN eLibrary, 2007.
- CME GROUP. Soybean Futures Contracts Specs CME, 2009.
- HERWARTZ, H. Econometric analysis of high frequency data. Allgemeines Statistisches Archiv, v. 90, n. 1, p. 89-104, 2006. http://dx.doi.org/10.1007/s10182-006-0223-3
- HOL, E.; KOOPMAN, S. J. Stock Index Volatility Forecasting with High Frequency Data Tinbergen Institute, 2002. Tinbergen Institute Discussion Paper, n. 068/4.
- JONES, B. Is ARCH useful in High Frequency Foreign Exchange Applications? Applied Finance Centre, Macquarie University, 2003. (Research paper, n.24).
- LI, H.-C.; LEE, Y.-H.; LEE, M.-C. Forecasting China Stock Markets Volatity via GARCH Models Using skewed-GED Distribution. Journal of Money, Investment and Banking, v. 7, 2009.
- MARTENS, M.; ZEIN, J. Predicting financial volatility: High-frequency time-series forecasts vis-à-vis implied volatility. Journal of Futures Markets, v. 24, n. 11, p. 1005-1028, 2004. http://dx.doi.org/10.1002/fut.20126
- SAVOR, P. G.; LU, Q. I. Do Stock Mergers Create Value for Acquirers? Journal of Finance, v. 64, n. 3, p. 1061-1097, 2009. http://dx.doi.org/10.1111/j.1540-6261.2009.01459.x
- TAYLOR, S. J.; XU, X. The incremental volatility information in one million foreign exchange quotations. Journal of Empirical Finance, v. 4, n. 4, p. 317-340, 1997. http://dx.doi.org/10.1016/S0927-5398(97)00010-8
- ZARNOWITZ, V.; MINCER, J. A. The Evaluation of Economic Forecasts New York, 1969.
Datas de Publicação
-
Publicação nesta coleção
28 Mar 2012 -
Data do Fascículo
2012
Histórico
-
Recebido
27 Jan 2010 -
Aceito
12 Out 2011