Resumos
O principal objetivo desse artigo é apresentar uma introdução intuitiva à técnica de análise de conglomerados. Metodologicamente, utilizamos os dados de Coppedge, Alvarez e Maldonado (2008) sobre as duas dimensões da poliarquia propostas por Dahl (1971): contestação e inclusividade. A partir dessas dimensões os regimes políticos são classificados em diferentes grupos (clusters) de acordo com o grau de similaridade entre eles. Em termos substantivos,esperamos indicar uma ferramenta metodológica para classificação dos regimes políticos e facilitar a compreensão da técnica de análise de conglomerados na Ciência Política.
regimes políticos; análise de cluster; Q analysis; classificação; métodos quantitativos
The principal aim of this paper is to provide a intuitive introduction to cluster analysis. Methodologically, we use data from Coppedge, Alvarez e Maldonado (2008) regarding the two dimensions of polyarchy proposed by Dahl (1971): contestation and inclusiveness. Based on these dimensions we classify political regimes in different groups (clusters) according to their similarity level. On substantive grounds, we hope to suggest a methodological tool to classify political regimes and facilitate the understanding of cluster analysis in Political Science.
political regimes; cluster analysis; Q analysis; classification; quantitative methods
Classificando regimes políticos utilizando análise de conglomerados
Dalson Britto Figueiredo Filho; José Alexandre da Silva Júnior; Enivaldo Carvalho da Rocha
Departamento de Ciência Política Universidade Federal de Pernambuco. dalsonbritto@yahoo.com.br; jasjunior2007@yahoo.com.br; enirocha@hotmail.com
RESUMO
O principal objetivo desse artigo é apresentar uma introdução intuitiva à técnica de análise de conglomerados. Metodologicamente, utilizamos os dados de Coppedge, Alvarez e Maldonado (2008) sobre as duas dimensões da poliarquia propostas por Dahl (1971): contestação e inclusividade. A partir dessas dimensões os regimes políticos são classificados em diferentes grupos (clusters) de acordo com o grau de similaridade entre eles. Em termos substantivos,esperamos indicar uma ferramenta metodológica para classificação dos regimes políticos e facilitar a compreensão da técnica de análise de conglomerados na Ciência Política.
Palavras chave: regimes políticos; análise de cluster; Q analysis; classificação; métodos quantitativos
ABSTRACT
The principal aim of this paper is to provide a intuitive introduction to cluster analysis. Methodologically, we use data from Coppedge, Alvarez e Maldonado (2008) regarding the two dimensions of polyarchy proposed by Dahl (1971): contestation and inclusiveness. Based on these dimensions we classify political regimes in different groups (clusters) according to their similarity level. On substantive grounds, we hope to suggest a methodological tool to classify political regimes and facilitate the understanding of cluster analysis in Political Science.
Keywords: political regimes; cluster analysis; Q analysis; classification; quantitative methods
"Classification of objects into meaningful sets - clustering - is an important procedure in all of the social sciences"
Richard G. Niemi
"Crude classifications and false generalizations are the curse of the organized life"
H. G. Wells
Introdução1 1 Agradecemos aos comentários de Natália Leitão a versões anteriores e ao professor Michael Coppedge por gentilmente disponibilizar o seu banco de dados. Eventuais imprecisões são exclusivamente creditadas aos autores. Nosso trabalho é financiado por duas principais fontes: CAPES e CNPQ.
Como classificar casos de forma sistemática? Como criar tipologias e taxonomias de forma objetiva? Partindo do pressuposto de que a classificação é um componente central do conhecimento científico, o principal objetivo deste artigo é apresentar a lógica da análise conglomerados (clusters) na classificação dos regimes políticos2 2 Para Pohlmann, "a análise de conglomerados tem sido referida como análise de clusters, Q analysis, typology, classification analysis e numerical taxonomy" (POHLMANN, 2007, p. 325). Neste artigo, por fins meramente estilísticos, utilizamos os termos análise de conglomerados, análise de cluster e análise de agrupamentos como sinônimos. . Em termos metodológicos, utilizamos o banco de dados elaborado por Coppedge, Alvarez e Maldonado (2008) com diferentes indicadores de democracia. Essas medidas são reduzidas a duas dimensões latentes: contestação e inclusividade, seguindo a definição de Dahl (1971). A partir dessas dimensões, os regimes políticos são classificados em diferentes grupos (clusters) de acordo com o grau de similaridade entre eles.
Uma motivação central que orienta este artigo é a tímida utilização dessa técnica nas Ciências Sociais brasileira3 3 Revisamos todos os números de quatro importantes periódicos da área (DADOS, Revista Brasileira de Ciências Sociais, Revista de Sociologia e Política e Opinião Pública) e, salvo melhor sistematização, não encontramos um único artigo que tenha utilizado alguma técnica de análise de conglomerados. Curi (2003) agrupa países de acordo com o padrão de vida. Lima et al (2005) utilizam a análise de cluster para identificar conglomerados de violência no estado de Pernambuco. No entanto, em ambos os casos, os artigos foram publicados em periódicos de Saúde Pública. . Acreditamos que esse fenômeno pode ser parcialmente explicado pela resistência dos cientistas sociais brasileiros aos métodos quantitativos (SOARES, 2005; WERNECK VIANNA et al, 1998; VALLE e SILVA, 1999 e SANTOS e COUTINHO, 2000). Um impedimento adicional referese à complexidade matemática envolvida na operacionalização das diferentes técnicas de análise de conglomerados (ALDENDERFER E BLASHFIELD, 1984; BAILEY, 1975). Parafraseando Mooney (1996), acreditamos que os benefícios associados à utilização da análise de agrupamentos ainda não são evidentes do ponto de vista conceitual. Por exemplo, Aldenderfer e Blashfield afirmam que "apesar de sua popularidade, os métodos de agrupamento ainda são vagamente compreendidos quando comparados com outras técnicas multivariadas como análise fatorial, análise discriminante e escalonamento multidimensional" (ALDENDERFER e BLASHFIELD, 1984, p. 9). Dessa forma, enquanto não ficarem claras as suas potencialidades, é improvável que esse repertório de técnicas seja incorporado ao cotidiano dos pesquisadores brasileiros. Por isso, nosso foco referese mais ao modus operandi da técnica e menos à interpretação substantiva dos resultados.
Mas o que é análise de conglomerados (cluster)? Ainda de acordo com Aldenderfer e Blashfield, "Análise de cluster é uma denominação genérica para um grande grupo de técnicas que podem ser utilizadas para criar uma classificação. Esses procedimentos formam empiricamente clusters ou grupos de objetos fortemente similares" (ALDENDERFER e BLASHFIELD, 1984, p.7). Para Hair et al, a "análise de conglomerados agrupa indivíduos ou objetos em clusters de modo que objetos em um mesmo cluster são mais parecidos entre si do que em relação a outros clusters" (HAIR et al, 2006, p. 555). É nesse sentido que o principal objetivo da análise de conglomerados é agrupar casos a partir de determinadas características que os tornam similares4 4 Uma forma bastante intuitiva de compreender a lógica da análise de conglomerados é imaginar a organização de um supermercado. Em geral, itens semelhantes são agrupados em um mesmo setor: cerveja, vinho e refrigerantes se agrupam no setor de bebidas. Banana, maçã e laranja se agrupam no setor de hortifrutigranjeiro, etc. . Para tanto, a análise de conglomerados procura não só minimizar a variância dentro do grupo (within group variance), mas também maximizar a variância entre os grupos (between group variance)5 5 Variância é um conceito central em Estatística e em análise multivariada de dados. Algebricamente: σ 2 = Onde, µ representa a média e N representa o tamanho da população. Para calcular a variância da amostra a fórmula é a seguinte: Onde, representa a média da variável na amostra e n representa o tamanho da amostra. Na análise de conglomerados, buscase garantir que tanto a homogeneidade dentro dos grupos ( clusters) quanto a heterogeneidade entre os grupos sejam maximizadas. .
Para tratar dessas questões, este artigo está dividido em cinco partes. A próxima seção revisa brevemente parte da literatura sobre a análise de conglomerados. O objetivo é fornecer ao leitor um ponto de partida para aprofundar seus conhecimentos sobre essa técnica. A segunda apresenta o planejamento, passo a passo, da análise de cluster. A meta é familiarizar o leitor com a terminologia utilizada bem como sistematizar os estágios que devem ser seguidos. A terceira seção oferece um exemplo de desenho de pesquisa utilizando a análise de conglomerados. Depois disso, apresentamos as principais estatísticas de interesse e sua respectiva interpretação. Por fim, a quinta parte apresenta as conclusões do artigo.
Breve revisão da literatura6 6 Para os propósitos deste artigo, o grau de complexidade matemática foi minimizado. Para os leitores interessados em aprofundar seus conhecimentos, sugerimos consultar a bibliografia citada: para trabalhos clássicos utilizando a análise de cluster, Zubin (1938), Tryon (1939), Driver e Kroeber (1932) e Sokal e Sneath (1963). Para uma revisão da literatura, ver Bailey (1975). Para uma introdução, ver Aldenderfer e Blashfield (1984). Para uma análise de cluster das votações congressuais, ver MacRae (1966). Para uma tipologia de famílias de rua utilizando a referida técnica, ver Danseco e Holden (1998). Para uma aplicação em demografia, ver Peters (1958). Para um exame de atitudes políticas utilizando análise de cluster, ver Fleishman (1986). Goldstein e Linden (1969) empregam análise de conglomerados para classificar 513 alcoólatras em quatro diferentes grupos. Para um estudo sobre mercado de trabalho, ver Vanneman (1977). Burton e Romney (1975) analisaram o papel de diferentes termos linguísticos a partir da referida técnica. Filsinger, Faulkner e Warland (1979) utilizaram análise de cluster para classificar indivíduos a partir da variável religião.
De acordo com Bailey (1975), a análise de cluster tem sua origem na psicologia a partir dos trabalhos pioneiros de Zubin (1933) e Tryon (1939) e na antropologia a partir do artigo "Quantitative expressions of cultural relationships" de Driver e Kroeber (1932)7 7 Os interessados podem acessar o referido trabalho a partir do seguinte endereço eletrônico: < http://digitalassets.lib.berkeley.edu/anthpubs/ucb/text/ucp031-005.pdf>. Outros textos importantes foram produzidos por Czekanowski (1911), Driver (1965) e Johnson (1967). . Para Aldenderfer e Blashfield (1984), uma importante contribuição ao desenvolvimento das técnicas de clustering (agrupamento) foi feita a partir do livro "Principles of Numerical Taxonomy" de Sokal e Sneath (1963). Em Economia, Fisher (1969), na Geografia, Berry e Ray (1966) e em Ciência Política, Kaiser (1966) foram pioneiros na aplicação da técnica em suas respectivas áreas de interesse (BAILEY, 1975). No entanto, tanto Aldenderfer e Blashfield quanto Bailey destacam que, durante muito tempo, as diferentes técnicas de análise de cluster ficaram restritas a um grupo mais reduzido de pesquisadores devido a sua complexidade matemática. Esses autores argumentam que o avanço computacional é um elemento central para explicar a propagação da técnica entre os diferentes ramos do conhecimento. Atualmente, os algoritmos matemáticos e os cálculos de distância entre os casos são realizados quase instantaneamente pela maior parte dos pacotes estatísticos, isso facilita a utilização da análise de conglomerados por pesquisadores que não dominam as complexidades matemáticas, mas compreendem a lógica intuitiva da técnica.
Mas para que serve a análise de cluster afinal? Hair et al (2006) afirmam que a "Análise de cluster é um grupo de técnicas multivariadas cujo principal objetivo é agrupar objetos a partir de suas características" (HAIR et al, 2006, p. 559). De acordo com Garson (2010), a "Análise de cluster (...) procura identificar subgrupos homogêneos de casos na população, quer dizer, a análise de cluster é utilizada quando o pesquisador não sabe a priori o número de grupos, mas deseja identificálos e analisar níveis de pertencimento" (GARSON, 2010).
Para Aldenderfer e Blashfield (1984), "o principal motivo para utilizar análise de conglomerados é encontrar grupos de objetos similares em uma amostra de dados. Esses grupos são convenientemente chamados de clusters" (ALDENDERFER e BLASHFIELD, 1984, p. 33). Em síntese, fica claro que o principal objetivo da referida técnica é agrupar casos de acordo com o grau de semelhança observado entre eles. Hair et al (2006) afirmam que a lógica subjacente à análise de cluster é semelhante à lógica da análise fatorial. A diferença básica é que, na análise fatorial, o pesquisador está interessado em representar um conjunto de variáveis observadas a partir de um número menor de fatores enquanto na análise de conglomerados o pesquisador procura representar um conjunto de casos a partir de um número menor de grupos (clusters). Em uma frase: na análise fatorial, agrupamse variáveis, na análise de conglomerados, agrupamse casos8 8 É importante lembrar que alguns pacotes estatísticos apresentam a opção de utilizar a análise de conglomerados para agrupar variáveis, é o caso, por exemplo, do Statistical Package for Social Sciences (SPSS). . A Figura 1 ilustra um tipo ideal de análise de conglomerados.
Os casos são agrupados de acordo com o grau de proximidade recíproca, é o que a literatura denomina de distância/similaridade. Existem diferentes formas de estimar quão distantes/próximas são as observações9 9 Aldenderfer e Blashfield (1984), Garson (2010) e Hair et al (2006) discutem diferentes métodos para estimar a distância/similaridade entre os casos. Para os propósitos deste artigo, optamos por não reproduzir integralmente o debate, nos limitando aos aspectos mais básicos da técnica. . Em geral, procurase garantir o máximo de homogeneidade dentro do cluster ao mesmo tempo em que se maximiza a heterogeneidade entre os grupos. Como é impossível maximizar duas variáveis ao mesmo tempo, esperase encontrar uma solução que otimize essa relação. Para tanto, é importante entender o conceito de variate. Para Hair et al, "A variate do conglomerado é um grupo de variáveis que representam as características utilizadas para comparar os objetos na análise de cluster" (HAIR et al, 2006, p. 559). É exatamente a partir da variate que os casos são classificados, formando os diferentes grupos (clusters)10 10 Uma forma mais intuitiva para pensar o conceito de variate é imaginar uma medida síntese que seja utilizada para calcular o nível de similaridade entre os casos analisados. Neste artigo, evitamos utilizar o termo variate, optando pelo termo variável. Agradecemos ao parecerista por essa sugestão. . A próxima seção ilustra o planejamento de uma análise de conglomerados.
Planejamento de uma análise de conglomerados11 11 Aldenderfer e Blashfield alertam para quatro precauções que os pesquisadores devem atentar antes de utilizar a análise de conglomerados em seus desenhos de pesquisa. Em primeiro lugar, os autores afirmam que "a maior parte dos métodos de análise de conglomerados são procedimentos relativamente simples que, em geral, não necessitam de extenso suporte estatístico" (ALDENDERFER e BLASHFIELD, 1984, p.14). Em segundo lugar, os autores afirmam que a análise de conglomerados está intimamente ligada ao desenvolvimento metodológico de diferentes disciplinas, carregando, dessa forma, os avanços e os vieses de diferentes ramos do conhecimento. Por exemplo, o que é importante em Psicologia pode ser dispensável em Ciência Política e viceversa. Nesse sentido, cabe ao pesquisador não só garantir que os procedimentos técnicos sejam devidamente seguidos, mas, principalmente, conferir interpretação substantiva aos resultados encontrados. Em terceiro lugar, Aldenderfer e Blashfield afirmam que "diferentes métodos de agrupamento podem e, em geral, produzem diferentes soluções para o mesmo conjunto de dados" (ALDENDERFER e BLASHFIELD, 1984, p.15). É importante que o pesquisador esteja atento a este fato na hora de replicar testes de outros pesquisadores e, sempre que possível, procure validar os resultados encontrados. Por fim, os autores destacam que "enquanto a estratégia da análise de cluster é structureseeking, sua operacionalização é structureimposing" (ALDENDERFER e BLASHFIELD, 1984, p.16), i.e., grupos (conglomerados) sempre serão criados, já que a análise parte do pressuposto de que existe uma estrutura inerente aos dados que não pode ser observada visualmente.
Que requisitos precisam ser satisfeitos para utilizar a técnica de análise de cluster em um determinado desenho de pesquisa (HAIR et al, 2006). O objetivo desta seção é sumarizar essas informações. A Tabela 1 sintetiza o planejamento de uma análise de conglomerados em cinco estágios.
O primeiro passo é definir a amostra. Para Hair et al (2006), o tamanho da amostra na análise de cluster não se relaciona com questões de inferência estatística como em análise de regressão, por exemplo. Ou seja, não se procura estimar em que medida os resultados encontrados na amostra podem ser estendidos à população. Na verdade, o tamanho da amostra deve garantir que os pequenos grupos da população sejam devidamente representados. Além disso, diferente de outras técnicas multivariadas, não existe uma regra geral para especificar o tamanho mínimo da amostra12 12 Formann (1984) sugere que o número de casos (n) deve ser igual a 5*2 k, onde k representa o número de variáveis. Logo, se o pesquisador utilizar três variáveis, ele deve contar com, no mínimo, (5* 2 3) = 40 casos. (DOLNICAR, 2002). Nossa recomendação é que ao se elevar a quantidade de variáveis incluídas na análise devese aumentar também o número de casos. Um procedimento importante que deve ser empregado ainda no primeiro estágio é a identificação de outliers. Isso porque a análise de conglomerados é sensível à presença de observações muito destoantes. Hair et al (2006) sugerem a inspeção gráfica do diagrama de perfil (profile diagram). O pesquisador também pode utilizar o blox-plot e gráficos de dispersão para identificar outliers, além dos testespadrão disponíveis nos diferentes pacotes estatísticos. Pohlmann sugere "calcular o escore padronizado Z e considerar como outliers as observações cujos escores, em valores absolutos, sejam maiores do que três" (POHLMANN, 2007, p. 333)13 13 Para padronizar uma variável, devese subtrair o seu valor pela média e dividir o resultado pelo desviopadrão. Algebricamente, Onde x1 representa o valor da observação, µ representa a média da população σ e ( representa o desvio padrão. .
Depois de selecionar a amostra (1º estágio), o pesquisador deve decidir que variáveis serão utilizadas para estimar a distância/similaridade entre os casos (2º estágio). Como a análise de cluster não diferencia entre variáveis relevantes e irrelevantes, é necessário que essa inclusão seja teoricamente orientada. Hair et al afirmam que devem ser incluídas apenas as variáveis que caracterizem os objetos que serão agrupados e se relacionem especificamente aos objetivos da análise de cluster (HAIR et al, 2006, p. 570). Para Aldenderfer e Blashfield, "a escolha das variáveis que serão utilizadas na análise de conglomerados é um dos passos mais importantes do processo de pesquisa, mas, infelizmente, um dos menos compreendidos" (ALDENDERFER e BLASHFIELD, 1984, p.19). Idealmente, o desenho de pesquisa deve selecionar apenas variáveis teoricamente relevantes para proceder à classificação dos casos. Os autores advertem que, caso contrário, existe um sério risco de o pesquisador enveredar por um empirismo ingênuo, produzindo resultados conceitualmente vazios e que não contribuem para o avanço do conhecimento. No que diz respeito ao nível de mensuração, Hair et al (2006) destacam as medidas correlacionais e as medidas de distância. As correlacionais permitem trabalhar com variáveis categóricas, já as de distância exigem variáveis métricas14 14 Aldenderfer e Blashfield (1984) argumentam que a mais importante discussão a respeito das diferentes medidas de distância/similaridade pode ser encontrada no trabalho de Sneath e Sokal (1973). . Outro ponto importante diz respeito à padronização das variáveis incluídas na análise de cluster. Alguns especialistas recomendam que variáveis medidas em diferentes escalas devem ser padronizadas (média zero e variância igual a um) para que a comparação entre elas seja inteligível. O problema da ponderação (criar pesos) também divide a opinião dos pesquisadores15 15 Para o leitor interessado em um debate inicial sobre esses temas, ver Aldenderfer e Blashfield (1984). Para uma discussão mais aprofundada, ver Everitt (1980). .
Depois de selecionar as variáveis utilizadas para estimar a similaridade entre os casos (2º estágio), o pesquisador deve definir a medida de similaridade utilizada (3º estágio). Pohlmann afirma que "a similaridade entre objetos (interobject similarity) é uma medida de correspondência, ou semelhança, entre os objetos a serem agrupados" (POHLMANN, 2007, p.333). Existem diferentes maneiras de calcular essas medidas e diferentes medidas tendem a produzir soluções distintas. Para Pohlmann, "existe frequentemente um grande grau de subjetividade envolvido na escolha da medida de similaridade. Importantes considerações incluem a natureza das variáveis (discretas, contínuas, binárias), escalas de medida (nominal, ordinal, intervalar, proporcional) e o conhecimento da matéria objeto da pesquisa" (POHLMANN, 2007, p.333334). Recomendamos que pesquisadores iniciantes utilizem as medidas de similaridade mais convencionais, incorporando diferentes medidas ao longo do seu processo de aprendizado.
Uma vez calculada a similaridade, o próximo passo é decidir o método (algoritmo matemático) de aglomeração. Ou seja, o pesquisador deve definir como as distâncias serão calculadas e quantos conglomerados (grupos) devem ser criados16 16 A versão 16 do SPSS contempla as seguintes medidas de similaridade para variáveis métricas: euclidian distances, squared euclidian distances, Cosine, Pearson correlation, Chebychev, Block, Minkowski e Customized. Como métodos de aglomeração o referido software dispõe do seguinte: between groupslinkage, within groupslinkage, Nearest neighbor, Furthest neighbor, Centroid clustering, Median clustering e Ward's method. Para uma discussão sobre cada um deles, ver Garson (2010). . O Statistical Package for Social Sciences, versão 16, fornece três abordagens gerais para criar os conglomerados: a) Hierarchical clustering (agrupamento hierárquico); b) K- means clustering e c) Twostep clustering17 17 Para as diferenças entre a s três abordagens, ver Garson (2010). . A abordagem Hierarchical clustering (HCA) é mais apropriada para amostras pequenas em geral, N<250 (GARSON, 2010). Na medida em que o tamanho da amostra cresce, a solução do algoritmo tende a ficar mais lenta, podendo, inclusive, travar o computador. Na HCA, os clusters são aninhados, ou seja, não são mutuamente exclusivos. O pesquisador pode escolher a amplitude do número de clusters ou a quantidade exata de grupos que devem ser criados a partir dos casos observados.
A opção K- means clustering é mais indicada para amostras maiores (N>1.000) já que ela não computa a matriz de proximidade de distâncias/similaridade entre todos os casos observados. Como medida de similaridade, a abordagem K- means clustering utiliza a distância Euclidiana18 18 Algebricamente, Onde d ij representa a distância entre os casos i e j; x ik é o valor da Kesima variável para o iesimo caso. Para evitar a utilização da raiz quadrada, é possível elevar o valor da distância ao quadrado (d ij 2) produzindo, dessa forma, a distância Euclidiana ao quadrado ( squared Eucledian distance). e o pesquisador deve especificar antecipadamente o número de grupos (conglomerados) que serão formados (GARSON, 2010).
A abordagem Twostep clustering é considerada ideal para grandes bases de dados, já que tanto o agrupamento hierárquico quanto a K- means clustering podem apresentar problemas de escalonamento quando a amostra é demasiadamente grande. Além disso, a saída do output apresenta mais opções, inclusive um gráfico que compara a importância de cada variável na formação dos conglomerados.
Depois de escolher a medida de similaridade e o método (algoritmo matemático) de aglomeração (3º estágio), o pesquisador deve identificar o número de grupos (K) que serão formados (4º estágio). Nesse momento, ele deverá utilizar a teoria para orientar a sua escolha. Por exemplo, se trabalhos anteriores sugerem a existência de três grupos, uma possibilidade analítica é replicar o número de grupos com o objetivo de verificar em que medida a solução encontrada é mais ou menos robusta. Na ausência de teoria sobre o assunto, o pesquisador pode adotar uma perspectiva exploratória e repetir a análise variando o número de grupos (K). As diferentes soluções devem ser comparadas à luz da literatura especializada sobre o tema em busca de uma explicação substantiva.
Por fim, no 5º estágio, o pesquisador deve validar os resultados encontrados. Hair et al alertam que "o pesquisador deve ter muito cuidado na validação e na garantia de significância prática da solução final" (HAIR et al, 2005, p.405). A validação consiste em garantir que a solução encontrada seja representativa da população, descrevendo um padrão relativamente estável para outras amostras. Um procedimento para executar a validação consiste no particionamento (divisão) da amostra original em outras separadas e comparar as soluções obtidas em ambos os casos, verificando a correspondência dos resultados (HAIR et al, 2005). Outro caminho é testar a capacidade preditiva da solução gerada a partir da comparação de uma variável aleatória que não tenha sido utilizada na solução inicial de geração dos conglomerados. Por exemplo, ao separar grupos de acordo com o hábito tabagista, esperase que, em média, a resistência física dos não fumantes seja maior do que a dos fumantes. Dessa forma, depois de separar os grupos, o pesquisador pode conduzir uma bateria de testes físicos e verificar se o grupo dos não fumantes, de fato, apresenta um rendimento superior à performance dos fumantes. Ou, ao classificar regimes políticos de acordo com o seu nível de democratização, o pesquisador pode estimar em que medida a desigualdade de renda varia entre os diferentes grupos de países, assumindo que democracias tendem a promover maior distribuição de renda do que não-democracias.
Exemplo de desenho de pesquisa: classificando regimes políticos
Retomando a questão de pesquisa: como classificar casos sistematicamente? Como criar tipologias e taxonomias de forma objetiva? Para responder a essas questões, utilizamos a análise de conglomerados para classificar regimes políticos. Em termos metodológicos, utilizamos o banco de dados elaborado por Coppedge, Alvarez e Maldonado (2008) (1º estágio), analisando as duas dimensões da poliarquia propostas por Dahl (1971): contestação e inclusividade (2º estágio)19 19 Coppedge, Alvarez e Maldonado (2008) utilizam um modelo de análise fatorial para reduzir diferentes indicadores de democracia nas duas dimensões da poliarquia propostas por Dahl (1971), contestação e inclusividade. Essas dimensões são utilizadas no presente artigo como as variáveis de referência para classificar os regimes políticos em diferentes conglomerados. Aldenderfer e Blashfield (1984), Hair et al (2006) e Garson (2010) advertem que a análise de conglomerados pode não ser eficientemente realizada quando as variáveis utilizadas são fatores ou componentes extraídos via análise fatorial. Essa preocupação se justifica por que, em muitas soluções, os fatores extraídos carregam pouca variância (S 2<60%), o que, de fato, pode prejudicar o poder aglomerativo das variáveis. A solução fatorial encontrada no presente banco de dados explica mais de 75% da variância total das variáveis observadas, o que assegura um maior nível de capacidade de as dimensões latentes (contestação e inclusividade) agruparem os casos observados em diferentes clusters. . A amostra contempla diferentes países no período entre 1950 e 2000. Finalizado o segundo estágio, o próximo passo é definir o tipo de distância e decidir o método de aglomeração (3º estágio). Para os propósitos deste artigo, utilizamos a medida mais comum: o quadrado da distância Euclidiana. Além disso, como a amostra é relativamente pequena e todas as variáveis são contínuas, optamos por utilizar as abordagens Hierarchical clustering e K- means clustering. Depois disso, essas dimensões (contestação e inclusividade) foram utilizadas para classificar os regimes políticos (4º estágio). Por fim, utilizamos a validação por amostras particionadas, além disso, comparamos nossa classificação, produzida via análise de conglomerados, com a classificação proposta por Mainwaring, Brinks e PérezLiñán (2001) (5º estágio).
Resultados20 20 Neste artigo, todo o trabalho computacional foi efetuado a partir do Statistical Package for Social Sciences (SPSS), versão 16. Para solicitar a análise de cluster no SPSS, o pesquisador deve escolher as opções Analyze, Classify e, então, optar pelo método de aglomeração desejado ( Hierarchical clustering ou K- means clustering ou Twostep clustering).
Os dados mais recentes disponíveis no banco referemse ao ano de 2000. Optamos por trabalhar com essas informações, totalizando 192 observações21 21 O banco de dados utilizado neste artigo está disponível no seguinte endereço eletrônico: < http://www.nd.edu/~mcoppedg/crd/datacrd.htm>. . Por motivos pedagógicos, selecionamos uma amostra aleatória de 20%, já que os resultados computacionais, produzidos utilizando todas as observações no método de agrupamento hierárquico, dificulta a edição das informações dada a magnitude das tabelas22 22 Como procedimento padrão, o Statistical Package for Social Sciences, versão 16, disponibiliza duas diferentes saídas: a) case processing summary e b) agglomeration schedule. O primeiro representa a frequência dos casos analisados, bem como o número de casos missing. Caso o pesquisador observe que o número de casos com informações ausentes seja alto, ele deve repensar a utilização da técnica e/ou preencher as informações faltantes. A segunda saída ilustra o processo de aglomeração. Ela indica, passo a passo, os casos que foram aglomerados para formar um determinado cluster.O linkage plot fornece a mesma informação em formato gráfico. . Dessa forma, foram selecionados 41 casos. Do método de agrupamento hierárquico, analisamos apenas o dendograma, concedendo mais atenção às saídas produzidas pelo método de agrupamento K- means clustering.
O dendograma é uma síntese gráfica da análise de conglomerados e agrupa os casos em função do padrão de similaridade, dispensando a determinação prévia da quantidade de grupos23 23 Além do dendograma, a saída computacional do método de aglomeração hierárquica fornece a matriz de proximidade, desde que requisitada na opção "estatísticas". Como ela estima a distância de cada caso em relação aos demais, quanto maior é o N, tanto mais complicada é a sua edição gráfica. Por esse motivo, nos furtamos de reportála aqui. O importante é observar que a matriz de proximidade resume o grau de semelhança/diferença de cada caso em relação aos demais ao mesmo tempo. . Os casos estão listados no eixo vertical, no caso, os países. Quanto mais casos, maior é o peso do conglomerado. O eixo horizontal ilustra a distância entre os clusters (grupos) quando eles são agrupados. É uma medida de diferenciação entre os grupos. Quanto maior a distância, maior é a diferença entre os casos.
Analisando o dendograma de cima para baixo, observase a existência de diferentes clusters. O primeiro conglomerado agrupa os seguintes países: Finlândia (FIN), Nova Zelândia (NZL), Dinamarca (DNK) e Áustria (AUT). O segundo grupo é formado por 10 observações, são elas: Suíça (CHE), Estados Unidos (USA), Costa Rica (CRI), Argentina (ARG), Islândia (ISL), Reino Unido (GBR), República Dominicana (DOM), Guiana (GUY), Brasil (BRA) e Belize (BLZ). O terceiro grupo reúne 10 casos: Sri Lanka (LKA), Ucrânia (UKR), Bulgária (BGR), Kiribati (KIR), San Marino (SMR), Cabo Verde (CPV), Mônaco (COM), Barbados (BRB), Andorra (ADO) e Peru (PER). O quarto cluster é formado por apenas um caso: Gana (GHA). O quinto conglomerado é formado por Cuba (CUB) e Uzbequistão (UZB). O sexto agrupamento conglomera três países: Argélia (DZA), Camarões (CMR) e Kazaquistão (KAZ). O sétimo cluster tem apenas um caso: Djibuti (DJI). O oitavo conglomerado é formado por dois casos, são eles, Baren (BHR) e Líbia (LBI). Por fim, o último grupo é formado por um único caso: Kuwait (KWT). Mas qual é a interpretação substantiva que o pesquisador pode extrair desses dados? Os resultados revelam que os casos que se encontram no mesmo grupo são, ao mesmo tempo, mais parecidos entre si e mais diferentes das observações que se localizaram nos demais grupos.
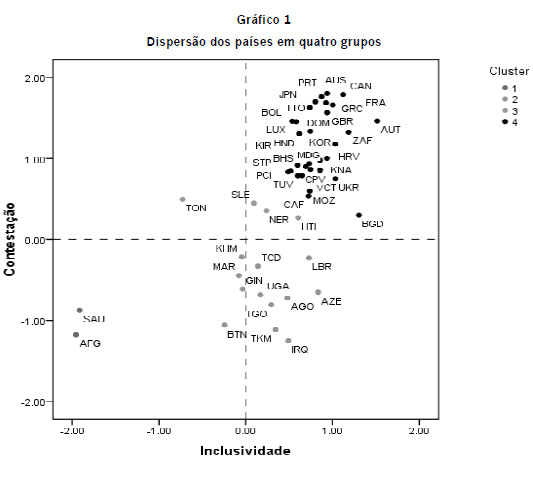
No entanto, é importante lembrar qque a definição do número de conglomerados é um processo subjetivo. Isso porque a análise de conglome erados sempre encontrará uma solução que separa os casos em grupos, mas cabe ao pesquisador deterrminar o número de grupos efetivamente extraídos. Nesse sentido, reforçamos a ideia de que essa té écnica deve ser utilizada com cautela em sua modalidade exploratória. É preferível que o pesquisador t tenha alguma motivação teórica para agrupar seus casos em diferentes grupos. Neste artigo, estimamos ccomo a análise de cluster classificaria os regimes políticos a partir das duas dimensões propostas por r Dahl (1971): inclusividade e contestação. O objetivo é comparar o agrupamento realizado através s da média com o agrupamento produzido via análise de cluster. Para colocar em prática essa opção,selecionamos o método de aglomeração K- means clustering. O Gráfico 1 ilustra a dispersão dos paíse es divididos em quatro clusters, lembrando que as linhas pontilhadas representam as médias das resppectivas variáveis.
Os valores estão padronizados dee tal modo que a média é zero e a distância entre as observações é calculado em termos de desviiopadrão. O cluster 1 é formado por Arábia Saudita (SAL) e Afeganistão (AFG), ambos os regimes apresentam baixa inclusividade e reduzida contestação pública. A maior parte dos regimes políticos do cluster 2 está acima da média na dimensão da inclusividade. Quanto à contestação, todos eles estão abaixo do termo médio. A exceção de Togo (TON), todos os países do conglomerado 3 estão acima da média nas duas dimensões. Similarmente, todos os países agrupados pelo cluster 4 também apresentam inclusividade e contestação acima da média. À primeira vista, o leitor seria levado a acreditar que a análise de cluster falhou em classificar os regimes políticos. Isso porque agrupou países com médias de contestação e inclusividade semelhantes dentro de diferentes conglomerados (clusters 3 e 4). No entanto, os conglomerados são criados de forma relacional, considerando todos os países ao mesmo tempo em função do centro do cluster. Temse, então, uma medida de similaridade entre os regimes políticos tendo como parâmetro não a média, mas sim a distância de cada um deles em relação ao centro do conglomerado. Por exemplo, ao se utilizar a média como referência, Haiti (HTI), Canadá (CAN) e França (FRA) formam um mesmo grupo, localizado no quadrante superior direito. Porém, via análise de cluster, o pesquisador chegaria a um resultado bem diferente e concluiria que o Haiti (HTI) é mais semelhante a Togo (TON) e Serra Leoa (SLE).
Mas quão diferentes são esses grupos (clusters)? Tecnicamente, o pesquisador pode avaliar em que medida a solução encontrada é estatisticamente aceitável. Garson (2010) recomenda analisar a distância média das observações em relação ao centro do cluster após a formação dos diferentes conglomerados. Quanto maior for a diferença entre essas médias, maior é o grau de diferenciação entre os grupos. A Tabela 2 sumariza essas informações.
Observando os valores da distância final de cada grupo (cluster) para cada uma das dimensões, temse que o cluster 4 apresenta os maiores níveis de inclusividade (0,83) e contestação (1,16). No outro oposto, o cluster 1 apresenta os valores mais reduzidos de inclusividade (1,94) e contestação (1,03). A Tabela 3 apresenta a estatística F e os respectivos níveis de significância estatística para cada dimensão analisada24 24 É importante lembrar que como a análise de cluster maximiza a diferença entre os grupos, a estatística F não pode ser interpretada como representando um teste de hipótese de diferença entre os grupos. A sua interpretação mais adequada deve se restringir ao aspecto descritivo .
Por fim, é importante validar os resultados encontrados. Neste artigo, optamos por duas formas de validação: a primeira consiste e em selecionar outra amostra aleatória a partir da amostra original e replicar a análise. O segundo proce edimento é comparar a classificação produzida via análise de conglomerados com a taxonomia proposta po or Mainwaring, Brinks e PérezLiñán (2000).
Em relação à primeira forma de valiidação, extraímos outra amostra aleatória a partir do banco de dados original. O Gráfico 2 ilustra a disperrsão dos países divididos em quatro clusters.
O cluster 1 se localiza integralmente no quadrante inferior esquerdo (ambas as dimensões abaixo da média) e agrupa Kuwait (KWT), Barém (BHR) e Líbia (LBI). O cluster 2, por sua vez, apresenta também distribuição homogênea, localizandose no quadrante superior direito (ambas acima da média). O cluster 3 agrupa os países com inclusividade acima da média e contestação abaixo do termo médio. Finalmente, o conglomerado 4 também agrupa os países com níveis de inclusividade e contestação acima da média. Em uma análise de dispersão convencional (olhando para as médias), o pesquisador seria levado a classificar os regimes políticos dos clusters 2 e 4 sob uma mesma categoria. No entanto, é visualmente perceptível a diferença que existe entre os regimes políticos dos clusters 2 e 4, registrese: os regimes políticos agrupados no grupo 4 são mais democráticos do que aqueles aglomerados no 2, embora eles estejam contidos no mesmo quadrante. Dessa forma, uma primeira vantagem associada à utilização da análise de conglomerados é o maior grau de precisão analítica que o pesquisador pode atingir. Como a classificação de um determinado regime político é mais objetiva, o pesquisador reduz a probabilidade de produzir classificações grosseiras. Além disso, é possível avaliar quão diferente é um caso em relação às demais observações do seu grupo bem como ponderar o nível de diferenciação entre os diferentes grupos.
O segundo procedimento adotado para validar os resultados é comparar as soluções encontradas via análise de conglomerados com a classificação elaborada por Mainwaring, Brinks e PérezLiñán (2000). Para tanto, realizamos uma nova aglomeração com os 19 casos analisados por esses autores, tendo o ano de 1999 como referência. Utilizamos o método K- means clustering de aglomeração e definimos a criação de quatro grupos. A Tabela 4 apresenta a classificação proposta por Mainwaring, Brinks e PérezLiñán (2000) bem como os níveis de contestação e inclusividade de cada país e o seu respectivo cluster.
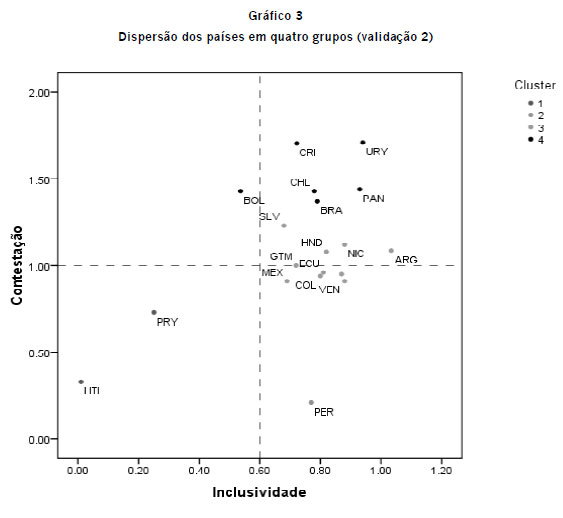
Seguindo a classificação proposta por Mainwaring, Brinks e PérezLiñán (2000), observase que 11 dos 19 regimes políticos são classificados como democráticos (57,89%), 36,84% dos casos são classificados como semidemocráticos (7 observações) e apenas o regime político do Haiti foi classificado como autoritário. No entanto, é interessante notar que países classificados com o mesmo regime foram agrupados em diferentes clusters, como é o caso de Argentina (cluster 3) e Bolívia (cluster 4). O Gráfico 3 ilustra a dispersão dos países analisados por Mainwaring, Brinks e PérezLiñán (2000) divididos em 4 grupos.
Em primeiro lugar, observase umma grande correspondência entre o cluster 3 e o grupo de países classificados como semidemocraciias segundo a tipologia elaborada por Mainwaring, Brinks e PérezLiñán (2000). A exceção fica por con nta do Peru (PER) cluster 2 e Paraguai (PRY) conglomerado 1. Em relação a este último, Mainwaring g, Brinks e PérezLiñán (2000), o classificam como semidemocracia. No entanto, a análise de clust ter sugere que o regime político paraguaio está mais próximo do Haiti (HTI), único país classificado com mo autoritário segundo a tipologia elaborada por Mainwaring, Brinks e PérezLiñán (2000). Além disso, o os países considerados democráticos pelos referidos autores estão divididos entre os clusters 3 e 4. Po or exemplo, Venezuela (VEN) cluster 3 e Uruguai (URY) cluster 4 estão agrupados sob a mesma a categoria: democracia. Todavia, os países do cluster 4 são nitidamente mais democráticos do que os regimes políticos do conglomerado 3. Isso quer dizer que a taxonomia proposta por Mainwaring, Brinks s e PérezLiñán (2000) não permite observar a variação dentro dos grupos. A depender de quanta variaçãoo esteja presente, correse o risco de chamar "urubu de meu louro". Em termos mais técnicos, correse o risco de produzir classificações e tipologias inconsistentes que não discriminam os casos de interesse a partir das categorias analíticas utilizadas.
Conclusão
Como elevar a precisão analítica de tipologias teoricamente orientadas? O principal objetivo deste artigo foi apresentar, passo a passo, a lógica intuitiva da técnica de análise de conglomerados. Isso porque acreditamos que a classificação de casos em categorias é uma etapa fundamental do conhecimento científico. Comparativamente, observouse que a classificação de regimes políticos via análise de agrupamentos fornece um maior grau de precisão do que classificações categóricas do tipo: democracia versus autoritarismo; democracia, semidemocracia e autoritarismo, etc. Com a análise de conglomerados, o pesquisador tem como estimar com maior precisão o grau de semelhança/diferença entre os seus casos de interesse. Entendemos que essa técnica proporciona um avanço metodológico importante e, caso seja aplicada adequadamente, pode nos ajudar a melhor classificar nossos casos em categorias teoricamente inteligíveis.
E qual é o problema de agrupar casos diferentes sob a mesma categoria? Fundamentalmente, perdese poder de sensibilidade analítica. Ou seja, a variável de interesse perde a sua capacidade explicativa em relação a outras variáveis. Por exemplo, se o pesquisador acredita que democracias tendem a promover um maior nível de redistribuição de renda, a classificação inadequada dos regimes políticos vai influenciar negativamente a capacidade de encontrar o efeito esperado. Não porque o efeito não existe e sim porque as categorias utilizadas não possuem poder discriminatório.
Atribuise a Charles Darwin a seguinte passagem: "A ignorância gera mais frequentemente confiança do que o conhecimento: são os que sabem pouco, e não aqueles que sabem muito, que afirmam de uma forma tão categórica que este ou aquele problema nunca será resolvido pela ciência". Acreditamos que a empreitada do conhecimento é um caminho tortuoso e quanto mais precisos forem nossos instrumentos para investigar a realidade, tanto mais capacitados estaremos para responder às questões que nos interessam. Com este artigo, esperamos ter facilitado a compreensão da técnica de análise de conglomerados nas Ciências Sociais em geral e difundido a sua aplicação prática na Ciência Política em particular.
Recebido para publicação em setembro de 2010.
Aprovado para publicação em junho de 2011.
- ALDENDERFER, M. S. e BLASHFIELD, R. K. "cluster Analysis". Sage University Paper Series: Quantitative Applications in the Social Science, 1984.
- BAILEY, K. D. "cluster Analysis". Sociological Methodology, vol. 6, p. 59-128, 1975.
- BERRY, B. J. L. and RAY, M. Multivariate socioeconomic regionalization: A pilot study in central Canada. Unpublished manuscript. Department of Geography, University of Chicago, 1966.
- BURTON, M. C. e ROMMEY, A. K. "A Multidimensional Representation of Role Terms". American Ethnologist, v. 2, n.3, p.397-407, 1975.
- COPPEDGE, M.; ALVAREZ, A.; MALDONADO, C. "Two Persistent Dimensions of Democracy: Contestation and Inclusiveness". Journal of Politics, v. 70, n. 3, p. 145, 2008.
- CZEKANOWSKI, J. "Objectiv Rriterien in der Ethnologie". KorrespondenzBlatt der Deutschen Gesellschaft fur Anthropologie, Ethnologie und Urgeschichte, 42, p.7175, Hamburg, 1911.
- DAHL, R. Poliarquia: Participação e Oposição. São Paulo: Edusp, 1971.
- DANSECO, E. R.; HOLDEN, E. W. "Are There Different Types of Homeless Families? A Typology of Homeless Families Based On cluster Analysis". Family Relations, v. 47, n. 2, p. 159-165.
- DOLNICAR, S. A review of unquestioned standards in used cluster analysis for datadriven market segmentation. Faculty of Commerce - Papers 2002. Disponível em: <http://ro.uow.edu.au/commpapers/273>
- DRIVER, H. E. Survey of numerical classification in anthropology. In: HYMES, D. (Ed.). The Use of Computers in Anthropology The Hague: Mouton, 1965.
- DRIVER, H. E.; KROEBER, A. L. Quantitative Expressions of Cultural Relation ships Berkeley: University of California Press, 1932.
- EVERITT, B.S. Cluster Analysis Second Edition, London: Heineman Educational Books Ltd, 1980.
- FILSINGER, E.; FAULKNER, J. & WARLAND, R. "Empirical taxonomy of religious individuals: An investigation among college students". Sociological Analysis, v. 40, 136-146, 1979.
- FISHER, W. D. Clustering and Aggregation in Economics Baltimore: Johns Hopkins, 1969.
- FLEISHMAN, J. A. "Types of Political Attitude Structure: Results of a cluster Analysis". The Public Opinion Quarterly, v. 50, n. 3, p. 371-386, 1986.
- FORMANN, A.K. Die Latent Class Analyse: Einführung in die Theorie und Anwendung. Weinheim: Beltz, 1984.
- GARSON, G. D. Statnotes: Topics in Multivariate Analysis [online]. Disponível em: <http://faculty.chass.ncsu.edu/garson/PA765/statnote.htm> Acesso em 22 jan. 2010.
- GOLDSTEIN, S. G. and LINDEN, J."Multivariate Classification of alcoholics by means of MMPI". Journal of abnormal Psychology, v. 14, n. 6, p. 661-669.
- HAIR, Jr; BLACK, W. C; BABIN, B. J.; ANDERSON, R. E.; TATHAM, R. L. Análise Multivariada de Dados Porto Alegre: Bookman, 2005.
- ______. Multivariate Data Analysis 6Ş edição. Upper Saddle River, NJ: Pearson Prentice Hall, 2006.
- JOHNSON, S. "Hierarchical clustering schemes". Psychometrika, 38, p.241-254, 1967.
- KAISER, H. F. "An objective method for establishing legislative districts". Midwest Journal of Political Science, v. 10, p. 200-213, 1966.
- KING, G.; KEOHANE, R.; VERBA, S. Designing Social Inquiry: Scientific Inference in Qualitative Research, Princeton: Princeton university Press, 1994.
- MACRAE, D. Jr. "cluster Analysis of Congressional Votes with the BC TRY System". The Western Political Quarterly, v. 19, n. 4, p. 631-638.
- MAINWARING, S.; BRINKS, D.; PÉREZLIÑÁN, A. "Classificando Regimes Políticos na América Latina, 1945-1999". Dados, v. 44, n. 4, 2001.
- MOONEY, C. Z. "Bootstrap Statistical Inference: examples and evaluation for Political Science". American Journal of Political Science, v. 40, n. 2, p. 570-602.
- PETERS, W. S. "cluster Analysis in Urban Demography", Social Forces, v. 37, n. 1, p. 38-44, 1958.
- POHLMANN, M. C. Análise de Conglomerados. In: CORRAR, L. J.; EDÍLSON, P.; DIAS FILHO, J. M. (Orgs.). Análise Multivariada São Paulo: Atlas, 2007.
- SANTOS, M. H; COUTINHO, M. "Política comparada: estado das artes e perspectivas no Brasil", BIB, v. 5, n. 4, p. 3-146, 2000.
- SOARES, G. "O calcanhar metodológico da ciência política no Brasil". Sociologia, Problemas e Práticas, v. II, n. 48, p. 27-52, 2005.
- SOKAL, R. R.; SNEATH, P. H. A. Principles of Numerical Taxonomy. San Francisco: W. H. Freeman, 1963.
- TRYON, R. cluster Analysis. New York: McGrawHill, 1939.
- VALLE e SILVA, N. Relatório de Consultoria sobre Melhoria do Treinamento em Ciência Social Quantitativa e Aplicada no Brasil Rio de Janeiro, Laboratório Nacional de Computação Científica, 1999.
- VANNEMAN, R. "The Occupational Composition of American Classes: Results from cluster Analysis". The American Journal of Sociology, v. 82, n. 4, p. 783-807, 1977.
- WERNECK VIANNA, L. et al. "Doutores e teses em ciências sociais", Dados, v. 41, n. 3, p. 453-515, 1998.
- ZUBIN, J. A. "A technique for measuring likemindedness". Journal of Abnormal and Social Psychology, 33, p.508-516, Oct.1938.
 Onde, µ representa a média e N representa o tamanho da população. Para calcular a variância da amostra a fórmula é a seguinte:
Onde, µ representa a média e N representa o tamanho da população. Para calcular a variância da amostra a fórmula é a seguinte:
 Onde,
Onde,
 representa a média da variável na amostra e n representa o tamanho da amostra. Na análise de conglomerados, buscase garantir que tanto a homogeneidade dentro dos grupos (
representa a média da variável na amostra e n representa o tamanho da amostra. Na análise de conglomerados, buscase garantir que tanto a homogeneidade dentro dos grupos (
 Onde x1 representa o valor da observação, µ representa a média da população σ e ( representa o desvio padrão.
Onde x1 representa o valor da observação, µ representa a média da população σ e ( representa o desvio padrão.
 Onde d
Onde d
Datas de Publicação
-
Publicação nesta coleção
10 Jul 2012 -
Data do Fascículo
Jun 2012
Histórico
-
Recebido
Set 2010 -
Aceito
Jun 2011