Resumen
El presente estudio analiza la capacidad de dos instrumentos de observación de aula, Classroom Assessment Scoring System (CLASS) y Mathematical Quality of Instruction (MQI), para describir el funcionamiento de aulas de matemática que pertenecen a escuelas municipales chilenas con trayectorias de mejoramiento. En concreto, se busca indagar, por una parte, cómo ambos instrumentos correlacionan y coinciden en encontrar determinados rasgos de la enseñanza, y por otra, en las descripciones cualitativas que esconden los puntajes asignados a cada sala. Los resultados nos indican, por un lado, que solamente la dimensión Diálogo Instruccional de CLASS correlaciona significativamente con algunas de las dimensiones de MQI y que los puntajes asignados a las aulas efectivamente permiten discriminar la calidad o frecuencia con que cada rasgo de la enseñanza aparece en cada aula. Sin embargo, las descripciones cualitativas mostraron que en cada sala es posible encontrar múltiples rasgos positivos de la enseñanza que permitieron a los profesores conducir una buena clase de matemática, con errores y elementos ausentes, pero que fueron reemplazados exitosamente por otros elementos de la enseñanza efectiva.
Observación de clases; Calidad matemática de la instrucción; Interacciones pedagógicas
Abstract
This study analyzes the capacity of two classroom observation instruments, Classroom Assessment Scoring System (CLASS) and Mathematical Quality of Instruction (MQI), to describe the functioning of mathematical classrooms in Chilean public schools with improved trajectories. In fact, it seeks to investigate how the two instruments correlate and agree on finding certain traits of teaching, and the qualitative descriptions that hide the scores assigned to each room. Results indicate that just the Instructional Dialogue dimension of CLASS correlates significantly with some of the dimensions of MQI, and that the scores assigned to the classrooms effectively discriminate the quality or frequency with which each trait of teaching appears in every class. However, qualitative descriptions showed that in each classroom it is possible to find multiple positive traits of teaching that allowed teachers to lead a good mathematics class, with errors and absent elements, but which were successfully replaced by other elements of effective teaching.
Class observation; Mathematical quality of instruction; Pedagogical interactions
Introducción
Recientemente, diversos investigadores han hecho importantes avances en la construcción de instrumentos para observar la sala de clases. CLASS - Classroom Assessment Scoring System (PIANTA; LA PARO; HAMRE, 2008PIANTA, Robert; LAPARO, Karen; HAMRE, Bridget. Classroom Assessment Scoring System™ (CLASS™). Baltimore: Paul H. Brookes, 2008.; PIANTA; HAMRE; MINTZ, 2012PIANTA, Robert; HAMRE, Bridget; MINTZ, Susan. Classroom assessment scoring aystem: upper elementary manual. Charlottesville: Teachstone, 2012.) e Framework for Teaching y Tripod 7Cs (FERGUSON; DANIELSON, 2014FERGUSON, Ronald; DANIELSON, Charlotte. How framework for teaching and tripod 7Cs evidence distinguish key components of effective teaching. In: KANE, Thomas; KERR, Kerry; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 98-143.) son algunos de los instrumentos orientados a analizar prácticas efectivas de la enseñanza en general, mientras que existen otros para observar asignaturas específicas como Protocol for Language Arts Teaching Observation - PLATO para el caso de lenguaje (MIHALY; MCCAFFREY, 2014MIHALY, Kata; MCCAFFREY, Daniel. Grade level variation in observational measures of teacher effectiveness. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 9-49.), MQI para el caso de matemáticas (HILL et al., 2008HILL, Heather et al. Mathematical knowledge for teaching and the mathematical quality of instruction: an exploratory study. Cognition and Instruction, London, v. 26, n. 4, p. 430-511, 2008., 2012HILL, Heather et al. Teacher quality and quality teaching: examing the relationship of a teacher assessment to practice. American Journal of Education, Chicago, v. 118, n. 4, p. 489-519, 2012.), y Quality Teaching in Science - QST para la enseñanza de las ciencias (SCHULTZ; PECHEONE, 2014SCHULTZ, Susan; PECHEONE, Raymond. Assessing quality teaching in science. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 444-492.). En parte, los avances en la construcción de dichos instrumentos han sido posibles gracias a los esfuerzos de la investigación por identificar aquellos atributos del quehacer docente y las interacciones pedagógicas al interior del aula que hacen que los niños alcancen más y mejores aprendizajes (HOPKINS; REYNOLDS, 2001HOPKINS, David; REYNOLDS, David. The past, present and future of school improvement: towards the third age. British Educational Research Journal, Abingdon, v. 27, n. 4, p. 459-475, 2001.; RIVERS; SANDERS, 2002RIVERS, June; SANDERS, Williams. Teacher quality and equity in educational opportunity: findings and policy implications. Teacher Quality, Standford, p. 13-23, 2002.; DARLING-HAMMOND et al., 2011DARLING-HAMMOND, Linda et al. Getting teacher tvaluation right: a background paper for policy makers. Washington: National Academy of Education, 2011.).
Estos instrumentos han adquirido relevancia el último tiempo en aquellos países donde, por una parte, existe consenso sobre la importancia de las interacciones pedagógicas para la calidad del sistema educativo, y por otro, se ha decidido que el camino para alcanzar la mejora es a través de la definición de estándares para las prácticas docentes, la rendición de cuentas, y los mecanismos de evaluación asociados (BARBER; MOURSHED, 2007BARBER, Michael; MOURSHED, Mona. How the world’s best-performing schools systems come out on top. Londres: McKinsey & Company, 2007.; PIANTA; KERR, 2014PIANTA, Robert; KERR, Kerri. Measuring effective teaching - the future starts now. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 583-590.).
En el contexto chileno, la observación de aula ha adquirido relevancia para la política educativa a través iniciativas del tipo pay for performance (MIZALA; SCHNEIDER, 2014MIZALA, Alejandra; SCHNEIDER, Ben Ross. Negotiating education reform: teacher evaluations and incentives in Chile (1990-2010). Governance, Medford, v. 27, n. 1, p. 87-109, 2014.) que se han manifestado por dos vías. Por una parte, las políticas de mejoramiento del cuerpo docente mediante la definición de estándares y evaluaciones. Estas políticas tomaron forma, primero, en el Programa de Asignación por Excelencia Pedagógica (AEP) y la Evaluación docente (RODRÍGUEZ, 2015RODRÍGUEZ, Beatriz. Historia del programa y antecedentes generales. In: RODRÍGUEZ, Beatriz et al. (Ed.). Reconociendo el mérito docente: programa de asignación de excelencia pedagógica 2002-2014. Santiago de Chile: MIDE UC: Pontificia Universidad Católica de Chile, 2015. p. 10-22.), y posteriormente, en el proyecto de ley que actualmente se discute sobre la creación de un Sistema de Desarrollo Profesional Docente (EYZAGUIRRE, 2014EYZAGUIRRE, Nicolás. Proyecto de ley de política nacional docente. Santiago de Chile: Ministerio de Educación, 2014.), que lleva asociadas mejoras salariales y profesionales al mejor desempeño en evaluaciones estandarizadas. Por otra parte, también la observación de aula ha adquirido relevancia en el sistema de Aseguramiento de la Calidad de la Educación, en el cual a través de las visitas de evaluación a las escuelas, entre otras cosas, se observa y analiza la calidad del desempeño docente (CHILE, 2014CHILE. Ministerio de Educación. Estándares indicativos de iesempeño para los establecimientos educacionales y sus sostenedores: evaluación, U. D. C. Y. Santiago de Chile: Ministerio de Educacción, 2014.).
Los instrumentos de evaluación de interacciones y prácticas de aula son un esfuerzo de décadas de investigación, en donde se ha logrado definir qué tipo de prácticas son más eficaces para lograr aprendizajes en los niños, y ciertamente han sido un gran aporte para la política educativa. Sin embargo, al tratarse de herramientas con fuerte conexión en la teoría, con estándares altamente exigentes, corren el riesgo de perder utilidad, mostrando poca capacidad de discriminación entre una buena y una mala sala de clases (CALLAHAN; SADEGHI, 2015CALLAHAN, Kathe; SADEGHI, Leila. Teacher perceptions of the value of teacher evaluations: New Jersey’s ACHIEVE NJ. NCPEA. International Journal of Educational Leadership Preparation, Houston, v. 10, n. 21, p. 46-59, 2015.), poniendo alta presión sobre los docentes y las escuelas al asociar algún tipo de consecuencias a la evaluación con estos instrumentos. En otras palabras, los instrumentos corren el riesgo de tomar distancia de los escenarios empíricos, perdiendo utilidad para el mejoramiento de las prácticas y el desarrollo profesional (CALLAHAN; SADEGHI, 2015CALLAHAN, Kathe; SADEGHI, Leila. Teacher perceptions of the value of teacher evaluations: New Jersey’s ACHIEVE NJ. NCPEA. International Journal of Educational Leadership Preparation, Houston, v. 10, n. 21, p. 46-59, 2015.; SANTIAGO et al., 2013SANTIAGO, Paula et al. OECD reviews of evaluation and assessment in education: teacher evaluation in Chile 2013. Paris: OECD, 2013.; FORD et al., 2015FORD, Timothy et al. Teacher self-efficacy, professional commitment, and high-stakes teacher evaluation policy in Louisiana. Thousand Oaks: Educational Policy, 2015.), y generando un efecto nocivo en las salas de clase por su uso para el accountability (FORD et al., 2015FORD, Timothy et al. Teacher self-efficacy, professional commitment, and high-stakes teacher evaluation policy in Louisiana. Thousand Oaks: Educational Policy, 2015.). Es preciso, por lo tanto, volver a mirar estos instrumentos de observación de aula y los rasgos de enseñanza efectiva que los sustentan, y contrastarlos con lo que realmente ocurre al interior de las aulas.
El objetivo de este artículo es analizar la capacidad de dos instrumentos de observación de aula, Classroom Assessment Scoring System (CLASS) y Mathematical Quality of Instruction (MQI), para describir el funcionamiento de aulas de matemática que pertenecen a escuelas chilenas con trayectorias de mejoramiento. En concreto, se busca indagar, por una parte, cómo ambos instrumentos correlacionan y coinciden en encontrar determinados rasgos de la enseñanza, y por otra, en las descripciones cualitativas que esconden los puntajes asignados a cada sala. Las aulas observadas pertenecen a escuelas vulnerables que han mejorado notoriamente sus resultados en los últimos diez años, lo que las convierte en un escenario ideal para examinar la forma en que este tipo de instrumentos logra captar adecuadamente las prácticas de enseñanza que aparecen empíricamente en escuelas efectivas.
Características de la enseñanza efectiva
Distintos estudios en diversos contextos coinciden en señalar que la enseñanza es efectiva cuando tiene las siguientes características (FERGUSON; DANIELSON, 2014FERGUSON, Ronald; DANIELSON, Charlotte. How framework for teaching and tripod 7Cs evidence distinguish key components of effective teaching. In: KANE, Thomas; KERR, Kerry; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 98-143.; SCHULTZ; PECHEONE, 2014SCHULTZ, Susan; PECHEONE, Raymond. Assessing quality teaching in science. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 444-492.; HOPKINS; REYNOLDS, 2001HOPKINS, David; REYNOLDS, David. The past, present and future of school improvement: towards the third age. British Educational Research Journal, Abingdon, v. 27, n. 4, p. 459-475, 2001.; MUIJS; REYNOLDS, 2011MUIJS, Daniel; REYNOLDS, David. Effective teaching: evidence and practice. 3. ed. Thousand Oaks: SAGE, 2011.; SAMMONS; HILLMAN; MORTIMORE, 1995SAMMONS, Pam; HILLMAN, Josh; MORTIMORE, Peter. Key characteristics of effective schools: a review of school effectiveness research. London: Institute of Education: University of London: OFSTED, 1995.; MARZANO, 2009MARZANO, Robert J. Setting the record straight on “high-yield” strategies. The Phi Delta Kappan, Arlington, v. 91, n. 1, p. 30-37, 2009.; MITCHELL; CAMERON; WYLIE, 2002MITCHELL, Linda; CAMERON, Marie; WYLIE, Cathy. Sustaining school improvement: ten primary schools’ journey. Wellington: New Zealand Council for Eduactional Research, 2002.; PIANTA; HAMRE; MINTZ, 2012PIANTA, Robert; HAMRE, Bridget; MINTZ, Susan. Classroom assessment scoring aystem: upper elementary manual. Charlottesville: Teachstone, 2012.; RACZYNSKI; MUÑOZ, 2006RACZYNSKI, Dagmar; MUÑOZ, Gonzalo. Factores que desafían los buenos resultados educativos de las escuelas en sectores de pobreza. In: CUETO, Santiago (Ed.). Educación y brechas de equidad en América Latina. Chile: Preal, 2006. p. 275-352.; ANFARA; BEAUMONT, 2007ANFARA, Vicent; BEAUMONT, Jesse. Defining the effectiveness of middle grades teachers. Middle School Journal, Westernville, v. 38, n. 5, p. 54-62, 2007.; APPELBAUM, 2009APPELBAUM, Peter. Taking action - mathematics curricular organization for effective teaching and learning. For the Learning of Mathematics, Ontario, v. 29, n. 2, p. 38-43, 2009.; ROUTMAN, 2012ROUTMAN, Regie. Mapping a pathway to schoolwide highly effective teaching. The Phi Delta Kappan, Arlington, v. 93, n. 5, p. 56-61, 2012.):
-
Organización eficiente de la clase: existencia de reglas de conducta y procedimientos para que las transiciones sean breves y estructuradas.
-
Estructuración de la clase, con objetivos claros que son comunicados a los estudiantes, y con monitoreo permanente de los aprendizajes de los niños.
-
Conexión emocional con los niños y sensibilidad ante necesidades académicas: relaciones afectuosas con los niños en un marco de respeto y confianza, donde cada niño sepa que el profesor está disponible para ayudarlo siempre y donde el profesor tiene un alto grado de conocimiento de sus estudiantes.
-
Altas expectativas sobre los niños: es deseable que docentes y escuela en su conjunto manejen altas expectativas, pero además que esto sea comunicado a los estudiantes. Algunos investigadores explicitan además la importancia del refuerzo positivo (SAMMONS; HILLMAN; MORTIMORE, 1995SAMMONS, Pam; HILLMAN, Josh; MORTIMORE, Peter. Key characteristics of effective schools: a review of school effectiveness research. London: Institute of Education: University of London: OFSTED, 1995.).
-
Foco en el desarrollo de los aprendizajes: instauración de una cultura del aprendizaje, tareas con alto desafío intelectual para los estudiantes mediante discusiones, fomento a la indagación y oportunidades para la práctica, etc.
-
Capacidad del docente de promover el involucramiento de los estudiantes, la conciencia de que cada uno es responsable de su propio aprendizaje y la motivación para lograr desarrollar tareas cognitivamente desafiantes.
-
Estrategias de aseguramiento para el aprendizaje significativo: clarificaciones para que todos los niños entiendan las lecciones, partir de los conocimientos previos de los estudiantes, dar adecuada retroalimentación y resolver las dudas de los niños de forma inmediata, utilizar distintos formatos para abordar diversos estilos de aprendizaje, etc.
-
Suficiente manejo por parte del profesor del contenido que se enseña, para así asegurar que los puntos señalados anteriormente tengan una base sólida.
Instrumentos de evaluación de la enseñanza efectiva
Los dos instrumentos utilizados en esta investigación, Classroom Assessment Scoring System (CLASS) y Mathematical Quality of Instruction (MQI) emergen de las categorías de enseñanza efectiva mencionadas más arriba.
CLASS permite captar interacciones pedagógicas entre el profesor y los estudiantes a partir de tres grandes dominios: Apoyo Emocional, Organización de la Sala y Apoyo Pedagógico (PIANTA; HAMRE; MINTZ, 2012PIANTA, Robert; HAMRE, Bridget; MINTZ, Susan. Classroom assessment scoring aystem: upper elementary manual. Charlottesville: Teachstone, 2012.). Las dimensiones asociadas a cada dominio se explican en el siguiente cuadro:
Por su parte, MQI permite evaluar la calidad matemática de una clase teniendo como base las interacciones que se producen entre el profesor y el contenido matemático, los estudiantes y dicho contenido, y la gestión por parte del profesor de esta última relación. Las dimensiones que se definen entre estas relaciones las podemos visualizar en el triángulo didáctico de la Figura 1.
En primer lugar, el instrumento evalúa si el trabajo de la clase está conectado con la matemática (Dimensión 1) y posteriormente evalúa 4 dimensiones, como en el cuadro 2.
Además de estas cinco dimensiones que son evaluadas dividiendo la clase en intervalos, existe una evaluación holística de la clase que considera elementos definidos en las dimensiones anteriores y algunos otros como uso del tiempo y percepción global de la calidad de la clase y el conocimiento del profesor.
Metodología
Instrumentos
CLASS mide la calidad de las interacciones pedagógicas entre profesor y estudiantes. Se utilizó CLASS en su versión Upper Elementary, que incluye las doce dimensiones de los tres dominios explicados arriba (PIANTA; HAMRE; MINTZ, 2012PIANTA, Robert; HAMRE, Bridget; MINTZ, Susan. Classroom assessment scoring aystem: upper elementary manual. Charlottesville: Teachstone, 2012.). La rúbrica tiene tres niveles (bajo, medio y alto) medidos en una escala de 7 puntos, donde: a) 1 y 2 son considerados resultados bajos; b) 3, 4 y 5 son intermedios; y, c) 6 y 7 son altos.
Por su parte MQI mide la calidad matemática de la instrucción en el aula asignando puntajes van de 0 a 3, lo que equivale a considerar que el indicador no está presente (0), bajo (1), medio (2) o alto (3) para cada una de las subdimensiones contenidas en el instrumento. Además asigna puntajes que van de 1 (bajo) a 5 (alto) a las subdimensiones de la dimensión holística que evalúa la clase completa.
Muestra
El tamaño muestral corresponde a 35 salas de 4º a 6º básico, pertenecientes a once escuelas con trayectorias de mejoramiento en el período 2002-2010. Para escoger estas escuelas se diseñó un Índice de Desempeño Educativo6 6 - El índice de Desempeño Educativo se construyó en base a un conjunto de indicadores de escuelas con quince o más estudiantes de 4º básico. Para mayor detalle ver la primera parte de Bellei y otros autores (2014). (IDE) creado para el estudio. Estas escuelas fueron escogidas bajo diversos criterios, entre los que destacan: sustentabilidad de la trayectoria, baja selectividad, diversidad de contextos socioeconómicos y que pertenecieran a las categorías de mejoramiento incipiente, en vías de institucionalización e institucionalizado. Además, los resultados del Sistema de medición de la calidad en educación (SIMCE) en 4º y 8º básico debían ser consistentes, y debían contar con un nivel mínimo en el IDE al final del trayecto estudiado. La selección de los casos cubrió intencionalmente tanto a escuelas municipales como particulares subvencionadas de distintos lugares del país (BELLEI et al., 2014BELLEI, Cristian et al.¿Qué se sabe sobre las escuelas que mejoran? In: BELLEI, Cristian et al. (Ed.). Lo aprendí en la escuela: ¿Cómo se logran procesos de mejoramiento escolar? Santiago de Chile: CIAE: Unicef, 2014. p. 17-27.).
De estas 35 salas, tres fueron escogidas para un posterior análisis cualitativo. Los criterios teóricos de selección tienen que ver esencialmente con las singulares características de las interacciones pedagógicas que muestran estas salas, de acuerdo al análisis cuantitativo realizado con CLASS y MQI.
Procedimientos y análisis
El análisis de interacciones pedagógicas a través de CLASS fue realizado a través de los siguientes pasos. Primero, se filmaron tres horas consecutivas de matemática; luego, éstas son divididas en segmentos codificables de 15 minutos cada uno, de los cuales se eligen cuatro, ubicados en distintos momentos de la clase. La codificación de los cuatro segmentos fue realizada por personas cuya confiabilidad fue certificada por Teachstone7 7 - La empresa creadora de CLASS y encargada de realizar los cursos y entregar certificaciones. , y se hizo un 20% de doble codificación, verificando consistencia adyacente superior al 80%. Se utiliza, como dato final, el promedio del puntaje obtenido en los cuatro segmentos, en cada dimensión.
Para MQI se utilizaron los mismos vídeos de CLASS. Para la codificación se dividen los videos en segmentos de 7,5 minutos y para cada uno se asignan puntajes a todos los indicadores que conforman las cinco primeras dimensiones. Una vez vista la clase completa se califica la dimensión seis de indicadores holísticos de la clase. Un 20% de las clases son doble codificadas por dos evaluadores que deben tener un alto nivel de coincidencia. En promedio se codifican veintidós segmentos para cada profesor y el puntaje que obtiene cada uno de ellos en cada subdimensión resulta de la media del total de segmentos.
El análisis de esta información se separa en dos etapas descriptivas: una de carácter cuantitativo que incluye todas las aulas y una cualitativa con tres de ellas. En la primera etapa, se calculan los coeficientes de correlación entre las dimensiones de Apoyo emocional y pedagógico de CLASS y las dimensiones de MQI.
En la segunda etapa se eligen, a partir de los resultados de la primera, tres casos que muestran buenos resultados en alguna de las dimensiones. El objetivo es analizar en detalle qué características tienen estas clases y de qué forma es una buena clase sin necesariamente contar con todos los elementos que los manuales de enseñanza efectiva.
Para esta segunda etapa se consideran únicamente los dominios de Apoyo pedagógico y Apoyo Emocional. Esto por dos razones: primero, teóricamente el dominio que debiese mostrar una correlación más robusta con MQI es el de apoyo pedagógico, dado que abordan elementos similares de la enseñanza. Segundo, empíricamente los datos mostraron correlaciones estadísticamente significativas con el dominio de Apoyo emocional.
Resultados
Estadísticos descriptivos y correlaciones
Los resultados muestran también un nivel medio en dimensiones del Apoyo emocional como Clima positivo y Sensibilidad del profesor. El Apoyo pedagógico se mantiene en niveles bajos en casi todas las dimensiones estudiadas, salvo en Formatos pedagógicos, donde casi alcanza un nivel medio, y en Comprensión del contenido, donde transita hacia un nivel medio-bajo. Existen dimensiones en niveles particularmente bajos como la Consideración por la perspectiva de los estudiantes, Análisis e Indagación y Diálogo instruccional. Estos resultados coinciden con otros estudios realizados en Chile (TREVIÑO; TOLEDO; GEMPP, 2013TREVIÑO, Ernesto; TOLEDO, Gabriela; GEMPP, René. Calidad de la educación parvularia: las prácticas de clase y el camino a la mejora. Pensamiento Educativo, Santiago de Chile, v. 50, n. 1, p. 40-62, 2013.; LEYVA et al., 2015LEYVA, Diana et al. Teacher-child interactions in Chile and their associations with prekindergarten outcomes. Child Development, Medford, v. 86, n. 3, p. 781-799, 2015.; ELACQUA et al., 2013ELACQUA, Gregory et al. Los efectos de las presiones de accountability sobre las políticas y prácticas pedagógicas en escuelas de bajo desempeño: el caso de Chile. Santiago de Chile: Programa de Promoción de la Reforma Educativa en América Latina y el Caribe, 2013.; TREVIÑO; DONOSO; MOLINA, 2013TREVIÑO, Ernesto; DONOSO, Francisca; MOLINA, Ángeles. Informe resultados: impacto del PAC en las prácticas pedagógicas. Santiago de Chile: Centro de Políticas Comparadas de Educación: Banco Interamericano de Desarrollo: Ministerio de Educación de Chile, 2013.; TREVIÑO; ROMO; GODOY, 2015TREVIÑO, Ernesto; ROMO, Francisca; GODOY, Felipe. Construcción de capacidades profesionales en educación parvularia: evidencia de “Un Buen Comienzo”. In: ELACQUA, Gregory; CORTÁZAR, Alejandra; CALVO, Esteban. Educación, el escenario pre-reforma. Santiago de Chile: Instituto de Políticas Públicas UDP. 2015. p. 37-46.).
En el caso de MQI cabe destacar que la dimensión que registra mejor puntuación es errores e imprecisiones de los profesores respecto del contenido matemático, es decir, que los profesores se caracterizan por no cometer errores ni ser poco claros en el desarrollo conceptual. Mientras que la dimensión peor puntuada es la que se refiere a la remediación de errores de los estudiantes y la utilización de las contribuciones matemáticas que éstos hacen. Cabe destacar que la subdimensiones que presentan mayor promedio son lenguaje matemático (D2) y demanda cognitiva de las tareas (D5).
La Tabla 1 indica que las salas estudiadas son altamente organizadas, con buen manejo de conducta, altamente productivas y con ausencia de clima negativo (GODOY et al., 2016GODOY, Felipe et al. Interacciones pedagógicas y percepción de los estudiantes en escuelas chilenas que mejoran: una aproximación exploratoria. Estudios Pedagógicos, Valdivia, v. 42, n. 3, p. 149-169, 2016.).
El siguiente análisis de correlación da cuenta de aquellos aspectos de la enseñanza efectiva según CLASS y MQI que aparecen de forma conjunta en las salas estudiadas.
Los resultados de la Tabla 2 indican que la dimensión de Diálogo Instruccional de CLASS correlaciona significativamente con varias dimensiones de MQI: Riqueza de la matemática, Trabajo con los alumnos y la matemática, y Participación de los alumnos en la creación de significado y razonamiento. El resto de las dimensiones de Apoyo pedagógico correlacionan solo episódicamente, e incluso, Comprensión del contenido no correlaciona con ninguna de las dimensiones de MQI.
Estos resultados levantan aspectos relevantes. Casi todas las relaciones encontradas son esperables desde la teoría, ya que todas se focalizan en el diálogo y el rol protagónico del estudiante. Sin embargo, la asociación entre Diálogo instruccional y Riqueza de la matemática aporta algo diferente. Mientras la primera se enfoca en las discusiones del grupo sobre el contenido, la Riqueza de la matemática capta la profundidad de la matemática desarrollada en la clase, a través de explicaciones, creación de significado y uso de patrones y generalizaciones. El hecho de que esta correlación exista en esta muestra de buenas clases, da cuenta de cuando el docente intenta desarrollar el contenido a partir de los aportes de los propios estudiantes, este diálogo es desarrollado sobre contenidos matemáticos tratados profunda y adecuadamente, es decir, forma y contenido tienden a coincidir en estas aulas.
La Tabla 3 muestra que las dimensiones asociadas al dominio de Apoyo emocional, correlacionan con varias de las dimensiones de MQI, mientras que las dimensiones de Organización del aula prácticamente muestran nula relación. Específicamente, Clima Positivo se relaciona con varias de las dimensiones de MQI que involucran la participación de los estudiantes y la consideración del profesor por sus contribuciones: Remediación de los errores, Uso de las contribuciones matemáticas de los alumnos, Estudiantes proveen explicaciones, y la Participación global de los alumnos en la creación de significado. Algo similar, pero en menor intensidad, ocurre con Sensibilidad del profesor y Consideración por la perspectiva de los estudiantes. Este análisis da cuenta, una vez más, de la consistencia entre ambos instrumentos, y de los rasgos que poseen las aulas estudiadas.
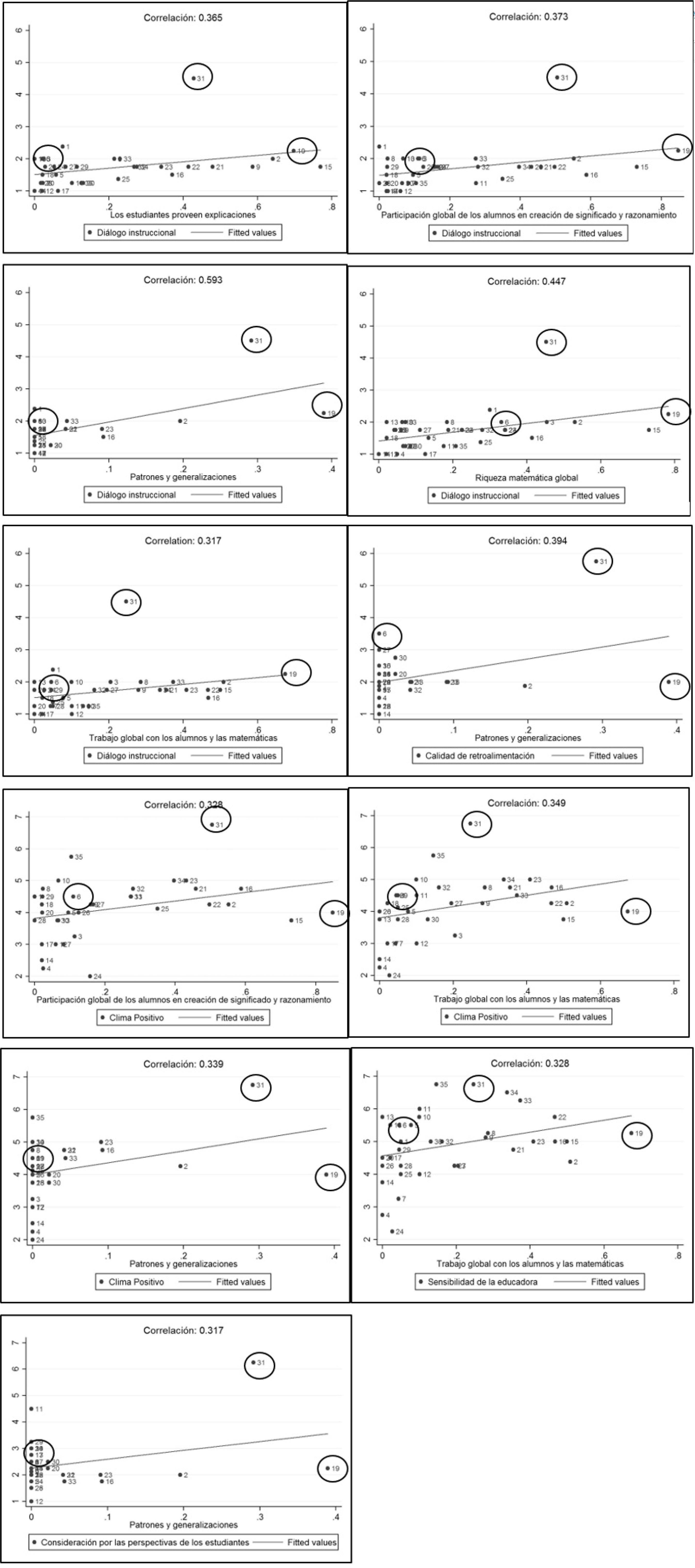
A partir de este análisis, de las correlaciones más significativas, y aquellas que involucran dimensiones globales de MQI, se grafica el comportamiento de los casos que posteriormente describiremos. La figura 2 muestra los gráficos de las correlaciones entre MQI y las dimensiones de Apoyo pedagógico CLASS que mostraron asociaciones más robustas. Acá resaltan tres casos. Primero, la sala 31 resalta por sobre todas las otras por sus altos puntajes en CLASS en todas las dimensiones, y un nivel por sobre la media en MQI. La sala 6, resalta por estar sobre la media en todas las dimensiones de CLASS, pero particularmente en la dimensión de Calidad de retroalimentación, donde casi alcanza un nivel medio. No obstante, el hecho de que esta sala obtenga puntajes tan bajos en MQI, hace que sea un caso interesante. Finalmente, la sala 19 es todo lo contrario: muestra niveles particularmente altos en los indicadores de MQI, pero en CLASS apenas supera la media predicha. Se trata, por tanto, de tres salas que destacan por razones muy distintas, y que vale la pena mirar en profundidad.
Diferentes tipos de clase, buenos resultados
Aula 31
Contexto: es un aula de quinto básico, en que la profesora desarrolla una serie de actividades con material concreto con el fin de determinar de manera experimental la probabilidad de un suceso, trabajando principalmente en torno a la idea qué es más probable que suceda. Es así como la profesora entrega a los estudiantes: una ruleta dividida en 5 partes iguales y dichas partes pintadas de distintos colores, un dado y tres monedas.
La profesora genera un clima propicio para el aprendizaje, mantiene una voz cálida y buen sentido del humor (al comentar, a propósito de la aleatoriedad en los lanzamientos del dado, que “por eso pierde plata la gente en los casinos”), así como también da muestras de sensibilidad para atender las necesidades académicas de los estudiantes (se pasea permanentemente entre los grupos de niños, se acerca constantemente a resolver dudas, y se muestra disponible para preguntas).
Esta clase se destaca por la existencia de un promedio de Apoyo Pedagógico considerablemente superior a la media de las salas analizadas. Esto se manifiesta principalmente en dos rasgos: las oportunidades para analizar e indagar sobre el contenido y las oportunidades para el diálogo instruccional. Sobre este último rasgo es posible observar múltiples ejemplos, donde los niños deben discutir y llegar a un acuerdo sobre sus hallazgos, para luego compartirlos con el resto del curso. Respecto de las oportunidades para analizar e indagar, además de los ejercicios en sí, es posible observar a la profesora haciendo repetidamente preguntas de alto desafío cognitivo a partir de las cuales los niños tienen la oportunidad de hipotetizar, analizar, y explicar sus razonamientos. Así lo muestra el siguiente ejemplo:
¿Cuál es el resultado más seguro que se puede obtener en la ruleta? No todas las ruletas son iguales por lo tanto cada grupo va a tener una respuesta distinta. Esa parte nos interesa, ¿por qué es más probable que salga esto y no lo otro? Discútanlo, pónganse de acuerdo.
Adicionalmente, la profesora ha diseñado tres actividades que tienen una primera fase exploratoria y posteriormente los estudiantes deben responder, frente al curso, la conclusión a la que han llegado argumentando por qué es válida. En muchas ocasiones la profesora pregunta al resto del curso “¿están de acuerdo con su compañero? ¿Por qué?”. Esto permite que existan explicaciones por parte de los estudiantes, en las que argumentan a partir del experimento realizado, por qué creen que algo es probable que suceda. A su vez, los estudiantes se comunican matemáticamente, no solo respecto de lo que ellos han realizado en sus grupos, sino que respecto de si están o no de acuerdo con lo realizado por los otros grupos, fundamentando su opinión en el trabajo matemático que han realizado.
Además existe trabajo en la búsqueda de patrones y generalizaciones. Esto se ve reflejado en la repetición de un experimento tendiendo a desarrollar la ley de los grandes números, con el fin de sacar conclusiones.
La calidad de la retroalimentación de esta clase es, no obstante, débil. En las múltiples preguntas abiertas realizadas, los estudiantes frecuentemente entregan respuestas erróneas que la profesora no trabaja ni corrige. Por ejemplo, la profesora les pregunta: ¿Qué números son más probables que salgan al lanzar un dado? Un niño responde: 2,3,6 y 5. Cuando la profesora le pregunta “¿por qué?”, el niño responde: “cuando tiré el dado, me dio eso”.
Aula 19
Contexto: durante esta clase de cuarto básico, la profesora trabaja la propiedad conmutativa de la adición. Para ello presenta una situación en la que los estudiantes indagan respecto del total de puntos que tendrían en una pieza de dominó al estar orientada de una u otra manera.
A pesar de que no se observe un clima positivo muy bueno, ya que la profesora no es particularmente cálida, los niños se notan cómodos y existe un clima de respeto. En ocasiones, la clase se vuelve bulliciosa y la profesora utiliza un tono de voz más firme para llamarles la atención, pero sin gritar en ningún momento. La profesora hace pasar estudiantes con frecuencia a la pizarra, pidiéndoles que inventen ejercicios que después sus propios compañeros tienen que resolver, lo cual facilita la autonomía y el liderazgo. El apoyo pedagógico de la clase también tiene elementos positivos y otros ausentes. Es posible encontrar algunos episodios en donde los niños proveen explicaciones sobre el contenido:
P: ¿Cómo supiste que era la misma pieza?
N: Porque yo creo que son la misma, porque si la doy vuelta me da la misma cantidad. Son la misma, porque si cualquiera de las dos la doy vuelta, me da la misma cantidad.
Así, independientemente de la calidad del argumento de los niños, éstos tienen múltiples oportunidades de proveer explicaciones gracias a las preguntas abiertas orientadas a reflexionar sobre el contenido que realiza la profesora. La profesora permanentemente les hace preguntas a los niños de “por qué” y “cómo”.
Además, se preocupa por el buen uso de los conceptos y sus componentes (por ejemplo, cuando les corrige el concepto suma por adición, y aclara que sus componentes son los sumandos y la suma). Esto también es altamente valorado por MQI, en el sentido de comunicarse sobre la matemática que hace otro. Un muy buen ejemplo de esto es que una vez que los estudiantes han establecido que, al resolver una adición, el orden de los sumandos no altera el resultado, en conjunto enuncian la propiedad conmutativa, haciendo especial énfasis en utilizar de manera correcta los términos matemáticamente correctos. Cuando ha sido correcta y completamente enunciada, la anotan en sus cuadernos. Es así como esta clase destaca por trabajar en la búsqueda de patrones y generalizaciones y en el uso del lenguaje matemático como dos elementos que le permiten destacarse en riqueza matemática. Además de dar un rol protagónico al estudiante en tanto elaboración de explicaciones como en la posibilidad de comunicarse respecto de la matemática que está en juego.
Sin embargo, se observa que la profesora prácticamente no entrega retroalimentación a los niños de forma individual, aunque sí de forma grupal (con todo el curso respondiendo alternadamente). Esto de por sí implica que CLASS califique con bajo puntaje la calidad de retroalimentación de esta sala. No obstante, es interesante profundizar un poco en la técnica de retroalimentación grupal que utiliza la profesora. Por ejemplo, se da el siguiente ciclo de retroalimentación con todo el curso:
Problema: Aníbal ha recorrido 270 kms en auto, y 370 kms en tren. Rosa recorrió 370 kms en auto, y 270 kms en tren. Rosa y Anibal recorrieron la misma distancia porque…
P: ¿Quién puede contestar? (…) ¿recorrieron los dos la misma distancia?
N (a coro): ¡Sí!
P: ¿Por qué?
N: Porque son los mismos números.
P: Ya, si yo digo que son los mismos números, me refiero a que son las mismas…
N (varios responden): cantidades.
P: La misma cantidad. Hablando de kilómetros son las mismas…
N: ¡Distancias!
P: Distancias, cierto. ¿Pero cuál sería la diferencia entre ellos dos?
N: Que Aníbal recorrió una distancia diferente en auto que Rosa.
P: Por ahí va.
Por último, en términos de diálogo instruccional no es posible encontrar discusiones sobre el contenido que involucren a más de un estudiante. El diálogo entre pares sobre el contenido no existe. No obstante, sí es posible observar en ocasiones que los niños tienen oportunidad de responder preguntas abiertas, y se trata de una clase en donde existe cierto balance entre la cantidad de tiempo que habla la profesora y la que hablan los estudiantes.
Aula 6
Contexto: el objetivo de la clase es presentar las fracciones propias e impropias, y sus diferencias. Para esto, la profesora comienza la clase recordando las partes de una fracción con todo el curso, y luego se hace un primer ejercicio utilizando gráficos de torta en la pizarra. Posteriormente, se realiza un ejercicio individual.
La profesora logra establecer un buen clima para el aprendizaje. Usa un tono de voz adecuado y no se muestra alterada en ningún momento. En la clase se muestra un clima de respeto, aunque la profesora suele llamar a los estudiantes por el apellido, y no por el nombre. Se muestra sensible ante las posibles necesidades de los estudiantes, lo que queda graficado en la actividad individual de los estudiantes, donde se pasea consultando si necesitan ayuda.
Dos aspectos llaman la atención del tipo de apoyo pedagógico que brinda esta profesora. Por una parte, la Calidad de retroalimentación. Si bien realiza el ejercicio con todo el curso, es frecuente (particularmente al inicio de la clase) que genere ciclos de retroalimentación con estudiantes de manera individual, a diferencia de la clase anterior. Por ejemplo:
P: Ahora, si yo quiero representar 5/4, ¿cómo lo podría hacer? (nota que varios levantan la mano, pero como son los mismos que participan siempre, no los elige), ¿quién más? ¿Quién más va a participar? ¿Pérez, a ver?
N: Ese no podría servir, tendría que hacer otro más (se refiere al gráfico de torta dividido en cuatro partes que está en la pizarra).
P: ¿Qué no me puede servir? (otros niños levantan la mano para contestar) A ver, esperemos que termine José.
N: El 5/4.
P: ¿Qué no me sirve de aquí? Si yo quiero trabajar con este entero (indicando el gráfico de 4/4), ¿a eso te refieres?
N: Sí.
P: ¿Por qué?
N: Porque son 5 espacios y ahí hay 4.
P: ¡Muy bien! ¿Lo mismo los demás, están de acuerdo?
Desde MQI esta clase destaca porque los estudiantes se comunican respecto de la matemática que se está trabajando y, por otra parte, en estos ciclos de retroalimentación la profesora es cuidadosa en el lenguaje matemático que utiliza, y además de promover el uso de éste entre los estudiantes.
El segundo elemento que llama la atención de esta clase es el Diálogo instruccional. Al principio de la clase, la profesora da algunas oportunidades para que los estudiantes entreguen respuestas y expliquen su razonamiento, lo cual suele ocurrir también en otras clases destacadas observadas para este estudio. No obstante, un aspecto novedoso que fue posible observar aquí fue un breve diálogo acumulativo entre estudiantes:
N1: (a propósito del ejercicio en donde se deben formar 5/4, un niño entrega una propuesta para hacerlo con los gráficos de la pizarra) También puede partir la mitad de un cuarto…
P: ¿Partir la mitad aquí? (indica la mitad de un cuarto en el gráfico).
N1: Sí.
P: ¿Qué dicen los demás? ¿Bruno?
N2: No, porque tiene que estar toda igual (se refiere a que todos los pedazos de la torta deben ser idénticos).
P: Cuando yo fracciono algo, es todo igual. Es lo mismo que cuando ustedes quieren repartir una pizza, o un pedazo de torta.
Resaltamos que, a lo largo de estos episodios de diálogo instruccional, además de que los estudiantes se comunican respecto de la matemática que se está trabajando en la clase, se trabaja de manera significativa en la creación de significado matemático. Específicamente, se hace énfasis durante la clase en dos elementos: que una fracción conlleva dividir un entero en partes iguales (como se puede apreciar en el diálogo anterior) y, por otra parte, en la relación entre numerador y denominador en una fracción propia e impropia, lo que además permite dar sentido a la fracción unidad.
Es así como en esta creación de significado surgen buenas explicaciones de parte de la profesora, lo que sumado al buen uso del lenguaje matemático hacen que esta clase tenga una puntuación aceptable en riqueza matemática, pero dado que el centro de esta actividad está en la profesora, no destaque por el trabajo de construcción conceptual por parte de los estudiantes.
Conclusiones
El objetivo del trabajo ha sido resaltar la capacidad de CLASS y MQI para describir las aulas de matemática que pertenecen a escuelas efectivas. En concreto, se buscó indagar, por una parte, en cómo ambos instrumentos correlacionan y coinciden en encontrar determinados rasgos de la enseñanza, y por otra, en las descripciones cualitativas que esconden los puntajes asignados a cada sala.
Respecto de las correlaciones, nuestra hipótesis era que aquellas dimensiones de CLASS más asociadas al contenido enseñado, como Comprensión del contenido y Análisis e Indagación, se asociarían mejor con las dimensiones de MQI, en vez de aquellas dimensiones asociadas a la forma de enseñar, tales como Diálogo instruccional o Calidad de la retroalimentación. Sin embargo, los resultados indican que solamente la dimensión Diálogo Instruccional correlaciona significativamente con las dimensiones de MQI: Riqueza de la matemática, Trabajo con los alumnos y la matemática, y Participación de los alumnos en la creación de significado y razonamiento. Una posible explicación para esto es la dificultad de CLASS para captar adecuadamente la precisión con que son expuestos los contenidos disciplinares, en este caso, de matemática. En otras palabras, esta relación tiene sentido, ya que es la actividad que más se relaciona con la construcción conceptual conjunta entre estudiantes y profesor.
La comprensión y descripción de lo que sucede al interior del aula es una tarea compleja que puede ser abordada desde distintos puntos de vista. Una muestra de ello es la variedad de información que se puede recoger con dos instrumentos complejos como son MQI y CLASS, dando dos miradas distintas de lo que sucede en la sala de clases. Estas miradas son distintas y complementarias, como vimos en los resultados.
Los resultados también muestran que los puntajes asignados a las aulas efectivamente permiten discriminar la calidad o frecuencia con que cada rasgo de la enseñanza aparece en cada aula. Sin embargo, las descripciones cualitativas mostraron aulas de alta calidad, pese a los bajos puntajes en algunas dimensiones. Así, en cada sala fue posible encontrar múltiples rasgos positivos de la enseñanza que permitieron a los profesores conducir una buena clase de matemática, con errores y elementos ausentes, pero que fueron reemplazados por otros elementos de la enseñanza efectiva que, probablemente, ellos dominaban mejor.
Por ejemplo, en las salas 31 y 10, ambos profesores destacan por tener un puntaje más alto que el común de docentes en riqueza matemática, sin embargo, dicha fortaleza responde a distintos elementos. Mientras el primero destaca por realizar una búsqueda sistemática de patrones, el otro pone énfasis en el uso y promoción de lenguaje matemático. En este sentido, si bien es deseable que una clase pudiera destacar en todos los indicadores, esto es inviable en la complejidad y especificidad de la sala de clases.
Instrumentos de observación de aula como CLASS y MQI efectivamente contribuyen a definir un norte claro respecto de la calidad de interacciones pedagógicas que deberían ocurrir en las aulas del sistema educativo chileno. Especialmente, si Chile ha optado por el camino de la definición de estándares y las políticas de pay for performance. No obstante, lo que nos muestran estos resultados es que deben tomarse precauciones al momento de utilizar dichos instrumentos para la evaluación de profesores, y entender que los números permiten entregar información de forma sistemática y precisa, pero a la vez esconden información y pueden reducir la complejidad de la realidad. La observación de estos buenos ejemplos permite visualizar este problema, y entregar algunas pistas sobre la dirección en la cual debemos avanzar. Estos instrumentos no deben convertir la estandarización de las prácticas de enseñanza efectiva en un fin, sino más bien, su función consiste en ser medios -útiles para profesores que operan en distintos contextos- que tienen habilidades y defectos particulares, pero que, por un camino u otro, deben lograr que sus estudiantes aprendan.
Referencias
- ANFARA, Vicent; BEAUMONT, Jesse. Defining the effectiveness of middle grades teachers. Middle School Journal, Westernville, v. 38, n. 5, p. 54-62, 2007.
- APPELBAUM, Peter. Taking action - mathematics curricular organization for effective teaching and learning. For the Learning of Mathematics, Ontario, v. 29, n. 2, p. 38-43, 2009.
- BARBER, Michael; MOURSHED, Mona. How the world’s best-performing schools systems come out on top. Londres: McKinsey & Company, 2007.
- BELLEI, Cristian et al.¿Qué se sabe sobre las escuelas que mejoran? In: BELLEI, Cristian et al. (Ed.). Lo aprendí en la escuela: ¿Cómo se logran procesos de mejoramiento escolar? Santiago de Chile: CIAE: Unicef, 2014. p. 17-27.
- CALLAHAN, Kathe; SADEGHI, Leila. Teacher perceptions of the value of teacher evaluations: New Jersey’s ACHIEVE NJ. NCPEA. International Journal of Educational Leadership Preparation, Houston, v. 10, n. 21, p. 46-59, 2015.
- CHILE. Ministerio de Educación. Estándares indicativos de iesempeño para los establecimientos educacionales y sus sostenedores: evaluación, U. D. C. Y. Santiago de Chile: Ministerio de Educacción, 2014.
- COHEN, David; RAUDENBUSH, Stephen; BALL, Deborah. Resources, instruction, and research. Educational Evaluation and Policy Analysis, Thousand Oaks, v. 25, n. 2, p. 1-24, 2003.
- DARLING-HAMMOND, Linda et al. Getting teacher tvaluation right: a background paper for policy makers. Washington: National Academy of Education, 2011.
- ELACQUA, Gregory et al. Los efectos de las presiones de accountability sobre las políticas y prácticas pedagógicas en escuelas de bajo desempeño: el caso de Chile. Santiago de Chile: Programa de Promoción de la Reforma Educativa en América Latina y el Caribe, 2013.
- EYZAGUIRRE, Nicolás. Proyecto de ley de política nacional docente. Santiago de Chile: Ministerio de Educación, 2014.
- FERGUSON, Ronald; DANIELSON, Charlotte. How framework for teaching and tripod 7Cs evidence distinguish key components of effective teaching. In: KANE, Thomas; KERR, Kerry; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 98-143.
- FORD, Timothy et al. Teacher self-efficacy, professional commitment, and high-stakes teacher evaluation policy in Louisiana. Thousand Oaks: Educational Policy, 2015.
- GODOY, Felipe et al. Interacciones pedagógicas y percepción de los estudiantes en escuelas chilenas que mejoran: una aproximación exploratoria. Estudios Pedagógicos, Valdivia, v. 42, n. 3, p. 149-169, 2016.
- HILL, Heather et al. Mathematical knowledge for teaching and the mathematical quality of instruction: an exploratory study. Cognition and Instruction, London, v. 26, n. 4, p. 430-511, 2008.
- HILL, Heather et al. Teacher quality and quality teaching: examing the relationship of a teacher assessment to practice. American Journal of Education, Chicago, v. 118, n. 4, p. 489-519, 2012.
- HOPKINS, David; REYNOLDS, David. The past, present and future of school improvement: towards the third age. British Educational Research Journal, Abingdon, v. 27, n. 4, p. 459-475, 2001.
- LEYVA, Diana et al. Teacher-child interactions in Chile and their associations with prekindergarten outcomes. Child Development, Medford, v. 86, n. 3, p. 781-799, 2015.
- MARZANO, Robert J. Setting the record straight on “high-yield” strategies. The Phi Delta Kappan, Arlington, v. 91, n. 1, p. 30-37, 2009.
- MIHALY, Kata; MCCAFFREY, Daniel. Grade level variation in observational measures of teacher effectiveness. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 9-49.
- MITCHELL, Linda; CAMERON, Marie; WYLIE, Cathy. Sustaining school improvement: ten primary schools’ journey. Wellington: New Zealand Council for Eduactional Research, 2002.
- MIZALA, Alejandra; SCHNEIDER, Ben Ross. Negotiating education reform: teacher evaluations and incentives in Chile (1990-2010). Governance, Medford, v. 27, n. 1, p. 87-109, 2014.
- MUIJS, Daniel; REYNOLDS, David. Effective teaching: evidence and practice. 3. ed. Thousand Oaks: SAGE, 2011.
- PAKARINEN, Eija et al. A validation of the classroom assessment scoring system in finnish kindergartens. Early Education and Development, Hove, v. 21, n. 1, p. 95-124, 2010.
- PIANTA, Robert; HAMRE, Bridget; MINTZ, Susan. Classroom assessment scoring aystem: upper elementary manual. Charlottesville: Teachstone, 2012.
- PIANTA, Robert; KERR, Kerri. Measuring effective teaching - the future starts now. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 583-590.
- PIANTA, Robert; LAPARO, Karen; HAMRE, Bridget. Classroom Assessment Scoring System™ (CLASS™). Baltimore: Paul H. Brookes, 2008.
- RACZYNSKI, Dagmar; MUÑOZ, Gonzalo. Factores que desafían los buenos resultados educativos de las escuelas en sectores de pobreza. In: CUETO, Santiago (Ed.). Educación y brechas de equidad en América Latina. Chile: Preal, 2006. p. 275-352.
- RIVERS, June; SANDERS, Williams. Teacher quality and equity in educational opportunity: findings and policy implications. Teacher Quality, Standford, p. 13-23, 2002.
- RODRÍGUEZ, Beatriz. Historia del programa y antecedentes generales. In: RODRÍGUEZ, Beatriz et al. (Ed.). Reconociendo el mérito docente: programa de asignación de excelencia pedagógica 2002-2014. Santiago de Chile: MIDE UC: Pontificia Universidad Católica de Chile, 2015. p. 10-22.
- ROUTMAN, Regie. Mapping a pathway to schoolwide highly effective teaching. The Phi Delta Kappan, Arlington, v. 93, n. 5, p. 56-61, 2012.
- SAMMONS, Pam; HILLMAN, Josh; MORTIMORE, Peter. Key characteristics of effective schools: a review of school effectiveness research. London: Institute of Education: University of London: OFSTED, 1995.
- SANTIAGO, Paula et al. OECD reviews of evaluation and assessment in education: teacher evaluation in Chile 2013. Paris: OECD, 2013.
- SCHULTZ, Susan; PECHEONE, Raymond. Assessing quality teaching in science. In: KANE, Thomas; KERR, Kerri; PIANTA, Robert (Ed.). Designing teacher evaluation systems: new guidance from measures of effective teaching project. San Francisco: Bill & Melinda Gates Foundation: Jossey-Bass: Wiley Brand, 2014. p. 444-492.
- TREVIÑO, Ernesto; DONOSO, Francisca; MOLINA, Ángeles. Informe resultados: impacto del PAC en las prácticas pedagógicas. Santiago de Chile: Centro de Políticas Comparadas de Educación: Banco Interamericano de Desarrollo: Ministerio de Educación de Chile, 2013.
- TREVIÑO, Ernesto; ROMO, Francisca; GODOY, Felipe. Construcción de capacidades profesionales en educación parvularia: evidencia de “Un Buen Comienzo”. In: ELACQUA, Gregory; CORTÁZAR, Alejandra; CALVO, Esteban. Educación, el escenario pre-reforma. Santiago de Chile: Instituto de Políticas Públicas UDP. 2015. p. 37-46.
- TREVIÑO, Ernesto; TOLEDO, Gabriela; GEMPP, René. Calidad de la educación parvularia: las prácticas de clase y el camino a la mejora. Pensamiento Educativo, Santiago de Chile, v. 50, n. 1, p. 40-62, 2013.
-
6
- El índice de Desempeño Educativo se construyó en base a un conjunto de indicadores de escuelas con quince o más estudiantes de 4º básico. Para mayor detalle ver la primera parte de Bellei y otros autores (2014)BELLEI, Cristian et al.¿Qué se sabe sobre las escuelas que mejoran? In: BELLEI, Cristian et al. (Ed.). Lo aprendí en la escuela: ¿Cómo se logran procesos de mejoramiento escolar? Santiago de Chile: CIAE: Unicef, 2014. p. 17-27..
-
7
- La empresa creadora de CLASS y encargada de realizar los cursos y entregar certificaciones.
-
1
- El desarrollo de este estudio se realizó con el apoyo del Proyecto PIA-CONICYT de financiamiento basal para centros científicos y tecnológicos de excelencia [grant number BF0003]; y por el proyecto PIA-CONICYT ANILLO [grant number SOC-1104].
Fechas de Publicación
-
Publicación en esta colección
2018
Histórico
-
Recibido
09 Jun 2016 -
Acepto
09 Ago 2016


 Fuente: adaptado de Cohen, Raudenbush, Ball (2003).
Fuente: adaptado de Cohen, Raudenbush, Ball (2003).
 Fuente: elaboración propia.
Fuente: elaboración propia.
 Fuente: elaboración propia.
Fuente: elaboración propia.