Abstracts
PURPOSE: To evaluate the influence of errors when two methods for assessing the available space in the dental arch are used. METHODS: A single investigator measured the available space in 30 plaster models by using two techniques: 1) with a digital caliper; and 2) by contouring the arch with a brass wire and subsequently straightening and measuring this wire with a millimeter ruler. Fifteen days later, data were collected using both methods with duplicate measurements, so that each method was used twice for each model. The random and systematic errors of each method under the conditions of repeatability and reproducibility were calculated. RESULTS: For method reproducibility, systematic errors were statistically significant (P<0.05) only when the brass wire method was used. The random errors were less than 1 mm under both conditions. With the brass wire, random errors were not significant for repeatability; however, for reproducibility, the mean value was 1.69 mm. CONCLUSION: In the digital caliper method, systematic and random errors were considered acceptable. The brass wire measurement method did not present errors under the condition of repeatability; for reproducibility, however, the systematic error was significant and the random error indicates that this method should be considered inappropriate to measure space in the dental arch.
Dental arch; space measurement; reproducibility
OBJETIVO: Avaliar a influência dos erros quando dois métodos para avaliação do espaço presente no arco dentário são utilizados. MÉTODOS: Um examinador único realizou a aferição do espaço presente em 30 modelos de gesso através de duas técnicas: 1) mensuração realizada com paquímetro digital; e 2) mensuração feita através do contorno do arco com fio de latão e medição deste com régua milimetrada. Após 15 dias, esta análise foi novamente realizada, utilizando os dois métodos, sendo que cada um deles foi empregado duas vezes consecutivas em cada modelo. Assim, foram obtidos dados em condição de repetibilidade e de reprodutibilidade e os erros sistemáticos e aleatórios de cada método nestas condições foram calculados. RESULTADOS: Os erros sistemáticos foram significativos (P<0,05) apenas na condição de reprodutibilidade para o método com fio de latão. Com paquímetro, a análise dos erros aleatórios mostrou que os erros presentes foram inferiores a 1 mm nas duas condições. Com fio de latão estes erros não existiram em condição de repetibilidade, porém foram de 1,69 mm em condição de reprodutibilidade. CONCLUSÕES: No método com paquímetro digital os erros sistemático e aleatório foram considerados aceitáveis. O método de medição com fio de latão não apresentou erro para repetibilidade. Para reprodutibilidade, no entanto, o erro sistemático foi significante e o erro aleatório encontrado fez com que este método fosse considerado no presente estudo como inapropriado.
Arco dental; medição de espaço; reprodutibilidade
ORIGINAL ARTICLE
Evaluation of two techniques to measure the available space in the mandibular dental arch using the method error
Avaliação de duas técnicas de aferição do espaço presente no arco dentário inferior quanto ao erro do método
Letícia Alves MachadoI; Oswaldo de Vasconcellos VilellaII; Lia Maria de Araujo Garcia AgostinhoIII
IClínica de Ortodontia da Odontoclínica Central da Marinha, Rio de Janeiro, RJ, Brasil
IIPrograma de Pós-Graduação em Odontologia - Área de Ortodontia, Universidade Federal Fluminense, Niterói, RJ, Brasil
IIIConsultório odontológico, Rio de Janeiro, RJ, Brasil
Correspondence Correspondence: Letícia A. Machado Rua Dois de Dezembro, 15/801 - Flamengo Rio de Janeiro, RJ - Brasil E-mail: letmachado@bol.com.br
ABSTRACT
PURPOSE: To evaluate the influence of errors when two methods for assessing the available space in the dental arch are used.
METHODS: A single investigator measured the available space in 30 plaster models by using two techniques: 1) with a digital caliper; and 2) by contouring the arch with a brass wire and subsequently straightening and measuring this wire with a millimeter ruler. Fifteen days later, data were collected using both methods with duplicate measurements, so that each method was used twice for each model. The random and systematic errors of each method under the conditions of repeatability and reproducibility were calculated.
RESULTS: For method reproducibility, systematic errors were statistically significant (P<0.05) only when the brass wire method was used. The random errors were less than 1 mm under both conditions. With the brass wire, random errors were not significant for repeatability; however, for reproducibility, the mean value was 1.69 mm.
CONCLUSION: In the digital caliper method, systematic and random errors were considered acceptable. The brass wire measurement method did not present errors under the condition of repeatability; for reproducibility, however, the systematic error was significant and the random error indicates that this method should be considered inappropriate to measure space in the dental arch.
Key words: Dental arch; space measurement; reproducibility
RESUMO
OBJETIVO: Avaliar a influência dos erros quando dois métodos para avaliação do espaço presente no arco dentário são utilizados.
MÉTODOS: Um examinador único realizou a aferição do espaço presente em 30 modelos de gesso através de duas técnicas: 1) mensuração realizada com paquímetro digital; e 2) mensuração feita através do contorno do arco com fio de latão e medição deste com régua milimetrada. Após 15 dias, esta análise foi novamente realizada, utilizando os dois métodos, sendo que cada um deles foi empregado duas vezes consecutivas em cada modelo. Assim, foram obtidos dados em condição de repetibilidade e de reprodutibilidade e os erros sistemáticos e aleatórios de cada método nestas condições foram calculados.
RESULTADOS: Os erros sistemáticos foram significativos (P<0,05) apenas na condição de reprodutibilidade para o método com fio de latão. Com paquímetro, a análise dos erros aleatórios mostrou que os erros presentes foram inferiores a 1 mm nas duas condições. Com fio de latão estes erros não existiram em condição de repetibilidade, porém foram de 1,69 mm em condição de reprodutibilidade.
CONCLUSÕES: No método com paquímetro digital os erros sistemático e aleatório foram considerados aceitáveis. O método de medição com fio de latão não apresentou erro para repetibilidade. Para reprodutibilidade, no entanto, o erro sistemático foi significante e o erro aleatório encontrado fez com que este método fosse considerado no presente estudo como inapropriado.
Palavras-chave: Arco dental; medição de espaço; reprodutibilidade
Introduction
The measurement of quantitative variables is a very common procedure in Orthodontic research (1) and clinical practice, since it is an important requirement for model analysis and for correct diagnosis and planning of orthodontic treatment. One key factor in model analysis is the assessment of the available space in the dental arch, which corresponds to the measurement of the space on the alveolar crest bone, in millimeters, from the mesial surface of the mandibular first permanent molars (2).
Previous studies have described several methods to measure the available space in the dental arch (3-8) and compared methods (9-11). For measurement of quantitative variables, an adequate evaluation of the errors in methodology is mandatory. Researchers must consider how these errors may affect the interpretation of their results (12). Inevitable errors are inherent to the procedures of each method, because not all factors that influence the results can be completely controlled in the experiment. Special attention should be given to aspects that contribute to improving the quality of scientific research, establishing the conditions for validating the measurement tests. Some factors may contribute to the variability of the test procedure: operator, equipment and time interval between measurements (13).
The term "precision of method" indicates the variability found between repeated tests on the same material, arising from the existence of inherent errors in the method. According to Leite (14), precision is the agreement between the various experimental values; the closer together they are, that is, the greater the precision, the lesser the amplitude of the measures. Quantitative measures of precision depend on stipulated (determined) conditions. The conditions of repeatability and reproducibility are particular cases of extreme conditions of variability (13). The repeatability condition occurs when there is no variation of the factors that may affect the variability of the results of a method; while reproducibility occurs when at least one of these factors is varied (13). Therefore, under the conditions of repeatability, all factors are kept constant and under conditions of reproducibility the same test method is used on the same material, the variable being the operator, the equipment or the time of the measurements, or any combination of variation of these factors.
An evaluation of the errors in a method under these conditions should be considered in studies involving the measurement of quantitative variables and attention should be given to the way in which these errors can affect the interpretation of the results. This is an important topic, not only for researchers, but also for the reader of any article that involves measurement (12). Each observed measurement can be analyzed through its real value and its error component.
The measurement error is defined as the difference between the value obtained in the process of measurement and the true value of the magnitude measurement (1). Two types of error can occur in measurements executed on an object: systematic error, also known as bias, and random error (12), also called casual. The systematic error is due to factors which, by having an effect on an instrument, on the measurement process, or even on the operator, affect the results in the same way. This means that the value which is found overstates or understates the true value of magnitude (1). Random error is defined as an error in which, due to competition between a number of factors, the difference between the measure and the measured magnitude may be positive or negative. The greater the number of measurements taken, the more clearly the sum of these differences tends to zero and becomes subject to a law of probability distribution, known as the Normal Distribution or Gauss-Laplace Curve (1). Even in the simplest of experiments, it is impossible to control all of the factors involved. Consequently, any experimental measurement will be affected to a greater or lesser extent by random errors and these errors must be considered (15).
In the model analysis to collect data for a correct diagnosis and subsequent treatment plan, the errors are also present due to a variety of factors. Often, an orthodontic treatment plan can be modified according to the model analysis. An error of 2 to 3 mm in relation to the real discrepancy, for example, may be sufficient to modify the treatment plan. This fact occurs in so-called borderline cases where the decision to extract or not extract teeth depends on the careful analysis of the diagnostic elements (16).
Therefore, this study aimed at evaluating the influence of systematic and random errors by using two methods for assessing the available space in the dental arch.
Methodology
The present study was conducted in accordance with resolution 196 of the National Health Council and monitored by the Committee for Ethics in Research of Universidade Federal Fluminense (UFF), Niterói, RJ, Brazil. Thirty plaster casts of the mandibular arch of patients of the UFF Orthodontic Specialization Course were randomly selected. As inclusion criteria, the models should have all permanent teeth fully erupted, except for second and third molars, as the available space was measured from the mesial face of the permanent first lower molars.
This study had a blinded design with a single examiner trained to analyze the available space present in the models, using two techniques.
The first technique was described by Proffit (17) and Bradley (4). In this technique, the available space was measured using a digital capiler. The available space was measured in four sections, from the mesial face of the first permanent molar on one side to the mesial face of the homologous tooth on the opposite side of the arch. It was performed with the digital caliper so that the sections were measured in the following order:
1. To measure the first section, one of the points of the caliper touched the contact point between the first molar and the second premolar, while the other point touched the point of contact between the canine and lateral incisor.
2. To measure the second section, one of the points of the caliper touched the contact point between the canine and lateral incisor, while the other point touched the point of contact between the central incisors.
3. To measure the third and fourth sections the procedure was repeated in the opposite half of the dental arch.
The length of each section for each of the models, in millimeters, was recorded, and the available space was calculated using the sum of the four sections.
The second technique using straightened brass wires was described by Sassouni (7). The available space was measured with a brass wire (diameter of 0.028-inch), which was adapted to the mesial face of the first molar on one side to the mesial face of its homologous tooth on the opposite side. The wire was adapted to the occlusal surface, passing over the contact points of the back teeth and along the incisal edges of the front teeth, making a smooth curve. To determine the available space, the wire was straightened, and its length was measured with a millimeter ruler.
Fifteen days after the first data collection, the analysis of available space was performed again on the thirty plaster casts by the same operator, using the two methods, in duplicate. The first measure was performed, and the second was obtained immediately after the first.
Thus, data was obtained under two conditions: with an interval of 15 days between measurements and in consecutive measurements. The systematic and random errors of each method under the two conditions were calculated. To perform the measurements, the models were selected in random sequence as defined by drawing lots.
The Student's paired t test was used to calculate the systematic errors (12), through the formula
where
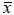 represents the average of the differences in each of the pairs formed by the two measurements, SD corresponds to the standard deviation of the differences and n is the number of pairs in the sample. In order to carry out the test, it is important to consider if a sufficient number of cases was replicated. If not, only large systematic errors will be revealed. If there are many small cases, even an important systematic error may not be detected as statistically significant.
represents the average of the differences in each of the pairs formed by the two measurements, SD corresponds to the standard deviation of the differences and n is the number of pairs in the sample. In order to carry out the test, it is important to consider if a sufficient number of cases was replicated. If not, only large systematic errors will be revealed. If there are many small cases, even an important systematic error may not be detected as statistically significant.In order to estimate the order of magnitude of the random, or casual, errors, the following formula proposed by Dahlberg (18) was used:
where d represents the difference between the two measures and n is the number of duplicate determinations.
A level of significance of 5% (P<0.05) was adopted for all tests.
Results
Table 1 shows the values of available space for the first collection of data (D0) and in the two consecutive measurements performed after 15 days (D15-1 and D15-2). The measurements obtained with the digital caliper had a precision of hundredths of a millimeter, while those obtained from the brass wire with the millimeter ruler have a precision of 0.5 of a millimeter.
Table 2 displays the systematic errors in both methods to measure the available space. For reproducibility, the Student's paired t test (12) was applied to compare the mean values of the first measurement (D0) with and the second  , since this was composed of two measurements. For repeatability, the same test was used to compare the values obtained in the second series of measurements (D15-1 and D15-2).
, since this was composed of two measurements. For repeatability, the same test was used to compare the values obtained in the second series of measurements (D15-1 and D15-2).
Table 3 shows the results of the verification of random errors, the variance and the reliability coefficient of the methods tested under the conditions of reproducibility and repeatability.
Discussion
In order to analyze the error in a method, careful replication of the measurements is necessary, demanding an increase in the time needed to perform the study and greater dedication of the researcher. In the present study, a sufficient number of cases (n=30) was replicated.
The verification of systematic errors of the methods to measure the available space indicated no significant difference between the two sets of measurements observed at different moments with the digital caliper. Nevertheless, when the values of the consecutive measurements were reported, the systematic errors were less than those measured after 15 days. In the consecutive measurements, the factors that could have contributed to the variability of the procedure of the assay probably tended to remain constant, thereby minimizing interferences in the methodology.
For the method with brass wire and millimeter ruler, the values of the first assessment were significantly different from those obtained in the second series of measurements. Uncontrolled variables such as temperature, luminosity and practical experience of the test operator, among others, may have contributed to the variability of the assay procedure and led to the inclusion of errors, making this method unsatisfactory for the condition of reproducibility. On the other hand, there was no statistical difference between the measurements performed consecutively on the 30 plaster models during the second series of measurements. In fact, all of the values of D15-1 and D15-2 were exactly the same. The interpretation that there were no errors under the condition of repeatability should be analyzed with caution. Obviously, if there is no difference between the values there can be no error, but it is probable that this result is more related to the low precision of the method (0.5mm), which may have influenced the operator with a biased assessment of the values in such a short space of time, than to the premise that all the factors were constant (Table 2).
For random errors, the method with digital caliper yielded errors less than 1 mm (0.92 mm between D0 and
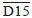 and 0.45 mm between D15-1 and D15-2). The reliability coefficients were 95.28% and 98.96%, respectively. In the first situation, the variance of the random error corresponds to 4.72% of the total variance and, in the second, to 1.04%. When the variance of an error is less than 3% of the total variance, the error of the method is considered to be of little importance and, when it is greater than 10%, the method of measurement is considered to be inappropriate (19).
and 0.45 mm between D15-1 and D15-2). The reliability coefficients were 95.28% and 98.96%, respectively. In the first situation, the variance of the random error corresponds to 4.72% of the total variance and, in the second, to 1.04%. When the variance of an error is less than 3% of the total variance, the error of the method is considered to be of little importance and, when it is greater than 10%, the method of measurement is considered to be inappropriate (19).For the method using brass wire and millimeter ruler, the random error was 1.69mm in comparing the values of D0 and
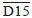 and the reliability coefficient was 85%, which means that the variance of the random error corresponds to 15% of the total variance. No difference was found between D15-1 and D15-2.
and the reliability coefficient was 85%, which means that the variance of the random error corresponds to 15% of the total variance. No difference was found between D15-1 and D15-2.Random errors arise from unpredictable factors and can be associated with the limitations of the equipment, the measurement procedure or a diverse variety of other factors. According to Houston (12), the main source of random error arises through the difficulty to identify or define reference points for the measurements. When a measurement is taken repeatedly, it is difficult to place the instruments in exactly the same position.
In the present study, under conditions of repeatability, both methods can be considered appropriate. Under the condition of reproducibility, the method with digital caliper was appropriate, despite the significant random error. In contrast, the method with brass wire and a millimeter ruler was considered inappropriate to measure the available space in the mandibular dental arch.
Conclusions
In the method with digital calliper, the systematic and random errors were considered acceptable. The method of assessment with a brass wire and a millimetre ruler did not present errors for repeatability; but for reproducibility, the systematic error was significant and the random error was greater than 10% of the total variance, which indicates that this method was considered inappropriate in the present study.
Received: September 28, 2011
Accepted: September 14, 2012
Conflict of Interests: The authors state that there are no financial and personal conflicts of interest that could have inappropriately influenced their work.
- 1. Mendes AJD, Santos-Pinto A. Algumas diretrizes estatísticas para avaliação do erro do método na mensuração de variável quantitativa. R Dental Press Ortodon Ortop Facial 2007;12:78-83.
- 2. Leal RC, Tanque LN, Gouveia SAS, Carmadella EG. Análises de modelos: uma revisão da literatura. R Clin Ortodon Dental Press 2006;5:64-76.
- 3. Nance HM. The limitations of orthodontic treatment. I - Mixed dentition diagnosis and treatment. Amer J Orthod Oral Surg 1947;33:177-223.
- 4. Bradley RE. The relationship between eruption, calcification, and crowding of certain mandibular teeth. Angle Orthodont 1961;31:230-6.
- 5. Musich DR, Ackerman JL. The catenometer: a reliable device for estimating dental arch perimeter. Am J Orthod 1973;63:366-75.
- 6. Moyers RE. Análise da dentição e oclusão. In: Moyers RE. Ortodontia. Rio de Janeiro: Guanabara Koogan; 1991. p. 187-207.
- 7. Sassouni V. Diagnosis and treatment plan. In: Sassouni V.Orthodontics in dental practice. St. Louis: Mosby; 1971. p. 327-54.
- 8. Mucha JN, Bolognese AM. Análise de modelos em ortodontia. R Bras Odont 1985;42:28-44.
- 9. Hoette F. Estudo comparativo entre vários métodos de medição de espaço presente do arco dental. [tese de mestrado]. Piracicaba (SP): Universidade Estadual de Campinas; 1974.
- 10. Blos JML, Vargas IA, Closs LQ. Avaliação da confiabilidade da discrepância de modelos realizada pelo método computadorizado em relação ao método convencional. Stomatos 2005;11:13-19.
- 11. Marques ALG. Aplicabilidade do cálculo da discrepância em dentadura mista por meio de tomografia computadorizada de feixe cônico [dissertação]. Rio Grande do Sul (RS): Universidade Federal do Rio Grande do Sul; 2009.
- 12. Houston WJB. The analysis of errors in orthodontic measurements. Am J Orthod 1983;83:382-90.
- 13. Albuquerque Junior HR, Pinto AS, Pinto LAMS. Precisão de medidas cefalométricas: validade de métodos de ensaio. R Dental Press Ortod Ortop Facial 2002;7:57-62.
- 14. Leite, F. Validação em análise química. 4Ş ed. Campinas: Editora Átomo;2002.
- 15. Barros Neto B, Scarminio IS, Bruns RE. Um pouco de estatística. In: Barros Neto B, Scarminio IS, Bruns RE. Planejamento e otimização de experimentos. Campinas: Editora da Unicamp; 1996. p. 21-53.
- 16. Toledo CEP, Quintão CCA, Rocha JM, Vitral RWJ. Avaliação de erro sistemático e discrepância das medições de modelos odontológicos utilizando-se paquímetro digital. Pesq Bras Odontoped Clin Integr 2009;9:55-61.
- 17. Proffit WR, Ackerman JL. Diagnóstico e planejamento do tratamento ortodôntico. In: Graber TM, Vanarsdall Jr RL. Ortodontia: princípios e tecnicas atuais. 2Ş ed. Rio de Janeiro: Guanabara Koogan; 1996.
- 18. Dahlberg G. Statistical methods for medical and biological students. New York: Interscience;1940.
- 19. Mitgaard J, Bjork G, Linder-Aronson S. Reproducibility of cephalometric landmarks and errors of measurement of cephalometric cranial distances. Angle Orthod 1974;44:56-61.
Correspondence:
Publication Dates
-
Publication in this collection
27 Nov 2012 -
Date of issue
2012
History
-
Received
28 Sept 2011 -
Accepted
14 Sept 2012






