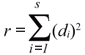Abstracts
We examined the species abundance distribution (SAD) of plant communities in: (1) a wet grassland, waterlogged throughout most of the year; (2) a seasonal savanna, with an annual dry season; and (3) a hyperseasonal savanna, with alternating drought and waterlogging over the year. We searched for differences in the abundance distributions of all species, as well as of the common and rare species. We tested whether the SADs fitted the lognormal, log-series, power fraction, and random assortment models. We found that environmental constraints may reduce the evenness of plant communities and change the SADs in savannas. We observed a lognormal abundance distribution in the wet grassland and a random abundance distribution in the hyperseasonal cerrado. The SAD of the seasonal savanna did not follow any model. The common species in the three communities were better fitted by the lognormal model. The rare species in the wet grassland and the hyperseasonal cerrado were better fitted by the random assortment model. The SAD of the rare species of the seasonal savanna did not follow any model. Seasonality seems to modify the lognormal distribution of the overall plant community, generating abundance distributions indistinguishable from random. However, differential community structuring between common and rare species may not be affected by seasonality. The different signatures of the abundance distributions of common and rare plants indicate that composite models are better predictors for SADs in savannas.
assembly rules; cerrado; environmental filter; evenness; relative abundance distribution
Examinamos as distribuições de abundâncias de espécies (DAEs) de comunidades de plantas em: (1) um campo úmido, alagado durante a maior parte do ano; (2) uma savana estacional, com uma estação seca anual; e (3) uma savana hiper-estacional, com uma estação seca e um alagamento alternantes durante o ano. Procuramos por diferenças na distribuição de abundância de todas as espécies, bem como das espécies comuns e raras. Testamos se as DAEs se ajustaram aos modelos normal-logarítmico, da série-logarítmica, da fração de potência e do agrupamento aleatório. Encontramos que as restrições ambientais podem reduzir a equabilidade das comunidades de plantas e podem mudar as DAEs em savanas. Observamos um modelo normal-logarítmico no campo úmido e um modelo do agrupamento aleatório na savana hiperestacional. A DAE da savana estacional não seguiu nenhum modelo. As espécies comuns das três comunidades se ajustaram melhor ao modelo normal-logarítmico. As espécies raras do campo úmido e da savana hiperestacional se ajustaram ao modelo do agrupamento aleatório. A DAE das espécies raras da savana estacional não seguiu nenhum modelo. A estacionalidade parece modificar o modelo normal-logarítmico da comunidade de plantas em geral, gerando distribuições de abundâncias aleatórias. Contudo, a organização diferencial da comunidade entre espécies comuns e raras pode não ser afetada pela estacionalidade. As diferentes assinaturas das distribuições de abundância das plantas comuns e raras indicaram que os modelos compostos são melhores preditores das DAEs em savanas.
cerrado; distribuição relativa de abundâncias; equabilidade; filtro ambiental; regras de montagem
ARTICLES
Abundance distribution of common and rare plant species of Brazilian savannas along a seasonality gradient
Distribuição de abundâncias de espécies de plantas comuns e raras de savanas brasileiras ao longo de um gradiente de estacionalidade
Igor Aurélio SilvaI,1 1 Corresponding author: igor6cordas@yahoo.com.br ; Marcus Vinicius CianciarusoII; Marco Antônio BatalhaI
IUniversidade Federal de São Carlos, Departamento de Botânica, São Carlos, SP, Brasil
IIUniversidade Federal de Goiás, Departamento de Ecologia, Goiânia, GO, Brasil
ABSTRACT
We examined the species abundance distribution (SAD) of plant communities in: (1) a wet grassland, waterlogged throughout most of the year; (2) a seasonal savanna, with an annual dry season; and (3) a hyperseasonal savanna, with alternating drought and waterlogging over the year. We searched for differences in the abundance distributions of all species, as well as of the common and rare species. We tested whether the SADs fitted the lognormal, log-series, power fraction, and random assortment models. We found that environmental constraints may reduce the evenness of plant communities and change the SADs in savannas. We observed a lognormal abundance distribution in the wet grassland and a random abundance distribution in the hyperseasonal cerrado. The SAD of the seasonal savanna did not follow any model. The common species in the three communities were better fitted by the lognormal model. The rare species in the wet grassland and the hyperseasonal cerrado were better fitted by the random assortment model. The SAD of the rare species of the seasonal savanna did not follow any model. Seasonality seems to modify the lognormal distribution of the overall plant community, generating abundance distributions indistinguishable from random. However, differential community structuring between common and rare species may not be affected by seasonality. The different signatures of the abundance distributions of common and rare plants indicate that composite models are better predictors for SADs in savannas.
Key words: assembly rules, cerrado, environmental filter, evenness, relative abundance distribution
RESUMO
Examinamos as distribuições de abundâncias de espécies (DAEs) de comunidades de plantas em: (1) um campo úmido, alagado durante a maior parte do ano; (2) uma savana estacional, com uma estação seca anual; e (3) uma savana hiper-estacional, com uma estação seca e um alagamento alternantes durante o ano. Procuramos por diferenças na distribuição de abundância de todas as espécies, bem como das espécies comuns e raras. Testamos se as DAEs se ajustaram aos modelos normal-logarítmico, da série-logarítmica, da fração de potência e do agrupamento aleatório. Encontramos que as restrições ambientais podem reduzir a equabilidade das comunidades de plantas e podem mudar as DAEs em savanas. Observamos um modelo normal-logarítmico no campo úmido e um modelo do agrupamento aleatório na savana hiperestacional. A DAE da savana estacional não seguiu nenhum modelo. As espécies comuns das três comunidades se ajustaram melhor ao modelo normal-logarítmico. As espécies raras do campo úmido e da savana hiperestacional se ajustaram ao modelo do agrupamento aleatório. A DAE das espécies raras da savana estacional não seguiu nenhum modelo. A estacionalidade parece modificar o modelo normal-logarítmico da comunidade de plantas em geral, gerando distribuições de abundâncias aleatórias. Contudo, a organização diferencial da comunidade entre espécies comuns e raras pode não ser afetada pela estacionalidade. As diferentes assinaturas das distribuições de abundância das plantas comuns e raras indicaram que os modelos compostos são melhores preditores das DAEs em savanas.
Palavras-chave: cerrado, distribuição relativa de abundâncias, equabilidade, filtro ambiental, regras de montagem
Introduction
Explaining differences in patterns of species abundance distribution (SAD) is an important stepping stone to understand how ecological communities are structured (McGill et al. 2007). The universal J curve produced when a histogram of number of species on the y-axis vs. abundance on the x-axis is plotted (Dewdney 2003) has motivated the development of many theoretical SAD models involving population dynamics (e.g., Hughes 1986; Hubbell 2001), niche partitioning (e.g., Tokeshi 1990; 1996), and spatial distributions (e.g., Harte et al. 1999; Borda-de-Água et al. 2002). However, most of these models did not establish any empirical pattern beyond the expected J-curve itself and, as a result, few were ever rejected (McGill et al. 2007). Environmental gradients provide a comparative basis for empirical tests of SADs theories (McGill et al. 2006; McGill et al. 2007). For instance, analyses of SADs along altitudinal gradients (Whittaker 1960; 1975) and latitudinal gradients (Hubbell 1979) have shown a general pattern of increasing evenness with productivity. Nevertheless, after these initial empirical studies, few investigations of models for SADs have attempted to explain the change of SADs along environmental gradients (McGill et al. 2007). Thus, a promising approach for assessing SADs is comparing them under different environmental constraints.
Recently, composite models for SADs (sensu Magurran 2004) have been proposed as an attempt to encapsulate ecological realism of the differential community structuring between common and rare species (Magurran & Henderson 2003; Ulrich & Ollik 2004). A general lognormal distribution has been found for common species (Magurran & Henderson 2003; Ulrich & Ollik 2004). However, rare species, which presented relatively high local extinction and immigration rates, were explained either by a log-series distribution (Magurran & Henderson 2003) or by a power function distribution (Ulrich & Ollik 2004). The former distribution follows if simple Poisson processes govern local abundances (Fisher et al. 1943). In general, a Poisson process can approximate the pattern of arrival of each species in a community. If a species follows a Poisson distribution, the variance to mean ratio will not be significantly different from 1.0 (Magurran & Henderson 2003). The latter distribution follows if patterns of rarity are self-similar (Moulliot et al. 2000). The self-similarity model predicts that changes in species richness are constant across temporal and spatial scales (Moulliot et al. 2000). Thus, the log-series as well as the power function distributions present, to a certain extent, stochastic properties. Structuring of common and rare species is expected to be differently influenced by biotic interactions and dispersal respectively (Magurran & Henderson 2003). Respective information on plant communities, nonetheless, is still lacking.
In South America, the largest savanna region is the Brazilian Cerrado, comprising originally an area of approximately 2 million km² (Gottsberger & Silberbauer-Gottsberger 2006). Most of the Cerrado region is composed of seasonal savannas (sensu Sarmiento 1983), with three to six months of rainless season (Gottsberger & Silberbauer-Gottsberger, 2006). However, there are also hyperseasonal savannas and wet grasslands scattered in Cerrado domain (Sarmiento 1983). Whereas wet grasslands remain waterlogged most of the year, hyperseasonal savannas undergo a dry season and a temporary waterlogging in the rainy season (Sarmiento 1983, Cianciaruso et al. 2005). Therefore, here we examined the abundance distribution of plants in a wet grassland, a seasonal cerrado, and a hyperseasonal cerrado, in central Brazil. We searched for differences in SADs along a seasonality gradient from the wet grassland to the hyperseasonal cerrado, passing through the seasonal cerrado. By fitting the lognormal (Preston 1948), log-series (Fisher et al. 1943), and power fraction models (Tokeshi 1996), that is, by fitting models that explain a successive decreasing of evenness, we investigated how increasing environmental constraints affect the SAD of all species, as well as the SADs of common and rare ones.
Methods
We carried out this study in the Emas National Park, one of the largest and most important cerrado reserves in central Brazil, with approximately 133,000 ha. We sampled three nearby herbaceous communities: a wet grassland (approximately, 18°15'40"S, 53°01'08"W), a seasonal cerrado (approximately, 18°17'34"S, 52°58'12"W), and a hyperseasonal cerrado (approximately, 18°18'07"S, 52°57'56"W). We conducted five surveys on each community: February 2003, at mid rainy season, when the hyperseasonal cerrado was waterlogged; May 2003, at late rainy season; August 2003, at dry season; November 2003, at early rainy season; and February 2004, at mid rainy season again. Total sampling effort was 50 quadrats of 1 m2 in each area in which we sampled all vascular plants excluding seedlings. Sampling sufficiency was demonstrated by Cianciaruso & Batalha (2008) with a curve of species richness versus sampled individuals.
Previous studies have shown that seasonality affects the plant communities in the seasonal and hyperseasonal cerrado. Seasonal changes in the environmental constraints of these areas lead to differences in plant community structure and dynamics (Cianciaruso et al. 2005; Silva & Batalha 2006; Cianciaruso & Batalha 2008; 2009). Whereas the wet grassland is largely stable, without changes in species composition and community structure (Cianciaruso & Batalha 2008), the hyperseasonal cerrado presents the highest floristic and structural changes along the year (Cianciaruso et al. 2005). For a detailed description of the studied areas and sampling methods, see Cianciaruso et al. (2005), Silva & Batalha (2006), and Cianciaruso & Batalha (2008; 2009).
First, we described structurally the three communities with indices of diversity and evenness to help us to explain the models of SAD. For each community, we summed the species and individuals sampled in the five surveys and computed: (1) total richness (S), as the number of species; (2) total number of individuals; (3) Shannon's diversity index (H'); and (4) Sheldon's evenness index, as eH'/S (Magurran 2004). H' ranges from 0, for communities with only a single species, to about 5, for communities with many species, each with few individuals. Evenness ranges from 0, when one species dominates the community completely, to 1, when all species present equally the same number of individuals. For a detailed description of theses indexes and of the procedures to compute them, see Magurran (2004).
To compare the SADs of the three areas, we plotted the data on diagrams of abundance classes, with classes of log2-transformed abundance on the x-axis vs. species number on the y-axis (Magurran 2004). We applied a heterogeneity chi-square analysis to answer whether the SADs of the three areas came from the same population of data (i.e., whether the SADs are homogeneous, Zar 1999). Then, we used the Kolmogorov-Smirnov two-sample test with the Bonferroni correction (Zar 1999) to test for differences between pairwise SADs (α = 0.025). Kolmogorov-Smirnov two-sample test can be used to compare two data sets directly, independently of any attempt to describe their abundance patterns (Tokeshi 1993). We also analyzed the SAD of the three vegetation communities with the deviation statistic 'V' (Caswell 1976) to compare the observed evenness with the evenness predicted by Caswell's (1976) neutral model. This model constructs an ecological community with the same number of species and individuals as the observed community, assuming certain neutral assembly rules, that is, random births, deaths, immigrations, and emigrations (Caswell 1976). Values of V > 2 or V < -2 denote a significant departure from neutrality and indicate a distribution less even than expected by the neutral model (Magurran 2004). We computed V with the Primer 5 software (Clarke & Gorley 2001).
We tested whether the SADs fitted the lognormal (Preston 1948), log-series (Fisher et al. 1943), and power fraction models (Tokeshi 1996) with the RAD fitting package (Ulrich 2002). RAD fitting package generates expected distributions of models for SADs. RAD is based on a least square statistic for finding the best solution. It compares the relative abundance of the species i of the data set with the mean density of the ith species of the fitting model (R). In this fitting procedure, the Euclidean distances between predicted and observed data points are minimized. The main fitting variable r can then be defined as:
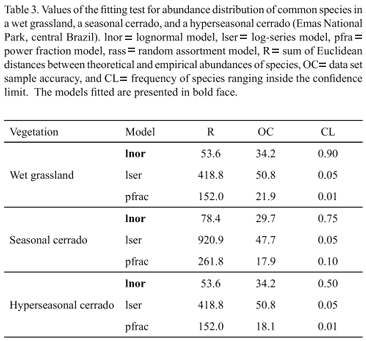
with di being the Euclidean distance between theoretical and empirical ln-transformed densities and S the number of species. However, due to the summation process the test statistic r depends on the total number of species S when comparing fits from assemblages of different species numbers. Therefore, to use r as a test at least a correction factor for density is necessary. We used the correction factors presented by Ulrich (2002). RAD also estimates the data set sample accuracy (OC). The OC test also computes squared differences; but, in this case, those of species numbers per binary density class (octave) between the model and the data set. Again, this measure depends on the total species number. We used the correction factors presented by Ulrich (2002). Values of R and OC around 10 indicate a good fitting; nevertheless, the fitting must be declined for values higher than 100.
RAD package also computes the frequency of species ranging inside the confidence limits (CL). This is particularly important when fitting stochastic models (power fraction models, for instance), although the discrimination power of this test is lower than those previous tests based on the least square statistic (Ulrich 2002). RAD computes 95% confidence limits of relative densities for samples comprising 70% of species. These confidence limits indicate a range of values of mean abundance for each rank likely to be encountered if a small sample is randomly drawn from the same parent population. We computed the SADs with the standard parameters of each model (i.e., z = 0.1 and X = 25 for lognormal; z = 5 and X = 0.9 for log-series; and z = 0.1 and X = 0 for power fraction model). Z and X are general parameters of the equations of each model. Z is the main generating parameter of the shape of all models and X is the second generating parameter of the shape of some models. We defined the ranges of the generating parameter z in the fitting procedures as described in Ulrich (2002). For the lognormal and log-series models, the relative abundances were estimated from expected species numbers per octave. This estimation was based on a random assignment at a log-scale of abundances inside the abundance range per octave (Ulrich 2002).
When the SADs were not fitted by any of the proposed models, we also tested for a random collection of species abundances with the random assortment model (Tokeshi 1990). We computed it with z = -0.9 and X = 0 (Ulrich 2002), also using the RAD package.
To analyze the SADs of common and rare species, we split the data sets of each community by a statistical criterion. Reliable model fitting is not possible for a low number of species (Wilson 1991). So, we considered the 20 most abundant species as common ones and the remaining species as rare ones. Then, we tested whether the common and rare species of each plant community fitted the lognormal, log-series, power fraction, and random assortment models, as described above.
Results
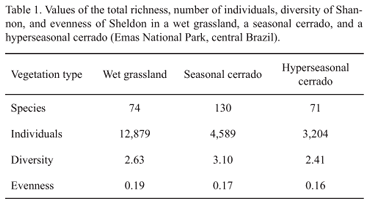
We sampled 12,879 individuals belonging to 74 species in the wet grassland; 4,589 individuals belonging to 131 species in the seasonal cerrado; and 3,204 individuals belonging to 71 species in the hyperseasonal cerrado. Among the species sampled, we considered 54 species as rare ones in the wet grassland (1,019 individuals); 110, in the seasonal cerrado (956 individuals); and 51, in the hyperseasonal cerrado (217 individuals). Overall diversity was higher in seasonal cerrado, followed by wet grassland and hyperseasonal cerrado (Tab. 1). However, overall evenness decreased following the increase of seasonality. The wet grassland presented the higher evenness, followed by the seasonal and hyperseasonal cerrados (Tab.1)
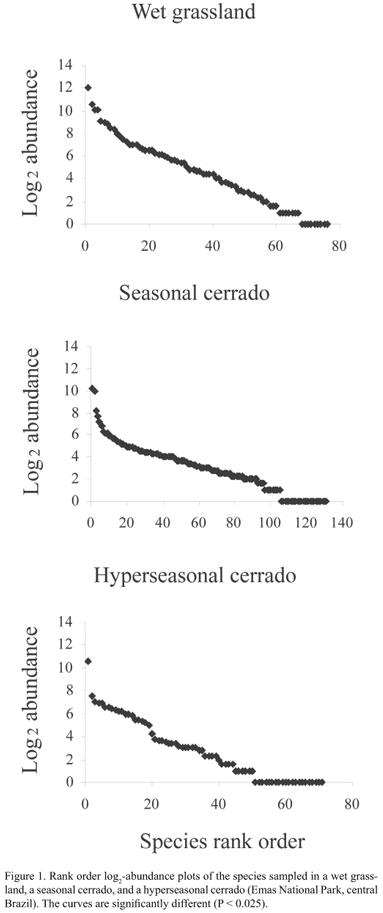
The SADs of the wet grassland, seasonal cerrado, and hyperseasonal cerrado presented heterogeneous hollow shapes (χ2 = 47.42, df = 18, P < 0.01; Fig. 1). When compared in pairs, the SADs were also different (df = 8, P < 0.025). The V values of the wet grassland, seasonal cerrado, and hyperseasonal cerrado were respectively -1.891, -5.667, and -4.404. The wet grassland species fitted the range of expected evenness for the neutral model. On the contrary, the seasonal and hyperseasonal cerrados were less even than expected for the neutral model.
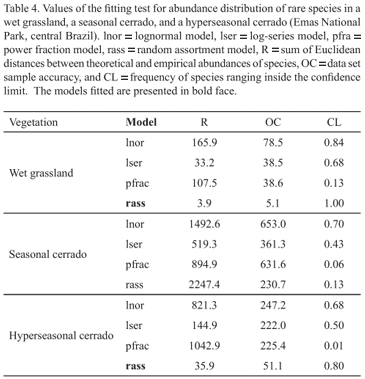
When we analyzed all species, the SADs of the wet grassland and hyperseasonal cerrado fitted better the lognormal and the random assortment models respectively (Tab. 2). The SAD of the seasonal cerrado did not fit any model (Tab. 2). The common species in the three areas were better explained by the lognormal model (Fig. 3; Tab. 3). In the wet grassland and the hyperseasonal cerrado, the rare species were better explained by the random assortment model, whereas, in the seasonal cerrado, they did not fit any model (Fig. 4; Tab. 4).
Discussion
The environmental constraints in the seasonal and hyperseasonal cerrados reduce the evenness of the plant communities and change the overall shaping of the SADs. Seasonality seems to modify the lognormal distribution of the species, generating abundance distributions indistinguishable from random. However, the differential community structuring between common and rare cerrado species may not be affected by seasonality. The common plant species were better fitted by the lognormal model, whereas the rare ones, by the random assortment model.
Although the wet grassland presents the more stable environmental conditions (Cianciaruso & Batalha 2008), we observed the highest values of richness and diversity in the seasonal cerrado. This is due to the size of the species pool. Species pool may be defined as 'a set of species that are potentially capable of coexisting in a certain community' (Eriksson 1993). Consequently, a species pool is ecologically delineated and is related to a given community type, the 'target community' (Pärtel et al. 1996). The number of cerrado species that can potentially colonize the seasonal cerrado is 600 species approximately (Batalha & Martins 2002). However, the number of species that can potentially colonize wet grasslands is smaller than that, since few species of the pool are expected to survive permanent waterlogging (Cianciaruso & Batalha 2008). Likewise, the richness of the hyperseasonal cerrado is also lower than seasonal cerrado because a small number of species is able to survive the period of waterlogging in the end of the wet season (Silva & Batalha 2006).
On the other hand, the wet grassland presented the highest number of individuals. Communities under stable conditions are expected to present saturated populations limited predominantly by interspecific competition (Tokeshi 1999). As environmental constraints imply death of certain individuals, the expected outcome of drought and waterlogging in the cerrados is the reduction of the size of the populations (Tokeshi 1999). Without environmental constraints removing individuals, the populations of the dominant species grow in the wet grassland. Nevertheless, the environmental constraints in seasonal and hyperseasonal cerrados prevent such population growth, reducing the total number of individuals.
Nonetheless, the species evenness seems to be the best measure to predict the seasonality gradient. Our results supported that higher environmental stability allows higher evenness in plant communities. The V values suggested that the pronounced drought in the seasonal cerrado as well as the contrasting stresses in the hyperseasonal cerrado reduce community evenness. Studies in boreal (Shafi & Yarranton 1973) and tropical forests (Cielo Filho et al. 2002; Sagar et al. 2003) also found this stability-evenness relationship. The wet grassland is stable, without significant changes in floristic composition, plant density, basal area, and cylindrical volume throughout the year (Cianciaruso & Batalha 2008). In savannas, however, there are few studies about evenness of plant communities across environmental gradients (see Bulla 1996 for references). Recently, Sankaran (2005) investigated the dynamics of tall grass savannas across a fire gradient and also observed a reduction in evenness at high levels of disturbance. Thus, the evenness of plant communities in savannas decreases as environmental severity increases.
Considering all species in the communities, we found a lognormal abundance distribution in the wet grassland, which presents more stable environmental conditions, and a random abundance distribution in the hyperseasonal cerrado, which experiences two contrasting environmental conditions (i.e., drought and waterlogging) along the year. The lognormal distribution is expected to occur in communities under few environmental constraints. Hill & Hamer (1998), for example, observed that the abundance distributions of butterflies fitted log-normal models in undisturbed forests and log-series in disturbed ones. Our results, however, supported that disturbances may generate abundance distributions indistinguishable from random instead of log-series distributions. The random assortment model was already predicted to occur in communities structured by constant environmental changes (see Tokeshi 1990). Nevertheless, we could not fit the abundance distribution of all species in the seasonal cerrado in any proposed model. So, we suggest that the intermediate level of disturbance in the seasonal cerrado leads to transitional shapes of SADs. Moreover, other SAD models that were not tested here might fit the SAD of the seasonal cerrado (see Magurran 2004 for examples).
As observed for marine fish communities (Magurran & Henderson 2003) and temperate forest hymenoptera (Ulrich & Ollik 2004), the common species in the three plant communities were also lognormal distributed. Lognormal distributions have been shown to commonly apply to many biological communities (see Magurran 2004 for reference). Thus, the lognormal model may be a pattern for SADs of common plants in savannas. However, contrary to previous studies that found a log-series distribution (Magurran & Henderson 2003) and a power function distribution (Ulrich & Ollik 2004), the SADs of the rare species in the wet grassland and the hyperseasonal cerrado followed the random assortment model. The random collection of species abundances, as predicted by this model (Tokeshi 1990), suggests that stochastic forces structure rare species in savannas. Magurran and Henderson (2003) also evoked the stochastic properties of the log-series distributions (see Fisher et al. 1943) to explain the SAD of rare marine fish. In general, random dispersal patterns are assumed to explain the abundance of rare species (Hubbell 2001; Magurran & Henderson 2003; Ulrich & Ollik 2004). In savannas, therefore, the abundance of rare plant species may also be structured by dispersal patterns. Environmental constraints, nonetheless, seem not to affect the SAD of common and rare plants.
The common species are expected to be permanent in the community and the rare species, occasional (Hanski 1982; Magurran & Henderson 2003; Ulrich & Ollik 2004). In this case, rare species are predicted to present high rates of local extinction and immigration (Magurran & Henderson 2003). Nevertheless, a remarkable characteristic of savanna plants is the resprouting ability after disturbances (Gottsberger & Silberbauer-Gottsberger 2006). The resprouting ability has been related to persistence of plant species in harsh environments (Grime 2001) and considered as an alternative pathway to avoid local extinction (Garcia & Zamora 2003). As a consequence, some rare species may be permanent in savanna communities. This expectation deserves more attention in future investigations of plant distributions in savannas, which should include temporal analyses of SADs.
In conclusion, the different signatures that common and rare plants left on the SADs of the plant communities we studied indicate that composite models are better descriptors for SADs in savannas. This difference may arise from a distinct community structuring between common and rare species (Magurran & Henderson 2003; Ulrich & Ollik 2004). However, although environmental constraints seem not to affect the abundance distribution of common and rare plant species, they may drive important changes in the SAD when all species are included, generating shapes indistinguishable from random.
Acknowledgments
We are grateful to Fundação de Amparo à Pesquisa do Estado de São Paulo, for financial support; to Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, for the scholarship granted to the first and second authors; to Conselho Nacional de Desenvolvimento Científico e Tecnológico, for the scholarship granted to the third author; to Instituto Brasileiro do Meio Ambiente e dos Recursos Naturais Renováveis, for research permission; to the Emas National Park staff, for logistical assistance; to herbaria of the Instituto de Botânica de São Paulo, Universidade de Brasília and Instituto Brasileiro de Geografia e Estatística; to Priscilla Amorim, Carlos Casali, André Jardim, Haroldo Lima, Renata Miotto, Fabíola Oliveira, Otávio Silva, and Mayla Valenti, for help in field; to the taxonomists Tarciso Filgueiras, and Regina Oliveira, for their assistance in the identification of species.
Recebido em 22/06/2009
Aceito em 19/02/2010
- Batalha, M.A. & Martins, F.R. 2002. The vascular flora of the cerrado in Emas National Park (Goiás, Central Brazil). Sida 20: 295-311.
- Borda-de-Água, L.; Hubbell, S.P. & McAllister, M. 2002. Species area curves, diversity indices, and species abundance distributions: A multifractal analysis. American Naturalist 159: 138-155.
- Bulla, L. 1996. Relationships between biotic diversity and primary productivity in savanna grasslands. Pp. 97-117. In: O.T. Solbrig, E. Medina & J.F. Silva (eds.). Biodiversity and savanna ecosystem process. A global perspective Berlin, Springer-Verlag.
- Caswell, H. 1976. Community structure: a neutral model analysis. Ecological Monographs 46: 327-354.
- Cianciaruso, M.V.; Batalha, M.A. & Silva, I.A. 2005. Seasonal variation of a hyperseasonal cerrado in Emas National Park, central Brazil. Flora 200: 345-353.
- Cianciaruso, M.V. & Batalha, M.A. 2008 A year in a Cerrado wet grassland: A non-seasonal island in a seasonal savanna environment. Brazilian Journal of Biology 68: 495-501.
- Cianciaruso, M.V. & Batalha, M.A. 2009. Short-term dynamics in seasonal and hyperseasonal cerrados. Brazilian Journal of Biology 69: 631-637.
- Cielo Filho, R.; Martins F.R. & Gneri M.A. 2002. Fitting abundance distribution models in tropical arboreal communities of SE Brazil. Community Ecology 3: 169-180.
- Clarke, K.R. & Gorley, R.N. 2001. PRIMER v5: user manual/tutorial. PRIMER-E, Plymouth, UK.
- Dewdney, A.K. 2003. The stochastic community and the logistic J-distribution. Acta Oecologica 24: 221-229.
- Eriksson, O. 1993. The species-pool hypothesis and plant community diversity. Oikos 68: 371-374.
- Fisher, R.A.; Corbet A.S. & Williams, C.B. 1943. The relation between the number of species and the number of individuals in a random sample from an animal population. Journal of Animal Ecology 12: 42-58.
- Garcia, D. & Zamora, R. 2003. Persistence, multiple demographic strategies and conservation in long-live Mediterranean plants. Journal of Vegetation Science 14: 921-926.
- Grime, J.P. 2001. Plant strategies, vegetation processes, and ecosystem properties Chichester, Wiley.
- Gottsberger, G. & Silberbauer-Gottsberger, I. 2006. Life in the cerrado: a South American tropical seasonal vegetation. Vol. 1. Origin, structure, dynamics and plant use Ulm, Reta Verlag.
- Hanski, I. 1982. Dynamics of regional distribution: the core and satellite species hypothesis. Oikos 38: 210-221.
- Harte, J.; Kinzig, A.P. & Green, J. 1999. Self-similarity in the distribution and abundance of species. Science 284: 334-336.
- Hill, J.K. & Hamer, K.C. 1998. Using species abundance models as indicators of habitat disturbance in tropical forests. Journal of Applied Ecology 35: 458-460.
- Hubbell, S.P. 1979. Tree dispersion, abundance and diversity in a tropical dry forest. Science 203: 1299-1309.
- Hubbell, S.P. 2001. The unified neutral theory of biodiversity and biogeography Princeton, Princeton University Press.
- Hughes, R.G. 1986. Theories and models of species abundance. American Naturalist 128: 879-899.
- Magurran, A.E. 2004. Measuring biological diversity Oxford, Blackwell publishing.
- Magurran, A.E. & Henderson, P.A.. 2003. Explaining the excess of rare species in natural species abundance distributions. Nature 422: 714-716.
- McGill, B.J.; Enquist, B.J.; Weiher, E. & Westoby, M. 2006. Rebuilding community ecology from functional traits. Trends in Ecology & Evolution 21: 178-185.
- McGill, B.J.; Etienne, R.S.; Gray, J.S.; Alonso, D.; Anderson, M.J.; Benecha, H.K.; Dornelas, M.; Enquist, B.J.; Green, J.L.; He, F.; Hurlbert, A.H.; Magurran, A.E., Marquet, P.A.; Maurer, B.A.; Ostling, A.; Soykan, C.U., Ugland, K.I. & White, E.P. 2007. Species abundance distributions: moving beyond single prediction theories to integration within an ecological framework. Ecology Letters 10: 995-1015.
- Moulliot, D.; Lepretre, A.; Andrei-Ruiz, M.C. & Viale, D. 2000. The fractal model: a new model to describe the species accumulation process and relative abundance distribution RAD. Oikos 90: 333-342.
- Pärtel, M.; Zobel, M.; Zobel, K. & Van Der Maarel, E. 1996. The species pool and its relation to species richness: evidence from Estonian plant communities. Oikos 75: 111-117.
- Preston, F.W. 1948. The commonness, and rarity, of species. Ecology 29: 254-283.
- Sagar, R.; Raghubanshi, A.S. & Singh, J.S. 2003. Tree species composition, dispersion and diversity along a disturbance gradient in a dry tropical forest region of India. Forest Ecology and Management 186: 61-71.
- Sankaran, M. 2005. Fire, grazing and the dynamics of tall-grass savannas in the Kalakad-Mundanthurai Tiger Reserve, South India. Conservation & Society 3: 4-25.
- Sarmiento, G. 1983. The savannas of tropical America. Pp. 245-288. In: D.W. Goodall (ed.). Ecosystems of the world - tropical savannas. Amsterdan, Elsevier.
- Shafi, M.I. & Yarranton, G.A.1973. Diversity, floristic richness, and species evenness during a secondary post-fire succession. Ecology 4: 897-902.
- Silva, I.A. & Batalha, M.A. 2006. Taxonomic distinctness and diversity of a hyperseasonal savanna in central Brazil. Diversity & Distribution 12: 725-730.
- Tokeshi, M. 1990. Niche apportionment or random assortment: species abundance patterns revisited. Journal of Animal Ecology 59: 1129-1146.
- Tokeshi, M. 1993 Species abundance patterns and community structure. Advances in Ecological Research 24: 111-186.
- Tokeshi, M. 1996. Power fraction: a new explanation of relative abundance patterns in species-rich assemblages. Oikos 75: 543-550.
- Tokeshi, M. 1999. Species coexistence. Ecological and evolutionary perspectives. Oxford, Blackwell Science.
- Ulrich, W. 2002. RAD - a FORTRAN program for the study of relative abundance distributions www.uni.torun.pl/~ulrichw
- Ulrich, W. & Ollik, M. 2004. Frequent and occasional species and the shape of relative abundance distributions. Diversity & Distributions 10: 263-269.
- Whittaker, R.H. 1960. Vegetation of the Siskiyou mountains, Oregon and California. Ecological Monographs 30: 279-338.
- Whittaker, R.H. 1975. Communities and Ecosystems New York, MacMillan Publishers.
- Wilson, J.B. 1991. Methods for fitting dominance diversity curves. Journal of Vegetation Science 2: 35-46.
- Zar, J.H. 1999. Biostatiscal analysis New Jersey, Prentice Hall.
Publication Dates
-
Publication in this collection
09 Aug 2010 -
Date of issue
June 2010
History
-
Received
22 June 2009 -
Accepted
19 Feb 2010