Abstract
This study aimed to develop and evaluate data driven models for prediction of forest yield under different climate change scenarios in the Gallies forest division of district Abbottabad, Pakistan. The Random Forest (RF) and Kernel Ridge Regression (KRR) models were developed and evaluated using yield data of two species (Blue pine and Silver fir) as an objective variable and climate data (temperature, humidity, rainfall and wind speed) as predictive variables. Prediction accuracy of both the models were assessed by means of root mean squared error (RMSE), mean absolute error (MAE), correlation coefficient (r), relative root mean squared error (RRMSE), Legates-McCabe’s (LM), Willmott’s index (WI) and Nash-Sutcliffe (NSE) metrics. Overall, the RF model outperformed the KRR model due to its higher accuracy in forecasting of forest yield. The study strongly recommends that RF model should be applied in other regions of the country for prediction of forest growth and yield, which may help in the management and future planning of forest productivity in Pakistan.
Keywords:
climate change; forest yield; RF and KRR models; prediction; Gallies forest; Abbottabad
Resumo
Este estudo teve como objetivo desenvolver e avaliar modelos baseados em dados para previsão da produção florestal em diferentes cenários de mudanças climáticas na divisão florestal Gallies do distrito de Abbottabad, Paquistão. Os modelos Random Forest (RF) e Kernel Ridge Regression (KRR) foram desenvolvidos e avaliados usando dados de produção de duas espécies (pinheiro-azul e abeto-prateado) como uma variável objetiva e dados climáticos (temperatura, umidade, precipitação e velocidade do vento) como preditivos variáveis. A precisão da previsão de ambos os modelos foi avaliada por meio de erro quadrático médio (RMSE), erro absoluto médio (MAE), coeficiente de correlação (r), erro quadrático médio relativo (RRMSE), Legates-McCabe’s (LM), índice de Willmott (WI) e métricas Nash-Sutcliffe (NSE). No geral, o modelo RF superou o modelo KRR devido à sua maior precisão na previsão do rendimento florestal. O estudo recomenda fortemente que o modelo RF seja aplicado em outras regiões do país para previsão do crescimento e produtividade florestal, o que pode ajudar no manejo e planejamento futuro da produtividade florestal no Paquistão.
Palavras-chave:
mudanças climáticas; produção florestal; modelos RF e KRR; predição; floresta das Galinhas; Abbottabad
1. Introduction
Recently, climate change is the biggest dilemma all over the world. Many researchers stated that atmospheric greenhouse gases emissions are the main source for changing global climatic conditions (Ashraf et al., 2015ASHRAF, M.I., MENG, F.R., BOURQUE, C.P.A. and MACLEAN, D.A., 2015. A novel modelling approach for predicting forest growth and yield under climate change. PLoS One, vol. 10, no. 7, pp. e0132066. http://dx.doi.org/10.1371/journal.pone.0132066. PMid:26173081.
http://dx.doi.org/10.1371/journal.pone.0...
; Hussain et al., 2014HUSSAIN, M., ZAIDI, S.M.H., MALIK, R.N. and SHARMA, B.D., 2014. Greenhouse gas emissions from production chain of a cigarette manufacturing industry in Pakistan. Environmental Research, vol. 134, pp. 81-90. http://dx.doi.org/10.1016/j.envres.2014.06.015.
http://dx.doi.org/10.1016/j.envres.2014....
, 2017HUSSAIN, M., NASEEM MALIK, R. and TAYLOR, A., 2017. Carbon footprint as an environmental sustainability indicator for the particleboard produced in Pakistan. Environmental Research, vol. 155, pp. 385-393. http://dx.doi.org/10.1016/j.envres.2017.02.024. PMid:28288441.
http://dx.doi.org/10.1016/j.envres.2017....
, 2018HUSSAIN, M., MALIK, R.N. and TAYLOR, A., 2018. Environmental profile analysis of particleboard production: a study in a Pakistani technological condition. The International Journal of Life Cycle Assessment, vol. 23, no. 8, pp. 1542-1561. http://dx.doi.org/10.1007/s11367-017-1385-9.
http://dx.doi.org/10.1007/s11367-017-138...
). The drift in global warming has been proved by the observation of climate, since 1900 the average temperature has been raised by 0.8% globally (Lindner et al., 2010LINDNER, M., MAROSCHEK, M., NETHERER, S., KREMER, A., BARBATI, A., GARCIA-GONZALO, J., SEIDL, R., DELZON, S., CORONA, P., KOLSTRÖM, M., LEXER, M.J. and MARCHETTI, M., 2010. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. Forest Ecology and Management, vol. 259, no. 4, pp. 698-709. http://dx.doi.org/10.1016/j.foreco.2009.09.023.), and since 1880 the 12 warmest years were observed in between 1990 and 2005 (Ciais et al., 2005CIAIS, P., REICHSTEIN, M., VIOVY, N., GRANIER, A., OGÉE, J., ALLARD, V., AUBINET, M., BUCHMANN, N., BERNHOFER, C., CARRARA, A., CHEVALLIER, F., DE NOBLET, N., FRIEND, A.D., FRIEDLINGSTEIN, P., GRÜNWALD, T., HEINESCH, B., KERONEN, P., KNOHL, A., KRINNER, G., LOUSTAU, D., MANCA, G., MATTEUCCI, G., MIGLIETTA, F., OURCIVAL, J.M., PAPALE, D., PILEGAARD, K., RAMBAL, S., SEUFERT, G., SOUSSANA, J.F., SANZ, M.J., SCHULZE, E.D., VESALA, T. and VALENTINI, R., 2005. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature, vol. 437, no. 7058, pp. 529-533. http://dx.doi.org/10.1038/nature03972. PMid:16177786.
http://dx.doi.org/10.1038/nature03972...
). Forests are very sensitive to changing climate, because rapid environmental variation does not allow trees to adapt due to their lengthy life span. There are numerous factors associated with climate change that are influencing forest ecosystem and which can act in combination or independently (Lindner et al., 2010LINDNER, M., MAROSCHEK, M., NETHERER, S., KREMER, A., BARBATI, A., GARCIA-GONZALO, J., SEIDL, R., DELZON, S., CORONA, P., KOLSTRÖM, M., LEXER, M.J. and MARCHETTI, M., 2010. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. Forest Ecology and Management, vol. 259, no. 4, pp. 698-709. http://dx.doi.org/10.1016/j.foreco.2009.09.023.). For instance, photosynthesis rates are increased by the rising concentration of carbon dioxide (CO2) in environment (Ainsworth and Long, 2005AINSWORTH, E.A. and LONG, S.P., 2005. What have we learned from 15 years of free‐air CO2 enrichment (FACE)? A meta‐analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2. The New Phytologist, vol. 165, no. 2, pp. 351-371. http://dx.doi.org/10.1111/j.1469-8137.2004.01224.x. PMid:15720649.
http://dx.doi.org/10.1111/j.1469-8137.20...
). The rate of tree growth may not rise correspondingly with increase in photosynthesis because of other limiting factors such as nutrients availability (Luo et al., 2004). Climate change posed significant threat for forests throughout the world (Fischlin et al., 2009FISCHLIN, A., AYRES, M., KARNOSKY, D., KELLOMÄKI, S., LOUMAN, B., ONG, C., PLATTNER, G.K., SANTOSO, H., THOMPSON, I., BOOTH, T.H. and MARCAR, N., 2009. Future environmental impacts and vulnerabilities. IUFRO World Series, vol. 22, pp. 53-100.). Forest productivity is directly affected from increase in temperature due to carbon dioxide concentration, changes in humidity, variations in timing and amount of rainfall, and altered storm and drought frequencies (Hyvonen et al., 2007HYVÖNEN, R., ÅGREN, G.I., LINDER, S., PERSSON, T., COTRUFO, M.F., EKBLAD, A., FREEMAN, M., GRELLE, A., JANSSENS, I.A., JARVIS, P.G., KELLOMÄKI, S., LINDROTH, A., LOUSTAU, D., LUNDMARK, T., NORBY, R.J., OREN, R., PILEGAARD, K., RYAN, M.G., SIGURDSSON, B.D., STRÖMGREN, M., VAN OIJEN, M. and WALLIN, G., 2007. The likely impact of elevated [CO2], nitrogen deposition, increased temperature and management on carbon sequestration in temperate and boreal forest ecosystems: a literature review. The New Phytologist, vol. 173, no. 3, pp. 463-480. PMid:17244042.). Similarly, pest attacks, variation in fire frequencies and distribution of tree species due to climate change would also affect the forest productivity (Medlyn et al., 2011MEDLYN, B.E., DUURSMA, R.A. and ZEPPEL, M.J., 2011. Forest productivity under climate change: a checklist for evaluating model studies. Wiley Interdisciplinary Reviews: Climate Change, vol. 2, no. 3, pp. 332-355. http://dx.doi.org/10.1002/wcc.108.
http://dx.doi.org/10.1002/wcc.108...
). Variation in global temperature might cause huge redistribution and shift of forests in the boreal region (Zhou et al., 2005ZHOU, X., PENG, C., DANG, Q.L., CHEN, J. and PARTON, S., 2005. Predicting forest growth and yield in northeastern Ontario using the process-based model of TRIPLEX1. 0. Canadian Journal of Forest Research, vol. 35, no. 9, pp. 2268-2280. http://dx.doi.org/10.1139/x05-149.
http://dx.doi.org/10.1139/x05-149...
). In response to the expected change in climate, several tree species data intelligent models have been developed in the previous twenty years (Ashraf et al., 2013ASHRAF, M.I., ZHAO, Z., BOURQUE, C.P.A., MACLEAN, D.A. and MENG, F.R., 2013. Integrating biophysical controls in forest growth and yield predictions with artificial intelligence technology. Canadian Journal of Forest Research, vol. 43, no. 12, pp. 1162-1171. http://dx.doi.org/10.1139/cjfr-2013-0090.
http://dx.doi.org/10.1139/cjfr-2013-0090...
, 2015ASHRAF, M.I., MENG, F.R., BOURQUE, C.P.A. and MACLEAN, D.A., 2015. A novel modelling approach for predicting forest growth and yield under climate change. PLoS One, vol. 10, no. 7, pp. e0132066. http://dx.doi.org/10.1371/journal.pone.0132066. PMid:26173081.
http://dx.doi.org/10.1371/journal.pone.0...
).
Forest managers are facing challenges in the implementation of sustainable forest management due to possible consequences of growing atmospheric temperature and carbon dioxide concentration on the productivity and growth of forest. For the estimation of total tree height, volume, and diameter at breast height (DBH), empirical statistical models of yield and growth have been used conventionally (Zhou et al., 2005ZHOU, X., PENG, C., DANG, Q.L., CHEN, J. and PARTON, S., 2005. Predicting forest growth and yield in northeastern Ontario using the process-based model of TRIPLEX1. 0. Canadian Journal of Forest Research, vol. 35, no. 9, pp. 2268-2280. http://dx.doi.org/10.1139/x05-149.
http://dx.doi.org/10.1139/x05-149...
). Due to absence of past data, inappropriately these models have been failed in simulation of the effects of climate change on forest stands and the growth dynamics of some regions’ forests. As, these models do not consider climate variables such as precipitation, temperature, and variation in carbon dioxide concentration, because these models only simulate forests yield and growth totally based on historic measurement (Peng, 2000PENG, C., 2000. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology and Management, vol. 132, no. 2-3, pp. 259-279. http://dx.doi.org/10.1016/S0378-1127(99)00229-7.
http://dx.doi.org/10.1016/S0378-1127(99)...
). Forest growth models could be utilized as an effective management tool, because growth models developed for management need simple and easily available data (Johnsen et al., 2001JOHNSEN, K., SAMUELSON, L., TESKEY, R., MCNULTY, S. and FOX, T., 2001. Process models as tools in forestry research and management. Forest Science, vol. 47, no. 1, pp. 2-8.). Growth and yield models are very convenient tools for managing large forests (Aghimien et al., 2016AGHIMIEN, E.V., OSHO, J.S.A., HAUSER, S., DENI, B. and ADE-ONI, V.D., 2016. Growth and yield models for uneven-aged secondary forest in IITA, Ibadan, Nigeria. Forest Research, vol. 5, no. 173, pp. 2.). Forest growth and yield models deliver quantitative evidence about continuous state of change in forest stand. These models are effective in future prediction of forest growth and yield, updating forest inventories, and making forest-harvesting plans (Weiskittel et al., 2011WEISKITTEL, A.R., HANN, D.W., KERSHAW JUNIOR, J.A. and VANCLAY, J.K., 2011. Forest growth and yield modeling. Hoboken: John Wiley & Sons. http://dx.doi.org/10.1002/9781119998518.
http://dx.doi.org/10.1002/9781119998518...
). With the help of information provided by management-oriented growth and yield models, efficient forest management plans can be made (Pretzsch, 2009PRETZSCH, H., 2009. Forest dynamics, growth and yield from measurement to model. Berlin: Springer, pp. 1-39.). Therefore, data intelligent models have been successfully applied globally to predict future forest yield using historical data. However, there is no study conducted for the prediction of forest yield using data intelligent models in Pakistan. Therefore, in the present study machine-learning models have been developed to predict forest yield to provide baseline information’s to forest managers in Pakistan. Thus, the objective of this study was to found out the future yield of two high-value principal tree species (blue pine and silver fir) under different climate change scenarios in the moist temperate forest of Gallies, Abbottabad, Pakistan.
2. Material and Method
2.1. Theoretical overview
2.1.1. Random forest
The Random Forests (RF) algorithm was projected by Leo Breiman for the first time in 1999 and can be widely utilized for regression and classification functions (Breiman, 2001BREIMAN, L., 2001. Random forests. Machine Learning, vol. 45, no. 1, pp. 5-32. http://dx.doi.org/10.1023/A:1010933404324.
http://dx.doi.org/10.1023/A:101093340432...
). This algorithm could be significant for the selection of different variables, interaction recognition, clustering and so on. The RF is a classification tool comprising of many tree classifiers, which uses two commanding machine-learning techniques, such as random selection of functions and bagging (Jiang et al., 2007JIANG, P., WU, H., WANG, W., MA, W., SUN, X. and LU, Z., 2007. MiPred: classification of real and pseudo microRNA precursors using random forest prediction model with combined features. Nucleic Acids Research, vol. 35, no. Web Server, suppl. 2, pp. W339-W344. http://dx.doi.org/10.1093/nar/gkm368.
http://dx.doi.org/10.1093/nar/gkm368...
). When bagging, training data comprising of bootstrap samples are used for the training of each tree, and then predictions are made by maximum tree votes. RF is a further development of bagging. When growing a tree, RF randomly selects a subset of features to split at each node rather than using all functions. To evaluate the predictive power of the RF model, it performs cross-validation in corresponding with the training step, by utilizing the so-called out-of-bag (OOB) samples. Specifically, each tree is grown during training with a specific sample of bootstrap. Since the bootstrapping exchanges samples from the training dataset, some of the sample’s sequences are skipped, while others in the sample are repeated. The skipped sequences create the OOB samples. On average, each tree is grown utilizing about of the training sequences, leaving as OOB. As, OOB sequences are not used in the building of tree but can be utilized to estimate the prediction performance (Svetnik et al., 2003SVETNIK, V., LIAW, A., TONG, C., CULBERSON, J.C., SHERIDAN, R.P. and FEUSTON, B.P., 2003. Random forest: a classification and regression tool for compound classification and QSAR modeling. Journal of Chemical Information and Computer Sciences, vol. 43, no. 6, pp. 1947-1958. http://dx.doi.org/10.1021/ci034160g. PMid:14632445.
http://dx.doi.org/10.1021/ci034160g...
). The algorithm of random forest is described below:
Draw bootstrap samples from the original data.
For every sample of bootstrap make an unpruned regression tree. At each node, sample of the predictors randomly instead of taking the best split among all predictors and select the best split from among those variables. (Bagging could be considered as the superior case of random forests attained when, the quantity of predictors).
An estimate of the error rate can be obtained, based on the training data, such as following:
-
a
At each bootstrap repetition, the data cannot be predicted in the bootstrap sample (called as out-of-bag, or OOB data) using the tree grown with the bootstrap sample;
-
b
The OOB predictions are aggregated (each data point would be OOB around 36% of the times on the average, so aggregate these predictions). Now calculate the rate of error, and name it the error rate of OOB (Bylander, 2002BYLANDER, T., 2002. Estimating generalization error on two-class datasets using out-of-bag estimates. Machine Learning, vol. 48, no. 1-3, pp. 287-297. http://dx.doi.org/10.1023/A:1013964023376.
http://dx.doi.org/10.1023/A:101396402337... ).
The key benefits of the advanced RF application are that it has been evidenced as the most accurate and strong algorithms in the prediction of many datasets (Caruana et al., 2008CARUANA, R., KARAMPATZIAKIS, N. and YESSENALINA, A., 2008. An empirical evaluation of supervised learning in high dimensions. In: Proceedings of the 25th international conference on Machine learning, 2008, New York, NY. New York: ACM Press, pp. 96-103. http://dx.doi.org/10.1145/1390156.1390169.
http://dx.doi.org/10.1145/1390156.139016...
). It can handle regression issues with multiple inputs and examine their relative importance. Also, the performance of RF is not very complex to its hyper parameters in the algorithm (Qi et al., 2018QI, C., FOURIE, A., DU, X. and TANG, X., 2018. Prediction of open stope hangingwall stability using random forests. Natural Hazards, vol. 92, no. 2, pp. 1179-1197. http://dx.doi.org/10.1007/s11069-018-3246-7.
http://dx.doi.org/10.1007/s11069-018-324...
; Kuhn and Johnson, 2013KUHN, M. and JOHNSON, K., 2013. Applied predictive modeling. New York: Springer. vol. 26. http://dx.doi.org/10.1007/978-1-4614-6849-3.
http://dx.doi.org/10.1007/978-1-4614-684...
). In most real-world applications, the RF algorithm is fast enough, but performance can be significant and further methods are preferred (Donges, 2018DONGES, N., 2018. The random forest algorithm. Toronto: Towards Data Science.). Figure 1 represents the schematic view of the RF model.
2.1.2. Kernel ridge regression
Kernel ridge regression (KRR) is a very simple but powerful machine learning model used for nonparametric regression, which is calculated by solving a linear system (Avron et al., 2017AVRON, H., CLARKSON, K.L. and WOODRUFF, D.P., 2017. Faster kernel ridge regression using sketching and preconditioning. SIAM Journal on Matrix Analysis and Applications, vol. 38, no. 4, pp. 1116-1138. http://dx.doi.org/10.1137/16M1105396.
http://dx.doi.org/10.1137/16M1105396...
). KRR is obtained by coupling the kernel trick with the ridge regression and is sometime termed as the linear least square regression with regularization of Tikhonov (Chu et al., 2011CHU, C., NI, Y., TAN, G., SAUNDERS, C.J. and ASHBURNER, J., 2011. Kernel regression for fMRI pattern prediction. NeuroImage, vol. 56, no. 2, pp. 662-673. http://dx.doi.org/10.1016/j.neuroimage.2010.03.058. PMid:20348000.
http://dx.doi.org/10.1016/j.neuroimage.2...
). Assume that we have a training data , where N represent the total number of training samples. X is a features matrix, , of size N × d and Y = is a N × 1 vector of class labels.
KRR depends on ridge regression and ordinary least square (OLS) (Saunders et al., 1998SAUNDERS, C., GAMMERMAN, A. and VOVK, V., 1998. Ridge regression learning algorithm in dual variables. In: ICML ’98: Proceedings of the Fifteenth International Conference on Machine Learning, 1998, San Francisco, CA. New York: ACM Press.; Rakesh and Suganthan, 2017RAKESH, K. and SUGANTHAN, P.N., 2017. An ensemble of kernel ridge regression for multi-class classification. Procedia Computer Science, vol. 108, pp. 375-383. http://dx.doi.org/10.1016/j.procs.2017.05.109.
http://dx.doi.org/10.1016/j.procs.2017.0...
). The purpose of OLS is to minimize the square loss:
where represents the L2 norm. A λ called ridge or shrinkage parameter is added in above Equation 1 to control the commutation among the variance and bias of the estimates, which generates the following equation:
Solution for the Equation 2 is where, I denote the identity matrix. The forecasted label of a new unlabeled x is represented by .
KRR uses the kernel trick which outspreads the linear regression into nonlinear and high dimensional or even into an infinite dimensional space. The data is replaced by the feature vectors: in X which is brought by the kernel where . Hence, the forecasted class label of new example x can be given as Equation 3:
here .
With KRR one can easily utilize the most commonly used functions, like polynomial or Gaussian or linear, without evaluating the feature vectors . Figure 2 represents the schematic view of the KRR model.
3. Data and Methods
3.1. Data collection
In this study, the acquired data includes environmental variables such as monthly rainfall, wind speed at 5am and pm, wind direction at 5am and pm, minimum and maximum temperature and humidity at 5am and pm, for the years 1963 to 2016 were collected from Pakistan Meteorological Department (PMD), Islamabad as can be seen in Table 1. While the yield data of two tree species (Silver fir and Chir pine) for selected region of study were obtained for the period of 1963 to 2016 from Pakistan Forest Institute Peshawar (PFI), Forest Working Circle Peshawar (FWC) and Forest Department, Khyber Pakhtunkhwa. Climate variables such as temperature, humidity, precipitation, rainfall and wind speed effect forest ecosystem composition and function as well as play a pivotal role in forest growth (Lindner et al., 2010LINDNER, M., MAROSCHEK, M., NETHERER, S., KREMER, A., BARBATI, A., GARCIA-GONZALO, J., SEIDL, R., DELZON, S., CORONA, P., KOLSTRÖM, M., LEXER, M.J. and MARCHETTI, M., 2010. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. Forest Ecology and Management, vol. 259, no. 4, pp. 698-709. http://dx.doi.org/10.1016/j.foreco.2009.09.023.). Forest growth and productivity are affected directly or indirectly through changes in climate variables (Gibbs et al., 2007GIBBS, H.K., BROWN, S., NILES, J.O. and FOLEY, J.A., 2007. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environmental Research Letters, vol. 2, no. 4, pp. 045023. http://dx.doi.org/10.1088/1748-9326/2/4/045023.
http://dx.doi.org/10.1088/1748-9326/2/4/...
). Increase in temperature disturbs the length of forest growing season and alter its geographical distribution due to which the habitat of forest species is likely to move from lower altitude to higher altitude (Backlund et al., 2008BACKLUND, P., JANETOS, A. and SCHIMEL, D., 2008. The effects of climate change on agriculture, land resources, water resources, and biodiversity in the United States. In: U.S. ENVIRONMENTAL PROTECTION AGENCY, ed. Synthesis and assessment product 4.3. Washington: Climate Change Science Program, 240 p.). Climate change is probable to raise in some regions the risk of drought and in others the risk of high rainfall and flooding. Warming temperature changes the time of snow melting, which disturbs the availability of water (Karl et al., 2009KARL, T.R., MELILLO, J.M., PETERSON, T.C. and HASSOL, S.J., eds., 2009. Global climate change impacts in the United States. Cambridge: Cambridge University Press.).
3.2. Study area
Present study was designed in the Gallies forest division of district Abbottabad (Figure 3). The forest division Gallies are in District Abbottabad Khyber Pakhtunkhwa Province, Pakistan. The total area of Gallies are 147753.72 hectares, mostly consist of moist temperate forest (Ali, 2018ALI, M., 2018 [viewed 9 June 2021]. Billions Trees Afforestation Project (BTAP) Restores 600,000ha Forests, Enhances KP's Forests Area By 6.3pc: PD. UrduPoint Network.Available from: https://www.urdupoint.com/en/pakistan/billions-trees-afforestation-project-btap-re-452211.html.
https://www.urdupoint.com/en/pakistan/bi...
). Northern latitudes of the Gallies are approximately 33°–55 and 34°-20, while eastern longitudes are 73°-20 and 63°-30. The total length of the forests present in the Gallies are about 39 km, extended from north to south. Main populated areas of the study area are Nathia Galli, Bagnotar, Donga Galli, Biran Galli and Bara Galli. The study area is surrounded by Abbottabad on its west, Haripur on the south, and Murree on the south east, while, Kunhar and Jhelum Rivers are located on its north and east respectively (Kayani et al., 2014KAYANI, S., AHMAD, M., ZAFAR, M., SULTANA, S., KHAN, M.P.Z., ASHRAF, M.A., HUSSAIN, J. and YASEEN, G., 2014. Ethnobotanical uses of medicinal plants for respiratory disorders among the inhabitants of Gallies-Abbottabad, Northern Pakistan. Journal of Ethnopharmacology, vol. 156, pp. 47-60. http://dx.doi.org/10.1016/j.jep.2014.08.005. PMid:25153021.
http://dx.doi.org/10.1016/j.jep.2014.08....
).
The total population of the study area are 880666 with major tribes inhibiting are Awan, Gujjars, Jadoons and Rajput. The population mainly rely on agriculture and livestock rearing, having literacy rate of 30%. Climatic conditions vary from sub-tropical in the lower areas to moist temperate in upper regions of the study area. Gallies receive heavy snowfall in winter while summer season is pleasant and average rainfall ranges from 1200 mm to 1700 mm annually. Geological structure is composed of Triassic, Jurassic and Cretaceous rocks (Kayani et al., 2014KAYANI, S., AHMAD, M., ZAFAR, M., SULTANA, S., KHAN, M.P.Z., ASHRAF, M.A., HUSSAIN, J. and YASEEN, G., 2014. Ethnobotanical uses of medicinal plants for respiratory disorders among the inhabitants of Gallies-Abbottabad, Northern Pakistan. Journal of Ethnopharmacology, vol. 156, pp. 47-60. http://dx.doi.org/10.1016/j.jep.2014.08.005. PMid:25153021.
http://dx.doi.org/10.1016/j.jep.2014.08....
). Gallies are categorized into three major forest types that are; Dry Sub-tropical Broad-Leaved Forest, Sub-tropical Pine Forest and Moist Temperate Forest. Major social hurdles of the area are poor literacy rate, bad infrastructure and poverty. Whereas, conversion of land, biodiversity loss and land sliding are the biophysical problems.
3.3. Model performance evaluation criteria
Performance of the RF and KRR models for the prediction of forest yield was evaluated from the independent validation data set by relating predicted values with observed values. The American Civil Engineering Society (Ali et al., 2018ALI, M., DEO, R.C., DOWNS, N.J. and MARASENI, T., 2018. Cotton yield prediction with Markov Chain Monte Carlo-based simulation model integrated with genetic programing algorithm: A new hybrid copula-driven approach. Agricultural and Forest Meteorology, vol. 263, pp. 428-448. http://dx.doi.org/10.1016/j.agrformet.2018.09.002.
http://dx.doi.org/10.1016/j.agrformet.20...
) recommends two categories of model assessment techniques, including statistics (or by comparing the simulated and observed data visually) and standardized performance metrics. For examining the dissimilarities among the factors maximum, minimum, mean, variance, skewness, kurtosis and standard deviation, statistical metrics are used however, standardized metrics are utilized to check the expected results against the observed data.
Following are the mathematical formulations (Prasad et al., 2017PRASAD, R., DEO, R.C., LI, Y. and MARASENI, T., 2017. Input selection and performance optimization of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmospheric Research, vol. 197, pp. 42-63. http://dx.doi.org/10.1016/j.atmosres.2017.06.014.
http://dx.doi.org/10.1016/j.atmosres.201...
; Dawson et al., 2007DAWSON, C.W., ABRAHART, R.J. and SEE, L.M., 2007. HydroTest: a web-based toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environmental Modelling & Software, vol. 22, no. 7, pp. 1034-1052. http://dx.doi.org/10.1016/j.envsoft.2006.06.008.
http://dx.doi.org/10.1016/j.envsoft.2006...
; Legates and McCabe Junior, 1999).
-
Correlation coefficient (r) is expressed as Equation 4:
-
Willmott’s index (WI) is expressed as Equation 5:
-
Nash-Sutcliffe coefficient (NSE) is expressed as Equation 6:
-
Root mean square error (RMSE) is expressed as Equation 7:
-
Mean absolute error (MAE) is expressed as Equation 8:
-
Legates-McCabe’s (LM) is expressed as Equation 9:
Where and are the observed and predicted ith values of forest yield , and are the observed and predicted means in the set of cross-validations (test) and represent the reference point number in the test set. The performance metrics regarding physical reasoning, it can be deduced that the coefficient of correlation, confined by (0,1) where 0 = relatively poor to 1,0 = perfect model, labels the variance proportion in observed forest yield that is explained by the KRR and RF models (Deo and Şahin, 2017DEO, R.C. and ŞAHIN, M., 2017. Forecasting long-term global solar radiation with an ANN algorithm coupled with satellite-derived (MODIS) land surface temperature (LST) for regional locations in Queensland. Renewable & Sustainable Energy Reviews, vol. 72, pp. 828-848. http://dx.doi.org/10.1016/j.rser.2017.01.114.
http://dx.doi.org/10.1016/j.rser.2017.01...
; Mohammadi et al., 2015MOHAMMADI, K., SHAMSHIRBAND, S., TONG, C.W., ARIF, M., PETKOVIĆ, D. and CH, S., 2015. A new hybrid support vector machine–wavelet transform approach for estimation of horizontal global solar radiation. Energy Conversion and Management, vol. 92, pp. 162-171. http://dx.doi.org/10.1016/j.enconman.2014.12.050.
http://dx.doi.org/10.1016/j.enconman.201...
). However, the equation is based on the consideration of the linear relationship between and and is therefore imperfect in its ability to deliver a strong notation as it standardizes observed and predicted means and variances. Though, the and can provide better predictive information whereby is used to measure the goodness-of-fit relevant to higher values while the is not focused on large events or small scale but evaluates all deviations from the observed values equal in method and independent of the sign. It is important to note that although can evaluate the model with a higher skill level than the correlation coefficient, this measure is calculated from the squared variances. Therefore, the performance evaluation is predetermined in favor of higher magnitude events, which in maximum cases have the large error and are unresponsive to lower magnitude sequences (Dawson et al., 2007DAWSON, C.W., ABRAHART, R.J. and SEE, L.M., 2007. HydroTest: a web-based toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environmental Modelling & Software, vol. 22, no. 7, pp. 1034-1052. http://dx.doi.org/10.1016/j.envsoft.2006.06.008.
http://dx.doi.org/10.1016/j.envsoft.2006...
). Hence, due to occasional large errors, the may be more sensitive than other performance measures because the squaring process can lead to very large errors leading to disproportionate weighting (Legates and McCabe Junior, 1999). To solve this problem, the Willmott’s index () was calculated by seeing the proportion of the mean squared error instead of the square of the differences, which offers an advantage over the values of , and . Considering the geographical variation between the current study sites, which may produce differences in the distribution of forest yield data, the relative root means square error () has also been calculated (Mohammadi et al., 2015MOHAMMADI, K., SHAMSHIRBAND, S., TONG, C.W., ARIF, M., PETKOVIĆ, D. and CH, S., 2015. A new hybrid support vector machine–wavelet transform approach for estimation of horizontal global solar radiation. Energy Conversion and Management, vol. 92, pp. 162-171. http://dx.doi.org/10.1016/j.enconman.2014.12.050.
http://dx.doi.org/10.1016/j.enconman.201...
; Prasad et al., 2017PRASAD, R., DEO, R.C., LI, Y. and MARASENI, T., 2017. Input selection and performance optimization of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmospheric Research, vol. 197, pp. 42-63. http://dx.doi.org/10.1016/j.atmosres.2017.06.014.
http://dx.doi.org/10.1016/j.atmosres.201...
) to evaluate and compare the model over different geographical locations. According to (Ertekin and Yaldiz, 2000ERTEKIN, C. and YALDIZ, O., 2000. Comparison of some existing models for estimating global solar radiation for Antalya (Turkey). Energy Conversion and Management, vol. 41, no. 4, pp. 311-330. http://dx.doi.org/10.1016/S0196-8904(99)00127-2.
http://dx.doi.org/10.1016/S0196-8904(99)...
), the degree of accuracy of a model is excellent if ˂ 10%, good if 10% ˂ ˂ 20%, fair if 20% ˂ ˂ 30%, and bad if ˃ 30%. Nash-Sutcliffe efficiency () is another standardized metric that determines the relative magnitude of the residual variance of the predicted data relative to measured variance. Legates-McCabes () is the most innovative and commanding metric than and , which uses the comparison fit to evaluate and . can be robust enough to evaluate outcomes by addressing weaknesses and using and baselines, as well as a and rating (Legates and McCabe Junior, 1999).
3.4. Model development
The RF and KRR models were developed in MATLAB R2016b programming environment (The Math Works Inc. USA). All the simulations were obtained on 2.93 GHz dual-core PC with Pentium 4 operating system. The models are developed in the following steps:
-
Data partitioning
The data are partitioned straightly 70% and 30% prior into training and testing subsets, respectively. Antecedent time lagged inputs (i.e., rainfall, wind speed, wind direction, minimum and maximum temperature and humidity) at (t – 1) are used to develop the models to predict yearly forest yields.
-
Normalization process
The data are normalized between [0, 1] using Equation 10 (Hsu et al., 2003HSU, A.L., MURPHY, C.T. and KENYON, C., 2003. Regulation of aging and age-related disease by DAF-16 and heat-shock factor. Science, vol. 300, no. 5622, pp. 1142-1145. http://dx.doi.org/10.1126/science.1083701. PMid:12750521.
http://dx.doi.org/10.1126/science.108370...
).
In Equation 10, represents the input/output, = the minimum value, = the maximum value of the data and = the corresponding normalized numeric value.
3.5. RF model
In the final phase of the modelling, the RF model is then applied to predict a year ahead forest yield by incorporating the environmental based input variables. After incorporating the input variables at (t – 1) lags into the RF model, different types of parameters were tuned that include the number of trees and number of predictors to train the model. The RF model is validated/tested independently. The performance of RF is benchmarked with KRR model. Different types of kernals (such as linear, gaussian, polynomial) are used to get the optimum KRR model.
4. Results and Discussion
4.1. Results
4.1.1. Box plots
In the present study boxplots of the Random Forest vs Kernel ridge regression models were designed to find out prediction error (PE) for the yield of blue pine and silver fir in the testing period of 1996 to 2016 as shown in Figure 4. Green box shows random forest model, blue box represents kernel ridge regression model, while the red colored + sign in both boxes show the outliers which signify the extreme magnitudes of the simulation error in the testing period. PE is the difference between the simulated values and observed values. If the difference between these values is more the model gives poor prediction, and when the difference is less the prediction will be better and model will be considered as best. Similarly, when the box size is bigger the model will perform poor, and when box is smaller the model will be good. These boxplots are showing that the box is smaller, and PE is less in random forest model for blue pine specie in response to the kernel ridge regression model whose box is bigger and PE is also more. Similarly, for silver fir specie the random forest model again showed less PE and smaller box than the KRR model. Therefore, by observing (Figure 4), RF model performed better than the KRR model for both species.
Box-plots of the Predicted error |PE| (cft) in testing period (1996-2016) for the RF and KRR models between the predicted and observed yields of Blue pine and Silver fir species.
4.1.2. Polar plots
In the present study polar plots were designed which demonstrate the Predicted error (PE) in Cubic feet (cft) for the RF and KRR models between the predicted and observed yields of blue pine and silver fir species in the testing period (1996-2016), as shown in (Figure 5). The green dots display the PE of RF model and the blue dots are showing the PE of KRR model which can be seen in (Figure 5). The model which has less predicted error will be considered as a better model. The results revealed that PE for the years 1997, 1998, 1999, 2000, 2001, 2004, 2005, 2007, 2008, 2009, 2011, 2013, 2014 and 2015 were significantly low for the RF model between the predicted and observed yields of blue pine. While, KRR model showed same results for blue pine in the years of 1996, 2002, 2003, 2006, 2010, 2012, and 2016. Similarly, PE was less in 1997, 1999, 2000, 2001, 2002, 2004, 2005, 2007, 2008, 2009, 2011, 2013, 2014, 2015, and 2016 in RF model in response to KRR model which revealed less magnitude of predicted error in 1996, 1998, 2003, 2006, 2010, and 2012 between predicted and observed yields silver fir. When both RF and KRR models were compared based on these results shown in (Figure 5), the RF model performed better presenting less magnitude of error than the KRR model.
Polar plots show the Predicted error |PE| (cft) in testing period (1996-2016) for the RF and KRR models between the predicted and observed yields of Blue pine and Silver fir species.
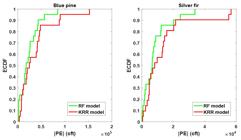
4.1.3. Empirical cumulative distribution function (ECDF)
In Figure 6, prediction performance of RF and KRR models were tested by plotting ECDF of the absolute PE between observed and predicted yields of blue pine and silver fir species in testing period (1996-2016). In the following Figure 6, the green line represents RF model, red line shows KRR model, Y-axis is ECDF ranging from 0 to 1, and X-axis is the PE, which ranges from 0 to 2 for blue pine and 0 to 6 for silver fir. The model having minimum error at ECDF 1 will be considered as best model. The results revealed that RF model bears 0.7 PE while, for KRR model the PE is 1.5 between the predicted and observed yields of blue pine. Similarly, for silver fir the PE’s were 3.4 and 5.6 for RF and KRR models respectively. Therefore, the (Figure 6) clearly showed that RF model was more precise than the KRR model in prediction for the yield of both blue pine and silver fir species.
Empirical cumulative distribution function (ECDF) of the Predicted error |PE| (cft) in testing period for the RF and KRR models between the predicted and observed yields of Blue pine and Silver fir species.
4.1.4. Taylor diagram
Taylor diagram was made as shown in (Figure 7), which quantified the similarities between the predicted and observed yields of blue pine and silver fir species in terms of their standard deviation and correlation for RF and KRR models. The Taylor diagram was made for the testing period of 20 years (1996-2016) which provided a more accurate and conclusive statement about the statistical results of how well the predicted yield matched with the observed yield in term of their correlation. Correlation of observed yield is 100% or 1 that can be seen in the following figure. In Figure 7, the red dot shows predicted yield of KRR model, green dot represents RF model, and observed yield is shown by the yellow dot. The model having minimum distance between the correlation of simulated yield and observed yield will be evaluated as better model. The results showed that the correlation coefficient for predicted yield of blue pine for RF model was 0.97 and 0.8 for KRR model. Similarly, for silver fir the correlation of RF model was 0.95 followed by KRR model which was 0.8. RF model was closer to the observed yield in both species as their correlation was 0.97 and 0.95 respectively, compared to KRR model having correlation of 0.8 and 0.8. So, RF model again performed better than the KRR model in terms of their correlation.
Taylor diagram showing the correlation coefficient between the predicted and observed yields (Blue pine and Silver fir) (cft) and standard deviation for the RF and KRR models.
4.1.5. Willmott’s index (Wi), Nash-Sutcliffe (Nse) and Legates-Mccabe’s (Lm) agreement
In the present project, the accuracy of RF and KRR model in testing period for both species (blue pine and silver fir) were evaluated based on WI, NSE and LM shown in Table 2. The model having higher value in terms of WI, NSE and LM is considered more accurate than the other model. Current results revealed that for blue pine and silver fir the proposed RF model attained the highest values of WI = 0.854 and 0.845, NSE = 0.866 and 0.864 and LM = 0.693 and 0.704 respectively followed by KRR model having values of WI = 0.713 and 0.682, NSE = 0.646 and 0.602, and LM = 0.529 and 0.521 respectively. The result showed that RF model was more accurate in prediction in response to the KRR model, and blue pine attained higher accuracy based on higher values of WI, NSE and LM agreement followed by silver fir.
Performance of RF vs. KRR models in testing period using Willmott’s index (WI), Nash-Sutcliffe (NSE) and Legates-McCabe’s (LM) agreement.
4.1.6. Root mean square error (Rmse), Mean absolute error (MAE) and coefficient of determination (r)
The accuracy of the developed RF model was evaluated in comparison with KRR model in terms of RMSE, MAE and r for the prediction of blue pine and silver fir species as revealed in Table 3. The RF model applied for the simulation of blue pine acquired higher values of RMSE = 31042.6 cft, MAE = 23461.6 cft and r = 0.964, followed by KRR model where RMSE = 11761.1 cft, MAE = 8277.0 cft and r = 0.80. Similarly, when applied for silver fir prediction, RF model again yielded higher values of RMSE = 50443.5 cft, MAE = 35960.7 cft and r = 0.957, followed by KRR model having RMSE = 20117.3 cft, MAE = 13382.4 cft and r = 0.799. Based on higher values of RMSE, MAE and r, it is evident that RF model outperformed KRR model in the yield prediction of both blue pine and silver fir.
Testing performance of RF vs. KRR models measured by root mean square error (RMSE), mean absolute error (MAE), coefficient of determination (r).
5. Discussion
Deforestation rate in Pakistan is considered second highest in the world. World Conservation Union (IUCN) has investigated that abrupt increase in population growth would leads to 3% increase in wood use in Pakistan annually. Hence it is predicted that if Pakistan continues the same rate of deforestation, there forests will be vanished within coming ten or fifteen years (Ali and Benjaminsen, 2004ALI, J. and BENJAMINSEN, T.A., 2004. Fuelwood, timber and deforestation in the Himalayas. Mountain Research and Development, vol. 24, no. 4, pp. 312-318. http://dx.doi.org/10.1659/0276-4741(2004)024[0312:FTADIT]2.0.CO;2.
http://dx.doi.org/10.1659/0276-4741(2004...
). Pakistan forest cover is 4.2 million hectares which is about 4.8% of the overall land area of the country (Zaman and Ahmad, 2012ZAMAN, S.B. and AHMAD, S., 2012. Wood supply and demand Analysis in Pakistan: key issues, managing natural resources for sustaining future agriculture. Research Briefings, vol. 4, no. 22, pp. 1-12.). Due to rapid increase in population, forest cover is also decreasing, because the local people depend on forest resources i.e., house construction, ecotourism, wooden furniture manufacture, fuelwood, and medicinal plants extraction. From 1996 to 2000 about 2.35 million m3 round wood was extracted for industrial use in Pakistan (Hussain et al., 2017HUSSAIN, M., NASEEM MALIK, R. and TAYLOR, A., 2017. Carbon footprint as an environmental sustainability indicator for the particleboard produced in Pakistan. Environmental Research, vol. 155, pp. 385-393. http://dx.doi.org/10.1016/j.envres.2017.02.024. PMid:28288441.
http://dx.doi.org/10.1016/j.envres.2017....
). According to global climate risk index 2019, Pakistan is the 7th most vulnerable country to climate change due to global warming (Eckstein et al., 2019ECKSTEIN, D., HUTFILS, M.L. and WINGES, M., 2019. Global climate risk index 2019: who suffers most from extreme weather events? Weather-related Loss Events in 2017 and 1998 to 2017. Berlin: Germanwatch e.V.).
Data intelligent models are an important tool in decision making for agriculture, hydrology, forest and wildlife to resolve issues caused due to global warming (Ali et al., 2018ALI, M., DEO, R.C., DOWNS, N.J. and MARASENI, T., 2018. Cotton yield prediction with Markov Chain Monte Carlo-based simulation model integrated with genetic programing algorithm: A new hybrid copula-driven approach. Agricultural and Forest Meteorology, vol. 263, pp. 428-448. http://dx.doi.org/10.1016/j.agrformet.2018.09.002.
http://dx.doi.org/10.1016/j.agrformet.20...
). Rapid changes in the climatic conditions are modifying tree growing environments by altering the site conditions. It is expected that the forest resources will be more influenced by climate change than the other natural resources (Ashraf et al., 2015ASHRAF, M.I., MENG, F.R., BOURQUE, C.P.A. and MACLEAN, D.A., 2015. A novel modelling approach for predicting forest growth and yield under climate change. PLoS One, vol. 10, no. 7, pp. e0132066. http://dx.doi.org/10.1371/journal.pone.0132066. PMid:26173081.
http://dx.doi.org/10.1371/journal.pone.0...
). Forest resources such as timber, fuelwood, medicinal plants, and wood production are limited in Pakistan and there is a prior need to manage those resources for the future (Zaman and Ahmad, 2012ZAMAN, S.B. and AHMAD, S., 2012. Wood supply and demand Analysis in Pakistan: key issues, managing natural resources for sustaining future agriculture. Research Briefings, vol. 4, no. 22, pp. 1-12.). For the better management of forest, we need advance and reliable predictive growth and yield model. In the present study two models such as RF and KRR model were developed for two tree species (Blue pine and silver fir) in Gallies forest division, Abbottabad to predict forest yield by using historical forest yield data and environmental variables from 1966 to 2016, as input predictors as can be seen in Appendix A
Appendix A
Environmental and forest yield variables Information’s for Gallies Forest Division, Pakistan.
Table 1A
Environmental and forest yield variables in the Gallies forest division of Abbottabad, Pakistan.
Year
Rainfall
min temp
max temp
humidity at 5am
humidity at 5pm
Wind speed at 5am
Wind speed at 5pm
Yield of Blue pine (Cft)
Yield of Silver fir (Cft)
1963
95.85833333
13.08333333
23.93333333
63.33333333
47.66666667
0.489692982
1.609868421
189779
35697
1964
102.425
12.44166667
23.19166667
64.08333333
47
0.489692982
1.609868421
179295
47212
1965
103.7666667
12.31666667
22.7
64.5
48.58333333
0.489692982
1.609868421
149709
56398
1966
121.5916667
12.50833333
23.44166667
63
47.66666667
0.489692982
1.609868421
157929
70476
1967
123.3833333
12.15
23.10833333
65
50.41666667
0.489692982
1.609868421
180610
47937
1968
105.7333333
12.2
22.99166667
66
48.83333333
0.489692982
1.609868421
208825
8537
1969
94.05
13.075
23.75833333
61
45
0.489692982
1.609868421
207907
18456
1970
96.56666667
13.3
24.025
62.16666667
43.58333333
0.489692982
1.609868421
190237
41527
1971
102.5166667
13.20833333
23.85833333
61.83333333
43.75
0.489692982
1.609868421
190191
39118
1972
107.7416667
11.71666667
22.55
66.33333333
45.5
0.489692982
1.609868421
174459
53809
1973
125.5
11.53333333
22.25833333
71.83333333
52.91666667
2.241666667
3.791666667
182191
45041
1974
96.69166667
10.81666667
22.45
68.08333333
46.66666667
2.258333333
4.166666667
181577
55669
1975
124.4
10.59166667
21.80833333
68.33333333
46.41666667
2.283333333
4.091666667
183270
44461
1976
131.6833333
10.425
21.86666667
70.83333333
49.75
1.991666667
2.775
199856
20508
1977
133.2166667
10.95833333
22.35833333
73.58333333
51.25
1.708333333
2.358333333
150883
79156
1978
134.5666667
10.80833333
22.3
71.5
54.16666667
1.625
2.233333333
161670
76123
1979
100.825
10.50833333
22.325
72.83333333
52.66666667
0.691666667
2.725
159791
77655
1980
111.3833333
10.65
22.61666667
72
53.33333333
0.483333333
2.05
148012
76888
1981
118.7666667
10.16666667
22.525
73.83333333
50.58333333
0.216666667
1.608333333
158100
74135
1982
118.5666667
9.991666667
21.475
75.83333333
53.91666667
0.175
1.425
168875
79361
1983
113.3416667
9.825
21.50833333
74.75
52.91666667
0.283333333
1.35
188121
66957
1984
115.2916667
10.325
22.53333333
70.25
48.08333333
0.191666667
1.233333333
146026
108981
1985
103.2666667
10.95
23.25833333
69.66666667
47.33333333
0.333333333
1.366666667
182683
72254
1986
133.5583333
10.05
21.80833333
75.16666667
52
0.3
1.158333333
182047
75044
1987
118.2416667
10.39166667
23.3
72.16666667
48.41666667
0.416666667
1.375
215631
40471
1988
107.8416667
11.31666667
23.59166667
67.91666667
46.75
0.341666667
2.05
226226
29029
1989
101.8583333
10.45
22.4
67.5
44.25
0.341666667
1.55
196879
58658
1990
141.9
11.525
22.91666667
73.08333333
52.33333333
0.325
1.058333333
205779
50288
1991
124.9583333
10
22.35
73.66666667
53.08333333
0.191666667
0.825
179081
76633
1992
146.6166667
9.941666667
22.05833333
74.58333333
55.66666667
0.125
1.025
163330
90865
1993
91.54166667
9.733333333
23.19166667
68.66666667
48.25
0.25
0.975
169879
89971
1994
133.3333333
9.058333333
22.1
77
57.16666667
0.141666667
0.775
202342
51273
1995
102.8666667
8.233333333
22.23333333
75.91666667
57
0.258333333
1.025
217604
48021
1996
117.425
10.575
22.53333333
72.91666667
51.5
0.208333333
0.858333333
205930
50447
1997
130.2916667
10.41666667
21.50833333
76.41666667
56.66666667
0.041666667
0.558333333
198549
59707
1998
106.7833333
11.2
23.66666667
71.08333333
51.08333333
0.008333333
0.608333333
177930
75031
1999
92
11.78333333
23.96666667
71.08333333
49
0.041666667
0.616666667
193511
70078
2000
95.18333333
10.84166667
24.10833333
73.91666667
48.16666667
0.058333333
1.183333333
189073
95949
2001
78.33333333
10.19166667
24.65833333
72.58333333
45.16666667
0.175
1
207833
77931
2002
86.46666667
11.14166667
24.44166667
73.25
45.25
0.133333333
2.3
8721
2687
2003
126.1166667
10.76666667
23.36666667
78
50.33333333
0.133333333
1.6
7956
3267
2004
97.60833333
11.24166667
24.33333333
76.16666667
48.5
0.125
1.583333333
7766
4335
2005
97.05
10.18333333
22.85
78.16666667
50.41666667
0.05
1.516666667
8433
1951
2006
112.225
11.15833333
23.575
79.75
51.75
0.083333333
1.425
8478
1747
2007
99.50833333
10.525
24.06666667
76.41666667
50
0.108333333
1.416666667
8522
3028
2008
117.3083333
10.5
23.60833333
79.58333333
51.83333333
0.091666667
1.35
7937
3844
2009
85.525
10.025
24.125
76.75
47.83333333
0.108333333
1.25
7973
2547
2010
97.86666667
10.25
24.78333333
78.66666667
49.91666667
0.066666667
0.916666667
8130
4127
2011
50.59
992
23.99
69.75431034
49.07758621
0.489692982
1.609868421
8187
3824
2012
3.320404153
9.592259918
23.21532783
69.75431034
49.07758621
0.489692982
1.609868421
8346
3560
2013
4.191148233
10.21493367
23.78962856
69.75431034
49.07758621
0.489692982
1.609868421
8355
2376
2014
3.630638121
10.01655082
23.28994006
69.75431034
49.07758621
0.489692982
1.609868421
8597
2068
2015
4.247571994
10.10961742
23.32796683
69.75431034
49.07758621
0.489692982
1.609868421
8087
3476
2016
3.066825794
10.96794124
25.1757221
69.75431034
49.07758621
0.489692982
1.609868421
8440
3002
Table 2A
Data t-1.
95.8583
13.0833
23.9333
63.33333333
47.66666667
0.489692982
1.609868421
179295
102.425
12.4417
23.1917
64.08333333
47
0.489692982
1.609868421
149709
103.767
12.3167
22.7
64.5
48.58333333
0.489692982
1.609868421
157929
121.592
12.5083
23.4417
63
47.66666667
0.489692982
1.609868421
180610
123.383
12.15
23.1083
65
50.41666667
0.489692982
1.609868421
208825
105.733
12.2
22.9917
66
48.83333333
0.489692982
1.609868421
207907
94.05
13.075
23.7583
61
45
0.489692982
1.609868421
190237
96.5667
13.3
24.025
62.16666667
43.58333333
0.489692982
1.609868421
190191
102.517
13.2083
23.8583
61.83333333
43.75
0.489692982
1.609868421
174459
107.742
11.7167
22.55
66.33333333
45.5
0.489692982
1.609868421
182191
125.5
11.5333
22.2583
71.83333333
52.91666667
2.241666667
3.791666667
181577
96.6917
10.8167
22.45
68.08333333
46.66666667
2.258333333
4.166666667
183270
124.4
10.5917
21.8083
68.33333333
46.41666667
2.283333333
4.091666667
199856
131.683
10.425
21.8667
70.83333333
49.75
1.991666667
2.775
150883
133.217
10.9583
22.3583
73.58333333
51.25
1.708333333
2.358333333
161670
134.567
10.8083
22.3
71.5
54.16666667
1.625
2.233333333
159791
100.825
10.5083
22.325
72.83333333
52.66666667
0.691666667
2.725
148012
111.383
10.65
22.6167
72
53.33333333
0.483333333
2.05
158100
118.767
10.1667
22.525
73.83333333
50.58333333
0.216666667
1.608333333
168875
118.567
9.99167
21.475
75.83333333
53.91666667
0.175
1.425
188121
113.342
9.825
21.5083
74.75
52.91666667
0.283333333
1.35
146026
115.292
10.325
22.5333
70.25
48.08333333
0.191666667
1.233333333
182683
103.267
10.95
23.2583
69.66666667
47.33333333
0.333333333
1.366666667
182047
133.558
10.05
21.8083
75.16666667
52
0.3
1.158333333
215631
118.242
10.3917
23.3
72.16666667
48.41666667
0.416666667
1.375
226226
107.842
11.3167
23.5917
67.91666667
46.75
0.341666667
2.05
196879
101.858
10.45
22.4
67.5
44.25
0.341666667
1.55
205779
141.9
11.525
22.9167
73.08333333
52.33333333
0.325
1.058333333
179081
124.958
10
22.35
73.66666667
53.08333333
0.191666667
0.825
163330
146.617
9.94167
22.0583
74.58333333
55.66666667
0.125
1.025
169879
91.5417
9.73333
23.1917
68.66666667
48.25
0.25
0.975
202342
133.333
9.05833
22.1
77
57.16666667
0.141666667
0.775
217604
102.867
8.23333
22.2333
75.91666667
57
0.258333333
1.025
205930
117.425
10.575
22.5333
72.91666667
51.5
0.208333333
0.858333333
198549
130.292
10.4167
21.5083
76.41666667
56.66666667
0.041666667
0.558333333
177930
106.783
11.2
23.6667
71.08333333
51.08333333
0.008333333
0.608333333
193511
92
11.7833
23.9667
71.08333333
49
0.041666667
0.616666667
189073
95.1833
10.8417
24.1083
73.91666667
48.16666667
0.058333333
1.183333333
207833
78.3333
10.1917
24.6583
72.58333333
45.16666667
0.175
1
8721
86.4667
11.1417
24.4417
73.25
45.25
0.133333333
2.3
7956
126.117
10.7667
23.3667
78
50.33333333
0.133333333
1.6
7766
97.6083
11.2417
24.3333
76.16666667
48.5
0.125
1.583333333
8433
97.05
10.1833
22.85
78.16666667
50.41666667
0.05
1.516666667
8478
112.225
11.1583
23.575
79.75
51.75
0.083333333
1.425
8522
99.5083
10.525
24.0667
76.41666667
50
0.108333333
1.416666667
7937
117.308
10.5
23.6083
79.58333333
51.83333333
0.091666667
1.35
7973
85.525
10.025
24.125
76.75
47.83333333
0.108333333
1.25
8130
97.8667
10.25
24.7833
78.66666667
49.91666667
0.066666667
0.916666667
8187
50.59
992
23.99
69.75431034
49.07758621
0.489692982
1.609868421
8346
3.3204
9.59226
23.2153
69.75431034
49.07758621
0.489692982
1.609868421
8355
4.19115
10.2149
23.7896
69.75431034
49.07758621
0.489692982
1.609868421
8597
3.63064
10.0166
23.2899
69.75431034
49.07758621
0.489692982
1.609868421
8087
4.24757
10.1096
23.328
69.75431034
49.07758621
0.489692982
1.609868421
8440
Table 3A
Normal Data t-1.
0.64578
0.00493
0.74307
0.12444
0.30061
0.21159
0.29142
0.78517
0.69161
0.00428
0.51889
0.16444
0.25153
0.21159
0.29142
0.64974
0.70097
0.00415
0.37028
0.18667
0.3681
0.21159
0.29142
0.68737
0.82536
0.00435
0.59446
0.10667
0.30061
0.21159
0.29142
0.79119
0.83787
0.00398
0.4937
0.21333
0.50307
0.21159
0.29142
0.92035
0.71469
0.00403
0.45844
0.26667
0.3865
0.21159
0.29142
0.91614
0.63316
0.00492
0.69018
0
0.10429
0.21159
0.29142
0.83526
0.65072
0.00515
0.77078
0.06222
0
0.21159
0.29142
0.83505
0.69225
0.00506
0.7204
0.04444
0.01227
0.21159
0.29142
0.76304
0.72871
0.00354
0.32494
0.28444
0.1411
0.21159
0.29142
0.79843
0.85264
0.00335
0.23678
0.57778
0.68712
0.98168
0.89607
0.79562
0.6516
0.00263
0.29471
0.37778
0.22699
0.98901
1
0.80337
0.84496
0.0024
0.10076
0.39111
0.20859
1
0.97921
0.87929
0.89579
0.00223
0.11839
0.52444
0.45399
0.87179
0.61432
0.65512
0.90649
0.00277
0.267
0.67111
0.56442
0.74725
0.49885
0.7045
0.91591
0.00262
0.24937
0.56
0.77914
0.71062
0.4642
0.69589
0.68044
0.00231
0.25693
0.63111
0.66871
0.30037
0.60046
0.64198
0.75412
0.00246
0.34509
0.58667
0.71779
0.20879
0.41339
0.68815
0.80565
0.00197
0.31738
0.68444
0.51534
0.09158
0.29099
0.73748
0.80425
0.00179
0
0.79111
0.76074
0.07326
0.24018
0.82557
0.76779
0.00162
0.01008
0.73333
0.68712
0.12088
0.2194
0.63288
0.7814
0.00213
0.3199
0.49333
0.33129
0.08059
0.18707
0.80068
0.69748
0.00276
0.53904
0.46222
0.27607
0.14286
0.22402
0.79777
0.90887
0.00185
0.10076
0.75556
0.61963
0.12821
0.16628
0.9515
0.80198
0.00219
0.55164
0.59556
0.35583
0.17949
0.22633
1
0.72941
0.00313
0.6398
0.36889
0.23313
0.14652
0.41339
0.86566
0.68765
0.00225
0.2796
0.34667
0.04908
0.14652
0.27483
0.9064
0.96708
0.00335
0.43577
0.64444
0.64417
0.13919
0.13857
0.78419
0.84886
0.0018
0.26448
0.67556
0.69939
0.08059
0.0739
0.71209
1
0.00174
0.17632
0.72444
0.88957
0.05128
0.12933
0.74207
0.61566
0.00152
0.51889
0.40889
0.34356
0.10623
0.11547
0.89067
0.9073
0.00084
0.18892
0.85333
1
0.05861
0.06005
0.96053
0.69469
0
0.22922
0.79556
0.98773
0.10989
0.12933
0.9071
0.79628
0.00238
0.3199
0.63556
0.58282
0.08791
0.08314
0.87331
0.88608
0.00222
0.01008
0.82222
0.96319
0.01465
0
0.77893
0.72202
0.00302
0.66247
0.53778
0.55215
0
0.01386
0.85025
0.61885
0.00361
0.75315
0.53778
0.39877
0.01465
0.01617
0.82993
0.64107
0.00265
0.79597
0.68889
0.33742
0.02198
0.17321
0.91581
0.52348
0.00199
0.96222
0.61778
0.11656
0.07326
0.1224
0.00437
0.58024
0.00296
0.89673
0.65333
0.1227
0.05495
0.48268
0.00087
0.85694
0.00258
0.57179
0.90667
0.49693
0.05495
0.28868
0
0.65799
0.00306
0.86398
0.80889
0.36196
0.05128
0.28406
0.00305
0.6541
0.00198
0.41562
0.91556
0.50307
0.01832
0.26559
0.00326
0.76
0.00297
0.63476
1
0.60123
0.03297
0.24018
0.00346
0.67125
0.00233
0.78338
0.82222
0.47239
0.04396
0.23788
0.00078
0.79547
0.0023
0.64484
0.99111
0.60736
0.03663
0.2194
0.00095
0.57367
0.00182
0.80101
0.84
0.31288
0.04396
0.19169
0.00167
0.6598
0.00205
1
0.94222
0.46626
0.02564
0.09931
0.00193
0.32987
1
0.7602
0.4669
0.40448
0.21159
0.29142
0.00265
0
0.00138
0.52604
0.4669
0.40448
0.21159
0.29142
0.0027
0.00608
0.00201
0.69964
0.4669
0.40448
0.21159
0.29142
0.0038
0.00216
0.00181
0.5486
0.4669
0.40448
0.21159
0.29142
0.00147
0.00647
0.00191
0.56009
0.4669
0.40448
0.21159
0.29142
0.00309
. RF model was compared with KRR model in the current study, the RF model showed better results based on higher values of RMSE, MAE and R. Due to the better performance of RF model it can be applied on other forest types of Pakistan to predict and manage forest yield as this department has been neglected so far.
In the present study yield of only two species were predicted, we can use the proposed model for the prediction of multiple forest species. Data regarding soil condition can be added to predict the forest yield as it influences the productivity of forest. Further data about uncontrolled grazing can be added in the follow-up work which is an important variable for yield prediction as it is an issue for sustainable forest management. Other variables such as solar radiation, light intensity, drought and geology of the site which directly affect the forest yield can also be coupled with meteorological data in the follow-up work to achieve better results regarding forest yield prediction. RF model and KRR model have not been used in forest yield prediction globally so far but some other models were used such as artificial neural network (ANN) and regression-based models were used by (Ashraf et al., 2013ASHRAF, M.I., ZHAO, Z., BOURQUE, C.P.A., MACLEAN, D.A. and MENG, F.R., 2013. Integrating biophysical controls in forest growth and yield predictions with artificial intelligence technology. Canadian Journal of Forest Research, vol. 43, no. 12, pp. 1162-1171. http://dx.doi.org/10.1139/cjfr-2013-0090.
http://dx.doi.org/10.1139/cjfr-2013-0090...
) for the development of volume increment model and individual tree based basal area (BA) (Ashraf et al., 2012ASHRAF, M.I., BOURQUE, C.P.A., MACLEAN, D.A., ERDLE, T. and MENG, F.R., 2012. Using JABOWA-3 for forest growth and yield predictions under diverse forest conditions of Nova Scotia, Canada. Forestry Chronicle, vol. 88, no. 6, pp. 708-721. http://dx.doi.org/10.5558/tfc2012-137.
http://dx.doi.org/10.5558/tfc2012-137...
), developed an individual-tree-based model (JABOWA-3) for the prediction of forest growth and yield.
In terms of model optimization for forest yield prediction, we can achieve better prediction by hybridizing different models rather than using single models. Therefore, the proposed model could be optimized with ensemble method (Ali et al., 2018ALI, M., DEO, R.C., DOWNS, N.J. and MARASENI, T., 2018. Cotton yield prediction with Markov Chain Monte Carlo-based simulation model integrated with genetic programing algorithm: A new hybrid copula-driven approach. Agricultural and Forest Meteorology, vol. 263, pp. 428-448. http://dx.doi.org/10.1016/j.agrformet.2018.09.002.
http://dx.doi.org/10.1016/j.agrformet.20...
; Lei and Wan, 2012LEI, K.S. and WAN, F., 2012. Applying ensemble learning techniques to ANFIS for air pollution index prediction in Macau. In: International Symposium on Neural Networks, 2012, Shenyang, China. Berlin: Springer, pp. 509-516. http://dx.doi.org/10.1007/978-3-642-31346-2_57.
http://dx.doi.org/10.1007/978-3-642-3134...
; Yun et al., 2008YUN, Z., QUAN, Z., CAIXIN, S., SHAOLAN, L., YUMING, L. and YANG, S., 2008. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 853-858. http://dx.doi.org/10.1109/TPWRS.2008.922249.
http://dx.doi.org/10.1109/TPWRS.2008.922...
) to attain more precise results. Another optimization method like the ANFIS algorithms can be used for forest yield prediction which is more precise and powerful (Yaseen et al., 2018YASEEN, Z.M., GHAREB, M.I., EBTEHAJ, I., BONAKDARI, H., SIDDIQUE, R., HEDDAM, S., YUSIF, A.A. and DEO, R., 2018. Rainfall pattern forecasting using novel hybrid intelligent model based ANFIS-FFA. Water Resources Management, vol. 32, no. 1, pp. 105-122. http://dx.doi.org/10.1007/s11269-017-1797-0.
http://dx.doi.org/10.1007/s11269-017-179...
). Moreover, some other more advanced models such as Optimization of Particle Swarm (Chen et al., 2005CHEN, G.C., YU, J.S. and GUO, W., 2005. Two sub-swarms substituting particle swarm optimization algorithm and its application. Huadong Ligong Daxue Xuebao (Ziran Kexue Ban). Journal of East China University of Science and Technology, vol. 31, no. 6, pp. 787-791.; Zhisheng, 2010ZHISHENG, Z., 2010. Quantum-behaved particle swarm optimization algorithm for economic load dispatch of power system. Expert Systems with Applications, vol. 37, no. 2, pp. 1800-1803. http://dx.doi.org/10.1016/j.eswa.2009.07.042.
http://dx.doi.org/10.1016/j.eswa.2009.07...
), Ensemble methods (Dietterich, 2002DIETTERICH, T.G., 2002. Ensemble learning. In: M.A. ARBIB, ed. The handbook of brain theory and neural networks. Cambridge: MIT Press.), chaos theory, Genetic algorithms (Davis, 1991DAVIS, L., 1991. Handbook of genetic algorithms. New York: Van Nostrand Reinhold.) and Firefly algorithms (Yang, 2010YANG, X.S., 2010. Nature-inspired metaheuristic algorithms. Frome: Luniver Press.) can be coupled with recently explored copulas (Nguyen-Huy et al., 2018NGUYEN-HUY, T., DEO, R.C., MUSHTAQ, S., AN-VO, D.A. and KHAN, S., 2018. Modeling the joint influence of multiple synoptic-scale, climate mode indices on Australian wheat yield using a vine copula-based approach. European Journal of Agronomy, vol. 98, pp. 65-81. http://dx.doi.org/10.1016/j.eja.2018.05.006.
http://dx.doi.org/10.1016/j.eja.2018.05....
; Nelsen, 2003NELSEN, R.B., 2003. Properties and applications of copulas: a brief survey. In: Proceedings of the First Brazilian Conference on Statistical Modeling in Insurance and Finance, 2003, Maresias. São Paulo: University Press USP, pp. 10-28.) which possibly will produce decent results because of their optimization capability. Least square support vector machine (Yuan et al., 2017YUAN, X., TAN, Q., LEI, X., YUAN, Y. and WU, X., 2017. Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy, vol. 129, pp. 122-137. http://dx.doi.org/10.1016/j.energy.2017.04.094.
http://dx.doi.org/10.1016/j.energy.2017....
) based copula (LSSVM-copula) and autoregressive fractionally integrated moving average-based copula (ARFIMA-copula) models can be utilized for the prediction of forest yield. Yield of different forest types in Pakistan can also be predicted by Extreme learning machine developed by Huang et al. (2006)HUANG, G.B., ZHU, Q.Y. and SIEW, C.K., 2006. Extreme learning machine: theory and applications. Neurocomputing, vol. 70, no. 1-3, pp. 489-501. http://dx.doi.org/10.1016/j.neucom.2005.12.126.
http://dx.doi.org/10.1016/j.neucom.2005....
and Support vector machine studied by (Cortes and Vapnik, 1995CORTES, C. and VAPNIK, V., 1995. Support-vector networks. Machine Learning, vol. 20, no. 3, pp. 273-297. http://dx.doi.org/10.1007/BF00994018.
http://dx.doi.org/10.1007/BF00994018...
). While the obstacle of model uncertainty is avoided by the standard statistical approaches which causes over-fitting and makes the decisions riskier, Bayesian model averaging (BMA) techniques (Raftery et al., 2005RAFTERY, A.E., GNEITING, T., BALABDAOUI, F. and POLAKOWSKI, M., 2005. Using Bayesian model averaging to calibrate forecast ensembles. Monthly Weather Review, vol. 133, no. 5, pp. 1155-1174. http://dx.doi.org/10.1175/MWR2906.1.
http://dx.doi.org/10.1175/MWR2906.1...
) can model uncertainty for more precise predictions. Hence, BMA techniques can be utilized to model uncertainty in forest yield that is resulted from different factors like extreme weather conditions, missing climate data and the more likely climate change influence. To enhance the scope of this study multi-resolution tools like frequency resolution could be utilized. Similarly, maximum overlap discrete wavelet transformation (Prasad et al., 2017PRASAD, R., DEO, R.C., LI, Y. and MARASENI, T., 2017. Input selection and performance optimization of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmospheric Research, vol. 197, pp. 42-63. http://dx.doi.org/10.1016/j.atmosres.2017.06.014.
http://dx.doi.org/10.1016/j.atmosres.201...
; Khalighi et al., 2011KHALIGHI, S., SOUSA, T., OLIVEIRA, D., PIRES, G. and NUNES, U. 2011, August. Efficient feature selection for sleep staging based on maximal overlap discrete wavelet transform and SVM. In: 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2011, Boston, MA. New York: IEEE, pp. 3306-3309. http://dx.doi.org/10.1109/IEMBS.2011.6090897.
http://dx.doi.org/10.1109/IEMBS.2011.609...
), empirical mode decomposition EMD (Rilling et al., 2003RILLING, G., FLANDRIN, P. and GONÇALVES, P., 2003. On empirical mode decomposition and its algorithms. In: Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing (NSIP), 2003, Grado, Italy. Piscataway: IEEE Circuits and Systems Society, vol. 3, no. 3, pp. 8-11.; Al-Musaylh et al., 2018AL-MUSAYLH, M.S., DEO, R.C., LI, Y. and ADAMOWSKI, J.F., 2018. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Applied Energy, vol. 217, pp. 422-439. http://dx.doi.org/10.1016/j.apenergy.2018.02.140.
http://dx.doi.org/10.1016/j.apenergy.201...
), and singular value decomposition (De Lathauwer et al., 1994DE LATHAUWER, L., DE MOOR, B. and VANDEWALLE, J., 1994. Blind source separation by higher-order singular value decomposition. In Proceedings of EUSIPCO-94 VIIth European Signal Processing Conference. EUSIPCO, 1994, Edinburgh, Scotland. Leuven: Katholieke Universiteit Leuven, vol. 1, pp. 175-178.), are superior models and can be utilized for the prediction of forest yield. Feature selection techniques (Salcedo-Sanz et al., 2018SALCEDO-SANZ, S., DEO, R.C., CORNEJO-BUENO, L., CAMACHO-GÓMEZ, C. and GHIMIRE, S., 2018. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Applied Energy, vol. 209, pp. 79-94. http://dx.doi.org/10.1016/j.apenergy.2017.10.076.
http://dx.doi.org/10.1016/j.apenergy.201...
; Guyon and Elisseeff, 2003GUYON, I. and ELISSEEFF, A., 2003. An introduction to variable and feature selection. Journal of Machine Learning Research, vol. 3, no. Mar, pp. 1157-1182.) is another way of model optimization for the simulation of forest yield with more precision and accuracy.
6. Conclusions and Recommendations
This study aimed to develop data driven models for the prediction of forest yield under climate change in the Gallies forests, Pakistan. In the present work RF and KRR models were developed using yield data of two species (Blue pine and Silver fir) as an objective variable and climate data (temperature, humidity, rainfall and wind speed) as predictive variables. Both models were compared based on their prediction accuracy, and it was found that the RF model outperformed the KRR model. The performance of RF model in comparison with KRR model was evaluated for blue pine and silver fir species by using the most advanced normalized metrics of Willmott’s index (WI), Nash-Sutcliffe (NSE), Legates-McCabe’s (LM) agreement, relative root mean square error (RRMSE) and coefficient of determination (r). Current results revealed that for blue pine and silver fir the proposed RF model attained the maximum values of WI = 0.854 and 0.845, NSE = 0.866 and 0.864 and LM = 0.693 and 0.704 respectively followed by KRR model having values of WI = 0.713 and 0.682, NSE = 0.646 and 0.602, and LM = 0.529 and 0.521 respectively. Moreover, RF model yielded relative percentage error of 50.3% for blue pine and 52.0% for silver fir while KRR yielded 81.7% for blue pine and 88.9% for silver fir. Whereas, RF model yielded the coefficient of determination (r) values of 0.964 for blue pine and 0.957 for silver fir in comparison with the KRR model having values of 0.80 for blue pine and 0.799 for silver fir in the Gallies forest division. This was the ever first study on forest yield prediction under climate change scenarios in Pakistan and it will contribute to the climate change adaptation activities based on sustainable forest management in Pakistan. This study will provide insight for future management and mitigation of climate change to save or protect the perilous effects of climate change on our forest yield and overall health and vigor. The proposed model can be applied to other forest types in other region of Pakistan as it can help forest department and forest managers in the management of forest and to address chronic effects of changing climate in a better way. Thus, it is highly recommended that RF model can be utilized for the prediction of forest yield in the future.
Appendix A Environmental and forest yield variables Information’s for Gallies Forest Division, Pakistan.
References
- AGHIMIEN, E.V., OSHO, J.S.A., HAUSER, S., DENI, B. and ADE-ONI, V.D., 2016. Growth and yield models for uneven-aged secondary forest in IITA, Ibadan, Nigeria. Forest Research, vol. 5, no. 173, pp. 2.
- AINSWORTH, E.A. and LONG, S.P., 2005. What have we learned from 15 years of free‐air CO2 enrichment (FACE)? A meta‐analytic review of the responses of photosynthesis, canopy properties and plant production to rising CO2 The New Phytologist, vol. 165, no. 2, pp. 351-371. http://dx.doi.org/10.1111/j.1469-8137.2004.01224.x PMid:15720649.
» http://dx.doi.org/10.1111/j.1469-8137.2004.01224.x - ALI, J. and BENJAMINSEN, T.A., 2004. Fuelwood, timber and deforestation in the Himalayas. Mountain Research and Development, vol. 24, no. 4, pp. 312-318. http://dx.doi.org/10.1659/0276-4741(2004)024[0312:FTADIT]2.0.CO;2
» http://dx.doi.org/10.1659/0276-4741(2004)024[0312:FTADIT]2.0.CO;2 - ALI, M., 2018 [viewed 9 June 2021]. Billions Trees Afforestation Project (BTAP) Restores 600,000ha Forests, Enhances KP's Forests Area By 6.3pc: PD UrduPoint Network.Available from: https://www.urdupoint.com/en/pakistan/billions-trees-afforestation-project-btap-re-452211.html
» https://www.urdupoint.com/en/pakistan/billions-trees-afforestation-project-btap-re-452211.html - ALI, M., DEO, R.C., DOWNS, N.J. and MARASENI, T., 2018. Cotton yield prediction with Markov Chain Monte Carlo-based simulation model integrated with genetic programing algorithm: A new hybrid copula-driven approach. Agricultural and Forest Meteorology, vol. 263, pp. 428-448. http://dx.doi.org/10.1016/j.agrformet.2018.09.002
» http://dx.doi.org/10.1016/j.agrformet.2018.09.002 - AL-MUSAYLH, M.S., DEO, R.C., LI, Y. and ADAMOWSKI, J.F., 2018. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Applied Energy, vol. 217, pp. 422-439. http://dx.doi.org/10.1016/j.apenergy.2018.02.140
» http://dx.doi.org/10.1016/j.apenergy.2018.02.140 - ASHRAF, M.I., BOURQUE, C.P.A., MACLEAN, D.A., ERDLE, T. and MENG, F.R., 2012. Using JABOWA-3 for forest growth and yield predictions under diverse forest conditions of Nova Scotia, Canada. Forestry Chronicle, vol. 88, no. 6, pp. 708-721. http://dx.doi.org/10.5558/tfc2012-137
» http://dx.doi.org/10.5558/tfc2012-137 - ASHRAF, M.I., MENG, F.R., BOURQUE, C.P.A. and MACLEAN, D.A., 2015. A novel modelling approach for predicting forest growth and yield under climate change. PLoS One, vol. 10, no. 7, pp. e0132066. http://dx.doi.org/10.1371/journal.pone.0132066 PMid:26173081.
» http://dx.doi.org/10.1371/journal.pone.0132066 - ASHRAF, M.I., ZHAO, Z., BOURQUE, C.P.A., MACLEAN, D.A. and MENG, F.R., 2013. Integrating biophysical controls in forest growth and yield predictions with artificial intelligence technology. Canadian Journal of Forest Research, vol. 43, no. 12, pp. 1162-1171. http://dx.doi.org/10.1139/cjfr-2013-0090
» http://dx.doi.org/10.1139/cjfr-2013-0090 - AVRON, H., CLARKSON, K.L. and WOODRUFF, D.P., 2017. Faster kernel ridge regression using sketching and preconditioning. SIAM Journal on Matrix Analysis and Applications, vol. 38, no. 4, pp. 1116-1138. http://dx.doi.org/10.1137/16M1105396
» http://dx.doi.org/10.1137/16M1105396 - BACKLUND, P., JANETOS, A. and SCHIMEL, D., 2008. The effects of climate change on agriculture, land resources, water resources, and biodiversity in the United States. In: U.S. ENVIRONMENTAL PROTECTION AGENCY, ed. Synthesis and assessment product 4.3. Washington: Climate Change Science Program, 240 p.
- BREIMAN, L., 2001. Random forests. Machine Learning, vol. 45, no. 1, pp. 5-32. http://dx.doi.org/10.1023/A:1010933404324
» http://dx.doi.org/10.1023/A:1010933404324 - BYLANDER, T., 2002. Estimating generalization error on two-class datasets using out-of-bag estimates. Machine Learning, vol. 48, no. 1-3, pp. 287-297. http://dx.doi.org/10.1023/A:1013964023376
» http://dx.doi.org/10.1023/A:1013964023376 - CARUANA, R., KARAMPATZIAKIS, N. and YESSENALINA, A., 2008. An empirical evaluation of supervised learning in high dimensions. In: Proceedings of the 25th international conference on Machine learning, 2008, New York, NY. New York: ACM Press, pp. 96-103. http://dx.doi.org/10.1145/1390156.1390169
» http://dx.doi.org/10.1145/1390156.1390169 - CHEN, G.C., YU, J.S. and GUO, W., 2005. Two sub-swarms substituting particle swarm optimization algorithm and its application. Huadong Ligong Daxue Xuebao (Ziran Kexue Ban). Journal of East China University of Science and Technology, vol. 31, no. 6, pp. 787-791.
- CHU, C., NI, Y., TAN, G., SAUNDERS, C.J. and ASHBURNER, J., 2011. Kernel regression for fMRI pattern prediction. NeuroImage, vol. 56, no. 2, pp. 662-673. http://dx.doi.org/10.1016/j.neuroimage.2010.03.058 PMid:20348000.
» http://dx.doi.org/10.1016/j.neuroimage.2010.03.058 - CIAIS, P., REICHSTEIN, M., VIOVY, N., GRANIER, A., OGÉE, J., ALLARD, V., AUBINET, M., BUCHMANN, N., BERNHOFER, C., CARRARA, A., CHEVALLIER, F., DE NOBLET, N., FRIEND, A.D., FRIEDLINGSTEIN, P., GRÜNWALD, T., HEINESCH, B., KERONEN, P., KNOHL, A., KRINNER, G., LOUSTAU, D., MANCA, G., MATTEUCCI, G., MIGLIETTA, F., OURCIVAL, J.M., PAPALE, D., PILEGAARD, K., RAMBAL, S., SEUFERT, G., SOUSSANA, J.F., SANZ, M.J., SCHULZE, E.D., VESALA, T. and VALENTINI, R., 2005. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature, vol. 437, no. 7058, pp. 529-533. http://dx.doi.org/10.1038/nature03972 PMid:16177786.
» http://dx.doi.org/10.1038/nature03972 - CORTES, C. and VAPNIK, V., 1995. Support-vector networks. Machine Learning, vol. 20, no. 3, pp. 273-297. http://dx.doi.org/10.1007/BF00994018
» http://dx.doi.org/10.1007/BF00994018 - DAVIS, L., 1991. Handbook of genetic algorithms. New York: Van Nostrand Reinhold.
- DAWSON, C.W., ABRAHART, R.J. and SEE, L.M., 2007. HydroTest: a web-based toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environmental Modelling & Software, vol. 22, no. 7, pp. 1034-1052. http://dx.doi.org/10.1016/j.envsoft.2006.06.008
» http://dx.doi.org/10.1016/j.envsoft.2006.06.008 - DE LATHAUWER, L., DE MOOR, B. and VANDEWALLE, J., 1994. Blind source separation by higher-order singular value decomposition. In Proceedings of EUSIPCO-94 VIIth European Signal Processing Conference. EUSIPCO, 1994, Edinburgh, Scotland. Leuven: Katholieke Universiteit Leuven, vol. 1, pp. 175-178.
- DEO, R.C. and ŞAHIN, M., 2017. Forecasting long-term global solar radiation with an ANN algorithm coupled with satellite-derived (MODIS) land surface temperature (LST) for regional locations in Queensland. Renewable & Sustainable Energy Reviews, vol. 72, pp. 828-848. http://dx.doi.org/10.1016/j.rser.2017.01.114
» http://dx.doi.org/10.1016/j.rser.2017.01.114 - DIETTERICH, T.G., 2002. Ensemble learning. In: M.A. ARBIB, ed. The handbook of brain theory and neural networks. Cambridge: MIT Press.
- DONGES, N., 2018. The random forest algorithm Toronto: Towards Data Science.
- ECKSTEIN, D., HUTFILS, M.L. and WINGES, M., 2019. Global climate risk index 2019: who suffers most from extreme weather events? Weather-related Loss Events in 2017 and 1998 to 2017. Berlin: Germanwatch e.V.
- ERTEKIN, C. and YALDIZ, O., 2000. Comparison of some existing models for estimating global solar radiation for Antalya (Turkey). Energy Conversion and Management, vol. 41, no. 4, pp. 311-330. http://dx.doi.org/10.1016/S0196-8904(99)00127-2
» http://dx.doi.org/10.1016/S0196-8904(99)00127-2 - FISCHLIN, A., AYRES, M., KARNOSKY, D., KELLOMÄKI, S., LOUMAN, B., ONG, C., PLATTNER, G.K., SANTOSO, H., THOMPSON, I., BOOTH, T.H. and MARCAR, N., 2009. Future environmental impacts and vulnerabilities. IUFRO World Series, vol. 22, pp. 53-100.
- GIBBS, H.K., BROWN, S., NILES, J.O. and FOLEY, J.A., 2007. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environmental Research Letters, vol. 2, no. 4, pp. 045023. http://dx.doi.org/10.1088/1748-9326/2/4/045023
» http://dx.doi.org/10.1088/1748-9326/2/4/045023 - GUYON, I. and ELISSEEFF, A., 2003. An introduction to variable and feature selection. Journal of Machine Learning Research, vol. 3, no. Mar, pp. 1157-1182.
- HSU, A.L., MURPHY, C.T. and KENYON, C., 2003. Regulation of aging and age-related disease by DAF-16 and heat-shock factor. Science, vol. 300, no. 5622, pp. 1142-1145. http://dx.doi.org/10.1126/science.1083701 PMid:12750521.
» http://dx.doi.org/10.1126/science.1083701 - HUANG, G.B., ZHU, Q.Y. and SIEW, C.K., 2006. Extreme learning machine: theory and applications. Neurocomputing, vol. 70, no. 1-3, pp. 489-501. http://dx.doi.org/10.1016/j.neucom.2005.12.126
» http://dx.doi.org/10.1016/j.neucom.2005.12.126 - HUSSAIN, M., NASEEM MALIK, R. and TAYLOR, A., 2017. Carbon footprint as an environmental sustainability indicator for the particleboard produced in Pakistan. Environmental Research, vol. 155, pp. 385-393. http://dx.doi.org/10.1016/j.envres.2017.02.024 PMid:28288441.
» http://dx.doi.org/10.1016/j.envres.2017.02.024 - HUSSAIN, M., MALIK, R.N. and TAYLOR, A., 2018. Environmental profile analysis of particleboard production: a study in a Pakistani technological condition. The International Journal of Life Cycle Assessment, vol. 23, no. 8, pp. 1542-1561. http://dx.doi.org/10.1007/s11367-017-1385-9
» http://dx.doi.org/10.1007/s11367-017-1385-9 - HUSSAIN, M., ZAIDI, S.M.H., MALIK, R.N. and SHARMA, B.D., 2014. Greenhouse gas emissions from production chain of a cigarette manufacturing industry in Pakistan. Environmental Research, vol. 134, pp. 81-90. http://dx.doi.org/10.1016/j.envres.2014.06.015
» http://dx.doi.org/10.1016/j.envres.2014.06.015 - HYVÖNEN, R., ÅGREN, G.I., LINDER, S., PERSSON, T., COTRUFO, M.F., EKBLAD, A., FREEMAN, M., GRELLE, A., JANSSENS, I.A., JARVIS, P.G., KELLOMÄKI, S., LINDROTH, A., LOUSTAU, D., LUNDMARK, T., NORBY, R.J., OREN, R., PILEGAARD, K., RYAN, M.G., SIGURDSSON, B.D., STRÖMGREN, M., VAN OIJEN, M. and WALLIN, G., 2007. The likely impact of elevated [CO2], nitrogen deposition, increased temperature and management on carbon sequestration in temperate and boreal forest ecosystems: a literature review. The New Phytologist, vol. 173, no. 3, pp. 463-480. PMid:17244042.
- JIANG, P., WU, H., WANG, W., MA, W., SUN, X. and LU, Z., 2007. MiPred: classification of real and pseudo microRNA precursors using random forest prediction model with combined features. Nucleic Acids Research, vol. 35, no. Web Server, suppl. 2, pp. W339-W344. http://dx.doi.org/10.1093/nar/gkm368
» http://dx.doi.org/10.1093/nar/gkm368 - JOHNSEN, K., SAMUELSON, L., TESKEY, R., MCNULTY, S. and FOX, T., 2001. Process models as tools in forestry research and management. Forest Science, vol. 47, no. 1, pp. 2-8.
- KARL, T.R., MELILLO, J.M., PETERSON, T.C. and HASSOL, S.J., eds., 2009. Global climate change impacts in the United States Cambridge: Cambridge University Press.
- KAYANI, S., AHMAD, M., ZAFAR, M., SULTANA, S., KHAN, M.P.Z., ASHRAF, M.A., HUSSAIN, J. and YASEEN, G., 2014. Ethnobotanical uses of medicinal plants for respiratory disorders among the inhabitants of Gallies-Abbottabad, Northern Pakistan. Journal of Ethnopharmacology, vol. 156, pp. 47-60. http://dx.doi.org/10.1016/j.jep.2014.08.005 PMid:25153021.
» http://dx.doi.org/10.1016/j.jep.2014.08.005 - KHALIGHI, S., SOUSA, T., OLIVEIRA, D., PIRES, G. and NUNES, U. 2011, August. Efficient feature selection for sleep staging based on maximal overlap discrete wavelet transform and SVM. In: 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2011, Boston, MA. New York: IEEE, pp. 3306-3309. http://dx.doi.org/10.1109/IEMBS.2011.6090897
» http://dx.doi.org/10.1109/IEMBS.2011.6090897 - KUHN, M. and JOHNSON, K., 2013. Applied predictive modeling New York: Springer. vol. 26. http://dx.doi.org/10.1007/978-1-4614-6849-3
» http://dx.doi.org/10.1007/978-1-4614-6849-3 - LEGATES, D.R. and MCCABE JUNIOR, G.J., 1999. Evaluating the use of “goodness‐of‐fit” measures in hydrologic and hydroclimatic model validation. Water Resources Research, vol. 35, no. 1, pp. 233-241. http://dx.doi.org/10.1029/1998WR900018
» http://dx.doi.org/10.1029/1998WR900018 - LEI, K.S. and WAN, F., 2012. Applying ensemble learning techniques to ANFIS for air pollution index prediction in Macau. In: International Symposium on Neural Networks, 2012, Shenyang, China. Berlin: Springer, pp. 509-516. http://dx.doi.org/10.1007/978-3-642-31346-2_57
» http://dx.doi.org/10.1007/978-3-642-31346-2_57 - LINDNER, M., MAROSCHEK, M., NETHERER, S., KREMER, A., BARBATI, A., GARCIA-GONZALO, J., SEIDL, R., DELZON, S., CORONA, P., KOLSTRÖM, M., LEXER, M.J. and MARCHETTI, M., 2010. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. Forest Ecology and Management, vol. 259, no. 4, pp. 698-709. http://dx.doi.org/10.1016/j.foreco.2009.09.023.
- LUO, Y., SU, B.O., CURRIE, W.S., DUKES, J.S., FINZI, A., HARTWIG, U., HUNGATE, B., MCMURTRIE, R.E., OREN, R.A.M., PARTON, W.J., PATAKI, D.E., SHAW, M.R., ZAK, D.R. and FIELD, C.B., 2004. Progressive nitrogen limitation of ecosystem responses to rising atmospheric carbon dioxide. Bioscience, vol. 54, no. 8, pp. 731-739. http://dx.doi.org/10.1641/0006-3568(2004)054[0731:PNLOER]2.0.CO;2
» http://dx.doi.org/10.1641/0006-3568(2004)054[0731:PNLOER]2.0.CO;2 - MEDLYN, B.E., DUURSMA, R.A. and ZEPPEL, M.J., 2011. Forest productivity under climate change: a checklist for evaluating model studies. Wiley Interdisciplinary Reviews: Climate Change, vol. 2, no. 3, pp. 332-355. http://dx.doi.org/10.1002/wcc.108
» http://dx.doi.org/10.1002/wcc.108 - MOHAMMADI, K., SHAMSHIRBAND, S., TONG, C.W., ARIF, M., PETKOVIĆ, D. and CH, S., 2015. A new hybrid support vector machine–wavelet transform approach for estimation of horizontal global solar radiation. Energy Conversion and Management, vol. 92, pp. 162-171. http://dx.doi.org/10.1016/j.enconman.2014.12.050
» http://dx.doi.org/10.1016/j.enconman.2014.12.050 - NELSEN, R.B., 2003. Properties and applications of copulas: a brief survey. In: Proceedings of the First Brazilian Conference on Statistical Modeling in Insurance and Finance, 2003, Maresias. São Paulo: University Press USP, pp. 10-28.
- NGUYEN-HUY, T., DEO, R.C., MUSHTAQ, S., AN-VO, D.A. and KHAN, S., 2018. Modeling the joint influence of multiple synoptic-scale, climate mode indices on Australian wheat yield using a vine copula-based approach. European Journal of Agronomy, vol. 98, pp. 65-81. http://dx.doi.org/10.1016/j.eja.2018.05.006
» http://dx.doi.org/10.1016/j.eja.2018.05.006 - PENG, C., 2000. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology and Management, vol. 132, no. 2-3, pp. 259-279. http://dx.doi.org/10.1016/S0378-1127(99)00229-7
» http://dx.doi.org/10.1016/S0378-1127(99)00229-7 - PRASAD, R., DEO, R.C., LI, Y. and MARASENI, T., 2017. Input selection and performance optimization of ANN-based streamflow forecasts in the drought-prone Murray Darling Basin region using IIS and MODWT algorithm. Atmospheric Research, vol. 197, pp. 42-63. http://dx.doi.org/10.1016/j.atmosres.2017.06.014
» http://dx.doi.org/10.1016/j.atmosres.2017.06.014 - PRETZSCH, H., 2009. Forest dynamics, growth and yield from measurement to model. Berlin: Springer, pp. 1-39.
- QI, C., FOURIE, A., DU, X. and TANG, X., 2018. Prediction of open stope hangingwall stability using random forests. Natural Hazards, vol. 92, no. 2, pp. 1179-1197. http://dx.doi.org/10.1007/s11069-018-3246-7
» http://dx.doi.org/10.1007/s11069-018-3246-7 - RAFTERY, A.E., GNEITING, T., BALABDAOUI, F. and POLAKOWSKI, M., 2005. Using Bayesian model averaging to calibrate forecast ensembles. Monthly Weather Review, vol. 133, no. 5, pp. 1155-1174. http://dx.doi.org/10.1175/MWR2906.1
» http://dx.doi.org/10.1175/MWR2906.1 - RAKESH, K. and SUGANTHAN, P.N., 2017. An ensemble of kernel ridge regression for multi-class classification. Procedia Computer Science, vol. 108, pp. 375-383. http://dx.doi.org/10.1016/j.procs.2017.05.109
» http://dx.doi.org/10.1016/j.procs.2017.05.109 - RILLING, G., FLANDRIN, P. and GONÇALVES, P., 2003. On empirical mode decomposition and its algorithms. In: Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing (NSIP), 2003, Grado, Italy. Piscataway: IEEE Circuits and Systems Society, vol. 3, no. 3, pp. 8-11.
- SALCEDO-SANZ, S., DEO, R.C., CORNEJO-BUENO, L., CAMACHO-GÓMEZ, C. and GHIMIRE, S., 2018. An efficient neuro-evolutionary hybrid modelling mechanism for the estimation of daily global solar radiation in the Sunshine State of Australia. Applied Energy, vol. 209, pp. 79-94. http://dx.doi.org/10.1016/j.apenergy.2017.10.076
» http://dx.doi.org/10.1016/j.apenergy.2017.10.076 - SAUNDERS, C., GAMMERMAN, A. and VOVK, V., 1998. Ridge regression learning algorithm in dual variables. In: ICML ’98: Proceedings of the Fifteenth International Conference on Machine Learning, 1998, San Francisco, CA. New York: ACM Press.
- SVETNIK, V., LIAW, A., TONG, C., CULBERSON, J.C., SHERIDAN, R.P. and FEUSTON, B.P., 2003. Random forest: a classification and regression tool for compound classification and QSAR modeling. Journal of Chemical Information and Computer Sciences, vol. 43, no. 6, pp. 1947-1958. http://dx.doi.org/10.1021/ci034160g PMid:14632445.
» http://dx.doi.org/10.1021/ci034160g - WEISKITTEL, A.R., HANN, D.W., KERSHAW JUNIOR, J.A. and VANCLAY, J.K., 2011. Forest growth and yield modeling Hoboken: John Wiley & Sons. http://dx.doi.org/10.1002/9781119998518
» http://dx.doi.org/10.1002/9781119998518 - YANG, X.S., 2010. Nature-inspired metaheuristic algorithms Frome: Luniver Press.
- YASEEN, Z.M., GHAREB, M.I., EBTEHAJ, I., BONAKDARI, H., SIDDIQUE, R., HEDDAM, S., YUSIF, A.A. and DEO, R., 2018. Rainfall pattern forecasting using novel hybrid intelligent model based ANFIS-FFA. Water Resources Management, vol. 32, no. 1, pp. 105-122. http://dx.doi.org/10.1007/s11269-017-1797-0
» http://dx.doi.org/10.1007/s11269-017-1797-0 - YUAN, X., TAN, Q., LEI, X., YUAN, Y. and WU, X., 2017. Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy, vol. 129, pp. 122-137. http://dx.doi.org/10.1016/j.energy.2017.04.094
» http://dx.doi.org/10.1016/j.energy.2017.04.094 - YUN, Z., QUAN, Z., CAIXIN, S., SHAOLAN, L., YUMING, L. and YANG, S., 2008. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment. IEEE Transactions on Power Systems, vol. 23, no. 3, pp. 853-858. http://dx.doi.org/10.1109/TPWRS.2008.922249
» http://dx.doi.org/10.1109/TPWRS.2008.922249 - ZAMAN, S.B. and AHMAD, S., 2012. Wood supply and demand Analysis in Pakistan: key issues, managing natural resources for sustaining future agriculture. Research Briefings, vol. 4, no. 22, pp. 1-12.
- ZHISHENG, Z., 2010. Quantum-behaved particle swarm optimization algorithm for economic load dispatch of power system. Expert Systems with Applications, vol. 37, no. 2, pp. 1800-1803. http://dx.doi.org/10.1016/j.eswa.2009.07.042
» http://dx.doi.org/10.1016/j.eswa.2009.07.042 - ZHOU, X., PENG, C., DANG, Q.L., CHEN, J. and PARTON, S., 2005. Predicting forest growth and yield in northeastern Ontario using the process-based model of TRIPLEX1. 0. Canadian Journal of Forest Research, vol. 35, no. 9, pp. 2268-2280. http://dx.doi.org/10.1139/x05-149
» http://dx.doi.org/10.1139/x05-149
Publication Dates
-
Publication in this collection
29 Oct 2021 -
Date of issue
2024
History
-
Received
09 June 2021 -
Accepted
23 July 2021