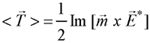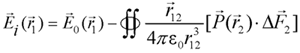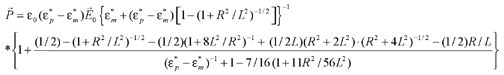Abstract
Electro-rotation can be used to determine the dielectric properties of cells, as well as to observe dynamic changes in both dielectric and morphological properties. Suspended biological cells and particles respond to alternating-field polarization by moving, deforming or rotating. While in linearly polarized alternating fields the particles are oriented along their axis of highest polarizability, in circularly polarized fields the axis of lowest polarizability aligns perpendicular to the plane of field rotation. Ellipsoidal models for cells are frequently applied, which include, beside sphere-shaped cells, also the limiting cases of rods and disks. Human erythrocyte cells, due to their particular shape, hardly resemble an ellipsoid. The additional effect of rouleaux formation with different numbers of aggregations suggests a model of circular cylinders of variable length. In the present study, the induced dipole moment of short cylinders was calculated and applied to rouleaux of human erythrocytes, which move freely in a suspending conductive medium under the effect of a rotating external field. Electro-rotation torque spectra are calculated for such aggregations of different length. Both the maximum rotation speeds and the peak frequencies of the torque are found to depend clearly on the size of the rouleaux. While the rotation speed grows with rouleaux length, the field frequency nup is lowest for the largest cell aggregations where the torque shows a maximum.
Electro-rotation spectra; Induced dipole moment; Mathematical modeling; Erythrocyte aggregates
Braz J Med Biol Res, February 2004, Volume 37(2) 173-183
Mathematical modeling of electro-rotation spectra of small particles in liquid solutions. Application to human erythrocyte aggregates
A. Zehe1, A. Ramírez2 and O. Starostenko3
1Facultad de Ciencias Físico-Matemáticas, Benemérita Universidad Autónoma de Puebla, Puebla, Pue., México
2Departamento de Microelectrónica, Instituto de Ciencias, Puebla, Pue., México
3Centro de Investigación CENTIA Cholula, Universidad de las Américas, Puebla, Pue., México
Text
References
Correspondence and Footnotes Correspondence and Footnotes Correspondence and Footnotes
Abstract
Electro-rotation can be used to determine the dielectric properties of cells, as well as to observe dynamic changes in both dielectric and morphological properties. Suspended biological cells and particles respond to alternating-field polarization by moving, deforming or rotating. While in linearly polarized alternating fields the particles are oriented along their axis of highest polarizability, in circularly polarized fields the axis of lowest polarizability aligns perpendicular to the plane of field rotation. Ellipsoidal models for cells are frequently applied, which include, beside sphere-shaped cells, also the limiting cases of rods and disks. Human erythrocyte cells, due to their particular shape, hardly resemble an ellipsoid. The additional effect of rouleaux formation with different numbers of aggregations suggests a model of circular cylinders of variable length. In the present study, the induced dipole moment of short cylinders was calculated and applied to rouleaux of human erythrocytes, which move freely in a suspending conductive medium under the effect of a rotating external field. Electro-rotation torque spectra are calculated for such aggregations of different length. Both the maximum rotation speeds and the peak frequencies of the torque are found to depend clearly on the size of the rouleaux. While the rotation speed grows with rouleaux length, the field frequency np is lowest for the largest cell aggregations where the torque shows a maximum.
Key words: Electro-rotation spectra, Induced dipole moment, Mathematical modeling, Erythrocyte aggregates
Introduction
The development of microdevices for applications in a wide range of biologically and medically related technologies is increasingly directed toward applying the advanced technologies of microelectronic structuring and fabrication. Such devices permit rapid analyses of small volume samples and have applications in medical and single-cell diagnostics or chemical detection. The bioparticles are suspended in a stationary fluid, and various force effects are imparted on them by the application of alternating current electric fields for dielectric characterization, manipulation, trapping or separation (1-12).
Calculations of the frequency dependence of force effects are primarily based on spherical or ellipsoidal models, the standard approach to biological cells. In particular, single-shell models with Maxwell's stress tensor (13) or the Laplace equation (14) are used. Interestingly, the general Laplace solution for the polarization of single-shell ellipsoids has been previously derived for a seemingly quite different case, i.e., the meteorological problem of dust particles covered with a fluid layer (15), prior to the application to biological cells (16,17). In order to arrive at explicit solutions of the Laplace equation, a homogeneous ellipsoid as the only material body with a constant local (internal) field has to be assumed. Integrating over this field leads to the induced dipole moment, providing the exposure of the ellipsoid to a homogeneous external field (18,19). The induced dipole moment is directly related to force effects acting on the particle. How precisely the frequency-dependent force effects and corresponding spectra can be reproduced depends on the precision of the calculus for the local field and the dipole moment.
However, many particles and biological cells, including erythrocyte cell aggregates, deviate from the ellipsoidal form, and in order to account for these specially shaped cells, more adequate models with shapes close to short cylinders have to be considered (20,21).
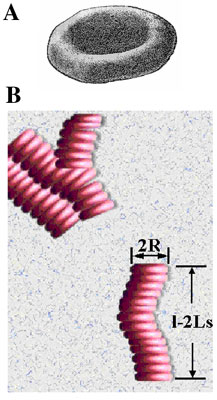
Normal human erythrocytes are non-nucleated biconcave disk-shaped cells of about 6.6-7.5 µm in diameter with edges that are thicker than the center part. Neither a spheroid model of rotational symmetry nor a spherical single-shell model approximates the cell shape very well. The biconcave shape of erythrocytes is usually flatter than the b/a-axis ratio of an ellipsoid would indicate, since the curvature at the equatorial zone of the cell is more critical for the polarization than the actual axis ratio (see Figures 1A and 2 Figure 2. Schematic representation of the electric field distribution for prolate ellipsoids (a > b = c) in field direction 0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R. ). The determination of the induced dipole moment for such a structure in the direction of the rotation axis will be possible only with a certain approximation, say, of a very short circular cylinder (disk) of radius R and half length L with L/R<<1.
A controlled formation of erythrocyte doublets has been shown recently by electrofusion (22), leading to an axis relation of 2L/R = 0.534. Rouleaux formation (Figure 1B) dominates the dielectric behavior of cell suspensions (23). Their size has been shown to be of clinical relevance (24).
The aggregation of disk-shaped objects to columns has a clear effect on the local field and the induced dipole moment. While the depolarizing factor in the direction of the cylinder axis (parallel to the external electric field) has a value close to 0 for L/R>>1, for the short cylinder or disk, this value is closer to 1.
It is important to visualize that the aggregation of individual erythrocytes generates columns of length l = s × d with d = 2L the thickness of a single disk (d = 2.2 µm) and s = 1, 2, 3, etc. Depending on the number s, the axis ratio of the columns L/R, the depolarizing factors f(q) and the induced dipole moments change correspondingly, and so does the electro-rotation torque acting on the cell aggregates.
Numerical methods most commonly used for field characterization within a biological structure are based on Mie theory (25-27) or the finite element and the finite difference time domain techniques. However, extensive computer calculations are required (7,28) and a simpler approach is desirable and often sufficient.
The rouleaux formation of erythrocytes due to side-by-side adherence of several individual cells translates into a cylindric cell model of variable but discrete cylinder height. Characterized by an integer factor of single cell heights, the aggregation of two, three or more cells changes the cell geometry from oblate to prolate. Thus, the local field and the polarization are affected considerably.
In the present study we calculated the electro-rotation spectra of erythrocytes under the aspect of cell aggregates of different stacking size. The multiplicity of these cell aggregates can be monitored by electro-rotation forces, and size-selective spectra appear, given a suitable suspending medium conductivity and frequency of the applied circular polarized electric field. The approximation procedure for dielectrics of general shape, departing from the simple ellipsoid approach, is included and applied to rouleaux of human erythrocytes of different length.
The problem is of practical importance since erythrocyte cell aggregation stems from the fact that rouleaux formation is caused by an increased blood concentration of fibrinogen, globulin or paraproteins. Associated clinical disorders include acute and chronic inflammatory disorders, macroglobulinemia, and multiple myeloma.
A, Approximate shape of a human erythrocyte with diameter 2R and thickness d at the outer rim of 2.2 µm. Neither a prolate ellipsoid (spheroidal cell model of rotational symmetry) nor a spherical single-shell model approaches the shape of the cell very well. B, Rouleaux formation of erythrocytes adhering side-by-side forming a cylindrical body of variable length. While the diameter 2R corresponds to that of the single erythrocyte, (2R = 7.5 µm), the rouleaux length l is proportional to the stack number s of adhered red blood cells, 2L x s. For s ³ 4, a short cylinder with cylinder symmetry axis of length l > 2R is formed.
Electro-rotation
A circularly polarized rotating electrical field induces a circulating dipole moment in a dielectric object. Due to ever-present dispersion processes in the exposed sample, a spatial shift between the external field vector and the induced dipole moment occurs. The interaction of the out-of-phase part of this dipole moment and the electrical field causes a torque on the object.
Very often only frequency dependencies of a physical measure are of interest. Thus, it is sufficient to consider the Clausius-Mossotti factor K(w), which is the frequency-dependent part of the induced dipole moment. The torque is proportional to the imaginary part of this factor and describes the frequency dependence of the rotation of an individual cell under study in or against the rotation sense of the external field.
The time-averaged rotational torque in circularly polarized external fields, excerted on a particle, is given by the vector product of induced dipole moment and conjugate field
The induced dipole moment  is proportional to the external field E, the suspending medium permittivity e*m and the volume V of the object. Let the principal axes of the (ellipsoidal) object be oriented parallel to the vectors of the base system, and then
is proportional to the external field E, the suspending medium permittivity e*m and the volume V of the object. Let the principal axes of the (ellipsoidal) object be oriented parallel to the vectors of the base system, and then  will be given by
will be given by

(Eq. 2)
(i, r - imaginary and real part, respectively, and j = (-1)1/2 - imaginary unit). With the external alternating current field written E = E0 × exp(jwt), and assuming that its components Ex, Ey, Ez are parallel to the same orthonormal base system, it follows from Equation 1 that
An electric field circulating at constant amplitude in the x-y plane can be written as

(Eq. 4)
For Ez considered to be zero, and as established in practical cases, where one of the principal axes of the ellipsoid is always perpendicular to the field plane, the k-th component of the acting torque results in

(Eq. 5)
For a homogeneous ellipsoidal particle, the Clausius-Mossotti factor (19) in the x direction is given by

(Eq. 6)
where e*p, e*m are the complex permittivity of the sample and the suspending medium, respectively, and fx(q) is the depolarizing factor along this direction with q being a number describing the axis relation (29-31). The Clausius-Mossotti factor is a measure of the effective polarizability of the particle and depends for fx(q) strongly on the geometrical shape of the ellipsoidal object.
With e the permittivity and s the conductivity of a dielectric medium, the complex permittivity is defined as

(Eq. 7)
Consequently, the Clausius-Mossotti factor depends on the frequency of the applied field in addition to the dielectric properties of particle and medium. When only frequency dependencies are important in the study, it is sufficient to consider K(w) as the only frequency-dependent part of the induced dipole moment. Variations of this factor give rise to the electro-rotation forces described in Ref. 5, which are unique to a special particle type. This concerns not only intrinsic dielectric properties, but also the geometrical shape via the depolarizing factors fx. It is this latter aspect that plays a particular role in the present study.
Shape variation of the particles affects K(w), leading to readily achievable electro-rotation spectra. The design and geometry of the microelectrodes used to generate the rotating electrical fields are of course important factors to be considered. To determine the orientation of particle movement, only the directions (signs) of the torque components corresponding to Equation 3 are needed. The sign of the torque about the z-axis, as considered in this report, is equivalent to that of the frequency-dependent K(w)-term:

(Eq. 8)
Thus, if the imaginary component of  is positive, corresponding to Equation 1, the exerted torque will be negative and cause the particle to rotate in a sense that opposes that of the rotating field.
is positive, corresponding to Equation 1, the exerted torque will be negative and cause the particle to rotate in a sense that opposes that of the rotating field.
Calculation of the induced polarization in linear rouleaux
In the Laplace model, a homogeneous ellipsoid always exhibits a constant local field. Integration over this field leads to induced polarization and thus to expressions related to the actions of force on the special object. On the other hand, in such important cases as a cube or a short cylinder it is difficult to calculate the depolarization factors without accepting an ellipsoid to substitute the shape of the object. But even then the best shape to be used and the next approximation step are not a straightforward choice. This chapter deals with an approximation procedure for the calculation of the internal depolarization field
i in a material body of general shape and a complex dielectric constant e*p, which is brought into an external field
in a material body of general shape and a complex dielectric constant e*p, which is brought into an external field  0
0 , acting inside a medium of dielectric permittivity e*m.
, acting inside a medium of dielectric permittivity e*m.
The problem can be formulated as follows (see Figure 2
Figure 2. Schematic representation of the electric field distribution for prolate ellipsoids (a > b = c) in field direction 0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R.
): the local field  i
i  causes a polarization
causes a polarization 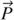 = e0(e*p - e*m)
= e0(e*p - e*m) i . This polarization generates on the surface element D
i . This polarization generates on the surface element D of the dielectric body a polarization charge Dq = spol . DF=
of the dielectric body a polarization charge Dq = spol . DF=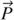 . D
. D , which by virtue of the Coulomb law, together with the unperturbed field
, which by virtue of the Coulomb law, together with the unperturbed field  0
0 , produces the local field of such a strength that
, produces the local field of such a strength that
The integration is carried out on the surface of the dielectric body; D points outward, and
points outward, and  12 combines the origin
12 combines the origin  1 with the integration element at
1 with the integration element at  2. We assume the relation between
2. We assume the relation between  0
0 and
and  i
i  to be linear:
to be linear:
In general, a  is a tensor since the directions of
is a tensor since the directions of  i and
i and  0 are not necessarily parallel. It further depends on the place inside the sample due to the locally different action of the polarization charges.
0 are not necessarily parallel. It further depends on the place inside the sample due to the locally different action of the polarization charges.
In order to calculate
 or
or 
 from Equations 9 and 10, we assume that a does not depend on
from Equations 9 and 10, we assume that a does not depend on  .
.
The polarization established inside the dielectric particle is due to the displacement of electrical charges enforced by the field  0
0 . Surface charges are built up and counteract the complete displacement which would correspond to the field
. Surface charges are built up and counteract the complete displacement which would correspond to the field  0
0 . We will assume here that the whole set of charges experiences the same displacement, which means that in Equation 10, a = constant. We further assume that the polarization vector
. We will assume here that the whole set of charges experiences the same displacement, which means that in Equation 10, a = constant. We further assume that the polarization vector 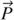 points more or less towards the direction of
points more or less towards the direction of  0
0 , i.e., we will consider the projection of the field generated by the polarization charges in the direction of
, i.e., we will consider the projection of the field generated by the polarization charges in the direction of  0
0 :
:

(Eq. 11)
This a1 value allows us to consider a first approximation of the polarization 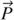 1, which generates charges on the surface of the dielectric and thus an additional field inside the dielectric. The problem would be completely solved if the total field at any place fulfilled the condition
1, which generates charges on the surface of the dielectric and thus an additional field inside the dielectric. The problem would be completely solved if the total field at any place fulfilled the condition

(Eq. 12)
but, in general, the polarization
1 of the first approximation step will not be sufficient to describe the real situation, and a field 1
1 will keep acting on the dielectric with the effect of the additional polarization
will keep acting on the dielectric with the effect of the additional polarization 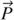 2
2 ,
,
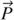 2
2 can be calculated with
can be calculated with  1
1 in the same way as
in the same way as 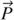 1
1 was calculated with
was calculated with  0
0 . The number of approximation steps needed to achieve the best result depends on the complexity of the shape of the dielectric body, as well as on the allowed error of the result.
. The number of approximation steps needed to achieve the best result depends on the complexity of the shape of the dielectric body, as well as on the allowed error of the result.
We will apply this procedure now to a cylinder-shaped object of the rouleau kind. Exact solutions proposed by Fuhr et al. (11) with a constant a are known for the sphere, as well as the infinitesimal thin wire (needle), and the infinitesimal extended disk (sheet). When our approach is applied here, the first approximation step (11) gives the exact solution, as it should, when a = a1 is a constant.
= a1 is a constant.
The polarization of a prolate spheroid (Figure 2 Figure 2. Schematic representation of the electric field distribution for prolate ellipsoids (a > b = c) in field direction 0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R. A), considered together with Equation 10 and the axis relation q2 = b2/(a2-b2), yields

(Eq. 14)
An oblate ellipsoid yields

(Eq. 15)
and consequently with q ® ¥ (or a = b = c) we obtain a1 = 3/(e*p +2e*m) for the sphere-shaped dielectric body, and thus the known result for the polarization vector

(Eq. 16)
which would be a rouleau of length l = 2Ls with s ³ 4.
Not so straightforward is the situation in the case of a short cylinder which would be a rouleau of length l = 2Ls with s £ 4 (see Figure 2 Figure 2. Schematic representation of the electric field distribution for prolate ellipsoids (a > b = c) in field direction 0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R. B). As a first approximation, we obtain

(Eq. 17)

(Eq. 18)
Such a homogeneous polarization is the first approximation and good enough only for long cylinders with L>>R or for disks with R>>L. Due to the choice of the center point at z = 0, the 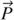 generated field will be too weak in the transversal plane at z = 0, but along the z-axis at the limiting surfaces of the cylinder it is too strong. A field
generated field will be too weak in the transversal plane at z = 0, but along the z-axis at the limiting surfaces of the cylinder it is too strong. A field  1
1 remains as given in Equation 13, which delivers the depolarization at the cylinder top and bottom surfaces in a second approximation.
remains as given in Equation 13, which delivers the depolarization at the cylinder top and bottom surfaces in a second approximation.
The integrations involved in this step are quite tedious and will not be presented here.
We obtain

(Eq. 19)
The surface charge density s2 = e0(e*p - e*m)a2  11 when added to s1 has the effect of reducing the charge density of the side surfaces, but increasing it on the cover area close to the side surfaces.
11 when added to s1 has the effect of reducing the charge density of the side surfaces, but increasing it on the cover area close to the side surfaces.
The dipole moment of the cylinder of length 2L in a second approximation yields then Equation 20:
By comparing this equation with Equation 10, an analytical expression for a is found after two approximation steps and can be used for rouleaux of different length.
Electro-rotation torque calculation and discussion
The frequency response of the electro-rotation torque on linear erythrocyte cell arrangements in rouleaux is governed by the corresponding Clausius-Mossotti factor, which is related to a (Equations 10 and 20) by

(Eq. 21)
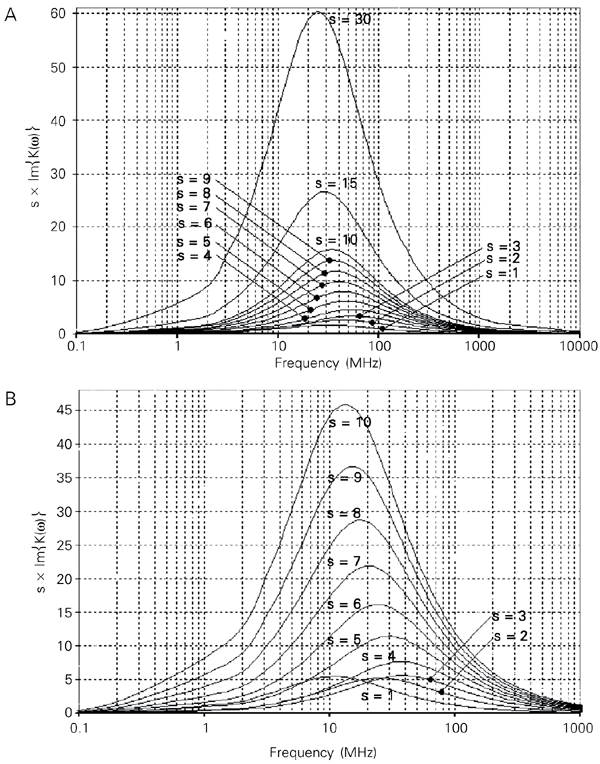
In the limiting cases of a long cylinder with a = 1/e*m, a sphere with a = 3/(e*p +2e*m), and a disk with a = 1/e*p, respectively, the relations known for ellipsoids are of course reproduced. In the present case, the rouleaux are approximated to solid homogeneous cylinders of length l = 2L × s (Figure 1C) with a relative permittivity ep = 50 and conductivity sp = 0.5 S m-1 (32). For s ³ 4, the aggregation length corresponds to short cylinders whose symmetry axis lines up with the external electric field vector, while for s £ 3 a reorientation will occur with the erythrocyte radius vector now in parallel to the external field. By applying the given electrical parameters, a plot of the frequency variation of the polarization factor estimated from Equation 20 was calculated as a function of frequency and rouleaux-length parameter s in medium conductivities of sm = 1 mS/m and 0.1 S/m, respectively.
Only the high frequency (positive torque) part is shown, which reproduces the cell behavior without accounting for the electrical properties of the cell envelope, but displays the effect of different rouleaux lengths. The results are shown in Figure 3. The dependence of the peak rotation speeds on the rouleaux size for a certain medium conductivity is given by the maximum value of each curve in this figure. Its theoretical height is and depends of course on the dielectric data of cell and medium, as well as on the cell shape via the depolarization factor f(q). Membrane data do not interfere with the high-frequency part of the spectrum.

(Eq. 22)
The fitting of theoretical electro-rotation spectra to experimentally determined data might require the consideration of hydrodynamic friction. Indeed, the counteracting frictional force will increase with cell volume too, and smaller rotation speeds are measured.
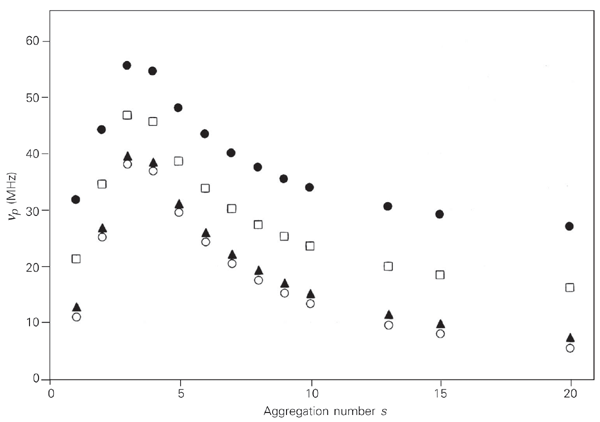
The peak frequency np of the rotation spectra for different rouleaux lengths is presented in Figure 4, showing a shift to lower values with increasing length parameter s. While these shifts are more pronounced between short rouleaux s ³ 4, a computer differentiated presentation [dT(w)/dw] would indicate with high precision the frequency maxima and their correlation with the length parameter s. In order to understand the positive peak frequency shift in np for values s = 1 to 4, one has to consider the orientation of the main (longest) particle axis with respect to the rotating electric field vector. Since the rouleaux length is defined by l = 2L × s, and the erythrocyte thickness at the rim by 2L = 2.2 µm, only for values s ³ 4 will the main particle axis be the rouleaux cylinder axis. The erythrocyte diameter 2R = 7.5 µm is wider for s £ 3 than the rouleaux length and correspondingly the radius vector aligns with the external field, i.e., the shorter rouleaux cylinder axis is the rotation axis.
The peak frequency is related to the cell and medium properties, as well as to the rouleaux size via the depolarization factor f(q) as

(Eq. 23)
Cells rotate around their small semi-axis. A reorientation of rouleaux occurs at the transition from s = 2 to 4. Rouleaux with s = 3 show an axis relation of approximately 1:1 and are not well defined in terms of reorientation.
The magnitude and polarity of the torque are related to both the geometrical structure and the dielectric properties of the rouleaux.
The experimental determination of electro-rotation spectra on the one hand, and the fitting to theoretically determined electro-rotation curves, particularly to the characterized frequencies np, on the other, allows us to determine the set of dielectric and geometric properties of the cells in corresponding frequency ranges.
The rotation can be observed using either digital image processing techniques or direct CCD analysis. The typical induced rotation speed is in the range of one revolution per second, and can of course be controlled by the driving voltage.
A, Electro-rotation spectra of erythrocyte rouleaux of different lengths l = s x 2L, at medium conductivity sm = 100 mS/m. 2L = 2.2 µm is the thickness of a single erythrocyte. The vertical axis displays a measure of the acting torque. Only the spectral range of positive torque is shown, where no membrane effects are involved. Cytoplasm parameters are ep = 50 and sp = 0.535 S/m. B, Same as A, but the medium conductivity is reduced to sm = 1 mS/m. The maximum torque on the particles is increased up to a factor of three.
Peak frequency np of the maximum torque on a rouleaux of length l = s x 2L, where s = 1 to 20 characterizes the length of the cell aggregation. At s £ 3 the particle rotation axis is the rouleaux cylinder axis, while for s ³ 4 the erythrocyte radius vector is the rotation axis. Medium conductivities are introduced as parameters: sm = 0.1 S/m (filled circles); sm = 0.05 S/m (open squares); sm = 0.01 S/m (filled triangles); sm = 0.001 S/m (open circles).
Acknowledgments
We are grateful to Ms. Guadalupe Leal Santos and Mr. Eduardo Ramírez Solís for help with computer programming and manuscript typing.
Address for correspondence: A. Zehe, Facultad de Ciencias Físico-Matemáticas, Benemérita Universidad Autónoma de Puebla, Apartado Postal 1505, 72000 Puebla, Pue., México. E-mail: azehe@prodigy.net.mx
Research supported by CONACyT, México. Received June 14, 2002. Accepted June 24, 2003.
- 1. Pauly H & Schwan HP (1959). Über die Impedanz einer Suspension von kugelförmigen Teilchen mit einer Schale. Ein Modell für das dielektrische Verhalten von Zellsuspensionen und von Proteinlösungen. Zeitschrift für Naturforschung, 14b: 125-131.
- 2. Jones TB (1995). Electromechanics of Particles Cambridge University Press, Cambridge, UK.
- 3. Pohl HA (1978). Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields. Cambridge University Press, Cambridge, UK.
- 4. Asami K, Hanai T & Koizumi N (1980). Dielectric approach to suspensions of ellipsoidal particles covered with a shell in particular reference to biological cells. Japanese Journal of Applied Physics, 19: 359-365.
- 5. Holzapfel C, Vienken J & Zimmermann U (1987). Rotation of cells in an alternating electric field: theory and experimental proof. Journal of Membrane Biology, 67: 13-26.
- 6. Griffin JL (1970). Orientation of human and avian erythrocytes in radio-frequency fields. Experimental Cell Research, 61: 113-120.
- 7. Miller RD & Jones TB (1993). Electro-orientation of ellipsoidal erythrocytes. Biophysical Journal, 64: 1588-1595.
- 8. Gimsa T, Müller T, Schnelle T & Fuhr G (1996). Dielectric spectroscopy of single human erythrocytes at physiological ionic strength: dispersion of the cytoplasm. Biophysical Journal, 71: 495-506.
- 9. Arnold WM & Zimmermann U (1982). Rotating-field-induced rotation and measurement of the membrane capacitance of single mesophyll cells of Avena sativa Zeitschrift für Naturforschung, 37c: 908-915.
- 10. Höltzel R (1997). Electrorotation of single yeast cells at frequencies between 100 Hz and 1.6 GHz. Biophysical Journal, 73: 1103-1109.
- 11. Fuhr G, Zimmermann U & Shirley SG (1996). Cell motion in time varying fields: principles and potential. In: Zimmermann U & Neil GA (Editors), Electromanipulation of Cells. CRC Press, Boca Raton, New York, London, Tokyo.
- 12. Stoylov SP (1996). Electric polarization of polyelectrolyte and colloid media: dielectric versus electro-optic approach. Biophysical Chemistry, 58: 165-172.
- 13. Wang X, Wang XB & Gascoyne PRC (1997). General expression for dielectrophoretic force and electrorotational torque derived using the Maxwell stress tensor method. Journal of Electrostatics, 39: 277-295.
- 14. Pastushenko VPh, Kuzmin PI & Chizmadshev YA (1985). Dielectrophoresis and electrorotation: a unified theory of spherically symmetrical cells. Studia Biophysica, 110: 51-57.
- 15. Bohren CF & Hoffman DR (1983). Absorption and Scattering of Light by Small Particles. Wiley, New York.
- 16. Paul R & Otwinowski M (1991). The theory of the frequency response of ellipsoidal biological cells in rotating electrical fields. Journal of Theoretical Biology, 148: 495-519.
- 17. Sokirko AV (1992). The electro-rotation of axisymmetrical cell. Biologicheskie Membrany, 6: 587-600.
- 18. Maxwell JC (1873). Treatise on Electricity and Magnetism Oxford University Press, London, UK.
- 19. Landau LD & Lifschitz EM (1985). Elektrodynamik der Kontinua Vol. 8. Akademie-Verlag, Berlin, Germany.
- 20. Gimsa J & Wachner D (1999). A polarization model overcoming the geometric restrictions of the Laplace solution for spheroidal cells. Biophysical Journal, 77: 1316-1326.
- 21. Morgan H & Green NG (1997). Dielectrophoretic manipulation of rod-shaped viral particles. Journal of Electrostatics, 42: 279-293.
- 22. Baumann M (1999). Dynamics of oscillating erythrocyte doublets after electrofusion. Biophysical Journal, 77: 2602-2611.
- 23. Chelidze T (2001). Dielectric spectroscopy of blood: experiment and theory. Proceedings of the 1st International Conference on Dielectric Spectroscopy in Physical, Chemical and Biological Applications (DS 2001), Jerusalem, Israel, March 12-15, 2001, 57.
- 24. Priezzhev AV, Forsov NN, Vyshlova MG, Lademann J, Richter H, Kiesewetter H & Mueller GJ (1999). Assessment of erythrocyte aggregation in whole blood samples by light backscattering: clinical applications. SPIE Proceedings, 3599: 9-14.
- 25. Stratton J (1941). Electromagnetic Theory McGraw-Hill, New York.
- 26. Benardi P, Cavagnaro M & d'Inzeo LM (1999). Cell modeling to evaluate EM field absorption in biological samples. Union Radio-Scientifique Internationale XXVI General Assembly, 616 (Abstract).
- 27. Liu LM & Cleary SF (1995). Absorbed energy distribution from radiofrequency electromagnetic radiation in a mammalian cell model: effect of membrane-bound water. Bioelectromagnetics, 16: 160-171.
- 28. Sebastián JL, Muñoz S, Sancho M & Miranda JM (2001). Analysis of the influence of the cell geometry, orientation and cell proximity effects on the electric field distribution from direct RF exposure. Physics in Medicine and Biology, 46: 213-225.
- 29. Stille U (1944). Der Entmagnetisierungsfaktor und Entelektrisierungsfaktor für Rotations-Ellipsoide. Archiv für Elektrotechnik, 38: 91-101.
- 30. Stoner EC (1945). The demagnetizing factors for ellipsoids. Philosophical Magazine, 36: 308-321.
- 31. Osborn JA (1945). Demagnetizing factors of the general ellipsoid. Physical Review, 67: 351-357.
- 32. Pauly H & Schwan HP (1966). Dielectric properties and ion mobility in erythrocytes. Biophysical Journal, 6: 6221-6239.
 0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R.
0 (A). An oblate ellipsoid corresponds to b > a = c. B, Dielectric cylinders of length 2L and diameter 2R.Correspondence and Footnotes
Publication Dates
-
Publication in this collection
30 Jan 2004 -
Date of issue
Feb 2004
History
-
Accepted
24 June 2003 -
Received
14 June 2002