Spectral derivation of the ornstein-zernike decay for four-point functions

Spectral derivation of the ornstein-zernike decay for four-point functions

F. Auil; J. C. A. Barata

Universidade de São Paulo, Instituto de Física and São Paulo, SP 05315-970, Brazil

ABSTRACT

In this note we discuss the relation between the Ornstein-Zernike decay of certain four-point functions (''energy-energy correlations'') in lattice spin systems and spectral properties of the transfer matrix, related to the property of two-particle asymptotic completeness in (massive) Euclidean lattice quantum field theories.

I. INTRODUCTION

In Statistical Mechanics, power-law corrections to the exponential decay provide an improved asymptotic description for two-point functions (or pair-correlation) away from the critical point. Such corrections have been analysed since the pioneering work of Ornstein and Zernike [1] and its nature has been associated to other underlying phenomena.

In this paper we study the Ornstein-Zernike (O-Z) behavior of four-point functions in the context of (massive) Euclidean quantum field theories on the d+1 dimensional integer lattice or, correspondingly, in the context of classical statistical mechanics spin systems described by the transfer matrix formalism. We follow closely the methods of Paes-Leme [9]. More precisely, our work attempts to extend that results to four-point functions and for the case of absolutely continuous energy-momentum spectrum. Therefore, the emphasis of the present work is to associate the O-Z corrections to spectral properties of the transfer matrix related to the absence of two-particle states and to properties of the dispersion curve of one-particle states near the origin.

Our main result is expression (III.6) in Theorem III.1 below. For the specific case of the Ising model at high temperatures in space dimension d = 1 or 2, our expression (III.6) is weaker than the known bound (obtained by more specific methods. See, e.g., [15]), while for d > 3 we are able to reproduce the bound known for that particular model (see [15]). In this context, it is opportune to remark that our results and methods are based on general hypotheses, valid in essentially any model described by the transfer matrix formalism and without two-particle bound states, as we discuss in Sec. . In fact, the exact asymptotics in d = 1 or 2 for the Ising model at high temperatures are, in the framework of this paper, due to of additional model-dependent properties of the function v in (III.5). See Sec. for some comments on this in our context or [15].

Rather than providing a replacement to other well-known methods employed in Statistical Mechanics for the analysis of decay properties of n-point functions, as random walk methods, our aim is to illuminate, in a model independent way, the relation between O-Z corrections and spectral properties associated to the particle structure of certain statistical mechanics systems, seen as lattice quantum field theory models through the transfer matrix formalism. Random walk methods may not be available in models exhibiting continuous symmetries, while our spectral hypotheses could in principle be verified even in such cases by other formalisms, like those employed in [17,18,20], that use ideas originated in [23].

To emphasise the features of our spectral approach, let us present a brief historical review of the O-Z properties. The original argument of Ornstein and Zernike consists basically on a local limit type computation based on suitable assumptions on the structure of correlations. In a technical sense, this description is valid (for classical systems) in the limit of infinitely weak long-range potentials [2]. Fisher [3] introduced a heuristic development of these results based on a Bethe-Salpeter (B-S) type expression 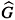= +r^–1

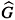for the Fourier transform of the pair-correlation G. Here, the ''B-S kernel'' is given by minus the inverse of the (mean) density r, the ''free resolvent'' is the so called ''direct correlation function'' C and, in this perhaps somewhat vague analogy, the critical point is identified, in some sense, with a ''pole'' of the ''resolvent'' G. Supported on symmetry arguments, the function C is assumed to be quadratic near the origin (see [4]).

In more recent studies (see, e.g. [5-7]) the presence of power-law corrections to the exponential decay (O-Z corrections) has been established by the use of convergent expansion methods, like polymer and cluster expansions or random walks. In the work of Campanino, Ioffe and Velenik [8], for instance, a refined expansion method was employed to derived a precise O-Z asymptotic formula for the decay of the two-point function, valid for all the region above the critical temperature in a wide class of finite range Ising type models.

A general spectral approach for two-point functions in the context of lattice spin systems, described by transfer matrices, and satisfying conditions required by lattice quantum field theories, can be found in the work of Paes-Leme [9]. There, the presence of O-Z corrections was associated to spectral properties of the transfer matrix related to the presence of a one-particle state and to properties of its dispersion curve near the origin (zero momentum).

The O-Z behavior was also analysed for four-point functions (or energy-energy correlations) and subsequently explored in the literature, mostly concerning the Ising Model [10-12]. Later elaborations are found in [5-7] where, for the analysis of four-point functions, correlation inequalities of the type derived in [13,14] were used. Further references and a survey of results can also be found there. Note that the relevance of energy-energy correlations for Statistical Mechanics is based on its use for the computation of the specific heat [4,10]. The case of arbitrary odd-odd and even-even correlations for the Ising model at high temperatures is considered in [15].

Our starting point is an explicit expression (eq. (III.5), below) for the Fourier transform of the connected part of a truncated four-point function. Assuming a ''local minimum (quadratic) behavior'' for the dispersion curve at the origin, we can use, as in [9], a multidimensional adaptation of Laplace method [16] for the asymptotic estimation of some integrals and, in this way, we get the O-Z decay property, namely a power-law correction as |t₀|^–d, t₀ being the ''time''-component of the coordinate t, defined in (III.3).

The main difference with respect to [9] is that our expression (III.5) is basically a paraphrase of the two-particle asymptotic completeness condition studied in [19], as we will remark in Sec.VI. Roughly speaking, this represents the absence of (two-particle) bound states. In a mathematical sense, the energy-momentum spectrum up 2m is, in this case, absolutely continuous and has multiplicity 1. Asymptotic completeness is verified under general hypotheses, as discussed in [19]. The Ising model at high temperatures, for instance, matches this condition [20].

Analogous results could be derived assuming the existence of two-particle bound states but, in this case, it seems plausible to expect that the exponential decay is corrected by |t₀|^–d/2, as in the case of the two-point function [9], instead of |t₀|^–d. See the final digression of Sec. IV and Sec.VII .

Our results provide a one-way proof that some suitable assumptions on the energy-momentum spectrum, related to two-particle asymptotic completeness, imply a definite O-Z decay. One would be naturally tempted to speculate on the opposite direction, and ask whether the knowledge of the O-Z decay of correlations provides information on the energy-momentum spectrum which could be interpreted in terms of properties of the particle states, such as asymptotic completeness. Unfortunately, however, to address such interesting general questions is beyond our present capabilities, and we leave this point without further comments.

This paper is organised as follows. In Sec. II we present the basic setting we will work with. In Sec. III we introduce the basic assumptions and state our main result, captured in Theorem . In Sec. we present some preparatory results to the proof of Theorem III.1, finally presented in Sec. V. In Sec. VI we derive the expression (III.5) under suitable hypotheses. Sec. VII is devoted to some final remarks.

II. BASIC HYPOTHESES

A model in lattice quantum field theory is specified by the choice of a state m (i.e., a linear, positive functional with norm 1) on the algebra C() of complex-valued, continuous functions on the set of configurations : = {j: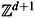® S}, with the product topology, where S Í is a conveniently topologized set. For instance, for the Ising Model we have S : = {–1, 1} with the discrete topology, but restrictions on S and its topology are not really serious neither relevant in the present context. As usual, 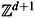is the lattice of integers in d+1 dimensions, with d>1, whose sites will be denoted by x = (x₀, x₁, ..., x_d) or (x₀, x), for short.

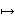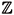Examples of functions in S are the projections at site x, j_x:jj(x), and the function identically equal to 1, denoted here by . For each i Î {0, 1,..., d} and a Î we define the semi-spaces L_i,a : = {(x₀, x₁, ..., x_d) Î 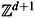: x_i> a}. We also define the lattice translations: t_x:y

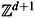y+x , " x, y Î , and the reflections q_i,a: y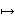(y₀, y₁, ..., y_i–1, 2a–y_i, y_i+1, ..., y_d), a Î 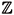/2. An example is the ''time'' reflection q : = q_0,0:(x₀, x)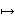(–x₀, x). The state m is interpreted as the vacuum state and is typically obtained as the thermodynamic limit of finite volume Gibbs states. Additionally, the state m is assumed to satisfy

A1 Invariance under reflections and translations: m = q_i,a = t_x, " i Î {1, ..., d}, " x Î 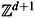and " a Î 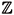/2.

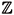A2 Reflection positivity: m(f)> 0, " f Î P(L_0,a) and " a Î /2.

Above, the bar indicates complex conjugation and (L) denotes the algebra generated by all the projections j_x with x Î L . The last two properties allow to construct the Hilbert space of physical states as the completion of the quotient (L_0,0)/{f : á f, f ñ₀ = 0}, a procedure similar to the GNS construction for C^*-algebras. Note that á f, g ñ₀ : = m(g) is a sesquilinear, Hermitian, non-negative form (by A2) on (L_0,0). The standard procedure gives additionally a canonical inclusion i:(L_0,0)® with dense image. For instance, i() = :W is the vacuum state vector. Functions f Î(L_0,0) act as multiplication operators on (L_0,0), :g fg. The action of functions and the lattice translations can also be extended through i, leading to operators acting on . Some relevant examples are:

i() =: F(x), the local fields, for x Î L_0;0,

i() =: T, the transfer matrix,

i() =: Tn, the generators of space trans lations, for n = 1; ..., d.

The local fields are bounded operators if S is a compact set, with ||F(x)||<sup{|s| : s Î S}. The transfer matrix is a positive self-adjoint operator with norm equal to 1 and the operators T_n, the generators of elementary space translations on the lattice, are unitaries, so they can be expressed as T_n = for certain self-adjoint operators P_n, with spectrum in (–p,p]. We can identify P = (P₁, ..., P_d) with the momentum operator. The Hamilton operator is defined on Ker (T)^{^} by H: = -ln(T|Ker (T)^{^}). Notice, however, that Ker (T) = {0} in many of the most interesting models (see [21]) and, hence, H will be defined on the whole Hilbert space. Thus, (H, P) will be called the energy-momentum operator.

Finally, for functions f on the lattice, the Fourier transform and anti-transform are defined by and , respectively. Above, is the (d+1)-dimensional torus: : = (–p,p]^d+1.

III. THE MAIN RESULT

The n-point Euclidean, or Schwinger, functions are defined by (x₁,..., x_n) : = m(j_x1... j_xn). As a consequence of translation invariance A1, we can express in terms of difference variables

We define the connected part of the truncated four-point function as

In terms of the new variables

and expressing the two-point and four-point functions in terms of difference variables (III.1), we get

The change of variables (III.3) requires certain care in the lattice context. This was discussed in [19], and here we omit these considerations. Denote R(k, p, q) : = (k, p, q), considering it as a family of integral operators [R(k)f](p) = R(k, p, q) f(q) dq indexed by k.

Our results on the four-point function will be obtained from the following single assumption, which we will derive from other more basic ones in Sec. VI.

a. Assumption: For each f in a ''suitable'' space of functions (see Sec. ), we have

where

(a)G(p, k) = [w(p+k)+w( p–k)]/2. Here, w is is a ''sufficiently differentiable'', real function defined in the torus (i.e. , periodic), with m : = w(0)<w(k), (grad w)(0) = 0, and such that the matrix B, whose entries are given by

is positive defined and non-singular. Furthermore, there exists m¢> m such that m¢<w(k) for all k outside a neighborhood of the origin. See Fig. 1.

(b)v(p, k) is a non-negative, C^¥ function.

(c)B(k)(f) is analytic in the strip |Im k₀| < m¢¢, where m¢¢> m¢> m.

By abuse of notation, we denote the map k₀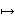 á f, R(k)f ñ by R and D = .

We are now in position to state our main result:

Theorem III.1 Under the assumptions above, we have

for t₀®¥, where m¢¢¢> m. Here, O*(K^–p) means O(K^–p+d) for alld> 0when K®¥.

Remarks. 1. The precise meaning of expression (III.6) is the following: there exists I(t) such that

where m¢¢¢ > m, and the expression I(t) satisfies:

as t₀®¥, for any d> 0. The function I(t) is the Fourier anti-transform of the first term at the r.h.s. in (III.5). See (IV.1) in Section below. 2. Our derivation of (III.6) from assumption (III.5) is valid in any space dimension d. As shown in Sec. , for the case d = 1 we derive relation (III.5) under some suitable hypotheses, among them the existence of a one-particle shell. In this case, the function w of condition (a) becomes the dispersion curve of the particle and m its mass. 3. From definition (III.3), note that the t coordinate is twice the difference between the ''center of mass coordinates'' (of points x₁ and x₂ and points x₃ and x₄, respectively), so the mass rate of the exponential decay in (III.6) is 2m, the expected one for that particular four-point function (compare, f.i., with [23,24]). 4. The condition on differentiability of w is not a physically restrictive condition. As will become clear from our proof of Theorem III.1 below, condition (b) is not essential and can be considerably weakened.

IV. SOME PREPARATORY REMARKS

Before we start the proof of Theorem III.1, let us make some preparatory comments on the decay properties of D(t). From (III.5), we have, by the analyticity of B(k)(f) in (c),

where I(t) is the Fourier anti-transform of the first term at the r.h.s. in (III.5)

The integral in k₀ (in brackets at the second line above) was easily evaluated by the method of residues, and its value is 2p e^{–G(p, k)|t0|}.

At this point we have to do a little digression. Let us denote by |p| the l^¥ norm of vectors p = (p₁,..., p_d) Î (or ), |p| : = max{ |p₁|, ..., |p_d|}. Define the set = {n Î : |n|< 1} and, for some conveniently small e> 0, consider the region

and

Note that for n Î we can write 2n = a+b with a, b Î and |a_i| = |b_i| "i = 1,...,d. Note also that if the two relations

are simultaneously valid for some n and m in , then n and m are not independent, because |p| < p and | k| < p. In fact, each component of the pair (n, m) admits just five possible values, (n_i, m_i) = (±1, 0), (0, ±1 or 0). From these two observations, the pair of relations (IV.3) is equivalent to

with a, b Î and |a_i| = |b_i| (for, just analyse each case separately and note that the original 9 = 3×3 cases are reduced to 5, by the second observation above). Define the translation T_{a, b}:(p, k) (p+pa, k+pb) and the ''rotation-reflection-dilatation'' given by the orthogonal matrix A = , where 1 denotes here the d×d identity matrix. Then, the pair of relations (IV.4) is equivalent to

for all a, b Î with |a_i|= |b_i|. Therefore, the region D is the image of the square of side 2e centered in 0 by the inverse of AT_{a, b}, for every a, b Î with |a_i|= |b_i|. Such a pairs (a, b) are the center and the corners of the dotted big square shown in Fig. 2, and the region D is the union of the five shaded diamond shaped sub-regions. 3

We split the dp dk integral in (IV.2) in two pieces, . The integral on D^c is O(), with m¢ > m. More delicate is the analysis of the integral on D. It can be written as a sum of integrals on each of the regions D_{a, b},

In the integral above we perform the change of variables given by the transformation AT_{a, b}, with Jacobian determinant (–2)^d, to get

where u: = v(AT_{a, b})^–1. Notice that the four regions in the corners of the big dotted square in Fig. 2 are identified as a single one on the torus. Therefore, the region D is actually the union of two diamond shaped regions on the torus. The proof of the Theorem III.1 will be continued from this exact point at the Sec.V below. The remaining of the present section is a digression.

Instead of condition (a) of the Assumption, consider the following weaker one:

(a')G(p, k) is a ''sufficiently differentiable'' function defined in the torus (i,e., periodic), depending on the variables p and k just in the combinations p+k and p–k respectively, m< G(p, k), and with the following property: there exists e > 0 such that the matrix B = B(p), whose entries are given by

is positive defined and non-singular for |p| < e. Furthermore, (grad_kG)(p, 0) = 0, for |p| < e.

As in [9], using the results of [16] the integral in brackets in (IV.7) can be estimated using the method of Laplace, which gets the asymptotic decay

The estimative in (IV.8) is valid for all regions D_{a, b} and is, therefore, valid for the integral on D. The power-law correction |p₀|^–d/2 to the exponential decay of the four-point correlations found above was obtained with a simple analysis, and a less restrictive condition on G. As we will show in the next section, they can be improved, leading to the stronger power-law correction |p₀|^–d, mentioned in Theorem III.1.

V. PROOF OF THEOREM III.1

Assuming the condition (a) for the function G

using (V.1) in (IV.1) we get

Now we can use, as in [9], the results of [16, p. 148 and ff.] on a multidimensional adaptation of the method of Laplace to estimate both integrals in (V.2), one at each time, beginning with the dk integral. We get that expression (V.2) decays asymptotically as

when t₀®¥. See ^{Appendix A} for the details. This bound, valid on each region D_{a, b}, extends immediately to the integral on D. The integral on D^c can be split into the integrals on two complementary regions, R and R^c Ç D^c, where R is the shaded region in Fig. 3.

In each rectangular sub-region R_{a, b}, just one of the integrals in (V.2) has an exponential decay with mass rate m/2 corrected by , while the other one has only an exponential decay with mass rate m¢/2, with m¢ > m. Therefore, these integrals decay as

As in the previous section, the integral on R^c Ç D^c has an exponential decay with mass rate m¢ > m. Finally, collecting the pieces, we have

being a positive constant. This completes the proof of Theorem III.1.

VI. DERIVATION OF EXPRESSION (III.5)

In this section we derive condition (III.5) from more basic hypotheses. The relation of the operator R(k) with the spectral measure of the energy-momentum operator, given by (VI.3), follows straightforwardly from the definitions introduced in Sec. II and at the beginning of Sec. III. The hypotheses H1-H3, stated below, are sufficient conditions for asymptotic completeness, as discussed in [19]. Moreover, a Radon-Nykodim derivative for the spectral measure of the energy-momentum operator (VI.5) can be explicitly derived in this case. Expression (III.5) of the Assumption is a direct consequence of the form of this Radon-Nykodim derivative. Directly from the definitions we have

where in the last equality we assumed x₀ = 0. Assuming now additionally h₀ = 0, identity (VI.1) takes the form

where Q(a):= [F(a)F(0)–m(j_aj₀)] W. Now, if f, g Î L²(⁺¹) are symmetrical, with purely spatial dependence, we have

Here, we have used (VI.2). Moreover, we denote Q(h):= å_xQ(x)h(–x), or

for the ''two-particle states'', and we have introduced the spectral measure of the energy-momentum operator dE_l: = d .

Let us briefly present some definitions. Let the unconnected four-point function be defined as (x₁,x₂,x₃,x₄) : = S₂(x₁,x₃)S₂(x₂,x₄)+S₂(x₁,x₄)S₂(x₂,x₃). As in expression (III.4), we can write in terms of the variables x, h and t, introducing D₀ as (x₁, x₂, x₃, x₄) = : D₀(t, x, h). Let the ''free resolvent'' R₀ be defined as R₀(k, p, q): = (k, p, q), considered as a family of integral operators indexed by k. Acting on symmetric functions, , f(p) = f(–p), it is given by R₀(k,p,q) = 2(2p)(k+p)(k–p)d(p+q) (see [19]). The so-called Bethe-Salpeter kernel K is defined by the Bethe-Salpeter equation R = R₀–R₀KR. Now, consider the following hypotheses:

H1 Existence of ''one-particle states'': The Fourier transform of two-point function is given by:

where Z(p) is a positive, C^¥ function; w(p) is real analytic, m,<w(p) < m+2d₀; 0 < d₀< m.

H2 Exponential decay of the Bethe-Salpeter kernel: The Bethe-Salpeter kernel K(k, p, q) is analytic in the region

for certain d_i > 0 (i = 1,..., d), and e> 0.

H3 ''Repulsive interaction'': K(k, p, q) = h 1+h²K₁(k, p, q), with K₁ satisfying H2. Here 1 is the function identically equal to 1 and h is a positive constant.

The hypotheses H1-H3 were verified in various models under several conditions by many authors (see [19] for a large list of references). We introduce also the following few definitions

It was proven in [19] that, for f in A_d, the measure d vanishes in (0, 2m) and, if d = 1, has a Radon-Nykodim derivative in [2m, 2(m+d₀)), given by

where, denoting (p₀, p) = (p₀, p₁), (k₀, k) = (k₀, k₁) and cos k₀–1 = x+iy, with x, y Î , we have

Replacing expression (VI.5) in the last integral in (VI.3), after the the change of variables given by p₁ = F^–1(l₀), we have

where

This establishes (III.5) under the above hypotheses.

VII. SOME FINAL COMMENTS

As a final remark, let us point that special mechanisms, eventually occurring in some model-specific situations and possibly related to particular symmetries or low-dimensional properties, can lead to some improvements of our estimates.

Expression (III.5) reflects the fact that the spectral measure dE_{(l0, –2k)} in (VI.3) is absolutely continuous below m¢¢ = 2(m+d₀). Physically, this fact reflects the absence of bound states. In the presence of two-particle bound states, additional d(l₀–2w(k)) terms must be added to the spectral measure, as in the case of the two-point function, studied by Schor in [22], where w is analogous to the dispersion curve w. In this case, a term like

has to be added to the r.h.s. of (III.5). As in the Sec. IV, it is easy to prove that such a term leads to a decay as (IV.8).

In terms of G, the convolution inverse of the two-point function, satisfying

the dispersion curve w is implicitly defined by (± i w(p), p) = 0, while the C^¥, positive function Z is defined by (see [22])

from which we get

By reflection invariance A1 (Sec.II), the two-point function is a symmetric function of p. From (VII.1), is equally symmetric and, finally, by (VII.3), the function Z is symmetric as well.

Assume that the function v in (III.5) is of the form v(p, k) = Z(p+k) Z(p–k) v₁(p), with Z symmetric. From the above observations and from (VI.7), this condition is not much restrictive. Under this hypothesis, the integral in (V.2) assumes the form

By the symmetry of Z, we have |Z(p)| ~ z₁+z₂|p|² near the origin, where z₁, z₂ are constants. Using this and the previously mentioned asymptotic estimates, expression (VII.4) becomes asymptotically

In specific models, it can happen that the constant c₁ above vanishes and the leading term becomes c₂/|t_0|^d+1. This behavior could also be reproduced provided the function v₁ above behaves as |v₁(p)|~|p|² near p = 0. This is possibly what happens in the high temperature Ising model in d = 2, where only the c₂-term reproduces the correct asymptotics. The precise analysis requires a model-specific study of the properties of the functions Z and v₁ that are beyond the scope of our general approach. See f.i. [15]. Note that the vanishing of either c₁ or c₂ is compatible with the claim > 0 in (V.5). The claim would be incompatible only if both c₁and c₂ of (VII.5) were simultaneously zero.

Received on 10 December, 2004

Considering the integral in (V.2), for any A, B, C positive numbers we can write

Now, as a consequence of equation (2.9.6) in [16, p. 149], we have

The Gaussian integral at the r.h.s. in (A.2) can be bounded by a term proportional to |t₀|^–d/2. Therefore

Analogously,

If we set A = C₃C₁|t₀|^–d, B = and C = C₃, using (A.3) and (A.4) the first term at the r.h.s. in (A.1) is bounded by B C₄C₂|t₀|^–(d+1)+2d = C₄C₂|t₀|^–1/2<C₄C₂, and for the second we have

Therefore, the l.h.s. in (A.1) is bounded by C₄C₂+C₃C₁ and this means that the integral in (V.2) is equal to A+O(B^–1), for any d> 0.

• [1] Ornstein, L. S., Zernike, F.: Accidental Deviations of Density and Opalescence at the Critical Point in a Single Substance. Proc. Acad. Sci. Amsterdam 17, 793-806 (1914).
• [2] Gates, D. J.: Correlation Functions for Classical Systems in the van der Waals Limit. J. Phys. A3, 223 (1970).
• [3] Fisher, M. E.: Correlation Functions and the Critical Region of Simple Fluids. J. Math. Phys. 5, 944 (1964).
• [4] Thomson, C. J.: Classical Equilibrium Statistical Mechanics Oxford: Clarendon Press, 1988.
• [5] Bricmont, J., Fröhlich, J.: Statistical Mechanical Methods in Particle Structure Analysis of Lattice Field Theories (I). General Theory. Nucl. Phys. B 251 [FS13], 517-552 (1985).
• [6] Bricmont, J., Fröhlich, J.: Statistical Mechanical Methods in Particle Structure Analysis of Lattice Field Theories II. Scalar and Surface Models. Commun. Math. Phys. 98, 553-578 (1985).
• [7] Bricmont, J., Fröhlich, J.: Statistical Mechanical Methods in Particle Structure Analysis of Lattice Field Theories. Part III: Confinement and Bound States in Gauge Theories. Nucl. Phys. B280 [FS18], 385-444 (1987).
• [8] Campanino, M., Ioffe, D., Velenik, Y.: Ornstein-Zernike Theory for the Finite Range Ising Models Above T_c Probab. Theory Relat. Fields 125, 305 (2003).
• [9] Paes-Leme, P. J.: Ornstein-Zernike and Analyticity Properties of Classical Lattice Spin Systems. Ann. of Phys. 115, 367-387 (1978).
• [10] Stephenson, J.: Ising Model Spin Correlations on the Triangular Lattice. II. Fourth-Order Correlations. Jour. Math. Phys. 7, 1123-1132 (1966).
• [11] Hecht, R.: Correlation Functions for the Two-Dimensional Ising Model. Phys. Rev. 158, 557-561 (1967).
• [12] Camp, W. J., Fisher M. E.: Behavior of Two-Point Correlation Functions at High Temperatures. Phys. Rev. Lett. 26, 73-77 (1971).
• [13] Aizenman, M.: Geometric Analysis of f⁴ Fields and Ising Models. Parts I and II. Commun. Math. Phys. 86, 1-48 (1982).
• [14] Fröhlich, J.: On the Triviality of lj_d⁴ Theories and the Approach to the Critical Point in d_(-)^>4 Dimensions. Nucl. Phys. B200 [FS4], 281-296 (1982).
• [15] Minlos, R. A. and Zhizhina, E. A.: Asymptotics of Decay of Correlations for Lattice Spin Fields at High Temperature. I. The Ising Model. Jour. Stat. Phys. 84 (1996), 85-118.
• [16] Sirovich, L.: Techniques of Asymptotic Analysis New York: Springer-Verlag, 1971.
• [17] Schor, R. S. and O'Carroll. M. Bound States in the Transfer Matrix Spectrum for General Lattice Ferromagnetic Spin Systems at High Temperature Phys. Rev. E 62, 1521-1525 (2000).
• [18] Schor, R. S. and O'Carroll M. Transfer Matrix Spectrum and Bound States for Lattice Classical Ferromagnetic Spin Systems at High Temperature J. Stat. Phys. 99, 1207-1223 (2000).
• [19] Auil, F., Barata, J. C. A.: Scattering and Bound States in Euclidean Lattice Quantum Field Theories. Annales Henri Poincaré 2, 1065-1097 (2001).
• [20] Auil, F.: Four-Particle Decay of the Bethe-Salpeter Kernel in the High-Temperature Ising Model. J. Math. Phys. 43 (2002), 6209-6223.
• [21] Fredenhagen, K.: On the Existence of the Real Time Evolution in Euclidean Lattice Gauge Theories. Commun. Math. Phys. 101, 579-587 (1985).
• [22] Schor, R. S.: The Particle Structure of n-Dimensional Ising Models at Low Temperatures. Commun. Math. Phys. 59, 213-233 (1978).
• [23] Spencer, T.: The Decay of Bethe-Salpeter Kernel in P(f)₂ Quantum Field Models. Commun. Math. Phys. 44, 143-164 (1975).
• [24] Spencer, T., Zirilli, F.: Scattering and Bounded States in lP(f)₂ Commun. Math. Phys. 49, 1-16 (1976).

APPENDIX A:  PROOF OF (V.3)

Publication Dates

• Publication in this collection
  06 Sept 2005
• Date of issue
  June 2005

History

• Received
  10 Dec 2004