Non Relativistic Limit in QFT: a Wilson Renormalization Group Approach in the Minkowski Space

Non Relativistic Limit in QFT: a Wilson Renormalization Group Approach in the Minkowski Space

A.J. da Silva^*

Instituto de Física, USP

C.P. 66318, 05389-970, São Paulo, SP, Brazil

Received on 19 April, 2001

We study the non relativistic limit of a model of fermions interacting through a Chern-Simons field, from a perspective that resembles the Wilson Renormalization Group (WRG) approach. The main difference of our approach to WRG is that instead of working in the Euclidean space, we directly work in Minkowski space. For the nonrelativistic limit this procedure admits a more direct interpretation of the results. As we will see, this modified WRG approach solves some difficulties, and gives a new understanding of non relativistic models that are not clear in the usual "classical" nonrelativistic (CNR) limit found in most text books. The method is general and our choice of the Chern-Simons as the gauge field is only for the sake of simplicity of illustration.

Models of a Chern-Simons [1] field interacting with non relativistic bosons [2] or fermions [3] have being studied in the literature both for its interest in general understanding of field theory by itself, as for its application to Condensed Matter Physics [4]. The use of these models face in general, the difficulties of their non renormalizability. This fact is the main reason for the interest, on the results of Bergman and Lozano [2], first in one loop, and later extended to three loops [5], that we pass to briefly reproduce. Their model consists of a non-relativistic boson field f of mass m, with a quartic self interaction and minimally interacting with a Chern-Simons field A^m, described by the Lagrangean

By explicitly writting the many n-point Green functions we can see that the only primitively divergent is the boson 4-point function. Up to one loop, the model can be made finite by the choice of a renormalized coupling constant l through the equation

where L is an ultraviolet (UV) cut-off and M an arbitrary constant (the renormalization scale) with dimension of mass. Their main observation is that at the critical value, l^* = ||, the one loop contribution vanishes and no renormalization of l is needed. At this choice of l the model regains the scale invariance that it has at classical level, and the relative wave function of two bosons reproduces the Aharonov-Bohm scattering amplitude [8] up to the second Bohr order. So, even being nonrenormalizable the model results to be finite.

The model of non relativistic fermions interacting with the Chern-Simons field was also shortly discussed in [2] and studied in more details in [3]. In this last paper it is shown that the one loop scattering of two fermions with spins of the same sign (in 2+1 dimensions the spin is a pseudo-scalar that assumes the values plus or minus 1/2 ) is finite in one loop. This is due to the contact interaction represented by the Pauli interaction, that is already present in the minimal interaction of the fermions with the gauge field, and that has a role similar to the contact interaction induced by the fine tuned l^*f⁴ term in the model discussed in the previous paragraph. As for the scattering of two fermions of opposite spins the Pauli interaction does not have any role and the amplitude is divergent [3] unless a quartic fermionic interaction of the form c(L) y^*y f^*f where y and f represent respectively fermions with spin plus and minus 1/2, and c is a constant that depends logarithmically on the UV cut off L. Nonrelativistic models are in general non renormalizable and the necessity of adding new monomials in the lagrangean at any new order of approximation is not unexpected. But from the relativistic point of view it poses a difficulty. If this non relativistic model is thought to be the low energy energy limit, in the way it is generally taken in most texts [9], of a model of relativistic Dirac fermions interacting with a Chern-Simons field, this monomial should come from a similar quartic interaction in the Dirac fermions that is non renormalizable! We will show that this is, in fact, a false problem. No quartic non renormalizable self interaction is needed in the "parent" relativistic model if a new perspective on the non relativistic limit in field theory is taken. Before going to the description of this new limit, lets us briefly resume, in an example, the "Classical Non Relativistic Limit", and discuss why it is not always correct. Let us consider, in 2+1 dimension, a 2 component Dirac fermion field Y, that represents a spin plus fermion and its anti-fermion, interacting with an external electromagnetic field A^m, as described by the Lagrangean density (the gamma matrices are g⁰s⁰,g¹is¹ and g²is² where s^m are the Pauli matrices)

The corresponding equation of motion is:

Let us now consider a positive energy solution Y of this equation. To make contact with the non relativistic description, in which the rest energy m of the particles is not included in the solution, lets make in the above equation of motion, the substitution

The result is the pair of one component equations

where P_± = P¹ ± P² , and Pⁱ=-i-eAⁱ. If we make the assumptions that: e|A⁰| << m and that the momentum space components of y and c are non null only for low momenta and energies, that is for (||, E ) << m , then the second equation can be approximately solved for c , and inserted in the first, giving:

where B = Ù is the magnetic field. The one component spinor y represent a fermion with spin plus. The last term is the Pauli magnetic moment-magnetic field interaction term. The Lagrangian density corresponding to this equation of motion is the so called Pauli Schrödinger (PS) lagrangean of non relativistic fermions in an external electromagnetic field

The essential facts behind the above "classical"non relativistic limit are the asumptions on the strength of A^m and the momentum space support of the field Y (this second assumption is not meaningfull without the first, since a low energy initial state of Y can be driven to a relativistic state by the action of a strong A^m field ). Suppose now that A^m is not an external, controllable field, but is a dynamical field with dynamics given by a Maxwell or Chern-Simons term (that must be thought as a new monomial added to the Lagrangean (3)). Let us now consider in this new theory, the scattering of two low energy fermions, their energy and momenta given by (p⁰ = m + , ±) with || << m. On Fig. 1 we draw a possible one loop contribution (among others) to this process. The corresponding amplitude is given by a Feynman integral in the loop momentum k^m:

Figure 1.
Vacuum polarization. The double line represent Dirac fermion propagators, and the wavy line the CS propagator.

The main observation on this equation is that, even if the process we are treating is a low energy one, the amplitude receives contributions of high energy intermediate states, represented by propagators whose dynamics is essentially relativistic, and so, not coming from the Feynman rules of the non relativistic Lagrangian (9). The bigger or lower suppression of the contribution of these high energy states to the whole integral above, depends on the dynamics of the exchanged A^m field. As we will explicitly see in one example below for the Chern-Simons field, they effectively give a contribution that can not be understood as coming from the non relativistic Lagrangean (9). What about the description of this same scattering process starting from the non relativistic theory given by (9) with a dynamical A^mu field? The amplitude for the same process of Fig. 1 is of the form

where now p⁰=||²/2m. Here also, the integral extends up to infinity momenta. High energy intermediate states also contribute to the amplitude, even with a bigger weight than to , as seen from the worse UV behavior of the Pauli-Schrödinger(PS) propagator. It must yet be observed, that from the view point of the Special Relativity, the PS propagator misses to represent the propagation of high energy intermediate states. Due to these facts, some authors in Field Theory [10] take the view of a Non Relativistic Field Theory as a Cutoff theory. This means that instead of considering, in a wrong way, the contribution of the high energy intermediate states, they prefer to decouple them from the theory, by limiting the integration in the Feynman integrals up to a maximal energy-momentum compatible with the newtonian description provided by the Pauli-Schrödinger propagator. This is also a view taken by some authors in Optics [11]. There, the typical energy involved in the scattering processes are of the order of the ionization energy of the atoms, that is, of order a²m, where a is the fine structure constant and m is the electron mass. The assumed cut off is L = a m, of the order of the inverse of the Bohr radius of the atom, much bigger than the typical energies involved in optical processes, but much smaller than the rest energy, m of the electron.

We will take a slight variation of these ideas, suited for understanding the results on non relativistic models with a CS field in the Coulomb Gauge, as treated in the literature [2, 3]. We will consider a non relativistic cutoff, only in the spatial momentum , of the Feynman integrals; that is, we will calculate the Feynman integrals, first freely integrating the k⁰ momentum component up to infinity, and then restricting the integration in || to the region (0, L) with L chosen so that || << L << m, where is a characteristic momentum of the low energy process in which of interest, and m is the mass of the fermion field. This choice has the additional technical advantage of not breaking the locality in the time direction and avoiding the appearence of higher order derivatives in time in the Lagrangean. The way, we are proposing these Cutoff (or Effective) non relativistic models are related to originally relativistic ones, is akin to the ideas of the Renormalization Group of Wilson [12]. Let us first outline the main ideas in a one dimensional toy model.

Consider a relativistic field theory in one space-time dimension, with dynamics given by a Lagrangian

^rel(F). Its functional generator is given by

where j is an external source for the field F, and F(p) dF(p). Suppose that we are only interested in describing "non relativistic" processes involving external particles with momenta p smaller than a certain value L << m, where m is the mass of the field F. This limitation can be implemented in the functional generator by choosing the external source to be non null only for the momentum region (0 , L). The F field can be separated in F(p) = f(p) + h(p) where f represents the low momenta modes and has support in (0, L) and h has support in (L, ¥) and represent the high momenta modes. The integration measure goes in F = fh, the Lagrangean separates in 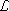^rel(F) = 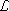^rel(f + h) = 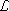^rel(f) + 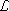₂(h) + 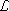_int(f, h), where 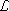₂(h) is the quadratic part of 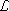^rel(h), and 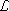_int (f, h) represents the interaction terms that depend on f and h. As j only have support in (0, L), the term j F gets reduced to j f. The functional generator becomes

and can be written in the form

where

^effect(f , L) =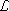 ^rel(f) + d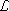(f , L) with

The effects of the high momenta modes h are incorporated in the effective dynamic of the low energy ones, through the additional term d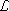(f, L). It is the effective Lagrangian, 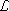^effect , in which the only remaining free momenta modes are the non relativistic ones, and not the original 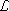^rel, that will give through the approximations called Classical Non Relativistic Limit (exemplified above), the same results as the original relativistic model, when calculating low energy processes.

The integration in h in (15) can in general be done by expanding the exponential in a series of powers of ò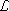_int(f, h), as indicated in the second line of the last equation above. The result will be a series of Feynman graphs with the propagator of h in the internal lines and the field f in the external legs. This means that the integrations in the loop momenta are restricted to the interval (L, ¥). The result is in general L dependent (as we will see the result of Bergman and Lozano is an exception) giving an Effective Lagrangian 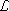^effect that is dependent on L.

Let us now return to the models that we want to treat in 2+1 dimensions. We will start with the relativistic Lagrangean

where Y (F) is a 2 component Dirac field representing a fermion and anti fermion of spin plus (minus). In the Coulomb Gauge, the CS propagator is (indices m, n,... runs from 0 to 2 and indices i, j,... runs over 1 and 2)

and will be represented by a wavy line. The Dirac propagators of the relativistic fermions will be represented by double straight lines. Through the same steps that led (3) to (9) we get the Classical Non Relativistic limit of this model

where y (f) are anti commuting one-component fields representing a spin plus (minus) fermion (nonrelativistic PS fermions). The fermionic PS propagator will be represented by a single straight line. This model has several different vertices : F^*FA⁰, F^*F, F^*FA^mA_m and F^*FB, where F stands for f or y. The F^*FB vertices (Pauli interactions) give a local interaction between two fermions, mediated by the the propagator

that we will represent by an dashed straight line.

We will leave the result above for future use, and return to the construction of the Effective Non Relativistic Model. This will be done by calculating different low energy processes in the Relativistic Theory and identifying the contributions that come from the low energy intermediate states (and are the same that come from the Classical Non Relativistic Model (19) with a cut off L) and the contributions that come from high energy intermediate states, and that must be incorporated in the Effective Non Relativistic Model, through new terms in the Lagrangian. We will restrict the calculations to the one loop order. The sum of Feynman graphs, written as a loop integral can be separated as

In the low momenta part, both || and || are smaller than L << m, and we can safely make the approximation w() = m + , for both p and k. The propagators and vertices collapse in the correspondent ones, gotten from the Lagrangean 16. In the high intermediate energy part this approximation can be taken for w(p) but not for w(k). As || << L and the integral is for || > L, the result, H(p, L), is analytic in p and can be expanded in a power series in p. Every term of this expansion is a contribution to the process, that can be represented by a (new) local term in the Lagrangean of the Effective Non Relativistic Model. The three processes that require renormalization are the Vacuum Polarization Tensor (Fig. 2) the Fermion Self energy (Fig. 3) and the Vertex Correction (Fig. 4). The calculation, of these quantities in covariant gauges are presented in many papers in the literature ([13]). In the Coulomb Gauge it was obtained in [6, 7]. The results, separating the contributions of the low (first bracket) and of the high (second bracket) intermediate momenta contributions are respectively

As indicated in these formulas, all the contributions to these functions come from the high momenta intermediate states. In fact it is well known that these same functions are zero when calculated in the classical non relativistic model [2]. As consequence the whole contribution to these functions, come only from the high momenta intermediate states and are independent of the cut off L. The effects of these terms in correcting the low energy dynamics of the fermions and the CS field are simulated by adding to the Lagrangean (19) the terms

From (25) and (19) we see that the CS field becomes a dynamical propagating field, the so called Maxwell-Chern-Simons field ([1]). We can also see that the magnetic momenta of the spin plus and minus fermions are corrected to [7]

(these results where obtained previously in the literature in covariant gauges in [13]).

Figure 2.
Fermion self energy.

Figure 3. Contributions ( in the Coulomb Gauge) to the scattering of a fermion by an external field A. The action of the external field is represented by a cross.

Figure 4.
Example of a one loop graph contributing to the scattering of two fermions.

Let us now look at the elastic scattering of two low energy fermions. For simplicity we will work in the Center of Momentum Reference Frame in which the incoming fermions have energy and momenta: (m + , ) and (m + , -) and the outgoing fermions have (m + -, -¢) and (m + , -¢) with || = |-¢| << L. The amplitude is a function of || and the angle between and -¢. We prefer to write it in terms of and the two vectors + -¢ and -¢- . In Fig. 5 are shown the non null graphs contributing to this process.

Figure 5.
Non null graphs contributing to the scattering of two Dirac fermions. On the right of the diagrams are represented the correspondent graphs in the classical non relativistic model.

For the scattering of one fermion of spin plus and other of spin minus, the contributions of these graphs are listed below, separated in two rows. In the first are the contributions of the low intermediate momenta states, (0, L), and in the second row, the local (independent of p) contributions of the high momenta intermediate states, (L, ¥).

Some observations are in order: 1. The (0, L) parts of each graph ( of the Relativistic Model ) are the same as calculated from the Classical Non Relativistic Model (19) with a cut off L, through the graphs drawn on Fig. 5, at the right of the corresponding relativistic ones. 2. The (0, L) part of each graph can depend on the non relativistic cut off L (see 5e) but the whole graph is independent of L ,as can be seen by adding , for each graph, the terms of the first and the second row. 3. Had we interpreted L as an UV cut off in the usual way, i.e. L® ¥, and (0, L) would be a divergent amplitude. 4. The (L, ¥) non null contributions of the graphs 5b and 5c could also be get by calculating 5a, starting from the already corrected Effective Lagrangian given by (19) plus (29). 5. The non null (L, ¥) part of diagram 5e instead, is a new term that must be incorporated in the Effective Lagrangian as a local quartic interaction of the form y^*y f^*f. It must be stressed that this term comes from the integration over the high momenta intermediate states of the Renormalizable Relativistic Model; no quartic term of the form Y^*Y F^*F is needed in the "parent"Relativistic Model to generate this quartic term in the Effective Non Relativistic Lagrangian. The Effective Non Relativistic Model incorporating all these terms can be written

The calculation of the magnetic moment of the fermions, the propagator of the (Maxwell) Chern-Simons, and of the low energy scattering of two fermions, in this theory, using a cut off L (up to one loop), give the same results as the calculation of the same quantities starting from the Relativistic Model (16). For example, the amplitude of scattering of one spin plus and one spin minus fermion ( the sum of the two rows in equation (27)) gives [14]

The calculation starting from the classical Non Relativistic Model, (the sum of terms in the first row in equation (27)) would instead, give the "divergent" result [3]

These results exemplify our main point: taking the non relativistic limit in the Lagrangian and equations of motion (Classical Non Relativistic Limit) and then calculating a process gives in general, a result different than, first calculating the same process in the relativistic theory and later taking the non relativistic limit of the result.

To finish this talk I will turn to the problem that motivated this study: the finite result for got in [2] for the scattering of two bosons and its extension [3] to the scattering of two spin plus fermions (we will think that the two fermions are not identical and we don't need to anti symmetrize the amplitude with respect to the outgoing particles). The non null graphs contributing to this process are the same of Fig. 5. The result is

The differences of these results to the ones in (27) come from the Pauli interaction of the magnetic field of each fermion with the magnetic moment of the other fermion. The effects of these interactions cancel in the scattering of a spin plus and a spin minus fermion and add in the case of two spin plus fermions. The results for ^effect and are now

The unexpected fact that this last result is finite, independent of L, is in the literature [2] related to the preservation at quantum level, of the scale invariance that the classical non relativistic model presents. In the model of bosons interacting with the CS field this only happens for the special value of the quartic self interaction discussed in the introduction. For fermions the same fact is provided by the Pauli interaction which already appear in the minimal interaction with the CS field; no fine tuning of coupling constants is needed. We here showed another aspect of this independence of L. Unusually, not only is independent of L: their high and low momenta intermediate energy contributions are separately independents of L. So the difference of the amplitudes got from the Classical or the Effective Non Relativistic Models is a finite constant independent of L. If the fermions are identical we must anti symmetrize the amplitudes (32) and (33) in the outgoing particles. In this case no difference at all appears in the final result. The amplitude got from both (32) and (33) is : i , and gives the Aharonov Bohm scattering amplitude for two identical fermions.

To finish the talk I should mention that one of the main utility of the effective non relativistic theory is in the calculation of low energy bound states, what is in general a very involved problem starting from a relativistic formulation, due to the mixing [10] of the several scales of energy involved.

Aknowledgements

This work was partially supported by CNPq (Conselho Nacional de Desenvolvimento Cientifico e Tecnologico) and by FAPESP ( Fundação de Amparo a Pesquisa do Estado de São Paulo). The author thanks M. Gomes for critically reading the manuscript.

References

[1] S. Deser, R. Jackiw and S. Templeton, Phys. Rev. Lett. 48, 975 (1982) and Ann. Phys.(NY) 140, 372 (1982) ; J. F. Schonfeld, Nucl. Phys. B185, 157 (1981).

[2] O. Bergman and G. Lozano, Ann. Phys.(NY) 229,416 (1994).

[3] C. R. Hagen, Phys. Rev. D 56 (1997) 2250.

[4] S. C. Zhang, T. H. Hansson and S. Kivelson, Phys. Rev. Lett. 62, 82 (1989).

[5] D. Z. Freedman, G. Lozano and N. Ruiz, Phys. Rev. D 49 1054 (1994).

[6] C. R. Hagen, Ann. Phys. (NY) 157,342 (1984).

[7] M. Fleck, A. Foerster, H. O. Girotti, M. Gomes, J. R. S. Nascimento and A. J. da Silva, Int. Journ. Mod. Phys. B 12, 2889 (1997).

[8] Y. Aharonov and D. Bohm, Phys. Rev. 115 (1959) 485

[9] V. B. Beretetskii, E. M. Lifshitz and L. P. Pitaevskii, Quantum Electrodynamics, Pergamon Press (1980). C. R. Hagen, Phys. Rev. D 31, O. Bergman, Phys. Rev. D 46,5474 (1992).

[10] W. E. Caswell and G. P. Lepage, Phys. Lett. B 167, 437 (1986); G. P. Lepage, Proc. of TASI 89, (1989).

[11] C. Cohen-Tannoudji, J. Dupont-Roc and G. Grinberg, Introduction to Quantum Electrodynamics, J. Willey and Sons (1989)

[12] K. G. Wilson, Phys. Rev.B 4, 3174 (1971).

[13] I. I. Kogan and G. Semenoff, Nucl. Phis. B 368, 718 (1992), I. I. Kogan, Phys. Lett. B 262, 83 (1991), G. Gat and R. Roy, Phys. Lett. B 340, 362 (1996).

[14] M. Gomes and A. J. da Silva, Phys. Rev. D57 (1998) 3579; H.O. Girotti, M. Gomes, J.R.S. Nascimento and A.J. da Silva, Phys. Rev. D 56 (1997) 3623. (The correspondent problem for scalars interacting with the CS field was studied in M. Gomes, J.M.C. Malbouisson, A.J. da Silva, Phys. Lett. A 236 (1997) 373; Ibid., Int. J. Mod. Phys. A 13 (1998) 3157).

Publication Dates

• Publication in this collection
  05 Mar 2002
• Date of issue
  June 2001

History

• Received
  19 Apr 2001