Quantum atom optics with trapped Bose-Einstein condensates

REGULAR ARTICLES

Quantum atom optics with trapped Bose-Einstein condensates

M. K. Olsen

Instituto de Física da Universidade Federal Fluminense, Boa Viagem 24210-340, Niterói, RJ, Brazil

ABSTRACT

Both Bose-Einstein condensates and optical fields are composed of bosons, so that the majority of the processes which have long been studied in quantum and nonlinear optics have equivalents in the field of Bose-Einsten condensation. However, due to the masses of the condensed atoms, the confining potentials and the huge collisional nonlinearities, the simpler theoretical approaches common to quantum optics can sometimes give misleading answers when applied to condensates. In this work we describe some of the areas where simplified treatments can be misleading, and compare and contrast the predictions of quantum many-body treatments with those of the single-mode type treatments which have been so successful in quantum optics.

1 Introduction

Quantum optics was possibly the first area of physics which allowed for simple investigations of many of the fundamental mysteries and paradoxes of quantum mechanics [1]. These investigations, both theoretical and experimental, were facilitated by the invention of the laser and the Fabry-Perot cavity and also by the fact that photons are essentially non-interacting in vacuum. The laser can provide a bright source of well stabilised coherent light which is the starting point for many quantum optics experiments, while Fabry-Perot cavities select a small number of resonant modes which can then interact with a nonlinear medium to produce light with nonclassical properties. The use of coherent states, the small number of modes which need to be taken into consideration, and the fact that any interaction is effectively only with the nonlinear medium all combine to simplify theoretical analyses. Even though the electromagnetic field is composed of many photons, an approximate theoretical approach not much more complicated than that used in single-particle quantum mechanics often gives valid predictions.

When we wish to consider trapped Bose-Einstein condensates (BEC), in principle there exist several ways to theoretically model the dynamics of interacting condensates, but in practice we find that our options are somewhat limited. A full and exact treatment requires a description in terms of quantum fields, but as the resulting functional Heisenberg equations of motion are highly nonlinear, this approach is impracticable. An equivalent option, the quantum master equation, is totally impractical as the dimension of the required Hilbert space is far beyond the capacities of any computer. Assuming non-vanishing expectation values for the field operators in the Heisenberg equations leads to the mean-field approach of the Gross-Pitaevskii equation (GPE) [2, 3], which, even though it is derived using quantum statistical considerations, cannot describe the effect of these on the dynamics. Worse, for systems of interacting fields, the GPE has been shown to give misleading predictions in some parameter regimes [4, 5]. An alternative approach which can say something about the quantum features is path-integral Monte Carlo [6], but this method is only really practical for calculating ground state properties and not dynamical evolution. Other recent developments have been the use of stochastic wave functions [7] to solve N-boson time-dependent problems, and a stochastic GPE, developed from the quantum kinetic master equation [8]. We note here that all these approaches are truly in the realms of many-body theory and hence more complicated than the methods normally used in quantum optics. In this work we will give several examples where an oversimplified theoretical approach, even though such approaches have enjoyed great success in quantum optics, can be shown to give misleading results.

2 Theoretical descriptions

2.1 An intracavity electromagnetic field

A single-mode non-interacting electromagnetic field can be described by a simple harmonic oscillator Hamiltonian,

where 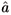is the well-known bosonic annihilation operator. If we wish to confine this mode inside an optical cavity, we must add pumping and damping terms,

where Î represents a classical pumping field and the G are bath operators which represent interactions, via the cavity mirrors, with a thermal reservoir. As optical frequencies are very high, we can assume that this thermal reservoir is at zero temperature. As photons are massless, we can make the Markov approximation and finally arrive at a simple set of Heisenberg equations for the intracavity field, in the rotating wave approximation [1],

where g represents the cavity loss rate. Of course, a pumped cavity is not a particularly interesting system, so we may wish to include the interaction with an intracavity nonlinear medium, so as to produce nonclassical states of light. With the inclusion of this interaction, the equations do not generally become much more complicated. We may also remember that it is difficult to make measurements on the intracavity field, so that we will need to relate the field inside the cavity to that outside, which may be measured. This is easily done by using a set of input-output relations [9]. The main reasons that these have a simple form are that we can consider a small number of modes and the fact that photons are massless, so that once they leave the cavity, they are gone forever. The latter fact allows for the use of the Born and Markov approximations.

2.2 A trapped condensate

One of the simplest possible condensate systems, from an experimental and theoretical point of view, is a single species trapped Bose-Einstein condensate, in some ways analogous to the intracavity electromagnetic field described above. There have been relatively few attempts to treat the full quantum dynamics of this simple system, and it is sometimes claimed that no computational approach is feasible [10], due to the large size of the many-body Hilbert space. The first published attempt to dynamically model this system as a spatially dependent field, while rigorously including the quantum features, was by Steel et al. [11], who developed functional positive-P [12] and Wigner [13] representations for a trapped one-dimensional condensate, which were then used to calculate quantities such as the first order coherence properties.

By comparison with the simplicity of Eq. 3, a quantum calculation of the evolution of the BEC field operator is a formidable task, a direct route using a number state basis not being a realistic option due to the enormous size of the Hilbert space. However, the phase-space techniques of quantum optics may be generalised to provide a complete description of the condensate field operator. The key to this approach is the representation of the density operator using phase-space quasi-probability functions. We will now outline the derivation of the equations resulting from the use of a functional positive-P representation.

A one-dimensional system can be considered by assuming a highly anisotropic harmonic trap with the longitudinal and radial trap frequencies (w_z and w_r respectively) satisfying l = w_z /w_r << 1. This corresponds to a cigar-shaped trap such as has commonly been used in experiments [14, 15]. The operator is then assumed to factorise so that we may write the one-dimensional longitudinal Heisenberg field operator as

where m is the atomic mass. Adopting harmonic oscillator units in the axial direction with a₀ = , t = w_zt, x = z/a₀ and 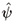(x, t) = (z, t), the one-dimensional second-quantised Hamiltonian is (dropping the spatial dependence for notational convenience)

where is the linear operator

m is the scaled chemical potential, and G = 2a/(la₀) is the scaled nonlinear constant with a the s-wave scattering length.

The positive-P field equations may be obtained by introducing the functional P-distribution [16, 17]

where r^(a) denotes the density operator r(t) antinormally ordered with respect to the field-operators 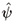, 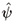^† in the Schrödinger picture. Putting the master equation obtained from the Hamiltonian (5) into antinormal order, and using the following functional analogues of the operator correspondences [18],

one finds the functional Fokker-Planck equation,

The diffusion matrix of this equation is not positive-definite and so there is no straightforward mapping onto a single stochastic differential equation [18]. A positive-P representation must be used, doubling the phase space with the mapping

where y₁(x, t) and y₂(x, t) are independent fields. Note that sometimes the notation y⁺(x, t) is used instead of (x, t), to denote the c-number field that corresponds to 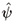^†. We now obtain a positive-definite diffusion matrix and finally derive the pair of Itô stochastic differential equations,

where the noise sources h₁ and h₂ are real, Gaussian and delta-correlated in time and space, with the correlations,

This set of coupled equations can then, in principle, be numerically integrated on a spatial lattice and averaged over a large number of trajectories to calculate any desired operator moments. In practice, the numerical integration presents severe difficulties, although some progress has been made toward overcoming these [19, 20, 21, 22, 23]. We readily see that even the simplest method which can hope to give a complete description of a trapped condensate is much more complicated than the equations used to describe an intracavity electromagnetic field. If we were to add the equivalents of the pumping and damping terms as in the optical case, the situation would become even more complicated. For example, although we can model the laser pumping of an optical cavity in a very simple manner, the equivalent with the condensate is possibly evaporative cooling of a cloud of thermal atoms, which again needs a sophisticated theoretical treatment [24].

3 Quantum state of a trapped condensate

Another operational difference between quantum optics and BEC lies in the ease which with quantum states, usually represented by the appropriate Wigner function, can be found. When we wish to numerically integrate stochastic differential equations to investigate the quantum dynamics of a given system, the initial conditions used can be very important. Generally in quantum optics, the laser which drives the system is accurately represented as a coherent state, whereas the quantum states of the interacting modes come naturally from the dynamics. However, for some quantum optical processes it has been shown that different initial states can result in quite different dynamics [25, 26]. As these processes have equivalents with BEC, we may assume that the initial state of the trapped BEC should also be important in theoretical investigations.

In quantum optics, some of the most utilised states are the coherent state, the Fock state and the thermal state. The coherent state gives a good description of a well-stabilised laser operating above threshold, as well as for the field of a cavity pumped by such a laser. The Fock state, which has a fixed number of quanta, arises naturally when we consider the decay of a single excited atom, for example. The thermal state describes the radiation emitted by black-bodies. While other states are important, they usually arise because of the dynamics of a system and are not important as an initial condition in physically realistic calculations.

On the other hand, the quantum state of a trapped condensate is almost certainly none of the above, although Fock and coherent states often appear as candidates in the literature. The coherent state appeals because of the coherence properties exhibited [14, 27, 28], but has the problem of a largish uncertainty in number, which is conceptually difficult to understand as atoms are not created or destroyed at typical temperatures. We should also remember that a coherent state is coherent to all orders, not just to first order as demonstrated by amplitude interference experiments. The Fock state is superficially an appealing choice, but as the condensate is in contact with an environment, particles can be added or removed. This state also has the problem that it has no defined phase. As the nonlinearity due to s-wave collisions between condensed atoms is equivalent to a Kerr interaction, we may expect to find that the actual state is none of the above. Several candidates have been offered in the literature, all making various levels of approximation. An early calculation [29] predicted an amplitude eigenstate, while a subsequent, more rigorous calculation [30], predicted a sheared Wigner function which approximated a number squeezed state. More recent attempts, using the Hartree approximation, found a Q-function which suggests both amplitude quadrature and number squeezing [31] and a function expressed in terms of generalised coherent states [32].

In fact, the calculation of the full Wigner function is a difficult task. The formal manner of calculating a Wigner (or other pseudo-probability function) distribution is to solve the appropriate Fokker-Planck equation. With a trapped BEC, this is complicated by the fact that the equation for the Wigner function has third-order derivatives, so that the usual methods cannot be used [11]. Even after discarding these terms, the task is still not simple, as the equation has both spatial and temporal dependence, is highly nonlinear, and contains kinetic energy and potential terms. Although the Hamiltonian exhibits some similarities to that of the Kerr amplifier, this latter system can be treated as zero-dimensional whereas this treatment is somewhat dubious for a trapped BEC. It seems that the actual Wigner function, once found, may prove to be spatially dependent as well as depending on the field variables. It is even possible that it may not be separable in terms of its different arguments, which would lead to a much more complicated function than any of those proposed to date. That the calculation or measurement of this Wigner function may be important has been shown in a series of articles which show that the process of photoassociation to form a molecular condensate exhibits dynamics which can depend on the actual initial quantum state [33, 34, 35, 36]. We will return to this subject in later sections.

4 Input-output relations

In quantum optics, the interaction of light with a nonlinear medium within a cavity is a common way of fabricating nonclassical states of the electromagnetic field. As measurements are made on the field outside the cavity, we need a means of theoretically relating the fields within the cavity to those outside. Using the Born and Markov approximations, Collett and Gardiner (see also Yurke [37]) developed the well-known input-output relations [9], which can be simply written as

which is a boundary condition relating each of the far-field amplitudes outside the cavity to the internal cavity field. g represents the cavity loss-rate. This relationship is easily transformed into frequency space, allowing for the simple calculation of output spectra. It can also provide, once measurements are made on the output fields, a simple way to calculate the field statistics inside the cavity.

The Born and Markov approximations which were used in the development of Eq. 13 have a restricted validity when we deal with trapped and outcoupled atomic systems as in, for example, Bose-Einstein condensates. The basic reason for this is that any atoms outcoupled from a trap tend to remain in the boundary region much longer than photons, which, being massless, exit at the speed of light. This means that there is a finite time during which the atoms remain in this region, still being able to interact with the trapped state. Hence the first and second Markov approximations are not valid because the system now has a finite memory and the outcoupling does not happen instantaneously. Formalisms to cope with general output coupling of trapped bosonic atoms have been developed [38, 39, 40, 41, 42, 43], allowing calculations to be made in the regime where the Markov approximation does not hold. These methods allow, for example, the calculation of the energy spectrum of the steady state output flux of a hypothetical continuous wave atom laser. It has also been shown in which regions of operation the Markov approximation may be valid, demonstrating that non-Markovian damping can lead to markedly different behaviours.

4.1 Non-Markovian output coupling

Following the approach of Hope et al. [42], we model a one-dimensional atom laser by separating it into three distinct physical regions and an interaction region, as shown in Fig. 1. Starting from the left, we have the pump reservoir, coupled to the trap by an irreversible process, described by the Hamiltonian _p. We do not specify a physical mechanism for the pump, but do state that it is not directly coupled to the output modes and is close enough to being a continuous process that we can consider the whole atom laser to be operating in the stationary regime.

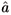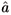The lasing mode is a condensate contained in an atomic trap with large enough energy spacing to be considered as effectively operating in the single-mode regime. In order to simplify the treatment, we will ignore collisional interactions between the trapped atoms. This means that we can approximately describe the lasing mode by bosonic annihilation and creation operators and ^† and the Hamiltonian _s. The external output field consists of atoms in a different electronic or magnetic state to the lasing mode atoms, so that it is no longer trapped by the potential. The output modes are described by the bosonic field operators 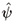(x) and 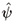^†(x) and the Hamiltonian _o. The coupling between the lasing mode and the output field is described by the Hamiltonian _i, so that the total Hamiltonian is written

with

where k(x, t) represents the form of coupling between the condensate and the output field, and w₀ represents the frequency of the lasing mode. Note that, without atom-atom interactions, w₀ does not depend on the mode occupation. As the pump does not couple directly to the external modes, the following commutation relationships hold

Hope et al. [42] have shown how it is possible to go to the Heisenberg picture, resulting in the general input-output relationship for this system,

where

_H(x, t) and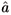 _H(t) are the Heisenberg operators corresponding to 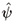(x) an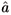d , and

The memory function, F, is proportional to a d-function in time in the Markovian case, giving the well known input-output relationships of quantum optics. More generally, it is written

where G(x, t, y, s) is the Green's function propagator due to the output Hamiltonian, _o, only. Eq. 20 allows us, in principal, to calculate any observables of the output field, provided that we know the appropriate Green's function and the history of 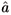_H(s). We should also note here that, in the stationary regime, F(x, t, s) is actually a function of (x, t - s).

4.2 Inverting the relation

In an actual experimental situation, it would be more common to perform measurements on the output of the atom laser, as it is this which is accessible. Hence we wish to invert the relationship (18) and thus find observables in the output which can be mapped onto properties of the lasing mode. Noticing that the integral in (18) is of the convolution type, we can use Laplace Transforms to find a formal solution as follows

so that

and

We can immediately see that, in the Markovian case this reduces to the usual quantum optical relationship, as the Laplace Transform of the memory function is a constant. In the more general situation, we know the Green's function propagator for free space with and without gravity [44]. In position space, the shape of the coupling is defined by the spatial wavefunction of the trapped state multiplied by the shape of the outcoupling device, which in the case of Raman outcoupling [45, 46], would be overlapping twin laser beams. Making the simplifying assumptions that no net momentum kick is given to the atoms and that the coupling is Gaussian in form,

where 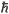s_k is the momentum width of the coupling and g the strength, the Green's function propagator in the presence of gravity is found as

where l = 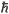/2M. Using (20), the memory function is found as

were Dt = t - u.

Setting g = 0 gives the memory function for coupling into free space, which decays as 1/ in the long time limit. This can be understood because, in the absence of a repulsive force or gravity, there is nothing to remove atoms from the region of the trap except for the spreading of the wavepacket. This happens on a time scale so long that it becomes difficult to decide at what time an atom has actually left the interaction region and can no longer be coupled back into the trapped condensate, resulting in a bound state. This is, of course, not the normal case with photons, which leave the region at the speed of light. In practice this means that to obtain full information about the lasing mode at a particular time, we would have to make measurements of the output over an infinite time. Fortunately, in a real atom laser the atoms will be repelled from the trap at least by gravity, and perhaps also by a repulsive potential, although the atoms will still leave at far less than the speed of light.

4.3 Intensity measurements

The obvious and simplest measurement to make on the output field is an intensity measurement, that is (t)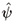_H(t), which can be made by atom counting techniques. From (18), we see that this can be expressed as

We find that this expression simplifies on taking expectation values,

but is still not easily inverted to give information about á

_Hñ.

It is instructive to follow the same procedure for the optical case, beginning with a measurement of (t)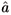_OUT(t). Using Eq. 13 and taking expectation values, we may immediately write

so that knowledge of the pumping and measurement of the output intensity tells us instantly the intensity inside the cavity.

4.4 Two-time correlation function

Another measurement which may be relatively easy in the near future, given recent advances in atom-interferometry [47] is the two-time amplitude correlation function. This can be measured by, for example, first-order interference experiments. In the optical case, the spectrum associated with this quantity is the same inside and outside the cavity, making inference of the intracavity spectrum totally trivial. In the case of the atom laser, we may wish to obtain information about the two-time correlation function of the lasing mode from measurements made on the output. There are at least two ways to achieve this, the first starting from the product of (27), but taken at different times, so that we have

which is an equation relating the two-time correlation functions of the lasing mode and the output. Assuming stationarity, that is that á(t + t) 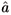_H(t)ñ is independent of t, where u = t + t, and also that the output is on an almost linear part of the dispersion curve (Note that, physically, this may be a difficult condition to fulfil, due to the quadratic dispersion of massive particles), we can take Fourier transforms to find a relationship between the power spectrum of the lasing mode and the power spectrum of the output,

where F_y(n) and F_a(n) are the Fourier transforms of the two-time correlation functions of the output and lasing mode respectively, and (n) is the transform of the memory function. Eq.(31) is then trivially rearranged to give the power spectrum inside the trap as a function of what is measured at the output,

This quantity can then be inverse Fourier transformed to give us the two-time correlation function and hence a measure of the first order coherence of the trapped state. In the limiting case where the coupling tends to Markovian, (n) is flat, meaning that the correlation time inside and outside the trap will be equal, as in the optical case. In general, however, because of the facts that the dispersion curve is not linear and the coupling is not Markovian, we see that the atomic case is more complicated.

We can also start with the relationship between the output energy flux and the two-time correlation function of the lasing mode [42]

which assumes that the output field was vacuum at t = 0. In the above, is the annihilation operator associated with the energy eigenstate of the output mode with position wavefunction u_p(x) and energy 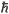w_p, so that

In the case where the only term in the output Hamiltonian is the kinetic energy, the eigenstates are the momentum eigenstates so that (p, t) is simply the Fourier transform of k(x, t). In the more realistic case, with gravity, the eigenstates are Airy functions with an energy-dependent displacement,

where N is a constant of normalisation and the length scale is given by b = (2m²g/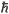²)^1/3. In this case (p, t) can be calculated numerically. We again see that the inversion of Eq. 33 to give knowledge of the internal atomic correlation function is much more difficult than in the optical case.

5 Raman superchemistry: coupled atomic and molecular condensates

The production of a molecular Bose-Einstein condensate (BEC) via Raman photoassociation of an atomic condensate has attracted a great deal of theoretical and experimental interest in the last few years. The process can be thought of as analogous to the well-known quantum optical process of second harmonic generation, where two low frequency photons interact with a nonlinear medium to create one photon of twice the frequency. That this analogous process should exist with atomic and molecular condensates was first stated by Drummond et al. [48], who developed an effective quantum field theory to describe coupled atomic and molecular BECs. An early suggestion that a molecular condensate could be produced via photoassociation came from Javanainen and Mackie [49], who proposed a two-mode, phenomenological Hamiltonian to model the process. A more complete proposal, using an atomic and two molecular fields with spatial dependence, coupled via a two colour Raman transition so as to minimise spontaneous emission losses, was developed by Heinzen et al. [50], who called this process superchemistry. Their model, using a mean-field, GPE approach, showed that the dynamics were quite different from those of normal chemical reactions. As shown by Hope and Olsen in one dimension [4], and Hope in three dimensions [5], full quantum treatments using the positive-P representation [11, 12] and initial coherent states may not always agree with mean-field predictions, as the quantum noise affects the dynamics. This result was expected, since a similar effect had been predicted in second harmonic generation [51, 52]. More recently, Olsen and Plimak [33], and Olsen [34] showed that the initial quantum state of the atomic condensate, as expressed by the Wigner function, can also have an effect on the dynamics. A later work showed that the magnitude of this effect could depend drastically on the dimensionality of the condensate [36], but this will be dealt with in a later section. Overall, what was demonstrated was that the superchemistry described in Ref. [50] can be even more different from standard chemistry than the original authors supposed.

5.1 Truncated Wigner approach

We will follow the treatment given in Refs. [33, 34] and show how a truncated Wigner representation can be used to model the dynamics of interacting atomic and molecular condensates. We consider that the initial atomic condensate is trapped such that one of the frequencies (w₀) is much smaller than the other two, leading to a cigar shaped condensate which may be approximated as one dimensional. We consider here a two laser Raman photoassociation scheme [50, 4, 5] where the excited molecular field will be adiabatically eliminated. The three different atomic and molecular fields with the laser couplings and detunings are shown schematically in Fig. 2, with the process being described by the functional Hamiltonian (note that we use units such that 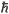= 1)

where m is the atomic mass, 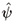_a(x) is the atomic field annihilation operator, 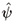_m*(x) is the excited molecular field annihilation operator, and 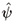_m(x) is the ground state molecular field annihilation operator. The Rabi frequency of the transition between atoms and excited molecules is represented by c(x) and W(x) is the Rabi frequency of the transition between excited and ground state molecules. In principle, these could also be time dependent. The bare detunings, D and d, are as shown in Fig. 2. The trapping potentials are represented by V_a (atoms), V_m (molecules) and V_m* (excited molecules). In the standard s-wave d-function approximation, U_aa is the atom-atom interaction strength, U_mm represents that between molecules, and U_am represents atom-molecule scattering. Note that we are considering only one field for the excited molecules as the lasers should be detuned so that their population will remain as small as possible. For this reason, and also because the strengths are not at all known, we have ignored spontaneous breakup of the excited molecules and any collisional interactions involving them.

Following the usual route [11, 18], we may map the Hamiltonian above onto a master equation and this onto a generalised Fokker-Planck equation. As stated above, although stochastic difference equations can be found which are equivalent to the generalised Fokker-Planck equation, they are difficult to use. After discarding the third-order derivatives, which are assumed to be small, we may map the resulting Fokker-Planck equation onto three coupled differential equations for y_j (j = a, m, m*), which are now the complex variables of the Wigner representation. Although the neglect of the third-order derivatives may be thought of as an uncontrolled approximation, it is an approximation that has previously given good results in many systems, especially when we only wish to calculate intensities. We note here that for a previous treatment of photoassociation using the positive-P representation [4], the truncated Wigner representation gives almost identical predictions for the atomic and molecular numbers.

As the detuning from the excited molecules should be large enough so that this level remains essentially unpopulated, we may adiabatically eliminate y_m* to write two coupled equations for the ground state atomic and molecular fields. Using the standard oscillator units, with time measured in units of and space in units of , and considering the laser couplings as spatially constant across the trap, we find (for details see Ref. [34])

where U^¢_aa = U_aa + c²/2D, and

The detuning from the Raman resonance is now represented by d^¢, which we will assume to be zero in our treatment. Note that we ignore interactions with any atoms of the thermal cloud which is usually found along with the condensed portion, as we are assuming that the condensate actually is at zero Kelvin. In all our investigations we will use U_am = -1.5U^¢_aa, U_mm = 2U^¢_aa, k = 1, d^¢ = 0, and a molecular trapping potential twice that of the harmonic atomic potential.

It must be stressed here that, although these equations have the form of coupled equations of the Gross-Pitaevskii type, they are not equations for the order parameter, the mean-fields, or for what are commonly called the macroscopic wavefunctions. They are equations for the complex variables of the Wigner representation of the two coupled condensates and these variables are in fact stochastic, with the initial conditions obeying a probability distribution. There are also differences in the self and cross interaction terms, which come purely from the Wigner distribution and which cause a shift in the Raman detuning. There are basically two advantages to using the truncated Wigner representation. Firstly, it allows for stable and rapid integration of the condensate equations when compared to the positive-P representation and, secondly, it allows for simple modelling of many initial quantum states.

As a harmonic trapping potential is most commonly used in theoretical investigations of trapped condensates, we consider this case here. For purposes of comparison, we also numerically integrate the GPE type equations, which give semiclassical results with the quantum statistics playing no part in the time evolution. We emphasise here that the GPE solutions are not really physically relevant where they disagree with the quantum predictions, as it is impossible to turn off the quantum noise. What we find is that the spatial dependence of the trapped condensates plays an important role in the process, with the coupling rates at different densities being different. For the parameters used, this causes an interesting structure to emerge, with spatial sidebands forming in the distributions. Over the times shown here, the kinetic energy of the condensates has little effect, with an averaging of the results of integration of spatially separate single-mode equations at each spatial point giving virtually identical predictions, both spatially and for the total particle numbers. This is not the case for longer interaction times, where the atoms have time to move around due to both the trapping potential and the s-wave scattering processes.

To model the initial quantum states of the condensates, each of the 512 points in the spatial grid is given an initial value on each trajectory, chosen from the Wigner distribution for the appropriate state. A coherent state is modelled by taking the (real) ground state GPE solution for the nth spatial point and adding real and imaginary numbers drawn from a normal Gaussian distribution, giving y_a(x_n) = (x_n) + .5(h₁(x_n) + ih₂(x_n)) / , where Dx is the spacing of the numerical grid. It is easily verified that the trajectory average will be |y_GP(x_n)|² + 1/2Dx at each point, with 1/2Dx needing to be subtracted at each point once the trajectory averaging has taken place. A minimum uncertainty squeezed state is modelled by adding .5(h₁(x_n)e^-r + ih₂(x_n)e^r) / at each point, where r is the squeezing parameter. A sheared state, typical of Kerr nonlinearities, as in Dunningham et al. [30], is simulated by transforming the added squeezed state noise by a factor exp(iqh₃(x_n)), where q is the shearing factor. The real noise terms have the correlations

Numerical checks of single-mode distributions produced using these methods show that they give the expected values for average numbers and quadrature variances. In our simulations for squeezed states, we use values of r = ±log0.5, while for the sheared state we used q = 0.005, which give results similar to the Wigner function shown in Dunningham et al. [30]. We also investigate a more extreme shearing of the distribution, with r = -log0.2 and q = 0.05, as we are treating a larger condensate than those considered in Refs. [30, 31]. This will hence possess a larger effective Kerr nonlinearity and be expected to have a more sheared Wigner distribution. We call this choice of initial condition a crescent state, due to the shape of the contours of the resulting Wigner distribution. The molecular field always begins as a coherent vacuum, with y_m(x_n) = .5(h₄(x_n) + ih₅(x_n)) / on each trajectory, with the random variables defined as in Eq. 39.

In Fig. 3 we show the mean atom numbers, defined as

where k labels the points on the numerical grid. What we see is that when we use an initial coherent state in the Wigner equations, we do not find the dramatic differences from the GPE predictions for the first atomic revival as reported previously [4, 5]. The reason is simply that we are working with different parameters, with the ratio between k and the strength of the nonlinear interactions being important in this regard. This was previously demonstrated to be the case in travelling wave second harmonic generation, with which, although it is not as rich a system as coupled condensates, a useful analogy can be made [52]. What we do see is that the oscillations predicted by Heinzen et al. [50] do not persist after the first atomic revival, once the quantum noise is taken into account. This feature is not due to interactions with thermal atoms, as in Góral et al. [53], as there are no thermal atoms present in our zero temperature treatment. Nor is it due merely to an averaging over different conversion rates at different positions within the condensates, as this averaging effect is also present in the GPE treatment. It is due to the quantum nature of the matter fields, cannot be represented by classical treatments, and is intrinsic to the process of photoassociation.

An initial atomic state with the same degree of amplitude squeezing and shearing as calculated in Ref. [30] also does not lead to vastly different dynamics from the initial coherent state, the difference between the two being almost negligible. However, a dramatic difference in the early dynamics occurs when we consider the initial crescent state. The initial conversion to molecules for this state is not as complete and the first revival in the atomic population is earlier and more pronounced than for the other initial states. Interestingly enough, the longer time behaviour is almost independent of the initial state, with the populations reaching a quasi-stationary state. Whether a later revival of the oscillations is present or not is difficult to predict using our methods, as the computational time required becomes prohibitive. However, we consider it unlikely as the system of interacting atomic and molecular condensates is probably too complicated to find the collapses and revivals predicted in, for example, the Jaynes-Cummings model of quantum optics [54].

The differences come in the first minimum of the atomic population and the subsequent revival and are readily explained by the degree of phase uncertainty in the initial state. It can be seen by examination of Eq. 37 that whether association or disassociation is predominant will partially depend on the phase of the products y_m and . As the crescent state has a larger phase uncertainty than the others considered, the photodisassociation process begins to dominate and the mean number of atoms begins to revive at an earlier time than for the other states.

5.2 The zero dimensional approach

The equivalent of the simple quantum optics approach to photoassociation would be to treat each of the interacting condensates as a single-mode, which can then be represented by a single variable, without any spatial dependence. This approach has been used, in a classical mean-field approximation [55], claiming that to reproduce the results for a condensate with spatial dependence, all one needs to do is to take the average of integrations for different points from the spatially dependent condensate. If the condensate did in fact obey the mean field equations this approach would actually give reasonable results for short times. For processes which take place over longer times, the kinetic energy has an effect and atoms and molecules can move around, changing the behaviour. However, after a short time, the mean-field approach can give completely wrong predictions for the populations, even when we begin with coherent states. This has previously seen in travelling wave second harmonic generation [51, 52], but is possibly not as important in that system due to the small nonlinearities and short interaction times of available c⁽²⁾ materials. With photoassociation, however, we do not have the same limits on interaction time. The process will continue as long as the Raman lasers are switched on and the condensate remains stable, which should be sufficient to produce a large number of the superchemistry type oscillations if the mean-field picture were correct.

We can investigate the zero dimensional system with the coupled equations

where a and b now represent atomic and molecular amplitudes, respectively. The other parameters are all as in Eq. 37. Note that the lack of potential and kinetic energy in this approach means that, apart from the detuning d^¢, these equations are mathematically equivalent to those used in Ref. [52]. One important difference from the optical case, however, is that the U_ij self and cross interaction terms are very much larger than those likely to be found in any optical system.

We show the results for the atomic dynamics in Fig. 4, comparing the predictions of the truncated Wigner with an initial coherent state to those of the classical approach, both for an initial atom number equal to |y_a|² at the centre of the densities used for the harmonic trap. Note here that this is not the same as the atomic number at the centre of the one-dimensional grid, which is Dx|y_a|², but is the number which enters into the one dimensional equations. The results for the other initial quantum states considered above are virtually indistinguishable from the coherent state. We find that the classical approach, which predicts regular periodic behaviour in this case, is reasonably accurate up to the second revival of atomic population, but then begins to differ from the quantum prediction. The quantum result shows a damping of the oscillations, due solely to the quantum noise. This serves to show that any averaging process using mean field solutions would eventually become an averaging over erroneous values and could not be expected to lead to correct predictions. We note also that it is very easy to find parameter regimes where the classical and quantum predictions are markedly different, even for early times. In this regard, the ratio between k and the s-wave interactions plays an important role, with the classical predictions becoming less accurate as k/U_aa is increased.

6 Fock state dynamics

In the absence of a complete solution for the Wigner function, obtained without making various approximations, researchers have sometimes chosen to use Fock states. The Wigner function for the Fock state |Nñ is

where L_N is the Laguerre polynomial of order N. This distribution is oscillatory and can obviously be either positive or negative, so cannot be easily simulated numerically. However, in the large N regime Gardiner has made the observation [8] that the cumulative distribution behaves very like a step function centered at |a|² = N. This distribution can then be approximated by a Gaussian with the right moments, at least for the mean and variance. The appropriate distribution is

where we have taken a = , with q uniform on [0, 2p). It can be shown that this approximation generates all moments of (42), up to a correction of order 1/N², which is negligible in the large N regime.

To simulate this distribution numerically, consider the choice (using a single mode for simplicity)

where h_i is a normal Gaussian random variable, and p and q are yet to be determined. As we are using a Gaussian approximation, it is sufficient to reproduce the first two moments of a². (Note that a is a real variable here, with the phase distribution still to be added.) We need to reproduce = N + 1/2 and = (N + 1/2)² + 1/4. This gives us

since = 0, = 1, and = 3, which leads to

Since p will be of the order of N and q will be less than one (q essentially gives the width of the Gaussian), we can neglect the term 2q⁴ to arrive at

The relation for the mean then gives us

from which we choose the solution

The a_i thus chosen is then multiplied by the factor exp(2ipx_i), where x is randomly chosen from the uniform distribution [0,1). Numerical tests with variables produced in this manner show that the required mean and variances are reproduced to a high degree of accuracy. Having now found a way to approximately reproduce the Wigner function for an initial Fock state, we may integrate the Raman photoassociation equations (37) with this initial condition.

6.1 Fock state in zero dimensions

By comparison with a zero-dimensional quantum optics type approach, sometimes used to represent Raman photoassociation of atomic condensates [55], we can show that the quantum statistics become more important as the dimension increases. The zero dimensional system can be investigated with the coupled equations given above (41). We find that the results for the atomic dynamics of an initial Fock state are almost indistinguishable from those shown in Fig. 4 for an initial coherent state. We find that the classical mean-field approach, which predicts regular periodic behaviour in this case, is reasonably accurate up to the second oscillation, but then begins to differ from the quantum prediction. The quantum result shows a damping of the oscillations, due solely to the quantum noise. In a zero-dimensional analysis, the choices of initial quantum state used here do not cause major differences, with the initial coherent state and the initial Fock exhibiting almost identical dynamics.

6.2 Fock state in one dimension

We will now return to a more realistic model which treats the interacting condensates as one dimensional. In Fig. 5 we show the results for the atomic numbers, using initial Fock, crescent and coherent states, all with the same initial mean numbers of atoms. Immediately obvious is that, for these parameters, the dynamics for the Fock state are completely different from the other two. Not only is the initial conversion rate less, but the degree of conversion to molecules is much less, and there are no oscillations seen between atoms and molecules. The different dynamics of the Fock state cannot be ascribed to the initial spatial intensity correlation, g⁽²⁾(x, x) (see Ref. [35, 56]), as this between 1 - 1/N for a Fock state, 1 for a coherent state, and 1.04 at the centre for the crescent state. As demonstrated above in Sec. 5, the more uncertainty in phase that a given state has by comparison with a coherent state, the more difference we see in the dynamics. A Fock state, which exhibits the maximum possible phase uncertainty of 2p, is therefore expected to differ most in its dynamics from the coherent state. That this phase uncertainty has a more pronounced effect in one dimension is because phase gradients are set up within the condensate on each trajectory, which means that the atoms will move around within the trap. Even though these movements may average out when we take the mean over the stochastic trajectories, they destroy the spatial coherence necessary to see oscillations.

Compared with the zero dimensional predictions, the results for the Fock state are quantitatively different. Although there is a difference for the coherent state, it is only quantitative. This is a clear example of the importance of the underlying dimensionality, which has long been appreciated in critical phenomena and is now shown to play a role in the quantum dynamics of interacting atomic and molecular condensates. We see that the zero-dimensional predictions, which can be found analytically under certain approximations, and have been used in, for example [57, 58] with initial Fock states, are far from the 1D results. We note here that, while there are certain physical conditions to be fulfilled so that a trapped BEC may be effectively considered as one-dimensional (see, for example, Ref. [56]), we are not aware of any physical conditions which would allow for the zero-dimensional models sometimes used to investigate photoassociation.

7 Twin beams via photodissociation

7.1 Parametric downconversion

The optical parametric amplifier (OPA) has long been used as a source of quantum states of the electromagnetic field in quantum optics. Because one high frequency photon can interact with a nonlinear medium to create two photons whose frequencies sum to that of the original photon, there is a high degree of quantum correlation between the produced low frequency photons. It can easily be shown theoretically that these twin photons are entangled and, in the nondegenerate case, allow for a demonstration of the Einstein-Podolsky-Rosen (EPR) paradox with continuous variables [59]. If we make the approximation that the pump field is undepleted, we can find analytical solutions. In the optical case, this is often a good approximation, as the conversion efficiency of commonly used nonlinear crystals can be of the order of 1 in 10¹³. We begin with the interaction Hamiltonian

where the

_j are annihilation operators for the low frequency modes and the coupling constant c is proportional to the nonlinearity of the medium and the pump amplitude. In this case we find solutions to the Heisenberg equations of motion as

which, starting from vacuum, predict a number of photons in each mode

where . We thus see that the effect of this device is to amplify the vacuum in the two low-frequency modes. An obvious consequence of this system is that the following conservation law holds:

which allows for a high degree of squeezing in the number difference.

What is more interesting for our purposes here is that the OPA also exhibits phase-dependent quantum correlations which can be used to demonstrate entanglement and the EPR paradox. Using the fact that two-mode squeezing is predicted in the combined quadratures Y_a + Y_b and X_a - X_b, (where X_a = 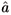+ 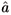^† and Y_a = -i( 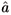- 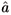^†) and the inseparability criterion proposed by Duan et al. [60], it may be shown that entanglement is guaranteed provided that [61]

With vacuum inputs, we may find analytical expressions for both these variances, as

showing that the degree of entanglement can, in principle, become perfect. In reality, the non-depleted pump approximation will break down and the entanglement will be found to be maximal for some finite interaction time [62].

A demonstration of the EPR paradox using this system has been outlined in Refs. [59, 61]. Essentially, the quadrature operators X_a,b and Y_a,b take the place of the position and momentum operators considered in the original treatment [63]. Basically, we can make linear estimates of the variances of two non-commuting quadratures, which, when multiplied together, seemingly violate the Heisenberg uncertainty principle. We define the inferred variances

where V(A, B) = áABñ - áAñ áBñ. All the quantities above can be calculated analytically, giving

whereas the product V(X_a)V(Y_a) > 1. Again, these analytical predictions lose their validity after a certain interaction time, as the undepleted pump approximation becomes untenable.

7.2 Molecular dissociation

We will now analyse the process of photodissociation of a molecular condensate to see how much physics can be added before the simple analyses of Sec. 7.1 lose their validity. Poulsen and Mølmer [64] have used the positive-P representation to predict squeezing in the number difference between two beams of dissociated atoms, considering the original molecular condensate as undepleted. The atomic state resulting from photo-dissociation is used as a squeezed input to the matter wave analog of a 50/50 beam splitter. The other input is a large conventional condensate of atoms in a different internal state, but with a well-defined relative phase. The squeezing in the particle number difference refers to the resulting two outputs of this atomic beam splitter. Kheruntsyan and Drummond have shown that, with the appropriate detunings on the Raman lasers, two spatially separated output beams can be produced directly from photodissociation, without the need for an atomic beamsplitter [65]. They predict a high degree of number squeezing between these beams. In both these analyses the full spatial problem was considered, but Ref. [65] also considered depletion of the molecular condensate.

We will outline here the treatment of Ref. [65], making various levels of approximation. The effective Hamiltonian for the atomic (

₁) and molecular (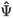₂) fields, taken for simplicity to be confined to one spatial dimension (See Ref. [56] for the necessary conditions), is:

with the commutation relations [

_i(x, t),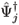(x^¢, t)] = d_ijd(x - x^¢). Here 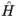_kin stands for the usual kinetic energy term, V_i(x) is the trapping potential (including internal energies), U₁₁ 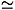4p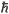a₁/(Am₁) represents the atom-atom scattering strength in one dimension, where m₁ is the mass, a is the three-dimensional S-wave scattering length, and A is the confinement area in the transverse direction, with similar results for the molecule-molecule and molecule-atom interactions. The term proportional to c(t) describes a coherent process of molecule-atom conversion via Raman photo-dissociation, where c(t) is the coupling constant related to the transition matrix elements and the amplitudes of the Raman lasers which have an overall frequency difference w.

The atoms are assumed to be untrapped longitudinally (they may be in an m = 0 magnetic sublevel) yet confined transversely (they may be in a transverse optical trap), so that the atomic field can effectively be treated as a free one-dimensional field, initially in a vacuum state. We neglect the atom-atom collisions since we restrict the coupling to short interaction times during which the atomic density remains small. The detuning D º V₁(0) - [V₂(x₀) + w]/2, where V₂(x₀) = V₂(0) + U₂₂n₂(0), is proportional to the energy mismatch between the atomic and molecular fields, with x₀ the axial half-length in the Thomas-Fermi approximation. The absolute value of the detuning |D| is chosen to be non-zero and much larger than the magnitude of U₁₂áñ so that the effect of atom-molecule s-wave scattering is also negligible. We now introduce characteristic length, d₀, and time scales, , and transform to dimensionless fields in rotating frames. Introducing a dimensionless detuning d = Dt₀ and coupling k(t) = c(t)t₀ / , we may write the Heisenberg equations of motion for the (dimensionless) field operators as,

Note that we have introduced an effective potential (x) = [V₂(xd₀) - V₂(x₀d₀)]t₀ + , where u = U₂₂t₀/d₀, for notational simplicity.

In Ref. [65], the positive-P version of the above equations was solved numerically to show that two spatially separated output atomic beams with a high degree of squeezing in the number difference could be created. In fact, for this correlation, an accurate insight was provided by the analytical solutions of single-mode type equations, as used above in Sec. 7.1. We will now move on to the phase-sensitive correlations required to show entanglement and the EPR paradox, demonstrating that the extrapolation from the simple equations is no longer so straightforward. To gain some analytical insight, we first consider an idealised model corresponding to an undepleted and uniform molecular condensate at density n₂(0), that fills the entire space from -l/2 to l/2, with periodic boundary conditions. The atom-molecule coupling c = c₀ is assumed to be constant during the whole evolution time from 0 to t. In a manner analogous to the undepleted pump approximation, the molecular field can be absorbed into an effective gain constant g = (where k₀ = c₀t₀ / ), which we assume to be real and positive. Solutions to the resulting linear equations for the atomic field are easily found in momentum space by expanding 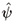₁(x, t) in terms of single-mode bosonic annihilation operators: 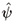₁(x, t) = , where q = d₀k is a dimensionless momentum. The corresponding Heisenberg equations of motion are

which simplifies the problem as the coupling is now between opposite momentum components only. The above equations have the solutions

where

while l_q º q² + d, and g_q º .

We can immediately see that these solutions are very similar to those given above, in Sec. 7.1. The parameter g_q can be identified with the coefficient c, while the parameter l_q is identified with an effective phase mismatch term. We note here, however that, unlike photons, the correlated atom pairs not distinguishable by frequency or polarisation, but by different momenta or spatial locations. Given the initial state of the atomic field, we can calculate any operator moments at time t. We will consider that all momentum components are initially in the vacuum state 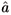_q(0) |0ñ = 0.

We now consider, following Ref. [59], the measurements that must be made to demonstrate the EPR paradox. It is readily seen that correlations exist between atomic quadratures of the beams with opposite momentum components. For example, a measurement of allows us to infer, with some error, the value of , and vice-versa. The same holds for the quadratures. This allows us to define, depending on which beam we measure, four inferred variances,

As the products of the non-inferred variances V(X_±q) and V(Y_±q) are bound by the Heisenberg uncertainty principal to be greater than or equal to one, the paradox exists for V^inf(X_q)V^inf(Y_q) < 1 or V^inf(X_-q)V^inf(Y_-q) < 1. As an example demonstrating the paradox we consider the correlations between the momentum components q = |d| and q = -|d| corresponding to the perfect phase matching condition with l_q = 0, where d < 0. In this simple case we obtain

which are identical to the OPA results of Eq. 57. As can be seen, this simple analysis shows an obvious demonstration of the EPR paradox.

It is extremely instructive to see what happens when we look at a more physical model. We return to the more realistic case as described by the full Hamiltonian of Eq. 58, which is mapped onto stochastic differential equations in the positive-P representation Including a term to describe possible linear losses at a rate g results in the equations:

Here y_i and are complex stochastic fields corresponding respectively to the operators 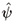_i and , v(x, t) = [V₂(xd₀) - V₂(x₀d₀)]t₀ + uy₂ represents the effective potential, and h_i , are four real independent delta-correlated Gaussian noise terms: áh_i(x, t)h_j(x^¢,t^¢)ñ = á(x, t)(x^¢, t^¢)ñ = d_ijd(x - x^¢)d(t - t^¢).

We consider the molecules as initially being in a (real) coherent state, represented spatially by the Thomas-Fermi solution, assuming repulsive molecule-molecule interactions. The time duration for the molecule-atom conversion is controlled via k(t) = k₀q(t₁ - t), so that k(t) = 0 for t > t₁, where q is the Heaviside function. Once the dissociation is stopped, we continue the evolution of the resulting atomic field in free space to allow spatial separation of the modes with positive and negative q values. What we find is that the product of the inferred variances for opposite momentum components is never less than one, in complete contradiction to the predictions of the simple model [66]. A clue as to why the correlations increase is found if we treat the initial molecular condensate as a plane-wave in space, also represented as a d-function in momentum. In this case we find a demonstration of the EPR paradox for some pair of output momentum components, and which is qualitatively similar to the analytical results of the simplified model. It seems that, as a realistic condensate has a spatial profile, it also includes components with different momenta, and these can become mixed in the output modes, thus degrading the quantum correlations. Although the simple model can give reasonable predictions for number difference squeezing, it misses this mode-mixing in momentum space completely and thus gives totally wrong predictions for entanglement and the inferred variances of the output modes. If we wish to demonstrate the EPR paradox with a realistic system, it seems that we will need a more sophisticated model than is provided by naively adopting the OPA equations to a spatially dependent condensate.

We can demonstrate the momentum mixing with a simple model, with two momentum components at ±k, which are strongly correlated and coupled by an interaction g₀. We then add interactions with other components at ±k ±Dk, with an adjustable parameter, g₁, which regulates the strength of the mode-mixing, represented here as a nearest neighbour type interaction in momentum space. In the undepleted case we can write an appropriate interaction Hamiltonian,

We will be interested in correlations between a₂(-k) and a₅(k), with the other modes being a₁(-k - Dk), a₃(-k + Dk) and a₄(k - Dk), a₆(k + Dk). By adjusting g₁, we can change the strength of the mode-mixing interactions.

The above Hamiltonian, being only quadratic in the operators, has an exact mapping onto stochastic equations for the Wigner variables, giving

where we have now included a detuning, D, which is equal to the momentum spacing between adjacent modes. The a_i are the stochastic variables of the Wigner representation which probabilistically represent symmetrically-ordered operator products.

We now wish to calculate the inferred variances,

and their equivalents for X₅ and Y₅, which will be equal due to the symmetry of the equations. Integrating these equations over 10⁴ stochastic trajectories, with initial states being the Wigner vacuum, gives the results shown in Fig. 6. In these results, we have set D = 184.1 and g₀ = 3.35×10³, equal to the numerical values used in the full equations. The time axis is within the limits of validity of the undepleted molecule approximation for g₁ = 0, with less than 1% molecular depletion. Overall, we see that the sensitivity to this mode-mixing is not linear, but that any non-zero amount of mode-mixing does act to degrade the correlations. By comparison with full spatial results, we see that a realistic effect coupling for this model is probably around g₁ = 0.75g₀. The fact that the products shown do not begin at exactly one is because of sampling error in the Wigner distribution, due to an averaging over a finite number of trajectories. We also note here that much is missing from this simple model, such as atom-atom, molecule-molecule and atom-molecule scattering, for example, but that it does show that a realistic spatial treatment of the trapped BEC is necessary if we wish to reproduce the physics of these EPR correlations.

We can also look at the variances for the combined quadratures, X₂ - X₅ and Y₂ + Y₅, shown in Fig. 7, which demonstrate the degree of entanglement between modes 2 and 5. Following the criterion of Duan et al. [60], entanglement is demonstrated when V(X₂ - X₅) + V(Y₂ + Y₅) < 4. In this case, with g₁ = 0, we find a result equivalent to that of Eq. 55. We see that including the interactions with the neighbouring momentum modes also serves to degrade this correlation, but to a lesser extent than for the inferred variances. For the highest degree of coupling considered, g₁ = 0.75g₀, there is still some degree of entanglement over a finite window of time. This effect is also seen in the full spatial model, where entanglement is more robust than the EPR correlations.

8 Conclusion

Possibly because a large number of theoreticians who work with BEC have their origins in quantum optics, it is common to find analyses which are performed using the simple models and techniques of quantum optics. Over many years, these models have been useful in many quantum optical situations, but may not have the same validity once we wish to treat the deeper quantum aspects of BEC. The mean-field models of interacting condensates, while they can treat the spatial dependence, can say nothing about the quantum features. To analyse these features requires a true many-body quantum approach, as we have shown in this review. We have given a number of examples where a simplified approach is not even approximately valid, but can give totally misleading predictions. These range from the input-output relations to atomic-molecular superchemistry. The input-output relations of quantum optics have limited validity once we wish to deal with massive atoms, which have different dispersion relations to massless photons, meaning that care must be taken with the Born and Markov approximations. In superchemistry, we have shown how quantum noise may act differently on the dynamics in different dimensions, becoming more important in one than in zero dimensions. This can mean that zero-dimensional predictions can be qualitatively wrong, as in the case of photoassociation with initial Fock states. We have also shown that taking realistic spatial profiles into account is very important when we wish to make predictions about entanglement and the EPR paradox with trapped condensates. Overall, the conclusion that we present is that, when we wish to perform theoretical investigations of trapped Bose-Einstein condensates, we must include sufficient physics to have some confidence that we are actually dealing with BEC and not some different, idealised system which exists only in our equations.

Acknowledgments

This work was supported by the New Zealand Foundation for Research, Science and Technology (Grant No. UFRJ0001). I would like to thank Stojan Rebi, Joe Hope, Ashton Bradley and Karén Kheruntsyan for ongoing and extremely useful discussions which helped with the preparation of this work.

References

[1] D.F. Walls and G.J. Milburn, Quantum Optics, Springer-Verlag, Berlin, (1995).

[2] L.P. Pitaevskii, Zh. Eksp. Teor. Fiz. 40, 646 (1961) [ Sov. Phys. JETP 13, 451 (1961)].

[3] E.P. Gross, Nuovo Cimento 20, 454 (1961).

[4] J.J. Hope and M.K. Olsen, Phys. Rev. Lett. 86, 3220 (2001).

[5] J.J. Hope, Phys. Rev. A 64, 053608 (2001).

[6] W. Krauth, Phys. Rev. Lett. 77, 3695 (1996).

[7] I. Carusotto, Y. Castin, and J. Dalibard, Phys. Rev. A 63, 023606 (2001).

[8] C.W. Gardiner, J.R. Anglin, and T.I.A. Fudge, J. Phys. B-At. Mol. Opt. 35, 1555 (2002).

[9] C.W. Gardiner and M.J. Collett, Phys. Rev. A 31, 3761 (1985).

[10] R.P. Feynman, Int. J. Theor. Phys. 21, 467 (1982).

[11] M.J. Steel, M.K. Olsen, L.I. Plimak, P.D. Drummond, S.M. Tan, M.J. Collett, D.F. Walls, and R. Graham, Phys. Rev. A 58, 4824 (1998).

[12] P.D. Drummond and C.W. Gardiner, J. Phys. A 13, 2353 (1980).

[13] E.P. Wigner, Phys. Rev. 40, 749 (1932).

[14] M.R. Andrews, C.G. Townsend, H.J. Miesner, D.S. Durfee, D.M. Kurn, and W. Ketterle, Science 275, 637 (1997).

[15] M.-O. Mewes, M.R. Andrews, D.M. Kurn, D.S. Durfee, C.G. Townsend, and W. Ketterle, Phys. Rev. Lett. 78, 582 (1997).

[16] R. Graham and H. Haken, Z. Phys. 234, 193 (1970).

[17] R. Graham and H. Haken, Z. Phys. 235, 166 (1970).

[18] C.W. Gardiner, Quantum Noise , Springer-Verlag, Berlin, (1991).

[19] L.I. Plimak, M.K. Olsen, and M.J. Collett, Phys. Rev. A 64, 025801 (2001).

[20] P. Deuar and P.D. Drummond, Comp. Phys. Commun. 142, 442 (2001).

[21] P. Deuar and P.D. Drummond, Phys. Rev. A 66, 033812 (2002).

[2] P.D. Drummond and P. Deuar, J. Opt. B: Quant. Semiclass. Opt. 5, S281 (2003).

[23] P.D. Drummond, P. Deuar, and K.V. Kheruntsyan, Phys. Rev. Lett. 92, 040405 (2004).

[24] P.D. Drummond and J.F. Corney, Phys. Rev. A 60, 2661 (1999).

[25] Y.R. Shen, Phys. Rev. 155, 921 (1967).

[26] M.K. Olsen, L.I. Plimak, and A.Z. Khoury, Opt. Commun. 201, 373 (2002).

[27] W. Ketterle and H.J. Miesner, Phys. Rev. A 56, 3291 (1997).

[28] J.M. Vogels, J.K. Chin, and W. Ketterle, Phys. Rev. Lett. 90, 030403 (2003).

[29] M. Lewenstein and L. You, Phys. Rev. Lett. 77, 3489 (1996).

[30] J.A. Dunningham, M.J. Collett, and D.F. Walls, Phys. Lett. A 245, 49 (1998).

[31] J. Rogel-Salazar, S. Choi, G.H.C. New, and K. Burnett, Phys. Lett. A 299, 476 (2002).

[32] V. Chernyak, S. Choi, and S. Mukamel, Phys. Rev. A 67, 053604 (2003).

[33] M.K. Olsen and L.I. Plimak, Phys. Rev. A 68, 031603 (2003).

[34] M.K. Olsen, Phys. Rev. A 69, 013601 (2004).

[35] M.K. Olsen and L.I. Plimak, Las. Phys. 14, 2, 313 (2004).

[36] M.K. Olsen, A.S. Bradley, and S.B. Cavalcanti, in press, Phys. Rev. A (2004).

[37] B. Yurke, Phys. Rev. A 29, 408 (1984).

[38] J.J. Hope, Phys. Rev. A 55, 2531 (1997).

[39] G.M. Moy and C.M. Savage, Phys. Rev. A 56, 1087 (1997).

[40] G.M. Moy, J.J. Hope, and C.M. Savage, Phys. Rev. A 59, 667 (1999).

[41] M.W. Jack, M. Naraschewski, M.J. Collett, and D.F. Walls, Phys. Rev. A 59, 2962 (1999).

[42] J.J. Hope, G.M. Moy, M.J. Collett, and C.M. Savage, Phys. Rev. A 61, 023603 (2000).

[43] A.S. Bradley, J.J. Hope, and M.J. Collett, Phys. Rev. A 68, 063611 (2003).

[44] See e.g. L. Schulman, Techniques and Applications of Path Integrals, Wiley (1981).

[45] M. Edwards, D.A. Griggs, P.L. Holman, C.W. Clark, S.L. Rolston, and W.D. Phillips, J. Phys. B-At. Mol. Opt. 32, 2935 (1999).

[46] E.W. Hagley, L. Deng, M. Kozuma, J. Wen, K. Helmerson, S.L. Rolston, and W.D. Phillips, Science 283, 1706 (1999).

[47] Y. Shin, M. Saba, T.A. Pasquini, W. Ketterle, D.E. Pritchard, and A.E. Leanhardt, Phys. Rev. Lett. 92, 050405 (2004).

[48] P.D. Drummond, K.V. Kheruntsyan, and H. He, Phys. Rev. Lett. 81, 3055 (1998).

[49] J. Javanainen and M. Mackie, Phys. Rev. A 59, 3186 (1999).

[50] D.J. Heinzen, R. Wynar, P.D. Drummond, and K.V. Kheruntsyan, Phys. Rev. Lett. 84, 5029 (2000).

[51] M.K. Olsen, R.J. Horowicz, L.I. Plimak, N. Treps, and C. Fabre, Phys. Rev. A 61, 021803 (2000).

[52] V.I. Kruglov and M.K. Olsen, Phys. Rev. A 64, 053802 (2001).

[53] K. Góral, M. Gajda, and K. Rza\.zewski, Phys. Rev. Lett. 86, 1397 (2001).

[54] J.H. Eberly, N.B. Narozhny, and J.J. Sanchez-Mondragon, Phys. Rev. Lett. 44, 1323 (1980).

[55] M. Kostrun, M. Mackie, R. Côté, and J. Javanainen, Phys. Rev. A 62, 063616 (2000).

[56] K.V. Kheruntsyan, D.M. Gangardt, P.D. Drummond, and G.V. Shlyapnikov, Phys. Rev. Lett. 91, 040403 (2003).

[57] J. Calsamiglia, M. Mackie, and K.-A. Suominen, Phys. Rev. Lett. 87, 160403 (2001).

[58] O. Dannenberg, M. Mackie, and K.-A. Suominen, Phys. Rev. Lett. 91, 210404 (2003).

[59] M.D. Reid, Phys. Rev. A 40, 913 (1989).

[60] L.-M. Duan, G. Giedke, J.I. Cirac, and P. Zoller, Phys. Rev. Lett. 84, 2722 (2000).

[61] K. Dechoum, P.D. Drummond, S. Chaturvedi, and M.D. Reid, in press, Phys. Rev. A (2004).

[62] M.K. Olsen, L.I. Plimak, and A.Z. Khoury, Opt. Commun. 215, 101 (2003).

[63] A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777 (1935).

[64] U.V. Poulsen and K. Mølmer, Phys. Rev. A 63, 023604 (2001).

[65] K.V. Kheruntsyan and P.D. Drummond, Phys. Rev. A 66, 031602 (2002).

[66] K.V. Kheruntsyan, M.K. Olsen, and P.D. Drummond, submitted to Phys. Rev. Lett.

Received on 19 April, 2004

Publication Dates

• Publication in this collection
  28 Jan 2005
• Date of issue
  Dec 2004

History

• Received
  19 Apr 2004