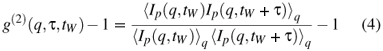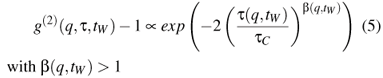Abstract
A dynamical freezing, which is the analogous of a glass transition, is observed at large concentrations in aqueous dispersions of maghemite nanoparticles. We study experimentally the structure and the dynamical properties of two dense ferroglass-formers in two very distinct states of interparticle interaction, either strongly repulsive or attractive. The static structure of the magnetic colloidal dispersions is probed by means of Small Angle X-ray Scattering both in and without the presence of an external magnetic field. Translational dynamics of the repulsive glassformer are investigated by X ray Photon Correlation Spectroscopy. Slow dynamics and aging properties, which both become anisotropic under an applied field, are here investigated.
75.50.Mn Magnetic liquids; 61.10.i Xray diffraction and scattering; 82.70.Dd Colloids; 64.70.Pf Glass transitions
Repulsive and attractive ferroglasses: a SAXS and XPCS study
E. WandersmanI; Y. ChushkinII; E. DuboisI; V. DupuisI; G. DemouchyI; A. RobertIII; R. PerzynskiI,* * Electronic address: regine.perzynski@upmc.fr
ILaboratoire des Liquides Ioniques et Interfaces Chargees, UMR 7612, Université Paris VICNRSESPCI − case 51, 4 place Jussieu, 75005, Paris , France
IIEuropean Synchrotron Radiation Facility − 6 rue J. Horowitz BP 220, 38043 Grenoble Cedex 9, France
IIIStanford Linear Acceleretor Center, Stanford University − LUSI/LCLS, 2575 Sand Hill road, MS43A, Menlo Park CA 94025, USA
ABSTRACT
A dynamical freezing, which is the analogous of a glass transition, is observed at large concentrations in aqueous dispersions of maghemite nanoparticles. We study experimentally the structure and the dynamical properties of two dense ferroglass-formers in two very distinct states of interparticle interaction, either strongly repulsive or attractive. The static structure of the magnetic colloidal dispersions is probed by means of Small Angle X-ray Scattering both in and without the presence of an external magnetic field. Translational dynamics of the repulsive glassformer are investigated by X ray Photon Correlation Spectroscopy. Slow dynamics and aging properties, which both become anisotropic under an applied field, are here investigated.
Keywords: 75.50.Mn Magnetic liquids;61.10.i Xray diffraction and scattering; 82.70.Dd Colloids; 64.70.Pf Glass transitions
I. INTRODUCTION
Magnetic Fluids, also called ferrofluids, are colloidal dispersions of magnetic nanoparticles in a solvent. Their technical applications are quite numerous ranging from actuators to optical modulators [1, 2]. They are also used in various medical issues [3], such as MRI contrast agents [4, 5] or in magnetothermotherapy [6]. In the latter cases, electrostatically stabilized nanoparticles in water are usually employed, forming ionic magnetic colloids, inside which the interparticle interaction can be finely tuned through the ionic strength of the dispersion [7]. Moreover, these dispersions can become densely packed for example if the nanoparticles are internalized inside living cells as magnetic endosomes [5]. For very large concentrations, these magnetic nanomaterials present a FluidSolid transition, which exhibits most of the features of the glasstransition of molecular systems [8, 9], namely slow dynamics and aging. A unified and complete understanding of the drastic dynamical slowing down observed at the glass transition in disordered systems remains a challenging question in statistical physics. For this purpose, soft glassy materials (colloidal glasses, gels, concentrated phases of micelles, .. [10, 11]) are adequate model systems to investigate the slow dynamics of the Glass transition. Indeed, the large intrinsic sizes of soft glassy materials shift their characteristic spatial and temporal scales toward ranges much more accessible experimentallly. Moreover in the case of soft ferroglasses considered here, an additional question is open: what is the influence of an anisotropic interparticle interaction, which can be introduced by applying a magnetic field ?
We investigate here the structural and the dynamical behavior of Ferroglasses by means of Small Angle X-ray Scattering (SAXS) and by X-ray Photon Correlation Spectroscopy (XPCS) respectively. Two different ferroglasses are investigated here. The first one has on average a very repulsive interparticle interaction and the second an attractive one. We investigate experimentally these two systems at the spatial scale of the interparticle distance both in zero field and under a magnetic field. Hereafter we first present the magnetic colloids used here, how they are prepared and their main characteristics. The second part describes the SAXS experiment and the resulting static structure of our ferroglasses. Last we describe the XPCS experiment performed on the repulsive ferroglass sample and discuss the obtained results concerning the slow dynamics of this glass-forming material both in zero field and under an applied field.
II. SAMPLES : PROPERTIES AND PHASE DIAGRAM
The systems used here consist of dispersions of maghemite (γ-Fe2O3) nanoparticles in water. The particles are chemically synthesized [12], and then coated with citrate molecules, which ensure a negative charge at neutral pH. The typical diameter of the particles is here 7-10 nm. In these dispersions, the surface charge is 2 e-/nm2 [13], the particles are dispersed in water at pH = 7.5 at volume fractions Φ ranging between 10-2 and 4.10-1. The ionic strength is due to the free sodium citrate concentration [cit]free, which has to be large enough (> 2.10-3 mol/L) in order to ensure the maximal charge of 2 e-/nm2. Note that, if [cit]free is lower than 2.10-3 mol/L, the charge of the particle decreases (at first order decreasing the repulsion intensity) however the ionic strength also decreases (which enhances the repulsion range). There is therefore a balance between those two parameters. We obtain stable dispersions with strong repulsive interparticle interactions down to [cit]free = 10-3 mol/L [7]. The colloidal suspensions obtained are thus stabilized by electrostatic repulsion.
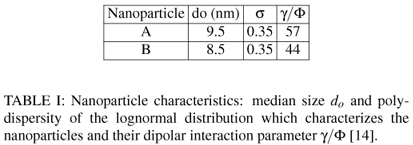
In the present work, two kinds of nanoparticles (see table 1) are used to prepare the dispersions. Their size distribution is deduced from the analyze of the field dependence of the magnetization of a stable and dilute dispersion consisting of individual nanoparticles. The Langevin formalism for paramagnetic materials is used, weighted by the size distribution of the nanoparticles [1]. The dipolar interaction parameter γ/Φ between the nanoparticles [14] is deduced from the initial susceptibility χo of the magnetization curve (γ/Φ = 3χo/Φ at low Φ).
Without magnetic field, at room temperature (i.e. 300 K) and for a given distribution of nanoparticle sizes, a dispersion is fully characterized by two parameters among the three following ones: its osmotic pressure Π, its volume fraction Φ, and its ionic strength I (fixed here by [cit]free ). The osmotic pressure can be measured for low pressures (< 4000 Pa). For larger pressures it is imposed, using the osmotic compression method [15]. The solution is placed in a dialysis bag which is itself put in a bath containing sodium citrate, which controls the ionic strength I, and polymer (dextran MW = 110000 g/mol, Fluka), which controls the osmotic pressure Π. After three weeks, the equilibrium is reached, and the pressures inside and outside the bag are equilibrated. Φ is measured by the chemical titration of iron using atomic absorption spectroscopy.
Controlling and varying the three parameters, pressure Π, volume fraction Φ and [cit]free allows us to build up the phase diagram of the system which is presented in [7, 16, 17] (see figure 1). This phase diagram is similar to the one of atomic systems: a gas, a liquid, a fluid and a solid phases can be observed, together with a critical point at the top of a Gas-Liquid like coexistence curve. The ordinate is the ratio ΠV/kT, V being the nanoparticle volume, in order to renormalize the influence of the mean size of the particle (Π is proportional to 1/V to first order). The critical point roughly corresponds to ΠV/kT ~ 0.04. For a given volume fraction, the ratio ΠV/kT (through the pressure Π) is decreased by increasing the ionic strength, meaning that the repulsion between particles is also decreased. The green dotted line in figure 1 associated with ΠV/kT = Φ corresponds to a second virial coefficient equal to zero (effective balance between attraction and repulsion). It bisects the diagram in two areas : the upper part where the effectice balance of interactions is repulsive and the lower part where the effective balance is attractive. Following a path at constant ionic strength in the upper part of the phase diagram (see figure 1), an increase of volume fraction increases the osmotic pressure (and thus the ratio ΠV/kT). At large volume fractions the system undergoes a Fluid/ Solid transition, which is experimentally observed by a freezing of the degrees of freedom of the nanoparticles [8].
In the upper part of the diagram, the thermal diffusion coefficient, as measured with a Forced Rayleigh Scattering device [18] through the determination of the massic diffusion coefficient and the Soret coefficient, decreases at increasing the volume fraction (see Figure 2). It drastically decreases while approaching a volume fraction Φ* above which the creation of the spatial concentration modulations produced in the experiment by the Soret effect is no longer possible in a reasonable time scale. This slowing down of the thermal diffusion (see Figure 2) is correlated with the decrease of isothermal compressibility of the dispersions as measured in the thermodynamic limit by Small Angle Neutron Scattering [19]. This expresses a freezing of the translational dynamics of the nanoparticles at volume fractions larger than Φ*.
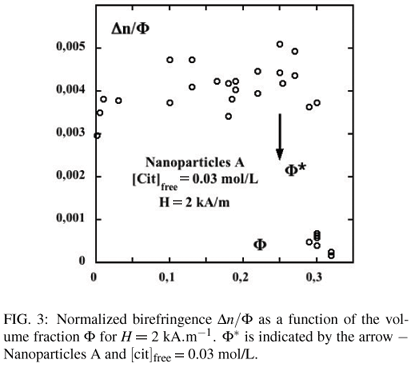
A probing of the rotational dynamics is also possible by using the intrinsic optical anisotropy of the nanoparticles, which is coupled to their magnetic moment. Indeed while submitted to a magnetic field, the dispersions show magneto-optical birefringence directly related to the orientation of the nanoparticles along the applied field. Figure 3 presents the intensity of the magneto-optical birefringence Δn normalized by the volume fraction Φ of the suspension at [cit]free = 0.03 mol/L for nanoparticles A under a low magnetic field H = 2 kA/m. At low volume fractions, Δn is to first order proportional to Φ. Δn/Φ is only weakly increasing with Φ up to a volume fraction Φ* above which the ratio Δn/Φ drastically slows down expressing the freezing of the rotational dynamics of the nanoparticles. This rotational freezing corresponds to the freezing of effective spheres of radius equal to that of the nanoparticles increased by the screening length. This has been extensively studied in [8, 20, 21] where it is shown how Φ* depends on the ionic strength of the dispersion and on the size of the nanoparticles. This freezing is necessarily associated with a small anisotropy of interaction in the system [8, 21]. In the following, we explore by X-ray scattering techniques the structure and the slow dynamics of repulsive glass-forming dispersions at volume fraction of the order of 30% (i.e. larger than Φ*) in the presence of a magnetic field. The structure under field of a dispersion at the same volume fraction 30% but located in the attractive area of the phase diagram of figure 1 is also undertaken, with nanoparticles B at [cit]free = 0.5 mol/L. In this last system no rotation of the nanoparticles is detected by a birefringence measurement.
Let us note that the efficient physico-chemical control of the dispersions also allows to prepare well-defined dispersions of repulsive individual nanomagnets. They constitute an appropriate system to finely probe another glass transition experienced by these magnetic fluids at low temperatures, namely the Super-SpinGlass transition [22-24] that we do not develop here.
III. SMALL ANGLE XRAY SCATTERING
The SAXS experiment is performed on the ID02 beamline at the European Synchrotron Radiation Facility (Grenoble - France) using 12 keV X-rays and two sample-to-detector distances. It gives access to scattering vectors in the range 5 ·10-2 nm-1
q 2 nm-1. The intensity is detected on a FReLON CCD. The concentrated samples are deposited on the wall of a capillary as a layer of thickness of the order of 50 µm. To prevent any water evaporation from the sample, the capillary is filled up with dodecane, which is non-miscible with water. A uniform magnetic field H, normal to the X-ray beam and in the plane of the sample, can be applied with an intensity ranging from 0 up to 800 kA/m.
2 nm-1. The intensity is detected on a FReLON CCD. The concentrated samples are deposited on the wall of a capillary as a layer of thickness of the order of 50 µm. To prevent any water evaporation from the sample, the capillary is filled up with dodecane, which is non-miscible with water. A uniform magnetic field H, normal to the X-ray beam and in the plane of the sample, can be applied with an intensity ranging from 0 up to 800 kA/m.
In zero magnetic field, the scattered patterns are isotropic. The scattered intensity I (q, Φ), radially averaged along rings at constant q is:
where F(q) and S(q, Φ) are the form factor and the static structure factor of the nanoparticles respectively. In order to determine the form factor F(q), a scattering experiment is performed, for each kind of nanoparticles A and B, on a dilute sample at a low volume fraction (Φd ~ 1%) and a concentration of free citrate species [cit]free = 0.03 mol/L, for which the structure factor equals 1. The structure factor is obtained using:
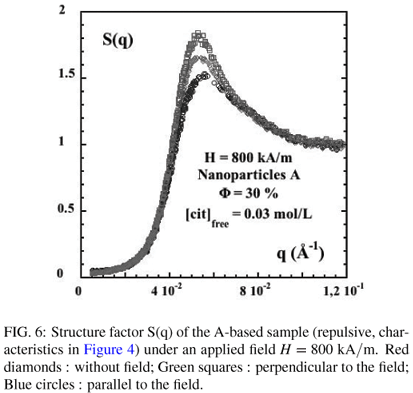
Figure 4 compares the structure factor of the two samples at Φ ~ 30%, respectively based on nanoparticles A and B. A clear difference is observed between the repulsive (A-based) and the attractive (B-based) samples. The first one presents a maximum at the mean interparticle distance 2π/qmax = 14 nm with a very low compressibility ( ~ 0.035) at low q while the second one is flat at large q and does not present any bump at any interparticle distance. On the contrary, it presents a correlation hole centered at q of the order of 0.2 nm-1 with an upturn of S(q) at low q's.
When submitted to a magnetic field H = 800 kA/m the dilute samples keep an isotropic shape (data not shown). this is no longer true for the concentrated samples. Figure 5 shows the scattering pattern under field of the A-based repulsive sample. It presents an obvious anisotropy at the scale of the interparticle distance. The B-based attractive sample looks isotropic except at very low q's. The intensity is averaged over sectors of width 20° leading to the intensity I||(q, H, Φ) (resp. I⊥(q, H, Φ)) along the direction parallel (resp. perpendicular) to the magnetic field. Anisotropic structure factors are then deduced from
They are presented in Figures 6 and 7. The anisotropy of the structure factor of the A-based repulsive sample is very close to that observed in repulsive fluid samples [25] based on comparable ionic nanoparticles: the anisotropy of the compressibility is small because the repulsion dominates, and the anisotropy is maximal in the q range around the peak of the structure factor. This means that the dispersion is less structured in the direction parallel to the field and more structured in the direction perpendicular to the field. Note that, due to the self magnetic field of the assembly of nanoparticles, the mean interparticle distance, as defined by the q value of the maximum of the structure factor, is 10% smaller along the applied field than perpendicularly to it. On the other hand, an anisotropy is only observed at small q for the B-based attractive sample. As for the repulsive samples, the compressibility of this suspension is lower (resp. higher) than without field in the direction parallel (resp. perpendicular) to the field. For more dilute samples, this behaviour resulting from collective demagnetizing effects can be modeled [25,26]. Although the model cannot be quantitatively applied for such concentrated samples, the results show that the hierarchy S||(q → 0) < SH = 0(q → 0) < S⊥(q → 0) is reproduced in these concentrated suspensions and that both for repulsive and attractive samples.
IV. X-RAY PHOTON CORRELATION SPECTROSCOPY
We investigate the out-of-equilibrium translational dynamics of the repulsive concentrated sample by X-ray Photon Correlation Spectroscopy. This technique allows to probe the ergodic - non ergodic dynamic properties of systems such as glass-forming ones [9]. The XPCS experiment is carried out at the ID10C branch of the TROIKA beamline at the European Synchrotron Radiation Facility (ESRF) with 7 keV X rays. Figure 8 gives typical speckle patterns obtained from XPCS experiment (a) in zero applied field and (b) under a field H = 320 kA/m as recorded by a Charge Coupled Device (CCD) camera with an appropriate resolution.
Long-time series of speckle patterns are recorded while the sample ages (over typically 10 to 12 hours). In order to determine the ensemble-averaged intensity auto-correlation at a certain age tW we evaluate the second order correlation function [27]
where Ip is the scattered intensity at pixel p of the CCD camera and < ... >q denotes the circular average over a ring of pixels corresponding to scattering vectors q of same amplitude and different azimutal directions. To calculate (g(2)(q,τ,tW) - 1) as a function of lag τ, a time average over a series of frames centered around time t = tW (within the time window Texp) is performed. The ensemble-average (required for glass-forming samples presenting non ergodic features) is thus realized. Age initialization tW = 0 is defined by the time at which the sample is placed in the sample cell and is no more exposed to any mechanical stress.
Figure 9 shows an example of the age-dependence of the calculated intensity auto-correlation functions (g(2)(q,τ,tW)-1) at the maximum qmax of the static structure factor for different ages increasing from left to right. In the experiment we do not detect the fast β-relaxation of the translational dynamics which is too fast for our experimental set-up. We only probe the α-process which is the final relaxation (g(2)(q,τ,tW)-1 tends to 0 at long times). The measured out-of-equilibrium translational dynamics captures on nanoscales generic features usually observed on microscales :
- a compressed exponential relaxation (see figure 9) described by
with β(q, tW) > 1
- an age-dependence of the characteristic time τC(q, tW) scaling as q-1 (as presented in figure 10) evolving from exponential at young age to a slower behavior at large ages [9].
- no deviation from these behaviours observed in the vicinity of q* - which corresponds to the strongest spatial correlations - thus excluding local rearrangements at the single scale of 2π/q* as driving force for aging in this system.
Such a ballistic-like relation of dispersion τC(q, tW)-1 ~ q is frequently observed in literature, essentially dealing with attractive systems. It rules out any cage-escape process for the present aging behavior. It is frequently addressed as the relaxation of randomly distributed stresses inside the system [10]. However, recent Time-Resolved dynamic light scattering experiments performed on strongly attractive gels [28] have shown that such observations could be associated with series of rearranging events that induce intermittent dynamics. The intermittency of the dynamics can be quantified by the dynamical susceptibility χ4 introduced in simulations of glass formers and corresponding to the volume integral of the four point correlator [29-31].
From our XPCS data, the analysis of the dynamical fluctuations of the speckel patterns in terms of Time Resolved Correlations [32] shows that the dynamics is temporally heterogeneous too [20, 33].
The slow dynamics under field is also recorded here with H = 320 kA/m. The observed dynamics is anisotropic (see Figure 8) and the analysis is performed in a similar way as the statics under field, i.e. along portions of annuli at constant q inside angular sectors of 40° around the direction parallel (resp perpendicular) to the applied field.
Figure 11 shows that in both directions the dynamics under field is faster than the zero-field one. This clearly indicates that the system is rejuvenated by the application of the external magnetic field. In the direction parallel to the magnetic field, where the position fluctuations of the nanoparticles are larger, the relaxation is faster. Under-field, anisotropic aging is also observed. This will be described in a forthcoming work.
V. DISCUSSION
To understand and control the interparticle interaction, as well as the structure and the dynamics of concentrated magnetic fluids is of paramount importance for the numerous technological developments in which they are involved in nanosciences [2] and in nanobiotechnologies [4,5]. The physico-chemical control of the dispersions as developed here is certainly a decisive point. Carrying on in parallel various experimental probing of their structural and dynamical properties reveals to be fruitful. Indeed complementary techniques such as SAXS, XPCS, Magneto-optical birefringence and Rayleigh Forced Scattering, give here a deep insight in the colloidal glass transition experienced by magnetic fluids at large concentrations. This insight is rather innovating in the general framework of the fundamental physics of complex systems.
- The present work extends the experimental investigations on the colloidal glass transition down to the nanoscale with quasi-spherical objects, 10 nm in size. Indeed such studies are usually undertaken with larger objects from100 nm to a few microns in size [10,34].
- The efficient control of the physico-chemical parameters of the studied dispersions gives the unique opportunity to probe the same system of nanoparticles with a simple tuning of interparticle interaction from repulsive to attractive on average Ð an eloquent example is given here.
- Third the magnetic nature of the nanoparticles provides the system with a powerful external parameter. Indeed applying a magnetic field produces an external stress on the dispersions, which is easily tunable. It allows with the present complex system to explore the well-known jamming diagram which has been proposed by Liu and Nagel in [11]. As expected, our XPCS probing shows that the magnetic colloidal system experiences a stress on the nanoscale, the (slow) dynamics of the system being accelerated under field and this rejuvenation of the system being here anisotropic.
VI. CONCLUSION
We investigate concentrated electrostatically stabilized ferrofluids. Both repulsive and attractive ferroglasses can be prepared, the structure of which is clearly different as evidenced by the SAXS experiments. Under field, both systems present anisotropic features : their compressibility is smaller in the direction of the field and larger in the direction perpendicular to the field. The effect is larger for attractive samples. This extends the results previously obtained for repulsive ferrofluids to all dense ferroglasses. Moreover, the static structure factor is anisotropic for lengthscales corresponding to the interparticle distance only for the repulsive sample.
From the dynamical point of view, rotational dynamics is slowed down in the repulsive glasses but remains however measurable. Whereas it becomes undetectable in attractive glasses. Therefore the translational dynamics has been studied by XPCS in the repulsive sample showing slow relaxations and aging behavior on the scale of several hours. Applying an external magnetic field acts as rejuvenating the sample, which then presents a strong anisotropy of slow dynamics and aging.
The attractive samples will be studied in more details in a future work. In particular we intend to approach carefully the glass transition to study the arrest of the dynamics as a function of the volume fraction, in order to elucidate the influence of the interparticle interaction parameters on the dynamics.
Beside a deeper investigation of the under-field aging properties of the systems presented here and of the attractive dispersions, an interesting prospect would be to study dense colloidal dispersions based on slightly larger nanoparticles. Indeed they could present at the same time at room temperature, a colloidal glass transition and a Super-SpinGlass transition, thus mixing together jamming and magnetic spinglass-like effects.
VII. ACKNOWLEDGEMENTS
We thank D. Talbot for help in the preparation of the ferrofluids. We acknowledge the ESRF for the beamtime allocation on ID02 and ID10, and P. Panine for his useful help as local contact on the beamline ID02 of ESRF during the experiment.
(Received on 1 July, 2008)
- [1] B. Berkowski, ed., Magnetic fluids and application handbook (Begell House (UNESCO), 1996).
- [2] S. Odenbach, ed., Magnetically controllable fluids and their applications (Springer Verlag (Berlin), 2003).
- [3] K. Kataoka, A. Harada, and Y. Nagasaki, Adv. Drug delivery Rev. 47, 113 (2001).
- [4] M. Martina, J. Fortin, C. Ménager, O. Clément, G. Barrat, C. GrabielleMadelmont, F. Gazeau, V. Cabuil, and S. Lesieur, J. Am. Chem. Soc. 127, 10676 (2005).
- [5] C. Rivière, C. Wilhelm, F. Cousin, V. Dupuis, F. Gazeau, and R. Perzynski, Eur. Phys. J. E 22, 1 (2007).
- [6] R. Hergt and S. Dutz, J. Magn. Magn. Mat. 311, 187 (2007).
- [7] F. Cousin, E. Dubois, and V. Cabuil, Phys. Rev. E 68, 021405 (2003).
- [8] G. Mériguet, E. Dubois, V. Dupuis, and R. Perzynski, J. Phys.: Condens. Matter 18, 10119 (2006).
- [9] A. Robert, E. Wandersman, E. Dubois, V. Dupuis, and R. Perzynski, Europhys. Lett. 75, 764 (2006).
- [10] L. Cipelletti and L. Ramos, J. Phys.: Condens. Matter 17, R253 (2005).
- [11] A. Liu and S. Nagel, Nature 396, 21 (1998).
- [12] R. Massart, C. R. Acad. Sci. Paris 291, 1 (1980).
- [13] E. Dubois, V. Cabuil, F. Boué, and R. Perzynski, J. Chem. Phys. 111, 7147 (1999).
- [14] F. Gazeau, F. Boué, E. Dubois, and R. Perzynski, J. Phys.: Condens. Matter 15, S1305 (2003).
- [15] V. Parsegian, N. Fuller, and R. Rand, Proc. Natl. Acad. Sci. U.S.A. 76, 2750 (1979).
- [16] G. Mériguet, E. Dubois, M. Jardat, A. Bourdon, G. Demouchy, V. Dupuis, B. Farago, R. Perzynski, and P.Turq, J. Phys.: Condens. Matter 18, S2685 (2006).
- [17] F. Cousin, E. Dubois, V. Cabuil, F. Boué, and R. Perzynski, Braz. J. of Phys. 31, 350 (2001).
- [18] G. Mériguet, G. Demouchy, E. Dubois, R. Perzynski, and A. Bourdon, Journal of NonEquilibrium Thermodynamics 32, 271 (2007).
- [19] E. Dubois, R. Perzynski, F. Boué, and V. Cabuil, Langmuir 16, 5617 (2000).
-
20[20] E. Wandersman, E. Dubois, V. Dupuis, A. Duri, A. Robert, and R. Perzynski, J. Phys.: Condens. Matter 20, 204124 (2008).
- [21] E. Wandersman, V. Dupuis, E. Dubois, and R. Perzynski, to be published (2008).
- [22] D. Parker, F. Ladieu, E. Vincent, G. Mériguet, E. Dubois, V. Dupuis, and R. Perzynski, J. of Appl. Phys. 97, 5002 (2005).
- [23] D. Parker, V. Dupuis, F. Ladieu, J. Bouchaud, E. Dubois, R. Perzynski, and E. Vincent, Phys. Rev. B 77, 104428 (2008).
- [24] E. Wandersman, V. Dupuis, E. Dubois, R. Perzynski, and S. Nakamae, to be published (2008).
- [25] G. Mériguet, F. Cousin, E. Dubois, F. Boué, A. Cebers, B. Farago, and R. Perzynski, J. Phys. Chem. B 110 (2006).
- [26] F. Gazeau, E. Dubois, J. Bacri, F. Boué, A. Cebers, and R. Perzynski, Phys. Rev. E 65, 031403 (2002).
- [27] L. Cipelletti and D. Weitz, Rev. Sci. Instrum. 90, 3214 (1999).
- [28] A. Duri and L. Cipelletti, Europhys. Lett. 76, 972 (2006).
- [29] S. Franz and G. Parisi, J. Phys.: Condens. Matter 12, 6335 (2000).
- [30] P. Mayer, H. Bissig, L. Berthier, L. Cipelletti, J. Garrahan, P. Sollich, and V. Trappe, Phys. Rev. Lett. 93, 115701 (2004).
- [31] L. Berthier, G. Biroli, J. Bouchaud, L. Cipelletti, D. E. Masi, D. L' Hôte, F. Ladieu, and M. Pierno, Science 310, 1797 (2005).
- [32] L. Cipelletti, H. Bissig, V. Trappe, P. Bastella, and S. Mazoyer, J. Phys.: Condens. Matter 15, 257 (2003).
- [33] E. Wandersman, A. Duri, A. Robert, E. Dubois, V. Dupuis, and R. Perzynski, J. Phys.: Condens. Matter 20, 6220 (2008).
- [34] V. Trappe, E. Pitard, L. Ramos, A. Robert, H. Bissig, and L. Cipelletti, Phys. Rev. E 76 (2007).
Publication Dates
-
Publication in this collection
03 July 2009 -
Date of issue
Apr 2009
History
-
Accepted
01 July 2008 -
Received
01 July 2008