A quantum formalism for a terahertz acoustic laser

Abstract

The aim of this work is to improve the study of a phonon laser (saser) proposed by us several years ago[1]. This is a device capable to generate an intense coherent beam of acoustical phonons. Our acoustic laser consists in a double barrier heterostructure tailored such the energy difference between the ground and the first excited state in the well is close to the energy of the LO phonon. The electrons are directly injected into the excited level. Therefore they decay producing a high rate of LO phonons. These phonons are confined inside the well and decay into a pair of phonons[2]: LO -> <img src="http:/img/fbpe/bjp/v29n4/lotil.gif">+ TA. The TA phonons escape the well in the [111] direction constituting an intense coherent beam. Recently were studied (and sometimes realized experimentally) several kinds of phonon lasers. Up to our knowledge our saser is the only that has a very short wavelength (smaller than 25 Å) and a very long range (greater than 1000 mum). Because of that, such beam could have applications to acoustic nanoscopy, acoustic nanolithography and phonoelectronics. In early articles[1, 3, 4, 5, 6] we get the kinetic equations for the averaged electron and phonon populations. Quantum fluctuations were not taken into account. The system Hamiltonian is H = He + Hph + He<FONT FACE=Symbol>-</FONT>ph + Hph<FONT FACE=Symbol>-</FONT>ph + He<FONT FACE=Symbol>-</FONT>e. To solve this Hamiltonian we expand their eigenfunctions in the basis of the eigenstates¦jn1n2n3<FONT FACE=Symbol>ñ</FONT> of the single particle part of it. We obtain a set of coupled equations for the expansion coefficients that can be solved with some approximations. The results are qualitatively similar to those obtained previously.

A Quantum Formalism for a Terahertz Acoustic Laser

Ihosvany Camps Rodríguez,

Physics Faculty, University of Havana, Cuba and

Instituto de Fí sica, Universidade Federal Fluminense,

Niterói - RJ, Brazil.

Sergio Saul Makler,

Instituto de Física, Universidade Federal Fluminense,

Niteroi-RJ, Brazil

and Enrique Victoriano Anda

Instituto de Física, Universidade Federal Fluminense, Niteroi-RJ, Brazil and

Departamento de Física, Pontificia Universidade Católica do Rio de Janeiro,

Caixa Postal 38071, 22452-970, Rio de Janeiro - RJ, Brazil Received February 6, 1999 2

Received February 6, 1999

The aim of this work is to improve the study of a phonon laser (saser) proposed by us several years ago[1]. This is a device capable to generate an intense coherent beam of acoustical phonons. Our acoustic laser consists in a double barrier heterostructure tailored such the energy difference between the ground and the first excited state in the well is close to the energy of the LO phonon. The electrons are directly injected into the excited level. Therefore they decay producing a high rate of LO phonons. These phonons are confined inside the well and decay into a pair of phonons[2]: LO ® + TA. The TA phonons escape the well in the [111] direction constituting an intense coherent beam. Recently were studied (and sometimes realized experimentally) several kinds of phonon lasers. Up to our knowledge our saser is the only that has a very short wavelength (smaller than 25 Å) and a very long range (greater than 1000 mm). Because of that, such beam could have applications to acoustic nanoscopy, acoustic nanolithography and phonoelectronics. In early articles[1, 3, 4, 5, 6] we get the kinetic equations for the averaged electron and phonon populations. Quantum fluctuations were not taken into account. The system Hamiltonian is H = H_e + H_ph + H_e-ph + H_ph-ph + H_e-e. To solve this Hamiltonian we expand their eigenfunctions in the basis of the eigenstates ½jn₁n₂n₃ñ of the single particle part of it. We obtain a set of coupled equations for the expansion coefficients that can be solved with some approximations. The results are qualitatively similar to those obtained previously.

I Introduction

In the recent years, the study of mesoscopic system has steadily grown. New theoretical approaches appeared at the time when new technologies were developed to produce systems of sizes ranging from 5 nm to 500 nm. In particular, double barrier heterostructures (DBH) have attracted a large attention due to its potential applications as ultra-high-frequency electronic oscillators, diodes, transistors and other electronic devices [7].

After the work of Goldman, Tsui and Cunningham [8, 9], it was realized the importance of electron-phonon interactions on the electronic properties of these structures. However, little importance has been given to the study of the phonons generated in this process, the way they propagate, their decay processes, etc.

This paper is dedicated mainly to the study of phonon generation in a DBH under the effect of an external applied bias. In previous works [3, 4, 6] this study was done through a set of phenomenological kinetic equations for the average populations. In this paper a set of quantum kinetic equations is obtained to describe the electron and phonon population using a full quantum treatment.

II The device

The device studied here consist on a DBH made of GaAs-AlGaAs. The sizes of the system are calculated in order to get De = e₁-e₀£ 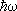₀ for an applied bias V such that the first excited level is above the Fermi level in the emitter. Here e₀ is the energy of the ground state in the well, e₁ is the energy of the first excited level and w₀ is the G-point LO phonon frequency. By increasing V the levels in the well are lowered in relation to . If is low enough then the ground state falls below the bottom of the conduction band and the current is almost suppressed until the level e₁ reaches . By further augmenting V the current begins to flow through the excited level, but since De remains much less than 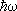₀phonon emission is inhibited. For a given bias V the resonant condition De » 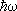₀ is achieved and the electrons begin to decay to the ground state by emitting LO phonons. The potential profile and the level positions at this resonant condition are shown in figure 1.

Figure 1.
Potential profile and energy levels at resonant condition.

As our system has wide barriers, the electrons remain confined in the well for long time. For an Al concentration greater than 0.25 [10] or 0.3 [11] the LO phonons are also confined inside the well. They can be also absorbed by exciting electrons from e₀ to e₁. This process acts in parallel with the decay of primary phonons due to anharmonicity. One of the products of this decay are the TA phonons. The device proposed here could produce a continuous beam of TA phonons in the range of 2 THz. These secondary TA phonons are coherent and form a beam that we call saser by analogy with a laser. The ultra short wavelength of these phonons permits potential applications that were discussed in a previous paper[5].

III The Hamiltonian

Our system is described by the Hamiltonian:

where

_o is the single particle Hamiltonian given by an electronic part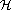 _e plus the contributions 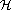_LO, 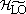, 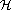_TA for the LO, 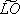and TA phonons respectively:

_int is the Hamiltonian that describes the electron-phonon (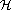_e-ph) and the phonon-phonon (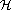_h-ph) interactions

The electronic system is described by a tight binding Hamiltonian with hoppings v between nearest neighbors. The Hamiltonian can be written in a Wannier basis, in terms of the electronic creation and annihilation operators c_jlm⁺, c_jlm at sites jlm,

with j, l, m = - , ¼, .

Because the system has translational symmetry in the directions perpendicular to the grow direction z, the Hamiltonian can be uncoupled. We expand the operators c_jlm in plane waves in the xy direction,

By doing that, we can treat the system as a sum over 1D Hamiltonians for each wave vector k_^ perpendicular to the current in the z direction

where = - 4v. The energies are measured from the bottom of the conduction band of the emitter and = e_j + . The energies e_j are chosen to describe the energy profile of the DBH.

For the sake of simplicity we will left implicit the dependence with k_^.

For the z direction we separate the space in three regions: the dispersion region and two semi-infinity unidimensional chains. To the left we will have planes with energy e_j= 0 for j £ 0 and to the right e_j = V for j ³ L+1, L is the length of the DBH. The corresponding eigenstates of these two regions are planes waves. If we disconnect the DBH from the left and right chains we get for the dispersion region the profile of an infinity (even not rectangular) well as it is shown in figure 2.

Figure 2.
The profile for the scattering region.

For the dispersion region we diagonalize a three-diagonal matrix of order L corresponding to the profile showed above getting the eigenvalues e_m and the eigenvectors |mñ of equation

Here,

_ez is the part of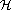 _ez that goes from the beginning of the left barrier to the end of the right one. Written in the basis of planes this is

After the diagonalization we get L discrete levels. We label these levels through the index m as m = 0, ¼. For the right chain we rename the planes, from L+1, L+2, ¼ to 1, 2, ¼; and for the left one, from 0, -1, -2,¼, - to , , ¼, . Therefore we get a new picture where we have two semi-infinity chains, the first one corresponding to the planes j = , ¼, and the other one corresponding to j = 1, ¼, . Between the L levels obtained from the diagonalization of the matrix (8), only the two states with lower energies will participate significantly in the electronic transport. The others are far over the Fermi level, thus they do not contribute. Therefore the dispersion region is represented by j = 0 for the fundamental level and j = for the excited level, with energies e₀ and respectively.

To connect the DBH with the left and right chains we computed the matrix elements

Only four values are relevant in our calculations: , , , and . Finally, the electronic Hamiltonian is

As it is well know [12], the dominant dispersion process in polar semiconductors is due to the coupling between electrons and LO phonons. In this work we also considered the phonons resulting from the decay of the LO phonons, i.e., the 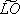and the TA phonons. The Hamiltonians 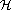_LO, 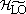, 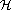_TA used here are the simplest for each kind of phonons considering just one mode. They are

where

₁,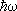 ₂, 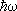₃ are the energies for LO, 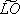and TA phonons respectively and 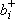, b_i are the creation and annihilation operators for phonons. In this case we introduce two imaginary terms ( ik₂ , ik₃) that take into account the decay by anharmonicity of 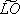and the escape of the TA phonons. The decay of LO phonons is described in detail by the term 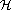_ph-ph. This is important because it describes the stimulated emission of TA phonons that is the main process of our device.

The electron-phonon interaction Hamiltonian has the form,

where g is a constant that measure the strength of the interaction.

The phonon-phonon interaction is given by[2]

This Hamiltonian describes the decay LO® 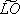+ TA and its inverse process (recombination).

Now we define the operators:

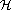The operators creates the eigenstates of _o:

formed by an electron at plane j and n₁LO phonons, n₂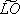 phonons, and n₃TA phonons.

Using the operators (16) and the Hamiltonian (1) we can calculate their equations of motion. In order to simplify the notation we call n for n₁,n₂,n₃:

For the stationary solutions (t) = (0)eⁱwt, the previous equations can be written as:

If we replace the Hamiltonian (1) into equation (19) we get the following equations:

where = e_j+n₁

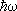₁+n₂( ₂-i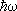k₂) + n₃( 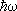₃-i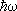k₃) and we defined n¢ º T(n₁-1),(n₂+1),(n₃+1); n¢¢ º (n₁+1),(n₂-1),(n₃-1); n^-º (n₁-1),n₂,n₃ and n⁺º (n₁+1),n₂, n₃.

We expand the eigenstates |Fñ of 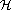in the eigenstates of 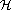_o

Due to the orthogonality of |jnñ the amplitudes can be calculated as = á jn|Fñ = á0||Fñ.

IV The kinetic equations

To obtain the kinetic equations that describe the population of electrons and phonons we need to obtain the equations of motion for the electron number operators

c_j and the phonon number operators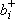 b_i.

Defining the averaged populations for electrons in the excited and ground states as:

and the averaged populations for the LO, 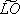, and TA phonons as:

and using the equations (23) we get the set of kinetic quantum equations:

The population rates in (24,25,26, 27,28) are: the electronic input rate from the emitter

and the output rate from the excited level to the collector,

The net balance between the emission and absorption of LO phonons via the electron transitions is given by

The input rate from the emitter directly to the ground state,

is equal to zero near the saser resonant condition because the products () are real numbers, when the ground state merges below the bottom of the conduction band at the emitter. This is due to the fact that the modes connected to the ground state at left are evanescent modes.

The output rate from the ground state to the collector is

The decay of one phonon LO by the emission of a pair of 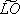and TA phonons, and the inverse process (i.e., recombination) are given by

The decay rate of the 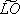population turns out to be

Finally the escape rate of the TA phonons is given by

A diagram for the input and output rates is shown in figure 3.

Figure 3.
Diagram for the several rates.

To put the kinetic equations (24,25,26,27,28) as a function of the populations we have to replace the amplitudes from (22). By doing that, we get a new set of kinetic equations something different form the previous one[5]. For the sake of comparison we show the equations derived in reference [5],

where G is the input current, and R₀ are the escape rate through the right barrier, w is the transition rate due to LO phonon emission, g_o is the decay rate of the LO phonons and t^-1 = k₂ is the escape rate of the TA phonons. Comparing (37) with (24) we see that the escape terms are coincident. By other hand, the second term appearing in (24) contain the second one in (37) plus some other cross terms that take into account that our system, due the escape of the electron from the dispersion region to the left chain, does not have levels but slightly hybridized peaks.

V The calculation of the current

In order to calculate the electronic current and the saser intensity we have to solve the system (22). In previous papers [4,6] we solved a restrict version of these equations in which the peaks corresponding to the excited level and the satellite of the ground state mixed in two polaronic branches. In that paper was not considered

_ph-ph in the calculation of the electronic current. In this paper the phonon-phonon term is taken into account explicitely. In figure 4 we can see the two polaronic branches when the lifetime of the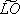 is t₂ = k₂^-1 = 0.05 ps. Such small liftime can occur when the 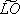decays by stimulated emission of other phonons. When this lifetime is increased to t₂ = 10 ps it appears a third peak corresponding mainly to one electron in the ground state with a pair ( 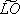+ TA) of phonons. The electronic current can be calculated from the amplitudes a_jn. In figure 5 can be seen the input current for the same lifetimes as above. For t₂ = 0.05 ps the result is the same as in our previous calculations. The current presents two peaks corresponding to the passage of the polaronic branches from the Fermi level to the bottom of the conduction band of the emitter. For t₂ = 10 ps the third peak in the transmittance produces a shoulder in the characteristic curve that can be seen more in detail in the inset. In figure 6 we can see the saser intensity for t₂ = 0.05 ps. This curve is obtained by solving the kinetic equations (24) to (28).

Figure 4.
Dashed line: the two polaronic peaks when the lifetime of the

Figure 5.
Dashed line: the electronic current when the lifetime of the

Figure 6.
The TA phonon population n₃ and the saser intensity S = k₃n₃.

VI Conclusions

In this work, a set of kinetic equations was obtained using a full quantum treatment. This set is different from those presented in previous works where the kinetic equations were derived phenomenologically. Also, we consider for the first time all the relevant phonons and their interactions in the calculation of the current.

It can be seen that, if the decay of the 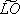phonons is very rapid, the current is the same as in previous calculations. Even if we consider a very long lifetime for these phonons, only small modifications are observed for the current.

In summary, an accurate full quantum calculation for a DBH phonon laser confirms the results obtained using rough phenomenological methods. The Hamiltonian presented here is suitable to study the synergetics of our laser.

Acknowledgments

One of us (IC) wants to acknowledge Latin American agency CLAF for financial support.

• [1] E. V. Anda, S. S. Makler, H. M. Pastawski, R. G. Barrera, Braz. J. of Phys. 24, 330 (1994).
• [2] F. Vallée, Phys. Rev. B 49, 2460 (1994).
• [3] S. S. Makler, D. E. Tuyarot, E. V. Anda and M. I. Vasilevskiy, Surface Science 361, 239 (1996).
• [4] D. E. Tuyarot, S. S. Makler, E. V. Anda and M. I. Vasilevskiy, Superlattices and Microstructures 22 (3) 427 (1997).
• [5] S. S. Makler, M. I. Vasilevskiy, E. V. Anda, D. E. Tuyarot, J. Weberszpil and H. M. Pastawski, J. of Phys. Cond. Matt. 10 (26), 5905 (1998).
• [6] J. Weberszpil, S. S. Makler, E. V. Anda and M. I. Vasilevskiy, Microelectronic Engineering 43 - 44, 471 (1998).
• [7] F. Capasso and S. Datta, Phys. Today 43, 74 (1990).
• [8] V. J. Goldman, D. C. Tsui and J. E. Cunningham, Phys. Rev. Lett. 58, 1256 (1987).
• [9] V. J. Goldman, D. C. Tsui and J. E. Cunningham, Phys. Rev. B 36, 7635 (1987).
• [10] B. Jusserand, F. Mallot, J.-M. Moison and G. Le Roux, Appl. Phys. Lett. 57, 560 (1990).
• [11] J. M. Jacob, D. M. Kim, A. Bouchalkha, J. J. Sony, J. F. Klem, H. Hou, C. W. Tu, H. Morkoç, Sol. State Comm. 91, 721 (1994).
• [12] H. Haken Quantum Field Theory of Solids, an Introduction, North-Holland, Amsterdam p. 218 (1996).

Publication Dates

• Publication in this collection
  23 Feb 2001
• Date of issue
  Dec 1999

History

• Received
  06 Feb 1999