The quantization of galilean duffin-kemmer-petiau field

The quantization of galilean duffin-kemmer-petiau field

L.M. Abreu^*; F.J.S. Ferreira^†; E.S. Santos^‡

Instituto de Física, Universidade Federal da Bahia, 40210-340, Salvador, BA, Brazil

ABSTRACT

We study the quantization of the Galilean covariant Duffin-Kemmer-Petiau (DKP) field in a five-dimensional manifold. The quantization is performed both in the canonical and in the path-integral scenario. It is considered a representation of the Duffin-Kemmer-Petiau matrices which provides the scalar sector of the model, generating the manifestly Galilei-covariant version of the quantized Schrödinger field in a consistent way. Besides, an analysis of the Green's function is done, as well as the basis of the interacting DKP field.

Keywords: Galilean Covariance, Duffin-Kemmer-Petiau formalism.

Introduction

The Duffin-Kemmer-Petiau (DKP) formalism was introduced about seven decades ago, and it is based on a first order wave equation for the description of relativistic scalar and vector fields [1, 2]. It remains currently attracting deal of interest in many different contexts [3-13]. In particular, in Ref. [5] is presented a discussion concerning the quantization of the DKP field, being proved the equivalence between the DKP and Klein-Gordon theories for charged scalar particles interacting with external or quantized electromagnetic field.

On the other hand, considering the non-relativistic scenario, there are in literature examples which prove the viability of the construction of Galilei-covariant first-order wave equations, these being associated to the covariant version of the Schrödinger and non-relativistic vector field equations [10-13]. An interesting physical motivation for this context is the study of condensed matter physics, as the Bose-Einstein condensation in dilute gases [14, 15] and non-relativistic systems such as fluids [16].

In general, Galilean covariance is based on the fact that the Galilean space-time can be implemented as an embedding in a five dimensions space-time, G, such that the coordinates x = (x, x⁴, x⁵) = (x,t,s) transform by [17-19]

where v, R, a and b represent the relative velocity, rotation, spatial and time translations between different reference frames, respectively. The coordinate s is defined in the interval [0, l], and it can be seen on physical grounds as canonical conjugate to the mass, up to a constant to fix the unit [17-19].

It is easy to note that the invariant scalar product under the transformations in Eq. (1) is g_µν x^µ x^ν, where g_µν is the Galilean metric given by

A natural question is about the of construction of quantum theory of the Galilean covariant DKP field, similarly to the relativistic context. In this work, we perform the quantization of the nonrelativistic DKP formalism in two ways: in the canonical and in the path-integral scenarios. Both cases are discussed in a representation of the DKP matrices which provides the scalar sector of the model, generating the manifestly Galilei-covariant version of the quantized Schrödinger field.

The paper is organized as follows. Section 2 is devoted to develop the Hamiltonian canonical approach for the Galilean DKP theory, as well as an analysis of the surface's structure of constraints is obtained. This is done by making use of a particular representation of the DKP matrices, which allows us to work in the component form. The equal-time commutation relations that define the quantization rules are also obtained, and the propagator of the free DKP field is defined and analyzed. In Section 3, the construction of the path-integral formalism in a matrix form is discussed, as well as the basis of the interacting DKP field. Finally, Section 4 presents some concluding remarks.

2 Canonical Quantization

2.1 Hamiltonian Formulation

Let us start with the Lagrangian density for the Galilean covariant free DKP field, defined as

where β^µ are matrices that satisfy the fundamental algebra,

with the indices µ,ν running from 1 to 5; ψ is the spinor representing the DKP field; and = ψ^†η is the adjoint spinor, with η = [(β⁴ + β⁵)² + 1] as usual [10-13]. The equivalence of DKP and Schrodinger equations is dicussed in ^{Appendix A} .

We choose the spinors ψ and expressed in a form such that ψ = ψ^*µψ_µ - ψ₆. In this context, the chosen six-dimensional representation for the β^µ matrices (shown in ^{Appendix B} ) describes a spin-0 representation of the DKP field. So, the Lagrangian density in Eq. (5) can be written in the component form as

From Eq. (7) it is possible to derive the canonical conjugate momenta,

The next step is to construct the Hamiltonian density H,

The constraints from Eq. (8) are written using combinations between them, resulting in m₁ = 10 primary constraints given by

where i = 1,2,3. In this scenario, we note that the subset is formed of second-class constrains, while are of first-class ones. Therefore, the matrix of the Poisson brackets for the primary constraints (10), denoted as , has a vanishing determinant and

Following the prescription of the well known method of quantization of constraint theories [21], let us introduce the modified Hamiltonian density,

where λ^α are parameters to be determined. Since the primary constraints must be time-independent, it implies that the time derivative of the constraints must vanish, i.e.

Thus, as a consequence of this conservation conditions for the set of second-class constraints in Eq. (10), we have

Notice that the other eight λ-functions are undetermined in the first stage, because m₁ - ρ₁ = 6. Then, the conservation conditions for the set first-class constraints in Eq. (10) provide the secondary constraints in the second stage,

where γ = 1, 2, and

The constraints given by Eqs. (10) and (14) constitute a set of second-class constrains. In this context, the total number of constraints is necessarily even. This follows from the fact that a nonsingular antisymmetric matrix always has an even rank [21]. Then, the conservation conditions that we must use for this second-class constraints are

where

The matrix composed of Poisson brackets of the constraints given by Eqs. (10) and (14) has the form

where ρ₂≡ rank({Φ_k, Φ_k^'}) = 8. Therefore, we can use Eq. (17) in (15) to obtain the λ-functions,

After that, we can write the new Hamiltonian density as

and the equations of motion for ψ₆ and as

Now we make use of secondary constraints in Eq. (14) to rewrite Eq. (19) in the form

Similarly, the equations of motion for ψ⁴ and are

Then, the use of Eq. (14) in (21) yields

Finally, after combining Eqs. (20) and (22), we obtain

Thus, we see that the components ψ₆ and of the DKP field satisfy a Klein-Gordon-like equation. However, in our context we consider that they obey the ansatz [17-19],

which allows us to interpret Eq. (23) as the manifestly Galilean covariant Schrödinger wave equations.

2.2 Quantization and the Green's function

The canonical quantization of a constrained classical theory is more difficult because the canonical coordinates become operators acting in the Hilbert space H, and these operators possess nontrivial commutation relations among each other. To implement the canonical quantization of a theory with second-class constraints, we consider that the canonical variables are

where Ω_k is the canonical set of constraints, being equivalent to the constraints Φ_k defined by Eq. (16).

Taking into account that the constraint surface is described by equations Ω_k = 0, the equal-time commutation relations that define the quantization rules are obtained from the Dirac brackets, i.e. { , }_{D (Ω}) → [ , ] , resulting in

At this point we are able to construct the two-point function of the Galilean covariant DKP field. As the first step, we write the operator solutions of the DKP equation for a free particle as

where p represents the five-momentum p^µ = (p, m, E) (m and E being the mass and energy, respectively), and the operators â(p), â^†(p), (p) and ^†(p) satisfy the following commutation relations,

Also, since the spinors u⁽⁺⁾ and u^(-) satisfy

their normalized solutions may be express as [10]

Therefore, Eq. (30) shows that a covariant Galilean field theory is in principle compatible with the idea of particles with energy ±E and ±m, which is in agreement with Refs. [23, 24]. Nevertheless, since the particles with negative energy -the antiparticles- are not physical significance in our Galilean context, we can use the solutions with negative energy in the intermediate steps of our model, and the predicted physical results cannot carry them.

From Eq. (30) it is possible to obtain the scalar products,

Noticing that these scalar products can be written in the form

then the projection operators for particle and anti-particle may be defined as

Let us introduce the Green's function of the Galilean DKP theory, G_DKP (x - x^' ) , such that it must satisfy the equation

where the Dirac delta function in G_{(4 + 1)} is defined as [23, 24]

It is interesting to note that the Fourier expansion of the G_DKP-function in Eq. (34) is written as

while the delta-function in Eq. (35) has the form

Then, using Eqs. (36) and (37) in (34) we find

which is in agreement with Ref. [5]. So, taking into account Eqs. (38) and (33), we can rewrite the G_DKP-function in Eq. (36) as

where K₀≡ (p²/2m) - (k²/2m). Finally, with the change of variable p⁵→ p⁵ - K₀ and the integration over p⁵, we obtain

Hence, as expected, we clearly see that the Green's function is associated to the 2-point function (the Feynman propagator of DKP formalism), i.e.

where | 0 〉 is the ground state of the Fock space and T[·] is the time-ordering operator.

The physical significance of the expression explicit in Eq. (41) can be clarified if we consider the component [G_DKP]₆₆ of the expression in Eq. (40), which gives

where Δ_F (x - x^') is the Galilean covariant version of the Green's function (the Feynman propagator) of the Schrödinger field, as it is remarked in Ref. [23]. This result proves the equivalence between the quantized Galilean DKP theory for free scalar particles developed here and the Schrödinger formalism for a non-relativistic Bose gas. Besides, one can notice that the absence of a term carrying the projector ∧_ in Eq. (40) forbids the simultaneous existence of particles and antiparticles, which is consistent with the non-relativistic scenario.

3 Generating functional for Green's functions

3.1 The non-interacting formalism

The aim of this Section is the development of the functional quantization of the Galilei-covariant DKP theory. Let us to use the DKP action given by Eq. (5) in matrix form for convenience. In this scenario, the canonical conjugate momenta are

and the Hamiltonian density is

Now we can write the first-stage constraints in matrix form,

and the second-stage constraints are,

where M = 1+β⁴β⁵ and N = 1+β⁵β⁴.

Let us consider in this Section the development of the functional quantization of the Galilei-covariant DKP theory. To do this, it is important to take into account the surface's constraints of the theory [22]. As can be seen from Eq. (8), the Lagrangian density is independent of the subset of velocities , making their equations in terms of the set {p_i, p_i^*, p₅, p₅^*, } undetermined. Such a case forces the use of secondary constraints, given by Eq. (49), to determine the physical subspace of the path integral measure.

Thus, following the usual path-integral formalism of quantum field theory, we define the generating functional as

where Z₀ = Z[ 0, 0] and we set det . Integrating over the momenta we obtain

We can introduce the auxiliary fields χ and to exponentiate the constraints, generating

where we have used the fact Mβ⁴ = β⁴N = 0. So, performing the functional integration over the fields ψ, , χ and and considering only physically relevant terms [27], we obtain

where G_DKP (x - x^') is given by Eqs. (34) and (36). Hence, from Eq. (53) we obtain the two-point function,

We notice that Eq. (54) is identical to (41), which shows the consistency of the functional formalism to obtain the two-point function of Galilean DKP field.

In a general way, we can define the n-point function of the Galilean DKP field as

After the analysis of the free quantized Galilean DKP formalism, we can conclude this study with the construction of the general aspects of the interacting theory.

3.2 The generating functional for the interacting formalism

In the situation of an interacting DKP formalism, we assume a Lagrangian density given by

where L is given by Eq.(7) and L_int is the interaction term, depending only on ψ e (without field derivatives).

Then, using standard methods, the modified generating functional has the form

So, the n-point functions of the Galilean DKP field can be derived from Eq. (55) by replacing Z[ J, ] with Z^'[ J, ].

The scattering amplitude can be determined by taking the ket |p₁,p₂, ..., p'_n〉 as representing the initial state of n particles and | p'₁,p'₂, ..., p'_n〉 the final state, then the amplitude is defined by

The operator S is given by

where are the DKP operator fields given by Eq. (27) in the initial configuration, O_x = β_µ∂^µ + k and : : denotes the normal ordering. By expanding the exponential of Eq. (58) and after some manipulations, the n-th order leads to the term in which we are interested,

where the τ_DKP -function is defined in Eq. (55). Thus, with the use of the Lehmann-Symanzik-Zimmermann (LSZ) reduction method and the formalism discussed in Ref. [23], we are able to calculate scattering amplitudes S_fi of interacting processes; the equivalence between the obtained result and the Schrödinger formalism is reached by taking into account the component [S_fi]₆₆, as it is similarly remarked at the end of Section 2.

4 Concluding remarks

The purpose of this paper has been to implement the quantization of the the scalar sector of the Galilean covariant DKP in both canonical and path-integral approaches. We have shown that this formulation generates a consistent Galilei-covariant version of the quantized Schrödinger field.

In the canonical quantization approach, an analysis of the surface's structure of constraints has been performed, yielding the correct equal-time commutation relations that define the quantization rules. The propagator of the free Galilean DKP field has been determined, which is consistently equivalent to the Schrödinger formalism for a non-relativistic Bose gas.

In addition, the path-integral formalism in a matrix form has been discussed, being possible to derive the n-point function of Galilean DKP field from the generating functional. Finally, we have developed the basis for the construction of an interacting DKP theory to study scattering processes.

Interesting topics related with the formalism studied above deserve future investigation. A natural question is to analyze the DKP field in a interacting context, as the presence of non-relativistic vector field and a version of the formalism which reproduces the physics of nonlinear Schrödinger equation.

Acknowledgements

This work was partially supported by the Brazilian agency CNPq.

[1] R. J. Duffin, Phys. Rev. 54, 1114 (1938); N. Kemmer, Proc. Roy. Soc. A 173, 91 (1939); G. Petiau, Acad. R. Belg. Cl. Sci. Mem. Collect. 8, 16 (1936) No. 2.

[2] For historical details of the original version of DKP equation, see R.A. Krajcik and M. M. Nieto, Am. J. Phys. 45, 818 (1977).

[3] A. A. Bogush, Rep. Math, Phys. 25, 27 (1988).

[4] V. Gribov, Eur. Phys. J. C 10, 71 (1999).

[5] B. M. Pimentel and V. Ya Fainberg, Theory. Math. Phys. 124,1234 (2000).

[6] J. T. Lunardi, B. M. Pimentel, R. G. Teixeira and J. S. Valverde, Phys. Lett. A 268, 165 (2000).

[7] J. T. Lunardi, B. M. Pimentel and R. G. Teixeira, Gen. Rel. Grav. 34, 491 (2002).

[8]R. Casana, V. Ya. Fainberg, B. M. Pimentel and J. S. Valverde, Phys. Lett. A 316, 33 (2003).

[9] R. Casana, B. M. Pimentel and J. S. Valverde, Phys. A 370, 441 (2006).

[10] M. de Montigny, F. C. Khanna, A. E. Santana, E. S. Santos and J. D. M. Vianna, J. Phys. A: Math. Gen. 33, L273 (2000).

[11] M. de Montigny, F. C. Khanna, A. E. Santana and E. S. Santos, J. Phys. A: Math. Gen., 34, 8901 (2001).

[12] M. C. B. Fernandes, A. E. Santana and J. D. M. Vianna, J. Phys. A Math. Gen. 36 3841 (2003).

[13] E. S. Santos and L. M. Abreu, J. Phys. A: Math. Theo. 41, 075407 (2008).

[14] M. H. Anderson, J. R. Ensher, M. R. Matthews, C. E. Wieman, E. A. Cornell, Science 269, 198 (1995); K. B. Davis, M. O. Mewes, M. R. Andrews, N. J. van Druten, D. S. Durfee, D. M. Kurn, W. Ketterle, Phys. Rev. Lett. 75, 3969 (1995); C. C. Bradley, C. A. Sackett, J. J. Tollett, R. G. Hulet, Phys. Rev. Lett. 75, 1687 (1995).

[15] F. Dalfovo, S. Giorgini, L.P. Pitaevskii, S. Stringari, Rev. Mod. Phys. 71, 463 (1999).

[16] M. de Montigny, F. C. Khanna, A. E. Santana, J. Phys. A 36, 2009 (2003).

[17] M. Omote, S. Kamefuchi, Y. Takahashi and Y. Ohnuki, Fortschr. Phys. 12, 933 (1989).

[18] A. E. Santana, F. C. Khanna and Y. Takahashi, Prog. Theor. Phys. 99, 327 (1998).

[19] M. de Montigny, F. C. Khanna, A. E. Santana and E. S. Santos, Ann. Phys. NY 277, 144 (1999).

[20] P. A. M. Dirac, Proc. Roy. Soc. A 246, 326 (1958).

[21] D. M.Gitman and I. V. Tyutin. Quantization of Fields with Constraints. (Berlin: Springer, 1990).

[22] L. D. Faddeev, Theoret. Math. Phys. 1, 1 (1970).

[23] L. M. Abreu, M. de Montigny, F. C. Khanna and A. E. Santana, Ann. Phys. NY 308, 244 (2003).

[24] M. de Montigny, F. C. Khanna and F. M. Saradzhev, eprint: hep-th/0706.4106v2.

[25] V. Ya Fainberg and B. M. Pimentel, Phys. Lett. A 271, 16 (2000).

[26] E. S. Santos, M de Montigny and F. C. Khanna, Ann. Phys. NY 320, 21 (2005).

[27] There is a term in the exponent of the Z-function in Eq. (48) proportional to . Notice, however, that it does not contribute to the physical elements of S-matrix, similarly to relativistic case pointed in Ref. [22].

(Received on 15 March, 2010)

In this Appendix we briefly show the equivalence of the nonrelativistic DKP and the Schrodinger equations. The equation of motion obtained from Lagrangian (5), which we simply call it as DKP equation, is given by

Notice that the multiplication of the DKP equation (A1) by the operator ∂_αβ^αβ^ν from the left, and after contracting it with ∂_ν, yields

Thus, each component of the spinor Ψ must obey a Klein-Gordon-like equation. However, considering that the DKP fields must obey the prescription [10, 11, 13, 17–19]

then Eq. (A2) can be rewritten as

which shows that each component of Ψ(x, t) obeys a Schrödinger equation, with m being the mass of particle and k is a irrelevant constant. Thus, Eq. (A2) can be understood as a Galilean covariant version of the Schrödinger equation, which is the right field equation of the nonrelativistic regime. Hence, in this scenario we interpret Eq. (A1) as the nonrelativistic DKP equation, and Ψ(x) the nonrelativistic DKP field.

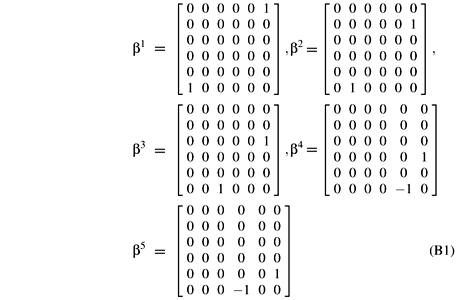
In this Appendix we explicit a possible choice for a 6- dimensional representation of the β matrices:

APPENDIX A:  THE EQUIVALENCE BETWEEN THE NONRELATIVISTIC DKP AND THE SCHRODINGER EQUATIONS

APPENDIX B:  SPIN 0 REPRESENTATION FOR THE GALILEAN DKP THEORY

Publication Dates

• Publication in this collection
  23 June 2010
• Date of issue
  June 2010

History

• Received
  15 Mar 2010