Consistent histories and contrary inferences

Consistent histories and contrary inferences

G. Nisticò

Istituto Nazionale Fisica Nucleare, Italy Dipartimento di Matematica, Università della Calabria, via P. Bucci 30b, 87036, Rende (Italy)

ABSTRACT

To perform a more transparent analysis of the problems raised by contrary inferences within Consistent History approach to Quantum Theory, we extend the formalism of the conceptual basis. According to our analysis, the conceptual difficulties arising from contrary inferences are ruled out.

1 Introduction

Consistent History Approach to quantum theory, introduced in explicit form by Griffiths [1], provides an extension of the interpretation of the formalism of quantum mechanics. While standard quantum theory is based on the concept of event, represented by a projection operator E of the Hilbert space describing the system, CHA is based on the concept of history, which is a finite ordered sequence h = (E₁,E₂,...,E_n) of events. Suitable families of histories can be selected by means of a criterion of consistency. According to CHA, only the histories of a consistent family have physical meaning. The occurrences of histories are the empirical facts the theory is concerned with.

One of the aims of CHA is to solve some conceptual difficulties of standard quantum mechanics. Griffiths and Omnès [2] argue that the famous quantum measurement problem [3] is solved by the extended interpretation provided by CHA.

However, the new theory raised some criticisms. One of the most debated problems is linked to the so called contrary inferences, illustrated in section 3 below. The debate provoked by this problem did not reach a shared conclusion. We think that a better clarity can be obtained if some natural concepts of CHA are better formalized, so that to allow a more transparent analysis of the debated questions.

We do this by extending the formalism of the conceptual basis of CHA with the introduction of the notion of support. Starting from it, new tools can be developed allowing a deeper analysis of some questions. Also the problem of contrary inferences can be submitted to such an analysis. Our result is that contrary inferences do not entail conceptual difficulties.

The plan of the paper is the following. In section 2 the basic concepts of CHA are outlined. The problem of contrary inferences is described is section 3. The notion of support of a family of histories is introduced in section 4, where the formalism stemming from this notion is developed. In section 4.2 some general implications of the extended formalism are derived. A deeper undestanding of CHA notion of compatible families is obtained in section 4.3.

Finally, the problem of contrary inferences is analyzed in section 5 on the basis of the extended formalism, showing that the related difficulties are ruled out.

2 Basic concepts of CHA

Let be the Hilbert space which describes the physical system according to standard quantum theory. Throughout this paper we assume that has a finite dimension N; moreover, the Heisenberg picture is adopted. Fixed a finite sequence of times t₁, t₂, ..., t_n, let us consider for each time t_k a decomposition of the identity E_k = {} which is a finite set of projection operators of Hilbert space , with ^ if i ¹ j and = 1. A family of histories, generated by E₁,E₂, ...,E_n, is the set of all sequences h = (E₁,E₂,...,E_n) such that E_k = å_{some i} . Projection operator E_k in a history h represents an event susceptible of occurring at time t_k. When every event E_k constituting a history h is just an event of E_k, i.e. if E_k Î E_k for all k = 1,2,...,n, then h is called elementary history. Hence the set 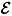of all elementary histories of is the cartesian product 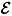= E₁×E₂×¼×E_n. For every history h = (E₁,E₂,...,E_n), by h we denote the following subset of elementary histories: h = {Î }. Two histories h₁ = (E₁,E₂,...,E_n),h₂ = (F₁,F₂,...,F_n) Î are summable if they differ in only one place, say k, hence E_j = F_j for all j ¹ k, and E_k ^ F_k; in such a case their sum is h₁+h₂ = (E₁,E₂,...,E_k+F_k,...,E_n) Î. The histories h₁ and h₂ are said to be alternative if there is k such that E_k ^ F_k.

Let h = (E₁,E₂,...,E_n) be a commutative history, i.e. such that all E_k commute with each other. According to quantum theory, the statement "h occurs'' means that all events E₁,E₂,...,E_n occur. Therefore, h is identified with the single event E₁·E₂¼E_n = E₁Ù E₂Ù¼ÙE_n. Though the mathematical notions of CHA are given within the usual quantum theoretical formalism, standard quantum theory is unable to consider and describe the occurrence of a history when it is not commutative. However, in the case that is weakly decohering, i.e. 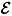if Re(Tr()) = 0 for all h₁,h₂Î , h₁¹ h₂, the functional pc:® [0,1], pc(h) = Tr(C_h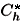) behaves as a probability which extends the probability predicted by standard quantum theory for commutative histories [4]. The basic principle of CHA establishes that when family satisfies the mathematical criterion of being weakly decohering then it is consistent, i.e.

(I) the set of all elementary histories of

is a "sample space of mutually exclusive elementary events, one and only one of which occurs'' [8].

The occurrence of history h means that an elementary history Î h occurs. Here the physical meaning of the notion of occurrence of a history, involved in (I), is the following

(O) A given history h = (E₁,E₂,...,E_n) occurs if all events E₁,E₂,...,E_n objectively occur at respective times t₁, t₂, ..., t_n. The occurrence of a history is an objective physical fact, independent of the performance of a measurement which reveals this occurrence.

Accordingly, if is consistent, any occurrence (or non-occurrence) of an elementary history in must be referred to an individual, concrete sample of the physical system.

Remark 1. The probability of occurrence of a history h, pc(h) = Tr(C_h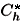), is clearly independent of the consistent family it belongs to. However, the symbol is kept in the formula for future convenience, as explained in remark 2 below.

3 Contrary inferences

To make predictions about occurrences of histories, the initial data, i.e. the known information about the physical system, are expressed as sentences involving histories of a consistent family , and assumed as true, i.e. objectively realized sentences. Conclusions can be derived by means of logical reasonings in which histories of are regarded as events of a classical sample space and by interpreting the number pc(h) = Tr(C_h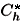) as the probability of occurrence of history h. These conclusions are the theoretical predictions to be regarded as objectively realized sentences.

However, the histories needed to express the same initial data belong, in general, also to another consistent family '. Therefore, another set of conclusions can be obtained by using ' instead of . A conclusion of this new set could contradict some conclusion derived from . To avoid these conflicts, CHA introduces the following rule.

Single Family Rule. All valid physical inferences are those obtained by using a single consistent family . In general, different conclusions drawn by using distinct consistent families do not hold together.

The possibility of contrary inferences is the main criticism opposed to CHA. They are a particularly effective example of the conflicts described above. Let us briefly describe them. Suppose that

₁ and ₂ are two different weakly decohering families such that h₁ = (E₀,E₁,E₂) Î₁ and h₂ = (E₀,F₁,E₂) Î₂, with E₁^ F₁, and h₀ = (E₀,1,E₂) Î₁Ç ₂. A. Kent [5] was able to find examples in which the conditional probabilities pc₁(h₁|h₀) = 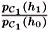and pc₂(h₂|h₀) = 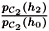are both 1. Therefore, according to CHA we may state that if h₀ occurs, then also E₁ occurs within the family ₁, but then also F₁ occurs within the family ₂; on the other hand, E₁^ F₁ means that the occurrence of E₁ excludes the occurrence of F₁: then we have two inferences which are contrary to each other. Contrary inferences do not entail logical incoherence for CHA because they take place in different consistent families, and thus the contradiction arises only by violating the single family rule.

The presence of contrary inferences in CHA is at the root of a rather lively debate. According to Kent, their occurrence makes it "hard to take it [CHA] seriously as a fundamental theory in its present form'' [5]. And about single family rule, which formally prevents contrary inferences from yielding theoretical contradiction [6], "any formalism [...] can be made free from contradiction by such a restriction'' [7]. The replies of Griffiths are essentially based on the following arguments.

1. The derivation of the contradiction violates the single family rule. In particular, the problem arises because Kent assigns to 'contrary' histories h₁ and h₂ the classical-logic meaning of word contrary, i.e. that the occurrence of h₁ always implies the non-occurrence of h₂. But this cannot be done because h₁ and h₂ cannot be compared without violating single family rule 3.

2. "The conceptual difficulty goes away if one supposes that the two incompatible frameworks are being used to describe two distinct physical systems that are described by the same initial data'' [9].

The critics of CHA were not satisfied by these arguments. To synthetically explain the reason for such a disagreement, let us consider the example of contrary inferences above outlined and two physicists, Alice and Bob. Suppose that the known data about a single physical system s are that E₀ and E₂ occur, i.e. h₀ occurs. In order to establish whether E₁ occurs or not, Alice uses family ₁ and, in accordance with CHA, she finds that E₁ occurs. Bob, for the same individual system s, chooses ₂, and he concludes that F₁ occurs. The fact that E₁ occurs or F₁ occurs seems to depend on the physicist. But, according to CHA itself, the occurrence of a history, once established by means of the theory, is to be considered an objective fact. As a consequence, both E₁ and F₁ should occur. But everybody rejects this conclusion because E₁^ F₁.

4 Extended formalism

Now we introduce the notion of support of a family of histories. In such a way we give formal content to some concepts, naturally stemming from the basic principles of CHA reflected by (I) and (O), which are not formalized in the standard formulation of CHA. Two basic axioms (1 and 2) shall be formulated as statements which arise from the physical meaning of support. Such an extension of the formalism supplies us with new tools which make possible a conceptually transparent analysis of some questions in CHA. According to the results of this analysis, the conceptual difficulties linked to contrary inferences are ruled out.

4.1 The notion of support

Given a family and a concrete specimen s of the physical system, there are two mutually exclusive possibilities: for this particular s either

i) one elementary history h of occurs and all other elementary histories do not occur,

or

ii) no one of the elementary histories of occurs.

In case (i) we say that the histories of

make sense for this s; in case (ii) we say that the histories of do not make sense.

For instance, if the physical system is a silver atom entering a Stern and Gerlach apparatus, we may consider two families of histories.

Family

^(a), which is the family generated by the following elementary histories

= "the atom emerges from the apparatus with spin up''

= "the atom emerges from the apparatus with spin down''.

Family

^(b), which is the family generated by the following elementary histories

= "the atom is democratic''

= "the atom is republican''.

For this particular s family

^(a) makes sense. On the contrary, family ^(b) does not.

By support of we mean the set b() of all concrete specimens of the physical system for which makes sense. The introduction of set b() allows us to formally express the consistency of a family by means of a simple definition which reflects the meaning of consistency expressed by (I) and (O).

Definition 1.A family

is consistent if and only if b(

) ¹ Æ.

As an evident insight, the (sufficient) condition which makes the conclusions of logical reasonings based on a family

valid for a specimen s of the physical system is

Remark 2. As a consequence, also the number pc(h) = Tr(C_h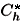) can be interpreted as probability of occurrence of h only if s Î b(). For this reason it makes sense to keep symbol in this formula.

Now we deduce a natural implication for the supports of two families

₁ and ₂ such that ₁Í₂. We consider the case in which b(₂) ¹ Æ. For every s Î b(₂), there is only one elementary history h₂(s) of ₂ which occurs, and all other elementary histories of ₂ do not occur. From ₁Í₂ it follows that all elementary histories of ₁ form a set, denoted by 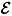₁, of albeit non-elementary histories of ₂. Only one history h₁Î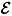₁ occurs, because there is a unique h₁Î 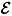₁ such that h₂(s) Îh₁. Analogously we find that all other h Î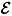₁ do not occur. Therefore, it is possible to state that only one elementary history of ₁ occurs and all other h Î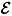₁ do not occur for this individual system s; thus, by definition 1, s Î b(₁). We state the result of this argument as the following axiom.

Axiom 1. Let

₁,

₂ be two families of histories. Then

₁Í ₂implies b(₂) Í b(₁).

Now we proceed to state another axiom. If h Î, by b₁(h;) (resp., b₀(h;)) we denote the subset of b() whose elements are the specimens for which h occurs (resp., does not occur). It is obvious to assume that

According to (O), the occurrence of h = (E₁,E₂,...,E_n) is equivalent to the occurrences of all events E₁, E₂, ...E_n at the respective times t₁, t₂, ...,t_n, and then it is independent of the family which h belongs to. Therefore, we can state the following axiom.

Axiom 2.If h Î Ç ', then b₁(h;) Ç b₀(h;') = b₁(h;') Ç b₀(h;) = Æ.

Axiom 2 establishes that a history h cannot occur as history of and do not occur as history of ', for the same specimen s.

4.2 General implications

Let X be any set of histories. The family generated by X is (X) = Ç_{c|XÍc}C. By axiom 1 we have that h Î implies b() Í b(({h})) = U_hÎc(). Therefore, b(h) º b(({h})) is the set of all specimens of the physical system for which single history h occurs or does not occur (h makes sense). By b₁(h) (resp., b₀(h))we denote the subset of those systems for which h occurs (resp., does not occur). Of course

According to the present approach, the fact that a given history h₀ occurs (or does not occur) for a physical system s₀ means that a family ₀ exists such that

Family

₀ = ({h₀}) fullfils these requirements. All histories of ₀ make sense for s₀. However, the eventuality that for a given system s history h Î occurs but s Ï b() is logically possible. Therefore, the fact that a family is consistent, and h Î does not imply that the inferences obtained by means of reasonings based on hold for an arbitrary physical system s for which h occurs.

Suppose that the following statement holds for s: "history h₀ occurs'' (initial data). Then s Î b₁(h₀), and hence s Î b(({h₀})), are true statements. Thus, all sentences obtained by logical deductions based on ({h₀}) hold for s.

Family ({h₀}) admits several refinements, i.e. various families may exist such that ({h₀}) Í . Deductions based on a refinement in general do not hold for s Î c(({h₀})); indeed, as already argued, ({h₀}) Í implies, by Axiom 1, b() Í b(({h₀})), and therefore s Î b() does not necessarily follow. Since ({h₀}) Í, all inferences obtained by reasoning with ({h₀}) can be obtained with ; this implies that the two set of sentences cannot contradict with each other; but inferences involving histories in \({h₀}) in general do not make sense if s Î b(({h₀}))\b().

Here is a profound difference between the "coarsest'' family (X) compatible with the available initial data relative to a physical system s and any refinement of (X): conclusions drawn by using (X) are true, i.e. objective facts, whereas the truth of conclusions obtained from a refinement is not ensured by the truth of the data (X) alone. As a consequence, in the present approach Griffiths' prescription: "Use the smallest, or coarsest framework which contains both the initial data and the additional properties of interest in order to analyse the problem.'' [9] is not always valid.

4.3 Compatibility of families

Now we come to analyze the notion of compatibility of families.

Definition 2.Two consistent families

₁ and

₂ are compatible if a third consistent family

exists such that

₁ È ₂Í .

According to standard CHA, the conclusions drawn in different families hold together in the case that these families are compatible. By axiom 1, compatibility implies b() Í b(₁) Ç b(₂); therefore, the conclusions drawn from ₁ and ₂ certainly hold together for the systems s Î b(). However, if s Î b(₁) Ç b(₂), then the predictions drawn in ₁ and ₂ hold together for this system s, no matter whether ₁ and ₂ are compatible or not. It is true that single family rule of CHA guarantees from conflicting inferences, but it makes the theory unable to describe this possibility.

Moreover, if s Î b(₁) and s Ï b(₂), then a conclusion drawn from ₂ does not necessarily hold for this s.

5 Analysis of contrary inferences

Contrary inferences were discovered by Kent within the framework of standard CHA. To can discuss them on the basis of our extended formalism, we make coincide the concept of consistency of definition 1 with that of standard CHA. This identification is formally realized by means of the following axiom.

Axiom CHA. A family

is consistent, in the sense of definition 1, if and only if it is weakly decohering. In this case pc(h) =

Tr(C_h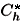) is the probability of occurrence of history h.

We begin our analysis of contrary inferences by formally showing, within our approach, that two mutually orthogonal projections represent events which cannot occur simultaneously.

Let E and F be two mutually orthogonal projections. The family generated by E and F, i.e. ({E,F}), has 3 elementary (one-event) histories: 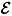= {E,F,G = 1–(E+F)}; it is the smallest family containing E and F. Then, following the argument of section 4.2, whenever both E and F make sense, all histories in ({E,F}) must make sense too. Therefore, the following proposition holds.

Proposition 1.If E ^ F, then s Î b(E) Ç b(F) implies s Î b(C({E,F})) and, therefore, b₁(E) Ç b₁(F) = Æ.

If families

₁ and ₂ in Kent's example of contrary inferences were compatible families, then we would have a contradiction.

Indeed, in this case a consistent family would exist such that ₁È ₂Í. By axiom 1 we get

Furthermore h₀ = (E₀,1,E₂) Î, because h₀Î₁ Ç ₂. Since pc(h₀) ¹ 0, there would exist a specimen Î b₁(h₀) Ç b(), and hence Î b(₁) Ç b(₂) by (5). Therefore, we should conclude Î b₁(E₁) and Î b₁(F₁), because pc₁(h₁| h₀) = pc₂(h₂ | h₀) = 1. Thus we would have a contradiction with b₁(E₁) Ç b₁(F₁) = Æ which follows from proposition 1, since E₁ ^ F₁.

However,

₁ and ₂ in contrary inferences example are not compatible families, therefore previous argument does not apply. We can show that the occurrence of history h₀ = (E₀,1,E₂) does not give rise to conceptual difficulties. The foregoing argument shows that the condition to be satisfied to avoid the contradiction is

If

₁ and ₂ are not compatible, (6) is logically consistent with the occurrence of h₀. Indeed, from

by axiom 1 we are simply led to

This relation is consistent with (6), contrary to what happen if

₁ and ₂ were compatible. Indeed, when h₀ occurs, i.e. if s Î b₁(h₀) Í b(h₀), we have 3 mutually exclusive and exhaustive possibilities:

p)s Î b(₁). In this case pc₁(h₁| h₀) = 1 must hold (see remark 2) and this entails that E₁ occurs. The consistency with (6) merely requires that s Ï b(₂) so that pc₂(h₂ | h₀) = 1 ('h₀ occurs implies F₁ occurs'), does not hold for this s. Regards to the occurrence of F₁ there are two possibilities:

p₁) s Î b(F₁)\b(₂). This possibility is consistent because F₁Î ₂ implies b(₂) Í b(F₁). In this case axiom 2 and proposition 1 imply that F₁ does not occur, i.e. s Î b₀(F₁);

p₂) s Ï b(F₁), therefore F₁ does not make sense, i.e. it neither occurs nor does not occur.

q)s Î b(₂). In this case pc₂(h₂ | h₀) = 1 holds, and then F₁ occurs. We have for E₁ the same conclusions of item (p) above for F₁.

r)s Ï b(₁) È b(₂). In this case no conclusion about E₁ or F₁ can be obtained with the available data.

Which of these alternatives (p), (q) and (r) is actually realized with our initial data (s Î b₁(h₀)) is a question which cannot be predicted without further data. However, no contradiction is implied.

Received on 26 January, 2005

• [1] R.B. Griffiths, J. Stat. Phys. 36, 219 (1984).
• [2] R.B. Griffiths and R. Omnčs, Physics Today (August 1999) 26.
• [3] Quantum theory of measurement, J.A. Wheeler and W.H. Zurek (eds.) (Princeton University Press, Princeton, 1983).
• [4] G. Nisticň, Found. Phys. 29, 221 (1999).
• [5] A. Kent, Phys. Rev. Letters 78, 2874 (1997).
• [6] R.B. Griffiths and J.B. Hartle, Phys. Rev. Lett. 81, 1981 (1998).
• [7] A. Kent, Phys. Rev. Lett. 81, 1982 (1998).
• [8] R.B. Griffiths, Phys. Rev. A 57, 1604 (1998).
• [9] R.B. Griffiths, Consistent Quantum Theory (Cambridge University Press, Cambridge, U.K., 2002).

Publication Dates

• Publication in this collection
  06 Sept 2005
• Date of issue
  June 2005

History

• Received
  26 Jan 2005