Interior problem in a ponsymmetric theory of gravitation

REGULAR ARTICLES

Interior problem in a ponsymmetric theory of gravitation

S. Ragusa^I; D. Bosquetti^II

^IInstituto de Física de São Carlos Universidade de São Paulo, C.P. 369, 13560-970 São Carlos, SP, Brazil

^IIFaculdade de Tecnologia de Botucatu Botucatu, SP, Brazil

ABSTRACT

The field equations of a previous metric nonsymmetric theory of gravitation are considered for the interior of a static spherically symmetric perfect fluid with a view to a study of stellar equilibrium. The equations are put into a form of four first-order differential equations which are ready for numerical integration.

Keywords: Nonsymmetric theory; Gravitation

I. INTRODUCTION

In previous papers [1-I,II] a metric nonsymmetric theory of gravitation has been developed by one of us and the solution for a point mass source was obtained. The theory was shown to be consistent with the four classical tests of general relativity (GR). In [2] it was shown that the theory is definitely free of ghost-negative radiative modes even when expanded around a Riemannian GR background space. In a more recent paper [3] the conservation laws of energy and momentum were established. Some application of the results were made for a static spherically symmetric perfect fluid with a view to future study of stellar equilibrium. This is the subject of which we start developing in this paper. The sources of the field are the energy-momentum-stress tensor T_ab and the fermionic current density S^a. For a macroscopic system this current is taken to be

where f_a is the coupling of the fermion specie a to the geometry, n_a is its rest number density found, for instance, in the description of the interior of stars (electrons, protons and neutrons) and u^a is the common velocity.

In this paper we study the interior problem for a static and spherically symmetric perfect fluid. Therefore, only the component S⁰ will survive. This will be focused with a view to a study of stellar equilibrium. It would be interesting to analyze what the modifications of the predictions of GR are for stellar equilibrium and collapse particularly by the fact that, together with the stress tensor, the matter current is also a source of gravitation.

The approach is similar to the one studied by Savaria [4] in the context of a different nonsymmetric theory. The equations are put into a form of four first-order differential equations which are ready for numerical integration. They are ready for application to the study of white dwarf and neutron stars, to discuss their stability as compared with the results of GR.

The set of four differential equations involve four quantities to be determined: the fermionic charge F(r) below the radial distance r, the two metric coefficients g₀₀(r) and g₁₁(r), the internal pressure p(r) and or the mass density r(r). The system must be supplemented by an equation of state relating the pressure and density as in GR, and information about f_an_a(r).

The paper is organized as follows. In Sec. II the field equations are presented In Sec. III we set their form for a static spherically symmetric sphere. In Sec. IV the first-order equations are written down and in Sec. V the limits at the centre and boundary are stated. In Sec. VI we present our conclusions and highlight plans for future work.

II. THE FIELD EQUATIONS

The field equations of the theory are [1-I], with k = 8pG,

and

We use the notation a_(ab) = (a_ab + a_ba)/2 and a_[ab] = (a_ab - a_ba)/2 for the symmetric and antisymmetric parts of a_ab and the notation a_[ab,g] = a_[ab],g + a_[ga],b + a_[bg],a for the curl of a_[ab]. In the first equation

symmetric because the second term is (see (2.12) below) and containing only the symmetric part of the connection, is the analogue of the Ricci tensor. L is the cosmological constant and in the right-hand side we have the symmetric part of the tensor

with T = g^abT_ab. The next two equations involve the symmetric and antisymmetric parts of g^ab = g^ab where g = det.(g_ab) and g^ab is the inverse of g_ab as defined by

Equation (2.4) involves the curl of the antisymmetric part of the metric and of the tensor in (2.6). The second field equation, (2.2), can be solved for the symmetric part of the connection [1-I] giving

with

where s_ab symmetric and with determinant s is the inverse of g^(ab) as defined by

Equation (2.4) came as the result of the equation

where G_a = is a vector involving contractions of the antisymmetric part of the connection. In deriving (2.8) from (2.2) we come across the relation

which can be re-obtained from that equation. One then sees that the second term on the right of (2.5) is in fact symmetric.

The Lagrangian density we end up with in [1-I] is

where L_M is the matter part of the Lagrangian. It is modeled after the one of GR, containing here the generalized matter energy-momentum-stress tensor T_ab and the fermionic current S^a, as given by

where

As d = g_µndg^µn/2, we have dg^ab = dg^ab - g^abg_µndg^µn/2, and (2.14) can also be written as

Equations (2.1)-(2.4) can be re-obtained from Eq. (2.13) by variations with respect to g^ab, and G_a. The first one gives U_ab + G_[a,b] + Lg_ab = k_ab, the symmetric and antisymmetric parts give (2.1) and (2.11), this last one leading to (2.4). The second variation gives (2.2) while the one with respect to G_a gives (2.3).

Together with the down-indices stress T_ab we will be working (1-I) with the upper-indices T^µn defined by the variation with respect to g_µn,

as in GR. This second stress is related to the first one by

which follows from the relation dg_µn = -g_ang_µbdg^ab resulting from the variation of Eq. (2.7). It should be kept in mind that Eq. (2.18) does not imply a rule for lowering indices because this operation is not defined for a nonsymmetric metric. A better name for the upper-indices stress tensor would probably be S^µn but we shall use the same T for both tensors. Notice that the inverse relation is T^µn = g^µbg^anT_ab and that both have the same trace g^abT_ab = g_µnT^µn.

We end this section by writing the matter-response equation. Working directly with dL_M [1-I] or going through the variational principle [3] the equation is of the form

where

Now consider the situation in which we are are interested in, dealing with a perfect fluid. Then it can be shown [3] that

r being the matter rest density, p the pressure and u^µ the velocity.

In the next section we will see the form acquired by the field equations and of (2.19) in the interior of a static spherically symmetric perfect fluid.

III. THE STATIC SPHERICALLY SYMMETRIC SPHERE

The static and spherically symmetric metric tensor in polar coordinates x⁰ = t, x¹ = r, x² = Q and x³ = F is of the form

and all other components equal to zero. The non-zero components of the inverse matrix are then

We need also the inverse s_ab to g^(ab), whose non-zero components are

The determinants have values

and

From (2.3) we have S^a_,a = 0 guaranteeing the conservation of the fermionic charge. For the static sphere we have uⁱ = 0 so according to (1.1) only the zero component survives in (2.3). From (3.2) and (3.4) that equation yields

where

is the conserved fermionic charge contained in a sphere of radius r. From (3.6) we have

With this result and equations (3.4) and (3.5), we have s/g = r⁴/(F² + r⁴) and equation (2.9) yields

where for short

For future use we note that from (3.7) we have

By multiplication by F and using (3.6) we obtain

and, from (3.10),

Let us go now to the calculation of the symmetric part of the connections, from (2.8). Putting the abbreviation B = F² + r⁴ a straightforward calculation yields ( = da/dr)

and all other components vanishes. Using all this information the nonzero components of U_ab are

and U₃₃ = U₂₂sin²Q.

From (2.18) and (2.21) equation (2.6) gives

As our fluid is in hydrostatic equilibrium we have

and, from u^au_a = 1,

From now on we will neglect the contribution of the cosmological constant as in GR. For the relevant components of (2.1) we then have from (3.19a),

and

On the other hand (2.11) becomes (with L = 0)

Only the 0,1 antisymmetric component of this relation is non-vanishing, giving

The matter-response equation (2.19) acquires [3] the simple form

On account of the previous equation and of (3.13) this equation becomes

IV. THE FIRST-ORDER EQUATIONS

As in GR we can obtain from (3.20) and (3.21) a relation involving only first-order derivatives of the metric by multiplying the first one by a/g and adding the result to second one. The calculation is delineated in ^{Appendix A}. After multiplication of the whole thing by B/2ar² we obtain

This result would hold even if L were present.

Next we use Eq. (3.17) in (3.22) and add and subtract to (4.1). After some algebra (see Apendix A) we obtain

and

Using equations (1.1), (3.8) and (3.13) in (3.11) we obtain

Equations (4.2), (4.3), (4.4) and (3.26) are the equations that define the behavior of the interior of our system. As promised they constitute a system of equations for the two metric coefficients g(r) and a(r), the fermionic charge F(r) below r,the density r, the pressure p and the fermionic coupling-density number f_an_a(r) for each component. This last quantity together with an equation of state f(r, p) = 0, as in GR, are required for the solution of the system of equations.

These equations can be put in a more interesting form by noticing that the last two terms on the left-hand side of (4.2) can be condensed as -r(1 + x)^-1((1 + x)²/a)'. Motivated by the form of a in GR we then introduce the variable m(r) defined by

When x is null, that is, when w is null this becomes the GR relation with m(r) equals the mass within a sphere of radius r. In terms of this quantity our four equations can be written as

and

The coefficient a is obtained from (4.5) and w comes from (3.8)

Having all this the total mass of the star can be calculated from equation (5-10) of [3], which is,

where

We give the details of the calculation in ^{Appendix B}, quoting here the final result. We have

As it will be discussed in the next section, this quantity can also be calculated from the continuity of a across the surface boundary R of the star.

V. CONDITIONS AT THE CENTER AND BOUNDARY

Because of divergent terms at r = 0 we expand the equations around that point. This will permit to perform the numerical integration from near the center on, all the way up to the radius R of the star.

Starting with (4.5) we see that m(0) = 0 to have a(0) finite. Thus, from (4.9) we see that F near the origin goes as r³ because F(0) = 0 from (3.7).Then, from (3.10) it follows that x goes as r². Then (4.6) tell us that m goes as r³, r(0) being finite. Next, from (4.8) p goes as p(0) plus a term of order r². Finally, (4.7) tell us that g goes as g(0) plus a term of order r². We fix now the coefficients. Calling

we have

where

and

where

Having (5.3) and (5.4), equation (4.5) gives for a(r)

At the surface the parameters r, p and S⁰ or x all vanish. Having a(r) inside, the mass of the star can be calculated from the continuity at r = R. We have

The exterior value is determined by the solution obtained outside in [1-II],

VI. CONCLUSIONS

The field equations of the metric nonsymmetric theory of gravitation developed in [1-I,II] have been analyzed for the interior of a static spherically symmetric perfect fluid with a view to a study of structure of stars.

The field equations have been reduced to a set of four first-order differential equations which is ready for numerical integration.

The obtained set of equations is appropriate to the study of the behavior of white dwarf and neutron stars. It will be interesting to see what the modifications of the prediction of GR are for their state of equilibrium.

Another topic for future work would be to establish the form of the field equations for a non-rotating perfect fluid aiming as a model to the study of stellar collapse.

Received on 27 January, 2006

After multiplication of (3.15) by a/g, a differentiation by parts of its first term gives

When added to (3.16) we obtain

From (3.20) and (3.21) we find, using (3.8),

Using (A2) and multiplying the whole thing by B/2ar² equation (4.1) follows.

Next, from (A3) and (3.22) we find

Using (3.7) and (A2), equations (4.2) and (4.3) follow.

In our case only the g^[01] component survives in the last term inside the parenthesis of (4.11). From (2.21) equation (4.12) gives

Thence, for our hydrostatic fluid, T₀ ⁰ = r and T_iⁱ = -3p. Next, using (3.8) in the last relation of (3.2) we have

Taking this together with (3.24) in (4.11) gives

From (3.4) and (3.8)

Using here (4.5) and taking the result into (B3) equation (4.13) follows.

• [1] S. Ragusa, Phys. Rev. D 56, 864, (1997). D in this paper is now named G.; Gen. Relat. Gravit. 31, 275 (1999). These papers will be refereed to as I and II, respectively.
• [2] S. Ragusa and Lucas C. Céleri, Braz. J. Phys. 33, 821 (2003).
• [3] S. Ragusa, Braz. J. Phys. 35, 1020 (2005). A factor G^-1 should be added to the last term of equation (6.4). Equation (3.26) should be written as in the present equation (2.19) and equation (3.28) should be dropped.
• [4] Pierre Savaria, Class. Quantum Grav. 6, 1003 (1989).

APPENDIX A:  PROOF OF (4.1)-(4.3)

APPENDIX B:  PROOF OF (4.13)

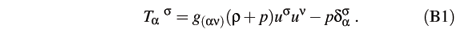
Publication Dates

• Publication in this collection
  31 July 2006
• Date of issue
  June 2006